Anomaly Detection for Industrial Big Data

Neil Caithness and David Wallom

Oxford e-Research Centre, Dept. of Engineering Science, University of Oxford, Oxford, U.K.

Keywords:

Industrial Internet of Things (IoT, IIoT), Industrial Big Data, Anomaly Detection, Ordination,

Singular Value Decomposition (SVD), Principal Components Analysis (PCA), Correspondence Analy-

sis (CA).

Abstract:

As the Industrial Internet of Things (IIoT) grows, systems are increasingly being monitored by arrays of

sensors returning time-series data at ever-increasing ‘volume, velocity and variety’ (i.e. Industrial Big Data.

An obvious use for these data is real-time systems condition monitoring and prognostic time to failure analysis

(remaining useful life, RUL). (e.g. See white papers by Senseye.io, Prognostics - The Future of Condition

Monitoring, and output of the NASA Prognostics Center of Excellence (PCoE)). However, as noted by others,

our ability to collect “big data” has greatly surpassed our capability to analyze it. In order to fully utilize

the potential of Industrial Big Data we need data-driven techniques that operate at scales that process models

cannot. Here we present a prototype technique for data-driven anomaly detection to operate at industrial scale.

The method generalizes to application with almost any multivariate data set based on independent ordinations

of repeated (bootstrapped) partitions of the data set and inspection of the joint distribution of ordinal distances.

1 INTRODUCTION

Data from energy smart meters represents an appro-

priate use-case for demonstrating a new method for

detecting anomalies in Industrial Big Data, speciﬁ-

cally where accurate system process models do not

exist and where data-driven techniques are sought in-

stead. The electricity network is a system being mon-

itored by arrays of sensors (smart meters), and repre-

sents appropriately high volume, velocity, and variety

of data (de Mauro et al., 2015).

Energy theft by meter tampering represents a sig-

niﬁcant threat to the UK energy industry. The cre-

ation of new opportunities for cyber theft and fraud

introduced by the imminent deployment of up to 50M

smart meters across the UK industry has prompted a

search for a data-driven solution to detecting possi-

ble theft or fraud events. In the DIET project (Data

Insight against Energy Theft

) we developed a new

technique using unsupervised machine learning for

the identiﬁcation of anomalous events based on data

collected exclusively from smart meters.

Electricity smart meters typically collect standard-

ized consumption data (kWh in 48 half-hour bins per

day) and an associated stream of non-standardized

or meter speciﬁc “event” or “logging” data. Event

Innovate UK, Grant Reference Number 102510.

streams may consist of nominal codes that track the

actions on the smart meter and may relate to activities

such as accessing the cache via modem, turning the

power supply off, or many more of increasingly tech-

nical nature. It is yet unknown whether meter tam-

pering for theft, fraud, or otherwise, carries with it

speciﬁc and detectable event sequence signatures (i.e.

there is no relevant process model in existence.)

The question then becomes, can theft or meter

tampering be credibly detected from the data streams

alone, without reference to deﬁning event sequence

signatures? Without credible and/or sizable training

sets of theft or fraud cases with which to train super-

vised machine learning systems, we position this task

instead in the context of anomaly detection, using un-

supervised machine learning techniques.

This is closely related to the ﬁeld of outlier detec-

tion in the data science literature, where, in a well-

known deﬁnition by Hawkins (1980) an outlier is

an observation which deviates so much from

other observations as to arouse suspicion that

it was generated by a different mechanism.

Or, according to Barnett and Lewis (1994)

an observation [...] which appears to be in-

consistent with the remainder of that set of

data.

Caithness, N. and Wallom, D.

Anomaly Detection for Industrial Big Data.

DOI: 10.5220/0006835502850293

In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 285-293

ISBN: 978-989-758-318-6

285

A resurgence of research activity on outlier detec-

tion algorithms was triggered by the seminal work of

Knorr and Ng (1997), and new models have contin-

ued to be developed (Aggarwal, 2013; Akoglu et al.,

2015; Chandola et al., 2009; Schubert et al., 2014),

though none has achieved universal acclaim as being

applicable and effective in all cases.

Campos et al. (2016) have systematically and thor-

oughly reviewed the literature and development of

unsupervised outlier detection algorithms and found

that “little is known regarding the strengths and weak-

nesses of different standard outlier detection models”,

that “the scarcity of appropriate benchmark datasets

with ground truth annotation is a signiﬁcant impedi-

ment to the evaluation of outlier methods”, and still

further that “even when labeled datasets are available,

their suitability for the outlier detection task is typi-

cally unknown”. Thus endeavors to develop and crit-

ically evaluate new unsupervised techniques are both

timely and warranted.

We refer to the general concept of outlier instead

as anomaly, to emphasize the suspected origin in a

different underlying mechanism as characterized by

Hawkins (1980) cited above, and to distinguish it

from outliers in the normal tail of a statistical distri-

bution produced by a single uniﬁed mechanism. In

this paper we present a new approach to the task of

anomaly detection speciﬁcally designed to accommo-

date datasets of different data-types on the same set of

cases (e.g. consumption and event data for a portfolio

of smart meters). We know of no comparable tech-

nique that can be used to perform independent analy-

ses of two data streams and then establish a combined

case-by-case measures of outlierness. Identiﬁcation

of potential anomalous cases is achieved by inspect-

ing the joint-distribution of distances derived from a

novel density analysis. This joint-distribution is sus-

ceptible to new and special statistical interpretation

that we introduce here, but which we will develop fur-

ther in subsequent publications. Our contention is that

in this application, meter tampering for theft, fraud,

or otherwise, will insert into the data set cases that

are not representative of the background mechanism

of the system as a whole.

Finally, we suggest that this procedure generalizes

to anomaly detection for almost any multivariate data

set with any combination of data-types by applying

independent analyses to two or more (possibly ran-

domized) partitions of the data set and then inspecting

the joint distribution of cases.

2 METHOD

For any system (here the electricity network) being

monitored by technical equipment (here a sensor ar-

ray comprising the set of smart meters) that generates

a multivariate cases-by-variables data set, we devise

the following method of analysis. It is useful here to

refer to a schematic diagram of the workﬂow of the

method as shown in Figure 1. We describe in detail

the ﬁve processes labeled S1-S5.

2.1 Partition (S1)

The ﬁrst novel aspect of the method is that datasets to

be studied are always split into two or more partitions,

vertically by variables, and each partition is analyzed

separately. Cases need not be present in all partitions

(or a case may have null data across the variables in

a partition) but anomalous cases can be detected only

from the set of cases in common across all partitions.

There are a number of criteria for partitioning:

2.1.1 Different Data Types

The smart meter event/consumption data set presents

time series data that is a mixture of data-types: in-

dividually time-stamped nominal-scale event codes;

and time-binned ratio-scale consumption data. Where

the downstream analysis requires different variants

depending in the data-types of the variables, then par-

titioning on data-type is a natural evolution of the

work-ﬂow.

2.1.2 Random Partitioning

Where partitions do not require different kinds of

analysis we make partitions at random and repeat

many times (a process with similar beneﬁts to statis-

tical bootstrapping (Efron and Tibshirani, 1994)).

2.2 Transform (S2)

There are two steps in the transform process: coding

and ordination.

2.2.1 Coding

For the nominal-scale event data we ﬁrst transform by

frequency count over some speciﬁed time period. We

found by inspection that three months is an effective

period: shorter and many events have zero count, so

this is effectively ignoring potentially relevant data;

longer and the anomalous data produced by the event

of a meter tamper could be so diluted by the back-

ground of normal operation as to go undetected. An

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

286

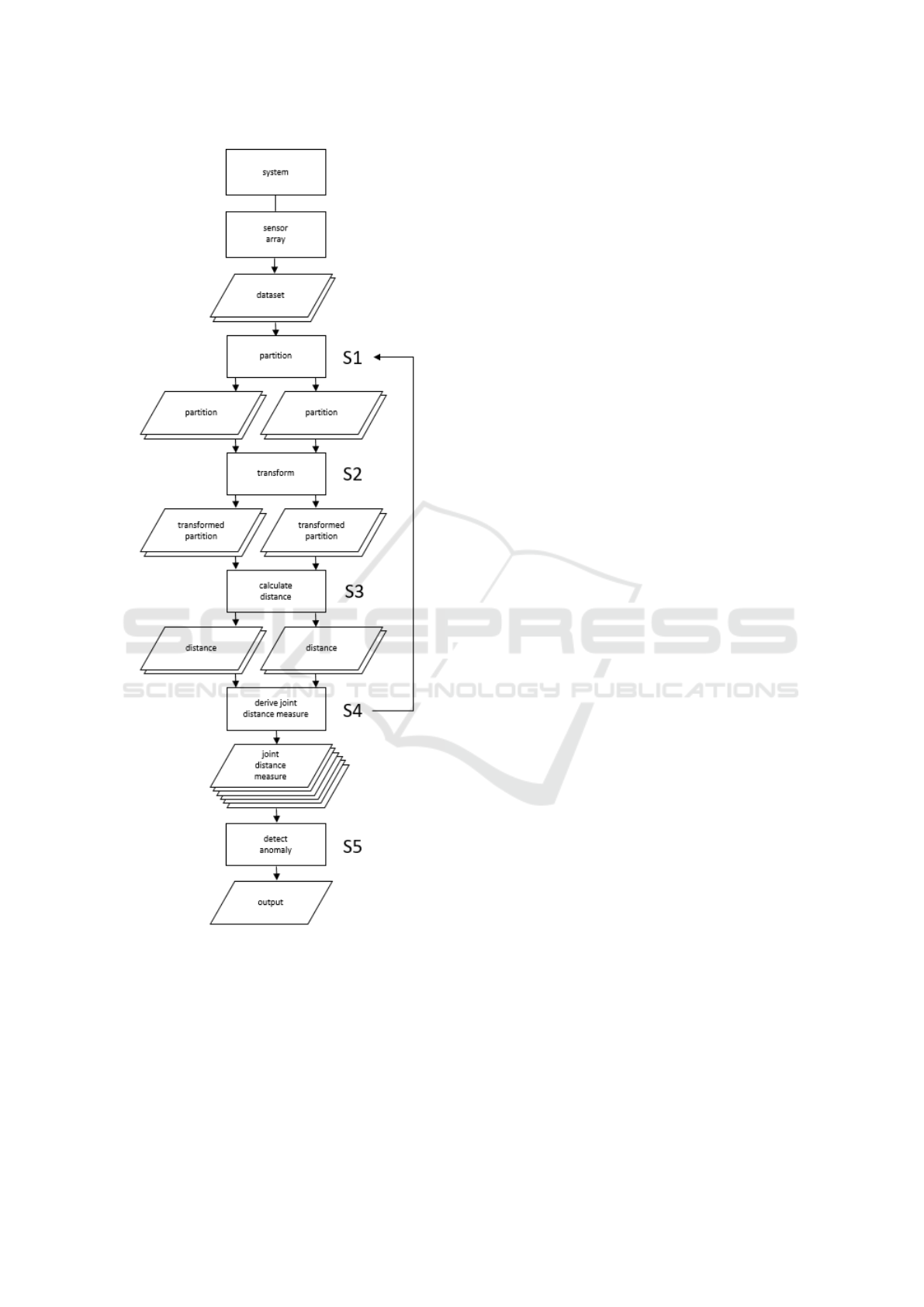
Figure 1: Schematic diagram of the method workﬂow.

alternative treatment for nominal-scale data would be

to apply a numeric coding. If the partitions are made

at random and repeated sampling is performed, and if

randomized numeric coding is applied with each rep-

etition, then the association between codes remains

unbiased.

For the ratio-scale consumption data, we wish to

capture a relevant cyclical frequency. There are clear

daily, weekly, and seasonal energy consumption pat-

terns, and although these cycles differ between do-

mestic and commercial properties, they remain the

dominant patterns for both types of property. In

our analysis we recode the standard 48 half-hourly

bins per day of consumption data collected by typical

smart meters to a total daily consumption, averaged

by day of the week. We emphasize that this coding

practice was found to be effective in application to

this data set, but is not itself integral to the technique;

there are many other data folding and coding possi-

bilities, and users may ﬁnd that other transformations

prove effective with their data.

2.2.2 Ordination

We use several variants of methods from the family

of dimension reduction techniques that employ sin-

gular value decomposition (SVD). Speciﬁcally, prin-

cipal components analysis (PCA) and correspondence

analysis (CA), depending on the data types of the par-

titions.

The biplot provides a convenient visualization of

the ordination but is not itself integral to the tech-

nique. We illustrate our results with various kinds of

plots, including biplots, in the following section.

The biplot (Greenacre, 2010) is a graphical de-

vice that shows simultaneously the rows and columns

of a data matrix as points and/or vectors in a low-

dimensional Euclidean space, usually just two or

three dimensions. Greenacre (2013) introduced the

contribution biplot in which the right singular vec-

tors (column contribution coordinates) of a dimension

reduction analysis show, by their length, the relative

contribution to the low-dimension solution. Contri-

bution biplots can be used with any of the methods

that perform dimension reduction by singular value

decomposition (SVD), these include correspondence

analysis (CA), principal component analysis (PCA),

log-ratio analysis (LRA), and various derived meth-

ods of discriminant analysis.

SVD is a factorization of a target matrix T such

that

T = UΓV

(1)

What distinguishes the various methods is the

form of the normalization applied to T before per-

forming the SVD. In CA this normalization is the ma-

trix of standardized residuals

T = D

−1/2

(P − rc

−1/2

(2)

where P is the co-called correspondence matrix

P = N/n, with N being the original data matrix and

n its grand total, row and column marginal totals of P

Anomaly Detection for Industrial Big Data

287

are r and c respectively, and D

and D

are the diago-

nal matrices of these.

In the analysis of a cases-by-variables data matrix,

the right singular vectors of the SVD, V, are the con-

tribution coordinates of the columns (variables). A

further transformation involving a scaling factor D

such that

F = D

−1/2

UΓ (3)

deﬁnes the principal coordinates of the rows (cases).

The joint display of the two sets of points in F and

V can often be achieved on a common scale, thereby

avoiding the need for arbitrary independent scaling to

make the biplot legible.

The appropriate normalizations and the derivation

of scaling factors for the alternative methods are de-

tailed in his Table 2 and in various equations given

in Greenacre (2013). We use CA for the ordination

of the event data, following a double log transform of

the frequency data, N

such that

N = ln(ln(N

+ 1) + 1) +1 (4)

Note that the successive additions (+1) in Equa-

tion (4) above are simply to avoid taking ln(0). This is

a convenience, introducing an appropriate scaling so

as to make the biplot legible, but does not otherwise

alter the analysis. For the ratio-scale consumption

data we use the PCA method of Greenacre (2013), af-

ter centering and standardizing the input data by vari-

able.

2.3 Calculate Distance (S3)

Both ordination techniques, whether CA or PCA, re-

sult in a matrix F of principal coordinates of the rows

(cases) as in Equation (3). This matrix has the same

number of dimensions (columns) as variables in the

raw input data, however the information content of

the data is now concentrated towards the higher order

components (i.e. towards the left-most columns of F).

This is the central purpose of the dimension reduction

performed by SVD, and typically, a scree plot is used

to inspect the degree of dimension reduction, essen-

tially a plot of the eigenvalues, Γ in Equation (1).

A decision needs to be made as to how many

components to retain, referred to as a stopping rule

(Jackson, 1993; Peres-Neto et al., 2005). A conven-

tional rule is to retain only those components with

corresponding eigenvalues >1 (known as the Kaiser-

Guttman criterion, (Nunnaly and Bernstein, 1994)),

which is the rule we apply here, though this is a tun-

able parameter of the method and a range of values

should generally be explored. Once a stopping rule

has been decided the case-by-case distances d from

the origin in Euclidean space are calculated for the k

number of retained dimensions. This is done sepa-

rately for each partition. The following code is pro-

vided for clarity.

e.g. Matlab Code

d = sum(F(:,1:k).ˆ2,2).ˆ(1/2)

2.4 Derive Joint Distance Measure (S4)

The second novel aspect of the method, after par-

titioning the data set, is to examine the joint-

distribution of distances derived from the separate or-

dinations of the partitions. Where the partitions have

vastly different numbers and types of variables, and

where the speciﬁc ordination techniques differ be-

tween partitions, (as in our case of event data, circa

250 variables of event frequency counts, analyzed

by CA, vs. consumption data, seven variables of

ratio-scale data, analyzed by PCA), then comparison

should be made on the rank order of distances, rather

than directly on the distances themselves.

If all the data across all the variables were gen-

erated by independent random processes, then there

would be no relationship between the rank-ordering

of cases in the two lists. If the variables are at least

partially correlated (as is usually the case for real-

world data) then we would expect a correlation be-

tween the rankings derived from the two partitions,

but we would still expect an even spread of associ-

ations. A scatter plot of the two rank ordered lists

will reveal the nature of the association. A correlation

among variables will manifest as a concentration of

points towards the diagonal, but from a uniﬁed under-

lying process we would not expect much departure

from an even spread along the diagonal. If a sec-

ond, distinct process inserts cases into the data set,

we could expect that these may be manifested as a

departure from the uniform density of points, possi-

bly forming locally high density clusters. We plan to

develop the statistics of this phenomenon further in

subsequent publications.

2.5 Detect Anomaly (S5)

Following on from the derivation of a joint distance

measure based on the density of points in the joint

distribution of rank orders, as described in S4, we

now standardize the measure and inspect the depar-

ture from the mean density in units of standard devi-

ation. Cases at the far extremes of departure from the

mean may well be interpreted as being so divorced

from the background process generating the bulk of

the data as to be anomalies produced by a different

mechanism (Hawkins, 1980).

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

288

This ﬁnal process in the method proceeds to ﬁnd

those cases at the far extremes of departure from the

mean density, and to report them as likely anomalies

that require an alternative explanation.

3 DATA

We analyzed a data set obtained from British Gas con-

sisting of anonymized records for circa 120,000 smart

meters with daily electricity consumption (kWh in 48

half hour bins) and individually time-stamped events

(for circa 250 different event codes) as logged by each

meter over a three-month period. According to the

data conﬁdentiality agreement we are unable to pro-

vide more speciﬁc details or to make these data avail-

able in supplemental material for this publication and

the data set has been returned to ownership of British

Gas. However, we believe the level of detail provided

is sufﬁcient for reproduciblity.

4 RESULTS

We present results of the analysis in a series of plots.

Figure 2 shows a biplot of the consumption data in the

ﬁrst two dimensions of the PCA ordination. Cases

(the blue dots) can be ranked by their distance from

the origin in any chosen number of dimensions (up to

seven). Interpreting the vectors of the variables (days

of the week) we see the weekend being orthogonal

to week days as we might expect for small business

properties.

The cloud of cases is roughly elliptical in the ﬁrst

two dimensions with clearly identiﬁable outliers, but

none that would necessarily arouse suspicion.

Figure 2: PCA biplot of consumption data.

Figure 3 shows a scree plot of the consumption

data ordination. We can be conﬁdent that there is

signiﬁcant dimension reduction (the concave shape).

The Kaiser-Guttman rule selects only the ﬁrst two

components with eigenvalues >1, however these two

components account for only 45.36% of the variance

of the original data.

Figure 3: Screeplot of consumption data.

Figure 4 shows a histogram of the consumption

PCA ordinal distances with a right-skew, and a not

exceptionally long tail.

Figure 4: Ordinal distance histogram of consumption data.

Figure 5 shows a biplot of the CA ordination of

the event data in the ﬁrst two dimensions. A hand-full

of variables dominate the solution, in two orthogonal

sets. The rest of the variables contribute only a minor

inﬂuence on the solution.

Figure 6 shows a scree plot of the event data or-

dination. Here we can be even more conﬁdent that

there is signiﬁcant dimension reduction. The Kaiser-

Guttman rule (Jackson, 1993) selects about 20 out of

circa 150 variables with eigenvalues >1, and these ac-

count for 88.61% of the variance of the original data.

Figure 7 shows a histogram of the event CA or-

dinal distances with a right-skew, and again a not ex-

ceptionally long tail.

Anomaly Detection for Industrial Big Data

289

Figure 5: CA biplot of event data.

Figure 6: Scree plot of event data.

Figure 7: Ordinal distance histogram of event data.

Figure 8 shows a scatter plot of the ranked dis-

tances from the two ordinations of consumption and

event data. This shows, for the most part, that the data

in the two partitions are independent (the more-or-less

even cloud of data points across the entire space.) If

the variables in the two partitions were partially cor-

related we would expect a concentration in density of

points towards the diagonal.

What we’re not expecting from a uniﬁed under-

lying process is (much) variation in density of points

along the diagonal. For these data we see a distinct

cluster of high density at high ranks in the upper right

corner.

Figure 8: Joint rank scatter plot.

Figure 9 shows the density of the joint ranks as a

contour plot where density has been scaled to units

of standard deviation. The high density cluster in the

upper right corner is from two to 40 standard devia-

tions away from the mean of the background process,

and contains no more that 560 cases, out of a total of

some 120k cases. A slight concentration towards the

diagonal is also evident for the background process.

Figure 9: Joint rank density plot.

Figure 10 shows a surface plot using the same

scaling in units of standard deviation. We interpret the

spike in density to indicate a set of anomalous cases

that are probably derived from a different underlying

mechanism to the rest of the dataset.

Figure 11 illustrates the long tail of the distribu-

tion and shows just 560 cases with std >2, out of a

dataset of some 120k cases.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

290

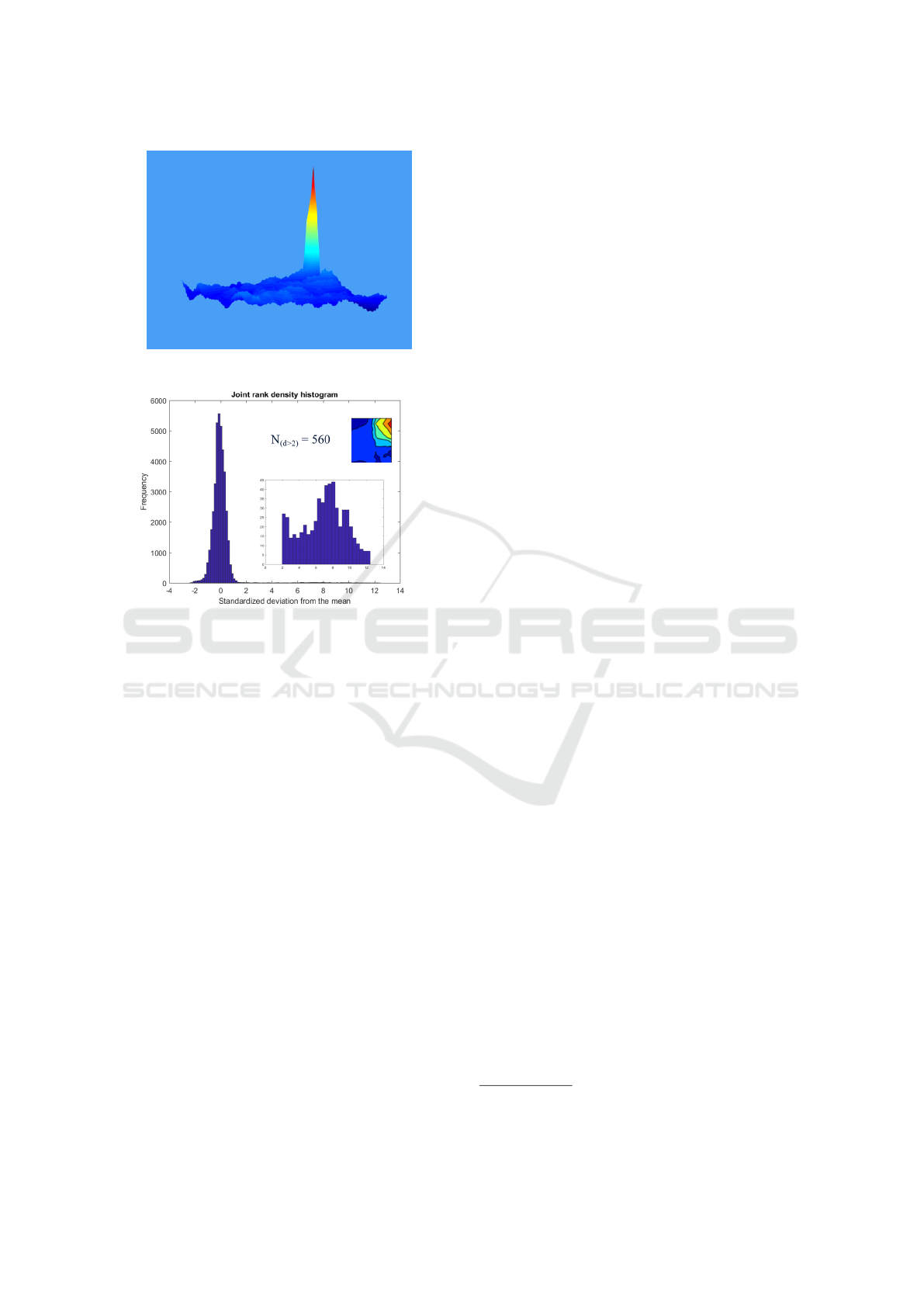
Figure 10: Joint rank density 3-d.

Figure 11: Joint rank density histogram.

5 PERFORMANCE

Computing the SVD in each ordination is the most

time consuming element of the method and the most

critical obstacle to scaling for Industrial Big Data. In

a series of experiments we tested three different im-

plementations and measured the performance as ex-

ecution time iterating over an increasing number of

dataset rows. Matlab code for the three implemen-

tations is shown in Sections 5.1 to 5.3. Tests were

run using Matlab(R) Version 9.3.0.713579 (R2017b)

on an ordinary desktop computer with an Intel(R)

Core(TM) i7-4790 CPU @ 3.60GHz, 3601 Mhz, and

Installed Physical Memory (RAM) of 16.0 GB.

Results of the performance tests are shown in Fig-

ure 12. The ‘naive’ but straightforward implemen-

tation following the mathematical notation and using

full diagonal matrices performs poorly, and is unus-

able for Big Data unless modiﬁed. Both the sparse

and vectorized implementations perform adequately

(vectorized being slightly better). These tests demon-

strate that the method does scale adequately to Indus-

trial Big Data, however further improvements by opti-

mizing the core SVD implementations should still be

investigated.

5.1 Full Diagonal Matrices

Notation follows Greenacre (2013, pp. 110–111).

Dr = diag(r);

% full diagonal

Dc = diag(c);

% full diagonal

T = Drˆ(-1/2)*(P-r*c’)*Dcˆ(-1/2);

% standardized residuals (Equation 4)

[U,S,V] = svd(T,0);

% singular value decomposition (economy size)

F = Drˆ(-1/2)*U*S;

% principal coordinates of the rows

5.2 Sparse Diagonal Matrices

Modiﬁcations to overcome the prohibitive size of the

diagonal matrices

rsq = 1./sqrt(r);

% inverse square root

nr = 1:numel(r);

% indices for sparse

rsp = sparse(nr,nr,rsq);

% sparse diagonal

csq = 1./sqrt(c);

% inverse square root

nc = 1:numel(c);

% indices for sparse

csp = sparse(nc,nc,csq);

% sparse diagonal

T = rsp*(P-r*c’)*csp;

% standardized residuals (Equation 4)

[U,S,V] = svd(T,0);

% singular value decomposition (economy size)

F = rsp*U*S;

% principal coordinates of the rows

5.3 Vectorised Loops

Modiﬁcations to improve speed as well as overcom-

ing the prohibitive size of the diagonal matrices

rsq = 1./sqrt(r);

% inverse square root

csq = 1./sqrt(c);

% inverse square root

T = P-r*c’;

for i = 1:size(T,2)

T(:,i)=(T(:,i).*rsq(:))*csq(i);

% standardized residuals (Equation 4)

end

[U,S,V] = svd(T,0);

% singular value decomposition (economy size)

F = U; s = diag(S);

for i = 1:size(F,2)

F(:,i) = (F(:,i).*rsq(:))*s(i);

% principal coordinates of the rows

end

Suggested by Odwa Sihlobo, Prescient SA.

Suggested by Stef Salvini, University of Oxford.

Anomaly Detection for Industrial Big Data

291

Figure 12: Performance evaluation plot.

6 CONCLUSIONS

In this paper we introduce a method for anomaly de-

tection to operate at industrial scale. The method has

relevance for system condition monitoring, prognos-

tic health maintenance, or any application where iden-

tiﬁcation of anomalous cases is advantageous. The

method aligns with the general trend in Industrial Big

Data applications towards data-driven discovery as an

alternative to process models which are unlikely to

operate at the scales required. The method can ac-

commodate high-dimensional data of heterogeneous

data types in a simple and scalable computational

framework of well-known and well understood ordi-

nation techniques (e.g. SVD, PCA, CA; Greenacre

(2010, 2013)), and spatial density analysis (e.g. Bad-

deley et al. (2015)).

The method has a well deﬁned workﬂow (refer to

Figure 1 and to the detailed descriptions in Section

2) and we demonstrate the method using data from

electricity smart meters (refer to Sections 3 and 4 and

to Figures 2 to 11). For the demonstration dataset

we ﬁnd a small number (N

(d>2)

= 560; <0.5%) of

cases with overwhelming indication that they origi-

nate from a mechanism that is different from the one

that produced the bulk of cases in the dataset.

This process discovers those cases most resistant

to ordination, and therefore least conforming to the

mechanism that generated the rest of the data, i.e. the

anomalies.

In future work we plan to explore:

(i) the statistical properties of the method, specif-

ically the departure from the mean background

process as measured by the joint rank density of

cases,

(ii) further optimization for operating at scale of

the well-known algorithms for singular value

decomposition (SVD) as applied in the special

case of the method, and

(iii) the properties of the method when applying

bootstrapped resampling as described in Sec-

tion 2.1.2.

ACKNOWLEDGEMENTS

Funding in support of this work was given by Inno-

vate UK, Grant Reference Number 102510. Useful

comments on the manuscript were provided by Laura

Shemilt and Glen Moutrie.

DISCLOSURE

The technical method described in this paper is pro-

tected by British patent applications 1713703.5 and

1713896.7, submitted on 25 and 30 August 2017.

REFERENCES

Aggarwal, C. C. (2013). Outlier Analysis. Springer, Berlin.

Akoglu, L., Tong, H., and Koutra, D. (2015). Graph-based

anomaly detection and description: a survey. Data

Mining and Knowledge Discovery, 29:626–688.

Baddeley, A., Rubak, E., and Turner, R. (2015). Spatial

Point Patterns: Methodology and Applications with R.

Chapman and Hall/CRC Press.

Barnett, V. and Lewis, T. (1994). Outliers in Statistical

Data. Wiley, New York, 3rd. edition.

Campos, G. O., Zimek, A., Sander, J., Campello, R. J.

G. B., Micenkov, B., Schubert, E., Assent, I., and

Houle, M. E. (2016). On the evaluation of unsuper-

vised outlier detection: measures, datasets, and an em-

pirical study. Data Mining and Knowledge Discovery,

30:891–927.

Chandola, V., Banerjee, A., and Kumar, V. (2009).

Anomaly detection: a survey. ACM Computing Sur-

veys, 41:1–58.

de Mauro, A., Greco, M., and Grimaldi, M. (2015). What

is big data? A consensual deﬁnition and a review

of key research topics. AIP Conference Proceedings,

1644(1):97–104.

Efron, B. and Tibshirani, R. J. (1994). An Introduction to

the Bootstrap. Chapman and Hall/CRC, New York.

Greenacre, M. (2010). Biplots in Practice. BBVA Founda-

tion, Madrid.

Greenacre, M. (2013). Contribution biplots. Journal of

Computational and Graphical Statistics, 22:107–122.

Hawkins, D. (1980). Identiﬁcation of Outliers. Chapman

and Hall, London.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

292

Jackson, D. A. (1993). Stopping rules in principal compo-

nents analysis: A comparison of heuristical and statis-

tical approaches. Ecology, 74:2204–2214.

Knorr, E. M. and Ng, R. T. (1997). A uniﬁed notion of

outliers: properties and computation. Proceedings of

the 3rd ACM international conference on knowledge

discovery and data mining (KDD), Newport Beach.

Nunnaly, J. C. and Bernstein, I. H. (1994). Psychometric

theory. McGraw-Hill, New York, 3rd edition.

Peres-Neto, P. R., Jackson, D. A., and Somers, K. M.

(2005). How many principal components? Stopping

rules for determining the number of non-trivial axes

revisited. Computational Statistics and Data Analy-

sis, 49:974–997.

Schubert, E., Zimek, A., and Kriegel, H. P. (2014). Local

outlier detection reconsidered: a generalized view on

locality with applications to spatial, video, and net-

work outlier detection. Data Mining and Knowledge

Discovery, 28:190–237.

Anomaly Detection for Industrial Big Data

293