OSPF Algebraic Formal Modelling using ACP

A Formal Description on OSPF Routing Protocol

Pedro Juan Roig

1,2

, Salvador Alcaraz

, Katja Gilly

and Carlos Juiz

Department of Physics and Computer Architecture, Miguel Hernández University, 03202 Elche (Alicante), Spain

Department of Computer Science, University of the Balearic Islands, 07122 Palma de Mallorca, Spain

Keywords: ACP, Formal Protocol Specification, Networking, OSPF.

Abstract: OSPF may well be the most popular routing protocol within Autonomous Systems, being used in all kind of

networks around the world. In this paper, we first design a basic model by focusing on the main tasks of a

router running OSPF, hence being neighbour discovery and a simplified route management, by means of

algebraic derivations using Algebra of Communicating Processes (ACP). Taking this model as a base case

scenario, we extend it by adding up some timing behaviour present in real OSPF implementations and by

detailing the packet exchanges involved in route management.

1 INTRODUCTION

We are living in an ever increasingly networked

world and routing protocols are key players in

supporting network communications. Focusing on

the OSI model (X200, 1994), communication among

network devices are mainly performed at layer 3,

namely, network layer.

As far as network communication is concerned,

layer 3 protocols are run in all interconnection

devices that belong to any network, providing an end

to end communication. Network communication

tasks are usually performed by routers, although it

might also be done by any layer 3 device with the

proper software package, such as switches, firewalls

or devices with multiple network adapters.

Those layer 3 devices communicate with each

other through routing protocols in order to exchange

their routing updates and build up and maintain their

own routing tables, which contain the best routes to

any attainable network according to common

criteria.

Routing protocols may be classified as Interior

Gateway Protocols (IGP) and Exterior Gateway

Protocols (EGP). A protocol belonging to the former

is implemented within an Autonomous System (AS),

thus among devices being managed by a common

administration, whereas the latter is reserved for

routing among different AS, like BGP.

Within IGP, protocols may be distinguished

between Distance Vector and Link State, the former

ones being like a route post, hence dealing with the

cost to get to a destination and pointing to the next

hop in the way there and the latter ones being like a

route map, thus having the aforesaid features and

also a topology map.

Among Link State protocols, there are two

protocols involved, being Intermediate System to

Intermediate System (IS-IS) and Open Shortest Path

First (OSPF), both standardized by IETF. The

former is mainly used in ISP environments and the

latter is the most widespreadly used, both in IPv4

(RFC 2328, 1998) and in IPv6 (RFC 5340, 2008)

domains. The aim of this paper is to get a realistic

approach model to OSPF behaviour.

The organization of this paper will be as follows:

first, Section 2 introduces formal description

techniques, then, Section 3 shows an OSPF informal

specification, next, Section 4 presents some Algebra

of Communicating Processes (ACP) fundamentals,

after that, Section 5 will get a basic router modelling

in an OSPF environment, afterwards, Section 6 will

render some examples of the basic modelling, later,

Section 7 will perform a detailed router modelling in

an OSPF environment, right after that, Section 8 will

perform a model verification and finally, Section 9

will draw the final conclusions.

2 FORMAL DESCRIPTION

TECHNIQUES

The use of Formal Description Techniques (FDT) in

Roig, P., Alcaraz, S., Gilly, K. and Juiz, C.

OSPF Algebraic Formal Modelling using ACP - A Formal Description on OSPF Routing Protocol.

DOI: 10.5220/0006838700550066

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 1: DCNET, ICE-B, OPTICS, SIGMAP and WINSYS, pages 55-66

ISBN: 978-989-758-319-3

order to study the ever growing complexity of

concurrent communication protocols is increasing as

it provides unambiguous descriptions in a more

precise way than any description made in natural

languages.

Because of that degree of complexity, there is

not a universal FDT to be employed in all cases but

it is necessary to deal with some of them, such that

one might better fit in some case scenario whereas

another one might do it in another situation.

Among all FDT, some of the tools most

commonly used tools are ESTELLE, LOTOS and

SDL (Turner, 1993). Otherwise, Petri Nets (Petri,

1966) are also widely used, as well as FSM and

Promela.

Eventually, Process Algebras may also be used

for that purpose, and among them, ACP (Bergstra

and Klop, 1985) might be one of the best suited for

dealing with distributed and concurrent systems, as

it abstracts away from the real nature of a system,

thus presenting it as a set of equations according to

its behaviour. The aforesaid equations are related to

the ACP axioms and processes are the solutions of

such systems of equations (Padua, 2011).

All Process Algebras share the concept of

Labelled Transition Systems (LTS) in order to

specify behaviour equivalence. Such systems are

formed by states whose transitions among them are

labelled with the proper associated actions. This

makes possible to model concepts regarding

distributed processing systems, such as OSI services

and protocols.

ACP is going to be used in order to get a formal

specification of OSPF, but before proceeding with it,

an OSPF informal specification will be presented so

as to later model those relevant features using ACP.

This work is going to extend a previous study on

formal description of OSPF by means of ACP (Roig

et al., 2018).

3 OSPF INFORMAL

SPECIFICATION

All routing protocols perform three basic functions,

such as identifying their neighbours on the network,

managing the route paths to all possible destinations

and making dynamic decisions as to where to

forward user traffic coming in. Those three actions

are necessary to build up and maintain the routing

table, thus forming control plane operations. Once

the routing table is completed, data plane will take

advantage of it in order to forward user traffic.

The first function may be known as neighbour

discovery and all OSPF routers exchange hello

messages through all their OSPF interfaces in order

to identify all their OSPF neighbours. All devices

within the same OSPF area must have the same hello

and dead timers, the same type of authentication, if

any, and the logical addressing of each interface

must be coherent with that of their link neighbours.

If this is the case, an OSPF neighbour relationship

will be established.

The second function may be known as route

management and all OSPF routers exchange routing

update messages in order to keep track of all

possible destinations available within the OSPF

environment.

In order to implement both functions, OSPF does

not use any transport protocol, such as TCP or UDP,

but it carries the data directly through an IP packet,

using protocol number 89 as the IP protocol field in

the IP header.

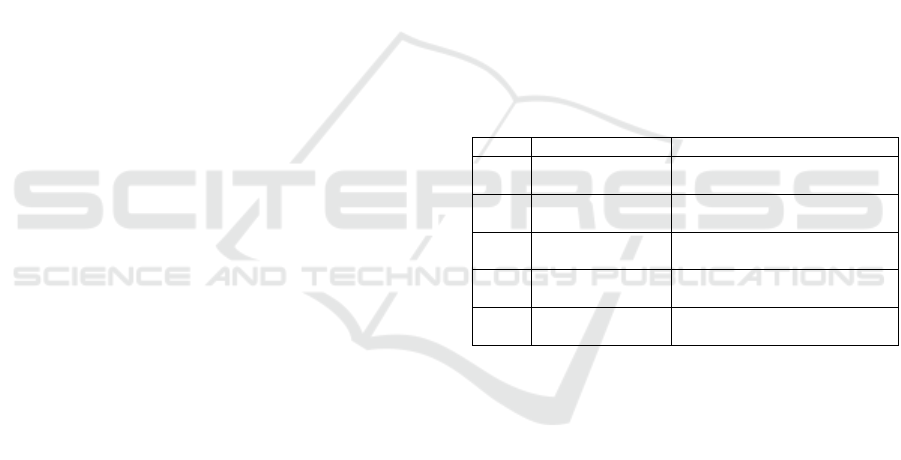
OSPF has five different types of packets, carried

inside an IP packet, whose functions are described in

Table 1.

Table 1: OSPF packet types.

Type Packet name Function

1 Hello

Discovering and maintaining

neighbors

Database

Description

Exchanging Data Base route

headers

Link State

Reques

Requesting Data Base route

updates

4 Link State Update

Sending Data Base route

updates

5 Link State ACK

Sending Acknowledgments to

route updates

Therefore, each local router running OSPF

implements the neighbour discovery function by

exchanging OSPF type 1 packets with all its OSPF

neighbouring routers, whereas the route

management function is performed by exchanging

the rest of OSPF packets types in the proper way.

As OSPF is a link state routing protocol, it holds

a Link State Data Base (LSDB) containing all routes

to all networks within the OSPF domain.

Furthermore, it implies all routers must have their

LSDB synchronised, meaning that all of them must

share the same information about the network

topology after the necessary route exchange, before

achieving the state of convergence. OSPF is a fast-

converging routing protocol, such as a network

composed by a few routers may converge just in a

few seconds.

Regarding router management, when a local

router has knowledge of any new route or a route

update, it sends an OSPF type 2 packet to its proper

DCNET 2018 - International Conference on Data Communication Networking

OSPF neighbouring routers. Those packets are also

known as Data Base Description (DBD) and they

contain a set of the route headers regarding those

routes. Upon receipt of a DBD, those OSPF

neighbouring routers check whether each route

header present within a DBD is also present within

their LSDB.

LSDB keeps not only the route headers but full

data about routes, allowing the buildup of a network

topology. Each LSDB entry belongs to a single route

and it is called Link State Advertisement (LSA).

Therefore, DBD packets contain summaries of the

LSA. Actually, the sending and receiving DBD is

called DataBase Exchange Process, where each LSA

has a sequence number and is acknowledged by

echoing it.

Each LSA header present in a DBD contains

some fields to identify in a unique way an LSA, such

as LS ID, LS type and Advertising Router, but in

order to determine which instance is more recent,

this is, the one inside the incoming DBD or the one

already stored within the LSDB, the fields to be

examined are LS Sequence Number, LS Age and LS

Checksum.

When a local router detects an LSA more recent

than its own database copy, then it sends an OSPF

type 3 packet to the OSPF neighbouring router

which sent that particular OSPF type 2 packet, so as

to request an update and in turn an OSPF type 4

packet will be deliver from that neighbour.

Eventually, each OSPF type 4 packet will be

acknowledged by an OSPF type 5 packet.

In addition to it, OSPF type 4 packets will be

sent from every local router to all of its proper OSPF

neighbours every 30 minutes by default, this is 1800

seconds, in order for them to refresh their LSA,

although some manufacturers might set different

values varying from 5 to 59 minutes. If such a

refreshment is not produced, the LSA will be flushed

from LSDB if its timer reaches its maximum aging

time, which is 1 hour, this is, 3600 seconds.

Special attention must be paid to OSPF type 4

packets, as those packets implement the flooding of

LSA, containing information about routing, metric

and topology regarding a particular section of the

OSPF network, thus being the relevant stuff about

routing updates. One particular OSPF type 4 packet

may contain a single LSA or multiple LSA.

LSA are used to fill and update LSDB, although

there is not only one sort of LSA but a few of them,

each one being employed for advertising different

OSPF networks. The mostly used LSA types are 1 to

5, although there are defined up to eleven types.

It must be taken into consideration that OSPF is

a highly scalable routing protocol because of the

concept of area, which permits the division of the

whole OSPF domain in different areas, hence routers

belonging to one particular area must have their

LSDB synchronised.

The connection among two or more areas is

performed by an Area Border Router (ABR) which

is a router that has interfaces in more than one area,

thus being able to propagate routes through all of

them. In addition to it, an Autonomous System

Boundary Router (ASBR) is a router being the edge

router with another routing domain, which also

might propagate some external routes inside. Those

OSPF multiarea concepts are depicted in Figure 1.

Figure 1: Multiarea OSPF routing domain.

Regarding LSA types, there are LSA types 1 and

2 that carry routes within the same OSPF area, thus

they are referred to as intra-area LSA. There are also

LSA types 3 and 4 that carry routes from one area to

another one, thus they are known as inter-area LSA.

Finally, there are LSA type 5 that carries external

routes redistributed into OSPF domain.

The mostly used LSA types are described in

Table 2, where the acronym DR will be described in

due course.

Table 2: OSPF LSA main types.

Type LSA name Function

1 Router LSA

Each router advertises all its

directly connected links

2 Network LSA

Each DR in a multi-access

network advertises all the

routers connected

3 Summary LSA

Each ABR advertises routes

from one area into other

connected areas

4 Summary ASBR LSA

Each ABR advertises routes

coming from an ASBR to show

where it is

5 AS external LSA

Each ABR advertises external

routes being redistributed into

OSPF domain

Apart from that, it is important that all

neighbours within a particular network segment

OSPF Algebraic Formal Modelling using ACP - A Formal Description on OSPF Routing Protocol

share the same OSPF network type. There are four

main types according to the standards, each of them

having particular characteristics. This fact makes

each of those network types a different case

scenario, as they might be exhibited in the following

points:

A. Broadcast (BRC)

There might be more than two neighbours within a

single network segment and then a Designated

Router (DR) and a Backup Designated Router

(BDR) must be assigned. The first one will be in

charge of receiving an LSA containing the routing

updates from a given neighbour and sending it back

to the rest of the neighbours, whereas the second one

will keep track of all receiving LSA but will not be

sending anything. With respect of the rest of

neighbours, they will be considered DROthers and

will not share LSA directly with any other

neighbour. The typical example of this network type

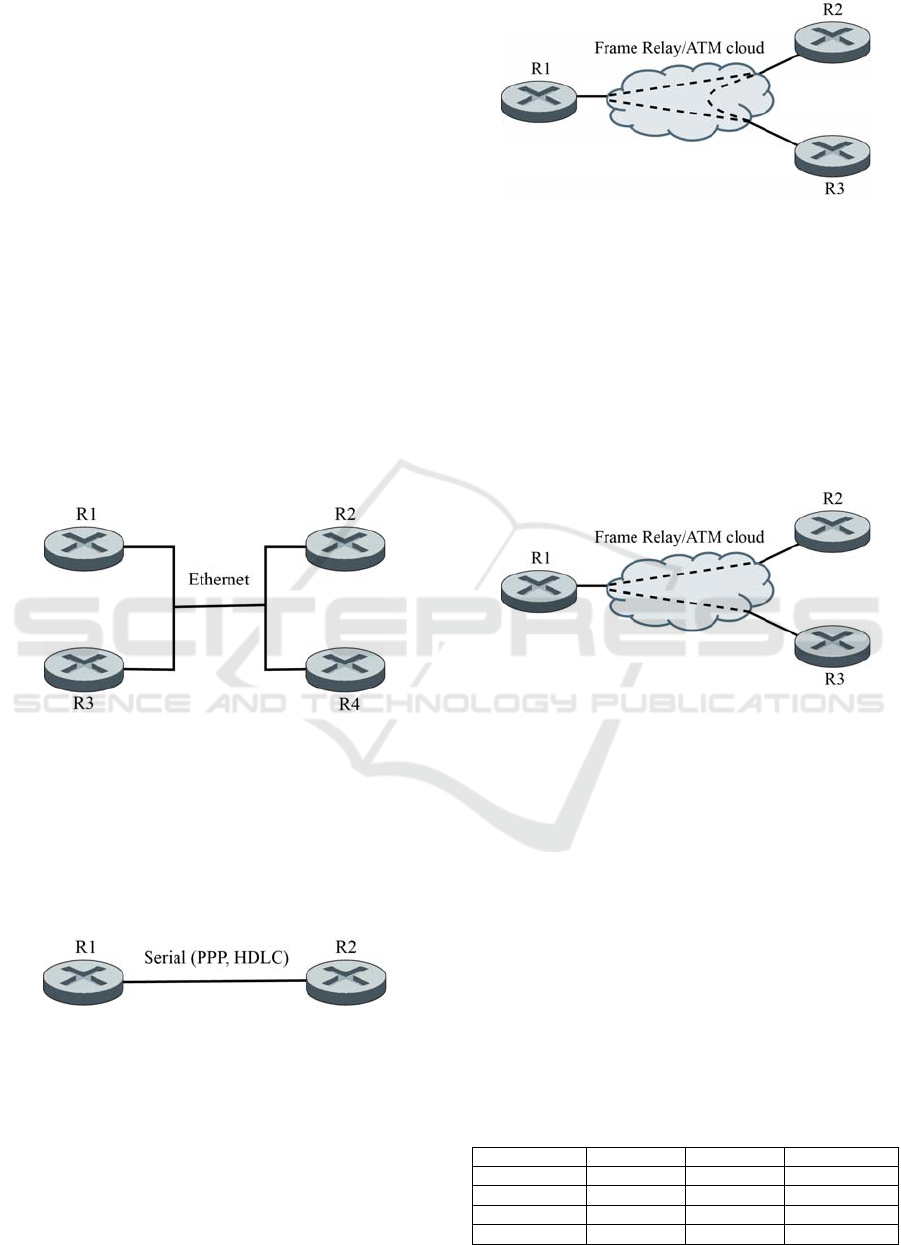
is an Ethernet environment, like in Figure 2.

Figure 2: OSPF Broadcast network.

B. Point to Point (P2P)

There are just two neighbours, so there is no need to

appoint a DR or a BDR as they both will be

exchanging LSA. A typical example of this network

type is a Serial link between two pairs, working with

layer two protocols PPP or HDLC, as in Figure 3.

Figure 3: OSPF Point to Point network.

A. Non Broadcast MultiAccess (NBMA)

It is found on non broadcast environments, such as

Frame Relay or ATM, and a multi-access topology

is needed, such as Full Mesh or Partial Mesh. There

might be present more than two neighbours,

therefore a DR and a BDR must be appointed, such

as in Figure 4.

Figure 4: OSPF Non Broadcast MultiAccess network.

B. Point to MultiPoint (P2MP)

It is present on non broadcast environments, such as

Frame Relay or ATM, and a Hub-and-Spoke

topology is implemented. In such a case, that

topology might be considered as a string of point to

point links, as all spokes routers must first

communicate with the hub in order to do it with

another spoke router, so there is pointless to assign a

DR and a BDR, as shown in Figure 5.

Figure 5: OSPF Point to MultiPoint network.

As stated before, neighbour discovery function

implies that all link neighbours share the same

values of hello timers and dead timers. There is a

timer set for each interface. The hello interval is

used to maintain neighbour relationships, thus being

reset upon each sending, whereas the dead interval is

used to delete such neighbour relationship after 4

silent hello intervals and it is reset upon receiving a

hello packet from a neighbour.

The hello interval defines how often a hello

packet is sent over whereas the dead interval sets the

waiting time for a hello packet before the neighbour

is declared dead. The default values of both timers

depend on the network type and they are described

in Table 3.

Table 3: Hello and Dead Timers –vs– Timer Types (TT).

Network Type Hello Time

Dead Time

Value

BRC 10 sec. 40 sec. TT = 0

P2P 10 sec. 40 sec. TT = 0

NBMA 30 sec. 120 sec. TT = 1

P2MP 30 sec. 120 sec. TT = 1

DCNET 2018 - International Conference on Data Communication Networking

In case any two neighbours are exchanging LSA,

an OSPF adjacency relationship will be established.

At that point they will start exchanging a full copy

of their LSDB and in turn they will be sending each

other any given routing update in order to keep their

LSDB synchronised.

Once LSDB belonging to all routers within a

given area are in synchronisation, then the Shortest

Path First (SPF) algorithm, also known as Dijkstra

algorithm (Dijkstra, 1959), will be run in each

router, taking itself as the root of the tree, in order to

get the shortest path tree from each router to all

networks present in the OSPF domain.

The SPF algorithm takes interface bandwidth in

order to calculate its cost, also known as metric. It

must be taken into account that the standard OSPF

v1 was released in the early 90s, so by that time a

FastEthernet link was the fastest and the original

expression to calculate it was the integer part of a

fraction where the numerator was 10

and the

denominator was the link bandwidth in bps, being 1

the least possible cost.

Therefore, a FastEthernet 100 Mbps link would

have an OSPF cost of 1 and also any faster link,

whereas a Serial 1.544 Mbps T1 link will have 64.

Later on, that formula was adjusted accordingly but

nowadays it is still considered as the default

implementation for backward compatibility

purposes.

On completion of the Dijkstra algorithm in each

router, the routes with the least cost from a particular

router to all those OSPF domain networks will be

selected and in turn they will be written into the

routing table.

At that stage, the third function exposed above

for any routing protocol will be fulfilled. Therefore,

the routing table will be built up, meaning that the

router will be ready to forward data packets to any

destination within the OSPF domain.

This is an OSPF informal specification, but we

are looking forward to achieving an OSPF formal

specification that captures the protocol behaviour.

4 ACP FUNDAMENTALS

The FDT chosen to model OSPF is going to be ACP,

which is a kind of process algebra that allows to

describe concurrent communication processes in an

abstract way, in a similar fashion as abstract algebras

do.

This is done by getting some ACP process terms

being behaviourally equivalent as the process to be

modelled, hence being OSPF, without caring about

other implementation details of that process being

described.

In order to achieve this, the concept of

bisimulation equivalence is used, also known as

bisimilarity, meaning that two processes may

execute the same string of actions and also have the

same branching structure (Fokkink, 2007).

Therefore, two bisimilar processes are considered to

behave in an equivalent manner.

ACP has its own set of axioms so as to prove that

two process terms have an equivalent behaviour.

Those axioms make use of the syntax and semantics

of ACP operators (Lockefeer et al., 2016).

The basic signature of a framework for ACP

consists of atomic actions, such as sending and

receiving data, which represent actions whose

behaviour may not be further divided, as well as

alternative operators, defined as sums, and

sequential operators, defined as products.

That may be extended with the use of concurrent

operators (||), whose behaviour may be described by

the left merge operator (||_) and the communication

merge operator (|) by means of the Expansion

Theorem, presented by Bergstra and Klop (Bergstra

and Klopp, 1984), where

}{}..{

1 in

XXXX 

and

},{}..{

jin

XXXXX 





XXXXXXX

_||)|(_||)||...||(

(1)

Therefore, depending on the number of concurrent

processes, the expression goes this way:

21122121

|_||_||)||(2 XXXXXXXXn 







132

231321

213312

321321

_||)|(

_||)|(_||)|(

)||_(||)||_(||

)||_(||)||||(3

XXX

XXXXXX

XXXXXXn















)||_(||)|()||_(||)|(

)||||_(||)||||_(||

||||||4

21433142

41323241

42314321

32144213

43124321

4321

XXXXXXXX

XXXXn











The behaviour of the left merge and the

communication merge operators is the following:

)||(_||)( yxvyxv







(2)

zyzxzyx _||_||_||)( 





(3)

OSPF Algebraic Formal Modelling using ACP - A Formal Description on OSPF Routing Protocol

)||()|()(|)( yxwvywxv 

(4)

zyzxzyx |||)( 

(5)

In addition to it, the encapsulation operator

)(



forces internal actions into communication. Joining

it with the concurrent operator shown above, the

outcome will only depend on whether the first factor

of each term belongs to set

or otherwise, where

constant



represents a deadlock and the set

represents all internal actions related to sending and

receiving messages.

Hvvv

 ,)(

(6)

Hvv

 ,)(



(7)



 )(

(8)

)()()( yxyx

HHH



(9)

)()()( yxyx

HHH



(10)

For a communication to take place in a channel, a

sending action is needed at one end whereas a

receiving action is needed at the other one, otherwise

deadlock

)(



will happen.

Therefore, communication is going to be

considered herein as unidirectional, hence, regarding

the channel where its sending point is

and its

receiving point is

jijiji

crs

,,,

| 

(11)





ijji

(12)





lkji

(13)

In summary, when applying the encapsulation

operator to the Expansion Theorem in order to

derive concurrent processes, only terms starting with

a communication merge operator having both the

same initial end and the same final end will prevail,

whereas all of the other terms will be discarded.

Furthermore, a conditional operation is declared

in order to distinguish whether a condition has been

accomplished or otherwise. This way, data can

influence process behaviour. As per its syntax, the

condition offers a Boolean data type and goes in the

middle of the expression, surrounded by two

triangles pointing outwards, whereas the True

condition goes ahead and the False condition goes

behind.

FalseConditionTrue ||

(14)

Those are the necessary ACP operators in order

to undertake the modelling of OSPF through

algebraic derivations. According to that, two

different models are presented:

 a basic model, making some assumptions over

the OSPF packet exchange in order to keep it as

simple as possible

a detailed model, following the actual OSPF packet

exchange in order to make it as close to real as

possible

5 BASIC ROUTER MODELLING

IN OSPF

The aim of this basic model is to get the big picture

of OSPF dynamics and a couple of assumptions are

to be made for that purpose.

The first one is to take the LSA exchange

process as a whole, thus considering the exchange of

OSPF packet types 2, 3, 4 and 5, as a single process

so as to keep things simple.

It is worth noting that the LSA exchange process

gets the synchronisation of LSDB belonging to all

OSPF routers within the same area so as to

eventually have the same contents within their

respective LSDB. That is why OSPF is considered a

link state routing protocol. At that point, the OSPF

routers are fully adjacent, thus making LSDB

synchronisation process possible in a predictable

time interval.

The second one is to ignore all the timers

involved in OSPF, namely, on one hand, hello timer

and dead timer in order to keep the neighbour

relationships and, on the other hand, the LSA refresh

timer and the max age LSA timer in order to keep

the each LSA entry in LSDB updated.

Keeping those assumptions in mind, a basic

OSPF model will be built up and for that purpose,

we have to deal with the three basic functions

describe in Section 3.

The first function was Neighbour Discovery,

where messages flow in all directions from all OSPF

routers looking for their OSPF neighbouring routers.

Using ACP syntax and semantics, it may be said

that a local OSPF router

exchanges hello

messages

)(h

through all its OSPF interfaces,

facing its

neighbouring OSPF routers, regardless

of the network type or which area they are located

in.

Therefore, Neighbour Discovery is modelled by

the following expression:

DCNET 2018 - International Conference on Data Communication Networking

))()((

,,1_

hrhsR

jii







(15)

When the sending and receiving actions from

neighbouring routers flow through the same channel

in the same direction (the same routers

and

, in

the same order), hello communication will occur,

therefore:

)()(|)(

,,,

hchrhs

jijiji



(16)

On the contrary, if both actions do not meet the

aforesaid requirements, it will yield deadlock (



This will get the expected result, such as

communication will take place between any router

and any of its neighbours, always in a unidirectional

fashion, hence all OSPF neighbours will be engaged

in a neighbour relationship.

The second function was Route Management and

the main difference with the previous one is that

network type is crucial, as LSA will be exchanged

by the routers having an adjacency relationship. It

must be taking into consideration that this basic

model assumes that the aforesaid function is

modelled as a single process.

According to the behaviour of DR and BDR

routers exposed above, the following table shows

whether LSA communication will take place

between a sender and a receiver. The role of each

sender will be shown as rows whereas the role of

each receiver will be seen as columns.

If a cell being the crossing point between a row

represented by a sender and a column represented by

a receiver shows 1, then LSA communication will be

held and LSA will be exchanged. Otherwise, if a cell

shows 0, then LSA communication will not be

produced between that sender and that receiver.

Needless to say that communication between a

single router being both sender and receiver is not

allowed. It all may be appreciated in Table 4.

Table 4: Valid Communication Channels.

BDR

DRO1

DRO2

DRO3

DRO4

- 1 1 1 1 1

BDR

1 - 0 0 0 0

DRO1

1 1 - 0 0 0

DRO2

1 1 0 - 0 0

DRO3

1 1 0 0 - 0

DRO4

1 1 0 0 0 -

In addition to it, it is also necessary to assign

different values to the four different network types

previously defined, depending whether DR and BDR

are appointed or otherwise, as seen in Table 5.

Table 5: Values assigned to network types (NT).

Network Type Nomenclature Value

Broadcas

BRC NT = 0

Point to Poin

P2P NT = 1

Non Broadcast

MultiAccess

NMBA NT = 0

Point to MultiPoin

P2MP NT = 0

In order to implement Table 4 in an equation, it

is first necessary to assign different values to the

different router roles and also keeping in mind the

values given by Table 5. This is shown in Table 6.

Table 6: Values assigned to router roles.

Network

Type

Router

Role

Naming Value

NT = 0 Designated Route

DR 3

NT = 0

Backup Designated

Route

BDR 2

NT = 0 DR Othe

DRO 1

NT = 1 Point to Point Routers - 0

Putting it all together, coefficients

will be

implemented in order to capture the behavior

exhibited in the previous tables. Those coefficients

have binary values, thus 1 or 0, depending on

whether communication exists in the channel

starting in a router

and ending in a router

Therefore, the coefficients will permit

communication between peers in a unidirectional

way or otherwise.

The role corresponding to the local router

will

be carried by variable

whereas the role

corresponding to its neighbouring router

will be

carried by variable

Those coefficients take their values from the next

equation, taking the integer part of a fraction

containing the role of both ends of the channel and

the network type:



















int

(17)

In order to get the roles for each router within each

network type, which will provide

and

values,

it is necessary to implement an algorithm having all

of the routers within a network segment

)(n

and its

network type

)(NT

as arguments, such as

Algorithm 1.

OSPF Algebraic Formal Modelling using ACP - A Formal Description on OSPF Routing Protocol

RouterRole(n,NT){

If (NT == 1)

Then

For (z = 0; z < count(n); z++)

z.Role = 0;

Done

Else

If (NT == 0)

Then

DR.priority = 0;

DR.router-id = 0;

BDR.priority = 0;

BDR.router-id = 0;

Flag = 0;

For (z = 0; z < count(n); z++)

If (z.priority > DR.priority)

Then

DR.priority = z.priority;

DR.router-id = z.router-id;

Flag = 1;

z.Role = 3;

Else

If (z.priority == DR.priority)

Then

If (z.router-id > DR.router-id)

Then

DR.router-id = z.router-id;

Flag = 1;

z.Role = 3;

EndIf

If (Flag == 0)

Then

If (z.priority > BDR.priority)

Then

BDR.priority = z.priority;

BDR.router-id = z.router-id;

Flag = 1;

z.Role = 2;

Else

If (z.priority == BDR.priority)

Then

If (z.router-id > BDR.router-id)

Then

BDR.router-id = z.router-id;

Flag = 1;

z.Role 2;

EndIf

If (Flag == 0)

Then

z.Role = 1;

EndIf

Done

EndIf

}

Algorithm 1: RouterRole(n,NT).

Using ACP syntax and semantics, it may be said

that a router

exchanges LSA messages

)(d

through its proper OSPF interfaces, this is, facing its

neighbours where the coefficients given by (17)

are 1 no matter the network type.

Therefore, Route Management is modelled by

the following expression:

))()((

,,,,2_

drkdskR

ijij

jijii







(18)

Analogously as the previous function,

communication will only take place in a

unidirectional fashion between a given sender and a

particular receiver, yielding deadlock (



) in the rest

of the cases.

)()(|)(

,,,

dcdrds

jijiji



(19)

The third function was Path Determination and

consists in making decisions about where to forward

each network message coming in, in other words,

filling up the routing table according to the Shortest

Path First (SPF) algorithm, also known as Dijkstra

algorithm.

Two actions need to be performed in order to

achieve that. The first action is running the Dijkstra

algorithm, considering the OSPF metric as the cost

to be minimised. It solves the problem of finding the

shortest paths from a source node to the rest of the

nodes within a network, providing all edges do have

non-negative weights.

Algorithm 2: Dijkstra(i,G).

A pseudocode algorithm implementing this

action, starting with router

as the root of the

shortest path tree for the weighted graph

),( VEG



representing the OSPF domain,

composed by all vertices

Vv

with edges acting

as the weight function

REw :

among those

Dijkstra(i,G){

dist[i] ← 0

for all v ∈ V–{i}

do dist[v] ← ∞

done

S ← ∅

Q ← V

while Q ≠ ∅

u ← mindistance(Q,dist)

S ← S ∪ {u}

for all v ∈ neighbors[u]

if dist[v] > dist[u] + weight(u,v)

then dist[v] ← dist[u] + weight(u,v)

endif

done

return dist

}

DCNET 2018 - International Conference on Data Communication Networking

vertices, would give a vector named dist. That array

contains the least path costs from the source router

to all destinations. The aforesaid algorithm is

Algorithm 2.

Regarding the second action, it is the election of

the least path cost from a local router to any other

destination. This action is performed right after the

Dijkstra algorithm has been executed and it just

takes its result as the outgoing interface and the path

cost to reach each network being part of the OSPF

domain and passes it on to the routing table.

In short, Path Determination would be modelled

by the following string of algorithms:

)(),(

iBestRoutesGiDijkstraR





(20)

But ACP does just deal with processes and that

implies that it does not deal with neither data nor

time (Fokkink, 2016), so this third function may not

be implemented. There are some ACP extensions

like mCRL2 (Groote and Mousavi, 2014) providing

data and time capabilities that might make possible

to implement Path Determination as described

above.

Hence, to wrap it all up, the modelling of an

OSPF router in this basic case scenario using ACP

syntax and semantics will take both neighbour

discovery and route management functions.































ijijjiji

ijji

drkdsk

hrhs

))()((

)(

,,,,

(21)

6 SOME EXAMPLES OF OSPF

BASIC MODELLING

In order to show the outcome of (21), we are going

to render some examples so as to prove that the

basic router model for OSPF using ACP mirrors the

real OSPF behaviour.

In those examples,

will represent the number

of routers within the same network segment and

will carry whether that network segment needs

to appoint a

BDRDR/

or otherwise.

A. n=2; NT=1; so there is no need of DR/BDR

))(1)(1())()((

1,22,11,22,11

drdshrhsR 





))(1)(1())()((

2,11,22,11,22

drdshrhsR 





))()((

))()(()||(

1,22,1

1,22,121

dcdc

hchcRR





B. n=2; NT=0; it yields the same result as A.

))()((

))()(()||(

1,22,1

1,22,121

dcdc

hchcRR







C. n=3; NT=0; it is supposed that R1 is DR, R2 is

BDR and R3 is DROther.

))(1)(1)(1)(1(

))()()()((

1,33,11,22,1

1,33,11,22,11

drdsdrds

hrhshrhsR









))(1)(0)(1)(1(

))()()()((

2,33,22,11,2

2,33,22,11,22

drdsdrds

hrhshrhsR









))(0)(1)(1)(1(

))()()()((

3,22,33,11,3

3,22,33,11,33

drdsdrds

hrhshrhsR









))()()()()((

))()()()(

)()(()||||(

2,31,33,11,22,1

2,33,21,33,1

1,22,1321

dcdcdcdcdc

hchchchc

hchcRRR









D. n=4; NT=0; it is supposed that R1 is DR, R2 is

BDR, R3 and R4 are DROther.

))(1)(1)(1)(1

)(1)(1())()(

)()()()((

1,44,11,33,1

1,22,11,44,1

1,33,11,22,11

drdsdrds

drdshrhs

hrhshrhsR











))(1)(0)(1

)(0)(1)(1())(

)()()()()((

2,44,22,3

3,22,11,22,4

4,22,33,22,11,22

drdsdr

dsdrdshr

hshrhshrhsR













))(0)(0)(0

)(1)(1)(1())(

)()()()()((

3,44,33,2

2,33,11,33,4

4,33,22,33,11,33

drdsdr

dsdrdshr

hshrhshrhsR













))(0)(0)(0

)(1)(1)(1())(

)()()()()((

4,33,44,2

2,44,11,44,3

3,44,22,44,11,44

drdsdr

dsdrdshr

hshrhshrhsR













))()(

)()()()()(

)(())()()()(

)()()()()(

)()()(()||||||(

2,42,3

1,44,11,33,11,2

2,13,44,32,44,2

2,33,21,44,11,3

3,11,22,14321

dcdc

dcdcdcdcdc

dchchchchc

hchchchchc

hchchcRRRR













OSPF Algebraic Formal Modelling using ACP - A Formal Description on OSPF Routing Protocol

7 DETAILED ROUTER

MODELLING IN OSPF

The aim of this detailed model is to get a more

realistic approach of OSPF dynamics and both

assumptions made in the previous basic model are to

be reverted for that purpose.

Regarding LSA exchange process, it must first

be considered the proper sequence of events. As

exposed in Section 3, it involves OSPF packet types

2 to 5, in a way that a local router sends a type 2

packet to each of its adjacent routers and then it

waits for receiving the acknowledgements in the

form of an echoing type 2 packet for each sending

one.

Alternatively, a local router waits for receiving a

type 2 packet from each of its adjacent routers and

after echoing that packet to the sender, then it runs

the Update algorithm in order to check whether any

of the LSA announced are more up to date that the

ones already stored in its LSDB.

If this is the case, a type 3 packet will be sent

back in order to ask for the more recent instance of

that particular LSA. Then, it will wait for receiving a

type 4 packet with the updated LSA and it will in

turn send a type 5 packet, meaning acknowledge

receipt of that LSA.

On the contrary, if this is not the case, it means

that it is an acknowledge receipt of a type 2 packet

previously sent to that adjacent router. This situation

implies that the local router will not be sending

further packets in response to it.

Regarding the Update algorithm, it is shown in

Algorithm 3. It takes the incoming OSPF type 2

packet and it checks each LSA header inside it

against those of the local LSDB corresponding to the

each proper LSA.

Algorithm 3: Update(i).

In order to keep the algorithm simple, the LSA is

uniquely identified by its LS ID field and the most

recent instance is considered to be the one with the

higher sequence number. Regarding the outcome of

that algorithm, if it gives 1, it means that LSA must

be updated but if it gives 0, it must not. Furthermore,

if an LSA does not exist in LSDB, it must also be

updated, so the algorithm gives 1 as well.

In summary, the LSA exchange process may be

described this way using ACP syntax and semantics.

The diverse OSPF Packet Types are expressed

herein as PTtypenumber.

























































ijjiijij

ijji

ijijijjiji

PTrPTsPTrk

iUpdatePTs

PTrPTs

PTs

PTrkPTrPTsk

)5()4()3(

|1)(|)5(

)4()3(

)2(

)2()2()2(

,,,,

,,,,,

(22)

Regarding the use of timers, there are four timers

involved in OSPF operations, as exposed in Section

III. The hello timer and dead timer values depend on

the network type, expressed by the variable TT, and

they have already been stated in Table III. However,

the LSA refresh timer and the maxAge LSA are

considered invariant of network type and they may

be expressed as per their default values.

As stated before, ACP rules do not show a way

to deal with time, as ACP represents LTS.

Nonetheless, LTS might be turned into Timed

Transition Systems (TTS) by making explicit at

which time an action takes place and that extension

would allow the introduction of timers into the

OSPF model. Actually, there are some ACP

extensions including time, such as mCRL2.

We herein consider that there are four constants

expressing the maximum amounts of seconds before

an action gets triggered. Those four maximum

values for the timers might be expressed in seconds

in an algebraic way.

TTT

MAXhello







2010

(23)

)2010(4

TTT

MAXdead







(24)

1800



MAXrefreshLSA

(25)

3600

_max



MAXAgeLSA

(26)

Furthermore, the four timers may be decreased and

evaluated as the time goes by, this is, at every

second. This action will be modelled for every router

by a function called Time(i), where

is life time

in OSPF, shown as Algorithm 4.

Update(i,DBD){

For Each LSID in DBD

If (DBD.LSID == i.LSDB.LSA.LSID)

Then

If (DBD.seqNo > i.LSDB.LSA.seqNo)

Then

Return 1;

Else

Return 0;

EndIf

Else

Return 1;

EndIf

Done

}

DCNET 2018 - International Conference on Data Communication Networking

Algorithm 4: Time(i).

Therefore, the use of timers might be modelled

as four synchronous processes being constantly

evaluated by means of the proper conditional

operators, whereas the function Time(i) represents

the time passing by, expressed as one second at each

execution of that function.

It is worth noting that hello packets will be

expressed as OSPF type 1 packets, to be coherent

with the naming convention used in the LSA

exchange process previously stated for this detailed

model.

Furthermore, the Init(i) function represents the

connection of a router

to the OSPF domain, so

0

when a router has just joined. On the

contrary, the Kill(i) function represents the

disconnection of that router

, so





. Also,

ResetX(i) functions just assign the maximum value

to timers given by (23)-(26), where X represents the

initial letter of the proper timer in capital letters.







































iMaxAgeijij

irefreshjiji

ideadij

ihelloji

tisetMPTrk

tisetRPTsk

jKilltisetDPTr

tisetHPTs

iTimeR

|0|)(Re)4(

)(|0|)(Re)1(

|0|)(Re)1(

)(

,,,

(27)

In summary, the modelling of an OSPF router in this

detailed case scenario using ACP syntax and

semantics will take some asynchronous terms and

some other synchronous terms. The former terms do

not depend on time and they are expressed by

shown in (22) and the latter do depend on time and

they are expressed by

as shown in (27).



)(|0|)( iInittRRiR

isa



(28)

8 MODEL VERIFICATION

In order to perform a model verification, it is to be

taken into account that ACP is a process algebra,

that being part of the abstract algebras family.

Therefore, a commonly used technique for

verification on those kinds of algebra may well be

used herein, such as proof by contradiction.

This technique states an initial proposition and

then some reasoning takes place in order to verify if

that proposition proves right, or otherwise, if a

contradiction appears, that will mean that the initial

proposition must be wrong.

It has been previously said that OSPF might be

broken into three components, such as Neighbour

Discovery, Route Management and Path

Determination. Hence, all of them will be assessed,

and if all three prove right, the model will be then

verified, as it will behave as stated on the OSPF

protocol standards.

First, neighbour discovery is done thanks to the

hello packets exchange, thus bringing up neighbour

relationships. In case they were not successfully

exchanged, those relationships could not take place,

so the model would not work as expected. But this is

not the case, as the model allows communication

from a particular sender to a particular receiver of

packets carrying such hello messages (h).

Second, route management is achieved due to the

LSA exchange, thus bringing up adjacent

relationships. In case those were not properly

exchanged, those relationships could not happen, so

the model would not meet the specifications. But

that is not the case, as the model allows

communication from a sender to its authorised

receiver of packets carrying such data (d).

Eventually, path determination is undertaken by

the layer 3 devices, in a way that the best possible

route from a particular device to any destination is

calculated thanks to the Dijsktra algorithm, which

gets feed from the LSA exchange. As such exchange

has just been proved right, so must be shortest path

tree obtained from the Dijkstra algorithm.

Therefore, this OSPF model has been verified.

9 CONCLUSIONS

In this paper we have been working on achieving a

formal modelling of OSPF through algebraic

derivations using ACP syntax and semantics. Two

models have been presented, hence a basic one and a

detailed one, both meeting the requirements.

Time(i){

hello,i

= t

hello,i

– 1;

dead,i

= t

dead,i

– 1;

refreshLSA,i

= t

refreshLSA,i

– 1;

maxAgeLSA,i

= t

maxAgeLSA,i

-1;

= t

+ 1;

return 1;

}

OSPF Algebraic Formal Modelling using ACP - A Formal Description on OSPF Routing Protocol

On one hand, the basic model makes

assumptions about taking the LSA exchanging

process as a single action and also about not

considering any timing constraints.

On the other hand, the detailed model reverts

those assumptions, thus making it closer to real

OSPF.

REFERENCES

X200, 1994. Information technology - Open Systems

Interconnection - Basic Reference Model: The basic

model. ITU.

RFC 2328, 1998. OSPF version 2. IETF.

RFC 5340, 2008. OSPF for IPv6. IETF.

Turner, K. J., 1993. Using Formal Description

Techniques: An Introduction to Estelle, Lotos and

SDL. Ed. John Wiley and Sons Ltd.

Petri, C. A., 1966. Communication with Automata.

RADC-TR-65-377, Volume 1.

Bergstra, J. A., Klopp, J. W., 1985. Algebra of

communicating processes with abstraction.

Theoretical Comp. Science, Vol. 37, pp. 77-121.

Padua, D. A., 2011. Encyclopedia of Parallel Computing.

Ed. Springer, 1

edition.

Roig, P. J., Alcaraz, S., Gilly, K., Juiz C., 2018. Study on

OSPF Algebraic Formal Modelling using ACP.

Elektronika ir Elektrotechnika 2018 (accepted for

publication).

Dijkstra, E. W., 1959. A note on two problems in

connexion with graphs. Numerische Mathematik,

Volume 1, pp 269-271.

Fokkink, W., 2007, Introduction to Process Algebra. Ed.

Springer, 2

edition.

Lockefeer, L., Williams, D. M., Fokkink, W,. 2016.

Formal specification and verification of TCP extended

with the Window Scale Option. Science of Computer

Programming, Vol. 118, pages 3-23.

Bergstra, J. A., Klopp, J. W., 1984. Verification of an

Alternating Bit Protocol by Means of Process Algebra.

LNCS, Vol. 215, pp. 9-23.

Fokkink, W., 2016. Modelling Distributed Systems. Ed.

Springer, 2

edition.

Groote, J. F., Mousavi, M. R., 2014. Modelling and

Analysis of Communicating Systems. Ed. MIT Press,

edition.

DCNET 2018 - International Conference on Data Communication Networking