
Algebraic Formal Modelling for EIGRP using ACP
Formal Description Modelling on EIGRP Routing Protocol
Pedro Juan Roig
1,2
, Salvador Alcaraz
1
, Katja Gilly
1
and Carlos Juiz
2
1
Department of Physics and Computer Architecture, Miguel Hernández University, 03202 Elche (Alicante), Spain
2
Department of Computer Science, University of the Balearic Islands, 07122 Palma de Mallorca, Spain
Keywords: ACP, EIGRP, Formal Protocol Specification, Networking.
Abstract: Fast-converging routing protocols are necessary in order to keep up with the interconnected world we are
living in and one of the quickest ones is EIGRP. In this paper, we are going to design two models for
network devices running EIGRP by focusing on the main events happening on them. First, a non-timing
model is going to be formally described, hence just studying the aforesaid main events without any time
constraints. Then, a timing model is going to extend the former with the proper time values associated with
each particular event. Both models are going to be formally described by means of manual algebraic
derivations using Algebra of Communicating Processes (ACP).
1 INTRODUCTION
Routing protocols are ever important as they support
the increasing network communications taking place
anywhere, anytime and anyhow.
Regarding network communications, it is crucial
to distinguish between routing and switching, the
former being communications among devices
belonging to the different networks, whereas the
latter coming about devices on the same network.
This fact means that they happen in different
layers on the OSI reference model (X200, 1994),
this is, routing takes place at layer 3, whereas
switching does it at layer 2.
In order to route traffic, two routing strategies
may be followed by network devices. On the one
hand, static routing, where routes are manually
specified on those devices. On the other hand,
dynamic routing, where routing updates are
exchanged among those devices in an autonomous
manner, according to the network topology existing
at a given time.
Focusing on dynamic routing protocols, they
may be divided into two different categories
according to their scope of action. This is, if they are
intended to work inside a unique Autonomous
System, namely, a set of networks being managed
by a single routing administrative domain, or
otherwise.
In case they do, they are called Interior Gateway
Protocols (IGP), and otherwise, they are named
Exterior Gateway Protocols (EGP). This
classification is exhibited in Figure 1, stating the
main protocols contained in each category.
Figure 1: Dynamic Routing Protocol Classification.
With regard to IGP, those routing protocols may
be separated into distance vector and link state. The
difference between them is that the network devices
taking part of the latter hold a synchronised Data
Base of the whole topology, whilst those belonging
to the former do not. Therefore, the way each
routing protocol approaches its update procedure
will depend a great deal on that.
As per the link state routing protocols, OSPF and
ISIS run the Shortest Path First algorithm, also
known as Dijkstra algorithm, in order for each
network device to build up its Shortest Path Tree,
meaning the minimum metric from each one to any
Roig, P., Alcaraz, S., Gilly, K. and Juiz, C.
Algebraic Formal Modelling for EIGRP using ACP - Formal Description Modelling on EIGRP Routing Protocol.
DOI: 10.5220/0006838802590266
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 259-266
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
259

other network within the topology, being the metric
a value related to the link bandwidth.
As per the distance vector, EIGRP runs the
Diffusing Update algorithm (DUAL), whose metric
is a composite one related to the link characteristics,
defaulting to its bandwidth and its delay, whilst RIP
runs the Bellman Ford algorithm, whose metric is
the hop count.
In enterprise networks, OSPF is more widely
used than ISIS, whereas EIGRP overcomes RIP.
Therefore, a comparison on whether EIGRP is more
convenient than OSPF arises. But there is not an
easy answer, as it depends on many factors.
There is some literature stating that EIGRP
performs generally better (Krishnan and Shobha,
2013), whereas there is some other claiming quite
the opposite (Kaur and Kaur, 2016). Eventually, it
all comes down to the features assessed and the
network topology being implemented.
The main key point for every routing protocol is
convergence time, that being the time necessary for
each network device being part of a single routing
domain to gather routing information about therein.
As said before, much discussion has been around
in the literature about which IGP routing protocol
converges the fastest. Obviously, the shorter the
better, and that makes EIGRP unbeatable under
certain circumstances that will be pointed out in due
course.
Regarding literature about computer simulations,
EIGRP protocol has been implemented and assessed
on a few simulation tools, such as Packet Tracer
(Mardedi and Rosidi, 2015), GNS3 (Chadha and
Gupta, 2014), Opnet (Vesely et al., 2017), Omnet++
(Hanif et al., 2015), NS2 (Vetriselvan et al., 2014)
and Maude (Riesco and Verdejo, 2009). However,
there is not much literature regarding algebraic
formal description of networking protocols and here
is where this paper fits in.
The organization of this paper will be as follows:
first, Section 2 introduces EIGRP fundamentals,
then, Section 3 shows some Algebra of
Communicating Processes (ACP) basic concepts,
next, Section 4 presents the nomenclature for the
EIGRP models, afterwards, Section 5 gives a draft
with the steps to understand and implement those
models, right after that, Section 6 performs a formal
description model for non-timing EIGRP, later,
Section 7 extends the aforesaid formal description
model with time constraints and finally, Section 8
will draw the final conclusions.
2 EIGRP FUNDAMENTALS
First of all, it is to be noted that EIGRP stands for
Enhanced Interior Gateway Routing Protocol and it
was designed by Cisco as a proprietary routing
protocol (Cisco Systems, 2005).
As a consequence of that, EIGRP could only be
run on Cisco devices, which was a handicap when
trying to interconnect network devices from
different manufacturers. As a matter of fact, EIGRP
was restricted to be used only in purely Cisco
environments, this is, when all network devices
within a routing domain were made by Cisco, due to
its proprietary nature.
On the contrary, other routing protocols such as
OSPF and ISIS were taking advantage in
multiplatform environments thanks to its free nature,
meaning that they could be implemented by all
manufacturers, thus allowing the use of network
devices made by different vendors in the same
routing domain.
This very fact was the turning point when trying
to choose a routing protocol, as EIGRP might be
rejected in favour of OSPF or ISIS in spite of
providing a better performance for a given network
topology and features (Hinds et al., 2013).
Therefore, in order to cope with this issue, Cisco
decided to make a partial release of EIGRP,
including all information necessary to implement it
along with its associated features, so as to let its
employment by other vendors, and in fact allow its
use in multivendor environments (Cisco Systems,
2013).
That aforesaid release of the basic EIGRP
features to the IETF led to its publication as an open
standard (RFC 7868, 2016), but most of the
manufacturers have decided not to implement it.
EIGRP may be considered as an advanced
distance vector protocol, or also a hybrid one, as it
has some features included in its link states
counterparts. Its most outstanding features are:
Use of the DUAL algorithm to calculate paths,
back-up paths and provide fast convergence;
Exchange of hello packets in order to form
neighbour adjacencies, hence checking up
network stability on a regular basis;
Incremental and bounded updates, thus reducing
the usage of network resources;
Use of Reliable Transport Protocol to send and
receive EIGRP packets;
Support for both equal and unequal cost load
balancing;
Support for MD5 and SHA2 authentication;
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
260

EIGRP has 5 different packet types in order to
undertake all its tasks, as explained in Table 1.
Table 1: EIGRP packet types.
Type
Packet name
Function
1
Hello
Discovering and maintaining
neighbours.
Unreliable delivery.
2
Acknowledgement
Hello packet with no data,
used to confirm reliable
delivery of other packets.
3
Update
Delivering routing updates to
neighbours.
Reliable delivery.
4
Query
Requesting alternative path to
an unavailable route.
Reliable delivery.
5
Reply
Responding to Query packets
if it has a route.
Reliable delivery.
As regards the frequency of sending Hello
packets, they might be tuned up, but the default
values vary if the link is a high bandwidth, thus
being greater than a T1 bandwidth, or otherwise, a
low bandwidth, hence being smaller than that value.
As a rule of thumb, broadcast links such as
Ethernet and Point-to-Point serial links such as
HDLC, PPP and Frame Relay subinterfaces may fit
into the first class, whereas Point-to-MultiPoint
serial links, such as Frame Relay multipoint
interfaces may fit the second class.
The counterpart of Hello timers are Hold timers,
which default to 3 times the former, and their
function is to certify the expiration of the neighbour
relationship previously formed. The default values
for both timers are stated in Table 2.
Table 2: Hello and Hold Timers.
Network Types
Hello
Timer
Hold
Timer
Broadcast interfaces
Point-to-Point interfaces
Frame-Relay subinterfaces
5
seconds
15
seconds
Frame-Relay multipoint
interfaces
60
seconds
180
seconds
As per the EIGRP messages, they are carried
using protocol number 88 as the IP protocol field
within the IP header and also an EIGRP header
carrying the packet type and the Autonomous
System. Eventually, the payload is in TLV format,
standing for Type, Length and Value, bringing all
necessary information for EIGRP to work. Figure 2
shows the full encapsulation within a frame.
Figure 2: EIGRP encapsulation headers within a frame.
For an EIGRP routing table to be fully
operational, there are some previous steps to be met,
namely, some other tables may be fulfilled. First of
all, the interface table shows the interfaces taking
part in the EIGRP routing domain. Then, the
neighbour table shows the neighbour adjacencies
formed among EIGRP neighbours. After that, the
topology table shows the metric among the different
network prefixes taking part within EIGRP domain.
And eventually, the routing table show the best
routes to reach each of those network prefix. This
flow chart is exhibited in Figure 3.
Figure 3: Flow chart for EIGRP tables to be fulfilled.
According to all previous information, the
EIGRP initial convergence process is depicted in
Figure 4, since the moment a new network device
joins the EIGRP routing domain, all the way to the
initial route discovery process, up to the moment its
routing table is updated, so EIGRP convergence has
been reached.
Figure 4: Flow chart for initial EIGRP convergence.
In the process of building up the topology table,
it is worth noting that each link between neighbours
has a particular distance depending on the EIGRP
metric used, and the distance of a path between two
non-neighbouring devices implies the bandwidth of
the slowest link in kilobits and the sum of all delays
on the route to destination in tenths of microseconds.
As stated before, the EIGRP metric is a
composite one, but most of the time the default
values are used, so that expression gets simplified
and becomes the following:
Algebraic Formal Modelling for EIGRP using ACP - Formal Description Modelling on EIGRP Routing Protocol
261
10
__10
256
7
delayofsum
bandwidth
metric
(1)
DUAL algorithm manages the concepts of
Successor and Feasible Successor, the former being
the neighbouring device with the least cost route to a
destination network, hence the next-hop according to
the routing table, and the latter being another
neighbouring device having an alternative loop-free
backup path to that same destination network.
Also, DUAL algorithm deals with the concepts
of feasible distance (FD) and reported distance
(RD), the former being the metric of the successor to
a destination, thus the metric quoted in the routing
table entry, and the latter being a neighbour’s
feasible distance to that same destination.
Putting it all together, in order to assure that a
feasible successor is loop-free, a feasibility condition
(FC) is imposed, such that a neighbour’s RD is less
than the local device’s FD. In such a case, it may be
stated that the alternative path to a given destination
is loop-free.
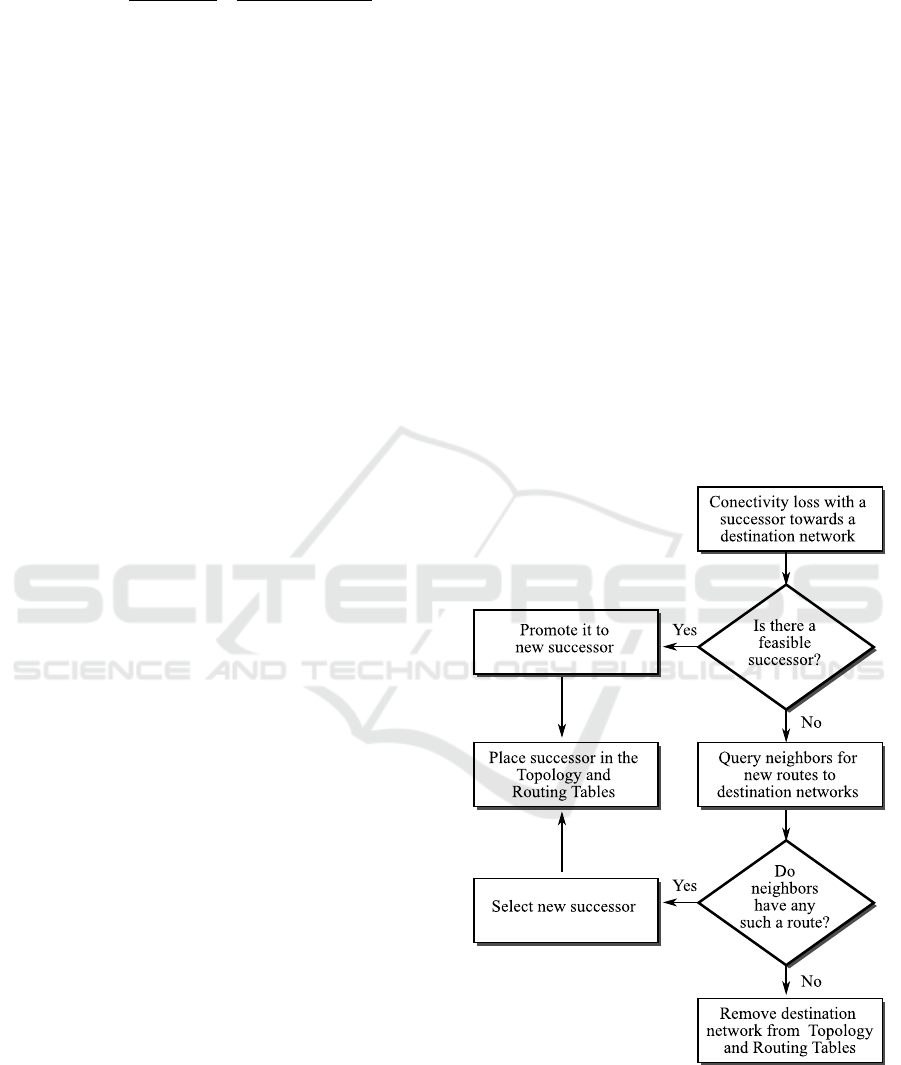
DUAL Finite State Machine (FSM) contains the
necessary logic for route calculation and
comparison, thus for making decisions on which
route is added up to the routing table. Therefore,
when a path to a successor going towards a
destination route goes down, two case scenarios may
happen:
There is a Feasible Successor: that will
immediately be promoted to successor for that
destination route and routing updates will be
sent to the rest of EIGRP devices;
There is no Feasible Successor: that will begin a
reconvergence process in order to obtain an
alternative path to that destination route;
Regarding reconvergence, DUAL puts that route in
Active state (Passive state means stable) and sends
EIGRP query packets to other devices for any path
to that route and waits for a reply.
If a neighbour has such a route, then it sends
back an EIGRP reply packet stating so, therefore the
local device’s routing table will be updated and in
turn routing updates will be sent out towards the rest
of neighbours to let them know.
Otherwise, if a neighbour does not have a route,
then it will send that query down to its own
neighbours, and it will wait for a reply from any of
them. If such a reply happens, then it will send back
that reply to the local device which started the query
and in turn will update its routing table and will send
out routing updates to its own neighbours.
However, it may happen that a neighbour
receives a query and it keeps waiting for a reply that
it does not arrive. In order to avoid waiting too long,
a timer is set for 180 seconds in the querying end,
and then, if there is no answer from the other end,
that device is put in a special state called Stuck in
Active (SIA) and the neighbour adjacency will be
killed.
Actually, a query timer is set for just half of that
time, namely 90 seconds, and when it expires,
another timer called SIA query timer is set for
another 90 seconds. This other timer is used to ask a
neighbour by means of SIA query packet if it has not
replied to the original query because it is still
waiting for a reply from any of its own neighbours.
If this is the case, that neighbour will send back a
SIA reply packet to the sender, meaning that the
neighbour is still up and running, although it is still
waiting. Otherwise, if it does not reply to the SIA
query packet, it must be because it has gone down.
All this reconvergence process is depicted in
Figure 5 as a flow chart.
Figure 5: Flow chart for EIGRP reconvergence.
Finally, retrieving the discussion about whether
EIGRP converges faster than other protocols, such
as OSPF or ISIS, the existence of a Feasible
Successor is key, as if this is the case, EIGRP wins
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
262

for sure as there are no recalculations for getting an
alternative path, but if this is not the case, then
EIGRP might be penalised by query and SIA query
waiting time, so other protocols might go swifter.
Anyway, EIGRP shows rapid convergence times
in case any change in the network topology comes
about, and those times are the fastest when there is a
feasible successor but may not be otherwise,
although those chances might be reduced by getting
a good network design, like applying stub routers or
summarizing routes, to avoid queries going deep.
3 ACP FUNDAMENTALS
ACP is going to be the formal description language
to model EIGRP, that being a sort of process algebra
allowing the description of concurrent
communication processes just focusing on such
processes and not on its real nature (Fokkink, 2007).
In fact, among process algebras, ACP is
considered the most abstract of all as processes are
treated as algebraic entities. Such notion of
abstraction permits that ACP is being included into
the abstract algebra family, along with the well-
known group theory, ring theory or field theory
(Padua, 2011).
This approach as an abstract algebra allows the
use of purely algebraic structures and reasoning to
deal with processes, which may be achieved by
obtaining some ACP process terms being
behaviourally equivalent as the process to be
modelled, which is known as bisimilarity or
bisimulation equivalence (Groote and Mousavi,
2014).
In order for two processes to be bisimilar, they
may not only execute the same string of actions but
they may also have the same branching structure
(Bergstra and Klop, 1985). If this is the case, two
bisimilar processes may be considered to behave in
an equivalent manner.
ACP contains a set of axioms in order to prove
that a couple of process terms have an equivalent
behaviour, and the aforesaid axioms may use the
syntax and semantics defined for ACP operators
(Lockefeer et al., 2016).
The most basic signature of a framework for
ACP contains atomic actions, like sending and
reading data, which might not be further divided
(Fokkink, 2016). Also, there is a bunch of operators
in order to reason about those atomic actions, the
main ones being shown in Table 3.
Table 3: ACP main operators.
ACP operator
meaning
symbol
Sequential operator
left process, and in
turn, the right
Alternate operator
left process or right
process
Summatory operator
a string of
alternatives
Concurrent operator
concurrent processes
||
Left merge Operator
left process, and in
turn, concurrent
_||
Communication
operator
Communication
between processes
|
Conditional operator
Condition c, being
True or False
FcT
Encapsulation operator
Turns send and read
into comm
H
Abstract operator
Hides internal details
of system
I
Sequential and alternate operators are the most
basic operators and work as the rules of its algebraic
counterparts, this is, product and addition.
Special attention may be dedicated to the
conversion of concurrent operators (||) into left
merge operator (||_) and communication merge
operator (|) by means of the Expansion Theorem,
presented by Bergstra and Klop (Bergstra and
Klopp, 1984), where
}{}..{
1 in
i
XXXX
and
},{}..{
1
,
jin
ji
XXXXX
:
ji
ji
i
in
XXXXXXX
,
1
_||)|(_||)||...||(
(2)
With respect to communication, it only takes
place if send and read actions have the same
direction, namely, the originating end and the
receiving end are the same for both actions,
otherwise, it results in deadlock (δ). That makes
communication unidirectional, coming from i to j.
jijiji
crs
,,,
|
(3)
yxji
rs
,,
|
(4)
In relation to the conditional operator, it allows
to make the decision of running different code if the
central condition is met or otherwise. This feature
may be used along with a sequence operator to
determine whether to run some code, if true, or not,
if false. This may be done as 1 is the neutral element
for multiplication, whilst 0 is its absorbing element.
Hence, if 1, the code is executed, and if 0, it is not.
Algebraic Formal Modelling for EIGRP using ACP - Formal Description Modelling on EIGRP Routing Protocol
263

FalseConditionTrue
(5)
...01 Condition
(6)
4 NOMENCLATURE FOR THE
EIGRP MODELS
First and foremost, it is to be defined the
nomenclature used to build up these models, which
is shown in Table 4.
Table 4: EIGRP modelling nomenclature.
ACP model
terms
meaning
)(xR
EIGRP model for device R
x
i
Local device running EIGRP
j
One particular neighbouring device
running EIGRP
k
Another particular neighbouring device
running EIGRP
m
All neighbouring devices running
EIGRP
m
j 1
...
Each neighbouring device running
EIGRP
}{
1
...
jm
k
Each neighbouring device running
EIGRP except a particular one
)(
,
xs
ji
Sending x packet from i to j
)(
,
xs
ij
Sending x packet from j to i
)(
,
xr
ji
Reading x packet in j, sent from i to j
)(
,
xr
ij
Reading x packet in i, sent from j to i
h
Hello packets
u
Update packets
ACK
Acknowledgement packets
i
D
Topology table of local device i, with
all Destination network prefixes
d
A single destination network prefix d
d
u
A single destination prefix inside an
Update packet
id
Du
states that network prefix d carried by
an Update packet is not inside the
topology table of i
i
Dd
states that network prefix d is included
inside the topology table of i
d
P
Destination network prefix d is set in
Passive state in the routing table,
meaning this is a stable route
j
n
All network prefixes having a particular
neighbour j as a next-hop to reach them
j
n
d 1
...
Each network prefix having a particular
neighbour j as a next-hop to reach them
)(
, kji
dFC
Feasible Condition met for local device
i going to prefix d using another route
through neighbour k instead of j
j
ñ
All network prefixes having a particular
neighbour j as a next-hop to reach them,
which do not meet Feasible Condition
j
ñ
d 1
...
Each network prefix having a particular
neighbour j as a next-hop to reach them,
which do not meet Feasible Condition
d
A
Destination network prefix d is set in
Active state in the routing table,
meaning the search for a new route
d
q
Query packets looking for a new route
for network prefix d
d
r
Reply packets providing a new route for
network prefix d
SIA
q
SIA Query packets
SIA
r
SIA Reply packets
kd
Dr
There is a reply packet coming from
neighbour k
i
Dd
states that network prefix d is excluded
out of the topology table of i
Next, it has to be defined the timing
nomenclature used to build up the extended model,
which is shown in Table 5.
Table 5: EIGRP timing nomenclature.
ACP model
terms
meaning
jihello
t
,_
Hello Timer for link going from i to j
ijhold
t
,_
Hold Timer for link coming from j to i
jiquery
t
,_
Query Timer for link going from i to j
jiSIA
t
,_
SIA Query Timer for link going from i to j
KT
hello
5
Maximum value for the Hello timer by
default (K=1 for all networks, except for
serial multipoint links, where K=12)
hellohold
TT 3
Maximum value for the Hold timer by
default (related to T
hello
value)
90
query
T
Maximum value for the Query timer by
default
90
SIA
T
Maximum value for the SIA timer by
default
Also, it is necessary to set up the initial values
for all timers used in the extended model to -1, so as
to get them initially disabled. This way, it is going to
be possible to establish the order in which each timer
applies. That is shown in Table 6.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
264

Table 6: Initial timing values.
ACP model
terms
meaning
1
,_
jihello
t
Hello Timer for link between i and j
1
,_
jihold
t
Hold Timer for link between i and j
1
,_
jiquery
t
Query Timer for link between i and j
1
,_
jiSIA
t
SIA Query Timer for link between i and j
5 EIGRP MODEL DRAFT
The first model to be implemented is going to be the
non-timing EIGRP, where all time constraints have
been dropped off. This way, only the different
actions established within the protocol specifications
will be taken into account in the model, each one
separated by a plus sign (+), no matter what time
they may happen. Then, the second model will
extend the previous one just by adding up the proper
time features.
The model applies for a particular network
device R(i) running EIGRP within an Autonomous
System. In order to get that design done, a draft is
presented to quote all EIGRP communication
packets flowing between a local device and its
EIGRP neighbours as a bullet point list with 8 items.
Initial exchange of Hello packets and Update
packets, both one way and another;
Exchange of Hello packets on a regular basis,
both one way and the other;
Exchange of Update packets on an occasional
manner, just when there are topology changes,
both one way or the other way around;
If a destination prefix is not available, check for
a feasible successor, or otherwise, start off the
query-reply process to search for a new
successor and, in case it is not possible, then
delete that destination;
In case the hold timer from a neighbour becomes
zero, then kill the neighbour adjacency with it
and search for new routes to all the destinations
being reached through it;
6 MODEL FOR NON-TIMING
EIGRP
m
j
n
d
dijiji
jijijiji
j
PDdACKsur
ACKsushrhs
iR
1
1
,,
,,,,
)()(
)()()()(
)(
)()(
)(
1
)(
)(
)()(
)()()()(
)()(
)()()()(
}{
1 1
,
}{
1
,
1
}{
1
,
,
}{
1
,,
1
,,
1
,
1
,
1
,,
1
,,,,
ij
jm
k
n
d
dkjid
jm
k
dkjid
m
j
id
jn
k
ki
ki
jn
d
di
ijij
m
j
jiji
m
j
ij
m
j
ji
m
j
ijij
n
d
di
ijijijij
DdLABELAdFCP
LABELAdFCP
Du
ACKr
us
PDd
ACKsur
ACKrushrhs
ACKrusPDd
ACKsurhshr
j
k
k
j
}{
1 1
,,
,,
,,
,,
,,
)()(
)()(
)()(
)()(
)()(
:
jm
k
ñ
d
ikd
dkidki
kiSIAki
kiSIAki
dkidki
kidki
j
DdDr
PACKsrr
ACKsrr
ACKrqs
PACKsrr
ACKrqs
LABEL
}{
1 1
}{
1
,,
,,
,,
,,
,,
,,
)()(
)()(
)()(
)(
)()(
)()(
jm
k
ñ
d
jm
u
ikSIAik
ikdik
dukduk
ukduk
ikdik
ikdik
j
PATCH
ACKsqr
ACKrrs
PACKsrr
ACKrqs
ACKrrs
ACKsqr
}{
1
,,
,,
,,
,,
,,
)()(
)()(
)()(
)()(
)()(
:
jm
u
iud
dukduk
ikSIAik
ukSIAuk
ukSIAuk
ikSIAik
DdDr
PACKsrr
ACKrrs
ACKsrr
ACKrqs
ACKrrs
PATCH
Algebraic Formal Modelling for EIGRP using ACP - Formal Description Modelling on EIGRP Routing Protocol
265

7 MODEL FOR TIMING EIGRP
The eight summing terms described above are
extended with their proper time constraints, each
term being given by (...) in the same order as listed
in the bullet point list given in the model EIGRP
draft, and besides, proper timing terms. Hence, R(i):
m
j
ijhelloijholdjihold
m
j
ijSIAijSIAjiSIA
jiSIA
m
j
ijqueryijquery
SIAjiSIAjiquery
jiquery
m
j
jihellojihellojihello
ijholdijhold
queryjiqueryholdijhold
ijhold
m
j
hellojihellojihello
m
j
hellojihello
holdijhold
ijhold
m
j
holdijhold
hellojihello
jihello
ttt
ttt
t
tt
Ttt
t
ttt
tt
TtTt
t
Ttt
Tt
Tt
t
Tt
Tt
t
1
,_,_,_
1
,_,_,_
,_
1
,_,_
,_,_
,_
1
,_,_,_
,_,_
,_,_
,_
1
,_,_
1
,_
,_
,_
1
,_
,_
,_
...1001
11...
001
1
)1(
...
001
101
1......
)(...)(
001
...)(001
...)(
)(
011
...)(
)(
011
8 CONCLUSIONS
In this paper, two formal description models for
EIGRP routing protocol, no-timed and timed, have
been presented using ACP syntax and semantics.
Both models meet the requirements set in the
EIGRP specifications, therefore, they are valid.
REFERENCES
X200, 1994. Information technology - Open Systems
Interconnection - Basic Reference Model: The basic
model. ITU.
Krishnan, Y. N., Shobha, G., 2013. Performance Analysis
of OSPF and EIGRP Routing Protocols for Greener
Internetworking. ICGHPC-2013.
Kaur, Y., Kaur M., 2016. A Survey of Various Routing
Protocols. IJARCSSE-2016, pp. 559-563.
Mardedi, L., Rosidi, A, 2015. Developing Computer
Network Based on EIGRP Performance Comparison
and OSPF. IJACSA-2015, Vol. 6, No. 9, pp. 80-86.
Chadha, A., Gupta, A., 2014. Attaining more Efficiency
from Enhanced Interior Gateway Routing Protocol.
IJCA-2013, No. 3, pp. 21-29.
Hanif, M., Talib, R., Ayub, N., Sarwar, M., Ullah, S.,
2017. OSPF vs EIGRP: A Comparative Analysis of
CPU Utilization using OPNET. IJACSA-2017, Vol. 8,
No. 7, pp. 468-471.
Vesely, V., Rek, V., Rysavy, O., 2015. Enhanced Interior
Gateway Routing Protocol with IPv4 and IPv6
Support for OMNeT++. SMMTA-AISC-2015, Vol.
402, pp. 65-82.
Vetriselvan, V., Patril, P., Mahendran, M., 2014. Survey
on the RIP, OSPF, EIGRP Routing Protocols. IJCSIT-
2014, Vol 5, pp. 1058-1065.
Riesco, A. and Verdejo, A., 2009. Implementing and
analyzing in Maude the Enhanced Interior Gateway
Routing Protocol. ENTCS-2009, Vol. 238, Issue 3, pp.
249-266.
Cisco Systems, 2005. Enhanced Interior Gateway Routing
Protocol. Document ID: 16406.
Hinds, A., Atojoko, A., Zhu, S. Y., 2013. Evaluation of
OSPF and EIGRP Routing Protocols for IPv6. IJFCC-
2013, Vol. 2, No. 4, pp. 287-291.
Cisco Systems, 2013. Enhanced Interior Gateway Routing
Protocol (EIGRP) Informational RFC Frequently
Asked Questions. Document ID: 1518931547541273.
RFC 7868, 2016. Cisco's Enhanced Interior Gateway
Routing Protocol (EIGRP). IETF.
Fokkink, W., 2007, Introduction to Process Algebra. Ed.
Springer, 2
nd
edition.
Padua, D. A., 2011. Encyclopedia of Parallel Computing.
Ed. Springer, 1
st
edition.
Groote, J. F., Mousavi, M. R., 2014. Modelling and
Analysis of Communicating Systems. Ed. MIT Press,
1
st
edition.
Bergstra, J. A., Klopp, J. W., 1985. Algebra of
communicating processes with abstraction.
Theoretical Comp. Science, Vol. 37, pp. 77-121.
Lockefeer, L., Williams, D. M., Fokkink, W,. 2016.
Formal specification and verification of TCP extended
with the Window Scale Option. Science of Computer
Programming, Vol. 118, pp. 3-23.
Fokkink, W., 2016. Modelling Distributed Systems. Ed.
Springer, 2
nd
edition.
Bergstra, J. A., Klopp, J. W., 1984. Verification of an
Alternating Bit Protocol by Means of Process Algebra.
LNCS, Vol. 215, pp. 9-23.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
266
