
Nonlinear Control Structure Design using Grammatical Evolution and
Lyapunov Equation based Optimization
Elias Reichensd
¨
orfer
1,2
, Dirk Odenthal
3
and Dirk Wollherr
4
1
BMW Group, Knorrstr. 147, 80788, Munich, Germany
2
Department of Electrical and Computer Engineering, Chair of Automatic Control Engineering,
Technical University of Munich, Theresienstr. 90, 80333, Munich, Germany
3
BMW M GmbH, Daimlerstr. 19, 85748 Garching near Munich, Germany
4
Department of Electrical and Computer Engineering, Chair of Automatic Control Engineering,
Technical University of Munich, Theresienstr. 90, 80333, Munich, Germany
Keywords:
Nonlinear Control Structure Design, Lyapunov Equation, Grammatical Evolution.
Abstract:
A new method for the automated synthesis of nonlinear control laws for nonlinear control systems using
grammatical evolution is presented. The controller structure, its parameterization and a quadratic Lyapunov
function are the result of a nonlinear, nonconvex optimization process. Evolutionary algorithms based on
grammatical evolution are used to find candidates for the control law. These are evaluated using a fitness
function incorporating eigenvalue specifications on the linearized closed loop system and bounds on the con-
trol input signals. The guaranteed domain of attraction subject to the closed loop performance and stability
specifications is maximized by evaluating the solution of the Lyapunov equation on the nonlinear system. The
method is tested on two different control systems that contain different types of nonlinearities. The results
show that the proposed approach is capable of outperforming state of the art methods by providing stronger
stability guarantees and/or better closed loop performance while making less restrictive assumptions.
1 INTRODUCTION
The Lyapunov method is one of the most power-
ful tools available to analyze stability properties of
nonlinear dynamical systems (Lyapunov, 1992). The
method provides a sufficient condition for stability
of a nonlinear system: the existence of a Lyapunov
function. Nevertheless, how to systematically find
suitable Lyapunov function candidates is still un-
solved. Although significant progress has already
been made—Sum-of-Square programming (Prajna
et al., 2002) partially solves the problem for polyno-
mial systems—however it is still open in the general
case. An extensive overview of Lyapunov function
synthesis is presented by (Giesl and Hafstein, 2015).
Even more challenging is to simultaneously find a
controller structure, its parameterization and a suit-
able Control Lyapunov function (CLF) to prove sta-
bility. In (Sontag, 1983), an explicit formula, also
known as “Sontag’s formula”, is presented to con-
struct a stabilizing controller for nonlinear input affine
systems assuming a predetermined CLF. While Son-
tag’s formula provides a direct way to compute a con-
troller for a nonlinear system, it still relies on the
choice of an appropriate CLF which indirectly deter-
mines the structure of the underlying controller.
For design and analysis of linear control systems
there exists a variety of methods like loop shaping or
pole placement (Zhou et al., 1996). Also, for a stable
linear system, a Lyapunov function can be computed
by solving the Lyapunov equation. This equation can
be solved efficiently by numerical methods (Bartels
and Stewart, 1972). To take advantage of the variety
of performance criteria from linear control theory, a
common approach is to linearize the nonlinear sys-
tem about an operating point. However, the domain
of attraction (DoA) of such a controller design might
be unacceptably small. Also, for some systems, non-
linear feedback might lead to better performance by
exploiting the nonlinear behavior of the system. Most
classical design approaches from control theory for
both linear and nonlinear controllers rely on several
structural assumptions.
Meta-heuristic search methods (MHSM), often in-
spired by nature, make very little assumptions on the
underlying solution structure (Glover and Kochen-
berger, 2006). One major branch of MHSM are evo-
lutionary algorithms (EA); a branch of EA are genetic
Reichensdörfer, E., Odenthal, D. and Wollherr, D.
Nonlinear Control Structure Design using Grammatical Evolution and Lyapunov Equation based Optimization.
DOI: 10.5220/0006839400550065
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 55-65
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
55

algorithms (GA) by (Holland, 1975). GA have been
extended to synthesize arbitrary programs by (Koza,
1992) with the method of genetic programming (GP).
A variation of GP is grammatical evolution (GE) by
(Ryan et al., 1998). Both GP and GE can not only
optimize parameters for a given structure, but are able
to optimize the mathematical structure itself. Due to
this generality, it is appealing to tackle the problem of
nonlinear control synthesis with these methods.
Meta-heuristic search methods have proven use-
ful in various practical control applications. In (Pre-
cup et al., 2015), input membership functions of
Takagi-Sugeno-Kang fuzzy models are tuned for an
anti-lock braking system using simulated annealing
and particle swarm optimization (PSO). The work
by (Saadat et al., 2017) applies different MHSM
for training echo state neural networks for time se-
ries prediction. In (Vrkalovic et al., 2017), differ-
ent MHSM are combined with linear matrix inequal-
ities for Takagi-Sugeno fuzzy controller design, ap-
plied to a cart pole. Identification of an optimal time
delay feedback for active vibration control using a
GA is shown in (Mirafzal et al., 2016), (Hosen et al.,
2015) use a GA and PSO to improve prediction capa-
bilities of neural networks for time series prediction.
Other applications include energy management of hy-
brid electric vehicles (Chen et al., 2014a), tuning of
proportional-integral-derivative (PID) controllers for
inductive power transfer systems (Chen et al., 2014b)
and heating systems (Singh et al., 2015). More appli-
cations can be found in (Haupt and Haupt, 1998) and
(Poli et al., 2008).
Evolutionary algorithms have already been used
for both structural controller design and Lyapunov
function synthesis. In (Shimooka and Fujimoto,
2000), GP is used to generate a controller for the
nonlinear inverted pendulum, while (Cupertino et al.,
2002) use structural chromosomes in their EA to gen-
erate controllers for a nonlinear DC drive with vari-
able load. In (Koza et al., 1999), the structure of a
controller for a linear three lag plant is synthesized
with GP, while in (Koza et al., 2000) the same control
system, extended by a time delay, is considered. Ro-
bust controllers have been evolved by GP for linear
interval plants (Chen and Lu, 2011) and for nonlinear
systems (Reichensd
¨
orfer et al., 2017) using GE. The
authors of (Gholaminezhad et al., 2014) use pareto
optimization to find the structure of a linear controller
with GP. All of these approaches focus on the synthe-
sis of control laws only. Stability is either investigated
using linear methods in a subsequent design step or by
heuristic arguments obtained with simulation. How-
ever, there also exists work on using EA for structural
optimization of Lyapunov functions.
In (Banks, 2002), GP is used to evolve Lyapunov
functions for nonlinear systems, while (Grosman and
Lewin, 2005) included a penalty term in their GP al-
gorithm to avoid overly complex solutions. Further,
(McGough et al., 2010) use GE for Lyapunov func-
tion synthesis. These methods focus on finding a Lya-
punov function for a system to prove stability, but
do not incorporate the search for control laws. In
(Tsuzuki et al., 2006), GP was used to find the struc-
ture of Control Lyapunov-Morse functions. However,
the controllers were constructed using Sontag’s for-
mula, not by using the EA directly. Finally, (Verdier
and Mazo Jr, 2017) used GP to construct a switching
rule based on CLF for a switched state feedback con-
troller. However, the modes of the controller were
limited to linear state feedback and actuator limits
were not taken into account. Also, simulations of the
switched state feedback controller showed high fre-
quency chattering, which is often undesirable in prac-
tice. In general, few research exists that has combined
CLF and EA so far.
In this paper, a new method is presented using GE
to synthesize the structure of control laws for a non-
linear system and generate the CLF by solving the
Lyapunov equation for the linearized system. The
generated Lyapunov function is then evaluated on the
nonlinear system as a performance measure. In the
current state of the art, there is no method available
to generate controller structures for nonlinear systems
using CLF and EA that includes constraints on both
the linearized dynamics and control effort. The main
contribution is the introduction of a novel fitness func-
tion that simultaneously aims to maximize the guar-
anteed domain of attraction while taking into account
constraints on the dynamics of the linearized closed
loop system, as well as limitations of actuators. The
motivation behind this is to identify controller struc-
tures that result in a predefined performance of the
system when it is close to its equilibrium. At the same
time, the domain of attraction is maximized in order
to make the controller robust with respect to inhomo-
geneous initial conditions and perturbations. The GE
algorithm chooses the structure of control laws such
that the requirements on the linearized closed loop
system are fulfilled and the domain of attraction of
the systems associated quadratic Lyapunov function
is maximized for the nonlinear system.
The remainder of this paper is organized as fol-
lows. In section 2, the concepts of Lyapunov stability
and GE are summarized. Section 3 introduces a novel
method for control structure design using GE. In sec-
tion 4, we evaluate the proposed method on two non-
linear control systems. Finally, in section 5, a conclu-
sion is drawn and an outlook for future work is given.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
56

2 BACKGROUND
2.1 Lyapunov Stability and CLF
We consider autonomous dynamical systems of the
form
˙x = f (x) (1)
with f : R
n
→ R
n
, f ∈ C
∞
and x ∈ X ⊆ R
n
, where x de-
notes the state vector of the system. We are interested
in the stability of equilibrium points of the system.
Definition 1. A state x
∗
is called an equilibrium if
f (x
∗
) = 0 ∀t.
Remark 1. We assume, without loss of generality,
that x
∗
= 0 since any non zero equilibrium can be
transformed into the origin by change of coordinates.
The stability of a given equilibrium is defined as
follows.
Definition 2. An equilibrium x
∗
of the system (1) is
called stable in the sense of Lyapunov if for every ε >
0 there exists some δ(ε,t
0
) such that
||x(t
0
)|| < δ ⇒ ||x(t)|| < ε, ∀t ≥ t
0
. (2)
Otherwise, the equilibrium is called unstable. If ad-
ditionally for ||x(t
0
)|| < δ ⇒ lim
t→∞
||x(t)|| = 0, the
equilibrium is called asymptotically stable.
First, the notion of positive and negative (semi)-
definiteness of a function is required.
Definition 3. Let X
0
⊆ R
n
be a connected set con-
taining the origin. A function V : R
n
→ R is called
positive definite on X
0
, if
V (0) = 0 (3)
V (x) > 0, x ∈ X
0
\ {0}, (4)
denoted by V (x) 0 and positive semi-definite if
inequality (4) is non-strict, denoted by V (x) 0.
A function V (x) is called negative (semi)-definite if
−V (x) is positive (semi)-definite, denoted by V (x) ≺ 0
and V (x) 0 respectively.
Stability of (1) can be determined using the direct
method of Lyapunov.
Definition 4. A function V : R
n
→ R is a Lyapunov
function for (1) if for x ∈ X
0
V (x) 0 (5)
˙
V (x) =
∂V
∂x
f (x) 0 (6)
and strict Lyapunov function if
˙
V (x) ≺ 0.
Existence of a (strict) Lyapunov function is suffi-
cient to proof (asymptotic) stability of an equilibrium.
If additionally X
0
= R
n
and lim
||x||→∞
V (x) → ∞, the
stability property holds true globally.
The domain of attraction is given by the next def-
inition.
Definition 5. Domain of attraction
D(x
∗
) = {x ∈ R
n
: lim
t→∞
ϕ(t,0, x) = x
∗
}, (7)
where ϕ(t,t
0
,x
0
) denotes the solution of (1) starting
at t
0
under the initial condition x
0
.
Now a dynamical system with static state feed-
back u(x) of the form
˙x = f (x, u(x)) (8)
is considered. Here u(x) ∈ R
m
is the control law to be
defined. The idea of CLF is now to choose u(x), such
that the Lyapunov conditions from definition 4 hold
true. Since this step is difficult in general, we want
to automatize it using GE. Before we proceed with
stating the optimization problem, an introduction to
the GE algorithm is given.
2.2 Grammatical Evolution
Common evolutionary algorithms simulate natural se-
lection mechanisms to evolve solutions. In this work,
the focus is set on genetic algorithms (Holland, 1975).
There, a fitness function determines the statistical sur-
vival probability of an individual within a population.
Individuals are then selected based on their fitness
and recombined by the crossover operator in order
to produce offspring. The mutation operator finally
adds additional diversity to the population by ran-
domly modifying solutions. The flowchart of a typ-
ical GA is illustrated in figure 1. GA are well known
for parameter tuning but have also been extended to
perform structure optimization (Koza, 1992), an ap-
proach called genetic programming.
Initialization
Fitness
Evaluation
Converged?
Selection
Crossover
Mutation
Finish
Yes
No
Figure 1: Flowchart of a genetic algorithm.
Grammatical evolution (Ryan et al., 1998), a vari-
ation of GP, is based on the idea to define a gram-
mar in Backus-Naur form (BNF) (Backus, 1959; Naur
et al., 1969) to parse an integer string into an exe-
cutable program. This works by interpreting a string
Nonlinear Control Structure Design using Grammatical Evolution and Lyapunov Equation based Optimization
57

of integer numbers as a programming language. The
GE algorithm compiles this language using a gram-
mar in BNF. The generated program, which in many
applications is just a mathematical formula, can then
be evaluated. The result of this evaluation is rated by
a user-defined metric, which serves as a fitness value
for the corresponding individual. A grammar in BNF
can be described by the following definition.
Definition 6. A context free grammar is the 4-tuple
G = (N ,Σ, P,S) where N is the finite set of non-
terminals, Σ the finite set of terminals with N ∩Σ =
/
0,
S ∈ N the start symbol. The vocabulary of G is V =
N ∪ Σ, which gives the finite set of production rules
as P ⊂ (V
∗
\ Σ
∗
) × V , each of the form N → V
∗
.
Here, ∗ denotes the Kleene star operator. Exam-
ple 1 shows, how this concept can be used to translate
an integer vector into a mathematical expression.
Example 1. We choose an example grammar G
like in definition 6 as N = {hei,hopi,hvi,hci},
Σ = {+, −,x, 1}, S = hei and P = {hei
r
1
→
hopi(hei,hei),hei
r
2
→ hvi,hei
r
3
→ hci,hopi
r
4
→ +,hopi
r
5
→
−,hvi
r
6
→ x,hci
r
7
→ 1}.
Consider an example individual, arbitrarily cho-
sen as i
GE
=
6 4 1 2 5 2
T
. Dispatching the
current rule r
k
is done using the modulo operator as
i
GE,k
mod p where i
GE,k
is called the k-th codon of i
GE
and p is the number of available rules from the cur-
rent non-terminal. This example starts with S = hei.
Since hei can be expanded by the three rules r
1
, r
2
,
r
3
, in the first step, p = 3. Modulo dispatch selects
the first rule since i
GE,1
mod p = 6 mod 3 = 0. The
translation process is then continued by unfolding all
nonterminals from left to right as shown in table 1.
Table 1: Parsing process on i
GE
using G.
i
GE,k
p i
GE,k
mod p Rule Expression
- - - S hei
6 3 0 r
1
hopi(hei, hei)
4 2 0 r
4
+(hei, hei)
1 3 1 r
2
+(hvi, hei)
2 1 0 r
6
+(x, hei)
5 3 2 r
3
+(x, hci)
2 1 0 r
7
+(x, 1)
This procedure shows that the example individ-
ual represents the expression x + 1. If the mapping
is not finished yet but ran out of codons, the wrapping
technique is used, starting from the beginning of i
GE
.
To avoid infinite loops, a maximum wrapping count
is defined. After exceeding this count, all recursive
rules are eliminated from P (in example 1 that would
be r
1
), such that the parsing is guaranteed to terminate
in a finite number of steps.
3 METHODS
3.1 Linear Performance Measures
For applicability and interpretability it is desirable to
define performance criteria from linear control theory
for the synthesized controllers. Therefore, we use Ja-
cobian linearization of the closed loop system about
the equilibrium x
∗
with δx = x − x
∗
. An approxima-
tion of the system dynamics by linearization is then
given by
δ ˙x =
h
∂ f
∂x
i
x=x
∗
δx = A
c
δx . (9)
The first step is therefore to insert the GE-
generated control law into (8) and perform the above
linearization. Afterwards, methods from linear con-
trol theory can be applied as performance measures.
In this work we use a common approach for pole
placement presented in (Ackermann et al., 2002),
where a suitable region Γ in the complex s-plane is
defined,
Γ
T
=
s = σ + jω : σ ≤ −
1
T
max
, (10)
Γ
ω
=
s = σ + jω :
p
σ
2
+ ω
2
≤ ω
max
, (11)
Γ
ζ
=
s = σ + jω : |ω| ≤
q
1 − ζ
2
min
ζ
min
|σ|
, (12)
Γ = Γ
T
∩ Γ
ω
∩ Γ
ζ
. (13)
Here, ζ
min
specifies the minimum damping of the
system, T
max
the maximum time constant and ω
max
the maximum frequency of the linearized system
from (9). The area spanned by this definition is a cir-
cular sector with “cropped top”, an example is shown
in figure 2.
−6
−4 −2 0
−2
0
2
s
C
α
Γ
Real axis [s
−1
]
Imaginary axis [s
−1
]
Figure 2: Example Γ-region (grey) for pole placement.
To assign a fitness value to a given controller, the
centroid of this region can be used. We propose the
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
58

following analytic formula for the centroid of the Γ-
region from figure 2.
Proposition 1. The centroid s
C
= σ
C
+ jω
C
of the
stability area Γ spanned in the complex s-plane by
equation (13) as a function of the design parameters
ζ
min
, T
max
and ω
max
with ζ
min
∈ (0,1], T
max
> 0 and
ω
max
> 1/T
max
is given by
ω
C
= 0, σ
C
=
M
1
+ M
2
A
1
+ A
2
, ∆ > 0 (14a)
M
1
/A
1
, ∆ ≤ 0 (14b)
where
∆ = ω
max
ζ
min
−
1
T
max
, (15)
A
1
=
1
4
ω
2
max
2α − sin(2α)
, (16)
M
1
= −
1
3
ω
3
max
sin
3
(α), (17)
A
2
=
q
1 − ζ
2
min
(ω
2
max
cos
2
(α)T
2
max
− 1)
2ζ
min
T
2
max
, (18)
M
2
=
−
q
1 − ζ
2
min
(ω
3
max
cos
3
(α)T
3
max
− 1)
3ζ
min
T
3
max
(19)
and
α =
arctan
q
1 − ζ
2
min
ζ
min
, ∆ > 0 (20a)
arccos
1
ω
max
T
max
, ∆ ≤ 0. (20b)
Proof. Because of the symmetry of the Γ-region, ω
C
has to be 0. It is sufficient to examine the curve above
the real axis. For the real part of the Γ-centroid, two
cases have to be considered.
Case 1. If ∆ ≤ 0, the Γ-region reduces to a circular
segment. Then σ
C
is given by M
1
/A
1
, the known stan-
dard formula for the centroid of a circular segment.
Case 2. If ∆ > 0, σ
C
can be derived by calculating the
centroids of the circular segment and the remaining
quadrilateral. The centroid and the upper half of the
area of the circular segment are known as
σ
C,1
= −
4ω
max
sin
3
(α)
3(2α − sin (2α))
, (21)
A
1
=
1
4
ω
2
max
(2α − sin (2α)). (22)
The area and momentum of the upper half of the
quadrilateral can be computed using integration
A
2
= −
q
1 − ζ
2
min
ζ
min
Z
−1/T
max
−ω
max
cos(α)
σdσ , (23)
M
2
= −
q
1 − ζ
2
min
ζ
min
Z
−1/T
max
−ω
max
cos(α)
σ
2
dσ , (24)
which then, with the relation σ
C,i
= M
i
/A
i
, yields
the above result for the composite centroid of the Γ-
region.
Now we can define a fitness measure for the GE
algorithm as follows.
Definition 7. Given the eigenvalues λ
i
from the sys-
tem matrix A
c
of a linearized system (9) and a Γ-
region defined by the triple (T
max
,ζ
min
,ω
max
) the first
part of the total fitness value is given by
φ
linear
= 1 +
1
n
n
∑
i=1
||λ
i
− s
C
||
2
2
, λ
i
/∈ Γ (25a)
0, λ
i
∈ Γ. (25b)
Remark 2. The value of φ
linear
describes the mean
deviation of the eigenvalues of A
c
not contained in Γ
from the geometrical mean (the centroid) of Γ. Note
that this only makes sense because Γ is convex and
connected. Otherwise the centroid is not guaranteed
to lie within the specified region.
Remark 3. In principle, different Γ-regions to the
proposed could be used. The advantage of this re-
gion however, is that it is widely used, compare (Ack-
ermann et al., 2002) or (Chilali and Gahinet, 1996),
can be parameterized by three meaningful values and
is both convex and connected, see remark 2.
Next, we want the controller not only to place the
poles of the linearized closed loop system (9) in the
Γ-region (13), but also to obtain a guaranteed domain
of attraction, which is as large as possible. We con-
tinue by stating this requirement as an optimization
problem and then propose a formulation compatible
to a GE algorithm, in order to make it computation-
ally tractable.
3.2 Domain of Attraction Estimation
To obtain an estimate for the stability region of the
synthesized controller, we use the fact that a subset of
the DoA (7), Ω
c
⊆ D(0) can be computed using
Ω
c
= {x ∈ R
n
: V (x) ≤ c}, (26)
with c ∈ R
+
, as long as V (x) fulfills the Lyapunov
conditions from definition 4 on Ω
c
. The task of find-
ing a controller that maximizes the domain of attrac-
tion and satisfies the constraints defined in section 3.1
Nonlinear Control Structure Design using Grammatical Evolution and Lyapunov Equation based Optimization
59

can then be stated as the constrained, bilevel opti-
mization problem
maximize
u ∈ U(G)
L(Ω
c
) (27a)
subject to Ω
c
= {x ∈ R
n
: V (x) ≤ c
}, (27b)
c
= minimize
x ∈ R
n
6=0
V (x)
subject to
˙
V (x) = 0,
(27c)
(27d)
λ
i
(A
c
) ∈ Γ ∀ i ∈ {1,. .. ,n} , (27e)
A
T
c
P + PA
c
+ Q = 0 , (27f)
P = P
T
0, (27g)
V (x) = x
T
Px , (27h)
|u
j
(x)| ≤ u
j,max
∀ j ∈ {1,. .. ,m} . (27i)
Here, L(Ω
c
) denotes the Lebesgue-measure of Ω
c
,
which can be interpreted as the maximum volume of
the estimated domain of attraction (26) for a given
u(x). Furthermore, U (G) is the function space of con-
trol laws u(x), that can be generated by a user-defined
grammar G, specified in definition 6. Following, u
max
is the actuator limit, λ
i
(A
c
) the i-th eigenvalue of A
c
(9) and Γ the region for pole placement (13). Equa-
tions (27c) and (27d) describe the standard optimiza-
tion problem of finding the largest level curve of V (x)
where
˙
V (x) 0, for example discussed in (Saleme
et al., 2011). In the proposed setup, this is only one
constraint of the outer optimization problem (27a),
(27b) of finding a suitable control law u(x). Con-
straint (27e) ensures that the poles of the linearized
system (9) are placed in the Γ-region (13), while (27i)
limits control effort.
In order to produce correct results, it is necessary
that V (x) 0, which can be difficult to test numer-
ically for arbitrary V (x). Therefore we use the so-
lution P of the Lyapunov equation, given Q 0, of
the linearized closed loop system (9) to construct a
symbolic representation of V (x) (27f), (27g), (27h).
In this work we choose Q as the identity matrix. Now
we perform a Monte Carlo sampling on V (x) and
˙
V (x)
within a region of interest of the state space X
c
⊂ R
n
.
The time derivative
˙
V (x) is calculated for the nonlin-
ear system symbolically by automatic differentiation.
The DoA is estimated using algorithm 1, which is a
modified version of the algorithm presented in (Na-
jafi et al., 2016): We store the samples V (x
i
) in a list
L (line 5), which is used to estimate the DoA (lines
8-11). This algorithm is used to solve the inner opti-
mization problem (27c), (27d).
The proportion k/N is then a normalized approx-
imation of the size of the domain of attraction on the
sample set by Monte Carlo integration and gives the
final fitness measure to be minimized by the GE algo-
Algorithm 1: Domain of attraction estimation.
1: procedure DOASIZE(V (x),
˙
V (x),X
c
,N)
2: Initialization: c ← ∞, k ← 0, L ←
/
0
3: for i ← 1 to N do
4: Pick random state x
i
∈ X
c
5: L ← (L,V (x
i
)) Store V (x
i
) in a list L
6: if V (x
i
) < c and
˙
V (x
i
) ≥ 0 then
7: c ← V (x
i
)
8: for i ← 1 to N do Estimate the DoA size
9: if L
i
< c then L
i
is the i-th element of L
10: k ← k + 1
11: return k/N
rithm, which includes (27a)-(27h),
φ =
φ
linear
, φ
linear
> 1 (28a)
1 − k/N , φ
linear
= 1 . (28b)
Additionally, we apply a smooth, symmetric satura-
tion with |u
j
(x)| ≤ u
j,max
(x) as shown in (Graichen
et al., 2010) to account for (27i). The function
u
j,sat
= u
j,max
−
2u
j,max
1 + exp(2u
j
/u
j,max
)
(29)
approximates a “hard” saturation, keeping u
sat
and
therefore the CLF differentiable.
Remark 4. While most methods cited in section 1 for
evaluating the quality of a Lyapunov function within
an EA framework for Lyapunov function synthesis use
some kind of sampling, most only count the propor-
tion of the samples that satisfy conditions in defnition
4. However, this measure is not very robust like the
example V (x
1
,x
2
) = x
2
1
demonstrates. Since with ran-
dom samples, it is practically impossible to hit a value
on the zero line x
2
= 0, the algorithm will not detect
positive semi-definiteness of V (x
1
,x
2
). This however
is crucial for stability analysis since V (x
1
,x
2
) 0 im-
plies that no conclusion about stability can be drawn.
Remark 5. Explicitly sampling on the axis x
2
= 0 us-
ing grid based techniques does not address the prob-
lem either as the example V (x
1
,x
2
) = (sin(β)x
1
+
cos(β)x
2
)
2
with some β ∈ (−π/2,π/2) \ {0} shows.
We therefore expect a more robust measure using the
proposed method, since V (x), generated as a solution
to (27f), is automatically positive definite. If (27f) is
not solvable for some generated controller, it is as-
signed the worst possible fitness, φ = ∞.
In the following section, we use a GE algorithm
to solve the optimization problem (27a)-(27i) for two
nonlinear benchmark systems in order to show the ef-
ficiency of the proposed method.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
60
4 EXPERIMENTS
4.1 Metrics and Setup
Table 2 shows the parameters of the GE algorithm.
Table 2: Grammatical evolution setup.
Parameter Value
Population size 100
Number of generations 5000
Mutation rate 0.05
Initial genome length ∼ U{10,20}
Initial genome values ∼ U{0,20}
Max. wrapping count 5
Max. tree depth 15
Selection Rank selection
Crossover Cut and splice
Mutation Uniform multi-point
Elitism rate 0.1
Selection pressure 1.5
Monte Carlo sample size 5000
The grammar G = (N ,Σ,P , S) used for the opti-
mization was chosen as
S = hei, (30)
N = {hei,hopi,hf i,hvi,hci}, (31)
Σ = {+,−, ×,/, sin,cos, arctan,x
1
,..., x
n
,C} , (32)
with the following mapping, denoted in BNF syntax,
by the production rules P ,
hei ::= hopi(hei, hei) | hf i(hei) | hvi | hci (33a)
hopi ::= + | − | × | / (33b)
hf i ::= sin | cos | arctan (33c)
hvi ::= x
1
| ... | x
n
(33d)
hci ::= C . (33e)
Here, C represents 10000 randomly generated con-
stants, drawn from a continuous uniform distribution
∼ U(−10,10). This provides a variety of different
constants for the GE algorithm, such that parameters
of the control law can be fine-tuned.
4.2 Nonlinear Oscillator Example
We validate the proposed method on two different test
systems. The first example is adopted from (Doyle
et al., 1996), describing a two dimensional oscillator
with highly nonlinear dynamics,
˙x
1
= x
2
(34)
˙x
2
= exp(x
2
)
cos(x
1
)sin(x
1
) − 2x
1
+ u
, (35)
with x
1
∈ [−4,4], x
2
∈ [−4,4]. Additionally we intro-
duce the constraint that u ∈ [−5,5]. The parameters
for the Γ-region were defined as T
max
= 1 s, ζ
min
= 0.7
and ω
max
= 5 s
−1
. After several iterations, the GE
algorithm produces the following control law of non
obvious structure
u
GE
= −3x
3
2
+ 2x
1
x
2
2
+ (x
1
− 2)x
2
, (36)
with the associated Lyapunov function
V (x) = 1.5x
2
1
+ 0.5x
2
2
+ x
1
x
2
. (37)
The eigenvalues of the closed loop system are both lo-
cated at (−1,0), satisfying the specified requirements
on the linearization of the system. We now use Jaco-
bian linearization (JL) of the uncontrolled, saturated
system and pole placement to generate a linear con-
troller with the same eigenvalues, given by
u
JL
= −2x
2
. (38)
Notice that both controllers (36) and (38) have the
same linearized closed loop eigenvalues and therefore
the same quadratic Lyapunov function (37) according
to equation (27f). While their performance is there-
fore locally equivalent, it differs when getting farther
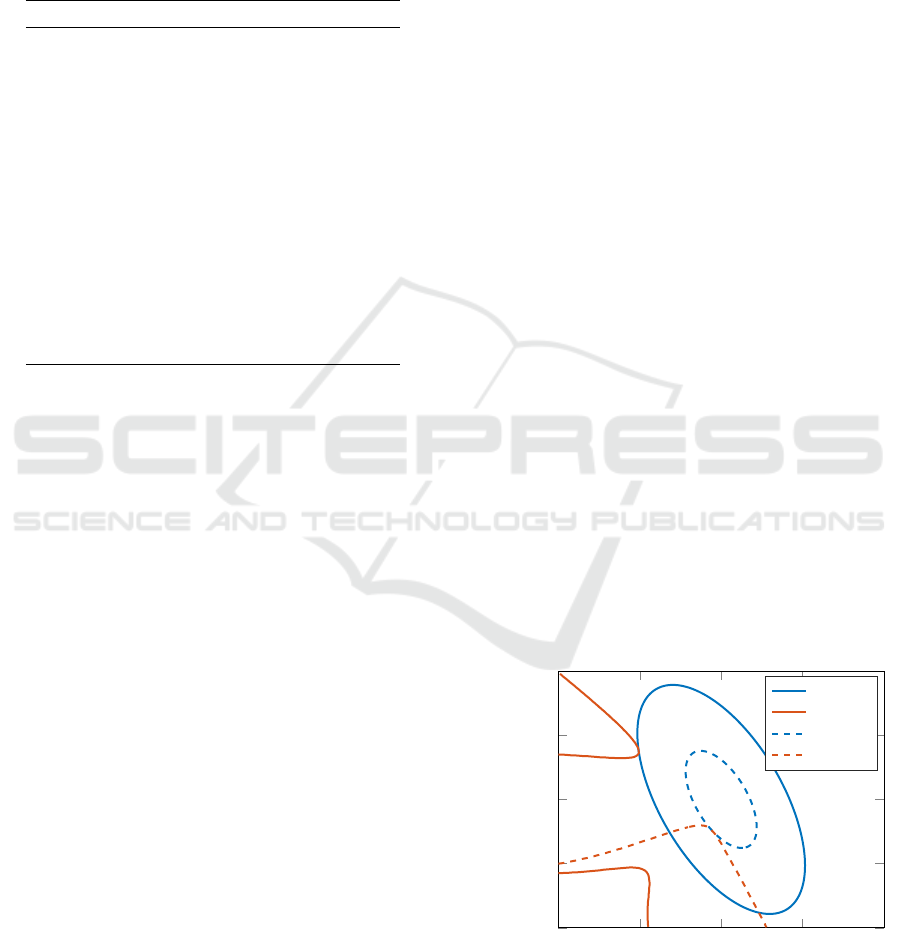
from the equilibrium. Figure 3 shows the estimated
domain of attraction for the GE controller (solid, blue)
and the linear controller (dashed, blue). The orange
lines indicate the level sets, where
˙
V (x) = 0 for the
GE controller (solid, orange) and the linear controller
(dashed, orange). The GE controller shows a guaran-
teed DoA larger by a factor of 4.57 compared to the
linear controller. This estimate was computed using
algorithm 1 with a sample size of N = 10
6
. Notice,
that for the optimization itself, a significantly smaller
sample size, namely N = 5000, as given in table 2,
was sufficient to achieve this result.
−2 −1 0 1 2
−2
−1
0
1
2
x
1
x
2
GE DoA
GE
˙
V = 0
JL DoA
JL
˙
V = 0
Figure 3: Comparison of domains of attraction.
One single optimization run on this example took
approximately 30 seconds on a 2.8 GHz CPU, with
Nonlinear Control Structure Design using Grammatical Evolution and Lyapunov Equation based Optimization
61

the algorithm implemented in C++, using the options
from table 2. Out of 100 different, randomly initial-
ized optimization runs, each run produced a controller
that satisfied the linear requirements. Also, the associ-
ated Lyapunov function guaranteed stability in an area
of the state space approximately of the size shown in
figure 3 within ±5% deviation.
4.3 Anti-lock Braking Example
Additionally, we test the proposed method on a non-
linear anti-lock braking system (ABS) with longitu-
dinal vehicle dynamics using a quarter car model.
This model serves as another benchmark problem to
demonstrate the method. The system equations are
J
˙
ω = −rF
x
− T
b
sign(ω) (39)
m ˙v = F
x
− F
a
. (40)
For details see for example (Petersen et al., 2001).
Here, ω is the angular velocity of the wheel, v the
longitudinal velocity of the vehicle and T
b
the brake
torque. Further, F
x
is the tire friction force, which
can be computed by the Pacejka tire model (Pacejka,
2005) as shown in (41) and F
a
the aerodynamic drag
force (42), given by
F
x
(λ,µ) = µ mg sin
C
p
arctan
B
p
λ
µ
, (41)
F
a
(v) =
1
2
c
w
ρA
s
v|v|, (42)
with λ, the longitudinal wheel slip defined as
λ =
ωr − v
max(|ω|r,|v|)
. (43)
The friction coefficient between tire and road is µ ∈
(0,1]. The other parameters are listed in table 3.
Table 3: Vehicle model parameters.
Name Description Value Unit
m Quarter car mass 450 kg
J Wheel moment of inertia 3 kgm
2
r Wheel radius 0.33 m
ρ Air density 1.1 kgm
−3
A
s
Vehicle front surface 2.4 m
2
c
w
Aerodynamic drag coef. 0.3 −
g Gravitational constant 9.81 ms
−2
B
p
Tire model slope coef. 10 −
C
p
Tire model shape coef. 1.3 −
T
act
Actuator time constant 0.025 s
Since the dynamics of the vehicle velocity evolve
significantly slower than the angular wheel velocity,
it is common to assume ˙v ≈ 0. For the braking case,
the slip dynamics can be derived, compare (Petersen
et al., 2001). The state vector includes the tire slip
error x
1
= λ − λ
set
, its integral x
2
=
R
t
0
λ − λ
set
dτ and
actuator dynamics x
3
as x =
x
1
x
2
x
3
T
. The state
equations of the augmented error dynamics including
actuator dynamics are given as
˙x
1
= −
r
Jv
rF
x
− u
max
(x
3
+ u
∗
)
−
F
x
mv
1 − λ
, (44)
˙x
2
= x
1
, (45)
˙x
3
=
1
T
act
u − x
3
, (46)
with λ = λ
set
+x
1
,
˙
λ
set
= 0 and u
∗
required for shifting
the equilibrium of the system to the origin given as
u
∗
= F
x
(λ
set
,µ)
mr
2
− J (λ
set
− 1)
u
max
r m
. (47)
The limit for the input is |u| ≤ 3000Nm = u
max
. The
region in the state space is defined as x
1
∈ [−1,1],
x
2
∈ [−0.2,0.2], x
3
∈ [−1,1], the parameters for the Γ-
region as T
max
= 0.1s, ζ
min
= 0.4 and ω
max
= 30 s
−1
.
For the optimization we set
˙
λ
set
= 0,λ
set
= 0.5,µ =
0.2 and v = 50 km/h. After several iterations, the GE
algorithm produces the following control law of non
obvious structure
u
GE
= −x
1
− 10.158x
2
+ x
2
arctan(ψ
1
), (48)
ψ
1
= x
1
− x
2
+ ψ
2
ψ
3
, (49)
ψ
2
= arctan(x
2
1
+ 11.16x
2
), (50)
ψ
3
= ψ
2
+ 11.16x
2
(x
2
− 11.16). (51)
The Lyapunov function associated to system (46) with
controller (48) saturated by (29) is derived to
V (x) = x
T
Px = x
T
0.0869 0.4663 0.0247
0.4663 9.9604 0.0012
0.0247 0.0012 0.0271
x .
(52)
The eigenvalues of the closed loop system are located
at (−11.13,±20.68) and (−17.51,0), matching the
specified requirements. We now use Jacobian lin-
earization of (48) to generate a linear PI controller,
u
PI
= −x
1
− 10.158x
2
. (53)
Notice that as in the previous example, both con-
trollers (48) and (53) have the same linearized closed
loop eigenvalues and therefore the same quadratic
Lyapunov function. Figure 4 shows the DoA esti-
mates of the two methods on system (46).
The GE controller shows a DoA that is approxi-
mately 3.55 times larger than that of the PI controller.
This estimate was obtained using algorithm 1 with
a sample size of N = 10
6
. The nonlinearity in the
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
62

−1
0
1
−0.1
0
0.1
−2
0
2
x
1
x
2
x
3
GE DoA GE
˙
V ≥ 0 PI DoA PI
˙
V ≥ 0
Figure 4: Comparison of domains of attraction.
control law (48) seems to be beneficial for increas-
ing the guaranteed DoA in this case. Additionally,
we evaluate the nonlinear controller on the original
system (40). For the simulation, the controller (48)
is discretized with a sample time of 10 ms and acts
as a limiter for the brake force commanded by the
driver. The integrator state x
2
is fed back with anti-
windup. Furthermore, we add Gaussian white noise
with a signal-to-noise ratio of 50 dB to both ω and v
in order to simulate measurement noise. Communi-
cation delay is modeled with a time delay of 10 ms
for both the actuator and the sensors. The simulation
starts at v = 130 km/h and λ = 0 on dry asphalt with
µ = 1. The driver starts braking at t = 0 with 40%
braking force. At t = 1 s, the friction coefficient of
the road drops to µ = 0.2 (snow). Therefore, the set-
point is changed to λ
set
= −3%. The controller gets
activated at t = 1.02 s, 20 ms after the event at t = 1 s.
Figure 5 shows the wheel slip λ as well as λ
set
, v, ω
and the control signal T
b
. The controller (48) iden-
tified by the GE algorithm successfully stabilizes the
nonlinear wheel dynamics. The wheel slip reaches
a peak value of ≈ 40%. The controller prevents the
wheels from decelerating further and therefore pre-
vents locking of the wheels.
One optimization run took again approximately
30 seconds on average. Figure 6 shows an example
error evolution of the best individual during one op-
timization run. It can be seen there that the linear
requirements are fulfilled at generation 281, where
φ ≤ 1 according to (28a) and (28b). At this point,
the constraints (27e)-(27i) are satisfied, as the poles
of the linearized closed loop system are located in the
specified Γ-region. Therefore, the Lyapunov equa-
tion (27f)-(27g) is guaranteed to have a unique so-
lution and a positive definite V (x) can be generated.
From thereon, the size of the guaranteed domain of at-
traction is increased over the subsequent generations.
0 1 2 3 4
5
−40
−20
0
Wheel slip [%]
λ
set
λ
0 1 2 3 4
5
0
50
100
150
Velocity [km/h]
v
ωr
0 1 2 3 4
5
0
500
1,000
1,500
Time [s]
T
b
[Nm]
Figure 5: Simulation of the tire slip controller (48).
0 1,000 2,000 3,000 4,000
5,000
10
−1
10
0
10
1
10
2
Generation
Fitness φ
φ = 1
Best φ
Figure 6: Example error evolution during the optimization.
Again, we evaluated the method for 100 different,
randomly initialized optimization runs, using the pa-
rameters from table 2 for the GE algorithm. As for
the nonlinear oscillator benchmark system from sec-
tion 4.2, each run produced a controller that placed the
poles of the linearized closed loop system in the de-
sired Γ-region. This was despite the fact that all runs
started with all, or at least some of the poles being
located outside of the Γ-region. The distance of the
poles to the centroid of the Γ-region was successfully
used as a performance measure for pole placement.
The average fitness achieved over all 100 optimiza-
tion runs was 0.4419 with a variance of 0.0662.
Nonlinear Control Structure Design using Grammatical Evolution and Lyapunov Equation based Optimization
63

5 CONCLUSION
A new method for controller synthesis based on gram-
matical evolution has been proposed. We derived an
explicit formula for the centroid of the considered sta-
bility region used for pole placement and integrated it
into a GE optimization algorithm. Additionally, the
GE algorithm was extended to maximize the guaran-
teed domain of attraction by using Monte Carlo inte-
gration in order to solve a bilevel optimization prob-
lem. On the considered nonlinear oscillator system
and the ABS control system, the method showed con-
vincing performance for maximizing the guaranteed
domain of attraction while satisfying the specified
constraints. For the ABS system, the generated con-
troller was validated by simulation. One limitation of
the presented approach is that it is computationally
expensive such that it cannot be applied as an online
optimization method.
Future work can extend the proposed approach in
different directions. One possibility is to include fur-
ther linear performance measures into the optimiza-
tion process. For example, the parameter space ap-
proach (Ackermann et al., 2002) provides measures
to ensure robustness of the controller with respect to
uncertain parameters for the linearized system. Also,
different Γ-regions than the proposed one might be
used for the optimization. Further, it would be in-
teresting to evaluate more algorithms for estimating
the domain of attraction, for example using a sam-
pling algorithm with memory as proposed in (Najafi
et al., 2016). Also, the MIMO (multi-input, multi-
output) case could be investigated. Finally, one could
remove the assumption of a quadratic Lyapunov func-
tion and let the GE algorithm search for the structure
of both the Lyapunov function and the control laws at
the same time. However, as mentioned in remarks
4 and 5, ensuring positive definiteness in this gen-
eral setup might be challenging. Future work could
therefore focus on creating algorithms that can reli-
ably detect positive semi-definiteness of general, non-
quadratic Lyapunov functions.
The presented approach is applicable for nonlinear
control synthesis for a large range of nonlinear sys-
tems with different types of nonlinearities. Input con-
straints and performance specifications adopted from
linear control theory can be incorporated into the con-
trol design process. In general, the system order is not
restricted. The method presents a nonlinear control
structure design tool which is applicable to a variety
of practical applications. Results suggest that reason-
able stability guarantees are achieved with the combi-
nation of structural control law optimization and do-
main of attraction maximization.
REFERENCES
Ackermann, J., Blue, P., B
¨
unte, T., G
¨
uvenc, L., Kaes-
bauer, D., Kordt, M., Muhler, M., and Odenthal, D.
(2002). Robust control: the parameter space ap-
proach. Springer Science & Business Media.
Backus, J. W. (1959). The syntax and semantics of the pro-
posed international algebraic language of the Zurich
ACM-GAMM conference. Proceedings of the Inter-
national Conference on Information Processing.
Banks, C. (2002). Searching for Lyapunov func-
tions using genetic programming. Virginia Poly-
tech Institute and State University, Blacksburg,
Virginia. Available online (last visit 24/05/2018):
http://www.aerojockey.com/files/lyapunovgp.pdf.
Bartels, R. H. and Stewart, G. (1972). Solution of the matrix
equation AX +XB = C: Algorithm 432. Communica-
tions of the ACM, 15(9):820–826.
Chen, P. and Lu, Y.-Z. (2011). Automatic design of ro-
bust optimal controller for interval plants using ge-
netic programming and Kharitonov theorem. Interna-
tional Journal of Computational Intelligence Systems,
4(5):826–836.
Chen, Z., Mi, C. C., Xiong, R., Xu, J., and You, C.
(2014a). Energy management of a power-split plug-in
hybrid electric vehicle based on genetic algorithm and
quadratic programming. Journal of Power Sources,
248:416–426.
Chen, Z., Yuan, X., Ji, B., Wang, P., and Tian, H. (2014b).
Design of a fractional order PID controller for hy-
draulic turbine regulating system using chaotic non-
dominated sorting genetic algorithm II. Energy Con-
version and Management, 84:390–404.
Chilali, M. and Gahinet, P. (1996). H
∞
design with pole
placement constraints: an LMI approach. IEEE Trans-
actions on automatic control, 41(3):358–367.
Cupertino, F., Naso, D., Salvatore, L., and Turchiano, B.
(2002). Design of cascaded controllers for DC drives
using evolutionary algorithms. In Evolutionary Com-
putation, 2002. CEC’02. Proceedings of the 2002
Congress on, volume 2, pages 1255–1260. IEEE.
Doyle, J., Primbs, J. A., Shapiro, B., and Nevistic, V.
(1996). Nonlinear games: examples and counterex-
amples. In Decision and Control, 1996., Proceed-
ings of the 35th IEEE Conference on, volume 4, pages
3915–3920. IEEE.
Gholaminezhad, I., Jamali, A., and Assimi, H. (2014). Au-
tomated synthesis of optimal controller using multi-
objective genetic programming for two-mass-spring
system. In Robotics and Mechatronics (ICRoM), 2014
Second RSI/ISM International Conference on, pages
041–046. IEEE.
Giesl, P. and Hafstein, S. (2015). Review on computational
methods for Lyapunov functions. Discrete and Con-
tinuous Dynamical Systems, Series B, 20(8):2291–
2337.
Glover, F. W. and Kochenberger, G. A. (2006). Handbook of
metaheuristics, volume 57. Springer Science & Busi-
ness Media.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
64

Graichen, K., Kugi, A., Petit, N., and Chaplais, F. (2010).
Handling constraints in optimal control with satura-
tion functions and system extension. Systems & Con-
trol Letters, 59(11):671–679.
Grosman, B. and Lewin, D. R. (2005). Automatic gener-
ation of Lyapunov functions using genetic program-
ming. IFAC Proceedings Volumes, 38(1):75–80.
Haupt, R. L. and Haupt, S. E. (1998). Practical genetic
algorithms, volume 2. New York: Wiley.
Holland, J. H. (1975). Adaptation in natural and artificial
systems: an introductory analysis with applications to
biology, control, and artificial intelligence. University
of Michigan Press.
Hosen, M. A., Khosravi, A., Nahavandi, S., and Creighton,
D. (2015). Improving the quality of prediction inter-
vals through optimal aggregation. IEEE Transactions
on Industrial Electronics, 62(7):4420–4429.
Koza, J. R. (1992). Genetic programming: on the program-
ming of computers by means of natural selection, vol-
ume 1. MIT press.
Koza, J. R., Keane, M. A., Yu, J., Bennett, F. H., Myd-
lowec, W., and Stiffelman, O. (1999). Automatic syn-
thesis of both the topology and parameters for a robust
controller for a nonminimal phase plant and a three-
lag plant by means of genetic programming. In Deci-
sion and Control, 1999. Proceedings of the 38th IEEE
Conference on, volume 5, pages 5292–5300. IEEE.
Koza, J. R., Keane, M. A., Yu, J., Mydlowec, W., and Ben-
nett, F. H. (2000). Automatic synthesis of both the
topology and parameters for a controller for a three-
lag plant with a five-second delay using genetic pro-
gramming. In Workshops on Real-World Applica-
tions of Evolutionary Computation, pages 168–177.
Springer.
Lyapunov, A. M. (1992). The general problem of the sta-
bility of motion. International Journal of Control,
55(3):531–534.
McGough, J. S., Christianson, A. W., and Hoover, R. C.
(2010). Symbolic computation of Lyapunov functions
using evolutionary algorithms. In Proceedings of the
12th IASTED International Conference, volume 15,
pages 508–515.
Mirafzal, S. H., Khorasani, A. M., and Ghasemi, A. H.
(2016). Optimizing time delay feedback for active
vibration control of a cantilever beam using a ge-
netic algorithm. Journal of Vibration and Control,
22(19):4047–4061.
Najafi, E., Babu
ˇ
ska, R., and Lopes, G. A. (2016). A fast
sampling method for estimating the domain of attrac-
tion. Nonlinear Dynamics, 86(2):823–834.
Naur, P., Backus, J. W., Bauer, F. L., Green, J., Katz, C.,
McCarthy, J., and Perlis, A. J. (1969). Revised report
on the algorithmic language Algol 60. Springer.
Pacejka, H. (2005). Tyre and vehicle dynamics. Butter-
worth-Heinemann, Oxford, 2 edition.
Petersen, I., Johansen, T. A., Kalkkuhl, J., and L
¨
udemann,
J. (2001). Wheel slip control in ABS brakes using
gain scheduled constrained LQR. In European Con-
trol Conference (ECC), pages 606–611. IEEE.
Poli, R., Langdon, W. B., and McPhee, N. F. (2008). A
field guide to genetic programming. Published via
http://lulu.com and freely available online (last visit
24/05/2018) http://www.gp-field-guide.org.uk. (With
contributions by J. R. Koza).
Prajna, S., Papachristodoulou, A., and Parrilo, P. A. (2002).
Introducing SOSTOOLS: A general purpose sum of
squares programming solver. In Decision and Control,
2002, Proceedings of the 41st IEEE Conference on,
volume 1, pages 741–746. IEEE.
Precup, R.-E., Sabau, M.-C., and Petriu, E. M. (2015).
Nature-inspired optimal tuning of input membership
functions of Takagi-Sugeno-Kang fuzzy models for
anti-lock braking systems. Applied Soft Computing,
27:575–589.
Reichensd
¨
orfer, E., Odenthal, D., and Wollherr, D. (2017).
Grammatical evolution of robust controller structures
using Wilson scoring and criticality ranking. In Eu-
ropean Conference on Genetic Programming, pages
194–209. Springer.
Ryan, C., Collins, J., and Neill, M. O. (1998). Grammati-
cal evolution: evolving programs for an arbitrary lan-
guage. In European Conference on Genetic Program-
ming, pages 83–96. Springer.
Saadat, J., Moallem, P., and Koofigar, H. (2017). Training
echo state neural network using harmony search algo-
rithm. International Journal of Artificial Intelligence,
15(1):163–179.
Saleme, A., Tibken, B., Warthenpfuhl, S. A., and Selbach,
C. (2011). Estimation of the domain of attraction for
non-polynomial systems: A novel method. IFAC Pro-
ceedings Volumes, 44(1):10976–10981.
Shimooka, H. and Fujimoto, Y. (2000). Generating robust
control equations with genetic programming for con-
trol of a rolling inverted pendulum. In Proceedings of
the 2nd Annual Conference on Genetic and Evolution-
ary Computation, pages 491–495. Morgan Kaufmann
Publishers Inc.
Singh, R., Kuchhal, P., Choudhury, S., and Gehlot, A.
(2015). Implementation and evaluation of heating sys-
tem using PID with genetic algorithm. Indian Journal
of Science and Technology, 8(5):413.
Sontag, E. D. (1983). A Lyapunov-like characterization of
asymptotic controllability. SIAM Journal on Control
and Optimization, 21(3):462–471.
Tsuzuki, T., Kuwada, K., and Yamashita, Y. (2006). Search-
ing for control Lyapunov-Morse functions using ge-
netic programming for global asymptotic stabilization
of nonlinear systems. In Proceedings of the 45th IEEE
Conference on Decision and Control, pages 5114–
5119. IEEE.
Verdier, C. and Mazo Jr, M. (2017). Formal controller syn-
thesis via genetic programming. IFAC-PapersOnLine,
50(1):7205–7210.
Vrkalovic, S., Teban, T.-A., and Borlea, I.-D. (2017). Stable
Takagi-Sugeno fuzzy control designed by optimiza-
tion. Int. J. Artif. Intell, 15:17–29.
Zhou, K., Doyle, J. C., Glover, K., et al. (1996). Robust and
optimal control, volume 40. Prentice hall New Jersey.
Nonlinear Control Structure Design using Grammatical Evolution and Lyapunov Equation based Optimization
65
