Extreme Learning Machine based Linear Homogeneous Ensemble for

Software Fault Prediction

Pravas Ranjan Bal and Sandeep Kumar

†

Department of Computer Science and Engineering, Indian Institute of Technology Roorkee, Roorkee, India

Keywords:

Extreme Learning Machine, Ensemble Model, Inter Release Prediction, Within Project Defect Prediction.

Abstract:

Many recent studies have experimented the software fault prediction models to predict the number of software

faults using statistical and traditional machine learning techniques. However, it is observed that the perfor-

mance of traditional software fault prediction models vary from dataset to dataset. In addition, the performance

of the traditional models degrade for inter release prediction. To address these issues, we have proposed li-

near homogeneous ensemble methods based on two variations of extreme learning machine, Differentiable

Extreme Learning Machine Ensemble (DELME) and Non-differentiable Extreme Learning Machine Ensem-

ble (NELME), to predict the number of software faults. We have used seventeen PROMISE datasets and ﬁve

eclipse datasets to validate these software fault prediction models. We have performed two types of predicti-

ons, within project defect prediction and inter release prediction, to validate our proposed fault prediction

model. The experimental result shows consistently better performance across all datasets.

1 INTRODUCTION

Software fault is an error in a software system that

causes a software system to behave abnormally or

to provide an unexpected result. Earlier prediction

of software faults help the software quality assu-

rance team to allocate the limited number of resour-

ces, before releasing of a software (Ostrand et al.,

2005; Menzies et al., 2007). Most of the resear-

chers have successfully experimented the software

fault prediction models to predict faulty or non-faulty

modules in a software project using different types

of classiﬁcation techniques (He et al., 2012; Bowes

et al., 2017; Li et al., 2016). In this paper, we have

used regression techniques to predict the number of

software faults in the release of a software.

Most of the earlier works have successfully de-

ployed statistical and traditional machine learning

techniques to build the software fault prediction mo-

dels. These classiﬁcation learning techniques incor-

porate logistic regression (James et al., 2013), arti-

ﬁcial neural network (Schmidhuber, 2015), support

vector machine (Ben-Hur et al., 2001), decision tree

(Quinlan, 1987), etc. Other regression techniques in-

cluding Poisson regression (Lambert, 1992), decision

tree regression (Quinlan et al., 1992), negative bino-

mial regression (Greene, 2003), etc., have also been

applied successfully to predict the number of software

faults and fault densities in a software project. Some

researchers have also used different types of ensem-

ble techniques such as bagging, boosting and stacking

approach to predict the number of software faults (Ra-

thore and Kumar, 2017b; Rathore and Kumar, 2017c)

and classify the faulty or non-faulty modules (Li et al.,

2016) in a software project.

Recently, most of the researchers have success-

fully deployed extreme learning machine for both

classiﬁcation and regression purpose in a wide appli-

cation area (Huang et al., 2012; Huang et al., 2015;

Rong et al., 2008). Following are some key features

that motivated to use extreme learning machine for

our experiment : (1) it is a faster technique in terms of

computation time, (2) it produces better accuracy due

to minimum norm output weight optimization met-

hod, (3) it has good generalization capability and (4)

it can ﬁnd the position of global minima with more

accuracy (Huang et al., 2006b). Due to this reasons,

we will present the extreme learning machine (ELM)

based ensemble in this paper.

Following are the contributions of this paper:

1. Extreme learning machine has not been explored

till now to predict the number of software faults.

2. We have proposed linear homogeneous ensem-

ble models for two variations of ELM, Diffe-

rentiable Extreme Learning Machine Ensemble

Bal, P. and Kumar, S.

Extreme Learning Machine based Linear Homogeneous Ensemble for Software Fault Prediction.

DOI: 10.5220/0006839500690078

In Proceedings of the 13th International Conference on Software Technologies (ICSOFT 2018), pages 69-78

ISBN: 978-989-758-320-9

(DELME) and Non-differentiable Extreme Lear-

ning Machine Ensemble (NELME), to predict the

number of software faults.

3. We have deployed proposed ensemble models for

both within project defect prediction and inter re-

lease prediction. The experimental results shows

that the proposed ensemble models have consis-

tent accuracy for both prediction scenario across

all datasets.

It is intended to answer following research questi-

ons from this work:

RQ 1. Is ELM based ensemble model prediction more

accurate than single predictor?

RQ 2. How does differentiable activation function ba-

sed ensemble model perform as compared to the non-

differentiable activation function based ensemble mo-

del for prediction of number of faults ?

RQ 3. Can we use differentiable and non-

differentiable function as activation function in

ELM to build ensemble model for prediction of

number of faults?

The rest of paper is organized as follows. Section

2 describes the related works of the software fault

prediction. Section 3 explains about proposed li-

near homogeneous ensemble model to predict soft-

ware faults. Section 4 describes the experimental se-

tup for proposed model. Section 5 presents the de-

tail experimental analysis and results of the proposed

model along with its comparative analysis. Section 6

presents threats to validity followed by conclusion in

section 7.

2 RELATED WORKS

Many researchers have deployed statistical and tra-

ditional machine learning techniques to predict the

number of software faults in last two decades. We

have explained some related works on software fault

prediction in terms to predict the number of software

faults and the use of ensemble models for software

fault prediction.

Rathore et al. (Rathore and Kumar, 2017b) propo-

sed two types of linear and non-linear heterogeneous

ensemble models to predict the number of software

faults. Fifteen PROMISE datasets had been used to

perform the experiments. The experiment conducted

for two scenarios of prediction, inter release and intra

release prediction. From the experimental results, it

is observed that the presented ensemble models per-

form better than single predictor based software fault

prediction models.

Li et al. (Li et al., 2016) proposed a three way

decision based ensemble classiﬁer to classify the soft-

ware modules being faulty or non-faulty and also rank

the software faulty modules. The ensemble model

was compared with traditional two way decision ba-

sed classiﬁer over NASA datasets. The experimental

results found that the proposed ensemble model pro-

vides higher prediction accuracy and lower decision

cost as compared to two way decision classiﬁer. In

addition, the proposed ensemble model performs bet-

ter as compared to the traditional classiﬁer for ranking

of software faulty modules.

Laradji et al. (Laradji et al., 2015) developed an

ensemble classiﬁer to classify the software modules

into faulty or non-faulty modules using some selected

features. The work suggested that greedy forward fe-

ature selection method outperformed on testing data-

sets. The experimental results found that the proposed

ensemble model achieved higher AUC performance

measure as compared to other conventional models.

Rathore et al. (Rathore and Kumar, 2017c) pro-

posed a heterogeneous ensemble model based on li-

near and non-linear combinational rule for prediction

of number of software faults. Eleven PROMISE data-

sets and seven eclipse datasets had been used to per-

form the experiments. The experimental results found

that the ensemble model had better prediction accu-

racy than single predictor across all datasets.

Graves et al. (Graves et al., 2000) proposed a

software fault prediction model using generalized li-

near regression for prediction of software faults. The

experiment has been performed using different types

of change metrics collected from large switching sy-

stem project dataset. The experimental results sug-

gested that the proposed model produced poor pre-

diction accuracy due to size of the module and other

complexity metrics. The model performed well when

the combination of different metrics are used.

Ostrand et al. (Ostrand et al., 2005) developed a

software fault prediction model using negative bino-

mial regression for prediction of software faults. Da-

tasets from two large industrial projects had been used

to perform the software fault prediction model. From

the experimental results, it is found that the accuracy

of negative binomial regression model was consistent

across all industrial datasets.

Huang et al. (Huang et al., 2006b) developed an

efﬁcient learning technique called extreme learning

machine for both classiﬁcation and regression purpo-

ses. The experimental results found that the learning

speed of extreme learning machine is relatively faster

and it had better generalization performance than gra-

dient based learning algorithm. In addition, this lear-

ning technique can used both differentiable and non-

differentiable function as activation function. Howe-

ICSOFT 2018 - 13th International Conference on Software Technologies

ver, these classiﬁcation models have not been explo-

red prediction of number of software faults.

Generally, gradient based learning algorithm like

back propagation neural network takes more compu-

tational time to ﬁnd the training error. If we will

use gradient based learning algorithm as base lear-

ner in the ensemble, then the computation time will

be again more. Thus, we have used extreme lear-

ning machine as base learner in the proposed ensem-

ble model. In this work, we have proposed linear ho-

mogeneous ensemble model to generate Differentia-

ble Extreme Learning Machine Ensemble (DELME)

and Non-differentiable Extreme Learning Machine

Ensemble (NELME) using extreme learning machine

to predict the number of software faults.

3 LINEAR HOMOGENEOUS

ENSEMBLE MODEL FOR

SOFTWARE FAULT

PREDICTION

In this work, we have used extreme learning ma-

chine (Huang et al., 2006b) and homogeneous ensem-

ble techniques called bagging method (Quinlan et al.,

1996) to build two types of linear homogeneous en-

semble models for prediction of number of software

faults. The details about extreme learning machine

and proposed ensemble model are explained in the

following subsection.

3.1 Extreme Learning Machine

ELM is a Single-hidden Layer Feed forward Neural

network (SLFN). Huang et al. (Huang et al., 2006b)

proposed the basic algorithm of an extreme learning

machine. Given an arbitrary training sample (x

, t

where, i = 1, · ·· , N and the output function of an ELM

with n hidden layer is deﬁned by Eq. (1)

(x) =

∑

i=1

(x) = Gβ (1)

Where,

G =







) . . . g

)

) . . . g

)

. . . .

) . . . g

)







and

β = [β

. . . β

]

Where, G is the hidden layer matrix with activa-

tion function g(x), β is the output weight matrix of an

ELM network and is deﬁned by Eq. (2).

β = G

†

T (2)

Where, G

†

is the Moore-Penrose generalized in-

verse of matrix G and T = [t

. . . t

]

. Singu-

lar Value Decomposition (SVD) method (Golub and

Reinsch, 1970) has been used to calculate the Moore-

Penrose generalized inverse for our experiment. Hu-

ang et al. (Huang et al., 2006b) suggested that

both differentiable and non-differentiable (threshold

function) functions can be used as activation functions

in the hidden layer of ELM. A differentiable function

is a continuous function whose derivative exists at

each point in its domain, otherwise, it is called non-

differentiable function. Further, Huang et al. (Hu-

ang et al., 2006a) proved that ELM can be directly

trained over threshold networks and it improves the

generalization performance better than other learning

algorithms. ELM of non-differentiable function takes

very less time to train the network than back propa-

gation and other learning algorithms. For our experi-

ment, we have used symmetric saturating linear trans-

fer function as threshold function and sigmoid trans-

fer function as differentiable function in the hidden

layer of ELM. Sigmoid and symmetric saturating li-

near transfer functions are deﬁned by Eq. (3) and Eq.

(4) respectively.

g(x) =

1 + e

−x

(3)

g(x) =











−1, if x ≤ −1

x, if −1 ≤ x ≤ 1

1, otherwise.

(4)

3.2 Proposed Ensemble Model

An overview of proposed ensemble model based on

bagging method for software fault prediction is shown

in Fig. 1. We have designed two ensemble models na-

mely Differentiable Extreme Learning Machine En-

semble (DELME) and Non-differentiable Extreme

Learning Machine Ensemble (NELME) to predict the

number of software faults. Both differentiable acti-

vation function based extreme learning machine and

non-differentiable activation function based extreme

learning machine have been used as base learner in

DELME and NELME ensemble models respectively.

The ﬁnal prediction result of the ensemble model is

combined by mean rule.

Extreme Learning Machine based Linear Homogeneous Ensemble for Software Fault Prediction

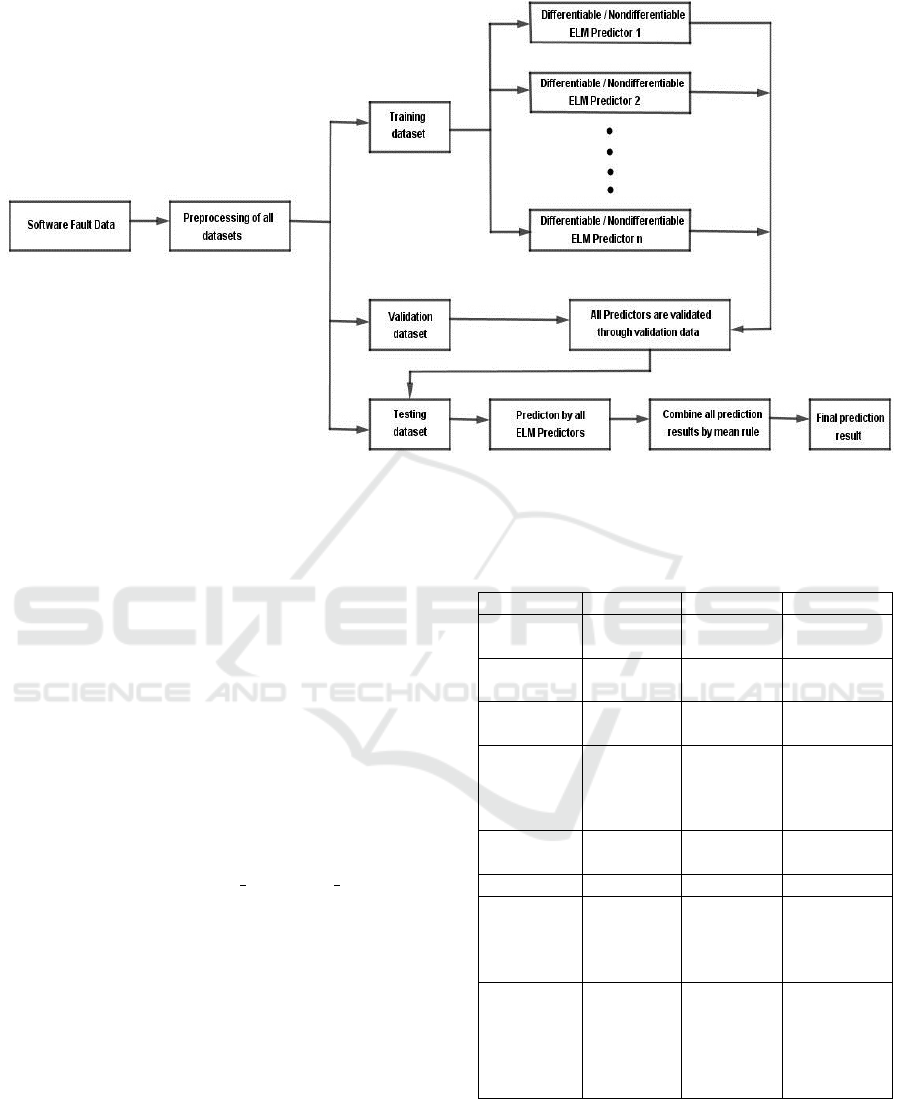
Figure 1: An overview of proposed ensemble model for software fault prediction.

4 EXPERIMENTAL SETUP

In this section, we will present experimental setups

required to validate the proposed software fault pre-

diction model.

4.1 Preprocessing of Software Fault

Datasets

We have used seventeen PROMISE (Menzies et al.,

2015) and ﬁve eclipse (D’Ambros et al., 2010) soft-

ware fault datasets for our experiment. Datasets con-

tain Object-Oriented (OO) metrics, wmc, dit, noc,

cbo, rfc, lcom, ca, ce, npm, lcom3, loc, dam, moa,

mfa, cam, ic, cbm, amc, max cc and avg cc as inde-

pendent variables and number of faults as dependent

variable. Most of the datasets contain imbalanced

value for number of software faults. Software fault

prediction models produce very poor prediction accu-

racy due to imbalanced nature of fault datasets. So,

we have used two stage data preprocessing method

to preprocess all datasets, before training of the soft-

ware fault prediction models. First, we have balan-

ced all datasets through SMOTER algorithm (Torgo

et al., 2013). Then, we have normalized all datasets

between a range [0, 1] through min − max normaliza-

tion method (Patro and Sahu, 2015). The details of

software faults datasets are explained in Table 1.

Table 1: An overview of Software fault datasets (Menzies

et al., 2015; D’Ambros et al., 2010).

Datasets # Features # Modules Defect Rate

Ant 1.5 20 293 12.26 %

Ant 1.7 20 745 28.67 %

Camel 1.2 20 608 55.1 %

Camel 1.4 20 872 19.94 %

Lucene 2.0 20 195 87.5 %

Lucene 2.2 20 247 139.8 %

Prop V4 20 3022 9.57 %

Prop V40 20 4053 12.99 %

Prop V85 20 3077 44.52 %

Prop V121 20 2998 16.51 %

Xalan 2.4 20 723 17.94 %

Xalan 2.6 20 885 86.7 %

Xerces 1.3 20 453 17.96 %

Jedit 4.0 20 306 32.46 %

Jedit 4.1 20 312 33.9 %

Jedit 4.2 20 367 15.04 %

Jedit 4.3 20 492 2.28 %

Eclipse 15 997 20.04 %

Equinox 15 324 66.15 %

Lucene 15 691 10.2 %

Mylyn 15 1862 15.15 %

Pde 15 1497 16.22 %

4.2 Performance Measures

For our experiment, we have used four performance

measures to validate the proposed ensemble model

for software fault prediction. These four performance

ICSOFT 2018 - 13th International Conference on Software Technologies

measures such as average absolute error (Willmott

and Matsuura, 2005), average relative error (Willmott

and Matsuura, 2005), measure of completeness value

(Briand and W

ust, 2002) and prediction at level l va-

lue (MacDonell, 1997) and are deﬁned as follows.

AAE =

∑

i=1

|(Y

−Y

)| (5)

ARE =

∑

i=1

|(Y

−Y

+ 1)

(6)

Where, k is the total number of samples, Y

is the

actual number of defects and Y

is the predicted num-

ber of defects. Sometimes, the ARE value provides

inﬁnity value, when the number of bugs are zero in

the module. Thus, we have added 1 in the denomi-

nator of Eq. (6) to avoid the inﬁnity values of ARE

performance measure (Gao and Khoshgoftaar, 2007).

MoC value =

Predicted number o f f aults

Actual number o f f aults

(7)

MoC value measures completeness of the soft-

ware fault prediction model. Nearly 100% complete-

ness value of the software fault prediction model pro-

vides best model.

Pred(l) value =

(8)

Where, k is the number of software modules whose

value must be less or equal to l and n is the total num-

ber of software modules. Pred(l) value calculates the

portion of number of software modules that are under

the threshold value of average relative errors. MacDo-

nell et al. (MacDonell, 1997) suggested that the thres-

hold value should be less than or equal to 30%. So, we

have set the threshold value to 0.3 for our experiment.

4.3 Tools and Techniques Used

We have used R studio to implement the proposed

ensemble model and other comparative models such

as extreme learning machine (Huang et al., 2006b)

and back propagation neural network (Kanmani et al.,

2007). For comparative analysis, we have imple-

mented Differentiable activation function based ELM

(D ELM), Non- differentiable activation function ba-

sed ELM (N ELM) and Back propagation neural net-

work (BPNN) along with Differentiable ELM based

ensemble (DELME) and Non-differentiable ELM ba-

sed ensemble (NELME). For balancing the imbalan-

ced datasets, we have used Weka tool to implement

the SMOTOR algorithm. We have chosen ﬁve hid-

den nodes and sigmoid transfer function as activation

function in the hidden layer for back propagation neu-

ral network. We have conducted two tailed Fried-

man’s test (Higgins, 2003) to know the signiﬁcance

of the proposed model and other comparative models.

5 EXPERIMENTAL RESULTS

AND ANALYSIS

In this section, we present experimental results and

analysis of the proposed model and comparative mo-

dels for both within project defect prediction and inter

release prediction. We have used 10 fold cross valida-

tion method to perform the experiments. Each dataset

is divided into 10 equal parts. One part is used for va-

lidation, another one part is used for test, and rest part

of the dataset is used for training dataset.

5.1 Within Project Defect Prediction

In within project defect prediction analysis, we have

used PROMISE and eclipse datasets to validate the

proposed ensemble model. Table 2 describes the per-

formance analysis of ﬁve software fault prediction

models for PROMISE datasets. Table 3 describes the

performance analysis of ﬁve software fault prediction

models for eclipse datasets. Measure of complete-

ness analysis of ﬁve software fault prediction models

for within project defect prediction on PROMISE and

eclipse datasets are shown in Fig. 2 and 3 respecti-

vely. From the performance analysis of within pro-

ject defect prediction, we concluded that in most of

the cases, both differentiable ELM based ensemble

(DELME) and non-differentiable ELM based ensem-

ble (NELME) performs best.

From Table 2 and 3 , it is observed that differen-

tiable ensemble (DELME) performs best prediction

accuracy in majority cases for PROMISE datasets and

non-differentiable ensemble (NELME) performs best

prediction accuracy in majority of cases for eclipse

datasets. From Fig. 2 and 3, it is observed that

the completeness of the proposed ensemble models

as well as single predictor models perform well for

within project defect prediction analysis.

5.2 Inter Release Prediction

In inter release prediction analysis, we have used

PROMISE datasets to validate the proposed ensem-

ble model. Table 4 describes the performance analy-

sis of ﬁve software fault prediction models. Measure

of completeness analysis of ﬁve software fault pre-

diction models for inter release prediction on PRO-

MISE datasets are shown in Fig. 4. From the per-

Extreme Learning Machine based Linear Homogeneous Ensemble for Software Fault Prediction

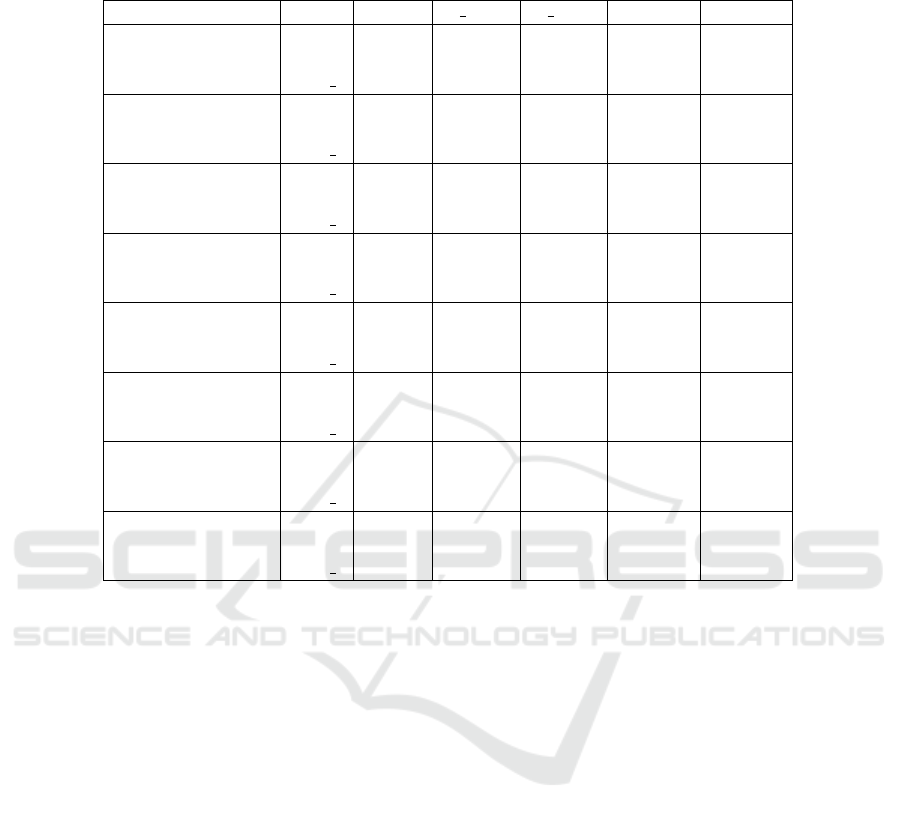
Table 2: Performance measure analysis of ﬁve software fault prediction models for within project defect prediction over

PROMISE datasets. Bold face values are best prediction accuracy and italic face values are second best prediction accuracy.

PROMISE datasets BPNN D ELM N ELM DELME NELME

Ant 1.7 AAE 0.0661 0.0583 0.0575 0.056 0.0694

ARE 0.0575 0.0524 0.0509 0.0476 0.0633

Pred l 99.62 98.68 99.6 98.68 98.68

Camel 1.2 AAE 0.042 0.0392 0.0448 0.0354 0.0355

ARE 0.0347 0.0366 0.0398 0.0334 0.0333

Pred l 99.71 100 99.35 100 100

Camel 1.4 AAE 0.0542 0.0413 0.0369 0.0342 0.0347

ARE 0.0486 0.0373 0.0337 0.0307 0.0317

Pred l 99.41 99.2 99.66 100 100

Prop V40 AAE 0.0235 0.0402 0.0374 0.037 0.0285

ARE 0.021 0.0369 0.0342 0.0338 0.0271

Pred l 99.63 99.37 99.46 99.53 99.76

Prop V121 AAE 0.0386 0.0406 0.0272 0.0241 0.024

ARE 0.0354 0.0373 0.025 0.0214 0.0222

Pred l 99.86 99.76 99.47 99.67 99.67

Jedit 4.1 AAE 0.0544 0.0435 0.0578 0.0423 0.0453

ARE 0.0482 0.0393 0.0494 0.0395 0.0382

Pred l 98.5 99.39 98.17 100 100

Jedit 4.2 AAE 0.0623 0.0407 0.0429 0.0494 0.0238

ARE 0.0539 0.0368 0.0387 0.0427 0.0218

Pred l 99.5 99.21 99.73 97.43 100

Xerces 1.3 AAE 0.0311 0.0271 0.0198 0.0202 0.0134

ARE 0.0284 0.026 0.0189 0.0194 0.013

Pred l 99.72 99.05 99.58 100 100

formance analysis of inter release prediction, we con-

cluded that both differentiable ELM based ensemble

(DELME) and non-differentiable ELM based ensem-

ble (NELME) performs best for almost all the data-

sets.

From Table 4 and Fig. 4, it is observed that

DELME performs best prediction accuracy as com-

pared to NELME in majority of cases. The comple-

teness of the proposed ensemble model is also impro-

ved as compared to single predictor for inter release

prediction.

5.3 Performance of Statistical Test

We have performed two tailed Friedman’s statistical

test to know whether software fault prediction mo-

dels under study are performing signiﬁcantly diffe-

rent or not. Table 5 describes the Friedman’s test

analysis of within project defect prediction for both

PROMISE and eclipse datasets. Table 6 describes the

Friedman’s test analysis of inter release prediction for

PROMISE datasets. It is evident from Table 5 and 6

with p−values of less than 0.5 indicating signiﬁcant

level.

We will discuss some research questions that were

deﬁned for our proposed work.

RQ 1. Is ELM based ensemble model prediction more

accurate than single predictor?

It is evident from Table 2, 3 and 4 that our propo-

sed ensemble models show best prediction accuracy

across all datasets in both cases, within project defect

prediction and inter release prediction. The proposed

ensemble models outperform as compared to single

predictors in both prediction scenarios.

RQ 2. How does differentiable activation function ba-

sed ensemble model perform as compared to non-

differentiable activation function based ensemble mo-

del for prediction of number of faults ?

From Table 2, 3 and 4, it is observed that there is

no signiﬁcant difference between two ensemble mo-

dels in terms of prediction accuracy. The measure of

completeness analysis of both ensemble models are

mostly similar for both prediction scenarios.

RQ 3. Can we use differentiable and non-

differentiable function as activation function in

ELM to build ensemble model for prediction of

number of faults?

Yes, we can use both differentiable and non-

differentiable function as activation functions in ELM

to build ensemble models for prediction of number of

ICSOFT 2018 - 13th International Conference on Software Technologies

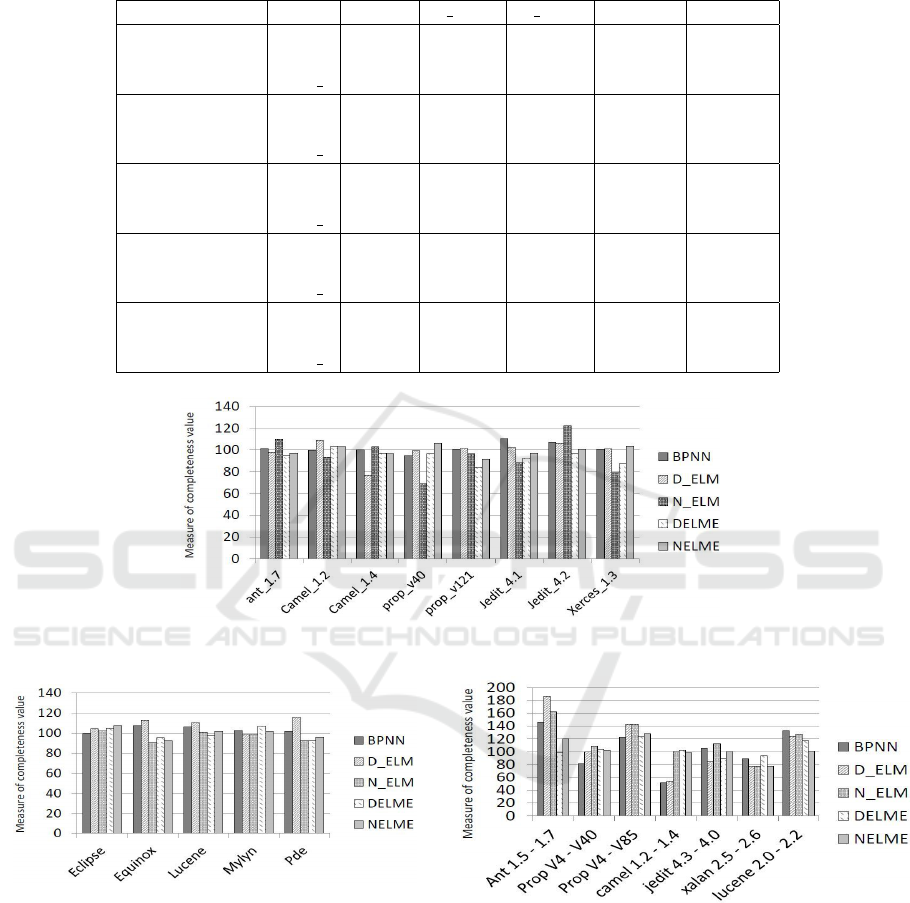
Table 3: Performance measure analysis of ﬁve software fault prediction models for within project defect prediction over

eclipse datasets. Bold face values are best prediction accuracy and italic face values are second best prediction accuracy.

Eclipse datasets BPNN D ELM N ELM DELME NELME

Eclipse AAE 0.0697 0.0558 0.0484 0.0445 0.0496

ARE 0.0604 0.0479 0.0429 0.0386 0.0448

Pred l 99.26 98.72 98.81 100 98.03

Equinox AAE 0.0539 0.0469 0.0425 0.0413 0.0283

ARE 0.0479 0.0425 0.0379 0.0359 0.0262

Pred l 99.22 98.88 99.72 100 100

Lucene AAE 0.0567 0.029 0.0272 0.0265 0.0344

ARE 0.0571 0.029 0.0244 0.0251 0.0303

Pred l 99.75 99.59 99.72 100 98.64

Mylyn AAE 0.0456 0.033 0.0406 0.0315 0.0251

ARE 0.0419 0.0309 0.0379 0.0291 0.0237

Pred l 99.84 99.54 98.67 100 100

Pde AAE 0.0242 0.0192 0.0231 0.0126 0.0109

ARE 0.0231 0.0161 0.0214 0.0121 0.0106

Pred l 99.92 99.54 98.63 99.01 100

Figure 2: Measure of completeness analysis of ﬁve software fault prediction models for within project defect prediction over

PROMISE datasets.

Figure 3: Measure of completeness analysis of ﬁve software

fault prediction models for within project defect prediction

over eclipse datasets.

faults. From Table 2, 3 and 4, it is observed that both

proposed ensemble models provide similar prediction

accuracy in both prediction scenarios.

6 THREATS TO VALIDITY

In this section, we have described some possible thre-

ats that might affect our prediction results.

Figure 4: Measure of completeness analysis of ﬁve soft-

ware fault prediction models for inter release prediction

over PROMISE datasets.

Internal Validity. In this work, we have used li-

near homogeneous technique called bagging method

to build the software fault prediction model for pre-

diction of number of software faults. Other types

of ensemble techniques such as linear and nonlinear

homogeneous ensemble methods, etc. may gene-

rate different prediction accuracy. Many researchers

have used object oriented metrics (Rathore and Ku-

mar, 2017a; Rathore and Kumar, 2017b; Rathore and

Extreme Learning Machine based Linear Homogeneous Ensemble for Software Fault Prediction

Table 4: Performance measure analysis of eight software fault prediction models for inter release prediction over PROMISE

datasets. Bold face values are best prediction accuracy and italic face values are second best prediction accuracy.

PROMISE datasets BPNN D ELM N ELM DELME NELME

Ant 1.5 - Ant 1.7 AAE 0.1225 0.1111 0.0964 0.0636 0.0682

ARE 0.1062 0.1037 0.0899 0.0567 0.0606

Pred l 90.8 96.84 98.81 98.55 98.94

Prop v4 - Prop v40 AAE 0.0734 0.0413 0.0455 0.0398 0.0396

ARE 0.0637 0.038 0.042 0.0365 0.0363

Pred l 98.41 99.46 99.25 99.53 99.39

Prop v4 - Prop v85 AAE 0.0314 0.029 0.0306 0.0261 0.0289

ARE 0.0292 0.027 0.0286 0.0244 0.0271

Pred l 99.74 99.68 99.58 99.82 99.63

Camel 1.2 - Camel 1.4 AAE 0.061 0.0597 0.037 0.0363 0.0354

ARE 0.0525 0.0514 0.0335 0.0328 0.0319

Pred l 99.27 99.2 99.32 99.66 99.66

Jedit 4.3 - Jedit 4.0 AAE 0.0983 0.0935 0.0602 0.0528 0.0655

ARE 0.0837 0.0792 0.0515 0.0468 0.0553

Pred l 92.1 96.26 97.19 98.75 98.13

Xalan 2.5 - Xalan 2.6 AAE 0.0768 0.0761 0.0761 0.0775 0.078

ARE 0.0683 0.0669 0.0668 0.0691 0.0687

Pred l 99.09 99.32 99.32 99.54 98.64

Lucene 2.0 - Lucene 2.2 AAE 0.0344 0.0416 0.0347 0.0317 0.032

ARE 0.0316 0.0383 0.0328 0.0296 0.0291

Pred l 99.59 99.19 99.19 100 99.59

Table 5: Friedman’s statistical test analysis for within pro-

ject defect Prediction.

Promise datasets (α = 0.05)

value df p-value

AAE 10.1 4 0.038

ARE 10 4 0.04

Eclipse datasets (α = 0.05)

value df p-value

AAE 14.24 4 0.0065

ARE 13.28 4 0.0099

Table 6: Friedman’s statistical test analysis for inter release

Prediction.

Promise datasets (α = 0.05)

value df p-value

AAE 12.57 4 0.013

ARE 11.08 4 0.025

Kumar, 2017c; Laradji et al., 2015; Nam et al., 2017)

as independent variables to train the fault prediction

model. We have used object oriented metrics of PRO-

MISE datasets to validate the proposed ensemble mo-

dels. Other software metrics can be used for pre-

diction of number of software faults.

External Validity. The experiments have been per-

formed over publicly available open source datasets.

Some industrial software fault datasets may contain

different types of defect pattern and that new types of

defect pattern may affect our prediction analysis. To

resolve this issue, we have developed ensemble mo-

dels using both differentiable and non-differentiable

activation functions of extreme learning machine.

Conclusion Validity. We have used Min Max nor-

malization algorithm to normalize the software fault

datasets. For balancing the imbalanced datasets, we

have used SMOTER algorithm to balance all imbalan-

ced datasets. Other types of normalization techniques

and preprocessing algorithms can be used to prepro-

cess the datasets.

7 CONCLUSION

In this paper, we have proposed linear homogeneous

ensemble models using extreme learning machine for

prediction of number of software faults. For better

prediction accuracy, we have used two stage data pre-

processing to preprocess the datasets, before training

the software fault prediction models. Seventeen PRO-

MISE datasets and ﬁve eclipse datasets have been

used to validate the proposed ensemble model. We

have used two types of activation functions, diffe-

rentiable function and non-differentiable function, for

extreme learning machine to build the ensemble mo-

del. From the experimental results and analysis, it is

ICSOFT 2018 - 13th International Conference on Software Technologies

observed that ensemble using differentiable function

based ELM as well as non- differentiable function ba-

sed ELM outperform as compared to other methods

across all datasets for both prediction scenarios within

project defect prediction as well as inter release pre-

diction. Overall, the proposed ensemble models have

consistent prediction accuracy across all datasets for

both prediction scenarios.

ACKNOWLEDGMENTS

The authors are thankful to Ministry of Electronics

and Information Technology, Government of India.

This publication is an outcome of the R&D work un-

dertaken in the project under the Visvesvaraya PhD

Scheme of Ministry of Electronics and Information

Technology, Government of India, being implemen-

ted by Digital India Corporation (formerly Media Lab

Asia).

REFERENCES

Ben-Hur, A., Horn, D., Siegelmann, H. T., and Vapnik, V.

(2001). Support vector clustering. Journal of machine

learning research, 2(Dec):125–137.

Bowes, D., Hall, T., and Petri

c, J. (2017). Software defect

prediction: do different classiﬁers ﬁnd the same de-

fects? Software Quality Journal, pages 1–28.

Briand, L. C. and W

ust, J. (2002). Empirical studies of qua-

lity models in object-oriented systems. In Advances in

computers, volume 56, pages 97–166. Elsevier.

D’Ambros, M., Lanza, M., and Robbes, R. (2010). An ex-

tensive comparison of bug prediction approaches. In

Mining Software Repositories (MSR), 2010 7th IEEE

Working Conference on, pages 31–41. IEEE.

Gao, K. and Khoshgoftaar, T. M. (2007). A comprehensive

empirical study of count models for software fault pre-

diction. IEEE Transactions on Reliability, 56(2):223–

236.

Golub, G. H. and Reinsch, C. (1970). Singular value de-

composition and least squares solutions. Numerische

mathematik, 14(5):403–420.

Graves, T. L., Karr, A. F., Marron, J. S., and Siy, H. (2000).

Predicting fault incidence using software change his-

tory. IEEE Transactions on software engineering,

26(7):653–661.

Greene, W. H. (2003). Econometric analysis. Pearson Edu-

cation India.

He, Z., Shu, F., Yang, Y., Li, M., and Wang, Q. (2012).

An investigation on the feasibility of cross-project

defect prediction. Automated Software Engineering,

19(2):167–199.

Higgins, J. J. (2003). Introduction to modern nonparametric

statistics.

Huang, G., Huang, G.-B., Song, S., and You, K. (2015).

Trends in extreme learning machines: A review. Neu-

ral Networks, 61:32–48.

Huang, G.-B., Zhou, H., Ding, X., and Zhang, R. (2012).

Extreme learning machine for regression and mul-

ticlass classiﬁcation. IEEE Transactions on Sys-

tems, Man, and Cybernetics, Part B (Cybernetics),

42(2):513–529.

Huang, G.-B., Zhu, Q.-Y., Mao, K., Siew, C.-K., Sarat-

chandran, P., and Sundararajan, N. (2006a). Can thres-

hold networks be trained directly? IEEE Transactions

on Circuits and Systems II: Express Briefs, 53(3):187–

191.

Huang, G.-B., Zhu, Q.-Y., and Siew, C.-K. (2006b). Ex-

treme learning machine: theory and applications.

Neurocomputing, 70(1-3):489–501.

James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013).

An introduction to statistical learning, volume 112.

Springer.

Kanmani, S., Uthariaraj, V. R., Sankaranarayanan, V., and

Thambidurai, P. (2007). Object-oriented software

fault prediction using neural networks. Information

and software technology, 49(5):483–492.

Lambert, D. (1992). Zero-inﬂated poisson regression, with

an application to defects in manufacturing. Techno-

metrics, 34(1):1–14.

Laradji, I. H., Alshayeb, M., and Ghouti, L. (2015). Soft-

ware defect prediction using ensemble learning on se-

lected features. Information and Software Technology,

58:388–402.

Li, W., Huang, Z., and Li, Q. (2016). Three-way decisions

based software defect prediction. Knowledge-Based

Systems, 91:263–274.

MacDonell, S. G. (1997). Establishing relationships bet-

ween speciﬁcation size and software process effort in

case environments. Information and Software Techno-

logy, 39(1):35–45.

Menzies, T., Greenwald, J., and Frank, A. (2007). Data

mining static code attributes to learn defect predictors.

IEEE transactions on software engineering, 33(1):2–

13.

Menzies, T., Krishna, R., and Pryor, D. (2015). The

promise repository of empirical software engineering

data. http://openscience.us/repo. North Carolina State

University, Department of Computer Science.

Nam, J., Fu, W., Kim, S., Menzies, T., and Tan, L. (2017).

Heterogeneous defect prediction. IEEE Transactions

on Software Engineering.

Ostrand, T. J., Weyuker, E. J., and Bell, R. M. (2005). Pre-

dicting the location and number of faults in large soft-

ware systems. IEEE Transactions on Software Engi-

neering, 31(4):340–355.

Patro, S. and Sahu, K. K. (2015). Normalization: A prepro-

cessing stage. arXiv preprint arXiv:1503.06462.

Quinlan, J. R. (1987). Simplifying decision trees. Internati-

onal journal of man-machine studies, 27(3):221–234.

Quinlan, J. R. et al. (1992). Learning with continuous clas-

ses. In 5th Australian joint conference on artiﬁcial

intelligence, volume 92, pages 343–348. Singapore.

Extreme Learning Machine based Linear Homogeneous Ensemble for Software Fault Prediction

Quinlan, J. R. et al. (1996). Bagging, boosting, and c4. 5.

In AAAI/IAAI, Vol. 1, pages 725–730.

Rathore, S. S. and Kumar, S. (2017a). An empirical

study of some software fault prediction techniques

for the number of faults prediction. Soft Computing,

21(24):7417–7434.

Rathore, S. S. and Kumar, S. (2017b). Linear and non-linear

heterogeneous ensemble methods to predict the num-

ber of faults in software systems. Knowledge-Based

Systems, 119:232–256.

Rathore, S. S. and Kumar, S. (2017c). Towards an ensemble

based system for predicting the number of software

faults. Expert Systems with Applications, 82:357–382.

Rong, H.-J., Ong, Y.-S., Tan, A.-H., and Zhu, Z. (2008).

A fast pruned-extreme learning machine for classiﬁ-

cation problem. Neurocomputing, 72(1-3):359–366.

Schmidhuber, J. (2015). Deep learning in neural networks:

An overview. Neural networks, 61:85–117.

Torgo, L., Ribeiro, R. P., Pfahringer, B., and Branco, P.

(2013). Smote for regression. In Portuguese confe-

rence on artiﬁcial intelligence, pages 378–389. Sprin-

ger.

Willmott, C. J. and Matsuura, K. (2005). Advantages of the

mean absolute error (mae) over the root mean square

error (rmse) in assessing average model performance.

Climate research, 30(1):79–82.

ICSOFT 2018 - 13th International Conference on Software Technologies