
Real-Time Non-linear Noise Reduction Algorithm for Video
Chinatsu Mori and Seiichi Gohshi
Kogakuin University, 1-24-2 Nishi-Shinjuku, Shinjuku-ku, Tokyo, 163-8677, Japan
Keywords:
Video Noise Reducer, 4KTV, 8KTV, Real Time, Non-linear Signal Processing, Image Quality.
Abstract:
Noise is an essential issue for images and videos. Recently, a range of high-sensitivity imaging devices
have become available. Cameras are often used under poor lighting conditions for security purposes or night
time news gathering. Videos shot under poor lighting conditions are afflicted by significant noise which
degrades the image quality. The process of noise removal from videos is called noise reduction (NR). Although
many NR methods are proposed, they are complex and are proposed as computer simulations. In practical
applications, NR processing of videos occurs in real-time. The practical real-time methods are limited and the
complex NR methods cannot cope with real-time processing. Video has three dimensions: horizontal, vertical
and temporal. Since the temporal relation is stronger than that of horizontal and vertical, the conventional
real-time NR methods use the temporal relation to reduce noise. This approach is known as the inter-frame
relation, and the noise reducer comprises a temporal recursive filter. Temporal recursive filters are widely
used in digital TV sets to reduce the noise affecting images. Although the temporal recursive filter is a simple
algorithm, moving objects leave trails when it reduces the high-level noise. In this paper, a novel NR algorithm
that does not suffer from this trail issue and shows better performance than NR using temporal recursive filters
is proposed.
1 INTRODUCTION
Imaging technology advanced in the 21st century and
HDTV (1920 × 1080) resolution cameras have be-
come a reasonably priced commodity. Recently, high-
sensitivity imaging devices have also become widely
available and video cameras can work under poor
lighting conditions. This high-sensitivity imaging
technology makes 4K/8K ultra-high-resolution video
systems possible. The size of one 4K imaging pixel
is 1/4 that of an HDTV pixel and the size of one 8K
pixel is 1/16 that of an HDTV pixel. The light en-
ergy collected by one pixel is proportional to the size
of the imaging cell; therefore, the light energy col-
lected by one 4K or 8K pixel is 1/4 or 1/16 that of
an HDTV pixel. Since imaging cells generate a volt-
age that is proportional to the collected light energy,
4K/8K imaging cells generate a lower voltage than
those of HDTV imaging cells. The light intensity is
often insufficient when 4K/8K imaging, which causes
noise to appear in videos, degrading the image qual-
ity.
Aside from 4K/8K videos, noise is also a crucial
issue in security cameras. Crimes are often commit-
ted after sunset. In the night time, the lighting condi-
tions are worse and the recorded videos usually con-
tain a lot of noise. When using recorded videos to
investigate a crime, noise is often a problem when try-
ing to identify the person of interest. Low noise and
high resolution, such as 4K/8K, are important factors
for high-quality videos. There are many signal pro-
cessing methods for reducing the noise and improv-
ing the resolution of recorded videos to achieve high-
quality videos.
Noise reduction (NR) is a signal processing
method for reducing noise in recorded videos, and
super-resolution (SR) is a signal processing method
for improving the video resolution. Unfortunately,
these two technologies are trade-offs. Noise occurs
as small dots that have high-frequency elements. The
high resolution is also created by high-frequency ele-
ments. If we try to reduce the noise in a video, the
high-frequency elements are reduced and the video
becomes blurry; this is the first issue with NR. The
second issue is real-time signal processing, which is
essential for all video systems. Although there are
many NR approaches, most of them are proposed for
still images. There are no real-time requirements for
still-image NR. The frame rates of video systems are
50/60 (analogue TV/HD/4K) or 120 Hz (8K). This
means that the NR processing for a frame has to be
finished within 25/16.7 ms for current practical video
Mori, C. and Gohshi, S.
Real-Time Non-linear Noise Reduction Algorithm for Video.
DOI: 10.5220/0006839803210327
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 1: DCNET, ICE-B, OPTICS, SIGMAP and WINSYS, pages 321-327
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
321

systems (analogue TV/HD/4K). Due to these time
constraints, it is impossible to adopt as complex NR
algorithms for videos as used for still images. In this
paper, a novel real-time NR algorithm for videos is
proposed. It exploits video characteristics that are dif-
ferent from those of still images and reduces noise
without blurring, unlike conventional NR algorithms
for videos.
2 PREVIOUS WORKS
Still images have horizontal and vertical (spatial)
axes, but videos havespatial and temporal axes. Many
two- (2D) and three-dimensional (3D) NR systems
have been proposed by researchers.
In (Malfait and Roose, 1997), (Kazubek, 2003),
(Piurica et al., 2004), (Nai-Xiang et al., 2006), (Se-
lesnick and Li, 2003), and (Pizurica et al., 2003), the
authors proposed the use of spatial (two-dimensional)
and spatiotemporal (three-dimensional) filters to re-
move video noise. However, spatial filters only con-
sider spatial information; therefore, these filters can
cause spatial blurring at high noise levels. Using
a combination of temporal and spatial information
can reduce this blurring effect. This approach can
also be used to improve the filtering performance at
low noise levels. In (Malfait and Roose, 1997), a
wavelet domain spatial filter in which the coefficients
are manipulated using a Markov random field im-
age model has been proposed. A Wiener filter was
utilized in the wavelet domain to remove the image
noise in (Kazubek, 2003). Noise reduction using
the wavelet transform was proposed in previous stud-
ies (Piurica et al., 2004)(Nai-Xiang et al., 2006)(Se-
lesnick and Li, 2003)(Pizurica et al., 2003)(Gupta
et al., 2004)(Mahmoud and Faheem, 2008)(Jovanov
et al., 2009)(Luisier et al., 2010), which provides a
high performanceand results in images of a high qual-
ity. However, currently, these approaches are only
feasible at the computer simulation level, and they
do not work in real time. The wavelet transform is
a complex algorithm; therefore, it is difficult to ap-
ply it to NR, and it is not cost-effective. Currently,
there are no practical real-time NR systems employ-
ing the wavelet transform method. The authors in (Pi-
urica et al., 2004) proposed a fuzzy logic-based image
noise filter that considers directional deviations.
In addition, a recursive estimator structure has
been proposed to differentiate a clean image from a
film-grain noisy image where the noise is considered
to be related to the exposure time in the form of a
non-Gaussian and multiplicativestructure (Nai-Xiang
et al., 2006). In addition, a pixel-based spatiotemporal
adaptive filter that calculates new pixel values adap-
tively using the weighted mean of pixels over mo-
tion compensated frames has been proposed in (Se-
lesnick and Li, 2003). An edge preserving spatiotem-
poral video noise filter that combines 2D Wiener and
Kalman filters has been presented in (Pizurica et al.,
2003). The authors of (Gupta et al., 2004) proposed
a nonlinear video noise filter that calculates new pixel
values using a 3D window. In this method, the pixels
are arranged with respect to the related pixel values
in the form of a 3D window according to their differ-
ence and the average of the pixels in the window af-
ter weighting them with respect to their sorting order,
which gives good results in the case of no or slow lo-
cal motion, but it deforms image regions in the case of
abrupt local motion. For local motion, the 3D filtering
performance of this method is low. To improvethe 3D
filtering performance of the method proposed in (Nai-
Xiang et al., 2006), video de-noising uses 2D and 3D
dual-tree complex wavelet transforms. The authors of
(9) proposed 2D wavelet-based filtering and temporal
mean filtering that uses pixel-based motion detection.
The authors in (Mahmoud and Faheem, 2008) pro-
posed 2D wavelet-based filtering and temporal mean
filtering that uses pixel-based motion detection. The
authors in reference (Jovanov et al., 2009) proposed
a wavelet transform-based video filtering technique
that uses spatial and temporal redundancy. A content
adaptive video de-noising filter was also proposed re-
cently (Luisier et al., 2010).This method filters both
impulsive and non-impulsive noises, but the filtering
performance is low in cases with Gaussian noise with
high variance. In this work, a new pixel-based spa-
tiotemporal video noise filter that incorporates motion
changes and spatial standard deviations into the de-
noising algorithm is proposed.
Bilateral filtering has also been proposed for NR
(Yang et al., 2009). Although it is a simple algorithm,
in principle, it could cause spatial blurring in station-
ary areas. Our eyes are sensitive to blurring in station-
ary areas than in moving areas. Stopping the video
signal, we perceive a large blur in the moving areas.
However, when playing the same video again, you
cannot find the same blur. The reason for this is that
our dynamic eyesihgt is inferior to the static eyesight.
Since NRs employing recursivetemporal filters do not
cause spatial blurring but cause blurring in moving ar-
eas, they give the perception of a better image qual-
ity. Many other proposals have been made to reduce
noise in images and videos (Dabov et al., 2007)(Le-
brun et al., 2013)(Portilla et al., 2003)(Kaur et al.,
2002)(Rudin and S.Osher, 1992)(Elad and Aharon,
2006). However, none of them are sufficiently fast
for their use with real-time videos.
SIGMAP 2018 - International Conference on Signal Processing and Multimedia Applications
322

Videos have a strong correlation along the tempo-
ral axis compared to the horizontal and vertical axes.
This characteristic has been used to reduce noise in
videos. Conventional real-time NR algorithms use
temporal correlation to reduce noise (Kondo et al.,
1994)(Brailean et al., 1995)(Yagi et al., 2004). Frame
memory is required to exploit temporal correlation.
This is called inter-frame signal processing. Although
the memory cost has been reduced, the overall cost is
still high if we use it for many frames. Traditionally, a
recursive temporal filter with one frame memory was
used in this configuration. Most of digital TV sets are
equipped with the recursive temporal type noise re-
ducers. However, there is an issue in the motion areas
which have blur trails becuse the recusive filters have
infinite responses. This issue is discussed in the next
section.
Figure 1: A conventional real-time video noise reducer.
Figure 2: A noisy video frame.
Figure 3: The processed result of Figure 2 using the con-
ventional method (Figure 1).
3 ISSUES WITH THE
CONVENTIONAL METHOD
A block diagram of a real-time noise reducer is shown
in Figure 1. The parameter, α, is set based on a range
0:1 (low level noise) to 0:3 (high level noise). It re-
duces the pixel value changes using a temporal re-
cursive low pass filter at every pixel. Currently, only
this type of noise reducer is practical since it is cost-
effective. It can work in real time and is commonly
used in TV systems (TI, 2011). AAs mentioned ear-
lier in this section, the stationary areas have the same
pixel values. However, the pixels in the moving areas
change their values in every frame. Although con-
ventional noise reducers successfully reduce noise in
stationary areas by averaging the values of each pixel,
they create a motion trail blur behind the moving ob-
jects.
Figure 2 shows a frame from a noisy video. In this
video, the camera is panning from left to right. Fig-
ure 3 shows the processed result using NR shown in
Figure 1. Although the noise is reduced in Figure 3,
there is a trail from left to right in accordance with
the camera panning direction. If the noise is high and
visible, the recursive filter in the noise reducer has to
work more heavily, i.e. with a larger recursive coeffi-
cient (α in Figure 1). The larger recursive coefficient
reduces the noise. However, as shown in Figure 3, it
also causes blur in the moving areas. This type of NR
involves a trade-off between the strength of NR and
the extent of blurry trails.
A video signal can be written as f(x, y, t). Here,
x is the horizontal axis, y is the vertical axis and t is
the temporal axis. We assume noise as n(t), and the
video with noise can be expressed as follows:
f
n
(x, y, t) = f(x, y, t) + n(t) (1)
The noise reduction process of the conventional
method shown in Figure 1 can be expressed as fol-
lows:
Fn(x, y, t) = (1− α) f
n
(x, y, t − 1) + αf
n
(x, y, t) (2)
The spatial position (x,y) is the same in all frames
and only the temporal parameter t changes. There-
fore, Equation 2 can be written as follows:
Fn(t) = (1 − α) f
n
(t − 1) + αf
n
(t) (3)
Equation 3 is a recursive filter that has an infinite im-
pulse response (IIR). Theoretically, IIR leads to in-
finite trails in movement areas. In the real video,
the trails continue until the output of the IIR filter
becomes smaller than the least significant bit (LSB)
level. A temporal finite impulse filter (FIR) does not
cause the long trails associated with IIR. However,
a couple of frames of temporal relation cannot re-
duce noise to the practically required level. If we
increase the number of frames in memory, blur/trail
occurs. The spatial processing (intra-frame) NR does
not cause trails or blur. It does not work well because
Real-Time Non-linear Noise Reduction Algorithm for Video
323

the spatial correlation is not strong compared with
the temporal relation in images/videos. The spatial
NR causes a spatial blur instead of the temporal blur
that is caused by temporal recursive NR. The conven-
tional NR is a kind of low pass filter (LPF). Noise
in videos looks like it comprises high-frequency el-
ements. However, noise comprises a wide range of
frequencies, including low-frequency elements and
DC. NR works as an LPF against noise which elimi-
nates the high-frequency elements while retaining the
low-frequency elements. Although the peak level of
noise decreases, the noise changes its shape and be-
comes low-level widespread spots. Since human eyes
are sensitive to the low-frequency elements, the fre-
quency shifted low-level noise becomes more visible.
This means that conventional NR changes the noise
shape and makes it more visible.
Figure 4: Proposed NR signal prosessing.
4 PROPOSED METHOD
Figure 4 shows an image comparison of the conven-
tional and the proposed NR. In Figure 4, the hori-
zontal axis is the horizontal/vertical line of the video
and the vertical axis is the level of the video. Fig-
ure 4(a) is the input of the NR filter, which is a video
with noise. Figure 4(b) is the conventional NR pro-
cessed result of Figure 4(a). As discussed in the pre-
vious section, the levels of noise are reduced but be-
come widespread, as shown in Figure 4(b). In Fig-
Figure 5: Block diagram of proposed NR signal prosessing.
Figure 6: Processed result of Fig. 2 by the proposed
method.
ure 4(b), the levels of noise are lower than those in
Figure 4(a) after the application of the LPF. How-
ever, the noise spreads over wider areas than that in
Figure 4(a). Noise becomes more visible with LPF
especially for high-noise videos that are shot under
poor lighting conditions. When these kinds of videos
are processed by the conventional NR equipped with
LPF, the low-level widespread noise appears every-
where. The conventional noise reducer changes the
noise frequency from high to low, which makes the
noise more visible. If the noise is converted to the
high-frequency areas , it becomes less visible. Fig-
ure 4(c) shows the processed result obtained by us-
ing the proposed method. In Figure 4(c), the levels
of noise become lower but the noise does not spread.
The ends of the noise become sharp edges that con-
tain high-frequency elements. Therefore, the noise is
successfully converted to the high-frequency areas.
We propose a novel nonlinear FIR for NR. Here,
we assume f(x, y, t− 1), f(x, y, t), and f(x, y, t +1) are
three sequential frames. The target frame for process-
ing is f(x, y, t). f(x, y, t − 1) and f (x, y, t + 1) are the
reference frames. We also assume the noise in the
video is Gaussian noise with deviation because it is
the most common noise for images created under poor
lighting conditions. Noise is the undesired signal. If
f(x, y, t) contains noise, the level of f(x, y, t) is higher
or lower compared with the true value. However, al-
though the video contains noise, f(x, y, t) may be the
true value. The proposed method changes the value of
SIGMAP 2018 - International Conference on Signal Processing and Multimedia Applications
324

f(x, y, t) according to the following three cases, which
occur depending on their probability.
• f(x, y, t − 1) ≤ f(x, y, t) ≤ f(x, y, t + 1) or
f(x, y, t + 1) ≤ f(x, y, t) ≤ f(x, y, t − 1) =⇒ the
output of the NR is f(x, y, t)
• f(x, y, t) is the highest=⇒ the output of the NR is
f(x, y, t) − δ
• f(x, y, t) is the lowest=⇒ the output of the NR is
f(x, y, t) + δ
Condition 1.: if f(x,y,t) is in the middle, f(x,y,t) does
not contain noise and no signal processing is neces-
sary for f(x,y,t). The output of the NR is f(x,y,t). Con-
dition 2.: if f(x,y,t) is the highest of the three sig-
nals, f(x,y,t)- is the output of the NR. Condition 3.:
if f(x,y,t) is the lowest of the three signals, f(x,y,t)+ is
the output of the NR. A block diagram of the proposed
signal processing is shown in Figure 5. The proposed
NR comprises two frame memories, one comparer,
one adder, one subtracter, and one selector. The com-
parer has three inputs. It compares f(x,y,t) with the
other two signals, f(x,y,t-1) and f(x,y,t+1). The output
of the comparer is three bits, which represent three
conditions: f(x,y,t) is the highest, f(x,y,t) is in the
middle, and f(x,y,t) is the lowest of the three values
. These three bits are introduced to the selector. This
approach is sufficiently simple to embody as a real-
time noise reducer.
In Figure 5, the top left is the video input of the
NR filter and the bottom right is the output of NR
filter. f(x,y,t-1), f(x,y,t), and f(x,y,t+1) are obtained
with the two frame memories. By comparing f(x,y,t)
with the other two values, the order of f(x,y,t) is ob-
tained. If the value of f(x,y,t) is in the middle (case 1),
f(x,y,t) is the output of the NR. If f(x,y,t) is the high-
est, f(x,y,t)- is the output of NR (case 2). If f(x,y,t) is
the lowest, f(x,y,t)+ is the output of NR. f(x,y,t)- and
f(x,y,t)+ are created by the adder and the subtracter.
The three paths, f(x,y,t), f(x,y,t)-, and f(x,y,t)+, are the
inputs of the selector, and one of them is selected as
the output of the comparer. The block diagram shown
in Figure 5 indicates practical hardware that could im-
plement the proposed algorithm. It is a simple and
compact design for the development of real-time NR
hardware.
5 EXPERIMENT
5.1 Simulation Results
Computer simulations were conducted to compare the
peak signal-to-noise ratios (PSNRs) of the proposed
and conventional NR methods. Figure 7 shows stills
from five video sequences. In Figures 7(a) and (e), the
train and marching people are moving and the cam-
era is panning slowly. In Figure 1(b), the camera was
moved using a circular dolly, whereas in Figure 7(d),
it was dollied in and then zoomed back. The woman
stood at the same place in both sequences and did not
move significantly. Figure7(c) shows a music concert
with flashing lights and confetti.
We preparedtest video sequences by adding Gaus-
sian noise ( = 7) to Figures 7(a)(e). We then compared
the PSNRs of the proposed NR method with those of
conventional NR using computer simulations. Ow-
ing to space limitations, only the results for Figures
7(a) and (b) are presented in Figures 8 and 9. Herein,
the horizontal axis shows the frame number, and the
vertical axis shows the PSNR. The blue lines show
the PSNRs for the videos with added noise compared
with the original videos. These stay constant because
a constant level of noise ( = 7) was added. The yellow
green and purple lines show the results of process-
ing the videos with conventional NR using parame-
ters = 0.2 and 0.5, respectively, whereas the brown
lines show the results of processing the videos using
the proposed method.
Although the conventional NR method reduced
the noise in the videos, its PSNRs are lower than those
for the noisy test videos. This means that it reduced
noise and degraded the resolution. In contrast, the
proposed method (brown lines) always yields PSNRs
higher than those of the noisy test videos, as shown in
both Figures 8 and 9. These results indicate that the
proposed NR method outperforms conventional NR.
5.2 Low Luminace Video
Figure 6 shows the processed result of Figure 2 using
the proposed method three times sequentially. Com-
paring Figure 3 with Figure 6, the image quality of
Figure 6 is better than that of Figure 3. Blur in Figure
6 is less than that in Figure 3 and noise is greatly re-
duced. Note that Figures 2, 3, and 6 are just computer
simulation results.
We apply the proposed method to an actual video.
Figure 10 shows a video frame shot under 3.5 lx il-
lumination by a high-sensitivity video camera. Al-
though 3.5 lx illumination is not sufficient for imag-
ing, noise is not visible. In the video, the doll is rotat-
ing and the hair ornament is curving due to centrifugal
force. Figure 11 shows a video frame shot under 0.4
lx illumination taken by the same video camera. Even
though a high-sensitivity camera is used, noise is visi-
ble everywhere. Figure 12 shows the processed result
of Fig. 10 by the proposed method. Comparing Fig-
Real-Time Non-linear Noise Reduction Algorithm for Video
325
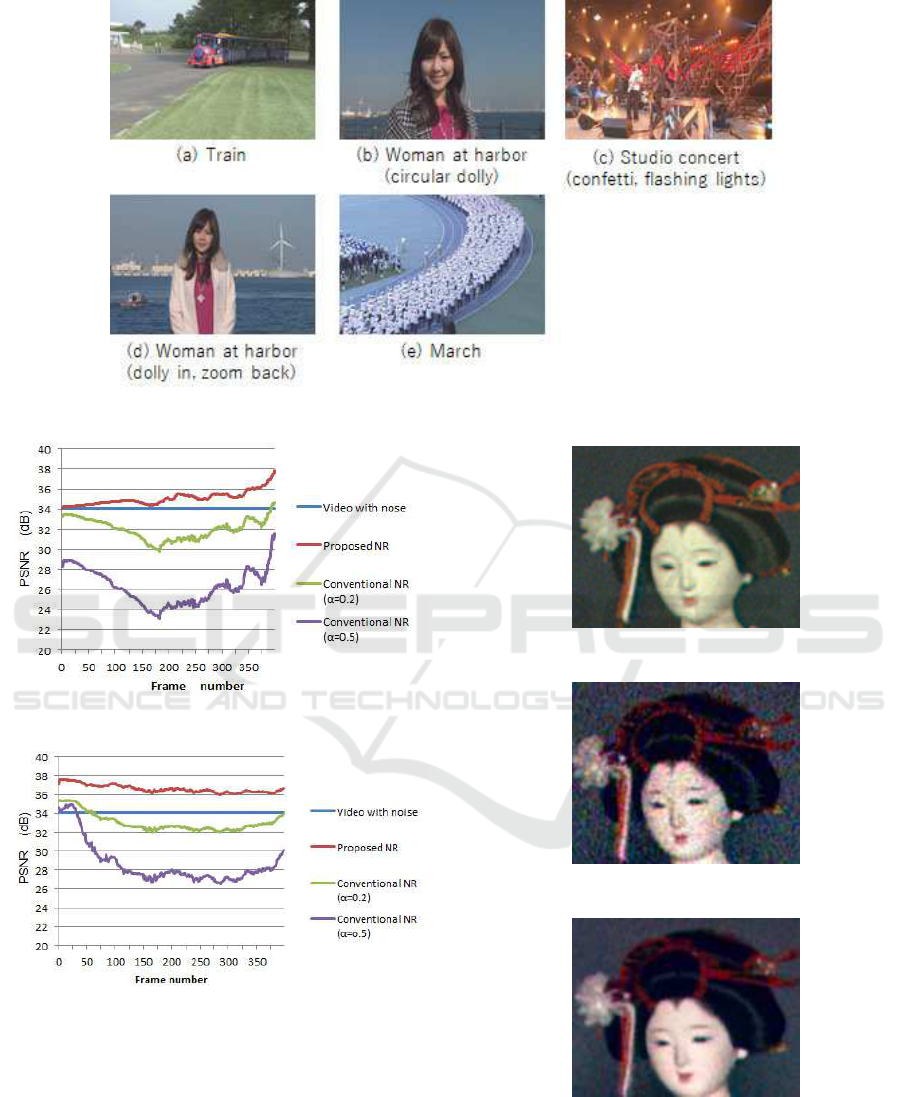
Figure 7: Video sequences.
Figure 8: Simulation results for the sequnce in Figure 7(a).
Figure 9: Simulation results for the sequnce in Figure 7(b).
ure 12 with Figure 11, noise is reduced and there is no
motion blur, which is apparent in Figure 3. In partic-
ular, the moving thin hair ornament that is curved due
to the motion is not blurry.
It should be noted that the proposed method does
not cause any blur in moving areas, unlike the conven-
tional NR. As shown in Figure 6 , the proposed NR
algorithm is simple, cost-effective, and can process
videos in real time. However, the noise levels differ
Figure 10: Image shot under 3.5 lx illumination.
Figure 11: Image shot under 0.4 lx illumination.
Figure 12: Processed result of Fig. 7 by the proposed
method.
depending on the video. It is necessary to precisely
detect the noise level to make the NR work in real
time. Future work will focus on developing a method
to detect the noise level automatically. Combining the
SIGMAP 2018 - International Conference on Signal Processing and Multimedia Applications
326

proposed NR and an automatic noise level detector
can reduce video noise effectively without human in-
tervention.
6 CONCLUSION
A novel NR algorithm that can process videos in real
time is was proposed. It does not sufferhave from
the artifactsartefacts that the afflict conventional NR
algorithmshas, such as trails behind moving objects
trails. The Computer simulations of a video with
added noise and shot in a dark room are were pre-
sented with the noise added video and the shot in a
dark room. Although the proposed NR is composed
with comprises a simple algorithm, it can remove
video noise effectively. Therefore, iIt is should not
be difficult to develop a real- time hardware based on
the proposed ideasmethod. The Future work should
focus on how to detect the noise level automatically.
REFERENCES
Brailean, J. C., Kleihorst, R. P., Efstratiadis, S., Katsagge-
los, A. K., and Lagenfdijk, R. L. (1995). Noise re-
duction filter for dynamic image sequeces : Review.
Proceedings of the IEEE, 83:1272–1292.
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2007). Image denoising by sparse 3-d transform-
domain collaborative filtering. IEEE Transactions on
Image Processing, 16(8):2080–2095.
Elad, M. and Aharon, M. (2006). Image denoising via
sparse and redundant representations over learned dic-
tionaries. IEEE Transactions on Image Processing,
15(12):3736–3745.
Gupta, N., Swamy, M. N., and Plotkin, E. (2004). Low-
complexity video noise reduction in wavelet domain.
IEEE 6th Workshop on Multimedia Signal Processing,
pages 239–242.
Jovanov, L., Pizurica, A., Schulta, S., Schelkon, P.,
Munteanu, A., Kerre, E., and Philips, W. (2009).
Combined wavelet domain and motion compensated
video denoiding based on video codec motion estima-
tion method. IEEE Transactions on Circuits and Sys-
tems for Video Technology, 19(3).
Kaur, L., Gupta, S., and Chauhan, R. (2002). Image denois-
ing using wavelet thresholdingh, indian conference on
computer vision. Graphics and Image Processing.
Kazubek, M. (2003). Wavelet domain image denoising by
thresholding and wiener filtering. IEEE Signal Pro-
cessing, 10(11):324–326.
Kondo, T., Fujimori, Y., Horishi, T., and Nishikata, T.
(1994). Patent: Noise reduction in image signals: Pct,
ep0640908 a1, ep19940306328.
Lebrun, M., Buades, A., and Morel, J.-M. (2013). A nonlo-
cal bayesian image denoising algorithm. SIAM Jour-
nal on Imaging Science, 6(3):1665–1688.
Luisier, F., Blue, T., and Unser, M. (2010). Surelet for
orthonormal wavelet domain video denoising. IEEE
Transactions on Circuits and Systems for Video Tech-
nology, 20(6).
Mahmoud, R. O. and Faheem, M. T. (2008). gcomparison
between dwt and dual tree complex wavelet transform
in video sequences using wavelet domain. INFOS.
Malfait, M. and Roose, D. (1997). Wavelet based image de-
noising using a markov random field a priori model.
IEEE Transaction on Image Processing, 6(4):549–
565.
Nai-Xiang, L., Vitali, Z., and Yap, T. P. (2006). Video
denoising using vector estimation of wavelet coeffi-
cients. ISPACS.
Piurica, A., Zlokolica, V., and Philips, W. (2004). Noise re-
duction in video sequences using wavelet-domain and
temporal filtering. Wavelet Applications in Industrial
Processing, Edited by Truchetet, Frederic. Proceed-
ings of the SPIE, 5266:48–49.
Pizurica, A., Zlokolica, V., and Philips, W. (2003). Com-
bined wavelet domain and temporal video denois-
ing. IEEE Conference on Advanced Video and Signal
Based Surveillance (AVSS2003), pages 334–341.
Portilla, J., Strela, V., Wainwright, M. J., and Simoncelli,
E. P. (2003). Image denoising using scale mixtures of
gaussians in the wavelet domain. IEEE Transactions
on Image Processing, 12(11):1338–1351.
Rudin, L. and S.Osher (1992). Nonlinear total variation
based noise removal algorithms. Physica D, 60(1-
4):259–268.
Selesnick, I. W. and Li, K. Y. (2003). Video denoising using
2d and 3d dual-tree complex wavelet transforms. In
Wavelet Applications in Signal and Image Processing
(SPIE 5207), 5207:607–618.
TI (2011). TVP5160 3D Noise Reduction Calibration Pro-
cedure Application Report: SLEA110 May, Texas In-
strument Manual.
Yagi, S., Inoue, S., Hayashi, M., Okui, S., and Gohshi, S.
(2004). Practical Video Signal Processing, pp. 143-
145, ISBN4-274-94637-1,. Ohmusha (in Japanese).
Yang, Q. X., Tan, K. I., and Ahuja, N. (2009). Real time
o(1) bilateral filtering. Computer Vision and Pattern
Recognition (CVPR).
Real-Time Non-linear Noise Reduction Algorithm for Video
327
