
Privacy-preserving Distributed Access Control for Medical Data
Christian Maulany
1
, Majid Nateghizad
1
, Bart Mennink
2
and Zekeriya Erkin
1
1
Cyber Security Group, Department of Intelligent Systems, Delft University of Technology, The Netherlands
2
Digital Security Group, Radboud University, Nijmegen, The Netherlands
Keywords:
Medical Data, Privacy, Secret Sharing, Polymorphic Encryption and Pseudonomysation.
Abstract:
The availability of wearable devices such as smartwatches and fitness trackers are a recent development.
Among other things, these devices can measure the activity and vital signs of their wearers. As the types of
data these devices are able to gather increases the potential for them to be used as a source of data grows.
This calls for a secure method of controlling the digital exchange of medical data between wearables and
healthcare providers, and healthcare providers in general. By enforcing the exchange of data to go through a
central authority, a patient can be given more control over who is able to access his medical data. This central
authority is then given the task of monitoring access and ensuring that all access requirements are met. Though
effective, this solution relies on a highly trusted central authority. In this work, we propose a scheme using
Polymorphic Encryption and Pseudonomysation and Secret Sharing to provide anonymous data storage and
data exchange. Our proposal removes the need for a central authority, and instead uses a group of authorities,
of which a quorum is needed to facilitate the exchange of data.
1 INTRODUCTION
In recent years there has been a rise in the number of
wearable devices, such as fitness trackers and smart-
watches (Wearables, 2017). These devices which of-
ten work in conjunction with a smartphone are be-
coming more accurate in their measurements and will
increasingly use cloud storage and become part of the
internet of things (Page, 2015). The increased adapta-
tion of these wearables goes hand in hand with Elec-
tronic Health Care (e-healthcare): the shift of health
care to the digital domain. In an e-healthcare setting,
patients are able to measure their medical condition at
home, using sensors placed in wearable devices. The
result is that medical measurements can be taken over
a longer period in an automated fashion. In this man-
ner costs on the number of hospital visits and work
performed by a doctor can be reduced. Furthermore,
the additional information gathered by these devices
can improve the quality of diagnosis.
Collecting and sharing medical data in e-
healthcare would benefit greatly from a cloud-based
solution, improving the availability of a patient’s
medical data and the ease of sharing. However, han-
dling medical data in such a manner causes privacy
concern. Medical data is highly sensitive; therefore,
a cloud Storage Provider (SP) should not be trusted
with it. A natural solution would be to store this
data in encrypted form, however, providing proper
access control and anonymity become two important
challenges. What is needed is a system where self-
monitoring devices and healthcare providers (HCPs)
are able to share medical data, while providing proper
access management and security.
Several countries allow a patient to decide who is
allowed to (digitally) access their medical data. This
is usually done through a Central Authority (CA). The
patient tells the CA which HCPs are allowed to ex-
change his/her medical data, fully trusting the CA to
not misuse this information, and furthermore monitor
and assist in this exchange accordingly. Usually only
certified HCPs are allowed to connect to this system.
This means third parties, such as wearable vendors
acting as SPs are unable to connect. The result is that
if provided at all, every vendor provides a different
method of sharing collected data with HCPs, making
it complicated to use data collected by wearables in
the medical domain.
1.1 Polymorphic Encryption and
Pseudonymisation
Polymorphic Encryption and Pseudonymisation for
Personalised Healthcare (PEP) by Verheul et al. (Ver-
322
Maulany, C., Nateghizad, M., Mennink, B. and Erkin, Z.
Privacy-preserving Distributed Access Control for Medical Data.
DOI: 10.5220/0006841403220331
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 322-331
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

heul et al., 2016) is a protocol that facilitates such
service. PEP allows patients and HCPs to store
data at SPs in ElGamal (El Gamal, 1984) encrypted
form, without the SP learning anything about the con-
tents and owners of the data. Anonymity is achieved
through pseudonymisation, the act of using different
identifiers for the same data at different parties. All
parties own a secret key that is derived from a mas-
ter secret key x, known only by a Key Server (KS).
The parties’ secret keys are related in such a way that
re-keying of encryptions can be done in an efficient
way, without knowing x. PEP has already been used
for medical purposes (PEP, 2017) and it seamlessly
fits the envisioned Dutch eID scheme (Verheul et al.,
2016).
Pivotal to PEP is the role of a Transcryptor (TR), a
trusted central authority through which all communi-
cation goes and who is able to re-key encryptions. For
example, if a user wants to get access to its storage at
an SP, it sends to TR an encryption of the pseudonym
under which it is known at TR. Consecutively, TR “re-
shuffles” this encryption to obtain an encryption of the
pseudonym under which the user is known at SP, “re-
keys” the encryption to match the key pair of SP, and
sends this re-shuffled encryption to SP. The SP can
then decrypt, obtain the pseudonym of the user, and
grant access. TR learns nothing about the content of
encryption, but only who is sharing data with whom.
Although PEP allows efficient communication
and transition of data, the KS and TR own secret data
that is crucial to the system. Indeed, KS’s knowledge
of the master secret key and TR’s ability to perform
re-key encryptions allows collusion of the two to de-
rive all individual secret keys. Even stronger, collu-
sion of TR with a user yields the master secret key.
Beyond the issue of collusion, TR forms a real liabil-
ity to the system, for various reasons:
• it learns all communication, can compute a map-
ping between pseudonyms and can perform ac-
cess monitoring;
• scalability becomes a concern with more and
more devices automatically storing medical data;
• if TR goes offline, the entire system stops work-
ing.
The liability of TR is acknowledged by Verheul et
al. (Verheul et al., 2016) and has also been pointed
out by Camenisch and Lehmann (Camenisch and
Lehmann, 2017).
1.2 Distributed Transcryptor
In this work, we isolate TR from the PEP protocol
and propose a solution to resolve liability issues. The
solution consists of distributing the role of TR over
a group of n TRs, of which a quorum of t TRs has
to collaborate in order to provide the mapping of
pseudonyms. Any group of less than t TRs is un-
able to learn decryption keys, perform re-shuffling of
pseudonyms, or whatsoever, even with the help of ad-
ditional HCPs or SPs.
Our solution relies on the threshold secret sharing
scheme (Shamir, 1979) used to share all secret data.
The re-randomisation, re-keying, and re-shuffling of
ElGamal encryptions in the PEP protocol are per-
formed using a neat junction of multiparty protocols
based on secret sharing (Ben-Or et al., 1988). A dif-
ficulty arises in that re-keying turns out to need expo-
nentiation of the inverse of the shared value, adding
up to the complexity of properly composing the in-
dividual protocols. Also, we introduce the re-key-
shuffling operation often used in PEP and demon-
strate that its multiparty computation protocol com-
pares favorably with the re-keying and re-shuffling
protocols individually. The protocol is described in
detail in Section 4.
From a security perspective, the individual ingre-
dients of our solution are all unconditionally secure
in the universal composability framework (Canetti,
2001) except with negligible probability. This read-
ily allows it to be used as black-box in PEP without
sacrificing security.
The improved security against collusion is there-
fore immediate. Beyond collusion, the mapping be-
tween pseudonyms cannot be performed by a single
TR, as at least t of them are needed to perform such a
mapping. The novel setup additionally increases the
scalability and availability of such a system: as long
as t TRs are online, the system will remain fully func-
tional. A formal security treatment is given in Sec-
tion 5.
We perform a complexity and performance anal-
ysis of our solution in Section 6. The number of
multiplications and exponentiations in the multiparty
phase (the most expensive steps) are O(t), where t
is the number of parties needed to evaluate success-
fully. In case of t = 1, i.e., the classical TR, re-key-
shuffling takes 671ms, whereas for t = 10 it takes
around 733ms and for t = 40 it takes around 931ms.
1
2 PRELIMINARIES
We will introduce the ElGamal cryptosystem in Sec-
tion 2.1, secret sharing in Section 2.2, and various
1
Optimization of our implementation may reduce the
running time, but it is expected this reduction is more ev-
ident for larger values of t.
Privacy-preserving Distributed Access Control for Medical Data
323

protocols for secret sharing in Section 2.3.
2.1 ElGamal Cryptosystem
ElGamal is an asymmetric cryptosystem relying on
the difficulty of computing discrete logarithms over
finite fields (El Gamal, 1984). Let p and q be large
primes such that p = 2q + 1. Let g ∈ F
∗
p
be a genera-
tor of multiplicative subgroup G
q
of order q. The se-
cret key is a random value x < q, from which the cor-
responding public key y = g
x
mod p is derived. En-
cryption under public key y is performed as E
y
(M) =
hb,ci = hg
r
,y
r
· Mi mod p, where r < q is a random
value. Decryption using secret key x is performed
as D
x
(hb,ci) =
c
b
x
=
y
r
·M
g
rx
= M mod p. The ElGamal
cryptosystem is semantically secure if the Decisional
Diffie-Hellman (DDH) problem, determine whether
a · b = c for given g, g
a
,g
b
,g
c
∈ G
q
, is hard on G
q
.
2.2 Secret Sharing
Let q be any positive integer. A (t, n) threshold
scheme allows a secret S < q to be shared among n
parties, in such a way that t colluding parties can re-
cover S but any set of t − 1 parties learns no informa-
tion about S. We denote by [S]
q
the event that S < q is
(t, n) threshold shared.
A (t,n) threshold scheme can be constructed us-
ing secret sharing (Shamir, 1979). Assume that q is
prime, and let f be a polynomial of degree t − 1 such
that f (0) = S. Value S is shared among n parties by
giving each party i a unique point (u
i
,v
i
) on f , where
u
i
is public while v
i
is kept secret. Given t unique
points on f , any point on the polynomial f , including
S = f (0), can be computed using Lagrange interpo-
lation. Let π be a sequence of t unique numbers in
{1,. .. ,n}. In order to obtain point x we calculate
f (x) =
∑
i∈π
`
i
(x) mod p , (1)
where
`
i
(x) = v
i
∏
j∈π, j6=i
x − u
j
u
i
− u
j
mod p . (2)
2.3 Secret Sharing Protocols
Multiparty computation based on the secret sharing
was first explored by Ben-Or et al. (Ben-Or et al.,
1988). Addition of secrets can be done by the n
parties trivially at no communication cost, but var-
ious more advanced protocols have appeared over
time (see, e.g., (Bar-Ilan and Beaver, 1989; Beaver,
2000; Cramer et al., 2000; Algesheimer et al., 2002;
Damg
˚
ard et al., 2006; Toft, 2009)). In this work, we
will require protocols for the addition of secrets, the
multiplication of secrets, and the generation of ran-
dom (invertible) secrets, all of which we derive from
Bar-Ilan and Beaver (Bar-Ilan and Beaver, 1989),
Damg
˚
ard et al. (Damg
˚
ard et al., 2006), and Toft (Toft,
2007). In addition, we will require a protocol for ex-
ponentiation with a secret, which differs from the for-
mer protocols in the setting, interface, and ultimately
the efficiency. We will elaborate on the security of
below protocols in Section 5.
2.3.1 Addition of Secrets
Consider two sharings [S]
q
and [T ]
q
. The parties
can generate a sharing [S + T ]
q
non-interactively by
adding their individual shares of S and T . In more
detail, if S and T are shared using polynomials f
and g of degree t − 1, every party i holds shares
f (u
i
) and g(u
i
) and can compute the share h(u
i
) =
f (u
i
) + g(u
i
) mod p corresponding to [S + T ]
q
. Poly-
nomial h is likewise of degree t − 1. We denote the
protocol by
add([S]
q
,[T ]
q
)
:
= [S + T ]
q
.
Note that the protocol immediately yields a protocol
for multiplication of a share with known value, as [S+
·· · + S]
q
= [S]
q
+ ··· + [S]
q
.
2.3.2 Multiplication of Secrets
The parties can generate a secret sharing over polyno-
mial h = f ·g with threshold t
h
= t
f
+t
g
−1 as follows.
Let π be a group of unique parties, with |π| = t
f
+t
g
−
1. Every party i computes h
0
(x
i
) = f (x
i
) · g(x
i
). The
degree of h
0
equals t
f
+t
g
− 2. In order to obtain a se-
cret sharing with threshold t
h
, every party i creates a
secret sharing for H
0
i
= h
0
(x
i
)
∏
j∈π, j6=i
x
j
x
i
x
j
, giving ev-
ery other party j share H
0
i, j
. After exchanging shares
every i computes their secret share of h as
∑
j∈π
H
0
j,i
.
We denote the protocol by
mult([S]
q
,[T ]
q
)
:
= [ST ]
q
.
2.3.3 Generation of Random Secret
In order to generate a sharing [R]
q
of a secret random
value R, every party i picks a random polynomial r
i
of
degree t −1 and gives every party j a share r
i, j
. Every
party j in turn computes
∑
n
i=1
r
i, j
as their secret share
of R. We denote the protocol by rand()
:
= [R]
q
.
2.3.4 Generation of Invertible Random Secret
The parties can generate a sharing of (R,R
−1
), where
R is a random invertible value, as follows: first, eval-
uate [R]
q
= rand() and [S]
q
= rand(), and compute
SECRYPT 2018 - International Conference on Security and Cryptography
324

[RS]
q
= rand([R]
q
,[S]
q
) and reveal T := RS. If T is
invertible, compute [T S]
q
= [(RS)
−1
S]
q
= [R
−1
]
q
non-
interactively. The protocol fails if T is not invertible,
which happens with probability at most 2/q. We de-
note the protocol by rand
∗
()
:
= ([R]
q
,[R
−1
]
q
).
2.3.5 Exponentiation with Secret
Consider a value M and a sharing [S]
q
. The parties
can compute M
S
as follows. Given π, a sequence of
t unique numbers in {1, .. ., n}, every member i in π
calculates S
i
= `
i
(0) using Eq. (2), and computes par-
tial result R
i
= M
S
i
. These partial results are com-
bined using
∏
i∈π
R
i
=
∏
i∈π
M
S
i
= M
∑
i∈π
S
i
= M
S
. (3)
We denote the protocol by
exp(M, [S]
q
)
:
= M
S
.
Damg
˚
ard et al. (Damg
˚
ard et al., 2006) gave a pro-
tocol for obtaining [T
S
]
q
from [T ]
q
and [S]
q
. In our
setting, it suffices to output a revealed value rather
than a shared value, and this allows us to simplify
the protocol significantly. The exponentiation proto-
col as outlined above appeared before, among others,
in (Desmedt and Frankel, 1989, Sect. 3.1) and (Jakob-
sson, 1999, Sect. 4).
3 POLYMORPHIC ENCRYPTION
AND PSEUDONYMISATION
The Polymorphic Encryption and Pseudonymisation
(PEP) protocol Verheul et al. (Verheul et al., 2016) al-
lows multiple parties to provide and/or use external
storage without parties learning each others’ identi-
ties. All parties are known by certain pseudonyms,
and a trusted transcryptor (TR) takes the task of
transforming encryptions and relaying them from one
party to another one. In the context of e-health, we
are mainly concerned with patients P and HCPs A.
At the core of PEP is a Key Server (KS), that
generates a master secret key x and publishes the
corresponding public key y = g
x
. Every party A in
the protocol holds a related key pair (x
A
,y
A
), where
x
A
= x · K
A
and y
A
= y
K
A
. The value K
A
is the key-
factor for A and is only known by TR. Patient P is
given a unique identifier pid
P
∈ G
q
. At every party A
providing or accessing data about P, P will be known
by a pseudonym of pid
P
, namely the value
pid
P
@A = pid
S
A
P
,
Table 1: Symbols and their meaning.
Symbol Description
x,y master key pair
x
A
,y
A
key pair of party A
K
A
key-factor for party A
S
A
pseudonym-factor for party A
pid
P
personal identifier of patient P
ppid
P
polymorphic pseudonym of P
pid
P
@A pseudonym of patient P at party A
epid
P
@A encrypted pid
P
@A
where S
A
is the S
A
is the pseudonym-factor of A, a
fixed random value known only by the TR. We refer
to Table 1 for an overview of the notation.
However, PEP does not operate on plain identi-
ties pid
P
, but rather on encryptions. Let ppid
P
=
E
y
(pid
P
) = hb, ci, an encryption of the identifier of
patient P under public key y. Taking advantage of the
homomorphic properties of ElGamal, the TR is able
to transformations between encrypted pseudonyms.
3.1 PEP Operations
PEP builds upon the following operations:
• re-randomisation takes an encryption hb,ci and a
random value r < q, and produces a randomized
encryption of the same message,
RR
r
(hb,ci)
:
= hg
r
· b,y
r
· ci mod p . (4)
• re-keying takes an encryption hb, ci encrypted un-
der public key y and a value K < q and produces
an encryption under public key y
K
(hence under
private key x
0
= x · K),
RK
K
(hb,ci)
:
= hb
K
−1
,ci mod p , (5)
where K
−1
is the inverse of K mod p.
• re-shuffling takes an encryption hb, ci of message
M and a value S < q and produces an encryption
of M
S
,
RS
S
(hb,ci)
:
= hb
S
,c
S
i mod p . (6)
3.2 Storing Data
An encrypted identifier ppid
P
is stored at all partic-
ipants supplying data for P. When a data supplier
DS wants to store data D at storage facility SF, it
first re-randomizes the ppid
P
to form a polymorphic
pseudonym, PP = RR
r
(ppid
P
) using random r. Next,
it encrypts the data D to obtain C = E
y
(D). The val-
ues PP and C are sent to the TR who re-keys and re-
shuffles PP using K
SF
and S
SF
, respectively, which
results in the encrypted polymorphic pseudonym:
epid
P
@SF = RS
S
SF
(RK
K
SF
(PP)). (7)
Privacy-preserving Distributed Access Control for Medical Data
325

TR sends epid
P
@SF and C to storage facility SF.
SF then decrypts epid
P
@SF using his private key:
D
y
SF
(epid
P
@SF) = pid
P
@SF = pid
S
SF
P
. SF stores C
using pid
P
@SF as a reference.
3.3 Retrieving Data
Let A be a participant authorized to retrieve data
D stored encrypted as C = E
y
(D) at storage facil-
ity SF. Since A is eligible to retrieve D he knows
ppid
P
= E
y
(pid
P
). A performs PP = RR
r
(ppid
P
) us-
ing random r and sends PP to the TR. TR computes
epid
P
@SF as in Eq. (7), and sends the result to SF.
SF decrypts epid
P
@SF to obtain pid
P
@SF as before,
and uses that to look up the requested encrypted data
C. SF re-randomizes C, C
0
= RR
s
(C) using random
s, and sends C
0
to TR. TR re-keys and re-shuffles
C
0
using the key-factor and pseudonym-factor of A,
R = RK
K
A
(C
0
), and forwards it to A. A can subse-
quently decrypt and obtain D
0
= D
x
A
(C
0
) = D.
3.4 Limitations of PEP
Through the pseudonymisation process, participants
have to communicate through the TR. This creates a
central party, who can perform access management,
logging and monitoring. However, this centraliza-
tion and other design decisions create several security
threats.
• The key server holds the master private key x. If it
collaborates with the storage facility, all data and
all polymorphic pseudonyms can be decrypted.
• TR holds secrets K
A
and S
A
for all parties A,
whereas each participant A holds x
A
= x · K
A
. If
TR collaborates with any party A, they can learn
x, creating the same security threat as compromis-
ing the key server. Furthermore, they can compute
any other private key, as x
B
= x ·K
B
. Furthermore,
they are able to learn personal identifier pid
A
0
from
any pseudonym of A
0
.
To prevent malicious behavior of the key server and
TR, PEP proposes the use of Hardware Security Mod-
ules (HSMs). These HSMs manage cryptographic
keys, key-factors and pseudonym-factors and all PEP
operations can only be performed inside these HSMs.
Though this prevents direct leakage of these secret
values, TR is still able to transform any data or
pseudonym, such that it can be decrypted by any par-
ticipant.
Besides security threats, the construction of PEP
can only be scaled vertically. Keeping the context of
wearables in mind, we can only expect the amount
of data which the TR needs to process to increase.
Furthermore, whenever TR goes offline, no exchange
of data can take place.
4 PRIVACY-PRESERVING
DISTRIBUTED ACCESS
CONTROL
In the original PEP a single TR is used to evaluate the
pseudonym and re-keying mappings of Section 3.1.
To obtain our solution where these operations are in-
stead performed by a quorum of t out of n TRs, we
first show how these operations can be performed in
a (t,n) manner (Section 4.1). Next, we demonstrate
how new parties and TRs can be added to the scheme
after setup (Section 4.2 and 4.3). Finally, we sug-
gest a way through which t
0
TRs can jointly perform
key generation and key management, which would re-
move the need for a trusted key server (Section 4.4).
4.1 Distributed PEP Operations
Let ppid
P
= E
y
(pid
P
) = hb,ci, an encryption of the
identifier of patient P. We describe how to com-
pute the PEP operations described in Section 3.1
in a distributed fashion. As generating [S
P
]
q
and
([K
P
]
q
,[K
−1
P
]
q
) are necessary for performing dis-
tributed PEP operations, TRs can pre-compute the
tuple of < [S
P
]
q
,[K
P
]
q
,[K
−1
P
]
q
> for each patient
P. Moreover, TRs can pre-compute [Q
P
]
q
:
= [K
−1
P
·
S
P
]
q
= mult([K
−1
P
]
q
,[S
P
]
q
), which is used later in op-
erations.
• Distributed re-keying of hb,ci for a shared value
[K]
q
with K < q is performed using the exponen-
tiation protocol of Section 2.3:
RK
K
(hb,ci) = hexp(b,[K
−1
]
q
),ci mod p . (8)
• Distributed re-shuffling of hb,ci of message M for
a shared value [S]
q
with S < q is performed using
the exponentiation protocol of Section 2.3:
RS
S
(hb,ci) = hexp(b,[S]
q
),exp(b,[S]
q
)i mod p .
(9)
PEP often performs re-keying and re-shuffling on the
same encryption consecutively, i.e., it often evaluates
RS
S
◦ RK
K
, where S and K correspond to the same
party. Instead of applying distributed re-keying and
re-shuffling independently, we can speed-up compu-
tation significantly by using the pre-computation of
[Q]
q
= [K
−1
· S]
q
, as the TRs do for every party. In
more detail, we define distributed re-key-shuffling: on
input of an encryption hb,ci, and shared values [Q]
q
SECRYPT 2018 - International Conference on Security and Cryptography
326
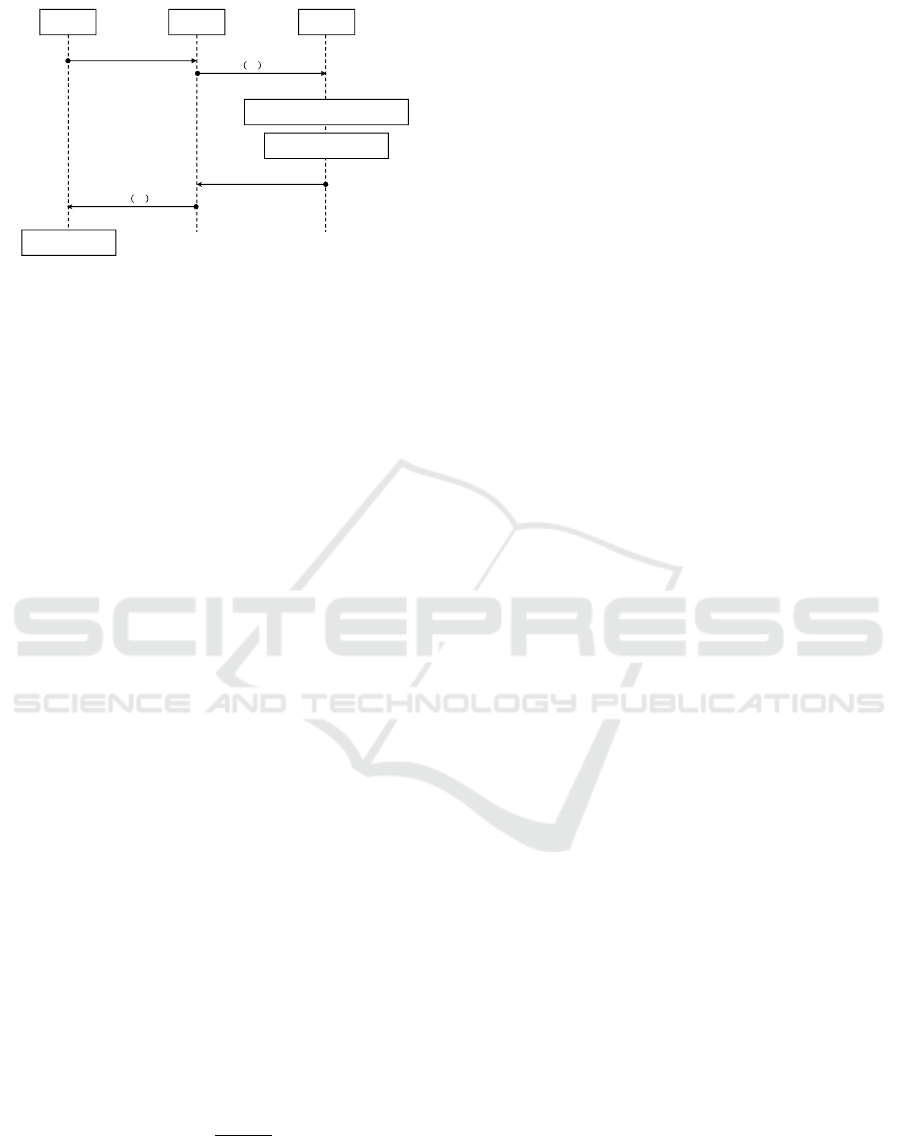
A
t TRs
SF
= ( ( ))
( )
= @
= ( @ )
Find the matching
′ = ( )
= (′ )
= ( )
Figure 1: Data retrieving in the distributed PEP.
and [S]
q
with Q,S < q, re-key-shuffling is performed
using the exponentiation protocol of Section 2.3:
RKS
Q,S
(hb,ci) = hexp(b,[Q]
q
),exp(b,[S]
q
)i mod p .
(10)
Re-key-shuffling by design satisfies RKS
K
−1
·S,S
=
RS
S
◦ RK
K
−1
.
Figure 1 shows the process of retrieving data from
SF in the distributed PEP, where an authorized party
A requests to obtain data D belong to a patient pid
P
.
The main differences between the original PEP and
the distributed version in retrieving data are the oper-
ations epid
P
@SF and R that are performed in a dis-
tributed fashion by using t TRs.
4.2 Generating New Key and
Pseudonym-factors
Let A be a new party given permission to access
some data owned by patient P. At least 2t − 1 TRs
(refer to Section 2.3.2) create secret sharings [S
A
]
q
,
([K
A
]
q
,[K
−1
A
]
q
), and [Q
A
]
q
= [K
−1
A
· S
A
]
q
. For any TR
not involved in the generation process, shares can be
generated using Lagrange interpolation.
4.3 Adding New Transcryptor
After setup, it is possible to add or replace a TR. Let
TR
k
be a new TR joining the setup. Given a (t,n)
secret sharing of secret Z ∈ G
q
, new shares for Z can
be generated using t TRs. Let π be a quorum of t TRs.
First, TR
k
is assigned a unique point u
k
not used by
any other TR. Every TR i ∈ π computes a partial result
for the secret share of Z for k as
Z
k,i
= Z
i
∏
j∈π, j6=i
u
k
− u
j
u
i
− u
j
mod p , (11)
and sends Z
k,i
to k. k can compute his secret share of
Z using
Z
k
=
∑
i∈π
Z
k,i
mod p . (12)
This way TR
k
can be given secret shares of all
pseudonym-factors, key-factors, and secret shares of
any pre-computations.
4.4 Master Key Generation
The role of a trusted key server can instead be dis-
tributed among t
0
TRs. Secret key x becomes a (t
0
,n)
threshold sharing of a secret random value. The ex-
ponentiation protocol of Section 2.3 allows the parties
to jointly compute and reveal y = g
x
.
For any participant P with (t,n) secretly shared
key-factor K
P
, t
0
+ t − 1 TRs can collaborate to com-
pute a share of the private key x
P
of P. First they com-
pute [x
P
]
q
= [x·K
P
]
q
= mult([x]
q
,[K
P
]
q
). The TRs can
send their partial results to P, who can combine those
to obtain his secret key x
P
.
Note that throughout this process no TR ever
learns nor holds the value of x. Furthermore, the se-
cret sharing of x can be done using t
0
greater than t,
improving the security of x. Also instead of giving all
TRs secret shares for x, shares can be given only to
TRs with increased trust.
5 SECURITY OF DISTRIBUTED
PEP
In this section, we provide proofs to show that our dis-
tributed PEP is simulation secure in the semi-honest
security model. Informally, we mean that the proba-
bility that an adversary can learn private information
from truly generated data by the parties in our pro-
tocols is at most negligibly more than the probability
that an adversary can learn from given randomly gen-
erated data. We use the simulatability paradigm (Lin-
dell, 2017) in our proofs, where the adversary takes
the control of the network and tries to obtain the fi-
nal result of the protocol by itself as the only party in
the protocol. In this paradigm, security is defined as
a comparison of computation work-flow in the “real
world” and the “ideal world”.
In real world, a protocol can be broken into sub-
protocols or computations that are carried out by each
party throughout the protocol. Let us denote π as
the distributed PEP protocol; we can split π into two
parts: π = π
T R
and π
SF
, which are performed in a
quorum of t TRs and SF, respectively. In retrieving
data, as an instance, π
T R
takes RR
r
(ppid
P
) as an in-
put from A and outputs epid
P
@SF to π
SF
. Then, π
SF
decrypts the given encryptions from π = π
T R
to ob-
tain pid
P
@SF and starts searching for corresponding
ciphertext C. Afterwards, π
SF
re-randomizes C and
Privacy-preserving Distributed Access Control for Medical Data
327

sends it to π = π
T R
. Thus, to retrieve specific en-
crypted data from the storage facility the encrypted
messages flow from one party to another party and
together they send back the result to the party A. As-
suming SF is corrupted by an adversary A, then A has
access to pid
P
@SF, and the encrypted search result
C. Similarly, when one of the TRs is corrupted, the
adversary has access to the intermediate computation
results.
In an ideal world, it is assumed that one of the par-
ties is corrupted by an adversary. Then, he uses a sim-
ulator to generate the outputs of the other parties. This
would be similar to performing the protocol with just
one corrupted party. In the ideal world, an adversary
´
A, who has control over SF, has only access to its pair
of (pid
P
@SF,C), and the garbage inputs given from
a simulator instead of the correct result of π
T R
. The
goal is to show that A can learn equal or negligibly
more than
´
A, meaning that they are computationally
indistinguishable. Then we can conclude that the pro-
tocol is a simulation secure protocol.
5.1 Security of Key Generation
Since, in our setting, the TRs are assumed to be semi-
trusted (not fully trusted like original PEP) we need
to show that any set of corrupted t − 1 TRs cannot
deduce any information about the secret.
Definition 5.1. Let the shared secret be a value S,
and algorithm π be a (t,n) threshold secret sharing
scheme, where π(S) = [s
1
,· ·· , s
n
]. Then, any adver-
sary A that has access to t − 1 shares from [s
1
,· ·· , s
n
]
cannot infer any information about the values of S.
5.2 Security of Storing Data
In the process of storing data, SF does
not have any input and is denoted by φ.
output
StoringData
i
(PP,C;S
SF
j
,K
SF
j
;φ; n) represents
the output of each party in storing data. The joint
output of two parties TRs and SF can be represented
as:
output
StoringData
(PP,C;S
SF
j
,K
SF
j
;φ; n))
= (output
StoringData
1
(PP,C;S
SF
j
,K
SF
j
;φ; n),
output
StoringData
2
(PP,C;S
SF
j
,K
SF
j
;φ; n)).
(13)
Definition 5.2. the process of storing data securely
computes f = (DS
f
,T R
f
,SF
f
) in the semi-honest se-
curity setting if there exist PPT algorithms Sim
T R
and
Sim
SF
such that:
{(Sim
T R
(1
n
,S
SF
,K
SF
,T R
f
, f ))}
c
≡ {(view
f
T R
(PP,C;
S
SF
j
,K
SF
j
;φ; n),output
f
(PP,C;S
SF
j
,K
SF
j
;φ; n))}.
(14)
and
{(Sim
SF
(1
n
,φ, SF
f
, f ))}
c
≡ {(view
f
SF
(PP,C;
S
SF
j
,K
SF
j
;φ; n),output
f
(PP,C;S
SF
j
,K
SF
j
;φ; n))}.
(15)
Denote the computation of PP = RR
r
(ppid
P
)
in the data supplier as DS
f
1
, C = E
y
(D) as
DS
f
2
, epid
P
@SF = RS
S
SF
(RK
K
SF
(PP)) as T R
f
1
,
and pid
P
@SF = D
y
SF
(epid
P
@SF) as SF
f
1
. Let
f = (DS
f
,T R
f
,SF
f
), where DS
f
= (DS
f
1
,DS
f
2
),
T R
f
= (T R
f
1
), SF
f
= (SF
f
1
) the f to be the
PPT functionality for storing data. The view of
the i
th
party i ∈ {DS, T R,SF} for storing data on
(PP,C;S
SF
j
,K
SF
j
;φ) and security parameter n is de-
noted by view
StoringData
i
(PP,C;S
SF
j
,K
SF
j
;φ; n) =
(w,r
i
;m
i
1
,· ·· , m
i
v
), where j ∈ {1, ·· · ,t},
w ∈ {PP,C, S
SF
,K
SF
,φ} based on i, r
i
is the
random number for i
th
party, and m
i
z
is the z
th
messages received by i
th
party.
Theorem 1. The protocol for storing data using dis-
tributed PEP securely computes the functionality f ,
when at most t − 1 TRs are corrupted by adversary A
in the presence of semi-honest adversaries.
Proof. We need to show that any set of t − 1 collud-
ing TRs cannot computationally distinguish between
generated messages and outputs from S
1
that is the
simulation of DS, and randomly generated data. TRs
receive two outputs from S
1
, PP and C. Given S
SF
,
K
SF
, and 1
n
(security parameter), storing data works
as follow:
1. S
1
chooses two random numbers r
1
and r
2
as
´
pid
P
and
´
D, respectively. Then, it performs DS
f
1
(r
1
)
and DS
f
2
(r
2
) to obtain
´
PP and
´
C and sends them
to a quorum of t TRs.
2. t TRs perform T R
f
1
to obtain epid
P
@SF, and
send it to DS together with C.
3. S
3
performs SF
f
1
to obtain pid
SF
P
, then stores the
pair (pid
SF
P
,
´
C) in its database.
The output of the simulation can be written
Sim
T R
(1
n
,S
SF
,K
SF
,T R
f
, f ) = (S
SF
,K
SF
;
´
PP,
´
C). The
real view of any TR involved in the protocol can be
represented as view
f
T R
(S
SF
,K
SF
) = (S
SF
,K
SF
;PP,C).
It can be observed that A cannot distinguish be-
tween C and
´
C since the ElGamal cryptosystem is se-
mantically secure. Moreover, since any set of t − 1
SECRYPT 2018 - International Conference on Security and Cryptography
328

corrupted TRs cannot decrypt any ciphertext; there-
fore, they are unable to distinguish between PP and
´
PP.
Theorem 2. The protocol for storing data using dis-
tributed PEP securely computes the functionality f ,
when SF is corrupted by adversary A in the presence
of semi-honest adversaries.
Proof. Assuming that SF is corrupted, we need to
show that A cannot distinguish between random gen-
erated results from other parties and the correct ver-
sions. SF receives two outputs from S
2
, as a simulator
for TRs, that are epid
P
@SF and C. The process of
storing data with the simulator S
2
, and given 1
n
as the
security parameter is as follows:
1. S
2
chooses three random numbers r
1
, r
2
, and r
3
as
´
pid
P
,
´
D, and S
SF
, respectively, then encrypts them
under public key y. Afterwards, S
2
performs T R
f
1
to obtain
´
epid
P
@SF and sends (
´
epid
P
@
´
SF,
´
C) to
SF.
2. SF performs SF
f
1
to get
´
pid
SF
P
, then stores the pair
(
´
pid
SF
P
,
´
C) in its database.
SF does not have access to the private key of DS,
thus it cannot decrypt
´
C and distinguish between
´
C
and C since the ElGamal cryptosystem is semantically
secure. Moreover, TRs re-shuffle the encrypted id be-
fore sending it to SF; therefore, SF cannot link
´
pid
SF
P
back to its owner. Therefore, we can conclude that
{(Sim
SF
(1
n
,φ, SF
f
, f ))}
c
≡ {(view
f
SF
(PP,C;
S
SF
j
,K
SF
j
;φ; n),output
f
(PP,C;S
SF
j
,K
SF
j
;φ; n))}.
(16)
5.3 Security of Retrieving Data
Assume that party A is authorized to retrieve
the data for pid
P
, denote the computation of
ppid
P
= E
y
(pid
P
) as A
f
1
, PP = RR
r
(ppid
P
) as A
f
2
,
epid
P
@SF = RS
S
SF
(RK
K
SF
(PP)) as T R
f
1
, pid
S
SF
P
=
D
y
SF
(epid
P
@SF) as SF
f
1
, C
0
= RR
s
(C) as SF
f
2
, and
R = RK
K
A
(C
0
) as T R
f
2
. Then, f = (A
f
,T R
f
,SF
f
),
where A
f
= (A
f
1
,A
f
2
), T R
f
= (T R
f
1
,T R
f
2
), and
SF
f
= (SF
f
1
,SF
f
2
).
Theorem 3. The protocol for retrieving data using
distributed PEP securely computes the functionality
f , when at most t − 1 TRs are corrupted by adversary
A in the presence of semi-honest adversaries.
Proof. We need to show that any of the TRs or a quo-
rum of t − 1 TRs cannot infer any information about
the private data after performing the protocol for re-
trieving data. Let S
1
be the simulator of party A and
S
3
the simulator of SF. Given S
SF
and K
SF
as the in-
puts of TRs and 1
n
as a security parameter, retrieving
data from SF for party A works as follows:
1. S
1
chooses a random number r
1
and performs
A
f
1
(r
1
) and A
f
2
to obtain
´
PP and sends it to a set
of t TRs.
2. TRs receive
´
PP and perform T R
f
1
to get
epid
P
@SF, then send it to S
3
.
3. S
3
performs SF
f
1
, encrypts a random number to
get C, executes
ˆ
C = SF
f
2
(C), and sends
ˆ
C to TRs.
4. TRs perform T R
f
2
and send R to S
1
.
The output of the simulation can be written
Sim
T R
(1
n
,S
SF
,K
SF
,T R
f
, f ) = (S
SF
,K
SF
;
´
PP,
ˆ
C). The
real view of any TR involved in the protocol can be
represented as view
f
T R
(S
SF
,K
SF
) = (S
SF
,K
SF
;PP,
´
C).
Since having at most t −1 corrupted TRs does not en-
able the decryption of the given messages, the TRs
cannot distinguish between PP and
´
PP, and
´
C and
ˆ
C.
Theorem 4. The protocol for retrieving data using
distributed PEP securely computes the functionality
f , when SF is corrupted by adversary A in the pres-
ence of semi-honest adversaries.
Proof. In the process of retrieving data securely, SF
plays an important role in finding the data in the re-
mote database. If SF becomes corrupted by an ad-
versary A, we need to guarantee that A can infer any
sensitive information from the given messages. SF re-
ceives epid
P
@SF from the TRs, decrypts it, and finds
the matching data. Let S
2
be the simulator for TRs,
then the process of retrieving data is as follows:
1. S
2
chooses two random numbers r
1
and r
2
as
´
PP
and S
SF
, respectively. Afterwards, S
2
performs
T R
f
1
(
´
PP,r
2
) to obtain
´
epid
P
@SF and sends it to
SF.
2. SF performs SF
f
1
(
´
epid
P
@SF) to get
´
pid
SF
P
and
checks all pairs of (pid
SF
P
,
´
C) in its database to
find the matching data. Then, it executes SF
f
2
and
sends the result back to the TRs.
The output of the simulation for retrieving data
when SF is corrupted is Sim
T R
(1
n
,pid
SF
P
,
´
C, SF
f
, f ) =
(pid
SF
P
,
´
C;
´
epid
P
@SF). The real view of any TR
involved in the protocol can be represented as
view
f
SF
(pid
SF
P
,
´
C; epid
P
@SF). Therefore. if A can-
not distinguish between epid
P
@SF and
´
epid
P
@SF,
Privacy-preserving Distributed Access Control for Medical Data
329

then we can conclude the protocol is simulation se-
cure. Note that both ciphertexts are encrypted with
K
SF
, thus SF can decrypt both to obtain pid
SF
P
and
´
pid
SF
P
. However, A is still unable to distinguish be-
tween pid
SF
P
and
´
pid
SF
P
, since they are re-shuffled with
different S
SF
values and A cannot track back to check
who is the owner of the data.
6 EFFICIENCY
6.1 Complexity
A complexity analysis of our distributed RR, RK, RS,
and RKS is given in Table 2. Here, the total amount
of multiplications and exponentiations is computed
in case t TRs participate. The merging of the pre-
computations (phase (ii) in RR, and the combination
step for exponentiation, Eq. (3)) is assumed to be eval-
uated by one participant. All operations show a com-
plexity of O(t). For comparison, in the original PEP,
operations have the complexity of O(1).
Table 2: Computational complexity of distributed PEP op-
erations.
Operation Mult. Exponen. Overall
RR 2t + 2 0 O(t)
RK t t O(t)
RS 2t 2t O(t)
RKS 2t 2t O(t)
For any distributed PEP operation the analysis
of the message complexity is as follows: a partici-
pant needs to send a polymorphic pseudonym and en-
crypted data C to t TRs, who subsequently perform
their operations and return their partial results to the
single receiver. This gives us a tight bound of θ(2t)
messages.
6.2 Performance
Although we have provided a distributed RR opera-
tion, this operation is not used by the TRs in our par-
ticular application, and we focus on distributed RKS.
We have implemented the protocol using C++ and the
GMP library
2
, and tested their performance on a ma-
chine running Windows 10.0, with an Intel Core i5-
7200 running at 2.50GHz.
To have a clear view on the cost of the individual
steps in the protocol, we have separated RKS as fol-
lows. Let π be a set of unique TRs in n with |π| = t.
2
See https://gmplib.org.
Let Q
i
, S
i
be the partial results of the Lagrange inter-
polation of secret shares [Q]
q
and [S]
q
for TR i (cf.,
Eq. (1)).
• Every TR i ∈ π computes a partial result as
PRKS
Q
i
,S
i
(hb,ci)
:
= hb
i
,c
i
i = hb
Q
i
,c
S
i
i. (17)
• One party combines the partial results as
CPR({hb
i
,c
i
i}
i∈π
)
:
= h
∏
i∈π
b
i
,
∏
i∈π
c
i
i. (18)
Table 3 gives the computation time for performing t
PRKS operations and combining the partial results us-
ing CPR, for different values of t. The PRKS compu-
tation time is the average time spend by a single TR,
averaged over 1000 evaluations.
Table 3: Average computation time of 1000 PRKS and CPR
operations.
t PRKS (ms) CPR (ms)
10 707 26
19 754 68
31 776 95
40 803 128
7 CONCLUSION
In this work, we proposed a solution for controlling
access in a fully distributed manner. The solution re-
lies on multiple applications of Secret Sharing, along
with multiparty computation protocols on shared val-
ues. Our solution performs well complexity and per-
formance wise, and is unconditionally secure as long
as no “too large group” collides. If combined with
the original PEP protocol by Verheul et al. (Verheul
et al., 2016), our distributed transcryptor thus allows
for improved security, while at the same time facili-
tating scalability and robustness.
REFERENCES
Algesheimer, J., Camenisch, J., and Shoup, V. (2002). Ef-
ficient computation modulo a shared secret with ap-
plication to the generation of shared safe-prime prod-
ucts. In Yung, M., editor, Advances in Cryptology
- CRYPTO 2002, 22nd Annual International Cryp-
tology Conference, Santa Barbara, California, USA,
August 18-22, 2002, Proceedings, volume 2442 of
Lecture Notes in Computer Science, pages 417–432.
Springer.
Bar-Ilan, J. and Beaver, D. (1989). Non-cryptographic
fault-tolerant computing in constant number of rounds
of interaction. In Rudnicki, P., editor, Proceedings of
SECRYPT 2018 - International Conference on Security and Cryptography
330

the Eighth Annual ACM Symposium on Principles of
Distributed Computing, Edmonton, Alberta, Canada,
August 14-16, 1989, pages 201–209. ACM.
Beaver, D. (2000). Minimal-latency secure function evalu-
ation. In (Preneel, 2000), pages 335–350.
Ben-Or, M., Goldwasser, S., and Wigderson, A. (1988).
Completeness theorems for non-cryptographic fault-
tolerant distributed computation (extended abstract).
In Simon, J., editor, Proceedings of the 20th Annual
ACM Symposium on Theory of Computing, May 2-4,
1988, Chicago, Illinois, USA, pages 1–10. ACM.
Camenisch, J. and Lehmann, A. (2017). Privacy-preserving
user-auditable pseudonym systems. In 2017 IEEE Eu-
ropean Symposium on Security and Privacy, EuroS&P
2017, Paris, France, April 26-28, 2017, pages 269–
284. IEEE.
Canetti, R. (2001). Universally composable security: A
new paradigm for cryptographic protocols. In 42nd
Annual Symposium on Foundations of Computer Sci-
ence, FOCS 2001, 14-17 October 2001, Las Vegas,
Nevada, USA, pages 136–145. IEEE Computer Soci-
ety.
Cramer, R., Damg
˚
ard, I., and Maurer, U. M. (2000). Gen-
eral secure multi-party computation from any linear
secret-sharing scheme. In (Preneel, 2000), pages 316–
334.
Damg
˚
ard, I., Fitzi, M., Kiltz, E., Nielsen, J. B., and Toft,
T. (2006). Unconditionally secure constant-rounds
multi-party computation for equality, comparison, bits
and exponentiation. In Halevi, S. and Rabin, T.,
editors, Theory of Cryptography, Third Theory of
Cryptography Conference, TCC 2006, New York, NY,
USA, March 4-7, 2006, Proceedings, volume 3876 of
Lecture Notes in Computer Science, pages 285–304.
Springer.
Desmedt, Y. and Frankel, Y. (1989). Threshold cryptosys-
tems. In Brassard, G., editor, Advances in Cryptol-
ogy - CRYPTO ’89, 9th Annual International Cryptol-
ogy Conference, Santa Barbara, California, USA, Au-
gust 20-24, 1989, Proceedings, volume 435 of Lecture
Notes in Computer Science, pages 307–315. Springer.
El Gamal, T. (1984). A public key cryptosystem and a sig-
nature scheme based on discrete logarithms. In Blak-
ley, G. R. and Chaum, D., editors, Advances in Cryp-
tology, Proceedings of CRYPTO ’84, Santa Barbara,
California, USA, August 19-22, 1984, Proceedings,
volume 196 of Lecture Notes in Computer Science,
pages 10–18. Springer.
Jakobsson, M. (1999). On quorum controlled asymmetric
proxy re-encryption. In Imai, H. and Zheng, Y., ed-
itors, Public Key Cryptography, Second International
Workshop on Practice and Theory in Public Key Cryp-
tography, PKC ’99, Kamakura, Japan, March 1-3,
1999, Proceedings, volume 1560 of Lecture Notes in
Computer Science, pages 112–121. Springer.
Lindell, Y. (2017). How to simulate it - A tutorial on the
simulation proof technique. In Tutorials on the Foun-
dations of Cryptography., pages 277–346.
Page, T. (2015). A forecast of the adoption of wearable
technology. IJTD, 6(2):12–29.
PEP (2017). Polymorphic encryption and pseudonymisa-
tion for personalised healthcare. https://pep.cs.ru.nl.
Preneel, B., editor (2000). Advances in Cryptology - EURO-
CRYPT 2000, International Conference on the The-
ory and Application of Cryptographic Techniques,
Bruges, Belgium, May 14-18, 2000, Proceeding, vol-
ume 1807 of Lecture Notes in Computer Science.
Springer.
Shamir, A. (1979). How to share a secret. Commun. ACM,
22(11):612–613.
Toft, T. (2007). Primitives and Applications for Multi-
party Computation. PhD thesis, University of Aarhus,
Aarhus.
Toft, T. (2009). Constant-rounds, almost-linear bit-
decomposition of secret shared values. In Fischlin,
M., editor, Topics in Cryptology - CT-RSA 2009, The
Cryptographers’ Track at the RSA Conference 2009,
San Francisco, CA, USA, April 20-24, 2009. Proceed-
ings, volume 5473 of Lecture Notes in Computer Sci-
ence, pages 357–371. Springer.
Verheul, E., Jacobs, B., Meijer, C., Hildebrandt, M., and
de Ruiter, J. (2016). Polymorphic encryption and
pseudonymisation for personalised healthcare. Cryp-
tology ePrint Archive, Report 2016/411.
Wearables (2017). Wearables market to be worth $25 billion
by 2019. http://www.ccsinsight.com/press.
Privacy-preserving Distributed Access Control for Medical Data
331
