A Quantum-Secure Niederreiter Cryptosystem using Quasi-Cyclic Codes

Upendra Kapshikar and Ayan Mahalanobis

IISER Pune, Pune, India

Keywords:

Niederreiter Cryptosystem, Post-quantum Cryptography, Quantum Fourier Sampling.

Abstract:

In this paper, we describe a new variant of Niederreiter cryptosystem over quasi-cyclic codes of rate

m−1

. We

show that the proposed cryptosystem is quantum secure, in particular, it resists quantum Fourier sampling and

has better transmission rate with smaller keys compared to the one using binary Goppa codes.

1 INTRODUCTION

In this paper, we develop a new Niederreiter cryp-

tosystem using

m−1

quasi-cyclic codes. These are

well known linear block codes. The main result in

this paper is, the Niederreiter cryptosystem built with

these codes is quantum-secure. Many attempts were

made by many distinguished authors to built new

McEliece or Niederreiter cryptosystems using differ-

ent codes. However, none of these authors demon-

strated that their cryptosystem is quantum-secure.

One of the main reason to study the Niederreiter cryp-

tosystem is that it can be quantum-secure. In today’s

world designing cryptosystem just got twice as hard.

One needs to ensure that it is secure from known clas-

sical attacks as well as secure from the known quan-

tum attacks, i.e., from the hidden subgroup problem

arising out of quantum Fourier sampling.

The concept of security which is tied to quan-

tum Fourier sampling for non-abelian groups has a

rich tradition in the work of Hallgreen et al. (Hall-

grean et al., 2003) and Kempe and Salev (Kempe and

Shalev, 2005). Dinh et al. (Dinh et al., 2011) us-

ing earlier work showed that the McEliece cryptosys-

tem built on binary Goppa codes is quantum-secure.

We use their theorem (Dinh et al., 2011, Theorem 4)

to show that our proposed cryptosystem is quantum-

secure. This work is part of ﬁrst author’s master’s

thesis (Kapshikar, 2018).

Description of the Parity Check Matrix Used for

the Proposed Niederreiter Cryptosystem. Recall

that we are talking about

m−1

quasi-cyclic codes over

. For the cryptosystem to be quantum-secure the

parity check matrix H for the [n = mp,k = (m − 1)p],

m−1

quasi-cyclic code should satisfy the following

conditions:

I. Integers m, p, such that p is a prime and m is

bounded above by a polynomial in p.

II. The matrix H is of size p × mp over F

III. The matrix H is of the form H =

= I |C

|... |C

m−1

], where each C

a circulant matrix of size p. Each C

for i > 0

should contain an element from a proper exten-

sion of F

. Furthermore, we denote the matrix

H as [I |C ] where C is the concatenation of the

circulant matrices C

, i > 0.

IV. We deﬁne T

corresponding to a matrix H as



∈ S

| ∃P

∈ S

p(m−1)

s. t. P

= C



where S

is the symmetric group acting on n let-

ters. It is easy to see that T

is a permutation

group action on p letters. The condition we im-

pose on H is that T

is not 2-transitive.

V. No two columns of C are identical.

For more on quantum security of the proposed cryp-

tosystem a reader can skip to Section 5.

2 REVIEW OF NIEDERREITER

CRYPTOSYSTEM

In 1978, Robert McEliece (McElice, 1978) suggested

a cryptosystem based on algebraic codes. The sys-

tem did not gain much popularity then because of its

large key sizes. However, with quantum computing

becoming a reality, McEliece cryptosystems have be-

come the center of attention for cryptographers. Un-

like RSA or ElGamal cryptosystem, McEliece cryp-

tosystem is based on a non-commutative structure

340

Kapshikar, U. and Mahalanobis, A.

A Quantum-Secure Niederreiter Cryptosystem using Quasi-Cyclic Codes.

DOI: 10.5220/0006843005060513

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 340-347

ISBN: 978-989-758-319-3

which allegedly makes it a strong candidate for post-

quantum cryptography. Compared to traditional cryp-

tosystems, a McEliece cryptosystem has following

advantages:

a) It is fast. Faster than RSA or ElGamal.

b) It is believed to be quantum secure.

The disadvantages are the following:

a) The key sizes are huge.

b) The ciphertext becomes much larger than the

plaintext because of the redundancy added by the

encoding process.

In this paper we focus on building a Niederreiter cryp-

tosystem. Apart from fulﬁlling the obvious require-

ment of a signature scheme, Niederreiter cryptosys-

tem is faster compared to a McEliece cryptosystem.

Li et al. (Li et al., 1994) proved that the security of a

McEliece cryptosystem and its Niederreiter counter-

part are equivalent under the Lee-Brickell attack (Lee

and Brickell, 1988). For these reasons, in this paper

our main focus is on building a Niederreiter cryp-

tosystem.

All codes in this paper are linear block codes

and our standard reference for coding theory is

Blahut (Blahut, 2003, Chapter 3). A binary linear

code C of length n and rank k is a k dimensional linear

subspace of F

. Hamming weight or simply weight t

of a codeword means that the codeword has t non-

zero entries. Standard distance on C is the hamming

distance. Distance of a linear code C is deﬁned as

minimum distance between two non-zero codewords.

Traditionally, such a code is denoted as [n,k] code.

The ratio

is the transmission rate of the code.

A generator matrix M of an [n,k] linear code C is

a k × n matrix such that C = {xG : x ∈ F

}. A gener-

ator matrix M of the form [I

] is said to be in the

systematic form. A parity check matrix H of an [n,k]

linear code C is an (n − k)×n such that H x = 0 if and

only if x ∈ C . A code generated by H is known as the

dual code and denoted by C

⊥

A decoding problem is given x ∈ F

ﬁnd a code-

word c ∈ C that is closest to x. This problem for a ran-

dom linear code is called the general decoding prob-

lem and is known to be NP-hard (Berlekamp et al.,

1978). But for some codes this decoding problem can

be solved efﬁciently. If such an algorithm is available

for a code C , we say that C has a decoder.

2.1 Quasi-Cyclic Codes

A quasi-cyclic code (QCC) is a block linear code

which is a simple generalisation of the cyclic code.

It is such that any cyclic shift of any codeword by m

symbols gives another codeword. We are particularly

interested in

m−1

rate codes. In particular our sys-

tem is based on

m−1

rate codes over F

. Such codes

along with quasi-cyclic codes of rate

were studied

in great detail by Gulliver (Gulliver, 1989).

Deﬁnition 2.1 (Circulant matrix). A square matrix is

called circulant if every row, except for the ﬁrst row,

is a circular right shift of the row above that.

A rate

m−1

systematic QCC has an p × mp parity

check matrix of the form H = [ I

| ... |C

m−1

]

where each C

is a circulant matrix of size p and I

the identity matrix of size p.

For compactness we denote H = [I |C ]. In a re-

cent work Aylaj et al. (Aylaj et al., 2016) found a

way to construct generator matrices for such codes

over F

. Since these generator matrices are in sys-

tematic form one can easily construct parity check

matrix from these generator matrices. As said pre-

viously, our main interest lies in codes over extension

ﬁelds. Gulliver (Gulliver, 1989, Chapter 6) shows that

quasi-cyclic codes over extension ﬁelds can be MDS

(maximum distance separable) codes. As the name

suggests, MDS codes can achieve large minimum dis-

tance and so there would be no low weight codewords.

This plays an imporatnt role in the classical security

of McEliece and Niederreiter cryptosystems, such as

the Stern’s attack and the Lee-Brickell attack. Though

Gulliver (Gulliver, 1989) only presents examples of

MDS codes with rate

, he does present a case to

study quasi-cyclic codes of rate

m−1

with large mini-

mum distances.

2.2 Decoding

Quasi-cyclic codes are well studied and well estab-

lished codes and depending on how one constructs

them there are various decoders available. We brieﬂy

mention some of them here. Gulliver (Gulliver, 1989,

Appendix B) presents a ML (majority logic) decod-

able QCCs. Another new and intersting way of de-

coding quasi-cyclic codes using Gr

obner basis can be

found in the work of Zeh and Ling (Zeh and Ling, ).

2.3 Niederreiter Cryptosystem

Let H be a k × n parity check matrix for a [n,n − k]

linear code C for which a fast decoding algorithm

exists. Let t be the number of errors that C can

correct.

Private Key: (A

,H ,B

) where A

∈ GL

) and B

is a permutation matrix of size n.

A Quantum-Secure Niederreiter Cryptosystem using Quasi-Cyclic Codes

341

Public Key: H

= A

H B

Encryption:

Let X be a n-bit plaintext with weight at most t. The

corresponding ciphertext Y of k-bits is obtained

by calculating Y = H

Decryption:

Compute y = A

−1

Y . Thus y = H B

Using Gaussian elimination ﬁnd a z such that weight

of z is at most t and H z

= y. Since y = H B



− B



= 0. Hence we have z−X B

∈ C .

Now use fast decoding on z with H to get X B

and

thus recover X .

For further details on Niederreiter cryptosystem the

reader is referred to (Niederreiter and Xing, 2009,

Chapter 6).

3 CLASSICAL ATTACKS

In this seciton we brieﬂy go over the generic classi-

cal attacks against McEliece and Niederreiter cryp-

tosystems. We also mention some attacks exploit-

ing the circulant structures in the keys. Interestingly,

Li et al. (Li et al., 1994, Section III) proved (see

also (Niederreiter and Xing, 2009, Theorem 6.4.1))

that both McElice and Niederreiter cryptosystems are

equivalent in terms of classical security. The proof

follows from the fact that the encryption equation for

one can be reduced to the other. This implies the

equivalence of security of both the cryptosystems for

attacks that try to extract the plaintext from a cipher-

text.

Most generic attacks over algebraic code based

cryptosystems are information set decoding at-

tacks(ISD). Two most popular ways of implementing

ISD attacks are by Lee and Brickell (Lee and Brick-

ell, 1988) and Stern (Stern, 1988). As mentioned by

Baldi et al. (Baldi et al., 2008) ISD attacks are the

best known attacks with the least work factor as far

as classical cryptanalysis is considered. Hence these

work factors are considered as security levels for a

McEliece and Niederreiter cryptosystems.

The basic idea behind one of the attacks was sug-

gested by McEliece himself. Lee and Brickell (Lee

and Brickell, 1988) improved the attack and added

an important veriﬁcation step where attacker conﬁrms

that recovered message is the correct one. In this

case, we are dealing with a McEliece cryptosystem

over a [n,k] linear code. The strategy is based on re-

peatedly selecting k bits at random from a n-bit ci-

phertext in hope that none of the selected bits are

part of the error. Similar attacks can also be im-

plemented over Niederreiter cryptosystems. Lee and

Brickwell also provided a closed-form equation for

complexity of the attack. As our system is based on

(n = mp,k = (m − 1)p, d

min

= 2E + 1) code the ex-

pression for minimal work factor (with α = β = 1 as

taken by Lee and Brickell) takes the following form

min

= W

= T



(m − 1)

+ (m − 1)pN



where T

+ Q

and Q





n−E

k−i







with N

= 1 + k +





In Table 1 we present numerical data for work fac-

tor for diferent values of parameters. Recently, Aylaj

et al. (Aylaj et al., 2016) developed an algorithm to

construct stack-circulant codes with high error cor-

recting capacity which makes the proposed Nieder-

reiter cryptosystem much more promising.

Other ISD attacks are based on a strategy given

by Stern. To recover the intentional error vector e in

a McEliece cryptosystem such strategies use an ex-

tension code C

generated by generator matrix M





. Bernstein et al. (Bernstein et al., ) later im-

proved this attack. Probability of success and work

factor for Stern’s attack is described in (Hirotomo

et al., 2005). In Table 1 we also provide probabil-

ity of success for parameters l = 16 and A

≈ n − k.

Both the parameters can be optimized further to ob-

tain the least work factor but not much variation is

seen as we change any of these parameters. With

such low probabilities, it is clear that the work fac-

tor for Stern’s attack is worse than the Lee-Brickell

attack. Even when one considers improvements sug-

gested by Bernstein et al. (Bernstein et al., ), Lee-

Brickell’s (Lee and Brickell, 1988) attack seems to

outperform the attack by Bernstein et al. as it pro-

duces speedup upto 12 times and hence the security

of the system against the Lee-Brickell attack should

be considered the security of the system. Key sizes

should be devised according to that.

Another attack worth mentioning for quasi-cyclic

codes is the attack on the dual code. This attack works

only if the dual code has really low weight codewords

and is often encountered only when sparse parity

check matrices are involved. For example, McEliece

with QC-LDPC (Baldi et al., 2008). Such attacks can

easily be stopped by choosing codes that do not have

low weight codewords. From the work of Aylaj et

al. (Aylaj et al., 2016) this can be achieved.

After this discussion on classical security we

now move towards quantum-security of the proposed

McEliece and Niederreiter cryptosystems which is

one of the major goal of this paper.

SECRYPT 2018 - International Conference on Security and Cryptography

342

4 QUANTUM ATTACKS

4.1 Hidden Subgroup Problem

Quantum Fourier sampling works behind the scene

for almost all known quantum algorithms. It is the

reason Shor’s algorithm for factoring and solving the

discrete logarithm problem works. The main idea

in this paper is to show that quantum Fourier sam-

pling will not work in some situations, in particular,

a Niederreiter cryptosystem using quasi-linear

m−1

codes.

However, before we go there let us brieﬂy sketch

how quantum Fourier sampling is used to break a

McEliece or Niederreiter cryptosystems. We recall,

the scrambler-permutation attack (Dinh et al., 2011,

Section 2). This structural attack is exactly same for

a McEliece or a Niederreiter cryptosystem except that

instead of ﬁnding a scrambler-permutation pair from

generator matrix M to M

one has to ﬁnd scrambler-

permutation pair from parity check matrix H to H

The problem essentially remains the same. In this at-

tack, we assume H and H

are known, the attack is to

ﬁnd A and B. Notice that ﬁnding any A

and B

such

that A

H B

= H

will also make the attack successful.

Deﬁnition 4.1 (Hidden Shift Problem). Let G be a

group. Let f

and f

be two functions from group G

to a set X. Given f

(g) = f

g) the task is to ﬁnd

a constant g

∈ G. Note that there can be many g

that satisfy the above condition. Hidden shift problem

asks us to ﬁnd any one of those constants.

Let M

= AMB. A Niederreiter cryptosystem will

be broken if we ﬁnd one possible pair (A,B) from

M and M

. Consider two functions from group G =

) × S

given by

(A,B) = A

−1

MB (1)

(A,B) = A

−1

B. (2)

Then one can check that f

(A,B) =

((A

−1

).(A,B)), that is A

−1

is the shift

between f

and f

. Hence, if one can solve the

hidden shift problem over G = GL

) × S

he can

break the Niederreiter cryptosystem. The general

procedure to solve this hidden shift problem is to

reduce it to a hidden subgroup problem.

Deﬁnition 4.2 (Hidden Subgroup Problem). Let G be

a group and f a function

from G to a set X. We know

that f (g

) = f (g

) if and only if g

H = g

H for some

subgroup H. The problem is, given f ﬁnd a generating

set for the unknown subgroup H.

The function f in the hidden subgroup problem is said to

be separating cosets of H as f is constant on a each coset

and different on different cosets.

We can now reduce the hidden shift problem with

functions f

and f

deﬁned above on the group G =

) × S

to the hidden subgroup problem over

(G × G) o Z

(Dinh et al., 2011, Section 2.2). The

hidden subgroup in this case is

K = (((H

−1

s),0) ∪ ((H

s,s

−1

),1)), (3)

where H

= {(A, P) ∈ GL

) × S

: A

−1

MP = M}

and s is a shift from f

to f

In short, the scrambler-permutation problem is

one of the key ways to attack a Niederreiter cryp-

tosystem. This problem can be formulated as a hidden

shift problem which further can be reduced to a hid-

den subgroup problem. So we can attack Niederreiter

cryptosystems by trying to solve a hidden subgroup

problem over (G ×G)o Z

where G = GL

)×S

4.2 Successful Quantum Attacks

In the previous section we saw that solving the hid-

den subgroup problem as a standard way to attack a

Niederreiter cryptosystem. An interesting question is,

when is the hidden subgroup problem hard to solve?

This way we can ensure the security of a Niederreiter

cryptosystem against known quantum attacks.

We brieﬂy sketch some thoughts behind effec-

tiveness of QFS. The algorithm of QFS in a gen-

eral scenario and its use for solving the hidden sub-

group problem is very well explained by Grigni et

al. (Grigni et al., 2001). Arguments particular to

Niederreiter cryptosystems and corresponding hidden

subgroup problem are described in details by Dinh

et al. (Dinh et al., 2011, Section 3). The standard

model of QFS yields a probability distribution as a

function of the hidden subgroup. The basic idea be-

hind indistinguisability of two subgroups H

and H

with probability distributions P

and P

is that P

and P

are very close. For the purpose of deﬁning

closeness we need to deﬁne a metric on the space

of probability distributions. In this case, the met-

ric chosen is the total variation distance between two

distributions. This follows from the work of Kempe

and Shalev (Kempe and Shalev, 2005). Later Dinh et

al. (Dinh et al., 2011) used the L

distance to deﬁne

distinguishibility. Furthermore, the probability distri-

bution for the hidden subgroup problem with the iden-

tity subgroup gives us the uniform distribution (Dinh

et al., 2011, Section 3.2). When that is the case, QFS

will not give us much information to solve the hid-

den subgroup problem. Kempe and Shalev (Kempe

and Shalev, 2005) provided a necessary condition to

distinguish a subgroup of S

from the trivial sub-

group hei. Later Dinh et al. (Dinh et al., 2011) ex-

tended this result while keeping the group relevant to

A Quantum-Secure Niederreiter Cryptosystem using Quasi-Cyclic Codes

343

a Niederreiter cryptosystem in mind. Their result can

be viewed as a study of the hidden subgroup problem

for the group G = (GL

) × S

)

o Z

which is the

group for Niederreiter cryptosystems. They demon-

strated a case when the hidden subgroup H can not

be distinguished from either its conjugate subgroups

gHg

−1

or the trivial subgroup hei and proved a gen-

eral result on a sufﬁcient condition for indistinguishi-

bility (Dinh et al., 2011, Theorem 4). We use their

result to prove that the proposed Niederreiter cryp-

tosystem is quantum-secure.

First note that weak Fourier sampling gives the

same distributions for all the conjugate subgroups,

i.e., P

is the same as P

gHg

−1

. Hence weak Fourier

sampling can not differentiate a subgroup from its

conjugate subgroup. Thus it sufﬁces to look at strong

Fourier sampling. Dinh et al. (Dinh et al., 2011), in-

spired by the work of Kempe and Shalev (Kempe and

Shalev, 2005) deﬁnes distinguishability of a subgroup

H by strong Fourier sampling.

Deﬁnition 4.3 (Distinguishability of a subgroup by

strong QFS). We deﬁne distinguishability of a sub-

group H of a group G, denote it by D

, to be the ex-

pectation of the squared L

distance between P

gHg

−1

and the uniform distribution, where g ∈ G. In other

words,

:= E

ρ,g



gHg

−1

(·|ρ) − P

hei

(·|ρ)k



A subgroup H is called indistinguishable by strong

Fourier sampling if D

≤ log

−ω(1)

|G|. The ρ above

belongs to the set of irreducible complex representa-

tions of the group G.

Note that if a subgroup H is indistinguishable ac-

cording to this deﬁnition then by Markov’s inequality,

for all c > 0, kP

gHg

−1

(·|ρ) − P

{e}

(·|ρ)k

t.v.

≤ log

−c

|G|

which is analogous to the deﬁnition provided by

Kempe and Shalev (Kempe and Shalev, 2005) for in-

distinguishability of a subgroup by weak Fourier sam-

pling.

We now deﬁne the minimal degree of a permuta-

tion group, the automorphism group of a matrix (as

deﬁned by Dinh (Dinh et al., 2011, Section 4.2)) and

recall the deﬁnition of T

for a k × n matrix M.

Deﬁnition 4.4 (Automorphism Group). The auto-

morphism group of M is deﬁned as Aut(M) = {P ∈ S

such that there exists A ∈ GL

), AMP = M}.

Deﬁnition 4.5 (Minimal Degree). The minimal de-

gree of a permutation group G 6 S

acting on set of n

symbols is deﬁned to be minimum number of elements

moved by a non-identity element of the group G.

Deﬁnition 4.6. Consider a k × n matrix M, we deﬁne

for the matrix M = [I

∗

] as T

= {P

∈ S

such

that there exists P

∈ S

n−k

with P

∗

= M

∗

We will use the following theorem which we state for

the convinience of the reader.

Theorem 4.1 (Dinh et al. (Dinh et al., 2011, Theorem

4)). Assume q

6 n

for some constant 0 < a < 1/4.

Let m be the minimal degree of the automorphism

group Aut(M). Then for sufﬁciently large n, the sub-

group K, D

6 O(|K|

−δm

), where δ > 0 is a con-

stant.

5 PROPOSED CRYPTOSYSTEM

In this section we explain the proposed Niederre-

iter cryptosystem and establish its quantum security

against the hidden subgroup attack.

Recall that our variant of the Niederreiter cryp-

tosystem consists of a parity check matrix H de-

ﬁned as follows: The matrix H is an array of

circulants in the systematic form

, that is, H =

= I |C

| ... |C

m−1

] where each C

is a circu-

lant matrix of size p (a prime) over F

. For sim-

plicity let us denote [C

| ... |C

m−1

] as C so that

H = [ I |C ]. Recall the conditions of the parity check

matrix H from Section 1. A parity check matrix H

satisfying these conditions is easy to construct. We

present a way to do so in the next section. Before

that, we prove security of the proposed Niederreiter

cryptosystem against quantum attacks.

5.1 Proof of Indistinguishability

We prove indistinguishibility in a sequence of lem-

mas.

Lemma 5.1. Let P ∈ Aut(H ) then P = P

⊕P

where

is a block of size p and P

is a block of size (m−1)p

and P

⊕P

is a block diagonal matrix of size mp×mp

with the top block P

and the bottom block P

Proof. Let P ∈ Aut(H ), from the deﬁnition of auto-

morphism there is an A such that AH P = H . This

implies that

A[I |C ]P = [A | AC ] P = [ I |C ].

As action of right multiplication by a permutation

matrix permute columns, the above equality shows

that [A|AC ] has same columns as [I |C ] possibly in

different order. Now since every column of C con-

tains an entry from a proper extension of F

, no col-

umn of A can be column of C. This forces A to have

same columns as I and AC to have same columns as

that of C. Hence P permutes ﬁrst p columns within

A systematic matrix is a matrix whose ﬁrst block is the

identity.

SECRYPT 2018 - International Conference on Security and Cryptography

344

themselves and last (m − 1)p columns in themselves.

Hence every P ∈ Aut(H ) can be broken into P

⊕ P

so that P

acts on I and P

acts on C. •

The next lemma is central to quantum-security. It

gives us a way to move from H to C by noting, the

from the P ∈ Aut(H ) is actually a member of T

Lemma 5.2. The cardinality of Aut(H ) is the car-

dinality of the set

{

)

}

that satisfy P

= C

where H = [ I |C ] as deﬁned earlier.

Proof. The proof follows from the fact, if P belongs

to Aut(H ), then P = P

⊕P

. Then A[I |C ]P = [I |C ]

translates into A [I |C ] (P

⊕ P

) = [I |C ]. Keeping in

mind the block diagonal nature of P, it follows that

[AIP

|ACP

] = [I |C ]. Then A = P

−1

and P

−1

C. This proves the lemma. •

The next lemma proves that for each P

there is atmost

one P

Lemma 5.3. Cardinality of the set {(P

) that sat-

isfy P

= C} equals |T

Proof. Recall that T

= {P

that satisfy P

= C}.

So it sufﬁces to show that for every P

there is at most

one P

. Since no two columns of C are identical, no

two columns of P

C are identical. Hence, there is at

most one way to re-order them to get back C. Thus

for every P

there is at most one P

. •

Theorem 5.4 (Burnside (Dixon and Mortimer, 1996,

Theorem 3.5B)). Let G be a subgroup of Sym(F

)

containing a p-cycle µ : ξ 7→ ξ + 1. Then G is either

2-transitive or G ≤ AGL

) where AGL

) is the

afﬁne group over p.

We prove a theorem on the size of the automorphism

group of H .

Theorem 5.5. If H satisﬁes conditions I,II and III

then |Aut(H )| 6 p(p − 1).

Proof. From Lemma 5.2 and Lemma 5.3, the group

Aut(H ) has same size as T

. It is now easy to check

that the circulant matrix µ with ﬁrst row [0, 1, 0,. . . , 0]

of size p belongs to T

. The corresponding P

will

be a block diagonal (m − 1)p matrix with blocks of

size p and each consisting of µ

−1

. Now notice that

the circulant matrix µ corresponds to the p-cycle ξ 7→

ξ + 1. By our condition III, T

is not 2-transitive.

Now by Burnside’s theorem T

≤ AGL

). Thus

|Aut(H )| 6 p(p − 1). •

After this bound on the size of the automorphism

group we move towards the minimal degree of the

Automorphism group.

Lemma 5.6. The minimal degree of Aut(H ) is

bounded below by p − 1.

Proof. Notice that any P ∈ Aut(H ) = P

⊕P

. By the

twist, from P ∈ Aut(H ) to P

−1

∈ T

, it is easy to see

that P

∈ AGL

). Then P

(x) = ax + b (mod q)

for some a,b ∈ F

. If P ﬁxes two distinct points, then

a = 1 and b = 0 is the only possible solution. This

corresponds to the identity element and thus a non-

identity element can not ﬁx more that one point. So

minimal degree of Aut(H ) is bounded below by p −

1. •

We now prove the main theorem of this paper.

Theorem 5.7. Let p be a prime and m a positive in-

teger bounded above by a polynomial in p, such that,

p ≤

m(logm + log p). Then the subgroup K (Equa-

tion 3) deﬁned above is indistinguishable.

Proof. We will use Theorem 4.1 in this proof. First

note, the minimal degree is bounded below by p −

1. Now it is well known that |K| = 2|H

and

|Aut(H )| ≤ p(p − 1) and it is easy to see that

|Fix(H )| = 1. Putting all these together, we see

that |K|

−δp

≤ 4p

−δp

for some positive constant

δ. However, from the bound on the size of m, it is

obviously true that 4p

−δp

≤ (mp log (mp))

−ω(1)

for

large enough p.

Now, if p ≤ am (log m + log p), then p

≤

amp (log m + log p) which gives 2

≤ (mp)

amp

for

0 < a <

. This satisﬁes the premise of Theorem 4.1

and hence K is indistinguishable. •

5.2 Constructing the Parity Check

Matrix

Now we address the last question about the proposed

Niederreiter cryptosystem, how to construct a matrix

H satisfying conditions I - V? Clearly, conditions I,

II and III are trivial to set up and deserve no special

attention. We suggest a particular way for construc-

tion of parity check matrix H so that condition IV is

satisﬁed. It should be noted that there may be other

ways to satisfy condition IV as well.

Choose a pair of distinct elements a,b ∈ F

. Now

construct H such that C

contains both a and b exactly

once in each column and no other C

contains both a

and b. We restate this condition as our condition IV

We could have replaced C

by any other C

for i > 1

and the proof remains the same. For sake of simplicity

we stick with C

Two distinct elements a,b ∈ F

occurs as entries

of C

exactly once in each column and no other C

contain both a and b.

A Quantum-Secure Niederreiter Cryptosystem using Quasi-Cyclic Codes

345

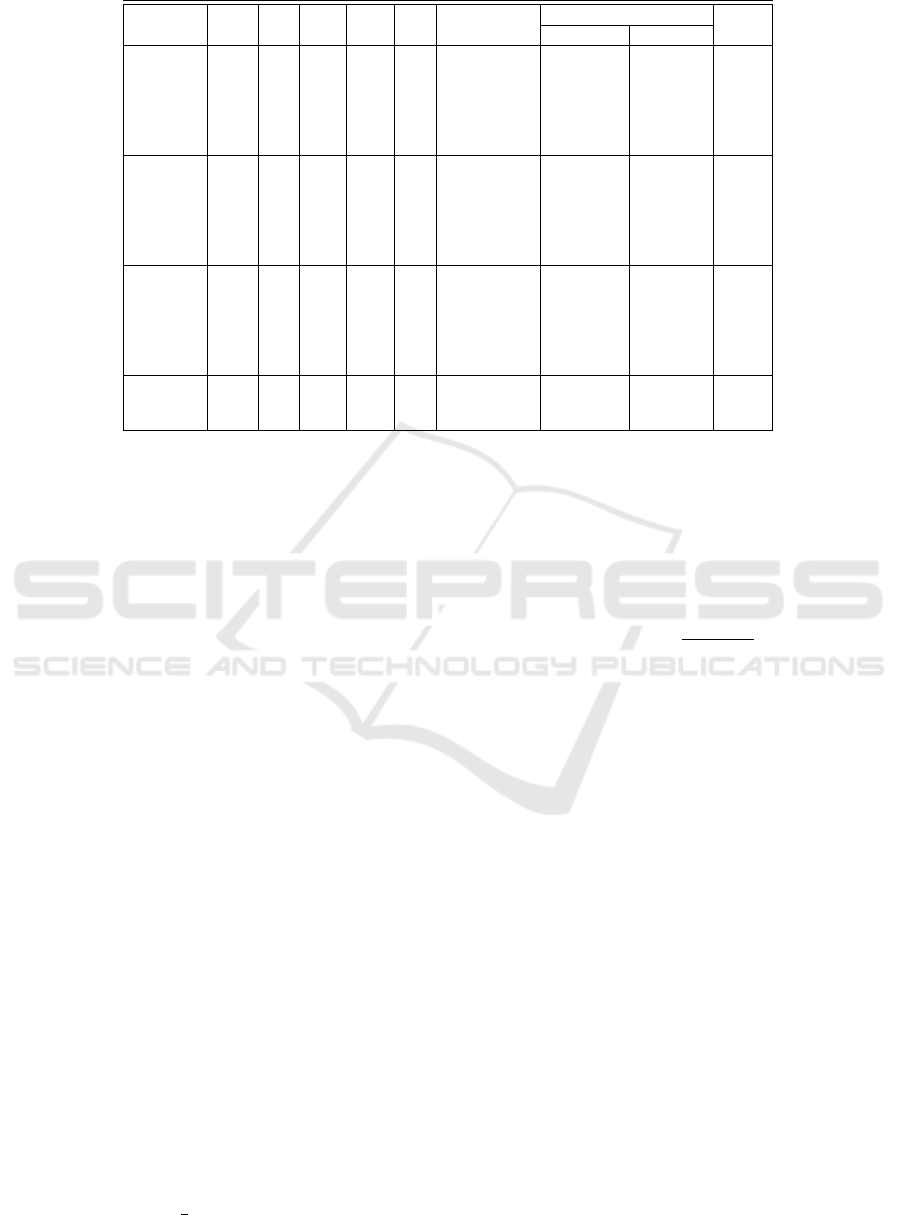
Table 1: Parameters for the proposed Niederreiter cryptosystem.

Security p t m

m Probability Public Key Size Rate

in bits of success No. rows No. cols

80-bits

101

15 17 35 35 2

−132

101 3535 0.60

20 9 35 35 2

−190

101 3535 0.77

211

35 4 62 62 2

−398

211 13082 0.71

40 3 62 62 2

−465

211 13082 0.80

100-bits

101

15 40 35 40 2

−136

101 4040 0.61

20 17 35 35 2

−190

101 3535 0.77

211

35 5 62 62 2

−398

211 13082 0.71

40 5 62 62 2

−465

211 13082 0.80

120-bits

101

15 95 35 95 2

−171

101 9595 0.67

20 32 35 35 2

−190

101 3535 0.77

211

35 8 62 62 2

−398

211 13082 0.71

40 6 62 62 2

−465

211 13082 0.80

256-bits 211

35 98 62 98 2

−443

211 20678 0.75

20 55 62 62 2

−465

211 13082 0.80

Lemma 5.8. If the matrix H satisﬁes IV

, it also sat-

isﬁes IV.

Proof. Let P

∈ T

. From P

= C it follows that

C should have the same set of columns as C but

possibly in a different order. Let α denote the row of

a in the ﬁrst column of C

and β denote the row of b

in the same column. Now notice that every column in

C that contains both a and b contains them such that

difference between rows of a and b is α − β mod p

where p is the size of each circulant matrix. Now let

σ ∈ T

such that it sends β to α and α to β. It then

follows from the fact that p is a odd prime, α = β

which contadicts our assumption. Hence, T

is not 2

transitive. •

Condition V can be easily satisﬁed using brute

force and other means and this completes the con-

struction of a parity check matrix H satisfying I - V

and hence, a Niederreiter cryptosystem that resists

quantum Fourier sampling is found.

6 ADVANTAGES OF THE

PROPOSED CRYPTOSYSTEM

One of the prime advantages of our proposed cryp-

tosystem is quantum-security. Apart from that it also

has high transmission rate which translated into high

encryption rate. It is known that the current McEliece

cryptosystem built on Goppa codes has transmission

rate of about 0.52. For a McEliece cryptosystem its

rate is same as that of the transmission rate of the un-

derlying code and is

. Niederreiter cryptosystems

have a slightly different rates due to difference in their

encryption algorithm. For a general cryptosystem its

encryption rate or information rate can be deﬁned as

follows (Niederreiter and Xing, 2009, Chapter 6):

Let S(C) denote possible number of palintexts and

T (C) denote possible number of ciphertexts then in-

formation rate of the system is deﬁned by

R (C) =

logS(C)

logT (C)

This information rate can be viewed as amount of in-

formation contained in one bit of ciphertext.

Our proposed Niederreiter cryptosystem have

good encryption rate (see Table 1). This gives the pro-

posed cryptosystem an edge over those constructed on

classical Goppa codes or with GRS codes (general-

ized Reed-Solomon codes).

As discussed before another problem with

McEliece and Niederreiter cryptosystems is large key

size. Circulant matrices is a good choice when

it comes to key-sizes. Matrices are 2-dimensional

objects but circulant matrices behave like a 1-

dimensional object as they can be described by their

ﬁrst row. Though this circulant structure is lost in

public key due to the scrambler-permutation pair, the

size of the key still remains smaller than the con-

ventional Niederreiter cryptosystem. Our system is

slightly better than original Niederreiter cryptosys-

tem because of the less number of rows in the pub-

lic key matrices. With p = 101, this number is less

than one-tenth of the original Niederreiter cryptosys-

tem. Though there are two factors that increases the

size of the matrix in our variant compared to origi-

nal McEliece: one, our matrices have large number

SECRYPT 2018 - International Conference on Security and Cryptography

346

of columns and two, our system is based on extension

ﬁeld F

which makes the effective size of the matrix

l times compared to McEliece which is based on F

However, in most cases due to less number of rows the

net result indicates that our system requires shorter

keys than original McEliece. For instance, at 80-bit

security with p = 101 and l = 3 our keys are almost

half of the keys corresponding to original McEliece

at same security level. At 256-bit security level with

p = 211,t = 40 and l = 3 the proposed cryptosys-

tem has key size of about one-forth of the original

McEliece.

In Table 1, we provide some parameters for the

proposed Niederreiter cryptosystem and show in de-

tails the beneﬁts of the proposed cryptosystem. There

are two kind of attacks – classical and quantum. For

the classical we come out with a value of m and call it

and for quantum we call it m

. The maximim of

these two is the m that one should use for that said pa-

rameter. As explained earlier we use p for the size of

the matrix and t as the error correcting capacity. We

also provide success probability from classical attack,

key size and the rate of the cryptosystem.

7 CONCLUSION

In this paper, we develop a Niederreiter cryptosys-

tem using quasi-cyclic codes that is both classically

and quantum secure against the current known at-

tacks. In particular, we show that for the proposed

cryptosystem the hidden subgroup problem from the

natural reduction of the corresponding scrambler-

permutation problem is indistinguishable by quantum

Fourier sampling. We also show that the proposed

cryptosystem has high encryption rate and shorter

keys compared to classical McEliece cryptosystems.

One of the important problem that needs to be ad-

dressed is ﬁnding quasi-cyclic codes that satisfy the

suggested parameter sizes. It would be interesting to

see if the cryptosystem remains classically secure if

we use other sparse keys. It is very clear that the sys-

tem remains secure against quantum computers as the

group structure for the system remains the same. This

is important because it could reduce key sizes sub-

stantially.

REFERENCES

Aylaj, B., Belkasmi, M., Nouh, S., and Zouaki, H. (2016).

Good quasi-cyclic codes from circulant matrices con-

catenation using a heuristic model. International jour-

nal of advanced computer science and applications,

7(9):63–68.

Baldi, M., Bodrato, M., and Chiaraluce, F. (2008). A new

analysis of the McEliece cryptosystem based on QC-

LDPC codes. Security and Cryptography for Net-

works, pages 246–262.

Berlekamp, E., McEliece, R., and Van Tilborg, H. (1978).

On the inherent intractability of certain coding prob-

lems (corresp.). IEEE Transactions on Information

Theory, 24(3):384–386.

Bernstein, D. J., Lange, T., and Peters, C. Attacking and de-

fending the McEliece cryptosystem. In Post-Quantum

Cryptography. PQCrypto 2008, pages 31–46.

Blahut, R. E. (2003). Algebraic codes for data transmission.

Cambridge University Press.

Dinh, H., Moore, C., and Russell, A. (2011). McEliece and

Niederreiter cryptosystems that resist quantum fourier

sampling attacks. volume 6841 of LNCS. Crypto2011.

Dixon, J. D. and Mortimer, B. (1996). Permutation Groups.

Graduate Texts in Mathematics. Springer, New York.

Grigni, M., Schulman, L., Vazirani, M., and Vazirani, U.

(2001). Quantum mechanical algorithms for the non-

abelian hidden subgroup problem. In Proceedings of

the thirty-third annual ACM symposium on theory of

computing, pages 68–74. ACM.

Gulliver, T. A. (1989). Construction of quasi-cyclic codes.

PhD thesis, University of Victoria.

Hallgrean, S., Russell, A., and Ta-Shma, A. (2003). The

hidden subgroup problem and quantum computation

using group representation. SIAM Journal of Compu-

tation, 32(4):916–934.

Hirotomo, M., Mohri, M., and Morii, M. (2005). A prob-

abilistic computation method for the weight distribu-

tion of low-density parity-check codes. In Interna-

tional Symposium on Information Theory.

Kapshikar, U. (2018). McEliece-type cryptosystems over

quasi-cyclic codes. Master’s thesis, IISER Pune.

https://arxiv.org/abs/1805.09972.

Kempe, J. and Shalev, A. (2005). The hidden subgroup

problem and permutation group theory. In Proceed-

ings of the sixteenth annual ACM-SIAM symposium

on discrete algorithms, pages 1118–1125. Society for

Industrial and Applied Mathematics.

Lee, P. J. and Brickell, E. F. (1988). An observation on

the security of McEliece’s public-key cryptosystem.

In Eurocrypt 1988, volume 330 of LNCS, pages 275–

280. Springer.

Li, Y. X., Deng, R. H., and Wang, X. M. (1994). On the

equivalence of McEliece’s and Niederreiter’s public-

key cryptosystems. IEEE Transactions on Information

Theory, 40(1):271–273.

McElice, R. J. (1978). A public key cryptosystem based on

algebraic coding theory. Technical report, Communi-

cations system research centre, NASA.

Niederreiter, H. and Xing, C. (2009). Algebraic Geometry

in Coding Theory and Cryptography. Princeton Uni-

versity Press.

Stern, J. (1988). A method for ﬁnding codewords of small

weight. In International Colloquium on Coding The-

ory and Applications, pages 106–113. Springer.

Zeh, A. and Ling, S. Decoding of quasi-cyclic codes up

to a new lower bound on the minimum distance. In

2014 IEEE International Symposium on Information

Theory, Honolulu, HI, 2014.

A Quantum-Secure Niederreiter Cryptosystem using Quasi-Cyclic Codes

347