Secure Grouping and Aggregation with MapReduce
Radu Ciucanu
1
, Matthieu Giraud
1
, Pascal Lafourcade
1
and Lihua Ye
2
1
LIMOS, Universit
´
e Clermont Auvergne, Aubi
`
ere, France
2
Harbin Institute of Technology, Harbin, Weihai, Shenzhen, China
Keywords:
Database Queries, MapReduce, Security, Grouping, Aggregation.
Abstract:
MapReduce programming paradigm allows to process big data sets in parallel on a large cluster. We focus on
a scenario where the data owner outsources her data on an honest-but-curious server. Our aim is to evaluate
grouping and aggregation with SUM, COUNT, AVG, MIN, and MAX operations for an authorized user. For
each of these five operations, we assume that the public cloud provider and the user do not collude i.e., the
public cloud does not know the secret key of the user. We prove the security of our approach for each operation.
1 INTRODUCTION
We address the fundamental problem of how to group
and aggregate data from a relation in a privacy-
preserving manner using MapReduce. We assume
that the data is externalized in the cloud by the data
owner and there is a user that queries it. We consider
the following five aggregation operations, which are
precisely those included in the SQL standard: SUM,
COUNT, AVG, MIN, and MAX.
We start by a running example to present the con-
cepts of grouping and aggregation, and of MapRe-
duce computations. Then, we present our problem
statement and illustrate with the same example the
privacy issues related to grouping and aggregation
with MapReduce.
Example 1. Assume there is a university storing the
relation R corresponding to the list of professors with
their associated department and salary. The grouping
and aggregation operation on the relation R, in the
case where we assume one group attribute and one
aggregate function, is denoted by γ
A,θpBq
pRq, where A
is the grouping attribute and θ is one of the five ag-
gregation operations applied on the attribute B dif-
ferent from the grouping attribute. In this example
(Figure 1), we consider the attribute “Department”
as the grouping attribute and SUM is the aggregation
operation applied on attribute “Salary”. Hence, for
each department we sum all the associated salaries.
Since Alice and Bob are in the Computer Science de-
partment, the sum of salaries associated to the Com-
puter Science department is 1900 ` 1800 “ 3700. In
the same way, we sum the salaries of Mallory and Os-
Name Department Salary
Alice Computer Science 1900
Mallory Mathematics 1750
Bob Computer Science 1800
Eve Physics 2000
Oscar Mathematics 1600
Figure 1: Relation R.
Department SUM (salary)
Computer Science 3700
Physics 2000
Mathematics 3350
Figure 2: Result of γ
Department,SUMpSalaryq
pRq.
car from the Mathematics department. Since Eve is
the only one in the Physics department, the sum cor-
responds to the salary of Eve which is equal to 2000.
For the query γ
Department,SUMpSalaryq
pRq, we obtain the
relation presented in Figure 2. Aggregation operati-
ons COUNT, AVG, MIN, or MAX work similarly.
Grouping-and-aggregation with MapReduce. An
algorithm to perform grouping and aggregation with
MapReduce is presented in Chapter 2 of (Leskovec
et al., 2014). First, a set of nodes has chunks of the
relation. The map function creates for each tuple a
key-value pair where key is equal to the value of the
grouping attributes in the considered tuple, and value
is equal to the value of the aggregation attribute of
the considered tuple. Then, the key-value pairs are
grouped by key, i.e., key-value pairs output by the
map phase which have the same key are sent to the
same reducer. For each key, the reduce function ap-
348
Ciucanu, R., Giraud, M., Lafourcade, P. and Ye, L.
Secure Grouping and Aggregation with MapReduce.
DOI: 10.5220/0006843803480355
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 348-355
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

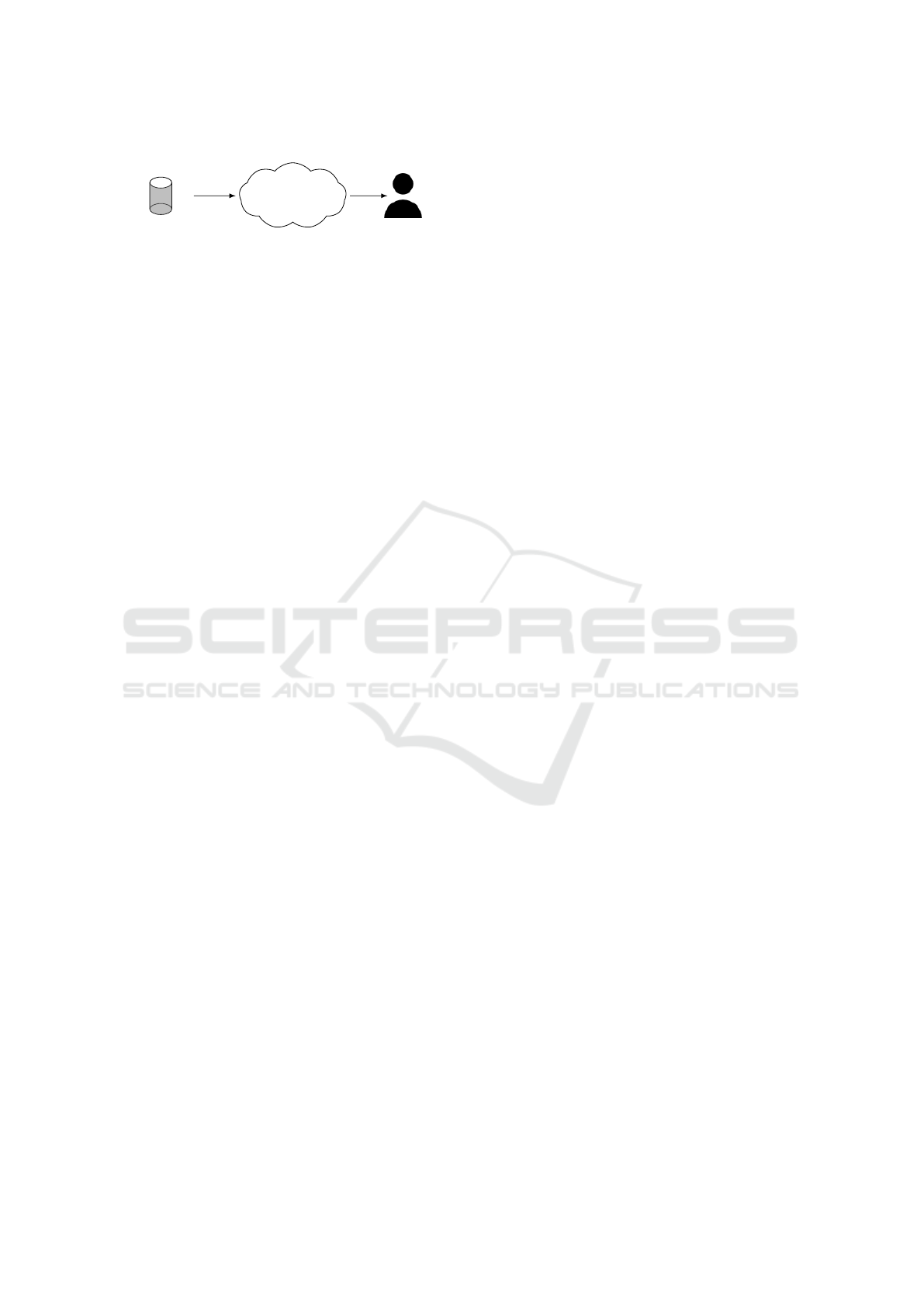
R
Data owner
Public Cloud
γ
A,θpBq
pRq
User
Figure 3: The system architecture.
plies the aggregate function on the associated values
of the considered key.
Example 2. Following Example 1, we perform grou-
ping and aggregation with MapReduce on the rela-
tion R where the grouping attribute is the attribute
“Department”, the aggregation attribute is the attri-
bute “Salary”, and the operation is the SUM. We
start grouping and aggregation with MapReduce by
applying the map function. Since the grouping attri-
bute is the attribute “Department” and that the ag-
gregation attribute is the attribute “Salary”, the map
function emits the pairs pComputer Science, 1900q,
pMathematics, 1750q, (Computer Science, 1800),
pPhysics, 2000q, and pMathematics, 1600q. Pairs
sharing the same key (i.e., same value of the grou-
ping attribute) are sent on the same reducer. Then, the
reduce function performs on each reducer the aggre-
gation, consisting here of the sum, and we obtain the
pairs pComputer Science, 3700q since 1900` 1800 “
3700, etc. We present the final result in Figure 2.
Problem Statement. We assume three participants:
the data owner, the public cloud and the user (pre-
sented in Figure 3). The data owner stores a relation
R in the distributed file system of some public cloud
provider. A user (who does not know the relation R)
is authorized to perform a grouping and aggregation
operation on R.
We assume that the public cloud is honest-but-
curious, i.e., it executes dutifully the computation task
but tries to learn the maximum of information on tu-
ples of R. In order to preserve the privacy of the data
owner, the cloud should not learn any plain input data,
contrary to what happens for standard algorithms as
found in Chapter 2 from (Leskovec et al., 2014) and
exemplified above.
We assume that the relation R is initially spread
over a set R of nodes, each of them storing a chunk
of R i.e., a set of elements of R. The final result
γ
A,θpBq
pRq is spread over a set of nodes Q before it
is sent to the user’s nodes U. We expect that none of
the nodes in Q can learn any information about rela-
tion R, or about the final result.
Notice that a straightforward solution would re-
quire the use of a fully homomorphic encryption
scheme e.g., (Gentry, 2009). Indeed, a fully ho-
momorphic encryption scheme would allow to exe-
cute directly in the encrypted domain all operations
needed for computing a grouping and aggregation
operation. Unfortunately, such an approach would
solve our problem only from a theoretical point of
view because making a fully homomorphic encryp-
tion scheme work in practice remains an open ques-
tion (as noted e.g., in (Gentry, 2009)).
Contributions. We revisit the standard algorithms
for MapReduce grouping and aggregation (as found
in Chapter 2 from (Leskovec et al., 2014)) to gua-
rantee the privacy of the data owner. More precisely,
neither the public cloud nor the user learn information
about the input data that belongs to the data owner.
Our approach, denoted SP for Secure-Private, works
for each of the considered five aggregation operations.
In each case, the SP approach is efficient from both
computational and communication points of view, in
the sense that the overhead is linear for each of the
two complexity measures.
Our technique is essentially based on two encryp-
tion schemes: (i) the well-known Paillier’s cryptosy-
stem (Paillier, 1999), which is partially homomorphic
i.e., it is additive homomorphic for COUNT, SUM,
and AVG operations, and (ii) the order-preserving
symmetric encryption scheme (Agrawal et al., 2004)
for MIN and MAX operations.
We summarize in Figure 4 the trade-offs between
computation cost and communication cost for our SP
approach vs the standard MapReduce approach for
grouping and aggregation for the five studied operati-
ons. In our communication cost analysis, we measure
the total size of the data that is emitted from a map or
reduce node.
Related Work. Since the seminal MapReduce pa-
per (Dean and Ghemawat, 2004), different proto-
cols have been proposed to perform operations in
a privacy-preserving manner (Derbeko et al., 2016)
such as search (Blass et al., 2012) (Mayberry et al.,
2013), count (Vo-Huu et al., 2015), matrix multiplica-
tion (Bultel et al., 2017) or joins (Dolev et al., 2016).
Chapter 2 of (Leskovec et al., 2014) presents an
introduction to the MapReduce paradigm. In particu-
lar, it includes the MapReduce algorithm for grouping
and aggregation that we enhance with privacy guaran-
tees. Very few approaches address the privacy preser-
ving execution for grouping and aggregation operati-
ons in MapReduce, and moreover they have different
assumptions than we do.
(Bonawitz et al., 2017) provides a technique
to compute secure aggregation, while relying on
Shamir’s secret sharing (Shamir, 1979) to compute
Secure Grouping and Aggregation with MapReduce
349

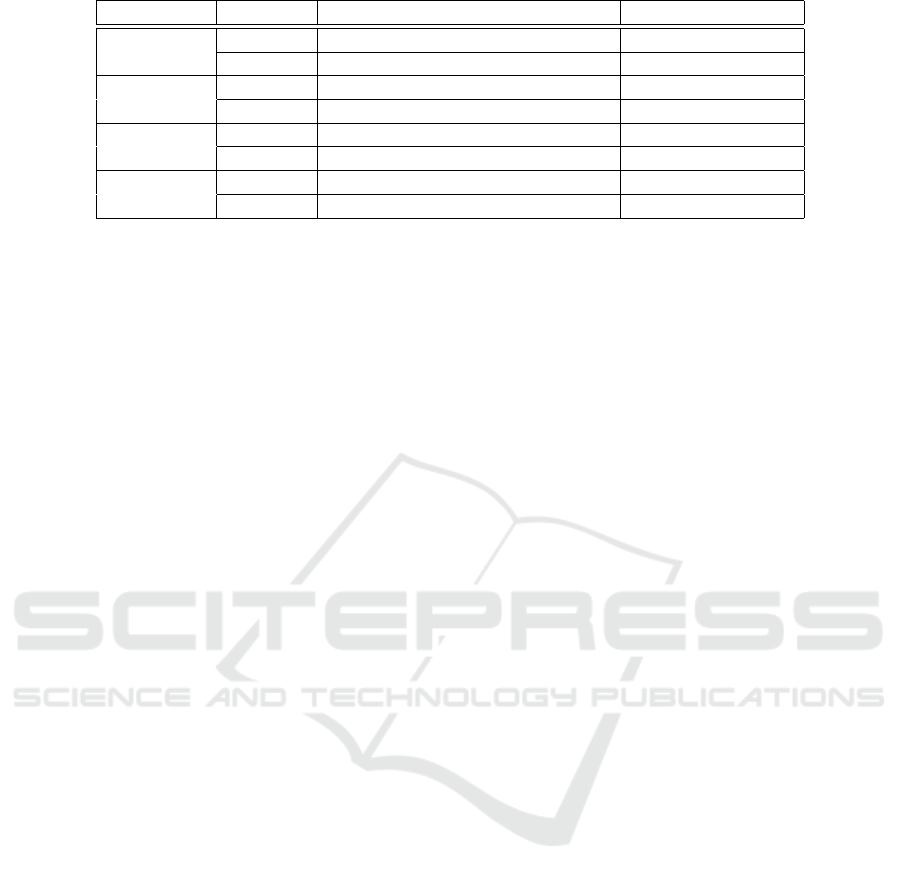
Alg. Approach Comp. cost (big-O) Comm. cost (big-O)
COUNT
Standard p1 `C
`
qn 2n
SP pC
f
` 2C
E
`C
ˆ
qn 3n
SUM
Standard p1 `C
`
qn 2n
SP pC
f
` 2C
E
`C
ˆ
qn 3n
AVG
Standard p1 ` 2C
`
`C
˜
qn 2n
SP pC
f
` 3C
E
` 2C
ˆ
qn 3n
MIN{MAX
Standard p1 `C
comp
qn 2n
SP pC
f
`C
E
ope
` 3C
E
`C
D
`C
comp
qn 3n
Figure 4: Summary of results. Let n be the number of tuples in the relation R. Let C
`
(resp. C
ˆ
, C
˜
, C
f
, C
E
ope
C
E
, C
D
) is the
cost of addition (resp. multiplication, division, pseudo-random function evaluation, order-preserving symmetric encryption,
asymmetric encryption, and asymmetric decryption) and 1 represents the cost to access to one tuple in the relation.
the sum of values coming from different sources. Si-
milarly, (Alghamdi et al., 2017) provides a techni-
que to compute secure aggregation for wireless sensor
networks. Contrary to us, these two approaches do not
consider the MapReduce paradigm and they cannot
be easily adapted for MapReduce because values of
shared attributes are encrypted in a non-deterministic
way. This is not a suitable choice for MapReduce
keys that need to be equal in order to aggregate the
key-value pairs on the same reducer.
(Dolev et al., 2016) proposed a technique for
executing MapReduce computations in the public
cloud while preserving data owner privacy. They use
the Shamir’s secret sharing and accumulating auto-
mata (Dolev et al., 2015). Among the five aggregati-
ons studied in this paper, they support only the count,
whose computation is done on secret-shares in the pu-
blic cloud, and at the end, the user performs the inter-
polation on the outputs. On the other hand, in our set-
ting, the user has only to decrypt the final query result,
contrary to the need of doing interpolations in (Dolev
et al., 2015).
On the other hand, substantial works has been
done on privacy-preserving functional queries on tra-
ditional rational database. Popa et al. (Popa et al.,
2011) designed CryptDB a system allowing a user to
execute queries over encrypted data. The authors con-
sider two threats. The first threat is a curious database
administrator who tries to learn private data while the
second threat is an adversary that gains complete con-
trol of application. In (Macedo et al., 2017), authors
proposed a generic framework called SafeNoSQL to
compute in a privacy-preserving manner on NoSQL
databases. This framework has a modular and exten-
sible design that enables data processing over multi-
ple cryptographic techniques applied on the same da-
tabase schema. Contrary to us, these two approaches
do not consider the MapReduce paradigm.
To the best of our knowledge, we are the first to
propose secure algorithms for grouping and aggre-
gation computation with the MapReduce paradigm
where the public cloud performs all the computations
and where the user has only to decrypt the result sent
by the cloud.
Outline. We introduce some preliminary notions in
Section 2. Then, we present our SP approach for these
five operations in Section 3. Finally, we outline con-
clusions and future work in Section 4.
2 PRELIMINARIES
2.1 Relational Algebra
A relation R is a set of n tuples. For a tuple t P R,
by π
X
ptq we denote the projection of the tuple t on
the attributes X i.e., the tuple obtained from t after
removing all attributes values that are not in X.
By γ
A,θpBq
pRq we denote the grouping and aggre-
gation operation on R, where A is the set of attributes
on which we group, B is the attribute for which we ap-
ply the aggregation function, and θ is an aggregation
function (SUM, COUNT, AVG, MIN, MAX).
2.2 Grouping and Aggregation with
MapReduce
We recall the MapReduce algorithms for grouping
and aggregation algorithms, as found in Chapter 2 of
(Leskovec et al., 2014): for COUNT in Figure 5(a),
for SUM in Figure 5(b), for AVG in Figure 5(c), and
for MIN in Figure 5(d). The algorithm for MAX is
very similar to the one for MIN and we omit it.
2.3 Cryptographic Tools
We present definitions of the cryptographic tools used
in our protocols: negligible function, pseudo-random
function, order-preserving encryption scheme, and
public key encryption scheme.
SECRYPT 2018 - International Conference on Security and Cryptography
350

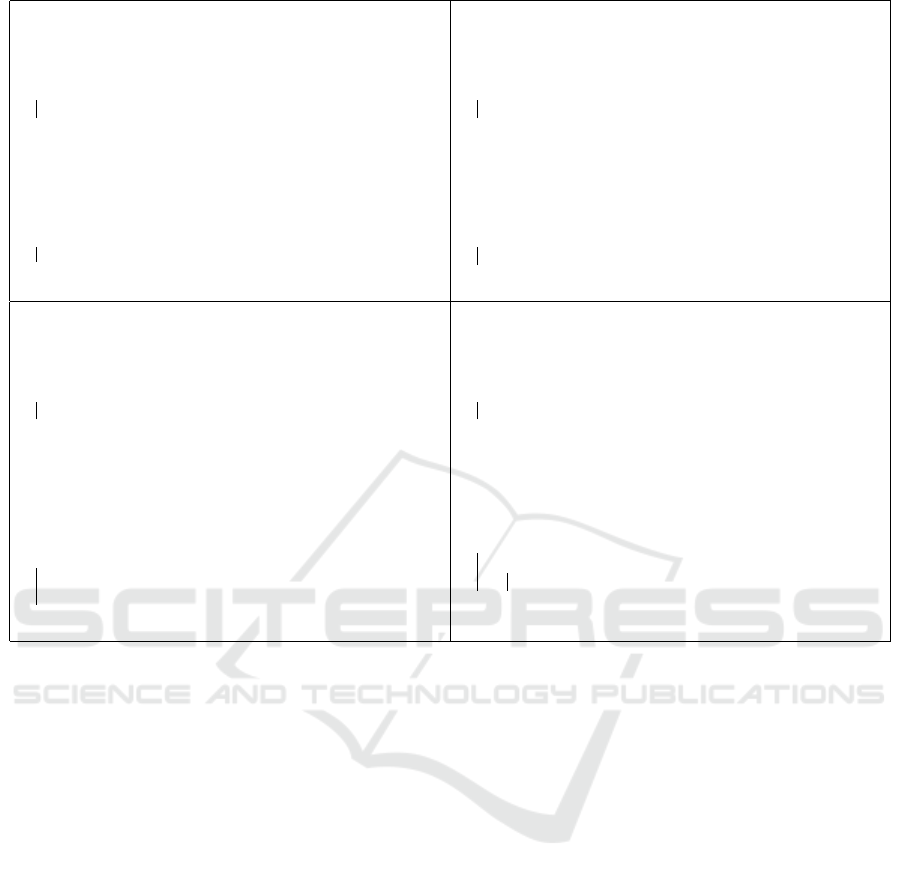
Map function:
Input: pkey, valueq
// key: id of a chunk of R
// value: collection of t P R
foreach t P R do
emit pπ
A
ptq, 1q.
Reduce function:
Input: pkey, valuesq
// key: π
A
ptq for t P R
// values: collection of 1
count Ð 0;
foreach 1 P values do
count Ð count ` 1;
emit pπ
A
ptq, countq.
(a) COUNT operation.
Map function:
Input: pkey, valueq
// key: id of a chunk of R
// value: collection of t P R
foreach t P R do
emit pπ
A
ptq, π
B
ptqq.
Reduce function:
Input: pkey, valuesq
// key: π
A
ptq with t P R
// values: collection of π
B
ptq with t P R
sum Ð 0
foreach π
B
ptq P values do
sum Ð sum ` π
B
ptq;
emit pπ
A
ptq, sumq.
(b) SUM operation.
Map function:
Input: pkey, valueq
// key: id of a chunk of R
// value: collection of t P R
foreach t P R do
emit pπ
A
ptq, π
B
ptqq.
Reduce function:
Input: pkey, valuesq
// key: π
A
ptq for t P R
// values: collection of π
B
ptq
cpt Ð 0;
sum Ð 0;
foreach π
B
ptq P values do
cpt Ð cpt ` 1;
sum Ð sum ` π
B
ptq;
emit pπ
A
ptq, sum{cptq.
(c) AVG operation.
Map function:
Input: pkey, valueq
// key: id of a chunk of R
// value: collection of t P R
foreach t P R do
emit pπ
A
ptq, π
B
ptqq.
Reduce function:
Input: pkey, valuesq
// key: π
A
ptq for t P R
// values: collection of π
B
ptq
min
$
Ð values;
foreach π
B
ptq P values do
if π
B
ptq ă min then
min Ð π
B
ptq;
emit pπ
A
ptq, minq.
(d) MIN operation.
Figure 5: Grouping and aggregation with MapReduce for COUNT, SUM, AVG, MIN operations.
Definition 1 (Negligible function). A function ε :
N Ñ N is negligible in η if for every positive poly-
nomial pp¨q and sufficiently large η, εpηq ă 1{ppηq.
Definition 2 (Pseudo-random function). A function
f : t0, 1u
η
ˆ t0, 1u
n
0
Ñ t0, 1u
n
1
is a pseudo-random
function if it is calculable in polynomial time in η and
if for all polynomial-size algorithm B,
ˇ
ˇ
Pr
“
B
f
k
p¨q
“ 1 : k
$
Ð t0, 1u
η
‰
´ Pr
“
B
gp¨q
“ 1 : g
$
Ð Funcrn
0
, n
1
s
‰
ˇ
ˇ
ď εpηq ,
where εp¨q is a negligible function in η, Func is
the space functions from domain t0, 1u
n
0
to dom-
ain t0, 1u
n
1
, and the probabilities are taken over the
choice of k and g.
Definition 3 (Order-Preserving Symmetric Encryp-
tion (Agrawal et al., 2004)). Let η be a security para-
meter. An order-preserving encryption (OPE) scheme
is defined by three algorithms pG
ope
, E
ope
, D
ope
q:
G
ope
pηq: returns a secret key K.
E
ope
K
pmq: returns a new key K
1
and a ciphertext c.
D
ope
K
pcq: returns the plaintext m.
such that for any two ciphertexts c
1
and c
2
with cor-
responding messages m
1
and m
2
we have c
1
ă c
2
if
and only if m
1
ă m
2
.
Definition 4 (Public Key Encryption (PKE)). Let η be
a security parameter. A public key encryption (PKE)
scheme is defined by three algorithms pG, E, Dq:
Gpηq: returns a public/private key pair ppk, skq.
E
pk
pmq: returns the ciphertext c.
D
sk
pcq: returns the plaintext m.
In the following, we require an additive homo-
morphic encryption scheme to secure the grouping
and aggregation with MapReduce. There exists se-
veral schemes that have this property (Okamoto and
Uchiyama, 1998; Paillier, 1999; Naccache and Stern,
1998). We choose Paillier’s cryptosystem (Paillier,
1999) to illustrate specific required homomorphic
properties. Our results and proofs are generic, since
any other encryption schemes having such properties
can be used instead of Paillier’s scheme.
We recall the key generation, the encryption and
decryption algorithms.
Key Generation. We denote by Z
n
, the ring of integers
modulo n and by Z
˚
n
the set of invertible elements of
Secure Grouping and Aggregation with MapReduce
351

Z
n
. The public key pk of Paillier’s encryption scheme
is pn, gq, where g P Z
˚
n
2
and n “ p ˆ q is the product
of two prime numbers such that gcdpp, qq “ 1. The
corresponding private key sk is pλ, µq, where λ is the
least common multiple of p ´ 1 and q ´ 1 and µ “
pLpg
λ
mod n
2
qq
´1
mod n, where Lpxq “
x´1
n
.
Encryption Algorithm. Let m be a message such that
m P Z
n
. Let g be an element of Z
˚
n
2
and r be a random
element of Z
˚
n
. We denote by E
pk
the encryption
function that produces the ciphertext c from a given
plaintext m with the public key pk “ pn, gq as follows:
c “ g
m
ˆ r
n
mod n
2
.
Decryption Algorithm. Let c be the ciphertext such
that c P Z
n
2
. We denote by D
sk
the decryption
function of the plaintext c with the secret key sk “
pλ, µq defined as follows: m “ L
`
c
λ
mod n
2
˘
ˆ µ
mod n .
Homomorphic Addition of Plaintexts. Paillier’s
cryptosystem is a partial homomorphic encryption
scheme. Let m
1
and m
2
be two plaintexts in Z
n
. The
product of the two associated ciphertexts with the pu-
blic key pk “ pn, gq, denoted c
1
“ E
pk
pm
1
q “ g
m
1
ˆr
n
1
mod n
2
and c
2
“ E
pk
pm
2
q “ g
m
2
ˆ r
n
2
mod n
2
, is the
encryption of the sum of m
1
and m
2
.
E
pk
pm
1
q ˆ E
pk
pm
2
q
“ c
1
ˆ c
2
mod n
2
“ pg
m
1
ˆ r
n
1
q ˆ pg
m
2
ˆ r
n
2
q mod n
2
“
`
g
m
1
`m
2
ˆ pr
1
ˆ r
2
q
n
˘
mod n
2
“ E
pk
pm
1
` m
2
mod nq .
3 SECURE PRIVATE APPROACH
We present our SP approach for the COUNT, SUM,
AVG, MIN, and MAX aggregation functions with
MapReduce. We denote respectively these five pro-
tocols: SP-COUNT, SP-SUM, SP-AVG, SP-MIN, and
SP-MAX. The algorithm for SP-MAX is very similar
to SP-MIN and we omit it to avoid redundancy.
3.1 SP Protocols
To avoid the cloud to learn the content of the relation
R, the data owner protects it before the outsourcing.
We denote the protected relation by
ˆ
R.
The data owner protects the relation using a
pseudo-random function with her secret key k and by
applying it on values of grouping attributes of each
tuples of the relation R. These deterministic pseudo-
random function evaluations allow the cloud to per-
form equality tests between values of grouping attri-
butes. Moreover, the data owner encrypts each va-
lue of the aggregation attribute either with Paillier’s
scheme (using the user public key pk
u
) or the OPE
scheme (using the shared secret key K between the
data owner and the user), depending on the aggrega-
tion function. We present the preprocessing phase in
Algorithm 1, where E represents either the Paillier en-
cryption (in the case of COUNT, SUM, AVG operati-
ons) or the OPE encryption (in the case of MIN and
MAX operations). We stress that A
f
and A
E
are just
notations making explicit the correspondences bet-
ween initial and outsourced data and that
ˆ
R is the
schema of
ˆ
R. For instance, if a relation R has two
attributes such that “Name” is the grouping attribute
and “Age” is the aggregation attribute, then
ˆ
R has at-
tributes “Name
f
”, “Name
E
” and “Age
E
”.
Algorithm: PreProcpRq
ˆ
R Ð H;
A
f
Ð tA
f
|A P Au;
A
E
Ð tA
E
|A P Au;
ˆ
R Ð A
f
Y A
E
Y B;
for t P R do
t
f
Ð
Ś
A
f
PA
f
f
k
pπ
A
ptqq;
t
E
Ð
Ś
A
E
PA
E
pE
pk
u
pπ
A
ptqqq;
ˆ
R Ð
ˆ
R Y tt
f
ˆt
E
ˆ Epπ
B
ptqqu;
Algorithm 1: Preprocessing of relations.
SP-COUNT (Figure 6(a)). Value of pairs sent by the
map function contains the Paillier encryption of the
grouping attribute value and the Paillier encryption of
1. Using the homomorphic property of the Paillier’s
scheme, each reducer multiplies encryption of 1 to
obtain the count of tuples sharing the same value of
the grouping attribute.
SP-SUM (Figure 6(b)). Value of pairs sent by the
map function contains the Paillier encryption of the
grouping attribute value and the Paillier encryption
of the aggregation attribute value. Similarly to
the SP-COUNT protocol, we use the homomorphic
property of the Paillier’s scheme allowing each
reducer to multiply encrypted aggregates to obtain
the encryption of the sum of tuples values sharing the
same grouping attribute value.
SP-AVG (Figure 6(c)). The protocol combines the
SP-COUNT protocol and the SP-SUM protocol. This
allows the MapReduce user to compute the average.
SP-MIN (Figure 6(d)). We stress that before to apply
the map function, the data owner must encrypt all va-
lues of the aggregate attribute using an OPE scheme
with the secret key K shared between the data owner
and the MapReduce user.
SECRYPT 2018 - International Conference on Security and Cryptography
352

Map function
Input: pkey, valueq
// key: id of a chunk of
ˆ
R
// value: collection of t P
ˆ
R
foreach t P
ˆ
R do
emit pπ
A
f
ptq, pπ
A
E
ptq, E
pk
u
p1qqq
Reduce function
Input: pkey, valuesq
// key: π
A
f
ptq for t P
ˆ
R
// values: collection of pπ
A
E
ptq, E
pk
u
p1qq
count Ð1
foreach pπ
A
E
ptq, E
pk
u
p1qq P values do
count Ð count ¨ E
pk
u
p1q
emit pπ
A
E
, countq
(a) SP-COUNT protocol.
Map function
Input: pkey, valueq
// key: id of a chunk of
ˆ
R
// value: collection of t P
ˆ
R
foreach t P
ˆ
R do
emit pπ
A
f
ptq, pπ
A
E
ptq, π
B
ptqqq
Reduce function
Input: pkey, valueq
// key: π
A
f
ptq for t P
ˆ
R
// value: collection of pπ
A
E
ptq, π
B
ptqq
sum Ð 1
foreach pπ
A
E
ptq, π
B
ptqqP values do
sum Ðsum ¨ π
B
ptq
emit pπ
A
E
ptq, sumq
(b) SP-SUM protocol.
Map function
Input: pkey, valueq
// key: id of a chunk of
ˆ
R
// value: collection of t P
ˆ
R
foreach t P
ˆ
R do
emit pπ
A
f
ptq, pπ
A
E
ptq, π
B
ptq, E
pk
u
p1qqq
Reduce function
Input: pkey, valueq
// key: π
A
f
ptq for t P
ˆ
R
// value: collection of pπ
A
E
ptq, π
B
ptq, E
pk
u
p1qq
cpt Ð 1
sum Ð 1
foreach pπ
A
E
ptq, π
B
ptq, E
pk
u
p1qq P values do
cpt Ð cpt ¨ E
pk
u
p1q
sum Ð sum ¨ π
B
ptq
emit pπ
A
E
ptq, cpt, sumq
(c) SP-AVG protocol.
Map function
Input: pkey, valueq
// key: id of a chunk of
ˆ
R
// value: collection of t P
ˆ
R
foreach t P
ˆ
R do
emit pπ
A
f
ptq, pπ
A
E
ptq, π
B
ptqqq
Reduce function
Input: pkey, valuesq
// key: π
A
f
ptq for t P
ˆ
R
// values: collection of pπ
A
E
ptq, π
B
ptqq
pv
1
, v
2
q
$
Ð values
min Ð D
sk
c
pv
2
q
foreach pπ
A
E
ptq, π
B
ptqq P values do
x Ð D
sk
c
pπ
B
ptqq
if x ă min then
min Ð x
emit pπ
A
E
ptq, E
pk
u
pminqq
(d) SP-MIN protocol.
Figure 6: Secure grouping and aggregation with MapReduce for COUNT, SUM, AVG, and MIN operations. The highlighting
emphasizes differences w.r.t. the standard non-secured approach cf. Figure 5.
Value of pairs sent by the map function contains
the encryption of the pre-computed OPE ciphertexts
using an IND-CPA public key encryption scheme
with the public key pk
c
of the public cloud. Since the
OPE encryption is deterministic, the additional public
key encryption avoids an eavesdropper between the
data owner and the public cloud to have any informa-
tion on repetitions of values sent by the data owner.
After received the key-value pairs, the public
cloud uses its secret key sk
c
to obtain OPE ciphers.
Using the property of the OPE scheme, each reducer
of the public cloud computes the minimum to obtain
the minimum value associated to the considered
value of the grouping attribute. Finally, the public
cloud uses the public key pk
u
of the user to encrypt
each OPE ciphertext and sends the result to the user.
Remark: As we can see in the SP-COUNT protocol
(Figure 6(a)), a public cloud knowing that it performs
the count operation can deduce the value of the count
even if it can not decrypt the encryption of 1. In fact,
the public cloud can count tuples that each reducer re-
ceives. Hence, it deduce the count result for the cor-
responding key. We stress that the plain value of the
key stay unknown from the public cloud since it does
not have the secret key sk
u
of the user to decrypt it.
In the following, we present the SP
comb
-COUNT and
the SP
comb
-AVG protocols in Figure 7 using combi-
ners (Leskovec et al., 2014) to avoid this leakage of
information.
3.2 Refinement: Combiners
Combiners allow to push some of what the reducers
do to the map function. In the case of the COUNT
operation, the map function counts tuples of the chunk
that share the same value for the grouping attribute.
Hence, each reducer receives key-value pairs, where
key is the grouping attribute value, and value is the
count of tuples sharing this key in the chunk.
We use homomorphic property of the Paillier’s
scheme to count in the map function the number of
Secure Grouping and Aggregation with MapReduce
353

Map function:
Input: pkey, valueq
// key: id of a chunk of
ˆ
R
// value: collection of pt
1
, t
2
, t
3
q P
ˆ
R
L Ð r s ; // Let L be a dictionary
foreach pt
1
, t
2
, t
3
q P
ˆ
R do
if pt
1
, t
2
q P L then Lrpt
1
, t
2
qs Ð Lrpt
1
, t
2
qs ¨
E
pk
u
p1q;
else Lrpt
1
, t
2
qs Ð E
pk
u
p1q;
foreach pt
1
, t
2
q P L do
emit pt
1
, pt
2
, Lrpt
1
, t
2
qsqq.
Reduce function:
Input: pkey, valuesq
// key: π
A
ptq for t P
ˆ
R
// values: collection of pE
pk
u
paq, E
pk
u
pbqq
count Ð 1;
foreach pE
pk
u
paq, E
pk
u
pbqq P values do
count Ð count ¨ E
pk
u
pbq;
emit pE
pk
u
paq, countq.
Figure 7: SP
comb
-COUNT protocol.
Map function:
Input: pkey, valueq
// key: id of a chunk of
ˆ
R
// value: collection of pt
1
, t
2
, t
3
q P
ˆ
R
L Ð r s ; // Let L be a dictionary
M Ð r s ; // Let M be a dictionary
foreach pt
1
, t
2
, t
3
q P
ˆ
R do
if pt
1
, t
2
q P L then Lrpt
1
, t
2
qs Ð Lrpt
1
, t
2
qs ¨
E
pk
u
p1q;
else Lrpt
1
, t
2
qs Ð E
pk
u
p1q;
if pt
1
, t
2
q P M then Mrpt
1
, t
2
qs Ð Mrpt
1
, t
2
qs ¨t
3
;
else Mrpt
1
, t
2
qs Ð t
3
;
foreach pt
1
, t
2
q P L do
emit pt
1
, pt
2
, Lrpt
1
, t
2
qs, Mrpt
1
, t
2
qsqq.
Reduce function:
Input: pkey, valuesq
// key: π
A
ptq for t P
ˆ
R
// values: collection of pE
pk
u
paq, E
pk
u
pbq, E
pk
u
pcqq
cpt Ð 1;
sum Ð 1;
foreach pE
pk
u
paq, E
pk
u
pbq, E
pk
u
pcqq P values do
cpt Ð cpt ¨ E
pk
u
pbq;
sum Ð sum ¨ E
pk
u
pcq;
emit pE
pk
u
paq, cpt, sumq.
Figure 8: SP
comb
-AVG protocol.
tuples in the chunk that share the same grouping attri-
bute value. Then, each reducer multiplies all encryp-
ted counts for the considered grouping attribute value
to obtain the final encrypted count sent to the user. We
present this refinement called SP
comb
-COUNT proto-
col in Figure 7.
Similarly, we can use combiners for the AVG ope-
ration. Even if the sum is encrypted, combiners hide
the count used for each grouping attribute value i.e.,
for each computed average. We present this refine-
ment called SP
comb
-AVG protocol in Figure 8.
We stress that we can also use combiners with
SUM, and MIN/MAX operations but they do not add
privacy as in previous operations.
3.3 Security Proofs
The security proofs of the SP-SUM protocol (Theo-
rem 1) and of the SP-MIN protocol (Theorem 2) are
presented in (Ciucanu et al., 2018). We emphasize
that the security for SP-(COUNT-AVG) protocols are
similar to the SP-SUM protocol so we do not present
them. Moreover, the security proofs for SP-MIN and
SP-MAX protocols are identical so we do not present
it too.
Theorem 1. The SP-SUM protocol securely computes
the grouping and aggregation for the SUM operation
in the ROM in the presence of semi-honest adversary
even if cloud nodes collude.
Theorem 2. The SP-MIN protocol securely computes
the grouping and aggregation for the MIN operation
in the ROM in the presence of semi-honest adversa-
ries even if cloud nodes collude.
4 CONCLUSION
We have presented efficient algorithms for grouping
and aggregation operations with MapReduce that en-
joy privacy guarantees such as none of the nodes of
the public cloud computing can learn the input or the
output relation. To achieve our goal, we relied on
Paillier’s cryptosystem and on Order-Preserving en-
cryption. We developed an efficient approach (SP) on
the computation cost side as the communication cost
side. We have compared this approach to the standard
algorithm with respect to three fundamental criteria:
computation cost, communication cost, and privacy
guarantees.
Looking forward to future work, we plan to study
the practical performance of our algorithms in an
open-source system that implements the MapReduce
paradigm as Hadoop
1
. Additionally, we aim to inves-
tigate the grouping and aggregation computation with
privacy guarantees in different big data systems (such
as Spark or Flink) whose users also tend to outsource
data and computations similarly to MapReduce.
ACKNOWLEDGEMENTS
This research was conducted with the support of the
FEDER program of 2014-2020, the region council
1
Apache Hadoop: https://hadoop.apache.org/
SECRYPT 2018 - International Conference on Security and Cryptography
354

of Auvergne-Rh
ˆ
one-Alpes, the support of the “Di-
gital Trust” Chair from the University of Auvergne
Foundation, the Indo-French Centre for the Promo-
tion of Advanced Research (IFCPAR) and the Cen-
ter Franco-Indien Pour La Promotion De La Re-
cherche Avanc
´
ee (CEFIPRA) through the project
DST/CNRS 2015-03 under DST-INRIA-CNRS Tar-
geted Programme.
REFERENCES
Agrawal, R., Kiernan, J., Srikant, R., and Xu, Y. (2004).
Order-Preserving Encryption for Numeric Data. In
Proceedings of the ACM SIGMOD International Con-
ference on Management of Data, pages 563–574.
Alghamdi, W. Y., Wu, H., and Kanhere, S. S. (2017). Reli-
able and Secure End-to-End Data Aggregation Using
Secret Sharing in WSNs. In 2017 IEEE Wireless Com-
munications and Networking Conference, WCNC, pa-
ges 1–6.
Blass, E., Pietro, R. D., Molva, R., and
¨
Onen, M. (2012).
PRISM - Privacy-Preserving Search in MapReduce.
In Privacy Enhancing Technologies - 12th Internatio-
nal Symposium, PETS, pages 180–200.
Bonawitz, K., Ivanov, V., Kreuter, B., Marcedone, A.,
McMahan, H. B., Patel, S., Ramage, D., Segal, A.,
and Seth, K. (2017). Practical Secure Aggregation
for Privacy-Preserving Machine Learning. In Pro-
ceedings of the 2017 ACM SIGSAC Conference on
Computer and Communications Security, CCS, pages
1175–1191.
Bultel, X., Ciucanu, R., Giraud, M., and Lafourcade, P.
(2017). Secure Matrix Multiplication with MapRe-
duce. In Proceedings of the 12th International Confe-
rence on Availability, Reliability and Security, pages
11:1–11:10.
Ciucanu, R., Giraud, M., Lafourcade, P., and Ye, L.
(2018). Secure grouping and aggregation with mapre-
duce. Cryptology ePrint Archive, Report 2018/501.
https://eprint.iacr.org/2018/501.
Dean, J. and Ghemawat, S. (2004). MapReduce: Simpli-
fied Data Processing on Large Clusters. In 6th Sym-
posium on Operating System Design and Implementa-
tion OSDI, pages 137–150.
Derbeko, P., Dolev, S., Gudes, E., and Sharma, S. (2016).
Security and privacy aspects in MapReduce on clouds:
A survey. Computer Science Review, 20:1–28.
Dolev, S., Gilboa, N., and Li, X. (2015). Accumula-
ting Automata and Cascaded Equations Automata for
Communicationless Information Theoretically Secure
Multi-Party Computation: Extended Abstract. In Pro-
ceedings of the 3rd International Workshop on Secu-
rity in Cloud Computing, SCC@ASIACCS ’15, pages
21–29.
Dolev, S., Li, Y., and Sharma, S. (2016). Private and Se-
cure Secret Shared MapReduce. In Data and Appli-
cations Security and Privacy XXX - 30th Annual IFIP
WG 11.3 Conference, DBSec, pages 151–160.
Gentry, C. (2009). Fully Homomorphic Encryption Using
Ideal Lattices. In Proceedings of the Forty-first Annual
ACM Symposium on Theory of Computing, STOC ’09,
pages 169–178. ACM.
Leskovec, J., Rajaraman, A., and Ullman, J. D. (2014).
Mining of Massive Datasets. Cambridge University
Press.
Macedo, R., Paulo, J., Pontes, R., Portela, B., Oliveira, T.,
Matos, M., and Oliveira, R. (2017). A practical fra-
mework for privacy-preserving nosql databases. In
36th IEEE Symposium on Reliable Distributed Sys-
tems, SRDS 2017, Hong Kong, Hong Kong, September
26-29, 2017, pages 11–20.
Mayberry, T., Blass, E., and Chan, A. H. (2013). PIRMAP:
Efficient Private Information Retrieval for MapRe-
duce. In Financial Cryptography and Data Security
- 17th International Conference, FC, pages 371–385.
Naccache, D. and Stern, J. (1998). A New Public Key Cryp-
tosystem Based on Higher Residues. In Proceedings
of the 5th ACM Conference on Computer and Commu-
nications Security, CCS ’98, pages 59–66, New York,
NY, USA. ACM.
Okamoto, T. and Uchiyama, S. (1998). A New Public-key
Cryptosystem as Secure as Factoring, pages 308–318.
Springer Berlin Heidelberg.
Paillier, P. (1999). Public-Key Cryptosystems Based on
Composite Degree Residuosity Classes. In Advan-
ces in Cryptology - EUROCRYPT ’99, International
Conference on the Theory and Application of Crypto-
graphic Techniques, pages 223–238.
Popa, R. A., Redfield, C. M. S., Zeldovich, N., and Bala-
krishnan, H. (2011). Cryptdb: protecting confidentia-
lity with encrypted query processing. In Proceedings
of the 23rd ACM Symposium on Operating Systems
Principles 2011, SOSP 2011, Cascais, Portugal, Oc-
tober 23-26, 2011, pages 85–100.
Shamir, A. (1979). How to Share a Secret. Commun. ACM,
22(11):612–613.
Vo-Huu, T. D., Blass, E., and Noubir, G. (2015). EPiC: Effi-
cient Privacy-Preserving Counting for MapReduce. In
Networked Systems - Third International Conference,
NETYS, pages 426–443.
Secure Grouping and Aggregation with MapReduce
355