
Scheduling Smart Loads in Modern Buildings
based on Metaheuristic Optimization
Mohammed Hijjo and Georg Frey
Chair of Automation and Energy Systems, Saarland University, 66123 Saarbrücken, Germany
Keywords: Load Scheduling, Smart Loads, Metaheuristic Optimization.
Abstract: Load scheduling is one of the most promising trends in smart grids. It enables renewable energy to be
efficiently utilized and accommodated in the smart buildings. In this work, we propose a comprehensive
scheduling approach of a group of non-preemptive loads in a ‘greedy’ manner in order to reduce the deficit
between the aggregate scheduled load and the available low-cost generation and therefore, the levelized cost
of energy (LCoE) can be minimized. In order to reduce the massive searching space and attain a good
schedule within a reasonable time, an efficient metaheuristic optimization framework is proposed and
implemented based on genetic algorithms. An illustrative example is used to carry out this work using
artificially created loads representing different facilities inside a building complex.
1 INTRODUCTION
Recently developed technologies in smart grid
sector, including smart loads and smart metering,
have enabled a highly efficient prediction and
identification of the electricity consumption of a
facility in a smart building. Besides, the numerous
adoption of renewable energy sources (RES) to
replace fossil fuel generation, both together, provide
the opportunity to maximize the efficiency of the
system by good coordination of the existing power
assets and loads in order to reduce the net gap
between the demand and the low-cost energy offered
by RES generation and the utility grid in the off-
peak times.
Until recently, various approaches have been
proposed and applied to coordinate the generation
sources in order to meet the varying demand while
keeping the electricity cost at optimal levels (Zhu,
2009). However, due to ever increasing demand and
motivated by the affordable prices of the renewable-
energy based systems, a growing desire exists to
control or optimize the demand growth in order to
facilitate the integration of RES into domestic and
industrial sectors.
Yet, the fluctuating nature and intermittency of
the RES are the still forming a barrier against
entirely relying on them as a main power provider or
even increasing their penetration level in generation
side. In spite of that, this obstacle can be overcome
by using a proper energy storage to stabilize the
operation and compensate the shortage (Pickard et
al., 2012). This solution is not always affordable,
especially in standalone and remote systems, or in
buildings subject to severe power outages, where the
fluctuating supply cannot be matched by a greater
energy storage on all occasions. Otherwise, this will
simply add cost and complexity to the system.
A potential alternative solution will be
influencing the load demand, totally or partially, in
order to lower the need for larger energy reserve. A
proper scheduling of some shiftable loads can
improve the reliability of power delivery for
customers during (macro)grid blackouts or
emergency islanded operation. Once the system is
integrated with some smart loads, that can be
scheduled in advance, an efficient algorithm could
be developed to reallocate these loads in another
time, in which, the total energy cost can be
minimized and the utilization of RES can be
maximized as well.
The need for some controllability over load is not
only to assist in accommodating more RES into
different power systems around the world, but also
there is an important and persistent need to develop
and apply such a solution in countries which have
weak power systems or suffer from continuously
interruption of the utility grid. Especially in
developing countries, a large number of buildings
Hijjo, M. and Frey, G.
Scheduling Smart Loads in Modern Buildings based on Metaheuristic Optimization.
DOI: 10.5220/0006846201190126
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 119-126
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
119

including healthcare facilities, schools and small
businesses are suffering from a serious lack of a
continuous and stable power supply. This issue has
forced the decision makers and the engineers to
develop some urgent solutions to meet the ever
increasing demand, usually depending on diesel
generators, which are costly and environmentally
unfriendly too. The reason behind not using such
logical approach previously, is the need for efficient
load forecasting techniques that can predict the
upcoming load accurately.
1.1 Related Works
A huge work has been done in the context of load
scheduling. A heuristic algorithm to schedule a
group of smart appliances in a smart building subject
to a real-time pricing has been proposed by (Lee et
al., 2013). Another work has been conducted on a
smart building environment but using a set of
household appliances that allow for a limited
interruption time (Caprino et al., 2015). A heuristic-
based load shifting optimization approach has been
proposed by (Logenthiran et al., 2012), where three
adjacent power networks have been chosen to carry
out the study.
Another load scheduling algorithm based on
game theory has been proposed by (Mohsenian-Rad
et al., 2010). The main objective was to optimize the
energy costs by reducing the aggregate peak-to-
average ratio of the total energy demand, while
respecting the privacy of the customers.
Considering the previously listed literature
review and the other ongoing work in this domain;
e.g. (Habib et al., 2016), (Manic et al. 2016), and
(O'Brien el al., 2016), it has been realized that the
number of studies that have discussed the problem
of scheduling dynamic non-preemptive loads from
the perspective of smart grids and smart buildings
are very few. Two reasons maybe behind that, which
are: the complexity of solving such a load
scheduling problem, which is agreed upon to be a
NP-hard problem (Baruah et al., 2004), and the
difficulties involved in modelling such continuously-
operating loads with a non-fixed power
consumption.
1.2 Scope of Work
This work takes care of the load scheduling in smart
building as an important function of the tertiary level
in controlling future microgrids. Thus, the scope of
this work does not include the voltage stability or
power quality at the point of common coupling
(PCC). However, it tackles the uppermost control
level, which has the longest discrete time steps; e.g.
ranging from intra-hours to intra-days. To this end,
this work offers a proactive scheduling plan for the
smart loads which announce their desired operation
pattern or the associated consumption profiles in
advance; e.g. a day ahead. In other words, the
proposed algorithm will attempt to reallocate the
aggregated loads to closely follow the low-price
available power; e.g. from utility grid or local RES
generation. The load profiles are known in
advanced, but they should be reallocated in better
time span in order to minimize the total energy cost.
Furthermore, the proposed approach will be
conducted on a deterministic system, where all load
profiles and RES generation as well as the off-peak
hours of the utility grid are known in advance. This
assumption provides the ‘best case’ scenario for a
stochastic system where the generation/demand
profiles are not precisely known ahead of time. Later
on the solution will be extended to include tackle the
uncertainty of the load as well as the RES
generation. Detailed description will be presented in
the following sections.
2 PROBLEM FORMULATION
Suppose that a part of a building complex consists of
several smart loads that declare their consumption
for the next day on the day ahead. These smart
loads, under this definition, can be called notified,
where the corresponding load profiles are known in
advance within a narrow margin of error. The load
profile per each is defined over T time slots
representing the schedule period (here is one day). A
time slot is chosen in consistence with the data rate
of the connected devices and the smart metering
system, which is usually taken as 10, 15, 30 or 60
minutes.
A non-empty set S consists of N smart shiftable
loads is assumed, =
ℓ∶ℓ∈ℕ
, where ℕ is the
set of the natural numbers, e.g. positive integers
greater zero. Each single load ℓ has a deterministic
load profile
ℓ
(
)
announced in advance in
accordance with the planned operation of the next
day.
The total unscheduled load profile of these
shiftable loads can be mathematically formulated as
given below in Equ. 1
(
)
=
ℓ
ℓ
(
)
1≤≤
(1)
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
120

2.1 Smart Shiftable Load
A smart load can be a single appliance or a cluster of
devices operate in a particular way to perform a
certain function in one of the facilities inside the
whole system. The corresponding load profile of
each load is predetermined, as it is smart, and the
preferred operation time is predefined too. However,
as illustrated in Figure 1, the activation time must be
commanded by the system operator (active mode).
Active mode
(Unscheduled)
Sleeping mode
Deadline
Earliest
Starting-time-
Power Consumption
Daytime
(e)
(d)
(L)
(A)
(B)
Figure 1: Example load profile of a smart shiftable load.
Several examples can be given for such smart
loads in different sectors, for instance, washing
machines and dryers in residential sector can be
considered as smart loads. Heating, ventilation, and
air conditioning (HVAC) systems are a good
example for smart loads in the commercial and
industrial sector, and they have been used as a load
service for large scale of buildings (Lu, 2012). In the
healthcare facilities, different loads and plants can
be good candidates for performing load scheduling,
such as: laundry, sterilization unit, and waste
disposal unit. All of these facilities, generally, can be
considered as ‘stand-alone’ plants or loads and their
load profile can be efficiently forecasted depending
on the different operation circumstances.
Ideally, a shiftable load ℓ is modelled by a
quadruple: (e
ℓ
, d
ℓ
, L
ℓ
, A
ℓ
), where e
ℓ
, d
ℓ
, L
ℓ
, and A
ℓ
are the earliest possible starting time, the deadline,
the duration of the active mode, and the load level
during the active mode respectively.
In this work, an advanced version of this model
is introduced, in which, the load can have multiple
modes of operation that feature the individual
functionalities associated with each smart load.
Thus, the resulting model will be modelled as a
quintuple. Specifically, the added element B
ℓ
represents a nother mode of operation, e.g., sleeping
mode, in which, the load consumes a much less
power than usual to be ready for the normal
operation upon request. Furthermore, the stochastic
nature of the each individual load is modelled using
some statistical properties added to each mode of
operation.
Three exemplary loads are defined in Table 1
and illustrated as shown in Figure 2, showing
different timings and power consumptions as well as
highlighting two modes of operation with their
means and standard deviations.
Table 1: Three exemplary shiftable smart loads.
Load
Tuples (units)
e
ℓ
(time)
d
ℓ
(time)
L
ℓ
(time)
A
ℓ
(,)
(power)
B
ℓ
(,)
(power)
ℓ
1
2 12 6 (135, 8) (15, 5)
ℓ
2
4 11 3 (220, 5) (20, 10)
ℓ
3
7 15 5 (60, 10) (0, 0)
Figure 2: Illustrative profiles of three smart loads.
Obviously, the presented loads here have two
modes of operation. However, the sleeping mode of
the third load is adjust to zero.
Here, the proposed algorithm is dedicated to
provide the operator with the optimal execution time
of each of these loads in order to minimize the LCoE
and maximize the net utilization of the local RES
generation. To this end, the permissible operation
interval
ℓ
of each load ℓ should be declared in
advance, in which, the active mode period must be
accomplished. See Equ. (2):
ℓ
=[
ℓ
,
ℓ
]
(2)
Under this definition, the latest activation time
ℓ
is given by Equ. (3):
ℓ
=
ℓ
−
ℓ
(3)
Thus, a mapping function should be defined in
order to shift the load in accordance with the
aforementioned parameters. A typical mapping
function may bring the selected load
τ
time-slots
forward or backward, as defined in Equ. (4):
ℓ
→
ℓ
=(
ℓ
)=
ℓ
[−
ℓ
]
(4)
Scheduling Smart Loads in Modern Buildings based on Metaheuristic Optimization
121

As the proposed algorithm is offline and deals
with a notified system, the value of the shifting
index can be positive or negative. However, in real-
time systems, in order to fulfill the causal
consistency condition, the shifting index
τ
associated
with a scheduling operator κ is chosen to be positive
integer.
2.2 Low-Price Power Signal
The low-price power signal has an important role in
solving this problem, where it must be tracked as
closely as possible. In isolated systems, which is
powered solely by renewables, this signal results
from the RES-power alone. On the other side, in
grid-connected systems, it can result from both; the
renewable generation and the incentive off-peak
periods of the utility grid, where the power price is
negligible, as compared with peaking times. In
modern power systems, this signal can be notified in
advanced as an incentive for customers to schedule a
part of their consumption accordingly.
In this work, it is assumed that the utility grid
adopts a two-level power price, in which, the off-
peak times follow a lower fixed price c
l
and the
counterpart peaking times follow a higher price c
h
as
given in Equ. (5):
(
)
=
,∈[
,
]
,ℎ
(5)
The low-price signal Υ() is represented by the
total sum of the solar generated power from the
installed array over the building and the utility grid
capacity during off-peak, ∈[
,
], see Figure 5.
The target is therefore to accumulate the greatest
possible amount of these loads in these time spans
without overriding the capacity limit of the main
power feeder.
2.3 Optimization Algorithm
In order to find the optimal scheduling operator κ
associated with each smart load in the system, we
chose here to penalize the absolute-value norm of
the error between the low-price power signal and the
aggregate scheduled load profiles as formulated in
Equ. (6):
(
)
=
Υ
(
)
−
ℓ
[−
ℓ
]
ℓ
(6)
Where Υ
(
)
is the low-price power signal and
P
ℓ
[−
ℓ
] is the shifted version of the smart load ℓ
corresponding to the scheduling operator κ. The
general overview of the proposed offline load
scheduling scheme is shown in Figure 3.
Figure 3: General overview of the proposed load
scheduling system.
The main idea is that to maximize the
autocorrelation between the low-price signal and the
aggregate load subject to the permissible activation
time of each load. It is important here to distinguish
between this problem and other classical constraint-
based scheduling problems (Wall, 1996), where the
tasks, i.e. the loads, are constant and require a
certain share of the resource. However, the dynamic
nature of the loads here makes it even harder to
solve the problem without using relaxation
techniques to eliminate the effect of the fluctuating
demand. As presented in Figure 3, the proposed
scheduling approach targets to reallocate the
different loads to minimize the difference between
announced low-price power profile and the
aggregate scheduled loads, so as to increase the
benefit from the available low-price power as much
as possible. The existing scheduling problem is a
complicated optimization problem, which is NP-
hard (Baruah et al., 2004). Therefore, finding an
optimal schedule for a huge set of schedulable loads
is very complicated problem and thus, the exact
solution might be hard to find without enumerating
all possible schedules and then evaluating them.
To elaborate on this issue, if we have a set of
loads with at least possible positions for each load
to start the active operation, the complexity of the
searching space will be
. Obviously, the
complexity of the problem is exponentially
increasing with the number of loads and/or the
possible schedules of each load. In order to cut down
the computation time, the developed optimization
approach applies the Genetic Algorithms to handle
this problem (Mitchell, 1996).
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
122
The genetic-based approach belongs to the
bigger class of evolutionary algorithms (EA), which
is one of the metaheuristic stochastic optimization
techniques that can provide a solution to an
optimization problem with less computational effort
than iterative ones. Compared to conventional
algorithms, metaheuristics sample a set of solutions
which is too large to be completely sampled. Thus,
by searching over a large set of feasible solutions,
metaheuristics can often find good solutions with
less computational effort than optimization
algorithms, iterative methods, or simple heuristics
(Blum et al., 2003).
A group of initial schedules are randomly
generated at the beginning. Some of the feasible
schedules are selected and then merged as a one
schedule by the crossover and mutation operations,
and then the schedule set is evolved by replacing a
schedule in the old set by the newly generated
schedule. This process is repeated until the schedule
set converges (Lee et al., 2013).
An abstract pseudo-code of the applied GAs is
given below in Figure 4.
1.Inputs
Load profiles, Possible schedules , Off-peak
periods, PV generation.
2.Initialization:
randomly seeded schedules.
3.Cost function evaluation (Equ. 6)
4.Selection:
Select the best candidate solution among the
present generation before step in the next
generation.
5.Crossover and mutation:
The new possible candidate solution is
generated from the parents which survived.
6.Evaluate the cost control function
again (STEP 4)
7.Termination:
After exceeding the time budget or generation
limit or satisfying the minimum criteria.
8.Output:
The values correspond to the best/final
solution.
Figure 4: Pseudo-code of the GA-optimization algorithm.
3 NUMERICAL EXAMPLE
A preliminary simulation is conducted using a
clinical facility building incorporating a group of six
shiftable loads. The low-price power signal is
generated from the aggregation of the off-peak
period from the utility grid in Gaza-city and the
onsite solar generation. Other essential loads are
assigned to be supplied using the conventional
generation as they need a continuous and stable
supply without any interruption. The building is
mainly supplied from the utility grid, which has a
feeder capacity of 18 kW. In spite of the low-price
power, the grid is interrupting on a daily basis,
which makes relying solely on it impossible.
Therefore, the building was fitted recently with a
20kW
p
solar array to assist the legacy standby diesel
generator.
The used diesel generator has a capacity of 20
kW and its associated fuel cost is modelled by fitting
the manufacturer data (Diesel Service, 1981). The
grid price is considered c
l
= 0.16 $/kWh during off-
peak hours and the price associated with diesel
operation under the rated load is c
h
= 0.56 $/kWh.
Half of the grid capacity is reserved for essential
loads and the second half is assigned for the
shiftable loads.
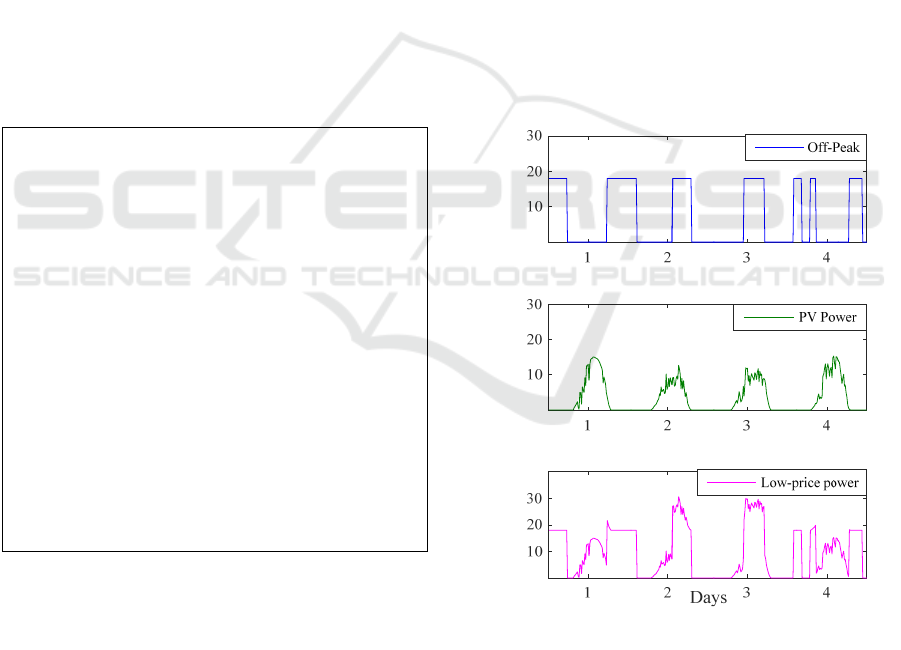
The off-peak signal and the available PV
generation over a four-days are shown below in
figure 5.
Figure 5: Sample 4-days off-peak and PV generation.
The system is modeled using MATLAB and the
optimization algorithm is conducted using the
provided optimization toolbox.
The optimization window is considered here as a
single day and then the optimization process should
be repeated in accordance with the new timing
Powe
r
Scheduling Smart Loads in Modern Buildings based on Metaheuristic Optimization
123

constraints for the day after. The convergence of the
optimization process for one sample day is depicted
in figure 6, where the searching process is converged
after about 100 generation, and then the
improvement rate is almost negligible. The resulting
value here (approx. 820) represents the penalized
absolute-value norm of the error between the low-
price power signal and the aggregate scheduled load
profiles as formulated in Equ. (6).
Figure 6: Convergence of the proposed GA-Scheduling.
The activation times of five sample loads are
expressed in figure 7, showing the original operation
and the proposed activation during the first day.
Figure 7: Scheduling results of three sample loads.
Figure 8 shows the final results over a four-days
simulation window. It presents the aggregated low-
price power (green), i.e. which has to be tracked as
well as the total loads before performing the
scheduling (dotted red) and finally, the total loads
after performing the scheduling (blue).
Figure 8: Scheduling results over four-days simulation.
Figure 9 illustrates the instantaneous energy cost
before (red) and after (blue) performing the
proposed scheduling algorithm.
Figure 9: Instantaneous end-price of energy.
Some performance indices and end results are
calculated and concluded in Table 2, presenting the
net utilization factor of the solar power and LCoE as
well.
Table 2: Performance indices.
Performance index
Before
scheduling
After
scheduling
Total PV
production (kWh)
323.48
Aggregate Shiftable
Loads (kWh)
388.63
Net PV usage
(kWh)
146.54 180.38
Total supply cost
($)
117.6 82.13
PV Utilization
Factor (%)
45.3 55.76
LCoE ($/kW) 0.30 0.21
4 DISCUSSION
Unlike other works, such as (Habib et al., 2016), and
(Leithon et al., 2017), where preemptive loads have
been used to reshape the aggregate load, e.g. that is
they can be supplied with interruptions, the proposed
work here aims at reallocating each shiftable load to
another time interval instead of reshaping them so
0 50 100 150
Generatio
n
820
860
900
940
Penalty value
Best: 821.459 Mean: 825.27
Best penalty value
Mean penalty value
0120
0
1
2
0120
0
1
2
0120
0
2
4
0120
0
2
4
0120
0
5
0120
0
5
0120
0
1
2
0120
0
1
2
0120
0
5
0120
0
5
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
124

that the resulting consumed energy after scheduling
is similar to their unscheduled counterpart. The
reason behind that is to avoid the so-called “rebound
effect”, because simply switching the loads ON and
OFF will not lead to the same desired performance if
they work continuously as usual. In such cases,
energy is naturally not saved and expectedly another
peak will be generated (Palensky et al., 2011).
Additionally, it is important here to highlight the
difference between the addressed model in this work
and other classical models (Ali et al., 2012) that use
4-tuples only expressing the timing constraints and a
constant power demand over a single mode of
operation, which makes the problem somehow
similar to constraint-based problems (Wall, 1996).
Unlikely, the presented model here expresses the
fluctuating nature of the load that can have multiple
operation modes with some variability on the power
consumption.
Another practical aspect is the scheduling
window, which is taken here as a single day and then
the algorithm is repeated for the next day using the
new data. In this regards, one load cannot be
requested more than once within the same window.
Otherwise, two or more identical loads with
different activation constraints should be used in
order not to allow any overlapping of the operation
of same load in that facility.
Formerly, the developed scheduling algorithms
were adopting some scheduling policies used in real-
time processing such as Earliest Deadline First
(EDF) and Least Laxity First (LLF) which assign the
tasks, e.g. loads, according to their deadlines or the
slack times (Subramanian et al., 2012). However, in
renewable energy systems with versatile loads, such
algorithms still need an accurate forecasting tools
and systems to handle the fluctuating nature of the
RES and the dynamic price of the grid.
Therefore, the matter of prioritizing loads should
consider both: timings of the loads and their
consumption level at each time slot. Obviously, the
dominants loads will be those with higher
consumption and less timing flexibility than others,
which will diminish the effect of other shiftable
loads but with lower consumption.
5 CONCLUSION AND OUTLOOK
An easy-to-implement load scheduling approach
based on the notified nature of the system was
proposed. Besides, a straightforward model for
smart shiftable loads was introduced in this work.
The proposed approach has adopted the GAs to cut-
down the searching space and find the optimal
schedule within a reasonable time budget.
There are three important topics that have not
been explored in this paper, and will be the subject
of our future publications:
(a) Reduction the capacity of the conventional
generation, e.g. diesel generator. The
economic basis for this issue should be
clearly justified through synthetic examples
and much more comprehensive simulations
using real data.
(b) The incorporated energy management
scheme, which will highlight the power
routing between all system components,
including the static and the essential loads
which cannot be shifted in time.
(c) Online adaptation of the resulting schedules
using shorter time window instead of
performing the algorithm once per day.
Thus, the improvement rate can be further
increased according to the recent
measurements of the RES generation and the
loads as well.
REFERENCES
Zhu, J., 2009. Optimization of Power System Operation,
Wiley publishing, Institute of Electrical and
Electronics Engineers
Pickard, W., Abbott, D., 2012. Addressing the
intermittency challenge: Massive energy storage in a
sustainable future, Proceedings of the IEEE, vol. 100,
no. 2.
Lee, E., B., Hyokyung, 2013. Electricity Usage
Scheduling in Smart Building Environments Using
Smart Devices, The Scientific World Journal
Caprino, D., Vedova, M., Facchinetti, T., 2015. Applying
limited-preemptive scheduling to peak load reduction
in smart buildings, IEEE 20
th
Conference on Emerging
Technologies & Factory Automation (ETFA),
Luxembourg
Logenthiran, T., Srinivasan, D., Shun, T., 2012. Demand
Side Management in Smart Grid Using Heuristic
Optimization, IEEE Transactions on Smart Grid, vol.
3, no. 3, pp. 1244-1252
Palensky, P., Dietrich, D., 2011. Demand side
management: demand response, intelligent energy
systems, and smart loads,” IEEE Transactions on
Industrial Informatics, vol. 7, no. 3, pp. 381–388
Habib, A. et al., 2016. Model predictive load scheduling
using solar power forecasting, American Control
Conference (ACC), Boston, MA.
Manic, M. et al., 2016. Building Energy Management
Systems: The Age of Intelligent and Adaptive
Buildings, IEEE Industrial Electronics Magazine, vol.
10, no. 1, pp. 25-39
Scheduling Smart Loads in Modern Buildings based on Metaheuristic Optimization
125

O'Brien, G., Rajagopal, R., 2016. Scheduling Non-
Preemptive Deferrable Loads, IEEE Transactions on
Power Systems, vol. 31, no. 2, pp. 835-845
Baruah, S., Goossens, J., 2004. Scheduling real-time tasks:
Algorithms and Complexity, in Handbook of
Scheduling: Algorithms, Models and Performance
Analysis, J.Y-T. Leung, Ed. Boca Raton, FL: CRC
Press,
Lu, N., 2012. An Evaluation of the HVAC Load Potential
for Providing Load Balancing Service, IEEE Trans-
actions on Smart Grid, vol. 3, no. 3, pp. 1263-1270
Wall, M., 1996. A Genetic Algorithm for Resource-
Constrained Scheduling, Massachusetts Institute of
Technology
Mohsenian-Rad, A., Wong, V., Jatskevich, J., Schober, R.,
Leon-Garcia, A., 2010. Autonomous demand-side
management based on game-theoretic energy
consumption scheduling for the future smart grid.
IEEE Transactions on Smart Grid, vol. 1, no. 3, pp.
320–331.
Goldberg, D., 1989. Genetic Algorithms in Search,
Optimization & Machine Learning, Addison-Wesley.
Conn, A. et al., 1997. A Globally Convergent Augmented
Lagrangian Barrier Algorithm for Optimization with
General Inequality Constraints and Simple Bounds,
Mathematics of Computation, vol. 66, no. 217, pp
261–288.
Mitchell, M. 1996. An Introduction to Genetic Algorithms.
MIT press Cambridge, MA, USA.
Blum, C., Roli, A., 2003. Metaheuristics in combinatorial
optimization: Overview and conceptual comparison.
35 (3). ACM Computing Surveys: 268–308.
Deep, K., Singh, K., Kansal, M.L., Mohan, C., 2009. A
real coded genetic algorithm for solving integer and
mixed integer optimization problems. Applied
Mathematics and Computation, 212(2), pp. 505–518.
Diesel Service, 1981. Diesel Fuel Consumption [online]
Available at: http://www.dieselserviceandsupply.com
[Accessed Feb. 2018].
Leithon, J., Sun, S., Lim, T. J., 2017. Demand Response
and Renewable Energy Management using
Continuous-Time Optimization, IEEE Transactions on
Sustainable Energy, Volume PP, Issue 99.
Subramanian, A., Garcia, M., Domínguez-García, A.,
Callaway, D., Poolla K., Varaiya, P., 2012. Real-time
scheduling of deferrable electric loads, American
Control Conference (ACC), Montreal, pp. 3643-3650.
Ali, S. Q., Maqbool, S. D., Ahamed T. P. I., Malik, N. H.,
2012. Pursuit Algorithm for optimized load
scheduling, IEEE International Power Engineering and
Optimization Conference, Malaysia, Melaka, pp. 193-
198.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
126
