On the Security of Linear Sketch Schemes against Recovering Attacks

Takahiro Matsuda

, Kenta Takahashi

and Goichiro Hanaoka

National Institute of Advanced Industrial Science and Technology (AIST), Tokyo, Japan

Hitachi Ltd., Yokohama, Japan

Keywords:

Fuzzy Signature, Linear Sketch, Recovering Attacks.

Abstract:

Recently, the notion of fuzzy signature was introduced by Takahashi et al. (ACNS 2015, ACNS 2016, ePrint

2017). It is a signature scheme in which signatures can be generated using “fuzzy data” (i.e. noisy data such

as biometric features) as a signing key, without using any additional user-speciﬁc data (such as a helper string

in the context of fuzzy extractors). One of the main building blocks in the existing fuzzy signature schemes, is

a primitive called linear sketch, which can be interpreted as a certain form of (one-way) encoding with which

fuzzy data is encoded, and is used in combination with an ordinary signature scheme with certain functional

and security properties, to construct a fuzzy signature scheme. Although the security of the underlying linear

sketch scheme is very important for the security of the constructed fuzzy signature schemes, a linear sketch

scheme is a relatively new primitive, and what security properties its deﬁnition and the existing constructions

satisfy, has not been understood well. In order to deepen our understanding of this primitive, in this paper we

clarify the security properties achieved by the existing linear sketch schemes. More speciﬁcally, we formalize

security of a linear sketch scheme against “recovering” attacks, and then clarify that the existing linear sketch

schemes achieve sufﬁciently strong security against them.

1 INTRODUCTION

1.1 Background and Motivation

Motivated mainly by application scenarios of biomet-

ric authentication, Takahashi et al. (Takahashi et al.,

2015; Matsuda et al., 2016; Takahashi et al., 2017)

recently introduced a special kind of digital signature

called fuzzy signature. In a fuzzy signature scheme,

signatures can be generated using “fuzzy data” (i.e.

noisy data such as biometric features) as a signing

key. There have been some approaches that achieve

a similar feature, and perhaps the most well-known

(and nowadays standard) approach would be to com-

bine an ordinary signature scheme with a fuzzy ex-

tractor (Dodis et al., 2008). However, as pointed

out by Takahashi et al., the fuzzy-extractor-based ap-

proach requires (public but) user-speciﬁc auxiliary

data to be present at the time of signing. Hence,

for example, a user has to carry it himself/herself,

or the device executing the signing algorithm has to

be on-line to retrieve the auxiliary data from some

(public) repository. What distinguishes a fuzzy signa-

ture scheme from the fuzzy-extractor-based approach,

is that the signing algorithm does not require user-

speciﬁc data (other than his/her own biometric fea-

ture) at the time of signing, and hence for example a

user can generate a signature even if he/she is com-

pletely empty-handed. This is quite attractive, and

fuzzy signatures are expected to be applied to various

applications.

We brieﬂy review the results by Takahashi et al.

(Takahashi et al., 2015; Matsuda et al., 2016; Taka-

hashi et al., 2017).

In (Takahashi et al., 2017), in

addition to formally deﬁne fuzzy signatures, they in-

troduced what they call a fuzzy key setting, which for-

malizes some necessary information about the setting

over which fuzzy data is considered, e.g. the met-

ric space to which fuzzy data belongs, the threshold

with which two sampled data are considered to be

measured from the same object, the distribution from

which each fuzzy data is assumed to be drawn, how

the ﬂuctuation of fuzzy data is modeled, etc. A fuzzy

signature scheme is associated with such a fuzzy key

setting. (Takahashi et al., 2017) also introduced a tool

that they call linear sketch, which is also a crypto-

Since (Takahashi et al., 2017) is the merged full version

of (Takahashi et al., 2015) and (Matsuda et al., 2016), from

here on, by “Takahashi et al.” we mean (Takahashi et al.,

2017) unless indicated.

Matsuda, T., Takahashi, K. and Hanaoka, G.

On the Security of Linear Sketch Schemes against Recovering Attacks.

DOI: 10.5220/0006847100760087

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 76-87

ISBN: 978-989-758-319-3

graphic primitive associated with a fuzzy key setting,

and is a kind of a pair of linear encoding and error

correction methods that we will detail later. (Taka-

hashi et al., 2017) then gave a generic construction of

a fuzzy signature scheme for a fuzzy key setting from

the combination of a linear sketch scheme (that is as-

sociated with the same fuzzy key setting) and an or-

dinary signature scheme that has some homomorphic

properties regarding signing/veriﬁcation keys. They

then gave two instantiations of concrete fuzzy signa-

ture schemes via their generic construction, where for

each construction, they speciﬁed a fuzzy key setting,

constructed a linear sketch scheme, and then com-

bined it with (a modiﬁed variant of) an existing or-

dinary signature scheme.

Linear Sketch. The main focus in this paper is on

a linear sketch scheme. As mentioned earlier, this

primitive can be understood as a pair of linear en-

coding and error correction methods. It is associated

with a fuzzy key setting and an abelian group K , and

consists of two algorithms

: “Sketch” and “DiﬀRec”

(where the second algorithm stands for “difference re-

construction”). The ﬁrst algorithm can be used to gen-

erate a “sketch” c of an element s ∈ K using a fuzzy

data x as a “key” (or a “mask”). The second algorithm

takes as input two sketches c and c

, where c (resp.

) is supposedly a sketch of an element s ∈ K (resp.

∈ K ) generated by using fuzzy data x (resp. x

and outputs the difference ∆s = s −s

if the two fuzzy

data x and x

are “close” (according to the threshold

t speciﬁed in the fuzzy key setting). In (Takahashi

et al., 2017), it is required that a linear sketch scheme

satisﬁes additional “linearity” and “weak simulatabil-

ity” properties that are used in the security proof for

the generic construction.

Our Motivation. Although the security of the un-

derlying linear sketch scheme is very important for

the security of the fuzzy signature schemes con-

structed from the generic construction of Takahashi

et al., a linear sketch scheme is a relatively new prim-

itive, and what security properties its deﬁnition and

the existing constructions satisfy, has not been well

understood. As mentioned above, in the formaliza-

tion in (Takahashi et al., 2017), a linear sketch scheme

is associated with a fuzzy key setting, which in turn

speciﬁes the underlying metric space and distribution

of fuzzy data. So far, we only have two concrete con-

structions of linear sketch schemes: the ﬁrst scheme

A linear sketch scheme actually also has the setup al-

gorithm Setup that outputs a public parameter used by the

other algorithms, but we omit them in the explanation in the

introduction. The formal deﬁnition appears in Section 3.

(denoted by “S

CRT

”) is based on the Chinese remain-

der theorem, and the second one (denoted by “S

Hash

”)

is based on a universal hash function family, and the

fuzzy data space for these constructions is the space

[0,1)

with the L

∞

-distance. Since the constructions

CRT

and S

Hash

seem tailored to this speciﬁc metric

space, they have to inherently deal with non-integer

numbers and furthermore they cannot be used with

fuzzy key settings with other natural metrics for bio-

metric authentication such as the edit distance and

Hamming distance over bit strings.

In fact, the earlier papers (Takahashi et al., 2015;

Matsuda et al., 2016) left the treatment of real num-

bers somewhat ambiguous, and Yasuda et al. (Yasuda

et al., 2017) showed that the linear sketch schemes

CRT

and S

Hash

could be vulnerable to so-called “re-

covering attacks” (which recover fuzzy data x and an

element s from a sketch c = Sketch(s,x)), if the real

numbers in these schemes are treated in an inappro-

priate way. Concurrently to (Yasuda et al., 2017), the

treatment of real numbers was unambiguously speci-

ﬁed in (Takahashi et al., 2017), and with their treat-

ment the attacks by (Yasuda et al., 2017) were shown

to no longer work. However, this situation suggests

that care must be taken in the deﬁnition of linear

sketch schemes.

The main motivation of this paper is to contribute

to deepening our understanding of this primitive, so

that we can come up with better constructions and ap-

plications, which potentially could lead to future new

constructions of fuzzy signatures (with fuzzy key set-

tings that are different from the existing schemes).

1.2 Our Contributions

In order to deepen our understanding of a linear

sketch scheme, in this paper we clarify a new aspect

of the security properties achieved by the existing lin-

ear sketch schemes.

More speciﬁcally, in Section 4, we introduce se-

curity of a linear sketch scheme against “recovering”

attacks, which directly captures the resistance against

the attacks of (Yasuda et al., 2017). Namely, it re-

quires that recovering fuzzy data x from a sketch c

(and a public parameter pp) is hard. Our formaliza-

tion uses the notion of average min-entropy (Dodis

et al., 2008), which naturally corresponds to the hard-

ness of guessing a secret given some leakage. Then,

as our main technical results, we show that the two

linear sketch schemes in (Takahashi et al., 2017), S

CRT

and S

Hash

, satisfy sufﬁcient level of security against

recovering attacks (when the treatment of real num-

bers in (Takahashi et al., 2017) is taken into account),

which are respectively shown in Sections 5 and 6.

On the Security of Linear Sketch Schemes against Recovering Attacks

These results directly imply that the attacks of (Ya-

suda et al., 2017) do not apply to the linear sketch

schemes in (Takahashi et al., 2017).

We remark that if a linear sketch scheme is vulner-

able to recovering attacks and is used in the generic

construction of (Takahashi et al., 2017), then the re-

sulting fuzzy signature scheme is also not secure. (In

this sense, security against recovering attacks can be

interpreted as a guideline for future designs of linear

sketch schemes.) Since (Takahashi et al., 2017) gives

security proofs for their fuzzy signature schemes, it

implies that the linear sketch schemes in (Takahashi

et al., 2017) are known to be secure against recover-

ing attacks. Our results show this fact more directly.

To show the security of the linear sketch schemes

against recovering attacks, we introduce the notion of

decomposability and partial hiding property of a lin-

ear sketch scheme. Informally speaking, the decom-

posability property requires that the computation of

c = Sketch(s,x) can be decomposed into two parts

and f

, where f

is independent of s, so that the

computation c = Sketch(s,x) is equivalent to c =

) = ( f

(s,x), f

(x)). The partial hiding prop-

erty requires that c

= f

(s,x) does not contain any in-

formation of x if s is chosen uniformly at random. We

will show that if a linear sketch scheme satisﬁes these

properties, then its security against recovering attacks

can be reduced to the hardness of recovering fuzzy

data x given only the leakage from the second com-

ponent f

(x), which means that the security against

recovering attacks can be analyzed by analyzing only

the distribution of x and f

. These properties make it

easier to show the security of linear sketch schemes

against recovering attacks, and we believe that their

formalizations are useful for future designs of linear

sketch schemes. We will show that the linear sketch

schemes S

CRT

and S

Hash

satisfy these properties in Sec-

tions 5.4 and 6.3, respectively. For the formal deﬁni-

tions and the more details on how they are useful, see

Section 4.

1.3 Paper Organization

The rest of this paper is organized as follows: In Sec-

tion 2, we review some basic notation, basic deﬁni-

tions and facts, and the treatment of real numbers. In

Section 3, we review the necessary deﬁnitions for lin-

ear sketch. In Section 4, we introduce security against

recovering attacks for a linear sketch scheme. There,

we also introduce decomposability and the partial hid-

ing property of a linear sketch scheme, and show a

useful lemma that is used in the subsequent sections.

In Section 5, we show how strong the ﬁrst linear

sketch scheme S

CRT

is against recovering attacks. In

Section 6, we do the same for the second linear sketch

scheme S

Hash

2 PRELIMINARIES

In this section, we review the basic notation, basic

deﬁnitions and facts, and the treatment of real num-

bers in this paper.

2.1 Basic Notation

N, Z, and R denote the sets of all natural numbers, all

integers, and all real numbers, respectively. If n ∈ N,

then we deﬁne [n] := {1, . . .,n}. If a,b ∈ N, then

“GCD(a,b)” denotes the greatest common divisor of a

and b. If a ∈ R, then “bac” denotes the maximum inte-

ger which does not exceed a (i.e. the rounding-down

operation), and “bae” denotes the integer that is the

nearest to a (i.e. the rounding operation). Through-

out the paper, we use the bold font to denote a vector

(such as x and a). We extend the deﬁnition of “b·e” to

allow it to take a real vector a = (a

,...) as input,

by bae := (ba

e,ba

e,...).

“x ← y” denotes that y is (deterministically) as-

signed to x. If S is a ﬁnite set, then “|S|” denotes its

size, and “x ←

S” denotes that x is chosen uniformly

at random from S. If Φ is a distribution (over some

set), then x ←

Φ denotes that x is chosen accord-

ing to the distribution Φ. If x and y are bit-strings,

then |x| denotes the bit-length of x, and “(x||y)” de-

notes the concatenation of x and y. “(P)PTA” denotes

a (probabilistic) polynomial time algorithm. If A is a

probabilistic algorithm, then “y ←

A(x)” denote that

A computes y by taking x as input and using an inter-

nal randomness that is chosen uniformly at random.

Throughout the paper, “k” denotes a security parame-

ter. A function f (·) : N → [0, 1] is said to be negligible

if for all positive polynomials p(·) and all sufﬁciently

large k, we have f (k) < 1/p(k).

2.2 Treatment of Real Numbers

Here, we recall the treatment of real numbers in

(Takahashi et al., 2017). The following explanations

are mostly taken verbatim from the “On the Treat-

ment of Real Numbers” paragraph in (Takahashi et al.,

2017, Section 6).

We assume that the signiﬁcand of all real num-

bers is expressed in an a-priori ﬁxed length (in bits)

λ, where λ is some natural number that is a polyno-

mial of a security parameter k. That is, a real num-

ber is expressed in the form

, where m is a λ-bit

integer that represents the signiﬁcand and −γ ∈ Z is

SECRYPT 2018 - International Conference on Security and Cryptography

the exponent.

Furthermore, if real numbers are in-

volved in some arithmetic operations such as addition

and multiplication, then the rounding-down operation

is naturally applied to the signiﬁcand of the result-

ing number, so that the result is always expressed in

the above form (i.e. its signiﬁcand is expressed with

λ bits). We stress that this setting is natural, taking

computer implementations into account.

For example, if we multiply a real number x =

(where m is a λ-bit integer and 0 ≤ γ ≤ λ) with an n-

bit integer a (where n ≤ γ), then the resulting number

x · a of the multiplication of x and a is treated as

m · a

· 2

−(γ−n)

. (1)

That is, its signiﬁcand is a λ-bit integer b

m·a

c and its

exponent is −(γ− n). This might not look straightfor-

ward at ﬁrst glance, but note that the signiﬁcand b

m·a

is the result of the multiplication m · a rounded down

to have a λ-bit precision (the denominator 2

is due

to the fact that a is an n-bit integer). The exponent is

correspondingly “shifted” to take into account that a

is an n-bit integer. See Figure 1 for an illustration for

the calculation of x · a.

2.3 Basic Deﬁnitions on Entropy

Here, we recall several basic deﬁnitions and a fact re-

lated to entropy used in this paper.

Deﬁnition 1. Let X be a distribution deﬁned over a

set X. The min-entropy of X , denoted by H

∞

(X ), is

deﬁned by H

∞

(X ) := −log

max

∈X

Pr[X = x

Deﬁnition 2 ((Dodis et al., 2008)). Let (X ,Y ) be a

joint distribution deﬁned over the direct product of

sets X ×Y . The average min-entropy of X given Y ,

denoted by

∞

(X |Y ), is deﬁned by

∞

(X |Y ) := −log



y←

max

∈X

Pr[X = x

|Y = y]

i

Note that the average min-entropy

∞

(X |Y ) nat-

urally captures the hardness of recovering a “secret”

x from a “leakage” y when (x,y) is sampled ac-

cording to (X ,Y ). More speciﬁcally, the deﬁni-

tion of average min-entropy

∞

(X |Y ) implies that

if (x,y) ←

(X , Y ), then given y, even a computa-

tionally unbounded algorithm can succeed in ﬁnding

x with probability at most 2

−

∞

(X |Y )

We will use the following simple fact formally

shown in (Dodis et al., 2008).

Lemma 1. Let (X ,Y ) be a joint distribution deﬁned

over the direct product of sets X ×Y . If |Y | ≤ 2

for

some t ∈ N, then

∞

(X |Y ) ≥ H

∞

(X ) − t.

For ease of treatment of decimal numbers, we use the

convention that a positive γ implies a negative exponent.

2.4 Universal Hash Function Family

Here, we ﬁrst recall the deﬁnition of a universal hash

function family, then the existence of a universal hash

function family with linearity.

Deﬁnition 3. Let H = {h

: D → R}

z∈Z

be a fam-

ily of hash functions, where Z denotes the seed space

of H . We say that H is a universal hash function

family if for all x,x

∈ D such that x 6= x

, we have

z←

(x) = h

)] ≤ 1/|R|.

In the linear sketch scheme S

Hash

in (Takahashi

et al., 2017), a universal hash function family with

a linearity property is used. (See e.g. (Cheraghchi,

2011) for a concrete construction.)

Lemma 2. Let F

be a ﬁnite ﬁeld with prime order p,

and let n ∈ N. There exists a family of universal hash

function H

lin

= {h

: (F

)

→ F

}

z∈F

such that for

all z ∈ F

, the following linearity property is satis-

ﬁed: For all x,x

∈ (F

)

and α,β ∈ F

, it holds that

α · h

(x) + β · h

) = h

(α · x + β · x

3 DEFINITIONS FOR LINEAR

SKETCH

Here, we review the deﬁnitions for a fuzzy key set-

ting in Section 3.1 and a linear sketch scheme in Sec-

tion 3.2.

In order to grasp how linear sketch schemes are

used in the constructions of a fuzzy signature scheme,

in Appendix, we review the deﬁnition of a fuzzy sig-

nature scheme as well as the two fuzzy signature

schemes proposed in (Takahashi et al., 2017).

3.1 Fuzzy Key Setting

A fuzzy key setting speciﬁes a metric space to which

fuzzy data (such as biometric data) belongs, the

threshold with which two sampled fuzzy data are con-

sidered close/far, the distribution from which each

fuzzy data is assumed to be sampled, and the error

distribution that models “ﬂuctuation” of fuzzy data.

The formalization of (Takahashi et al., 2017) adopts

the so-called universal error model, which assumes

that for all objects U that produce fuzzy data that we

are interested in, if U produces a data x at the ﬁrst

measurement (e.g. at the registration), and the same

object is measured next time, then the measured data

follows the distribution {e ←

Φ; x

← x + e : x

Formally, a fuzzy key setting F consists of

((d,X),t,X ,Φ,ε

), each of which is deﬁned as fol-

lows:

On the Security of Linear Sketch Schemes against Recovering Attacks

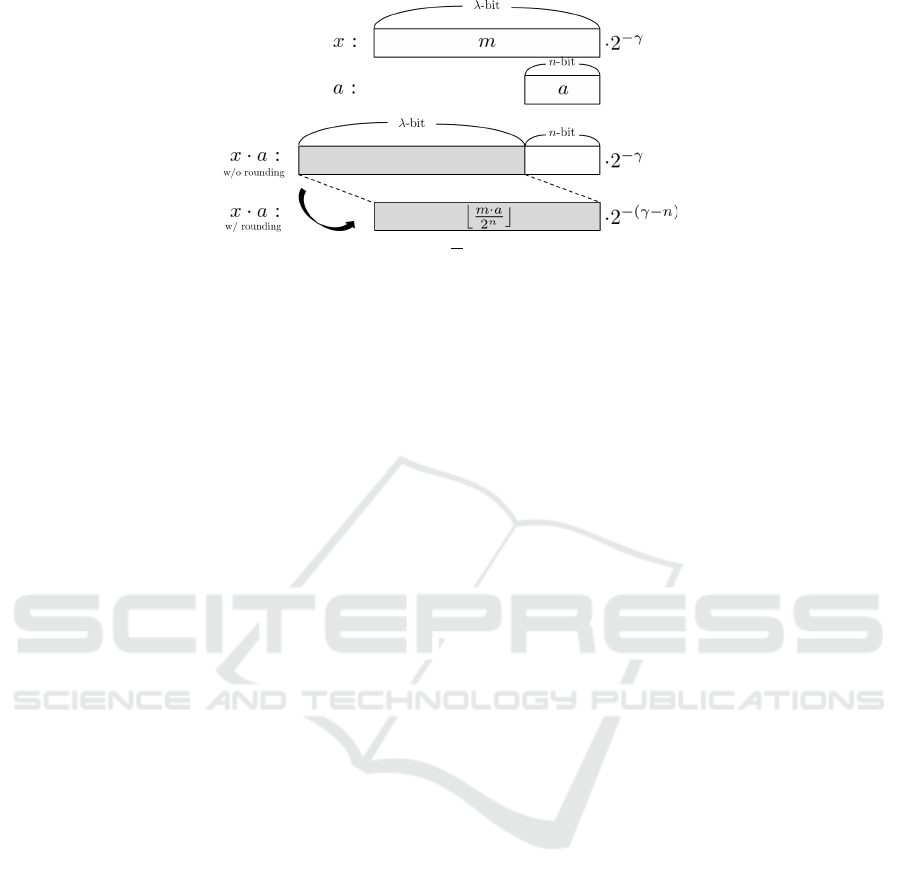
Figure 1: An illustration of multiplication of a real number x =

and an n-bit integer a. (This picture is taken from (Takahashi

et al., 2017, Fig. 5).)

(d,X): This is a metric space, where X is a space

to which a possible fuzzy data x belongs, and

d : X

→ R is the corresponding distance func-

tion. We furthermore assume that X constitutes

an abelian group.

t: (∈ R) This is the threshold value, determined by

a security parameter k. Based on t, the false ac-

ceptance rate (FAR) and the false rejection rate

(FRR) are determined. We require that FAR :=

Pr[x,x

←

X : d(x,x

) < t] is negligible in k.

X : This is a distribution of fuzzy data over X .

Φ: This is an error distribution (see the above expla-

nation).

: (∈ [0,1]) This is an error parameter that represents

FRR. We require that for all x ∈ X, FRR := Pr[e ←

Φ : d(x,x + e) ≥ t] ≤ ε

We remark that the false acceptance/rejection rate

FAR and FRR, the error distribution Φ, and the error

parameter ε

are not directly used in our paper be-

cause they do not directly affect the security of linear

sketch schemes.

3.2 Linear Sketch

Here, we review the deﬁnition of a linear sketch

scheme in (Takahashi et al., 2017).

Let F = ((d,X),t, X ,Φ,ε

) be a fuzzy key setting,

and let K be a ﬁnite abelian group. A linear sketch

scheme S for (F ,K ), consists of the following three

algorithms (Setup,Sketch,DiﬀRec):

Setup is the “setup” algorithm that takes 1

, and out-

puts a public parameter pp.

Sketch is the “sketching” algorithm that takes pp, an

element s ∈ K , and fuzzy data x ∈ X as input, and

outputs a “sketch” c.

DiﬀRec is the (deterministic) “difference reconstruc-

tion” algorithm that takes pp and two values c, c

(supposedly output by Sketch) as input, and out-

puts the “difference” ∆s ∈ K .

For correctness, it is required that for all k ∈

N, all x, x

∈ X such that d(x, x

) < t, all

pp output by Setup(1

), and all s,∆s ∈ K ,

we have DiﬀRec(pp,Sketch(pp, s, x), Sketch(pp,s +

∆s,x

)) = ∆s.

Besides, the properties called linearity and weak

simulatability are formalized in (Takahashi et al.,

2017). Informally, the linearity ensures that given

pp, a sketch value c output from Sketch(pp, s, x), and

“shift” values ∆s ∈ K and ∆x ∈ X , it is possible to

compute a sketch value c

that is distributed as if it is

computed from Sketch(pp,s + ∆s, x + ∆x). The weak

simulatability captures a weak form of conﬁdentiality

that c does not leak the information of the content s

if s is chosen uniformly at random from K and x is

sampled from X . Since we do not directly use these

properties, we omit the formal deﬁnitions. See (Taka-

hashi et al., 2017) for the formal deﬁnitions.

4 DEFINING SECURITY

AGAINST RECOVERING

ATTACKS

In this section, we introduce security of a linear sketch

scheme against recovering attacks. We then introduce

structural properties of a linear sketch scheme that we

call the decomposability and partial hiding property.

Finally, we show a lemma that is useful for analyz-

ing the security of linear sketch schemes that satisfy

these properties. This lemma plays the main role in

the subsequent sections.

In the following deﬁnitions, let F = ((d,X),t,X ,

Φ,ε

) be a fuzzy key setting, let K be an abelian

group, and let S = (Setup,Sketch,DiﬀRec) be a lin-

ear sketch for (F ,K ).

Deﬁnition 4. Let ε

= ε

(k) ∈ [0, 1]. We say that a

linear sketch scheme S for (F , K ) is ε

-secure against

recovering attacks if Adv

recover

(k) := 2

−

∞

(X |P ,C )

≤

holds, where (P ,C ) is the joint distribution deﬁned

SECRYPT 2018 - International Conference on Security and Cryptography

as follows:

(P , C ) := { pp ←

Setup(1

); x ←

X ;

s ←

K ; c ←

Sketch(pp,s,x) : (pp,c) }. (2)

(Note that (X , P ,C ) forms a joint distribution.)

As mentioned earlier, the average min-entropy

∞

(X |P ,C ) (in the form of 2

−

∞

(X |P ,C )

) gives an up-

per bound of the best (computationally unbounded)

adversary’s advantage in guessing x given (pp,c),

when (x, pp, c) is sampled according to the joint dis-

tribution (X ,P ,C ). Hence, if ε

is (negligibly) small,

-security against recovering attacks guarantees that

recovering x from (pp,c) is hard.

Next, we introduce a structural property for a

linear sketch scheme that we call decomposability,

which means that an execution of Sketch(pp,s, x) can

be decomposed into computing two sub-functions f

and f

, where f

is a (possibly probabilistic) func-

tion whose output depends on (pp,s, x), while f

a deterministic function whose output depends only

on (pp,x) (and independent of s), so that a sketch

c consists of the outputs from f

and f

, i.e., c =

( f

(pp,s,x), f

(pp,x)). We also require the prop-

erty that we call partial hiding, which requires that

the ﬁrst function f

hides the information of x from

its output c

if the input s is chosen randomly. (We

do not require the same for f

, and hence the name

“partial”.) The usefulness of the decomposability and

partial-hiding property will be evident later.

Deﬁnition 5. We say that a linear sketch scheme S for

(F ,K ) is decomposable, if there exist the following

two efﬁciently computable functions f

, f

• f

is a (possibly probabilistic) function that takes

pp (output by Setup), s ∈ K , and x ∈ X as input,

and outputs some value c

• f

is a deterministic function that takes pp (output

by Setup) and x ∈ X as input, and outputs some

value c

It is required that for all pp output by Setup, x ∈ X ,

and s ∈ K , the following two distributions D

and D

are identically distributed:

:= {c = (c

) ←

Sketch(pp,s,x) : c },

:= {c

←

(pp,s,x); c

← f

(pp,x) : (c

)}

and f

are called the decomposed functions of

Sketch.

Furthermore, we say that a decomposable linear

sketch scheme S (with the decomposed functions f

and f

) is partially hiding if for all pp output by

Setup, the distribution {x ←

X ; s ←

K ; c

←

(pp,x,s) : c

} is independent of the original fuzzy

data distribution X .

We now show that any decomposable linear sketch

scheme S = (Setup, Sketch,DiﬀRec) with partial hid-

ing property, satisﬁes a convenient property that its se-

curity against recovering attacks can be analyzed only

from X and f

(irrelevantly to f

, s, or c).

Lemma 3. Let S = (Setup,Sketch,DiﬀRec) be a lin-

ear sketch scheme S for (F , K ). Assume that S sat-

isﬁes decomposability (with decomposed functions f

and f

) and the partial hiding property. Then, it holds

that Adv

recover

(k) = 2

−

∞

(X |P , f

(P ,X ))

Proof of Lemma 3. Consider the following distribu-

tion that outputs (pp,c

{ pp ←

Setup(1

); x ←

X ; s ←

K ;

←

(pp,s,x); c

← f

(pp,x) : (pp,c

) }.

Let P , C

, and C

be the distributions that correspond

to computing and outputting pp, c

and c

in the

above distribution, respectively. Note that (P ,C

)

forms a joint distribution, and furthermore we have

= f

(P , X ) by deﬁnition. Due to the decompos-

ability of S, the joint distribution (P ,C ) (deﬁned

in Eq. (2)) and the joint distribution (P ,C

) are

equivalent, and thus it holds that

∞

(X |P ,C ) =

∞

(X |P ,C

)

∞

(X |P ,C

, f

(P , X )).

Furthermore, by the partial hiding property and

the fact that X is independent of the generation

of a public parameter, X and C

are guaranteed

to be independent, which means that we have

∞

(X |P ,C

, f

(P , X )) =

∞

(X |P , f

(P , X )).

Combining the above arguments, we obtain

Adv

recover

(k) = 2

−

∞

(X |P ,C )

= 2

−

∞

(X |P , f

(P ,X ))

This completes the proof of Lemma 3.

5 RECOVERING ATTACK

SECURITY OF LINEAR

SKETCH SCHEME S

CRT

In this and next sections, we show our main results:

security of the linear sketch schemes in (Takahashi

et al., 2017) against recovering attacks. In this sec-

tion, we do this for the ﬁrst linear sketch scheme S

CRT

This section is organized as follows: In Sec-

tion 5.1, we recall a concrete fuzzy key setting F

with which the linear sketch scheme S

CRT

is associ-

ated. Then, in Section 5.2, we review some math-

ematical background for describing S

CRT

. In Sec-

tion 5.3, we give the description of S

CRT

. Finally, in

Section 5.4, we show how secure the linear sketch

scheme S

CRT

is against recovering attacks.

On the Security of Linear Sketch Schemes against Recovering Attacks

A large part of Sections 5.1, 5.2, and 5.3 is taken

verbatim from Sections 6.1, 6.2, and 6.3 of (Takahashi

et al., 2017), respectively.

5.1 Speciﬁc Fuzzy Key Setting F

Here, we recall a concrete fuzzy key setting F

((d,X),t,X ,Φ,ε

) for which the linear sketch scheme

CRT

is constructed.

Metric space (d,X): We deﬁne the space X by X :=

[0,1)

⊂ R

, where n is a parameter speciﬁed by

the context (e.g. an object from which we mea-

sure fuzzy data). We use the L

∞

-distance as the

distance function d : X × X → R. Namely, for

x = (x

,...,x

) ∈ X and x

= (x

,...,x

) ∈ X , we

deﬁne d(x,x

) := kx − x

∞

:= max

i∈[n]

− x

Note that X forms an abelian group with respect

to coordinate-wise addition (modulo 1).

Threshold t: For a security parameter k, we deﬁne

the threshold t ∈ R so that

k = b−n log

(2t)c. (3)

Furthermore, we require that n = O(log

k), so

that 2

can be considered to be upper-bounded by

some polynomial of k. This property was used in

(Takahashi et al., 2017) to show the weak simu-

latability of the linear sketch scheme S

CRT

Distribution X : The uniform distribution over a

“discretized” version of X = [0,1)

. Speciﬁcally,

let λ ∈ N be the natural number that denotes the

representation length of a real number (see Sec-

tion 2.2). We require that each coordinate x

of a data x = (x

,...,x

) ∈ X be distributed as

{ j

←

}. Furthermore, we require λ to

be sufﬁciently large (at least dk/ne).

Error distribution Φ and Error parameter ε

: Φ

is any efﬁciently samplable distribution over X

such that FRR ≤ ε

for all x ∈ X.

5.2 Mathematical Preliminaries

We recall some mathematical background that is nec-

essary for describing the ﬁrst linear sketch scheme

CRT

in (Takahashi et al., 2017).

Let n ∈ N, and w

,...,w

∈ N be positive inte-

gers with the same bit length (i.e. dlog

e = ·· · =

dlog

e), such that

∀i ∈ [n] : w

≤

, and ∀i 6= j ∈ [n] : GCD(w

) = 1,

(4)

and W =

∏

i∈[n]

= Θ(2

), where k is deﬁned as in

Eq. (3). Note that Eqs. (3) and (4) imply that we have

≤ 2

dk/ne

for all i ∈ [n]. We assume that there exists

a deterministic algorithm WGen that on input (t, n)

outputs w = (w

,...,w

) satisfying the above.

For vectors v = (v

,...,v

) ∈ N

, we deﬁne

v mod w := (v

mod w

,...,v

mod w

). (5)

For vectors v

∈ N

, we deﬁne the equivalence re-

lation “∼” by

∼ v

def

⇐⇒ v

mod w = v

mod w,

and let Z

:= Z

/ ∼ be the quotient set of Z

by ∼.

Note that (Z

,+) constitutes an abelian group, where

the addition is modulo w as deﬁned in Eq. (5).

According to the Chinese remainder theorem

(CRT), each element in Z

can be uniquely repre-

sented as an element in Z

, and vice versa. Let

CRT

: Z

→ Z

be the mapping that transforms an

element in s ∈ Z

into s ∈ Z

via the CRT, and we

denote by CRT

−1

the inverse function of CRT

. Note

that for all v

∈ Z

, it holds that

CRT

+ v

) = CRT

) + CRT

) mod W.

Similarly to Z

, we deﬁne R

:= R

/ ∼ to be the

quotient set of real vector space R

by the equivalence

relation ∼, where for a real number y ∈ R, we deﬁne

r = y mod w

by the number such that ∃n ∈ Z : y =

+ r and 0 ≤ r < w

Let E

: R

→ R

be the following function:

(x) := (w

,...,w

) ∈ R

where x = (x

,...,x

) ∈ R

. Note that it holds that

(x + e) = E

(x) + E

(e) (mod w). (6)

Let C

: R

→ Z

be the following function:



,...,y

)





+ 0.5c,...,by

+ 0,5c



(7)

We note that the rounding-down operation by

+ 0.5c

in C

can be regarded as a kind of error correction.

Speciﬁcally, by the conditions in Eq. (4), the fol-

lowing properties are satisﬁed: For any x,x

∈ X, if

d(x,x

) = |x − x

∞

< t, then we have



(x) − E

)



∞

< t · max

i∈[n]

} ≤ 0.5.

Therefore, for such x,x

, it always holds that



(x) − E

)



= 0. (8)

Additionally, for any x ∈ R

and s ∈ Z

, the following

holds:

(x + s) = C

(x) + s (mod w). (9)

SECRYPT 2018 - International Conference on Security and Cryptography

5.3 Scheme Description

Let F

= ((d, X ),t,X , Φ, ε

) be the fuzzy key setting

deﬁned in Section 5.1, and let w = (w

,...,w

) =

WGen(t,n), where n is the dimension of X , and

let W =

∏

i∈[n]

. Let CRT

, CRT

−1

, E

, and

be the functions deﬁned in the previous subsec-

tion. Using these objects, the linear sketch scheme

CRT

= (Setup,Sketch,DiﬀRec) for F

and the addi-

tive group (Z

,+), is constructed as in Figure 2.

Note that the setup algorithm Setup in this lin-

ear sketch scheme actually does nothing, and the

main algorithms Sketch and DiﬀRec are determinis-

tic. Furthermore, recall that the rounding-down op-

eration is applied after multiplication of a real num-

ber and an integer is performed, so that the result-

ing real number has a λ-bit signiﬁcand. Concretely,

let s ∈ Z

and s = (s

,...,s

) = CRT

−1

, and sup-

pose that c = (c

,...,c

) ∈ R

is a sketch output

from Sketch(pp,s, x), where x = (x

,...,x

) ←

and thus each x

is of the form x

for some λ-bit

integer j

. Then, since each w

is a dk/ne-bit inte-

ger, x

= w

results in b

· j

dk/ne

c · 2

−(λ−dk/ne)

. Conse-

quently, each c

∈ R

is of the following form:

= s

· j

dk/ne

· 2

−(λ−dk/ne)

mod w

. (10)

It was shown in (Takahashi et al., 2017) that S

CRT

satisﬁes correctness, and also satisﬁes the linearity

and weak simulatability properties.

5.4 Security against Recovering Attacks

In this subsection, we show how secure the linear

sketch scheme S

CRT

is against recovering attacks. To

this end, we ﬁrst show that S

CRT

satisﬁes decompos-

ability with the partial hiding property.

Lemma 4. The linear sketch scheme S

CRT

satisﬁes the

decomposability and partial hiding property.

Proof of Lemma 4. Let s ∈ Z

and s = (s

,...,s

) :=

CRT

−1

(s) ∈ Z

. Let c = (c

,...,c

) ∈ R

a sketch output from Sketch(pp,s,x), where x =

,...,x

) ←

X and thus each x

is of the form

for some λ-bit integer j

. As mentioned in the

previous subsection, due to the rounding-down opera-

tion performed at each multiplication w

· x

, each co-

ordinate c

of the sketch c is computed as in Eq. (10).

Here, we consider the “integer” part c

(i)

and the “dec-

imal” part c

(i)

of c

, which are as follows:

(i)

= bc

c = s

· j

dk/ne

· 2

−(λ−dk/ne)

mod w

(11)

(i)

= c

mod 1 =

· j

dk/ne

· 2

−(λ−dk/ne)

mod 1.

(12)

Note that c

(i)

∈ Z

and c

(i)

∈ [0, 1). Note also that the

decimal part c

(i)

is independent of s

due to “ mod 1”.

We can make use of this fact, and deﬁne the decom-

posed functions f

(pp,s,x) and f

(pp,x) as follows:

(pp,s,x): This function outputs c

= (c

(1)

,...,

(n)

) ∈ Z

, where each c

(i)

is computed as in

Eq. (11).

(pp,x): This function outputs c

= (c

(1)

,...,c

(n)

)

∈ [0, 1)

, where each c

(i)

is computed as in

Eq. (12).

Furthermore, it is straightforward to see that f

satisﬁes the partial hiding property. Speciﬁcally, if

s ∈ Z

is chosen uniformly at random, then s =

,...,s

) = CRT

−1

(s) is distributed uniformly over

. Hence, each s

acts as a key for one-time pad

encryption, and thus each c

(i)

∈ Z

does not contain

any information of x

. Therefore, when s ∈ Z

is cho-

sen uniformly at random, the output c

of f

(pp,s,x)

becomes independent of x. This completes the proof

of Lemma 4.

We now show how secure the linear sketch scheme

CRT

is against recovering attacks.

Theorem 1. The linear sketch scheme S

CRT

satisﬁes

−k

-security against recovering attacks.

Proof of Theorem 1. Due to Lemmas 3 and 4, and the

fact that P does not involve any probabilistic opera-

tion, we have

Adv

recover

CRT

(k) = 2

−

∞

(X |P , f

(P ,X ))

= 2

−

∞

(X | f

(P ,X ))

Moreover, due to our treatment of real numbers,

each coordinate c

(i)

of the output of f

can have at

most 2

λ−dk/ne

values. Hence, the entire output of f

can take at most (2

λ−dk/ne

)

≤ 2

n·λ−k

values. Since

∞

(X ) = n · λ holds due to the assumption on the

fuzzy data distribution, by applying Lemma 1, we can

estimate

∞

(X | f

(P , X )) as follows:

∞

(X | f

(P , X )) ≥ H

∞

(X ) − (n · λ − k)

= n · λ − (n · λ − k) = k.

Combining the two inequalities, we obtain

Adv

recover

CRT

(k) ≤ 2

−k

, which means that S

CRT

satisﬁes 2

−k

-security against recovering attacks. This

completes the proof of Theorem 1.

On the Security of Linear Sketch Schemes against Recovering Attacks

Setup(1

) :

Return pp ← (w

,...,w

,W).

Sketch(pp,s ∈ Z

,x ∈ [0, 1)

) :

c ← (CRT

−1

(s) + E

(x)) mod w

Return c.

DiﬀRec(pp,c,c

) :

∆s ← C

− c)

∆s ← CRT

(∆s)

Return ∆s.

Figure 2: The linear sketch scheme S

CRT

= (Setup, Sketch,DiﬀRec) for the fuzzy key setting F

. In the ﬁgure, addi-

tions/subtractions are done in R

6 RECOVERING ATTACK

SECURITY OF THE LINEAR

SKETCH SCHEME S

Hash

In this section, we show the security of the second

linear sketch scheme S

Hash

in (Takahashi et al., 2017)

against recovering attacks.

This section is organized as follows: In Sec-

tion 6.1, we recall a concrete fuzzy key setting F

with which the linear sketch scheme S

Hash

is associ-

ated. Then in Section 6.2, we give the description of

Hash

. Finally, in Section 6.3, we show how secure

the linear sketch scheme S

Hash

is against recovering

attacks.

A large part of Sections 6.1 and 6.2 is taken ver-

batim from Sections 7.1 and 7.2 of (Takahashi et al.,

2017), respectively.

6.1 Speciﬁc Fuzzy Key Setting F

Here, we recall a concrete fuzzy key setting F

((d,X),t,X ,Φ,ε

) for which the linear sketch scheme

Hash

is constructed.

Metric space (d,X): The space X is deﬁned by X :=

[0,1)

⊂ R

, where n ∈ N is a parameter spec-

iﬁed by the context (e.g. an object from which

we measure fuzzy data) and a security parame-

ter k. The distance function d : X × X → R is

the L

∞

-distance. Namely, for x = (x

,...,x

) ∈ X

and x

= (x

,...,x

) ∈ X, we deﬁne d(x,x

) :=

kx − x

∞

:= max

i∈[n]

− x

|. Note that X forms

an abelian group with respect to coordinate-wise

addition (modulo 1).

Threshold t: For a security parameter k, we require

the threshold t ∈ R to satisfy

k ≤ b−n log

(2t)c. (13)

For notational convenience, let T := 1/(2t).

Distribution X : An efﬁciently samplable distribu-

tion over a “discretized” version of X = [0,1)

That is, letting λ ∈ N denote the length of the sig-

niﬁcand of a real number, if x = (x

,...,x

) is

sampled from X , then each x

is of the form

where j

is some λ-bit integer. (See Section 2.2.)

We require T ≤ 2

Furthermore, we require that X satisfy the as-

sumption on the average min-entropy that we state

later.

Error distribution Φ and Error parameter ε

: Φ

is any efﬁciently samplable distribution over X

such that FRR ≤ ε

for all x ∈ X.

The Requirement on the Distribution of Fuzzy

Data X . Let X

be the “scaled-up” version of X ,

namely, X

is the distribution obtained by multiply-

ing the value T = 1/(2t) to the outcome of the dis-

tribution X , where the rounding-down operation is

performed for each coordinate of X

as explained in

Section 2.2. Since X is a distribution over [0,1)

is a distribution over [0,T )

. Now, let us divide

into the “integer” part X

and the “decimal” part

. Namely, let x

= (x

,...,x

) be a vector pro-

duced from X

. Then, X

is the distribution of the

n-dimensional vector whose i-th element is the inte-

ger part of x

. Similarly, X

is the distribution of

the n-dimensional vector whose i-th element is the

decimal part of x

. Note that each coordinate of the

integer part X

is represented by dlog

T e bits, and

thus each coordinate of the decimal part X

will have

(λ − dlog

T e)-bit precision, so that the signiﬁcand of

the entire x

is expressed in λ bits. Note also that the

joint distribution (X

) contains the same infor-

mation as X

The requirement on the distribution X is that we

have

∞

) ≥ log

p + ω(log

k), (14)

where p is the order of the ﬁeld over which the uni-

versal hash family H

lin

(guaranteed by Lemma 2) is

constructed.

6.2 Scheme Description

Let F

= ((d, X ),t,X , Φ, ε

) be the fuzzy key setting

as deﬁned above. Let F

be a ﬁnite ﬁeld with prime

order p satisfying p ≥ T = 1/(2t). Here, we iden-

tify F

with Z

, and interpret an element in the for-

mer set as an element in the latter set, and vice versa.

Let H

lin

= { h

: (F

)

→ F

}

z∈F

be the universal

hash function family with linearity as guaranteed by

Lemma 2. For each z ∈ F

and s ∈ F

, we deﬁne

SECRYPT 2018 - International Conference on Security and Cryptography

“h

−1

(s)” as the set of preimages of s under h

. That

is, h

−1

(s) := {a ∈ (F

)

(a) = s}. Hence, the nota-

tion “a ←

−1

(s)” means that we choose a vector a

uniformly from the set h

−1

(s).

Then, using these ingredients, the linear sketch

scheme S

Hash

= (Setup, Sketch,DiﬀRec) for F

and

the additive group (Z

,+), is constructed as de-

scribed in Figure 3.

We remind the reader that we are treating real

numbers as explained in Section 2.2. We remark

that as in the ﬁrst linear sketch scheme S

CRT

, the

rounding-down operation is applied after the multi-

plication T · x, so that the resulting real number in

each coordinate has a λ-bit signiﬁcand. Concretely,

let s ∈ Z

, and let a = (a

,...,a

) ∈ h

−1

(s), and

suppose that c = (c

,...,c

) ∈ (R

)

is output from

Sketch(pp,s,x), where x = (x

,...,x

) ←

X and

thus each x

is of the form x

for some λ-bit in-

teger j

. Then, for each i ∈ [n], x

= T · x

results in

T · j

dlog

T e

c · 2

−(λ−dlog

T e)

. Consequently, each c

∈ R

is of the following form:

= a

T · j

dlog

T e

· 2

−(λ−dlog

T e)

mod p. (15)

It was shown in (Takahashi et al., 2017) that S

Hash

satisﬁes correctness, and also satisﬁes the linearity

and weak simulatability properties.

6.3 Security against Recovering Attacks

In this subsection, we show how secure the linear

sketch scheme S

Hash

is against recovering attacks. To

this end, we ﬁrst show that S

Hash

satisﬁes decompos-

ability with the partial hiding property.

Lemma 5. The linear sketch scheme S

Hash

satisﬁes

the decomposability and partial hiding property.

Proof of Lemma 5. Let s ∈ Z

and a = (a

,...,a

) ∈

−1

(s). Let c = (c

,...,c

) ∈ (R

)

be a sketch out-

put from Sketch(pp, s, x), where x = (x

,...,x

) ←

X and thus each x

is of the form x

for some

λ-bit integer j

. As mentioned in the previous subsec-

tion, due to the rounding-down operation performed

at each multiplication T · x

, each coordinate c

of the

sketch c is computed as in Eq. (15). Here, we con-

sider the “integer” part c

(i)

and the “decimal” part c

(i)

of c

, which are as follows:

(i)

= bc

c = a

T · j

dlog

T e

· 2

−`

mod p, (16)

(i)

= c

mod 1 =

T · j

dlog

T e

· 2

−`

mod 1. (17)

where `

= λ − dlog

T e. Note that c

(i)

∈ Z

and c

(i)

∈

[0,1). Note also that the only component that depends

on s is a, but due to “mod 1,” the decimal part c

(i)

becomes independent of it. Similarly to the ﬁrst linear

sketch scheme S

CRT

, we can deﬁne the decomposed

functions f

(pp,s,x) and f

(pp,x) as follows:

(pp,s,x): This function is a probabilistic function,

which ﬁrst picks a = (a

,...,a

) ∈ h

−1

(s) uni-

formly at random, and outputs c

= (c

(1)

,...,c

(n)

)

∈ (Z

)

, where each c

(i)

is computed as Eq. (16).

(pp,x): This function outputs c

= (c

(1)

,...,c

(n)

)

∈ [0, 1)

, where each c

(i)

is computed as Eq. (17).

Furthermore, it is not hard to see that f

satisﬁes

the partial hiding property. Speciﬁcally, recall that

given s ∈ Z

, Sketch chooses a = (a

,...,a

) ∈ (Z

)

uniformly at random from the set h

−1

(s). Due to

the linearity of the underlying universal hash family

lin

, if s ∈ Z

is also chosen uniformly at random,

a is distributed uniformly in (Z

)

. Hence, each a

acts as a key for one-time pad encryption, and thus

each c

(i)

∈ Z

does not contain any information of x

Therefore, when s ∈ Z

is chosen uniformly at ran-

dom, the output c

of f

(pp,s,x) becomes indepen-

dent of x. This completes the proof of Lemma 5.

We now show how secure the linear sketch scheme

Hash

is against recovering attacks.

Theorem 2. The linear sketch scheme S

Hash

satisﬁes

−1

· k

−ω(1)

)-security against recovering attacks.

Proof of Theorem 2. Due to Lemmas 3 and 5, and

the fact that f

does not use a public parameter pp = z

and thus independent of P , we have

Adv

recover

CRT

(k) = 2

−

∞

(X |P , f

(P ,X ))

= 2

−

∞

(X | f

(P ,X ))

Moreover, it is straightforward to see that the dis-

tribution f

(P , X ) is exactly the distribution X

in-

troduced in Section 6.1, namely, the distribution

of the vector of the “decimal”-part of the scaled-

up version X

of X . Note also that given X

guessing the original distribution X is a harder

task than guessing the “integer”-part X

. Hence,

we have

∞

(X | f

(P , X )) ≥

∞

) ≥ log

p +

ω(log

k). Due to Eq. (14), we can estimate

Adv

recover

Hash

(k) as follows:

Adv

recover

Hash

(k) = 2

−

∞

(X | f

(P ,X ))

≤ 2

−

∞

)

≤ 2

−(log

p+ω(log

k))

= p

−1

· k

−ω(1)

Hence, S

Hash

satisﬁes (p

−1

· k

−ω(1)

)-security against

recovering attacks. This completes the proof of The-

orem 2.

On the Security of Linear Sketch Schemes against Recovering Attacks

Setup(1

) :

z ←

Return pp ← z.

Sketch(pp,s ∈ Z

,x ∈ [0, 1)

) :

a ←

−1

(s)

c ← a + T · x

Return c.

DiﬀRec(pp,c,c

) :

∆c ← c

− c

∆s ← h

(b∆ce)

Return ∆s.

Figure 3: The linear sketch scheme S

Hash

= (Setup,Sketch,DiﬀRec) for the fuzzy key setting F

. In the ﬁgure, the addi-

tions/subtractions are done in (R

)

REFERENCES

Cheraghchi, M. (2011). Capacity achieving codes from

randomness condensers. http://arxiv.org/pdf/0901.

1866v2. pdf. Preliminary version appeared in ISIT

2009.

Dodis, Y., Ostrovsky, R., Reyzin, L., and Smith, A. (2008).

Fuzzy extractors: How to generate strong keys from

biometrics and other noisy data. SIAM J. Comput.,

38(1):97–139.

Goldwasser, S., Micali, S., and Rivest, R. (1988). A digi-

tal signature schemes secure against adaptive chosen-

message attacks. SIAM J. Computing, 17(2):281–308.

Matsuda, T., Takahashi, K., Murakami, T., and Hanaoka, G.

(2016). Fuzzy signatures: Relaxing requirements and

a new construction. In Proc. of ACNS 2016, volume

9696 of LNCS, pages 97–116. Springer.

Schnorr, C. (1990). Efﬁcient signature generation for smart

cards. In Proc. of CRYPTO 1989, volume 435 of

LNCS, pages 239–252. Springer.

Takahashi, K., Matsuda, T., Murakami, T., Hanaoka, G.,

and Nishigaki, M. (2015). A signature scheme with

a fuzzy private key. In Proc. of ACNS 2015, volume

9092 of LNCS, pages 105–126. Springer.

Takahashi, K., Matsuda, T., Murakami, T., Hanaoka, G.,

and Nishigaki, M. (2017). Signature schemes with a

fuzzy private key. IACR Cryptology ePrint Archive:

Report 2017/1188. https://eprint.iacr.org/2017/1188.

This is the merged full version of (Takahashi et al.,

2015) and (Matsuda et al., 2016).

Waters, B. (2005). Efﬁcient identity-based encryption with-

out random oracles. In Proc. of EUROCRYPT 2005,

volume 3494 of LNCS, pages 114–127. Springer.

Yasuda, M., Shimoyama, T., Takenaka, M., Abe, N., Ya-

mada, S., and Yamaguchi, J. (2017). Recovering at-

tacks against linear sketch in fuzzy signature schemes

of ACNS 2015 and 2016. In Proc. of ISPEC 2017,

volume 10701 of LNCS, pages 409–421. Springer.

APPENDIX

Here, we provide a minimal deﬁnition of a fuzzy sig-

nature scheme. Then, in order to grasp how the linear

sketch schemes S

CRT

and S

Hash

are used to construct

fuzzy signature schemes, we brieﬂy review the ﬁrst

and second fuzzy signature schemes in (Takahashi

et al., 2017).

Syntax. A fuzzy signature scheme Σ

for a fuzzy

key setting F = ((d,X),t,X ,Φ,ε) consists of the four

algorithms (Setup

,KG

,Sign

,Ver

Setup

: This is the setup algorithm that takes 1

input (where k determines the threshold value t of

F ), and outputs a public parameter pp.

: This is the key generation algorithm that takes

pp and a fuzzy data x ∈ X as input, and outputs a

veriﬁcation key vk.

Sign

: This is the signing algorithm that takes pp, a

fuzzy data x

∈ X, and a message m as input, and

outputs a signature σ.

Ver

: This is the (deterministic) veriﬁcation algo-

rithm that takes pp, vk, m, and σ as input, and

outputs either > (“accept”) or ⊥ (“reject”).

Let δ = δ(k) ∈ [0,1]. A fuzzy signature scheme

for a fuzzy key setting F = (d,X),t,X ,Φ,ε

) sat-

isﬁes δ-correctness if it holds that

pp ←

Setup

); x ←

X ;

vk ←

(pp,x); e ←

Φ;

σ ←

Sign

(pp,x + e,m) :

Ver

(pp,vk,m,σ) = >

≥ 1 − δ

for all k ∈ N and all messages m.

In (Takahashi et al., 2017), as a security require-

ment for a fuzzy signature scheme, an analogue of

the standard existential unforgeability against cho-

sen message attacks (EUF-CMA security) (Goldwasser

et al., 1988) was deﬁned. We omit the formal deﬁni-

tion since we do not directly deal with it in this paper.

First Scheme Σ

FS1

. This scheme is constructed for

the speciﬁc fuzzy key setting F

, from the combina-

tion of the linear sketch scheme S

CRT

and a variant of

the Waters scheme (Waters, 2005) (called the mod-

iﬁed Waters signature (MWS) scheme in (Takahashi

et al., 2017)). (For the fuzzy key setting F

and the

linear sketch scheme S

CRT

, see Sections 5.1 and 5.3,

respectively.)

Let ` = `(k) be a positive polynomial that denotes

the length of messages. Let F

= ((d,X ),t,X , Φ, ε

)

be the fuzzy key setting deﬁned in Section 5.1, where

SECRYPT 2018 - International Conference on Security and Cryptography

Setup

FS1

) :

g,h, u

,...,u

←

Let z be an element of Z

∗

of order W .

Return pp ← (g,h,u

,(u

)

i∈[`]

,z).

FS1

(pp,x) :

sk ←

; vk ← g

c ← (CRT

−1

(sk) + E

(x)) mod w

Return V K ← (vk, c).

Sign

FS1

(pp,x

,m) :

Parse m as (m

k...km

) ∈ {0, 1}

sk ←

;

vk ← g

; r ←

;

← g

← h

· (u

∏

i∈[`]

)

c ← (CRT

−1

(

sk) + E

)) mod w

Return σ ← (

vk,

c).

Ver

FS1

(pp,VK, m, σ) :

(vk, c) ← V K; (

vk,

c) ← σ

Parse m as (m

k...km

) ∈ {0, 1}

If e(

∏

i∈[`]

) · e(

vk, h)

6= e(

,g) then return ⊥.

∆s ← C

(

c − c); ∆sk ← CRT

(∆s)

If (vk)

∆sk

vk then return > else return ⊥.

Setup

FS2

) :

g ←

G; z ←

Let H : {0,1}

∗

→ Z

be a cryptographic hash function.

Return pp ← (g,z,H).

FS2

(pp,x) :

sk ←

; vk ← g

a ←

−1

(sk); c ← a + T · x

Return V K ← (vk, c).

Sign

FS2

(pp,x

,m) :

sk ←

;

vk ← g

; r ←

; R ← g

h ← H(Rkm);

s ← r + (

sk) ·

h mod p

←

−1

(

sk);

c ← a

+ T · x

Return σ ← (

vk,

c).

Ver

FS2

(pp,VK, m, σ) :

(vk, c) ← V K; (

vk,

c) ← σ

R ← g

· (

vk)

−

If H(Rkm) 6=

h then return ⊥.

∆c ←

c − c; ∆sk ← h

(b∆ce)

If vk · g

∆sk

vk then return > else return ⊥.

Figure 4: (Left) The description of the fuzzy signature scheme Σ

FS1

= (Setup

FS1

,KG

FS1

,Sign

FS1

,Ver

FS1

), and (Right) the

description of the fuzzy signature scheme Σ

FS2

= (Setup

FS2

,KG

FS2

,Sign

FS2

,Ver

FS2

). In both of the descriptions, the steps

related to the underlying linear sketch schemes are highlighted with the box .

t (and n) are determined according to the security pa-

rameter k. let w = (w

,...,w

) = WGen(t,n), where

n is the dimension of X, and let W =

∏

i∈[n]

. Let

CRT

, CRT

−1

, E

, and C

be the functions de-

ﬁned in Section 5.2. Let (G,G

,e, p) be a descrip-

tion of symmetric bilinear groups with prime order

p = Ω(2

) such that W |p − 1, where G and G

are

groups of prime order p and e : G × G → G

is an

efﬁciently computable bilinear map.

Then, using these ingredients, the fuzzy signature

scheme Σ

FS1

= (Setup

FS1

,KG

FS1

,Sign

FS1

,Ver

FS1

)

for the fuzzy key setting F

is constructed as in Fig-

ure 4 (left).

It was shown in (Takahashi et al., 2017) that this

fuzzy signature scheme satisﬁes ε

-correctness, and is

secure if the computational Difﬁe-Hellman assump-

tion holds in G.

Second Scheme Σ

FS2

. This scheme is constructed

for the speciﬁc fuzzy key setting F

, from the com-

bination of the linear sketch scheme S

Hash

and the

Schnorr signature scheme (Schnorr, 1990). (For the

For all generators g ∈ G and a, b ∈ Z

, it holds that

e(g

) = e(g,g)

∈ G

fuzzy key setting F

and the linear sketch scheme

Hash

, see Sections 6.1 and 6.2, respectively.)

Let F

= ((d,X),t,X ,Φ,ε

) be the fuzzy key set-

ting that we speciﬁed in Section 6.1, and suppose

the dimension of the fuzzy data space is n. Let

(G, p) be the description of a group G of prime or-

der p = Ω(2

). Let H

lin

= {h

: (F

)

→ F

}

z∈F

be the universal hash family with linearity as guar-

anteed by Lemma 2. (We identify F

with Z

.) Let

H : {0, 1}

∗

→ Z

be a cryptographic hash function

(modeled as a random oracle).

Using these building blocks, the second fuzzy

signature scheme Σ

FS2

= (Setup

FS2

,KG

FS2

,Sign

FS2

Ver

FS2

) for the fuzzy key setting F

is constructed as

in Figure 4 (right).

It was shown in (Takahashi et al., 2017) that this

fuzzy signature scheme satisﬁes ε

-correctness, and is

secure in the random oracle model (where H is mod-

eled as a random oracle) if the discrete logarithm as-

sumption holds in G.

On the Security of Linear Sketch Schemes against Recovering Attacks