Training Process Modeling of Hammer Throwers Taking into

Account Peculiarities of Stress Adaptation

Alexander Bolotin and Vladislav Bakayev

Institute of Physical Education, Sports and Tourism, Peter the Great St. Petersburg Polytechnic University,

St. Petersburg, Russian Federation

Keywords: Stress Adaptation, Qualification Norm, Computer Simulations, Training Process Forecasting, Hammer

Throwers.

Abstract: The article considers the solution of the forecast problem to improve the efficiency of the training process of

hammer throwers taking into account the peculiarities of their adaptation to the load. This problem was

solved by computer modelling. To solve this problem, restrictions were set on the control and managed

parameters. The number of parameters that were entered into the model was determined by the methods of

expert assessments. These parameters were adjusted in the process of modelling the dynamics of the

training system in time on a personal computer. Basing on the results of forecasting it was revealed that

taking account the peculiarities of stress adaptation in hammer throwers training led to doubled number of

sportsmen’s who fulfilled the qualification norm successfully.

1 INTRODUCTION

At present the problem of increased efficiency of the

training process in hammer throwers is very urgent

(Bolotin et al., 2017). For this purpose, computer

modeling is widely used. The development of such a

model is intended for solving the problem of training

process prognostication in hammer throwers taking

into account their stress adaptation (Bolotin et al.,

2014; Hopkinset al., 2009). Practice has shown that

the organizational and pedagogic management of the

training process in hammer throwers becomes a

classical task in the management theory (Bartonietz

et al., 1997; Bartonietz et al., 1988; Murofushi et al.,

2007; Malcata and Hopkins, 2014). If limitations for

control and controlled parameters are set such

problem has a solution. Maximization of the number

of hammer throwers who fulfilled the qualification

norm successfully for participation in international

competitions was the target function in our problem

settings (Winter, 2005).

2 ORGANIZATION AND

METHODS

We consider the equation of computer model for

prognostication of training process efficiency in the

form of a year’s full training cycle.

The following flows act in the system:

information flow - I, number of training sportsmen’s

, number of trainers N

tr.

Let us designate the initial number of training

sportsmen as N

and their number after completion

of the year’s full training cycle as N

, where T is

the year’s full training cycle. N

nТ

is summed up

from: N

nТs,

the number of sportsmen who fulfilled

the qualification norm; N

nТn,

the number of

sportsmen which did not fulfill the qualification

norm and N

nl,

the number of sportsmen who left the

training camp and who were not selected for the

competitions because of different reasons.

The general objective of the organizational and

pedagogic ma nagement of the training process is to

maximize N

nТs

, i.e. the number of sportsmen who

fulfilled the qualification norm. The method of

computer modeling belongs to heuristic methods and

a significant number of parameters included in the

model are determined by the methods of expert

assessment. These parameters may be corrected

Bolotin, A. and Bakayev, V.

Training Process Modeling of Hammer Throwers Taking into Account Peculiarities of Stress Adaptation.

DOI: 10.5220/0006847300790083

In Proceedings of the 6th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2018), pages 79-83

ISBN: 978-989-758-325-4

during the modeling process of training system

(model on PC) dynamics over time using PC.

Let us designate the number of intervals during

which the model will turn to the final condition as

M. It is convenient to use the number of training

cycles of 2 months each, i.e. 6 cycles, as M. Thus,

we obtain the possibility to compare the actual

training results with results revealed in the model

and to make quick correction (to implement

feedback). Then the model increment size is

Δt=T/N. At the initial time point: N

nТs0

= N

(all

sportsmen wishing to fulfill the qualification norm)

and N

nТn0

= N

. So, the number of sportsmen was

determined successfully. The values introduced for

components of this flow at any time point i are the

level of this flow.

The finite-difference equation of the simulation

model for the flow of the number of training

sportsmen has the form:

ni+1

= N

+ N

ni+

- N

ni-

ni+1

≤ N

here N

ni+

is the rate (increase rate of sportsmen

number). If we consider that reinstatement is

impossible after dismissal of sportsmen from the

training process, then N

ni+

=0.

If reinstatement is possible after appearance of

vacancies then Nni+=1 at the time of appearance of

a vacancy in the team.

ni-

– decrease rate of sportsmen number.

This rate is summed up from a complex of

factors favoring the effective continuation of the

training process:

- psychologic compatibility of sportsman with a

trainer,

- selection of the training program and training

method in accordance with individual resources of

sportsmen,

- successful sportsmen’ adaptation to the training

process,

- efficient fulfillment of the training program by

a sportsman,

- sportsmen’s motivation to achieving high sports

results etc.

The trainer’s role should be considered in the

form of coefficient which is composed from the

requirements to the trainer.

The linear relationship is usually supposed at the

initial stage of modeling basing on the results of the

previous training cycle. The pedagogic methods

such as subject-subject relations between a

sportsman and a trainer, current and midterm test

should be used to minimize N

, i.e. to implement the

organizational and pedagogic management.

The information flow is described by the

following equation:

кn+1

= I

+ I

ni+

- I

ni-

where I

ni+1

is information about sportsmen at

time point i+1, I

ni+

is rate of positive information

about sportsmen (fulfillment of control norms,

participation in interim competitions, increase of

physical fitness parameter values etc.); I

ni-

is rate of

negative information (disciplinary misdeeds,

violations of sports regimen, non-fulfillment of the

training program etc.).

If I

ni-

has non-zero value (negative feedback

functions) it is necessary to correct the rate N

ni+

immediately (listen to the trainer’s and sportsman’s

report, provide assistance in training of sportsmen

etc.).

The model validity is checked by solving the

prognostication problem for several previous periods

(training cycles) because when modeling the process

for previous periods the modeling result is known in

advance, therefore, it is possible to select some

model coefficients as per the program.

3 RESULTS AND DISCUSSION

Constructing the simulation model is bаsed on the

reports on results of the training process for a

sufficiently long time period and our additional

studies. Table 1 presents a fragment of summarized

reporting data on training of hammer throwers in

2013-2016.

Table 1: Summarized reported results of training for 2013-2016 used for selecting initial and final conditions.

Analyzed years

Number of training

sportsmen

Number of sportsmen who

fulfilled the qualification norm

2013

2014

2015

2016

Standardized mean

1.00

0.31

icSPORTS 2018 - 6th International Congress on Sport Sciences Research and Technology Support

Basing on Table 1 we form the initial and final

conditions for solving the problem of determining

simulation model coefficients (solving the

prognostication problem from known past to known

present events).

When solving prognostication problems

standardized units are commonly used because the

trend in change of the test parameters is of the main

interest.

When selecting the computer modeling program

we used the AnyLogic program

(www.anylogic.com). It is recommended for

construction of the computer model as the most

general one and at the same time it has an

understandable interface.

During the preliminary study we revealed factors

determining the efficiency of the training process of

hammer throwers. For this purpose, we conducted

questioning of coaches and sportsmen. Results of

this study are presented in Table 2. Of course, the

transition from non-parametric criteria to parametric

ones (ranking: r

, …, r

) requires parameter

standardization. Therefore, it is necessary to

standardize them by rank size, thereby, to make the

variable models “equal in rights”.

Therefore, in accordance with Table 2 we obtain

eight independent variables (x

, …, x

) where x

/0,198 etc. x

/0.052.

Practice has shown that the main causes for

leaving the training process by sportsmen include

impossibility of sportsmen ‘adaptation to physical

stress or other force-major circumstances (Bakaev et

al., 2015; Bakaev et al., 2016; Bolotin and Bakayev,

2016; Bolotin and Bakayev, 2017; Bakayev and

Bolotin, 2017; Bolotin et al., 2015; Osipov et al.,

2016; Rojas-Ruiz and Gutiérrez-Dávila, 2009; Kim

et al., 2011). In order to remove these causes it is

necessary to create appropriate psychologic and

pedagogic conditions required for successful

adaptation of hammer throwers to the training

process. When solving this study task we questioned

72 respondents. Results of this study are presented in

Table 3.

The similar method is used to standardize also

the conditions favoring effective sportsmen’ stress

adaptation after transition to parametric values (y

…, y

) where y

/0,213 etc. y

/0,037. The

decrease and increase rate of the number of

sportsmen N

ni-

and N

ni+

are linear functions of

independent variables (x

, …, x

) and (y

, …, y

Table 2: Factors determining the training process efficiency of hammer throwers (n=72).

Factors

Rank test (%)

Optimum height and weight parameters of hammer throwers

19.2

Use of individual approach to training of hammer throwers

17.3

Orientation of the training of hammer throwers to fulfillment of the qualification norm

15.7

Availability of favorable environment during the training process

14.4

Availability of target nature of the training process of hammer throwers

10.6

Objective registration sportsmen ‘ training process quality

9.3

High level of trainers’ personal responsibility for high-quality training of sportsmen

7.7

Availability of permanent monitoring of physical fitness level of hammer throwers in the

year’s training cycle

5.8

Table 3: Rank structure of psychologic and pedagogic conditions required for effective adaptation of hammer throwers to

the training process (n=72).

Psychologic and pedagogic conditions

Rank (%)

Inclusion of separate programs for formation of skills of training by sportsmen themselves in

their training process

21.3

Formation of aspiration for permanent growth of sport results in sportsmen

19.7

Use of innovative training methods during training of hammer throwers

15.2

Formation of hammer throwers’ striving for fulfillment of the qualification norm

12.8

Development of a complex of measures for controlling the level of physical and psychologic

parameters in sportsmen required for achievement of high sports results

12.2

Development of objective assessment criteria of the level of physical and psychological

parameters in sportsmen

9.8

Implementation of measures for searching ways to increase sportsmen’ interest and motivation to

the training process

5.3

Creating the environment for manifestation of high sports mastery of hammer throwers

3.7

Training Process Modeling of Hammer Throwers Taking into Account Peculiarities of Stress Adaptation

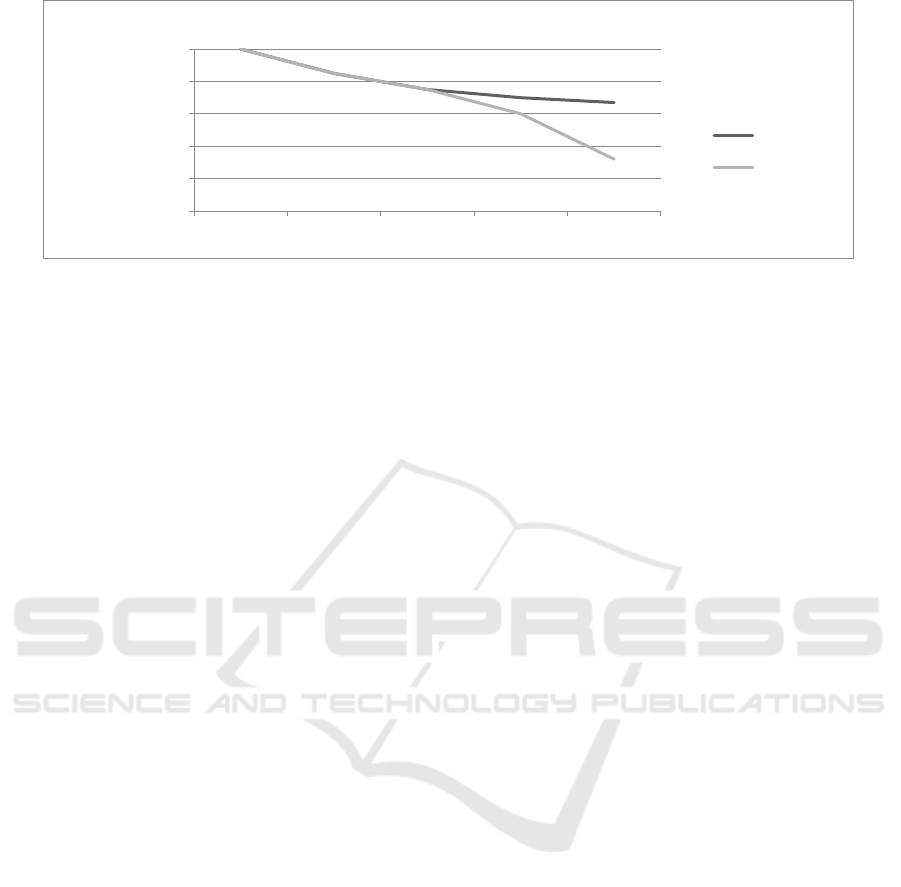
Figure 1: Solving the prognostication problem from known to present events (innovative technologies and new training

conditions are included in 2016).

coefficients of which are calculated by the program

when solving the problem of computer modeling.

4 CONCLUSIONS

When using developed pedagogic methods for

increasing the training process efficiency:

implementation of individual-oriented approach to

selection of training means and methods, optimum

selection of physical stress in accordance with

sportsmen’ individual resources, continuous

methodical support of the training process with

trainer's participation, criterion conditions presented

in Tables 2 and 3 will be met (Bolotin and Bakayev,

2016; Bolotin and Bakayev, 2017).

Figure 1 presents forecasting results for 2018

with existing organization of the training process

and in case of introduction of the innovative training

methods suggested by us (meeting conditions of

Tables 2 and 3). Figure shows sportsmen number

dynamics with the standard training system and the

prognostication result in case of introduction of the

innovative training process technologies in 2018.

The use of simulation modeling has shown the

high efficiency for solving the problem of training

process prognostication in hammer throwers taking

into account peculiarities of their stress adaptation. It

is found that if limitations for controlling and

controlled parameters of the training process of

hammer throwers are set the problem for

prognostication of training efficiency has solution.

Maximization of the number of hammer throwers

who fulfilled the qualification norm successfully for

participation in the international competitions was

the target function for solving our problem.

REFERENCES

Bakaev, V.V., Bolotin, A.E., & Vasil'eva, V.S. (2015).

Factors determining sports specialization of cross

country skiers. Teoriya i Praktika Fizicheskoy Kultury,

(2), 40-41.

Bakaev, V.V.,Bolotin, A.E.,Aganov, S.S. (2016). Physical

training complex application technology to prepare

rescuers for highland operations. Teoriya i Praktika

Fizicheskoy Kultury, (6), pp.6-8.

Bakayev, V., & Bolotin, A. (2017). Pedagogical model of

children swimming training with the use of method of

substitution of hydrogenous locomotion. In D.

Milanovic, G. Sporis, S. Salaj & D. Skegro (Eds.),

Proceedings Book of 8th International Scientific

Conference on Kinesiology, Opatija, 2017, (pp. 763-

767). Zagreb: Faculty of Kinesiology, University of

Zagreb.

Bartonietz, K., Barclay, L. & Gathercole, D. (1997).

Characteristics of top performances in the women's

hammer throw: basics and technique of the world's

best athletes. New Studies in Athletics, 12(2), 101–109.

Bartonietz, K., Hinz, L., Lorenz, G. & Lunau, G. (1988).

The hammer: the view of the DVfL of the GDR on

talent selection, technique and training of throwers

from beginner to top level athlete. New Studies in

Athletics, 3(1), 39–56.

Bolotin, A.E., Schegolev, V.A., & Bakaev, V.V. (2014).

Educational technology of use of means of physical

culture to adapt students for future professional work.

Teoriya i Praktika Fizicheskoy Kultury, (7), 5-6.

Bolotin, A.E., Bakayev, V.V., & Vazhenin, S.A. (2015).

Educational technology of using the system of Pilates

for the prevention of spine disorders of female

students. Journal of Physical Education and Sport,

15(4), 724-729.

Bolotin, A., & Bakayev, V. (2016). Educational

technology for teaching survival skills to pilots using

training routines. Journal of Physical Education and

Sport, 16(2), 413-417.

Bolotin, A., & Bakayev, V. (2016). Factors that determine

high efficiency in developing speed and strength

0,85

0,75

0,7

0,67

0,85

0,75

0,6

0,32

0,2

0,4

0,6

0,8

2014 2015 2016 2017 2018

Standardized sportsmen

number

Years

New conditions

Innovative

Standard

icSPORTS 2018 - 6th International Congress on Sport Sciences Research and Technology Support

abilities of female hurdlers. Journal of Physical

Education and Sport, 16(3), 910-913.

Bolotin, A., & Bakayev, V. (2016). Efficacy of using

isometric exercises to prevent basketball injuries.

Journal of Physical Education and Sport, 16(4), 1177-

1185.

Bolotin, A, & Bakayev, V. (2017). Peripheral circulation

indicators in veteran trail runners. Journal of Physical

Therapy Science, 29(8), 1092–1094.

Bolotin, A., Bakayev, V., Orlova, N., & Kozulko, A.

(2017). Peculiarities of time structure and of

biomechanical organization of a construction of motor

actions in the hammer throw. In D. Milanovic, G.

Sporis, S. Salaj & D. Skegro (Eds.), Proceedings Book

of 8th International Scientific Conference on

Kinesiology, Opatija, 2017, (pp. 137-141). Zagreb:

Faculty of Kinesiology, University of Zagreb.

Bolotin, A., & Bakayev, V. (2017). Pedagogical

conditions necessary for effective speed-strength

training of young football players (15-17 years old).

Journal of Human Sport and Exercise, 12(2), 405-413.

Hopkins, W., Marshall, S., Batterham, A., & Hanin, J.

(2009). Progressive statistics for studies in sports

medicine and exercise science. Medicine & Science in

Sports & Exercise, 41(1), 3-12.

Malcata, R., & Hopkins, W. (2014). Variability of

competitive performance of elite athletes: a systematic

review. Sports Medicine, (44), 1763-1774.

Murofushi, K., Sakurai, S., Umegaki, K. & Takamatsu, J.

(2007). Hammer acceleration due to thrower and

hammer movement patterns. Sports Biomechanics, (6),

301–314.

Osipov, A., Kudryavtsev, M., Kuzmin, V., Salyamova, P.,

Gavrilyuk, O., Struchkov, V., Galimov, G., &

Zakharova, L. (2016). Methods of operative and

informative control of the muscle loading level used

during the training of sambo wrestlers. Journal of

Physical Education and Sport, 16(4), 1247-1252.

Rojas-Ruiz, F., & Gutiérrez-Dávila, M. (2009). The

relation between angular displacement of the hammer

in the double support phase and its velocity in the

hammer throw. Journal of Human Sport and Exercise,

4(3), 254-261.

Kim, T.-S., Ryu, J.-S., Lee, M.-S., Yoon, S.-H., & Park,

J.-M. (2011). Analysis of Projectile Factors and

Biomechanical Characteristics of Men's Hammer

Throwing during Turning Phases. Korean Journal of

Sport Biomechanics, 21(2), 141-152.

Winter, D. A. (2005). Biomechanics and motor control of

human movement, (3rd ed.). Hoboken: John Wiley &

Sons, Inc.

Training Process Modeling of Hammer Throwers Taking into Account Peculiarities of Stress Adaptation