
COnfECt: An Approach to Learn Models of Component-based Systems
S
´
ebastien Salva and Elliott Blot
LIMOS - UMR CNRS 6158, Clermont Auvergne University, France
Keywords:
Model Learning, Passive Learning, Component-based Systems, Callable-EFSM.
Abstract:
This paper addresses the problem of learning models of component-based systems. We focus on model lear-
ning approaches that generate state diagram models of software or systems. We present COnfECt, a method
that supplements passive model learning approaches to generate models of component-based systems seen
as black-boxes. We define the behaviours of components that call each other with Callable Extended FSMs
(CEFSM). COnfECt tries to detect component behaviours from execution traces and generates systems of
CEFSMs. To reach that purpose, COnfECt is based on the notions of trace analysis, event correlation, model
similarity and data clustering. We describe the two main steps of COnfECt in the paper and show an example
of integration with the passive model learning approach Gk-tail.
1 INTRODUCTION
Delivering high quality software to end-users has be-
come a high priority in the software industry. To help
develop high quality products, the software engineer-
ing field suggests to use models, which can serve as
documentation, for verification or testing. But mo-
dels are often written by hand, and such a task is dif-
ficult and error-prone, even for experts. To make this
task easier, model learning approaches have proven
to be valuable for recovering the model of a system.
In this paper, we consider one specific type of formal
models, namely state machines, which are crucial for
describing system behaviours. In a nutshell, model
learning approaches infer a behavioural formal model
of a system seen as a black-box, either by interacting
with it (active approaches), e.g., with test cases, or by
analysing a set of execution traces resulting from the
monitoring of the system (passive approaches).
Although it is possible to infer models from some
realistic systems, several points require further inves-
tigation before entering in an industrial phase. Among
them, we observed that the current approaches consi-
der a black-box system as a whole, which takes in-
put events from an external environment and produ-
ces output events. Yet, most of the systems being
currently developed are made up of reusable featu-
res or components that interact together. The model-
ling of these components and of their compositions
would bring a better readability and understanding of
the functioning of the system under learning.
We focus on this open problem in this paper and
propose a method called COnfECt (COrrelate Extract
Compose) for learning a system of CEFSMs (Calla-
ble Extended FSMs), which describes a component-
based system. COnfECt aims at completing the pas-
sive model learning approaches, which take execution
traces as inputs. The fundamental idea considered
in COnfECt is that a component of a system can be
identified from the others by its behaviour. COnfECt
analyses execution traces, detects sequences of dis-
tinctive behaviours, extracts them into new trace sets
from which CEFSMs are generated. To do this, COn-
fECt uses the notions of event correlation, similarities
of models and data clustering. More precisely, the
contributions of our work are:
• the definitions of the CEFSM model and of a sy-
stem of CEFSMs allowing to express the behavi-
ours of components calling each other;
• COnfECt, a method supplementing the passive
model learning approaches that generate EFSMs
(Extended FSMs). COnfECt consists of two steps
called Trace Analysis & Extraction and CEFSM
Synchronisation. The first step splits traces into
event sequences that are analysed to build new
trace sets and to prepare the CEFSM synchroni-
sation. The second step proposes three strategies
of CEFSM synchronisation, which help manage
the over-generalisation problem, i.e., the problem
of generating models expressing more behaviours
than those given in the initial trace set. This step
returns a system of CEFSMs. We briefly show
264
Salva, S. and Blot, E.
COnfECt: An Approach to Learn Models of Component-based Systems.
DOI: 10.5220/0006848302640271
In Proceedings of the 13th International Conference on Software Technologies (ICSOFT 2018), pages 264-271
ISBN: 978-989-758-320-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

how COnfECt can be combined with the passive
approach Gk-tail (Lorenzoli et al., 2008). We call
the new approach Ck-tail. We show how to ar-
range the steps of Gk-tail and COnfECt to ge-
nerate a system of CEFSMs from the traces of a
black-box system.
The remainder of the paper is organised as fol-
lows: Section 2 presents some related work. Section
3 provides some definitions about the CEFSM model.
The COnfECt method is presented in Section 4. We
finally conclude and give some perspectives for future
work in Section 5.
2 RELATED WORK
We consider in this paper that model learning is de-
fined as a set of methods that infer a specification by
gathering and analysing system executions and con-
cisely summarising the frequent interaction patterns
as state machines that capture the system behaviour
(Ammons et al., 2002). Models can be generated
from different kinds of data samples such as affirma-
tive/negative answers (Angluin, 1987), execution tra-
ces (Krka et al., 2010; Antunes et al., 2011; Durand
and Salva, 2015), or source code (Pradel and Gross,
2009). Two kinds of approaches emerge from the li-
terature: active and passive model learning methods.
Active learning approaches repeatedly query sys-
tems or humans to collect positive or negative obser-
vations, which are studied to build models. Many ex-
isting active techniques have been conceived upon the
L
∗
algorithm (Angluin, 1987). Active learning cannot
be applied on all systems though. For instance, un-
controllable systems cannot be queried easily, or the
use of active testing techniques may lead a system to
abnormal functioning because it has to be reset many
times. The second category includes the techniques
that passively generate models from a given set of
samples, e.g., a set of execution traces. These techni-
ques are said to be passive since there is no interaction
with the system to model. Models are often con-
structed with these passive approaches by represen-
ting sample sets with automata whose equivalent sta-
tes are merged. The state equivalence is usually defi-
ned by means of event sequence abstractions or state
based abstractions. With event sequence abstractions,
the abstraction level of the models is raised by mer-
ging the states having the same event sequences. This
process stands on two main algorithms: kTail (Bier-
mann and Feldman, 1972) and kBehavior (Mariani
and Pezze, 2007). Both algorithms were enhanced to
support events combined with data values (Lorenzoli
et al., 2008; Mariani and Pastore, 2008). In particu-
lar, kTail has been enhanced with Gk-tail to generate
EFSMs (Lorenzoli et al., 2008; Mariani et al., 2017).
The approaches that use state-based abstraction, e.g.,
(Meinke and Sindhu, 2011), adopted the generation
of state-based invariants to define equivalence clas-
ses of states that are combined together to form final
models. The Daikon tool (Ernst et al., 1999) were ori-
ginally proposed to infer invariants composed of data
values and variables found in execution traces.
None of the current model learning approaches
support the generation of models describing the be-
haviours of components of a system under learning.
This work tackles this research problem and proposes
an original method for inferring models as systems
of CEFSMs. Our main contribution is the detection
of component behaviours in an execution trace set by
means of trace analysis, event correlation, model si-
milarity and data clustering.
3 CALLABLE EXTENDED
FINITE STATE MACHINE
We propose in this section a model of components-
based systems called Callable Extended Finite State
Machine (CEFSM), which is a specialised FSM in-
cluding parameters and guards restricting the firing of
transitions. Parameters and symbols are combined to-
gether to constitute events. A CEFSM describes the
behaviours of a component, which interacts with the
external environment, accepting input valued events
(i.e. symbols associated with parameter assignments)
and producing output valued events. In addition,
the CEFSM model is equipped by a special internal
(unobservable) event denoted call(CEFSM) to trigger
the execution of another CEFSM. This event means
that the current CEFSM is being paused while anot-
her CEFSM C
2
starts its execution at its initial state.
Once C
2
reaches a final state, the calling CEFSM re-
sumes its execution after the event call(CEFSM). We
do not consider in this paper that a component is able
to provide results to another one.
Before giving the CEFSM definition, we assume
that there exist a finite set of symbols E, a domain of
values denoted D and a variable set X taking values
in D. The assignment of variables in Y ⊆ X to ele-
ments of D is denoted with a mapping α : Y −→ D. We
denote D
Y
the assignment set over Y . For instance,
α = {x := 1,y := 3} is a variable assignment of D
{x,y}
.
α(x) = {x := 1} is the variable assignment related to
the variable x.
Definition 1 (CEFSM). A Callable Extended Finite
State Machine (CEFSM) is a 5-tuple hS,s0,Σ,P, T i
where :
COnfECt: An Approach to Learn Models of Component-based Systems
265
• S is a finite set of states, S
F
⊆ S is the non-empty
set of final states, s0 is the initial state,
• Σ ⊆ E = Σ
I
∪ Σ
O
∪ {call} is the finite set of sym-
bols, with Σ
I
the set of input symbols, Σ
O
the set
of output symbols and call an internal action,
• P is a finite set of parameters, which can be assig-
ned to values of D
P
,
• T is a finite set of transitions. A transition
(s
1
,e(p),G,s
2
) is a 4-tuple also denoted s
1
e(p),G
−−−→
s
2
where :
– s
1
,s
2
∈ S are the source and destination states,
– e(p) is an event with e ∈ Σ and p = hp
1
,..., p
k
i
a finite tuple of parameters in P
k
(k ∈ N),
– G : D
P
→ {true, f alse} is a guard that restricts
the firing of the transition.
A component-based system is often made up of
several components. This is why we talk about sys-
tems of CEFSMs in the remainder of the paper. A sy-
stem of CEFSMs SC consists of a CEFSM set C and
of a set of initial states S0, which also are the initial
states of some CEFSMs of C. SC is assumed to in-
clude at least one CEFSM that calls others CEFSMs
and whose initial state is in S0:
Definition 2 (System of CEFSMs). A System of CEF-
SMs is a 2-tuple hC,S0i where :
• C is a non-empty and finite set of CEFSMs,
• S0 is a non-empty set of initial states such that
∀s ∈ S0,∃C
1
= hS, s0,Σ,P,T i ∈ C : s = s0.
We also say that a CEFSM C
1
is callable-complete
over a system of CEFSMs SC, iff the CEFSMs of SC
can be called from any state of C
1
:
Definition 3 (Callable-complete CEFSM). Let SC
= hC, S0i be a system of CEFSMs. A CEFSM
C
1
= hS, s0, Σ,P,T i is said callable-complete over
SC iff ∀s ∈ S,∃s
2
∈ S : s
call(EFSM),G
−−−−−−−−→ s
2
, with G :
_
C
2
∈C\{C
1
}
CEFSM = C
2
A trace is a finite sequence of observable valued
events in (E × D
X
)
∗
. We use ε to denote the empty
sequence.
4 THE COnfECt APPROACH
COnfECt (COrrelate Extract Compose) is an appro-
ach for learning a system of CEFSMs from the exe-
cution traces of a black-box system. COnfECt ana-
lyses traces and tries to detect components and theirs
respective behaviours, which are modelled with CEF-
SMs. COnfECt aims to complement the passive mo-
del learning methods and requires a trace set to ana-
lyse them and identify the components of a black-box
system. And the more traces, the more correct the
component detection will be.
The system under learning SUL can be indetermi-
nistic, uncontrollable (it may provide output valued
events without querying it with a valued input event)
or can have cycles among its internal states. Howe-
ver, SUL and its trace set denoted Traces have to
obey certain restrictions to avoid the interleaving of
events. We consider that SUL is constituted of com-
ponents whose observable behaviours are not carried
out in parallel. One component is executed at a time;
a caller component is being paused until the callee ter-
minates its execution. Furthermore, we consider ha-
ving a set Traces composed of traces collected from
SUL in a synchronous manner (traces are collected by
means of a synchronous environment with synchro-
nous communications). Traces can be collected by
means of monitoring tools or extracted from log fi-
les. Furthermore, we do not focus this work on the
trace formatting, hence, we assume having a mapper
(Aarts et al., 2010) performing abstraction and retur-
ning traces as sequences of valued events of the form
e(p
1
:= d
1
,..., p
k
:= d
k
) where p
1
:= d
1
,..., p
k
:= d
k
are parameter assignments.
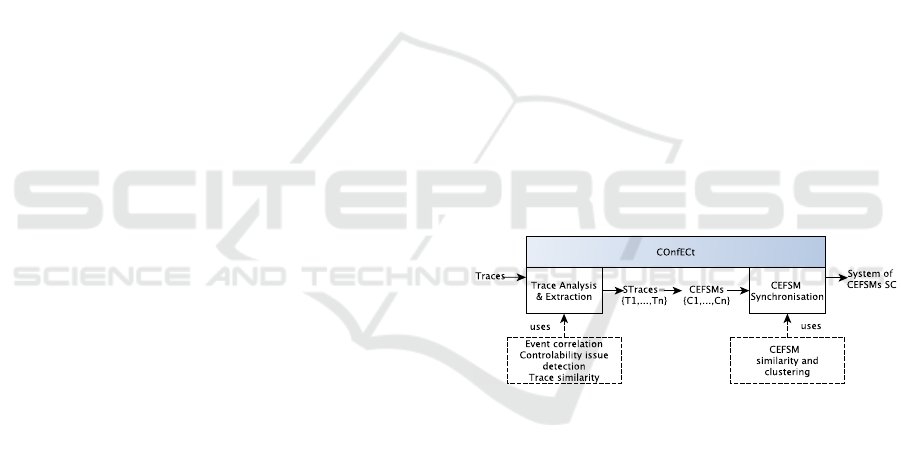
Figure 1: The COnfECt approach overview.
As depicted in Figure 1, COnfECt is composed of
two main stages called Trace Analysis & Extraction
and CEFSM Synchronisation. The former tries to de-
tect components in the traces of Traces and segments
them into a set of trace sets called STraces. The se-
cond stage proposes three CEFSM synchronisation
strategies and provides a system of CEFSMs SC. The-
ses stages are presented below. We believe they can
be interleaved with the steps of several passive model
learning techniques, e.g., (Mariani and Pastore, 2008;
Lorenzoli et al., 2008).
4.1 Trace Analysis & Extraction
This stage tries to identify components in the traces
of Traces by means of Algorithm 1. This algorithm is
based on three notions implemented by three procedu-
ICSOFT 2018 - 13th International Conference on Software Technologies
266

res. It analyses every trace of Traces with Inspect, it
segments them and builds the new trace sets T
1
,..., T
n
with Extract. Finally, it analyses the first trace set T
1
to detect other components with Separate. The algo-
rithm returns the set STraces, which is itself compo-
sed of trace sets. Each will give birth to a CEFSM.
Algorithm 1: Inspect&Extract Algorithm.
input : Traces = {σ
1
,.. . ,σ
m
}
output: STraces = {T
1
,.. . ,T
n
}
1 T
1
= {};
2 STraces = {T
1
};
3 foreach σ ∈ Traces do
4 σ
0
1
σ
0
2
... σ
0
k
=Inspect(σ);
5 STraces=Extract(σ
0
1
σ
0
2
... σ
0
k
,T
1
,STraces);
6 STraces=Separate(T
1
,STraces);
7 return STraces;
4.1.1 Trace Analysis
We assume that a component can be identified by
its behaviour, which is materialised by valued events
composed of symbols and data. We also observed
in many systems, in particular in embedded devices,
that the observation of controllability issues, i.e., ob-
serving output events without giving any input event
before, is often the result of a component interacting
with the external environment.
From these observations, we firstly analyse traces
by means of a Correlation coefficient. This coefficient
aims to evaluate the correlation of successive valued
events, in other words, their links or relations. We
define the Correlation coefficient between two valued
events by means of a utility function, which involves a
weighting process for representing user priorities and
preferences, here towards some correlation factors.
We have chosen the technique Simple Additive Weig-
hting (SAW) (Yoon and Hwang, 1995), which allows
the interpretation of these preferences with weights:
Definition 4 (Correlation Coefficient). Let e
1
(α
1
),
e
2
(α
2
) be two valued events of (E × D
X
), and
f
1
(e
1
(α
1
),e
2
(α
2
)),... f
k
(e
1
(α
1
),e
2
(α
2
)) be correla-
tion factors.
Corr(e
1
(α
1
),e
2
(α
2
)) is a utility function,
defined as: 0 ≤ Corr(e
1
(α
1
),e
2
(α
2
)) =
∑
k
i=1
f
i
(e
1
(α
1
),e
2
(α
2
)).w
i
≤ 1 with w
i
∈ R
+
0
and
∑
k
i=1
w
i
= 1.
The factors must give a value between 0 and 1.
They can have a general form or be established with
regard to the system context and addressed by an ex-
pert. We give below two general factor examples:
• f
1
(e
1
(α
1
),e
2
(α
2
)) =
freq(e
1
e
2
)
freq(e
1
)
+
freq(e
1
e
2
)
freq(e
2
)
with
freq(e
1
e
2
) the frequency of having the two sym-
bols one after the other in Traces and freq(e) the
frequency of having the symbol e. This factor,
used in text mining, computes the frequency of the
term e
1
e
2
in Traces over e
1
and over e
2
to avoid
the bias of getting a low factor when e
1
is greatly
encountered (resp. e
2
);
• f
2
(e
1
(α
1
),e
2
(α
2
)) = |param(α
1
) ∩ param(α
2
)|
/min(|param(α
1
)|,|param(α
2
)|) with param(α)
= {p | (p := v) ∈ α} is the overlap of the
shared parameters between two valued events
e
1
(α
1
),e
2
(α
2
). We have chosen the Overlap coef-
ficient because it is more suited for comparing sets
of different sizes. We recall that the overlap of two
sets X and Y is defined by |X ∩Y |/min(|X|, |Y |).
From this Correlation coefficient, we define two
relations to express what a strong and weak event cor-
relations are. Unfortunately, experts in data mining
often claim that this depends on the considered con-
text. This is why we use two thresholds X and Y in the
following. Both are factors between 0 and 1, which
need to be appraised, for instance after some iterative
attempts.
Definition 5 (Strong and Week Event Correlations).
Let e
1
(α
1
), e
2
(α
2
) be two valued events of (E × D
X
)
such that e
1
6= call and e
2
6= call.
e
1
(α
1
) weak-corr e
2
(α
2
) ⇔
de f
Corr(e
1
(α
1
),
e
2
(α
2
)) < X.
e
1
(α
1
) strong-corr e
2
(α
2
) ⇔
de f
Corr(e
1
(α
1
),
e
2
(α
2
)) > Y .
These relations are specialised on two valued
events. We complete them to formalise the strong
correlation of valued event sequences. We say that
strong-corr(σ
1
) holds when σ
1
has successive valued
events that strongly correlate. We are now ready to
identify the behaviours of components. We define the
relation σ
1
mismatch σ
2
, which holds when the last
event of σ
1
weakly correlates with the first one of σ
2
or when a controllability issue is observed between σ
1
and σ
2
:
Definition 6 (Valued Event Sequence Correlation).
strong-corr(σ) iff
σ = e(α) ∈ (E × D
X
),
σ = e
1
(α
1
)...e
k
(α
k
)(k > 1),∀(1 ≤ i < k) :
e
i
(α
i
) strong-corr e
i+1
(α
i+1
)
Let σ
1
= e
1
(α
1
)...e
k
(α
k
), σ
2
= e
0
1
(α
0
1
)...e
0
l
(α
0
l
) ∈
(E × D
X
)
∗
. σ
1
mismatch σ
2
iff
σ
2
= ε,
e
k
(α
k
) weak-corr e
0
1
(α
0
1
),
e
0
1
is an output symbol ∧ e
k
is an output symbol
The trace analysis is performed with the proce-
dure Inspect given in Algorithm 2, which covers every
trace σ of Traces and tries to segment σ into sub-
sequences such that each sub-sequence has a strong
COnfECt: An Approach to Learn Models of Component-based Systems
267

Figure 2: Sequence extraction example.
correlation and has a weak correlation with the next
sub-sequence. We consider that these sub-sequences
result from the execution of components.
4.1.2 Trace Extraction
Every trace σ ∈ Traces was segmented into
σ
0
1
σ
0
2
...σ
0
k
by means of the relations strong-corr and
mismatch. Every time σ
0
i
mismatch σ
0
i+1
holds bet-
ween two successive sub-sequences, we consider ha-
ving the call of other components by the current one
because both sub-sequences exhibit different behavi-
ours. σ is modified by the procedure Extract to ex-
press these calls.
The procedure Extract(σ,T, STraces), given in
Algorithm 2, takes the trace σ = σ
1
...σ
k
, transforms
it and then adds the new trace into the trace set T . For
a sub-sequence σ
id
of the trace σ = σ
1
...σ
k
, the pro-
cedure Extract tries to find another sub-sequence σ
i
such that strong-corr(σ
id
σ
i
) holds (lines 10,11). The
sequence σ
id+1
...σ
i−1
or σ
id+1
...σ
k
(when σ
i
is not
found) exposes the behaviour of other components
that are called by the current one. If this sequence
is itself composed of more than two sub-sequences,
then the procedure Extract is recursively called (li-
nes 13,14). Otherwise, the sequence is added to a
new trace set T
n
. In σ, the sequence σ
id+1
...σ
i−1
(or σ
id+1
...σ
k
) is removed and replaced by the va-
lued event call(CEFSM := C
n
) (lines 12,19). Once,
the sequence σ is covered by the procedure Extract, it
is placed into the set T .
Let us consider the example of Figure 2, which il-
lustrates the transformation of a trace σ. This trace
was initially segmented into 6 sub-sequences. A) We
start with σ
1
. We suppose the first sequence that
is strongly correlated with σ
1
is σ
5
. σ is transfor-
Figure 3: Component call example.
med into σ
1
call(CEFSM := C
2
)σ
5
σ
6
. Recursively,
Extract(σ
2
σ
3
σ
4
,T
2
) is called to split σ
0
= σ
2
σ
3
σ
4
. B)
We suppose σ
2
σ
4
strongly correlates, hence, σ
0
is mo-
dified and is equal to σ
0
= σ
2
call(CEFSM := C
3
)σ
4
.
The sequence σ
3
is a new trace of the new set T
3
.
As σ
0
is completely covered, σ
0
is added to the new
trace set T
2
. C) We go back to the trace σ at the sub-
sequence σ
5
. As there is no more sub-sequence that
strongly correlates with σ
5
, the end of the sequence σ,
i.e., σ
6
, is extracted and placed into the new trace set
T
4
. The trace σ is now equals to σ
1
call(CEFSM :=
C
2
)σ
5
call(CEFSM := C
4
). This trace is placed into
the trace set T
1
. At the end of this process, we have
recovered the hierarchical component call depicted in
Figure 3. And we get four trace sets.
When the procedure Extract terminates, Algo-
rithm 1 yields the set Straces = {T
1
,T
2
,...,T
n
} with
T
2
,..., T
n
some sets including one trace and T
1
a set of
modified traces, originating from Traces. As we do
not suppose that Traces expresses the behaviours of
only one component, T
1
may include traces resulting
from different components. Hence, T
1
needs to be
analysed as well and possibly partitioned.
4.1.3 Trace Clustering
The trace set T
1
is analysed with the procedure Sepa-
rate, which returns an updated set STraces. The pro-
cedure aims at partitioning T
1
into trace sets exclusi-
vely composed of similar traces. We consider that si-
milar traces exhibit a behaviour provided by the same
component. We evaluate the trace similarity with re-
gard to the symbols and parameters shared between
pairs of traces. Several general similarity coefficients
are available in the literature for comparing the simi-
larity and diversity of sets, e.g., the well-known Jac-
card coefficient. We have once more chosen the Over-
lap coefficient because the symbol or parameter sets
used by two traces may have different sizes.
Definition 7 (Trace Similarity Coefficient). Let σ
i
(i = 1,2) be two traces in (E × D
X
)
∗
.
Σ(σ
i
) = {e | e(α) is a valued event of σ
i
} is the sym-
bol set of σ
i
.
P(σ
i
) = {p | e(α) is a valued event of σ
i
,(p := v) ∈
α} is the parameter set of σ
i
.
Similarity
Trace
(σ
1
,σ
2
) = Overlap(Σ(σ
1
),Σ(σ
2
)) +
Overlap(P(σ
1
),P(σ
2
))/2.
ICSOFT 2018 - 13th International Conference on Software Technologies
268

With this coefficient, the procedure Separate
builds the sets of similar traces from T
1
by means
of a clustering technique. In short, the coefficient is
evaluated for every pair of traces to build a similarity
matrix, which can be used by several clustering al-
gorithms to find equivalence classes. The clustering
techniques here return the clusters of similar traces
T
S
11
,...T
S
1k
. These sets are added into STraces. The
sets T
S
1i
are marked with the exponent S to denote they
are composed of execution traces observed from com-
ponents that were not called by other components at
the beginning of these executions.
Algorithm 2: Procedures Inspect, Extract and Se-
parate.
1 Procedure Inspect(σ) : σ
0
1
σ
0
2
... σ
0
k
is
2 Find the no-empty sequences σ
0
1
σ
0
2
... σ
0
k
such that:
σ = σ
0
1
σ
0
2
... σ
0
k
, strong-corr(σ
0
i
)
(1≤i≤k)
, (σ
0
i
mismatch
σ
0
i+1
)
(1≤i≤k−1)
;
3 Procedure Extract(σ = σ
1
σ
2
... σ
k
,T,STraces): STraces is
4 id := 1;
5 while id < k do
6 n := |STraces| + 1;
7 T
n
:= {};
8 STraces := STraces ∪ {T
n
};
9 σ
p
is the prefix of σ up to σ
id
;
10 if ∃i > id: strong-corr(σ
id
σ
i
) then
11 σ
i
is the first sequence in σ
id
... σ
k
such that
strong-corr(σ
id
σ
i
);
12 σ := σ
p
σ
id
call(CEFSM := C
n
)σ
i
... σ
k
;
13 if (i −id) > 2 then
14 Extract(σ
id+1
... σ
i−1
,T
n
);
15 else
16 T
n
:= T
n
∪ {σ
id+1
};
17 id := i;
18 else
19 σ := σ
p
σ
id
call(CEFSM := C
n
);
20 if (k − id) > 1 then
21 Extract(σ
id+1
... σ
k
,T
n
);
22 else
23 T
n
:= T
n
∪ {σ
k
};
24 id := k;
25 T := T ∪ {σ};
26 return STraces;
27 Procedure Separate(T, STraces): STraces is
28 ∀(σ
i
,σ
j
) ∈ T
2
Compute Similarity
Trace
(σ
i
,σ
j
);
29 Build a similarity matrix;
30 Group the similar traces into clusters {T
11
,.. . T
1k
};
31 STraces = STraces \ {T
1
} ∪{T
S
11
,.. . ,T
S
1k
};
4.2 The CEFSM Synchronisation Stage
This stage aims to organise the component synchro-
nisation with regard to the event call(CEFSM). The
choice of integration of this stage within an existing
model learning approach mainly depends on the steps
of this approach. But it sounds natural to focus on
models, here CEFSMs, for applying different syn-
chronisation strategies. Thus, we consider that the
set STraces has been lifted to a system of CEFSMs
SC = hC,S0i by means of a passive learning met-
hod, e.g., (Lorenzoli et al., 2008). C is composed of
the CEFSM C
i
such that C
i
is derived from a trace
T
i
∈ STraces. In particular, a marked set T
S
j
(com-
posed of traces observed from components that were
not called by other components) gives the CEFSM
C
j
= hS
j
,s0
j
,Σ
j
,P
j
,T
j
i whose initial state s0
j
is also
an initial state of the system of CEFMs SC (s0
j
∈ S0).
We propose three general CEFSM synchronisa-
tion strategies in the paper, which provide systems
of CEFSMs having different levels of generalisation.
These strategies are implemented in Algorithm 3 and
described below:
Strict Synchronisation (Algorithm 3 lines(1,2)). We
want a system of CEFSMs SC in such a way that
a CEFSM of SC cannot repetitively call another
CEFSM. The callee CEFSM must be composed of
one acyclic path only (one behaviour). This strategy
aims to limit the over-generalisation problem, i.e. the
fact of generating models expressing more behaviours
than those given in the initial trace set Traces. This
strategy was already almost achieved by the previous
stage Trace Analysis & Extraction. Indeed, each sub-
sequence extracted from a trace is placed into new
trace set T
i
and is replaced by one valued event of
the form Call(CEFSM := C
i
). Hence, it remains to
transform the trace sets of STraces into CEFSMs for
obtaining a system of CEFSMs organised with a strict
synchronisation.
Weak Synchronisation (Algorithm 3 lines(3-16)).
This strategy aims at reducing the number of com-
ponents and allows repetitive component calls. The
previous stage has possibly created too much trace
sets, therefore the system of CEFSMs SC may in-
clude several similar CEFSMs modelling the functi-
oning of the same component. The similarity notion
is once more defined and evaluated by a Similarity
coefficient.
Definition 8 (CEFSM Similarity Coefficient). Let
C
i
= hS
i
,s0
i
,Σ
i
,P
i
,T
i
i (i = 1,2) be two CEFSMs.
Similarity
CEFSM
(C
1
,C
2
) = Overlap(Σ
1
,Σ
2
) +
Overlap(P
1
,P
2
)/2.
The similar CEFSMs of SC are once more grou-
ped by means of a clustering technique, which
uses the Similarity coefficient. The CEFSMs of
the same cluster are joined by means of a disjoint
union. Furthermore, the guards of the transitions
s
1
call(CEFSM),G
−−−−−−−−−→ s
2
are updated accordingly so that
the correct CEFSMs are being called. In addition,
COnfECt: An Approach to Learn Models of Component-based Systems
269
every transition s
1
call(CEFSM),G
−−−−−−−−−→ s
2
is replaced by a
self loop (s
1
,s
2
)
call(CEFSM),G
−−−−−−−−−→ (s
1
,s
2
) by merging the
states s
1
and s
2
.
Strong Synchronisation (Algorithm 3 lines(4-20)).
This strategy provides more over-generalised models
by generating callable-complete CEFSMs. It is based
on the previous strategy: we join the similar CEFMSs
of SC into bigger CEFSMs and we transform the tran-
sitions labelled by call as previously. In addition, we
complete every state s with new self-loop transitions
of the form s
call(CEFSM),G
−−−−−−−−−→ s so that all the CEFSMs
become callable-complete over the system of CEF-
SMs SC. This strategy seems particularly interesting
for modelling component-based systems having inde-
pendent components that are started any time.
Algorithm 3: CEFSM synchronisation strategies.
input : System of CEFSMs SC = hC,S0i, strategy
output: System of CEFSMs SC
f
= hC
f
,S0
f
i
1 if strategy = Strict synchronisation then
2 return SC;
3 else
4 ∀(C
i
,C
j
) ∈ C
2
Compute Similarity
CEFSM
(C
i
,C
j
);
5 Build a similarity matrix;
6 Group the similar CEFSMs into clusters {Cl
1
,.. .Cl
k
};
7 foreach cluster Cl = {C
1
,.. . ,C
l
} do
8 C
Cl
:=Disjoint Union of the CEFSMs C
1
,.. . ,C
l
;
9 if s0
i
∈ S0(1 ≤ i ≤ l) then
10 S0
f
= S0
f
∪ s0
Cl
;
11 C
f
= C
f
∪ {C
Cl
};
12 foreach C
i
= hS, s0,Σ,P,V, T i ∈ C
f
do
13 foreach s
1
call(CEFSM),G
−−−−−−−−→ s
2
∈ T with
G : CEF SM = C
m
do
14 Find the Cluster Cl such that C
m
∈ Cl;
15 Replace G by G : CEF SM = C
Cl
;
16 Merge (s
1
,s
2
);
17 if strategy = Strong synchronisation then
18 foreach C
i
= hS, s0,Σ,P, T i ∈ C
f
do
19 Complete the states of S with self-loop
transitions so that C
i
is callable-complete;
20 return SC
f
We studied the integration of COnfECt with se-
veral passive learning approaches. We have imple-
mented a combination of the approach with kTail
to generate Labelled Transition Systems (LTS). The
source code as well as examples are available in
(Salva et al., 2018).
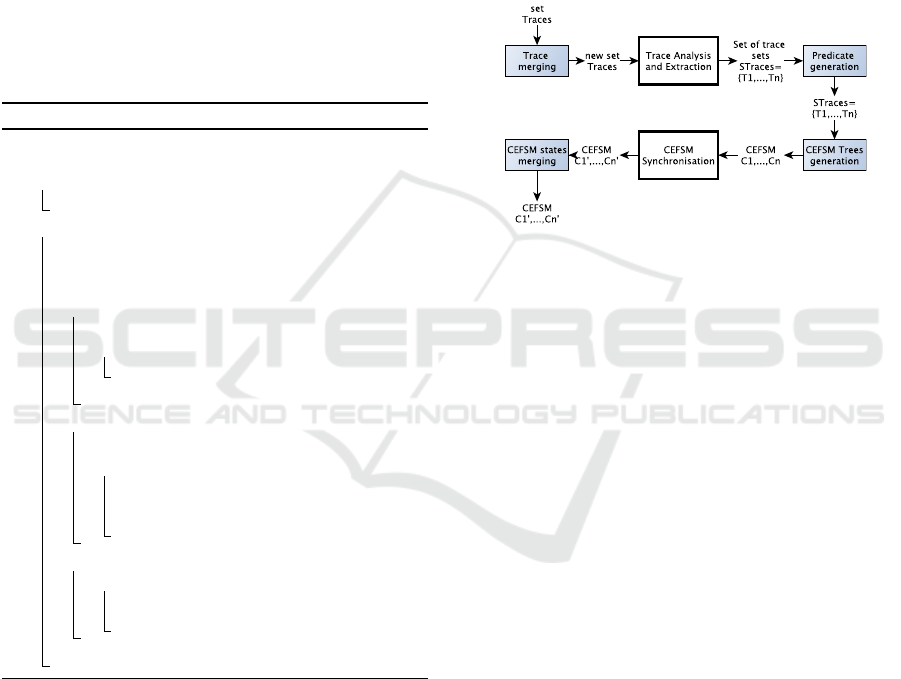
We are also studying the integration of COnfECt
with Gk-tail to generate systems of CEFSMs. Fi-
gure 4 illustrates how the COnfECt and Gk-tail steps
can be organised. The COnfECt steps are given with
white boxes. We call the resulting approach Ck-tail.
Step 2 corresponds to the first step of COnfECt. We
placed it after Step 1 (trace merging) to have less trace
to analyse, and before Step 3 (guard generation) to
measure the event correlation on symbols and real va-
lues. The CEFSM Synchronisation step of COnfECt
is the fifth step of Ck-tail. It is performed after the
CEFSM tree generation, and before Step 6 (state mer-
ging) because it sounds more interesting to group the
similar CEFMS and to merge their equivalent states
after, as more equivalent states should be merged if
we follow this step order. We illustrate this integration
with a example based upon a real system (an IOT (In-
ternet Of Things) thermostat) in (Salva et al., 2018).
Figure 4: Ck-tail: Integration of COnfECt with Gk-tail.
5 CONCLUSION
We have presented COnfECT, a method that com-
plements existing passive model learning approaches
to infer systems of CEFSMs from execution traces.
COnfECT is able to detect component behaviours by
analysing traces by means of a Correlation coeffi-
cient and a Similarity coefficient. In addition, COn-
fECT proposes three model synchronisation strate-
gies, which help manage the over-generalisation of
systems of CEFSMs.
In future work, we intend to carry out more evalu-
ations of COnfECT on several kinds of systems. The
main issue concerns the implementation of monitors
and mappers, which are required to format traces. We
also intend to tackle the raise of the abstraction le-
vel of CEFSMs. Indeed, while the trace analysis, the
successive computations of the Correlation coefficient
could also be used to perform event aggregation in
accordance with event correlation and some CEFSM
structural restrictions.
ACKNOWLEDGMENT
Research supported by the French Project VASOC
(Auvergne-Rhne-Alpes Region) https://vasoc. li-
mos.fr/
ICSOFT 2018 - 13th International Conference on Software Technologies
270

REFERENCES
Aarts, F., Jonsson, B., and Uijen, J. (2010). Generating mo-
dels of infinite-state communication protocols using
regular inference with abstraction. In Petrenko, A.,
Sim
˜
ao, A., and Maldonado, J. C., editors, Testing Soft-
ware and Systems, pages 188–204, Berlin, Heidel-
berg. Springer Berlin Heidelberg.
Ammons, G., Bod
´
ık, R., and Larus, J. R. (2002). Mining
specifications. SIGPLAN Not., 37(1):4–16.
Angluin, D. (1987). Learning regular sets from queries
and counterexamples. Information and Computation,
75(2):87 – 106.
Antunes, J., Neves, N., and Verissimo, P. (2011). Reverse
engineering of protocols from network traces. In Re-
verse Engineering (WCRE), 2011 18th Working Con-
ference on, pages 169–178.
Biermann, A. and Feldman, J. (1972). On the synthesis of
finite-state machines from samples of their behavior.
Computers, IEEE Transactions on, C-21(6):592–597.
Durand, W. and Salva, S. (2015). Passive testing of pro-
duction systems based on model inference. In 13.
ACM/IEEE International Conference on Formal Met-
hods and Models for Codesign, MEMOCODE 2015,
Austin, TX, USA, September 21-23, 2015, pages 138–
147. IEEE.
Ernst, M. D., Cockrell, J., Griswold, W. G., and Notkin, D.
(1999). Dynamically discovering likely program in-
variants to support program evolution. In Proceedings
of the 21st International Conference on Software En-
gineering, ICSE ’99, pages 213–224, New York, NY,
USA. ACM.
Krka, I., Brun, Y., Popescu, D., Garcia, J., and Medvido-
vic, N. (2010). Using dynamic execution traces and
program invariants to enhance behavioral model in-
ference. In Proceedings of the 32Nd ACM/IEEE In-
ternational Conference on Software Engineering - Vo-
lume 2, ICSE ’10, pages 179–182, New York, NY,
USA. ACM.
Lorenzoli, D., Mariani, L., and Pezz
`
e, M. (2008). Automa-
tic generation of software behavioral models. In Pro-
ceedings of the 30th International Conference on Soft-
ware Engineering, ICSE ’08, pages 501–510, New
York, NY, USA. ACM.
Mariani, L. and Pastore, F. (2008). Automated identification
of failure causes in system logs. In Software Reliabi-
lity Engineering, 2008. ISSRE 2008. 19th Internatio-
nal Symposium on, pages 117–126.
Mariani, L., Pezz, M., and Santoro, M. (2017). Gk-tail+
an efficient approach to learn software models. IEEE
Transactions on Software Engineering, 43(8):715–
738.
Mariani, L. and Pezze, M. (2007). Dynamic detection
of cots component incompatibility. IEEE Software,
24(5):76–85.
Meinke, K. and Sindhu, M. (2011). Incremental learning-
based testing for reactive systems. In Gogolla, M. and
Wolff, B., editors, Tests and Proofs, volume 6706 of
Lecture Notes in Computer Science, pages 134–151.
Springer Berlin Heidelberg.
Pradel, M. and Gross, T. R. (2009). Automatic generation
of object usage specifications from large method tra-
ces. In Proceedings of the 2009 IEEE/ACM Interna-
tional Conference on Automated Software Engineer-
ing, ASE ’09, pages 371–382, Washington, DC, USA.
IEEE Computer Society.
Salva, S., Blot, E., and Laurenc¸ot, P. (2018). Model Lear-
ning of Component-based Systems. Limos research
report. http://sebastien.salva.free.fr/useruploads/files/
SBL18a.pdf.
Yoon, K. P. and Hwang, C.-L. (1995). Multiple attribute
decision making: An introduction (quantitative appli-
cations in the social sciences).
COnfECt: An Approach to Learn Models of Component-based Systems
271
