A Novel Big-data-based Estimation Method of Side-slip Angles
for Autonomous Road Vehicles
D
´
aniel F
´
enyes, Bal
´
azs N
´
emeth and P
´
eter G
´
asp
´
ar
Institute for Computer Science and Control, Hungarian Academy of Sciences,
Kende u. 13-17, H-1111 Budapest, Hungary
Keywords:
Side-slip Estimation, Regression Analysis, Big Data, Kalman Filtering.
Abstract:
In the paper a novel side-slip estimation algorithm, which is based on big data approaches, is proposed. The
idea of the estimation is based on the availability of a large amount of information of the autonomous vehicles,
e.g. yaw-rate, accelerations and steering angles. The significant number of signals are processed through
big data approaches to generate a simplified rule for the side-slip estimation using the onboard signals of the
vehicles. Thus, a subset selection method for time-domain signals is proposed, by which the attributes are
selected based on their relevance. Furthermore, a linear regression using the Ordinary Least Squares (OLS)
method is applied to derive a relationship between the attributes and the estimated signal. The efficiency of the
estimation is presented through several CarSim simulation examples, while the WEKA data-mining software
is used for the OLS method.
1 INTRODUCTION AND
MOTIVATION
The spread of autonomous driving is predicted to be a
future tendency of intelligent transportation systems.
Several research institutes have focused on the new
challenges posed by autonomous vehicles, such as en-
vironment detection and the accurate estimation of
vehicle states. One of these signals is the side-slip
angle, which has relevance in the evaluation of the
vehicle stability. In several research projects filtering
methods and observers are designed to estimate the
side-slip angle, see (Stephant et al., 2004; Coyte et al.,
2014). The precise estimation using Kalman filtering
requires sensor fusion with GPS measurements, but
these solutions suffer from the loss of signals in urban
locations and tunnels (Grip et al., 2009).
Therefore, several further techniques have been
published in the literature. Big data were used in the
prediction of vehicle slip through the combination of
individual measurements of the vehicle and database
information (Jeon et al., 2015). In (Sasaki and Nishi-
maki, 2000) a layered neural network was developed
to compute the side-slip angle. An artificial neural
network method for slip estimation using accelera-
tion, velocity, inertial and steering angle information
was also proposed in (Kato et al., 1994). Moreover,
in (Boada et al., 2015) an adaptive neuro-fuzzy infer-
ence system approach was applied with various signal
measurements. Another formulation of the neural net-
works, such as the general regression for the side-slip
angle estimation, was used in (Wei et al., 2016).
In this paper a novel side-slip angle estimation
method which is based on linear regression is pre-
sented. As a first step, a subset selection method
is proposed, which is able to prioritize the attributes
based on their relation to the estimated signal. In
the method the time-domain measurements of the at-
tributes are processed through probability-based com-
putations. Secondly, the OLS method is used to ex-
press the relationship between the attributes and the
estimated signal in a linear form. In this process
the pace regression algorithms of the WEKA data-
mining software are performed (Wang and Witten,
1999). The advantage of the method is that it requires
little on-line computation, while the complex opera-
tions are solved off-line. Moreover, in the estimation
method only the onboard signals of the vehicle are
used, which are available without a loss in communi-
cation.
The structure of the paper is the following. Sec-
tion 2 provides a subset selection method, by which
priorities between the attributes can be set. The re-
sults of the selection are used through linear regres-
sion, which is presented in Section 3. The results of
the big-data-based method are illustrated through var-
ious simulations in Section 4. Finally, the contribu-
420
Fényes, D., Németh, B. and Gáspár, P.
A Novel Big-data-based Estimation Method of Side-slip Angles for Autonomous Road Vehicles.
DOI: 10.5220/0006849504200426
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 420-426
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tions of the paper and further challenges are summa-
rized in Section 5.
2 SUBSET SELECTION FOR THE
SIDE-SLIP ESTIMATION
The purpose of subset selection is to find the attributes
which have relevance in the estimation of the side-slip
angle. A difficulty in the subset selection method may
be the high number of attributes, which can lead to
the infeasibility of the problem. Thus, in the gener-
ation of subset models, it is necessary to reduce the
complexity of the big data analysis, while informa-
tion loss from the data is negligible (Wang and Wit-
ten, 2002). Several ranking algorithms have been pro-
posed for the relationships between event-based at-
tributes (Shibata, 1981; Thompson, 1978). However,
in the side-slip estimation problem the attributes con-
tain time-domain instances. Thus, it requires the eval-
uation of the measurement in the time-domain, which
is proposed in the following.
Consider a simple linear equation (1) with only
one variable.
y = c
k,0
+ c
k,1
x
k
, (1)
where y is the output (estimated attribute), x
k
∈ X is
a selected variable from the set of the measured at-
tributes (X), c
k,0
and c
k,1
are the fitting parameters.
Since, in this case, the attributes are time-domain vari-
ables, the relative derivatives can be derived from (1).
d
dt
y
x
k
= c
k,1
. (2)
Then, the statistical parameters of c
k,1
are computed,
such as σ
c
k,1
variance and ˆc
k,1
mean. It can be seen
that if the linear model (1) provides the perfect fitting
(the correlation between the two variables is 1)
σ
c
k,1
= 0, (3a)
ˆc
k,1
= c
∗
k,1
, (3b)
where
∗
denotes the parameters of the real model.
Furthermore, if the linear model gives the worst fitting
(the correlation between the two variables is 0)
σ
c
k,1
→ ∞, (4a)
ˆc
k,1
= 0, (4b)
If y 6= 0, x
k
6= 0 and y 6= b + x
k
, where b is a constant
bias parameter.
As the previous equations show, the relevance of
an attribute depends on the variance and the mean of
its c
k
1
parameter. If the normal distribution of c
k,1
is
assumed, then the relationship between these param-
eters is given by the gaussian distribution function:
G
k
(c
k,1
) =
1
σ
c
k,1
√
2π
e
−
1
2

c
k,1
−ˆc
k,1
σ
c
k,1

2
(5)
The relevance of an attribute can be expressed by
integrating the gaussian function and taking into ac-
count the sign of c
k,1
.
D
k
(c
k,1
) =
Z
∞
−∞
sign(c
k,1
)G(c
k,1
)dc
k,1
= (6)
=
1
σ
c
k,1
√
2π
Z
∞
−∞
sign(c
k,1
)e
−
1
2

c
k,1
−ˆc
k,1
σ

2
dc
k,1
D
k
(c
k,1
) yields a value D
k
(c
k,1
) ∈ [0,1], which indi-
cates the correctness of c
k,1
according to its sign, but
ignores the variance σ
c
k,1
. Therefore, the relevance of
an attribute is formed as:
R
k
=
D
k
(c
k,1
)
σ
c
k,1
(7)
Finally, the attribute with the highest relevance on y is
the attribute whose R is the highest.
max
x
(R ) (8)
3 ESTIMATION OF THE
SIDE-SLIP ANGLE BASED ON
THE OLS METHOD
The background of the estimation of the side-slip an-
gle is the combination of the ordinary linear regres-
sion method and the subset selection procedure. In
the following the most important features are summa-
rized and a detailed description is found in (Wang and
Witten, 1999).
In the method a dataset with n independent in-
stances is considered with k input variables and one
output variable. The instances are written in the form
of an n ×k design matrix X. Furthermore, the param-
eter vector of the true model is ζ
∗
. Using the paame-
ter vector of the true model and the matrix of the in-
stances, the output vector y is formed as
y = X ζ
∗
+ ε (9)
where ε is the noise vector, of which elements have
normal distribution N(0, σ
2
). Its variance is σ, and σ
2
is assumed to be known or estimated. The estimation
of σ is denoted by
ˆ
σ
2
. (9) describes the true model
M (ζ
∗
), which is approximated with a fitted, linear
model M (ζ), which has a unique parameter vector ζ.
A Novel Big-data-based Estimation Method of Side-slip Angles for Autonomous Road Vehicles
421

The goal of the estimation problem is to find a
model from the entire model space M = {M (ζ) : ζ ∈
R
k
}, whose predictive accuracy is the greatest on the
given dataset. The task can be solved through several
algorithms, such as the OLS method, the OLS subset
selection, shrinkage, RIC, CIC methods, see (Wang
and Witten, 1999). These methods can reduce the di-
mension of the models by discarding the redundant
variables.
It is defined a distance D between the candidate
model and the true model for the evaluation of the
estimation method. D is defined in the form of
D(M (ζ
∗
),M (
ˆ
ζ)) =
||y − ˆy||
2
σ
2
, (10)
where ||·|| denotes the L
2
norm and σ
2
is replaced by
its estimated value
ˆ
σ
2
. Moreover, ˆy is the prediction
output vector.
Thus, the estimation problem is to minimize the
distance between the models, which is represented by
the following expression
min
ζ
D(M (ζ
∗
),M (ζ)) (11)
In the OLS regression the prediction is expressed
in the following way
ˆy = X
ˆ
ζ (12)
where
ˆ
ζ is the parameter vector of the prediction
model. The distance (10) can be reformulated as
D(M (ζ
∗
),M (
ˆ
ζ)) =
||y −X
ˆ
ζ||
2
σ
2
, (13)
which can be expressed by the following form of the
training sets:
(y −X
ˆ
ζ)
2
σ
2
=
ω
∑
i=1
||y
i
−X
i
ˆ
ζ||
2
σ
2
(14)
where y
i
and X
i
are one of the training sets, while ω is
the number of the training sets.
The solution of the optimization task (11) can be
achieved by the partial derivation of (13) according to
ˆ
ζ. The solution is the following:
ˆ
ζ = (X
T
X)
−1
X
T
y. (15)
Thus, the predicted output ˆy in the vector form ˆy can
be expressed by using the orthogonal projection ma-
trix
P = X (X
T
X)
−1
X
T
such as
ˆy = P y. (16)
The estimation of the side-slip angle β(k) is based
on the optimization. The prediction model is formed
as
ˆ
β(k) = ζ
1
+
k
∑
i=k−j
ζ
2,i
a
x
(i) +
k
∑
i=k−j
ζ
3,i
a
y
(i)+
+
k
∑
i=k−j
ζ
4,i
˙
ψ(i) +
k
∑
i=k−j
ζ
5,i
δ
s
(i) (17)
in which past signals are applied in the estimation to
take into consideration the possible regressions. Al-
though their incorporation may improve the accuracy
of the prediction, the increase in j results in a more
complex model.
The number of the past elements can be assisted
through a spectrum analysis of β(k), with which the
dominant frequencies can be determined. It results in
the sampling time T and the entire time horizon of the
past is j ·T .
The measured elements of X
k
are
X
k
=

a
x
(k) a
y
(k)
˙
ψ(k) δ
s
(k)

T
with
• longitudinal acceleration a
x
,
• lateral acceleration a
y
,
• yaw-rate
˙
ψ,
• angle of the steering wheel δ
s
.
Furthermore, the side-slip angle y
k
= β(k) as a ref-
erence for the OLS regression analysis is also mea-
sured. The result of the optimization is the vector
ˆ
ζ = [ζ
1
ζ
2,k−j
... ζ
2,k
ζ
3,k−j
... ζ
3,k
...
ζ
4,k−j
... ζ
4,k
ζ
5,k−j
... ζ
5,k
]
T
. (18)
4 SIMULATION RESULTS OF
THE ESTIMATION METHODS
The efficiency of the proposed estimation method is
demonstrated through simulation examples, using the
high-fidelity vehicle dynamic software CarSim.
Several simulations have been performed, which
resulted in a training set for big data analysis. In the
simulations a D-class sedan passenger car has been
used, whose sprung mass is 1320kg, during the col-
lection of the signals the noises of the sensors were
considered.
The car has been driven along the Michigan Wa-
terford Hill Race Course (Figure 1) several times at
various longitudinal velocities (Figure 2), which has
resulted in the collection of more than 2 million in-
stances.
The prediction model also contains the past val-
ues of the attributes, see the relationship (17). The
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
422

−200 −100 0 100 200 300
−200
−150
−100
−50
0
50
100
150
X (m)
Y (m)
Figure 1: Simulation scenario.
0 20 40 60 80 100 120 140 160
Time (s)
0
10
20
30
40
50
60
V (km/h)
Figure 2: Velocity during the scenario.
Figure 3: Spectrum analysis of β.
T sampling time of the signals from the past is com-
puted through the Fourier spectrum analysis, whose
results are found in Figure 3.
They show that the frequency domain of the power
spectral density of the side-slip signal is between 0−8
Hz. Thus, the sampling time of the past values, ac-
cording to the Nyquist-Shannon sampling criteria, has
been chosen at 16 Hz. Moreover, 6 past values of all
attributes have been considered in the model estima-
tion, which corresponds to 0.375 sec horizon back-
wards. The relevance of the selected attributes is eval-
uated by the algorithm presented in Section 2.
Figures 4 shows the relative derivatives of the
measured signals. It can be seen that the means of the
acceleration signals (a
x
,a
y
) are close to zero and their
variances are relatively high, which indicates low rel-
evance on the estimated variable (β). The mean of the
yaw rate (
˙
ψ) and the steering angle (δ) are above zero
and their variances are significantly smaller, which
implies that these signals have high relevance on the
selected output.
0 20 40 60 80 100
Time (s)
-4
-2
0
2
4
6
Relative derivatives
0 20 40 60 80 100
Time (s)
-3
-2
-1
0
1
2
3
Relative derivatives
Figure 4: Relative derivatives of the selected attributes.
Table 1 summarizes the computed relevance of all
signals. In the following the predefined order of the
attributes is determined by their calculated relevance.
Furthermore, the OSL subset selection method has
created a model using the predefined order of the at-
tributes, whose correlation coefficient is 0.911.
Figure 5 illustrates a scenario of the slip estima-
tion, in which the car is driven along the test track
at various velocities. In the example the bias and the
variances of the sensors are selected in the following
way:
• inertial sensor: bias = 0.15 m/s
2
, variance = 0.1
2
• qyroscope: bias = 0.01 rad/s, variance = 0.01
2
The error of the estimation is very low, although
the velocity of the vehicle varies significantly, see Fig-
A Novel Big-data-based Estimation Method of Side-slip Angles for Autonomous Road Vehicles
423

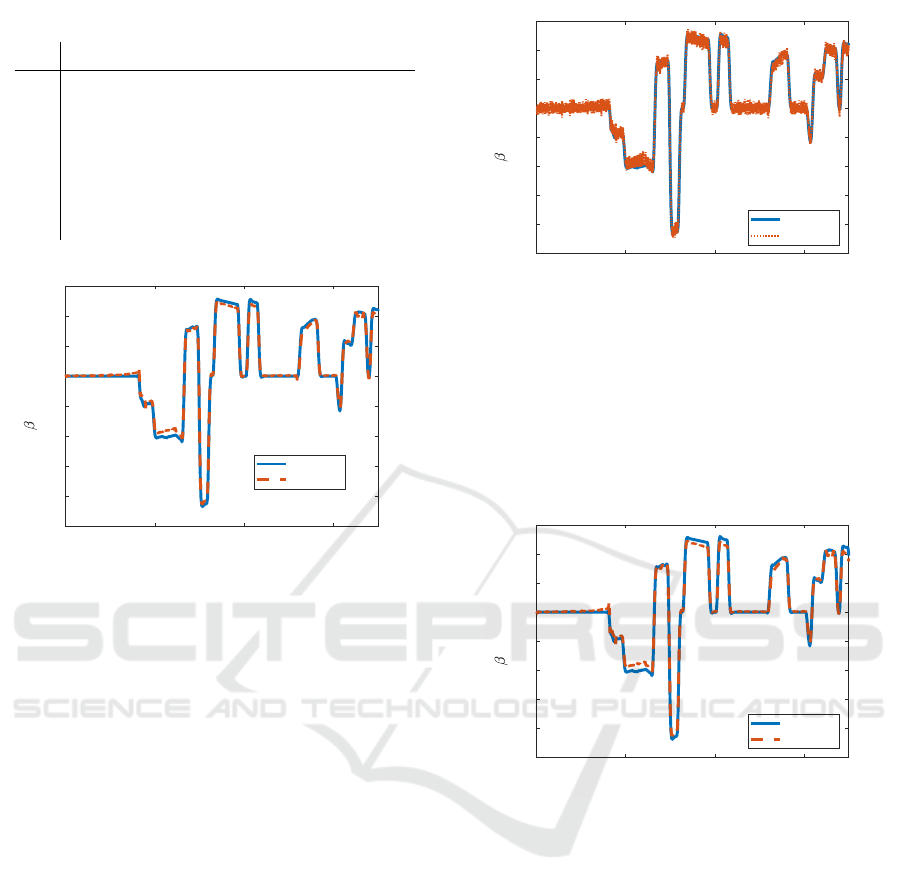
Table 1: Relevance of attributes.
T R
a
x
R
a
y
R
˙
ψ
R
δ
t 0.00013 0.00449 0.14336 0.58502
t-1 0.0002 0.00266 0.01528 0.00082
t-2 0.00095 0.00074 0.00103 0.00086
t-3 0.00216 0.00003 0.00236 0.00592
t-4 0.001 0.0007 0.00022 0.01225
t-5 0.00284 0.00217 0.00156 0.00455
t-6 0.00044 0.00287 0.00165 0.00133
0 50 100 150
Time (s)
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
(deg)
Reference
Predicted
Figure 5: Estimation of the side-slip angle.
ure 2. In the following, the accuracy and the capabil-
ity of the generated predictive model are examined in
various situations.
4.1 Increased Noise
In the first situation the impact of the increasing noise
on the predictive accuracy is examined. In practice,
the inertial sensors and the gyroscope are significantly
affected by sensor noises, while the angle of the steer-
ing wheel can be relatively well measured. In this sce-
nario the parameters of the sensors are significantly
modified to:
• inertial sensor: bias = 0.3 m/s
2
, variance = 0.4
2
• gyroscope: bias = 0.02 rad/s, variance = 0.04
2
Figure 6 shows the result of the simulation with the
modified sensor parameters. It can be seen that the
variation of the noise has only a slight effect on the
prediction. The estimated model predicts the side-slip
angle accurately despite the increased noises.
4.2 Variation of Vehicle Mass
Secondly, the effect of the car mass variation on the
accuracy of the prediction is investigated. The nomi-
nal sprung mass of the passenger car is m = 1320kg,
which is modified in two ways: the mass is reduced to
0 50 100 150
Time (s)
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
(deg)
Reference
Predicted
Figure 6: Effect of the increased noise on the prediction.
m = 1000kg and then it is increased to m = 1740kg.
The results of the changes can be seen in Figure 7.
Apart from a short section, the applied model has high
predictive accuracy, which means that the variation of
the mass has no significant influence on the predic-
tion. Therefore, the calculated model can resist the
change in the vehicle mass.
0 50 100 150
Time (s)
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
(deg)
Reference
Predicted
Figure 7: Effect of the variation of mass on the prediction
(m = 1000kg).
4.3 Variation of the Adhesion
Coefficient
In the third case the variation of the adhesion coeffi-
cient µ is simulated. The initial value of the adhesion
coefficient is µ = 1. In the simulations its value is de-
creased to µ = 0.7 and then to µ = 0.4. The results of
the simulations are shown in Figure 8. In the case of
µ = 0.7 it can be seen that the model predicts the side-
slip angle as accurately as in the normal case, see Fig-
ure 5. In the case of µ = 0.4 the model also operates
appropriately apart from two short sections between
80 −90s and 110 −120s. In these sections the vehi-
cle reaches its stability boundary, and therefore, the
effect of the steering angle on the lateral dynamics
decreases. Nevertheless, the applied model operates
accurately in all other sections.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
424

0 50 100 150
Time (s)
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
(deg)
Reference
Predicted
Figure 8: Effect of the variation of the adhesion coefficient
on the prediction (µ = 0.4).
4.4 Highway Analysis
Below, the predictive model is tested on a highway
route. In the example the highway between Ulm and
Stuttgart in Germany, which is one of the most hilly
highway sections in Europe, is selected. Since all of
the regression models can be easily overfitted, it is
important to guarantee that the calculated model op-
erates in other cases. In this case the passenger car
is driven at high velocity v
x
∼ 130 km/h. The side-
slip angle and its prediction are shown in Figure 9.
The simulation shows that the applied model is able
to predict the side-slip angle accurately. Its predic-
tive accuracy is still relatively high despite the low
side-slip values. It means that the proposed predictive
model is generally able to predict the side-slip angle.
0 50 100 150
Time (s)
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
(deg)
Reference
Predicted
Figure 9: Side-slip angles on the highway.
4.5 Comparison of the Results with
Kalman Filtering
Finally, the OLS estimation is compared with the
results of a Kalman filtering technique. Although
Kalman filtering and the presented OLS method are
close to each other (Otter, 1978), the design technique
of the filter and the computation algorithm with the
huge number of data can lead to slightly different re-
sults. For example, in case of the Kalman filter de-
sign the selection of the weights has an important role.
Moreover, in this application of the Kalman filtering
a sensor fusion algorithm is used, which incorporates
in the signals of GPS and IMU. The purpose of sen-
sor fusion is to use the precise longitudinal and lateral
velocity information of the GPS module, whose sam-
pling time is relatively high. Therefore, in the fusion
the less precise longitudinal and lateral acceleration
signals a
x,IMU
,a
y,IMU
of the IMU with low sampling
time are also incorporated (Ryu et al., 2002). The
goal of the comparison is to illustrate that the big data
based estimation can also be an acceptable method for
the estimation problem of vehicle side-slip angle.
The simulation results are illustrated in Figure 10.
It can be seen that both methods can provide accurate
results. However, the Kalman filter has higher preci-
sion at increased side-slip signals, while the proposed
big-data-based approach is more efficient at low β val-
ues.
0 20 40 60 80 100 120 140
Time (s)
-2
-1
0
1
2
3
(deg)
Measured
Predicted
Kalman-Filter
Figure 10: Comparison of the Kalman filter method and the
prediction method.
5 CONCLUSIONS
In the paper a big-data-based algorithm for vehicle
side-slip estimation has been proposed. Vehicle dy-
namic simulations have illustrated that the proposed
method can be an efficient alternative algorithm to
the conventional Kalman-filtering techniques. First,
a subset selection method has been proposed, which
provided priorities between the different attributes,
such as longitudinal and lateral accelerations, the
front wheel steering angle and the yaw rate. Second, a
linear regression fitting based on the OLS method has
been performed. As a future challenge in the research,
the proposed method will be demonstrated through
hardware-in-the-loop simulations and real test vehi-
cle measurements.
A Novel Big-data-based Estimation Method of Side-slip Angles for Autonomous Road Vehicles
425

ACKNOWLEDGEMENTS
This work was supported by the GINOP-2.3.2-15-
2016-00002 grant of the Ministry of National Econ-
omy of Hungary.
REFERENCES
Boada, B. L., Boada, M. J. L., Gauch
´
ıa, A., Olmeda, E.,
and D
´
ıaz, V. (2015). Sideslip angle estimator based
on ANFIS for vehicle handling and stability. Journal
of Mechanical Science and Technology, 24(4):1473–
1481.
Coyte, J., Li, B., Du, H., Li, W., Stirling, D., and Ros,
M. (2014). Decision tree assisted EKF for vehicle
slip angle estimation using inertial motion sensors. In
IEEE International Joint Conference on Neural Net-
work (IJCNN 2014), Beijing, China.
Grip, H., L.I.Imsland, Johansen, T., Kalkkuhl, J., and Su-
issa, A. (2009). Vehicle sideslip estimation. design,
implementation, and experimental validation. IEEE
Control Systems Magazine, 29(5):36–52.
Jeon, J., Lee, W., Cho, H. J., and Lee, H. (2015). A big data
system design to predict the vehicle slip. In 2015 15th
International Conference on Control, Automation and
Systems (ICCAS), pages 592–596.
Kato, M., Isoda, K., and Yuasa, H. (1994). Estimation of
vehicle side slip angle with artificial neural network.
SAE Review, 15:79–82.
Otter, P. W. (1978). The discrete Kalman filter applied
to linear regression models: statistical considerations
and an application. Statistica Neerlandica, 32(1):41–
56.
Ryu, J., Rossetter, E. J., and Gerdes, J. C. (2002). Vehi-
cle sideslip and roll parameter estimation using GPS.
In 6th Int. Symposium on Advanced Vehicle Control,
Hiroshima, Japan.
Sasaki, H. and Nishimaki, T. (2000). A side-slip angle est-
mation using neural network for a wheeled vehicle.
Shibata, R. (1981). An optimal selection of regression vari-
ables. Biometrika, 68:45–54.
Stephant, J., Charara, A., and Meizel, D. (2004). Experi-
mental validation of vehicle sideslip angle observers.
In IEEE Intelligent Vehicles Symposium, 2004, pages
150–155.
Thompson, M. L. (1978). Selection of variables in multiple
regression. International Statistical Society B, 46:1–
21 and 129–146.
Wang, Y. and Witten, I. H. (1999). Pace Regression. (Work-
ing paper 99/12). Hamilton, New Zealand: University
of Waikato, Department of Computer Science.
Wang, Y. and Witten, I. H. (2002). Modeling for optimal
probability prediction. In Proceedings of the Nine-
teenth International Conference in Machine Learning,
pages 650–657, Sydney, Australia.
Wei, W., Shaoyi, B., Lanchun, Z., Kai, Z., Yongzhi, W., and
Weixing, H. (2016). Vehicle sideslip angle estimation
based on general regression neural network. Mathe-
matical Problems in Engineering.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
426