LSHADE Algorithm with a Rank-based Selective Pressure Strategy
for the Circular Antenna Array Design Problem
Shakhnaz Akhmedova, Vladimir Stanovov and Eugene Semenkin
Department of System Analysis and Operations Research, Reshetnev Siberian State University of Science and Technology,
“Krasnoyarskiy Rabochiy” avenue, 31, Krasnoyarsk, Russia
Keywords: Optimization, Circular Antenna Array Design Problem, Communication Systems, Differential Evolution,
LSHADE, Mutation Strategies, Selective Pressure.
Abstract: A new algorithm called LSHADE-RSP, which is based on a modification of the Differential Evolution
technique, namely the LSHADE algorithm, with a rank-based selective pressure strategy, is presented in this
paper. The basic idea of the proposed approach LSHADE-RSP consists in the adaptation of its mutation
strategy, DE/current-to-pbest/1, using the linear rank-based selective pressure. LSHADE-RSP is built to
tackle complex high-dimensional global optimization problems, and firstly it has been successfully tested on
the CEC 2018 benchmark functions. Then the LSHADE-RSP was used for solving a real-life engineering
global optimization problem, more specifically, the circular antenna array design problem. The objective of
the stated problem is to vary the current and phase excitations of the antenna elements and try to suppress
side-lobes, minimizing beam width, and to achieve null control at the desired directions. From the obtained
results, the workability and usefulness of the new approach were confirmed. In addition, it can be concluded
that the proposed optimization algorithm demonstrates competitive results in comparison with most
alternative algorithms, thus, LSHADE-RSP can be recommended for solving optimization problems instead
of them.
1 INTRODUCTION
Antenna arrays are intensively used in radar
(Akcakaya and Nehorai, 2011), sonar (Bellettini and
Pinto, 2002) and wireless communication systems
(Zaker et al., 2007) among others. Therefore, the
optimum design of array patterns is an important
task in order to increase the channel capacities of
these systems, broadening their coverage areas and
ensuring an efficient spectrum utilization
(Civicioglu, 2013).
The aim of the circular antenna array design
problem is to obtain its optimum parameters, thus
determining the positions of array elements (Das and
Suganthan, 2010). Many researchers have conducted
different studies on this subject, for example
(Dessouky, 2006). In this study, a new modification
of the well-known LSHADE algorithm (Tanabe and
Fukunaga, 2014), which, in its turn, is a
modification of the Differential Evolution technique
(Storn and Price, 1997), is proposed for solving the
stated problem.
Although generally the original LSHADE
algorithm successfully solves various difficult
optimization problems, there are still difficulties in
keeping the balance between exploration and
exploitation when solving complex multimodal
problems. In order to achieve better performance, in
this study the problems of premature convergence
and search diversification were solved using a
modification of the LSHADE technique’s mutation
operator. Namely, the rank-based selective pressure
strategy (Jebari and Madiafi, 2013) was used for its
mutation strategy.
The developed technique was called the
“LSHADE Algorithm with Rank-Based Selective
Pressure Strategy” or LSHADE-RSP. Firstly, the
efficiency of LSHADE-RSP was examined on test
problems taken from the CEC 2018 competition on
real-parameter single objective optimization (Awad
et al., 2016). Experimental results demonstrated that
LSHADE-RSP performs better in comparison with
the alternative algorithms. Thus, LSHADE-RSP was
then used for solving the circular antenna array
design problem. It was established that the proposed
Akhmedova, S., Stanovov, V. and Semenkin, E.
LSHADE Algorithm with a Rank-based Selective Pressure Strategy for the Circular Antenna Array Design Problem.
DOI: 10.5220/0006852501490155
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 149-155
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
149

optimization algorithm shows competitive results in
comparison to different alternative algorithms.
In this paper, firstly a brief description of the DE
algorithm and consequently its modification
LSHADE is given. Then the proposed LSHADE-
RSP technique and its parameters settings and
adaptation are presented. In the next section, the
experimental results obtained by the new developed
LSHADE-RSP algorithm are demonstrated and
discussed. Finally, some conclusions are given in the
last section
2 DIFFERENTIAL EVOLUTION
Differential evolution (DE) is a global optimization
evolutionary meta-heuristic first introduced in 1997
for solving continuous optimization problems (Storn
and Price, 1997). It is one of the most effective
methods for complex high-dimensional problems,
and thus, it became one of the most popular and
often prize-winning optimization techniques.
The DE algorithm is simple in its
implementation due its compact structure.
Furthermore, it has fewer control parameters in
comparison to other evolutionary algorithms.
As with biology-inspired methods, the DE is a
population-based algorithm, and the population
contains a number of solutions. Thus, the DE starts
with a population of N candidate solutions, which
may be represented as x
i,j
, where i = 1, … , N
denotes individual’s index in the population and j =
1,…,D denotes a variable’s index (or coordinate).
The DE’s work process depends on the manipulation
and efficiency of three main operators: mutation,
crossover and selection.
One of the main features of a DE is the mutation
scheme, which was shown to automatically adapt to
the scale of the optimized function, improving the
performance. Therefore, the key idea of differential
evolution is in constructing a mutant vector using
the difference between two other vectors from the
current population.
The LSHADE algorithm (Tanabe and Fukunaga,
2014) is an extension of the SHADE algorithm
(Tanabe and Fukunaga, 2013), based on one of the
adaptive DE modifications JADE (Zhang and
Sanderson, 2009). LSHADE was first presented at
CEC 2014, and ranked as the winner-algorithm for
bound-constrained continuous optimization.
The original LSHADE algorithm uses the
DE/current-to-pbest/1 mutation scheme, shown
below:
   
jrjrjijbjij
xxFxxFxv
,2,1,,,

(1)
Here x
i,j
is the j-th coordinate of the i-th individual
x
i
, r1 and r2 are mutually random numbers
representing indexes of the individuals, v
j
is the so-
called mutant vector, which will be used in
crossover operation, and x
b
is randomly chosen as
one of the top 100p% individuals of the current
population with p from the range (0, 1]. The scaling
factor F is the parameter, usually in range [0, 1]. The
random index r2 is uniformly selected from the joint
set of the population and the external archive. The
external archive keeps parent individuals which
were replaced by new solutions.
The next step is the crossover, which is
performed for each individual x
i
as a calculation of
the trial vector t with the crossover rate Cr. The j-th
variable of the trial vector t is the same as the j-th
variable of the mutant vector d if a randomly
generated number in the range (0, 1) is smaller than
the crossover rate Cr or if j is equal to jrand, where
jrand is a randomly chosen index from 1 to D,
otherwise it is the same as the corresponding
variable of the individual x
i.
 








Crrandx
jrandjCrrandd
t
ji
j
j
,
1,0,
,
(2)
In the last formula, Cr is the control parameter of the
algorithm in the range [0, 1]. Cr = 1 means that there
is no crossover, and the trial vector is equal to the
mutant vector. The jrand index ensures that at least
one variable is taken from the newly generated
vector.
The selection step is performed after calculating
the fitness value of the trial vector. If the trial vector
is better than the i-th individual in the population,
than it is replaced by the trial vector.
In addition, it should be noted that the LSHADE
algorithm uses the Linear Population Size Reduction
(LPSR) scheme (Tanabe and Fukunaga, 2014),
which significantly boosts its performance. This
scheme decreases the number of individuals in the
population by deleting the least fit ones at every
generation.
3 PROPOSED APPROACH
In this section, the proposed algorithm LSHADE-
RSP is introduced. Firstly, a description of the
LSHADE-RSP is given and then the parameter
settings of the new algorithm are presented.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
150

3.1 LSHADE-RSP
In this section, the modification of the LSHADE
algorithm with a Rank-based Selective Pressure
mutation (LSAHDE-RSP) is described. The rank-
based mutation scheme, which was called current-
to-pbest/r, modifies the current-to-pbest/1 strategy
so that the second part containing two random
vectors receives selective pressure. More precisely,
r1 and r2 are selected according to the rank selection
typically used in genetic algorithms (Jebari and
Madiafi, 2013), with the ranks assigned as follows:
 
1 iNkRank
i
(3)
The largest rank is assigned to the individual with
the largest fitness, and the smallest rank to the least
fit, i.e. here i taken from the range [1, N] is the index
in a sorted fitness array. We are considering a
minimization problem, so larger fitness means a
smaller goal function value. In (3) k is the scaling
factor responsible for the greediness of the rank
selection. Thus, the probability that the individual i
will be selected is calculated as follows:



N
j
j
i
i
Rank
Rank
pr
1
(4)
The new mutation strategy, current-to-pbest/r, tends
to select individuals with larger fitness values more
often, although even the worst individual still has a
possibility of being selected for the mutation
operation. The motivation behind this is that rank-
based selection should boost the exploitation
capabilities of the mutation strategy without
significantly affecting the exploration. The resulting
mutation strategy uses the modification proposed for
the jSO algorithm (Brest et al., 2017), i.e. different
scaling factors for the first (Fw) and second part (F)
of the equation. Additionally, the scaling factor Fw
depends on the scaling factor F. At the beginning of
the search, while NFE<NFE
max
*0.2, Fw is set to be
equal to 0.7F. Next, while NFE<NFE
max
*0.4, Fw =
0.8F, and Fw = 1.2F for the rest of the search, where
NFE is the current number of function evaluations
and NFE
max
is the total available number of goal
function evaluations.
3.2 Parameter Settings
The two parameters adapted in LSHADE-RSP, are
the scaling factor F and crossover rate Cr. The
adaptation uses the same scheme as the original
LSHADE algorithm, but the initial values and some
constraints are taken from (Brest et al., 2017). The
scaling factor F for every mutation operation is
computed using a Cauchy distribution with location
parameter μF
r
and scale parameter 0.1, while Cr is
computed using a normal distribution with mean
μCr
r
and variance 0.1.
Moreover, µF
r
and µCr
r
are randomly chosen
from the memory M of successful parameter settings
(where the memory size is defined as H), and r is a
uniformly chosen random index. Initially all µF
r
are
set to 0.3, and µCr
r
are set to 0.8, and in addition to
this, one memory cell always keeps µF
r
and µCr
r
,
which are equal to 0.9. The values in µF
r
and µCr
r
in one memory cell are updated at the end of each
generation using the Lehmer mean, which takes into
consideration the fitness improvement.
While the memory is being updated, the new
values are calculated as the mean of the old F or Cr
value and the newly generated value.
For the first 0.6NFE
max
evaluations, (here NFE
max
denotes the maximum number of function
evaluations) the F value is constrained to be not
larger than 0.7 and not larger than 1.0 during the
remaining computation resource. The p value for the
current-to-pbest/r strategy, responsible for the
greediness of the search, is computed by the
following formula:
max
085.0085.0
NFE
NFE
p 
(5)
The idea behind increasing the number of best
individuals is to prevent premature convergence by
gradually decreasing the selective pressure as the
algorithm runs.
4 EXPERIMENTAL RESULTS
The efficiency of the new LSHADE-RSP was
investigated firstly on a set of benchmark problems
taken from the CEC 2018 competition on real-
parameter single objective optimization (Awad et
al., 2016). Then, a real-world engineering problem,
namely the circular antenna array design problem,
was solved by the proposed technique.
Subsequently, the experiments as well as the
obtained results are described.
4.1 CEC 2018 Benchmark Problems
Firstly, the algorithm performance was evaluated on
the CEC 2018 Competition on Single Objective Real
Parameter Numerical Optimization (Awad et al.,
2016). Therefore, the workability of the new
LSHADE Algorithm with a Rank-based Selective Pressure Strategy for the Circular Antenna Array Design Problem
151

algorithm was tested on 30 benchmark functions,
which were shifted and rotated. The functions in the
competition were tested for the corresponding
numbers of variables: 10 (10D), 30 (30D), 50 (50D)
and 100 (100D). The computational resource for all
algorithms and all dimensions was equal and was
calculated as 10000D.
In the performed experiments, the parameter k
for rank-based selection varied from 1 to 9, to be
more specific k was equal to 1, 2, 3, 5, 7 and 9 in
this study. However, only the results obtained with k
= 3 and 10 variables are presented here in Table 1.
Table 1: Algorithm results for 10D.
№
Worst
Best
Mean
Std. Dev
f
1
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
2
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
3
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
4
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
5
2.985e+00
0.000e+00
1.405e+00
7.155e-01
f
6
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
7
1.281e+01
1.067e+01
1.180e+01
5.087e-01
f
8
2.999e+00
0.000e+00
1.446e+00
6.647e-01
f
9
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
10
2.240e+02
2.339e-01
1.717e+01
4.244e+01
f
11
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
12
6.244e-01
0.000e+00
3.632e-01
2.054e-01
f
13
5.584e+00
0.000e+00
3.464e+00
2.303e+00
f
14
0.000e+00
0.000e+00
0.000e+00
0.000e+00
f
15
5.000e-01
8.096e-06
1.742e-01
2.067e-01
f
16
9.357e-01
4.094e-02
5.644e-01
2.172e-01
f
17
1.625e+00
7.174e-02
6.615e-01
4.071e-01
f
18
5.000e-01
3.935e-05
1.685e-01
2.003e-01
f
19
1.973e-02
0.000e+00
8.150e-03
9.504e-03
f
20
6.243e-01
3.122e-01
4.224e-01
1.492e-01
f
21
2.039e+02
1.000e+02
1.221e+02
4.210e+01
f
22
1.003e+02
1.000e+02
1.000e+02
6.716e-02
f
23
3.046e+02
3.000e+02
3.012e+02
1.533e+00
f
24
3.340e+02
1.000e+02
2.531e+02
1.082e+02
f
25
4.433e+02
3.977e+02
4.024e+02
1.350e+01
f
26
3.000e+02
3.000e+02
3.000e+02
0.000e+00
f
27
3.895e+02
3.890e+02
3.894e+02
1.762e-01
f
28
6.118e+02
3.000e+02
3.061e+02
4.323e+01
f
29
2.450e+02
2.267e+02
2.343e+02
3.406e+00
f
30
8.176e+05
3.945e+02
1.642e+04
1.133e+05
During the algorithm run, the error was
calculated as the difference between the current best
solution f(x) and the global optimum f(x*). If this
difference was less than 10
–8
, then it was considered
to be small enough and taken as zero. Table 1
contains the worst, best, mean and standard
deviation values for every function calculated over
51 program runs for 30 variables.
The performance of the LSHADE-RSP
algorithm was compared to the other methods
participating in the CEC 2017 competition on single
objective bound constrained optimization, including
the original LSHADE algorithm. This was possible
due to the fact that the test functions were the same
for the CEC 2017 and the CEC 2018 competitions.
Therefore, all methods had the same amount of
computational resources and runs. To compare
different methods, the Wilcoxon’s rank sum test
with p = 0.05 was used. For comparison, the jSO
(Brest et al., 2017), the EBOwithCMAR (Kumar et
al., 2017), and the LSHADE-SPACMA (Mohamed
et al., 2017) algorithms were chosen.
Table 2: Comparison with other methods using statistical
tests.
D
EBOwith
CMAR
jSO
LSHADE-
SPACMA
LSHADE-
RSP
(k = 0)
10
8+/12=/10-
2-
2+/26=/2-
0
12+/14=/4-
8+
2+/25=/3-
1-
30
10+/8=/12-
2-
7+/19=/4-
3+
12+/11=/7-
5+
8+/21=/1-
7+
50
13+/7=/10-
3+
13+/13=/4-
9+
13+/12=/5-
8+
10+/19=/1-
9+
100
13+/8=/9-
4+
16+/9=/5-
11+
8+/6=/16-
8-
15+/15=/0-
15
The numbers in the table represent the number of
wins (+), losses (-) and equal results (=) when
comparing LSHADE-RSP (k = 3) with other
methods. The obtained results demonstrate that the
proposed approach outperformed most of the
alternative optimization techniques, including jSO,
and was outperformed only by the winners of the
CEC 2017 competition for some dimensions.
Furthermore, LSHADE-RSP is more successful in
comparison to other optimization techniques when
the number of variables increases. Thus, it can be
concluded that the selective pressure gives an
improvement and the workability and usefulness of
the new LSHADE-RSP algorithm were established.
4.2 Circular Antenna Array Design
Problem
As was mentioned before, the circular shaped
antenna arrays find various applications in sonar,
radar, mobile and other communication systems. Let
us consider N antenna elements spaced on a circle of
radius r in the x-y plane (Das and Suganthan, 2010).
The antenna elements are said to constitute a circular
antenna array. The array factor for the circular array
is written as follows:
     



N
n
nn
krIAF
1
21
coscosexp 
(6)
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
152

where
n
ang
 
1
,
n
ang
 
02
,
Ndkr 
. In this
formula, the following denotations were used:

 
12  n
n
ang

is the angular position of the n-th
element on the x-y plane;
 k is the wave number;
 d is the angular spacing between elements;
 r is the radius of the circle defined by the antenna
array;

0

is the direction of maximum radiation;


is the angle of incidence of the plane wave;
 I
n
is the current excitation;
 β
n
is the phase excitation of the n-th element.
The current and phase excitations of the antenna
elements should be varied in order to suppress side-
lobes, minimize beam width and achieve null control
at desired directions. In addition, a symmetrical
excitation of the circular antenna array was
considered due to (Das and Suganthan, 2010). Thus,
the objective function is taken as follows:
 
 
 
 




num
k
kdes
l
sll
IAR
IDIR
IAR
IAR
OF
1
00
0
0max
0
,,,
,,
1
,,,
,,,




(7)
The first component attempts to suppress the side-
lobes.
sll

is the angle at which a maximum side-
lobe level is attained. The second component
attempts to maximize the directivity of the array
pattern. Nowadays, directivity has become a very
useful figure of merit for comparing array patterns.
The third component strives to drive the maxima of
the array pattern close to the desired maxima
des

.
The fourth component penalizes the objective
function if sufficient null control is not achieved.
num is the number of null control directions and
k

specifies the k-th null control direction.
The following parameters were also used for this
study:
 the number of elements in circular array was
equal to 12;
 the input string can be any string within the
bounds;
 null = [50,120] in radians (no null control);
 d is the angular spacing between elements;

180
des

;
 the distance was equal to 0.5.
The first six optimized variables for this problem
are in the range [0.2, 1], while the second six are in
the range [-180,180], and the problem has only
bound constraints. For our experiments, we have set
the maximum number of function evaluations equal
to 150000, as stated in (Das and Suganthan, 2010),
allowing the results to be compared to those
achieved by other researchers.
To show the advantage of using selective
pressure in the LSHADE-RSP algorithm, we have
performed several tests, first for the algorithm
without selective pressure (k=0), and next for
different coefficients k. Table 3 contains the best,
average and standard deviation of the results. There
were 25 runs performed for each algorithm
configuration.
Table 3: Results of LSHADE-RSP for the Circular
Antenna Array Design Problem.
RSP
Mean
Best
Std. Dev
Reliability
k = 0
-21.6376
-21.6445
0.03214
0.00
k = 1
-21.6675
-21.8425
0.08624
0.16
k = 2
-21.6519
-21.8424
0.03889
0.04
k = 3
-21.6600
-21.8425
0.05380
0.08
k = 5
-21.6773
-21.8425
0.08855
0.20
k = 7
-21.6599
-21.8425
0.05383
0.08
k = 9
-21.6996
-21.8426
0.08908
0.28
The reliability of the algorithm is according to
the value of the best known solution, found by
LSHADE-RSP, so if at the end of the search the
found value was lower than -21.8, the run was
considered as successful, and the ratio of the number
of successful runs to the total number of runs was a
reliability estimation. The algorithm with the highest
selective pressure coefficient, k = 9, achieved the
best results in terms of the mean value and best
found value. However, the mutation strategy without
selective pressure had a lower standard deviation. It
should be mentioned that applying even small
selective pressure with k = 1 allows the algorithm to
find very good solutions, whose goal function is
close to -21.8425, while the algorithm without
selective pressure could not achieve this goal
function value.
In Figure 1, the graphs of the average goal
function values achieved at different stages of the
search process, namely, 0.01, 0.1, 0.2, …, 1.0 are
presented. The goal function values are shifted up by
21.9, and the graphs are built in logarithmic scale so
that the difference can be seen more easily.
From the graphs, it can be seen that most of the
variants of the algorithm achieve the best solution at
around 0.5 of the available computational resource,
LSHADE Algorithm with a Rank-based Selective Pressure Strategy for the Circular Antenna Array Design Problem
153

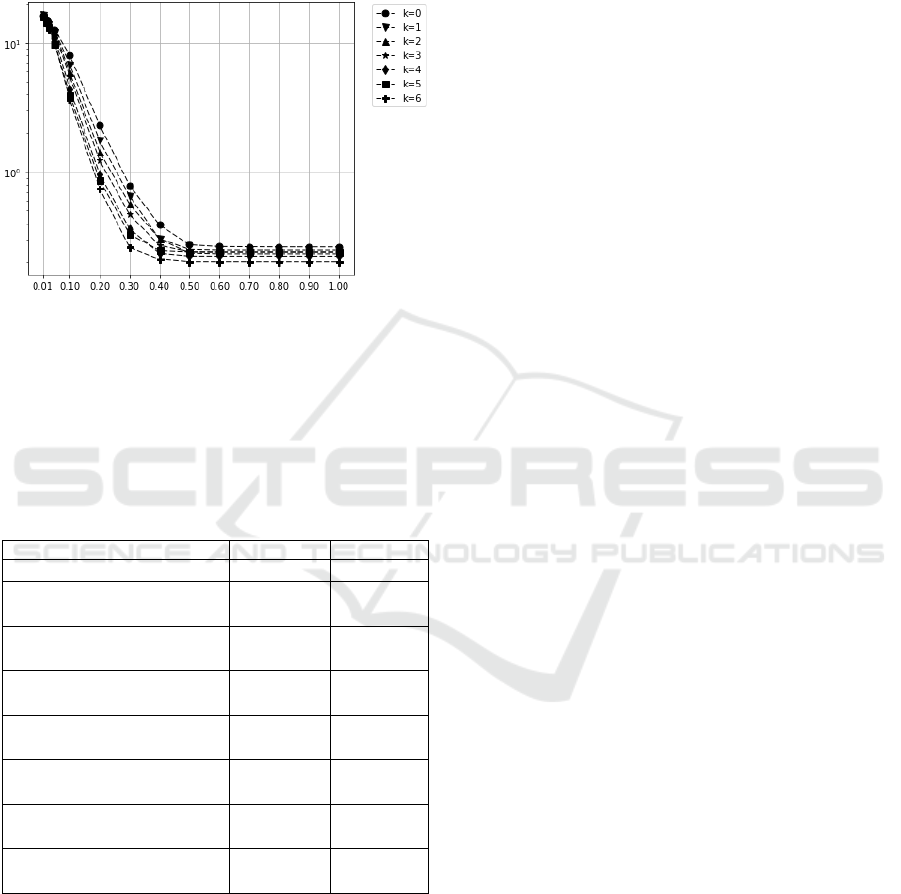
i.e. 75000 function calculations. However,
algorithms with higher selective pressure tend to
converge faster at the beginning of the search.
Moreover, as the selective pressure grows,
LSHADE-RSP is capable of finding better solutions,
i.e. it increases its search capabilities.
Figure 1: Comparison of the effect of different selective
pressures on the convergence speed.
The comparison to other algorithms used to solve
the same problem is presented in Table 4. The
amount of computational resource was the same for
all methods.
Table 4: Comparison of LSHADE-RSP with other
methods for the Circular Antenna Array Design Problem.
Algorithm
Mean
Best
LSHADE-RSP
-21.6996
-21.8426
OXCoDE
(Li and Yin, 2011)
-21.591
-21.865
WI-DE
(Haider et al, 2011)
-21,70
-21.80
GA-MPC
(Elsayed et al., 2011a)
-21.702
-21.8425
ED-DE
(Wang et al., 2011)
-21.421
-21.832
Adap.DE171
(Asafuddoula et al., 2011)
-20.958
-21.808
EA-DE-MA
(Singh et al., 2011)
-21.2554
-21.7956
SAMODE
(Elsayed et al., 2011b)
-21.6589
-21.8216
The comparison shows that although LSHADE-
RSP is outperformed in terms of the best value by
one method, and in terms of the mean value by
another, the difference in the performance is
insignificant. Considering both mean and best
values, the closest method is GA-MPC, which has
almost the same best value found, and similar
average performance.
5 CONCLUSIONS
In this paper, the LSHADE-RSP algorithm was
presented, which is a modification of Linear
population size reduction Success History based
Adaptive Differential Evolution with Rank-based
Selective Pressure. This algorithm implements a
number of various parameter adaptions, but most
importantly, it uses the modified mutation strategy,
current-to-pbest-w/r, which allows the convergence
speed of the algorithm to be improved.
The problem of designing the Circular Antenna
Array was solved by LSHADE-RSP with different
selective pressure parameters, and it was observed
that higher selective pressure results in better results
in terms of both mean and best values. The achieved
results are comparable to the best known up-to-date
results for this problem.
ACKNOWLEDGEMENTS
Research is performed with the support of the
Ministry of Education and Science of the Russian
Federation within State Assignment project №
2.1680.2017/ПЧ.
REFERENCES
Asafuddoula, Md., Ray, T., Sarker, R., "An Adaptive
Differential Evolution Algorithm and its Performance
on Real World Optimization Problems", in Proc.
Congress on Evolutionary Computation, pp. 1057 -
1062, New Orleans, June 2011.
Akcakaya, M., Nehorai, A., 2011. Adaptive MIMO Radar
Design and Detection in Compound-Gaussian Clutter,
IEEE Transactions on Aerospace and Electronic
Systems. Vol. 47, No. 3.
Awad, N.H., Ali, M.Z., Liang, J.J., Qu, B.Y., Suganthan,
P.N., 2016. Problem Definitions and Evaluation
Criteria for the CEC 2017 Special Session and
Competition on Single Objective Bound Constrained
Real-Parameter Numerical Optimization. Technical
report, Nanyang Technological University, Singapore.
Bellettini, A., Pinto, M.A., 2002. Theoretical Accuracy of
Synthetic Aperture Sonar Micronavigation Using a
Displaced Phase-Center Antenna, IEEE J. Oceanic
Eng. Vol. 27, No. 4.
Brest, J., Maucec, M.S., Boskovic, B., 2017. Single
Objective Real-Parameter Optimization Algorithm
jSO. In IEEE Congress on Evolutionary Computation.
IEEE Publications.
Civicioglu, P., 2013. Circular Antenna Array Design by
Using Evolutionary Search Algorithms, Progress in
Electromagnetics Research B. Vol. 54.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
154

Das, S., Suganthan, P.N., 2010. Problem Definitions and
Evaluation Criteria for CEC 2011 Competition on
Testing Evolutionary Algorithms on Real World
Optimization Problems. Technical report, Jadavpur
University, India; Nanyang Technological University,
Singapore.
Dessouky, M., Sharshar, H., Albagory, Y., 2006. A Novel
Tapered Beam Forming Window for Uniform
Concentric Circular Arrays, Journal of
Electromagnetic Waves and Applications. Vol. 20, No.
14.
Elsayed, S., Sarker, S., Essam, D., "GA with a New Multi-
Parent Crossover for Solving IEEE-CEC2011
Competition Problems", in Proc. Congress on
Evolutionary Computation, pp. 1034 - 1040, New
Orleans, June 2011.
Elsayed, S., Sarker, S., Essam, D., "Differential Evolution
with Multiple Strategies for Solving CEC2011 Real-
world Numerical Optimization Problems", in Proc.
Congress on Evolutionary Computation, pp. 1041 -
1048, New Orleans, June 2011.
Jebari, K., Madiafi, M., 2013. Selection Methods for
Genetic Algorithms, International Journal of
Emerging Sciences. Vol. 3(4).
Haider, U., Das ,S., Maity, D., Abraham, A., Dasgupta, P.,
"Self Adaptive Cluster Based and Weed Inspired
Differential Evolution Algorithm For Real World
Optimization," in Proc. Congress on Evolutionary
Computation, pp. 750 - 756, New Orleans, June 2011.
Kumar, A., Misra, R.K., Singh, D., “Improving the local
search capability of Effective Butterfly Optimizer
using Covariance Matrix Adapted Retreat Phase”,
Proceedings of the IEEE Congress on Evolutionary
Computation, pp. 1835‒1842, 2017.
Li X., Yin M., "Enhancing the Exploration Ability of
Composite Differential Evolution through Orthogonal
Crossover", in Proc. Congress on Evolutionary
Computation, pp. 153 - 177, New Orleans, June 2011.
Mohamed, A.W., Hadi. A.A., Fattouh, A.M., Jambi, K.M.,
“LSHADE with Semi-Parameter Adaptation Hybrid
with CMA-ES for Solving CEC 2017 Benchmark
Problems”, Proceedings of the IEEE Congress on
Evolutionary Computation, pp. 145‒152, 2017.
Singh, H.K., Ray, T., "Performance of a Hybrid EA-DE-
Memetic Algorithm on CEC 2011 Real World
Optimization Problems", in Proc. Congress on
Evolutionary Computation, pp. 1322 - 1326, New
Orleans, June 2011.
Storn, R., Price, K., 1997. Differential Evolution – a
Simple and Efficient Heuristic for Global
Optimization over Continuous Spaces, Journal of
Global Optimization. Vol. 11(4).
Tanabe, R., Fukunaga, A., 2013. Success-History Based
Parameter Adaptation for Differential Evolution. In
IEEE Congress on Evolutionary Computation. IEEE
Publications.
Tanabe, R., Fukunaga, A., 2014. Improving the search
performance of SHADE using linear population size
reduction. In IEEE Congress on Evolutionary
Computation. IEEE Publications.
Wang, Y., Li, B., Zhang, K., "Estimation of Distribution
and Differential Evolution Cooperation for Real-world
Numerical Optimization Problems", in Proc. Congress
on Evolutionary Computation, pp. 1315 - 1321, New
Orleans, June 2011.
Zaker, R., Ghobadi, C.H., Nourinia, J., 2007. A Modified
Microstrip-Fed Two-Step Tapered Monopole Antenna
for UWB and WLAN Applications, Progress in
Electromagnetics Research. Vol. 77.
Zhang, J., Sanderson, A.C., 2009. JADE: Adaptive
differential evolution with optional external archive,
IEEE Transactions on Evolutionary Computation.
Vol. 13, No. 5.
LSHADE Algorithm with a Rank-based Selective Pressure Strategy for the Circular Antenna Array Design Problem
155