Dynamical Investigation of Crawling Motion System based on a

Multistable Tensegrity Structure

Philipp Schorr

, Valter B

ohm

, Lena Zentner

and Klaus Zimmermann

Technical Mechanics Group, Department of Mechanical Engineering, Technical University of Ilmenau,

Max-Planck-Ring 12, 98693 Ilmenau, Germany

Technical Mechanics, Department of Mechanical Engineering, Ostbayerische Technische Hochschule Regensburg,

Galgenbergstr. 30, 93053 Regensburg, Germany

Compliant Systems Group, Department of Mechanical Engineering, Technical University of Ilmenau,

Max-Planck-Ring 12, 98693 Ilmenau, Germany

Keywords:

Worm-like Motion, Multistable Tensegrity Structure.

Abstract:

The basic idea of this article is the utilization of the multistable character of a compliant tensegrity struc-

ture to control the direction of motion of a crawling motion system. A crawling motion system basing on a

two-dimensional tensegrity structure with multiple stable equilibrium states is considered. This system is in

contact with a horizontal plane due to gravity. For a selected harmonic actuation of the system small oscillati-

ons around the given equilibrium state of the tensegrity structure occur and the corresponding uniaxial motion

of the system is evaluated. A change of the equilibrium state of the tensegrity structure yields to novel con-

ﬁguration of the entire system. Moreover, the motion behavior of the novel conﬁguration is totally different

although the actuation strategy is not varied. In particular, the direction of motion changes. Therefore, this

approach enables a uniaxial bidirectional crawling motion with a controllable direction of motion using only

one actuator with a selected excitation frequency.

1 INTRODUCTION

The increasing signiﬁcance of mobile robotics in en-

gineering applications requires a continuous impro-

vement of the current systems respective to the ope-

rating sensors and actuators. Moreover, as conse-

quence of the advanced demands on those systems

even the investigation of novel motion principles is

necessary. For example, applications like the mini-

mal invasive surgery allow only an extremely limited

working space which prevent the use of conventional

motion systems basing on wheels or legs. Therefore,

innovative motion principles basing on the direct in-

teraction to the environment are required.

A promising approach is the investigation of cra-

wling motion systems. This principle is copied from

the motion behavior of earth worms observed in the

nature. The peristaltic motion bases on the alternating

shortening and lengthening of several body segments.

Moreover, the presence of spike which are added at

the body of the earth worm are essential for the mo-

tion. Hence, a forward or backward motion occurs

depending on the orientation of these spikes.

Beside the biological aspects of the worm-like

motion groups of researchers are also interested in

this motion principle from the mechanical point of

view. In (Steigenberger and Behn, 2012), (Zimmer-

mann et al., 2009a) and (Zimmermann et al., 2013)

the earth worm is modeled by a ﬁnite number of rigid

body which are connected by kinematic drives. The

mechanical behavior of the mentioned spikes is mo-

deled by anisotropic friction properties and the occur-

ring motion behavior is investigated. But as conse-

quence of the anisotropy of the friction properties a

preferred direction of motion occurs and the use of

the opposite direction of motion is not possible for

a harmonic actuation. In (Bolotnik et al., 2006) and

(Zimmermann et al., 2009b) the actuation of an addi-

tional internal mass is investigated in order to control

the direction of motion for isotropic friction proper-

ties. Moreover, in (Fang and Xu, 2011) and (Fang

and Xu, 2012) the actuation by the kinematic drive is

varied to maximize the steady state velocity. Howe-

ver, for isotropic friction properties advanced requi-

rements are demanded on the actuator of the system.

Hence, the current state of the art not satisfying.

The use of compliant tensegrity structures in mo-

bile robotics enables advantages like high weight-to-

122

Schorr, P., Böhm, V., Zentner, L. and Zimmermann, K.

Dynamical Investigation of Crawling Motion System based on a Multistable Tensegrity Structure.

DOI: 10.5220/0006852701220130

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 122-130

ISBN: 978-989-758-321-6

load ratio, shock resistance and adjustable dynamical

behavior. Therefore, those structures are considered

for the application in motion systems. In (Sabelhaus

et al., 2015), (Kim et al., 2016), (Hustig-Schultz et al.,

2016), (Liu et al., 2016) and (Chen et al., 2017) the ca-

pability of shape change is used to realize successive

tilting sequences which yield to a controllable motion.

The shape change is realized by the manipulation of

mechanical parameter values. Furthermore, the use

of tensegrity structures in vibration driven motion sy-

stems is investigated in (Rieffel et al., 2010), (B

ohm

and Zimmermann, 2013), (B

ohm et al., 2013), (Kha-

zanov et al., 2014) and (B

ohm et al., 2015). The dyn-

amics of the tensegrity structure can be inﬂuenced by

varying the prestress states. This is also realized by

a variation of the mechanical properties. In (Schorr

et al., 2017) a vibration driven motion system based

on a multistable tensegrity structure is investigated.

The dynamical properties are varied to discrete va-

lues by changing the equilibrium state. In (Tietz et al.,

2013) a crawling motion system is realized by a ten-

segrity structure consisting of several segments con-

nected in series. The actuation strategy is investiga-

ted for different evironmental conditions. However,

because of number of segments many actuators are

required and a enormous control effort is necessary.

In this article a crawling motion system basing on

a two-dimensional multistable tensegrity structure in-

spired by (B

ohm et al., 2017) and (Sumi et al., 2017)

is considered. The system is in contact to a horizon-

tal plane due to gravity. A selected harmonic actu-

ation of the system yields to a crawling motion. As

consequence of a change of the equilibrium state the

conﬁguration of the entire systems is modiﬁed (con-

tact points are changing as consequence of a tilting

sequence). Therefore, totally different motion cha-

racteristics occur for an identical actuation strategy.

In particular, the direction of motion can be control-

led by changing the equilibrium state of the tensegrity

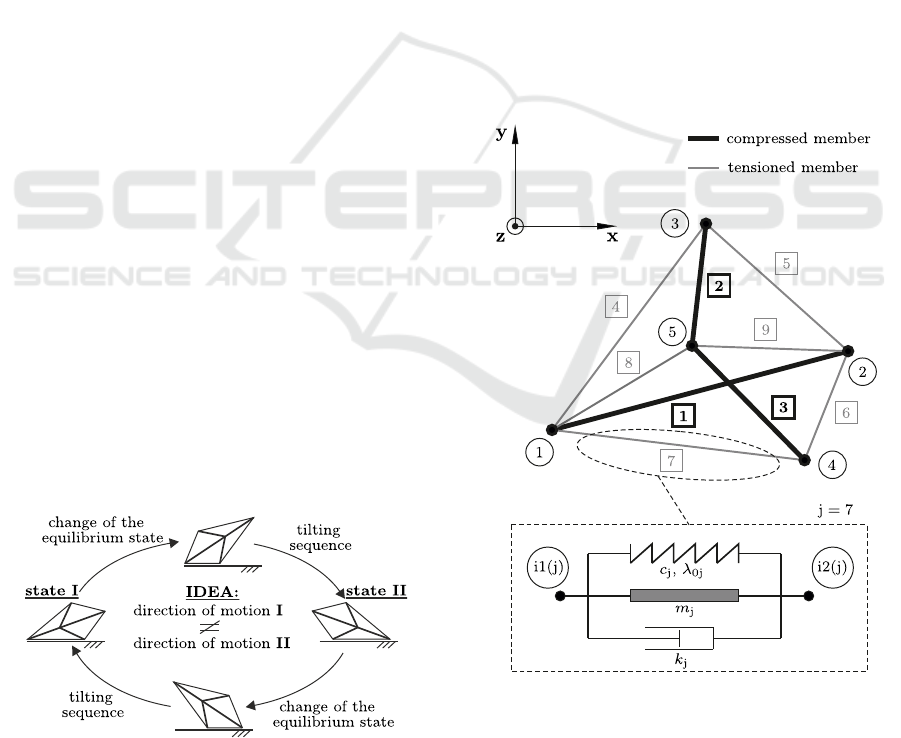
structure. This idea is illustrated in Figure 1.

Figure 1: Supposed behavior of the motion system.

Thus, this approach enables a uniaxial bidirecti-

onal crawling motion with only one actuator using a

selected actuation frequency. Therefore, the presence

of anisotropic friction properties and the application

of high-end actuators is not necessary anymore.

2 MECHANICAL MODEL OF

THE MOTION SYSTEM

2.1 Dynamics of the Multistable

Tensegrity Structure

The tensegrity structure shown in Figure 2 is con-

sidered. This structure consists of 9 members

(j = 1, 2,.. .,9) which are connected in 5 nodes

(i = 1, 2,.. .,5). These nodes are modeled as fricti-

onless revolute joints. With regard to the occurring

stress at the equilibrium state the members are divided

in compressed members and tensioned members. For

the given structural topology, the elements j = 1, 2,3

are classiﬁed as compressed members. The members

j = 4, 5,6,7, 8,9 are declared as tensioned members.

Figure 2: Two-dimensional multistable tensegrity structure

and the mechanical model of a single member.

The current conﬁguration of the tensegrity struc-

ture is deﬁned by the position of the nodes i. These

position are evaluated respective to the Cartesian in-

ertial coordinate system {x,y,z} to ~r

= (x

)

Dynamical Investigation of Crawling Motion System based on a Multistable Tensegrity Structure

123

Furthermore, the structure is supposed to be two-

dimensional in the x-y-plane. Therefore, the z-

component of the node positions is identical to zero

≡ 0). This yields to a degree of freedom of 10

for the considered tensegrity structure. As generali-

zed coordinates the components of the node positions

and y

are selected. These parameters are combined

in the vector ~q = (x

,. .., x

)

In order to describe the dynamics of the tensegrity

structure all acting loads have to be speciﬁed. The-

refore, the forces as consequence of the deformations

of the members have to be taken into account. The

deformation behavior of a single member is modeled

with a linear spring which is described by the accor-

ding stiffness c

and its initial length λ

0,j

. The cor-

responding energy dissipation as consequence of the

material damping properties is given by a linear dam-

per with the damping coefﬁcient k

. Furthermore, the

inertia of each element has to be taken into account.

The element j with the mass m

is modeled by a linear

link element known from the ﬁnite element method.

Therefore, the inertia is given by the according mass

matrix. For the following investigations the mass of

the tensioned members is assumed to be neglectable

= 0 for j = 4,5, 6,7,9.) The resulting mechanical

model of a single member of the tensegrity structure

is given by a parallel arrangement of the mentioned

components (see Figure 2). The deformation of the

member j is given by the position of the node i1(j) at

its beginning and the node i2(j) at its end. The corre-

sponding spring force

c,j

and the damping force

k,j

are formulated in (1) and (2).

c,j

= −c

| − λ

0,j

)

=~r

i2(j)

−~r

i1(j)

(1)

k,j

= −k

i2(j)

−

i1(j)

(2)

With regard to the topology of the tensegrity struc-

ture these forces are combined to the vectors

C(~q) and

~q,~q). This approach is shown in (3) and (4).

C(~q) = −







−

c,1

−

c,4

−

c,7

−

c,8

c,1

−

c,5

−

c,6

−

c,9

−

c,2

c,4

c,5

−

c,3

c,6

c,7

c,2

c,3

c,8

c,9







(3)

~q,~q) = −







−

k,1

−

k,4

−

k,7

−

k,8

k,1

−

k,5

−

k,6

−

k,9

−

k,2

k,4

k,5

−

k,3

k,6

k,7

k,2

k,3

k,8

k,9







(4)

The inertia of the tensegrity structure is taken into ac-

count by the mass matrix M. Hence, the nonlinear sy-

stem of equations of motion shown in (5) results.

M ¨q +

~q,~q) +

C(~q) =

0 (5)

For the following investigations the parameter values

listed in Table 1 are used.

Table 1: Topology and selected parameter values of the ten-

segrity structure.

El. Nodes λ

0,j

j i1 − i2 [m] [N/m] [Ns/m] [kg]

1 1 − 2 0.10 10

0.2 0.1

2 3 − 5 0.02 10

0.2 0.02

3 4 − 5 0.02 10

0.2 0.02

4 1 − 3 0.02 3000 0.2 0

5 2 − 3 0.02 3000 0.2 0

6 2 − 4 0.02 3000 0.2 0

7 1 − 4 0.02 3000 0.2 0

8 1 − 5 0.01 10000 0.2 0

9 2 − 5 0.01 10000 0.2 0

2.2 Modeling of the Crawling Motion

System

In order to realize a crawling motion an ac-

tuation of the tensegrity structure is required.

For the following investigations free length of

the tensioned member 8 is manipulated by a

harmonic excitation function s(t) = a sin(2π ft)

(a - amplitude of excitation, f - actuation frequency).

The corresponding actuation force is given in (6).

(t) = (c

s(t) + k

˙s(t))

(6)

The multistable tensegrity structure is in contact with

a horizontal plane due to gravity (~g = −g

). There-

fore, beside the actuation force the equations of mo-

tion have to be completed by the gravitational forces

as well as the contact forces. Moreover, occurring

friction effects at the contact points have to be taken

into account.

The gravitational forces are divided into compo-

nents acting on the nodes i. The resulting force vector

G is deﬁned in (7).

G = −

(0,m

,0, m

+ m

)

(7)

The contact interface between the nodes i and the

ground is represented by isolated points. The defor-

mation of the ground at those contact points is mo-

delled by a parallel arrangement of a linear damper

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

124

= 100 Ns/m and a linear spring c

= 10

N/m.

The deformation of the contact node of the tensegrity

structure is assumed to be neglectable. The corre-

sponding contact force at the node i is given by the

vector

contact,i

= (F

F,i

N,i

)

. The component F

F,i

describes the occurring friction forces at the contact

node i and F

N,i

the acting contact force. The deﬁni-

tion of the component F

N,i

is given in (8).

N,i











0 if y

≥ 0

−c

if y

< 0 and

≥ 0

−c

− k

else

(8)

Occurring friction at the contact nodes are mo-

deled by COULOMB’S LAW OF FRICTION. To mo-

del stiction effects like stick-slip despite of the nu-

merical accuracy the friction model is expanded by

KARNOPP’S METHOD. Therefore, a parameter δ =

−4

m/s is introduced. The resulting friction model

is given in (2.2). The static and the dynamic friction

coefﬁcients are given by the parameters µ

and µ. The

parameter F

res,i

describes the sum of all acting forces

except the friction force on the node i along the x-axis.

F,i











−µF

N,i

sign(

) if |

| ≥ δ

−µF

N,i

sign(F

res,i

) if |

| < δ

and |F

res,i

| ≥ µ

N,i

−F

res,i

else

(9)

All the mentioned components are combined to the

generalized force vector

~q,~q,t). Thus, the nonli-

near system of equation of motion of the entire craw-

ling motion system formulated in (10) results.

M ¨q +

~q,~q) +

C(~q) =

~q,~q,t) (10)

with

~q,~q,t) =

G +







contact,1

contact,2

contact,3

contact,4

contact,5













−







The resulting mechanical model of the investigated

crawling motion system is illustrated in Figure 3.

Figure 3: Mechanical model of the crawling motion system

- actuation of tensioned member 8 (two-head arrow), nodes

1 and 4 in contact with ground.

3 SIMULATION OF THE

CRAWLING MOTION

3.1 Initial Conditions of the Crawling

Motion System

The working principle of the crawling motion system

requires two equilibrium states I and II as shown

in Figure 1. These conﬁgurations have to differ re-

spective to the corresponding contact nodes. For

the determination of the equilibrium states the non-

actuated motion system (

≡

0) is considered for

~q = ~q

and

~q =

0. Basing on (10) these conditions

yield to a nonlinear system of equations formulated

in (11).

C(~q

) =

0,~q

) (11)

However, because of the piecewise smooth con-

tact and friction modelling conventional methods (e.g.

NEWTON-RAPHSON) cannot be applied to calculate

the conﬁguration ~q

and additional numerical effort

is required instead. Therefore, at ﬁrst the interaction

between the contact nodes and the ground is approxi-

mated by a static support.

Inspired by Figure 1, the nodes 1 and 4 are as-

sumed to be in contact with the ground. The con-

tact is simpliﬁed by the supports A and B (see. Fi-

gure 4). The according support reaction are deﬁned

A = (A

)

and

B = (0,B

)

. This approxima-

tion yields to smooth nonlinear system of equations

given in (12) which can be solved numerically.

C(~q

) =

G + (

(12)

Each solution of (12) has to be checked additio-

nally (y

≥ 0, y

≥ 0). Furthermore, only

stable equilibrium conﬁgurations are relevant for the

following investigation. Therefore, the Hessian of the

potential energy is considered. The potential energy

is given in (13).

E =

∑

j=1

|−λ

0,j

)

i1(j)

+~r

i2(j)





(13)

Figure 4: Mechanical model of the crawling motion system

for the determination of the relevant stable equilibrium sta-

tes I and II.

Dynamical Investigation of Crawling Motion System based on a Multistable Tensegrity Structure

125

The Hessian of the energy term is evaluated re-

spective to the generalized coordinates ~q. An equili-

brium state is deﬁned as stable if all eigenvalues of the

Hessian are positive. Otherwise, the state is declared

as instable and is not taken into account anymore.

This approach yields to two stable conﬁgurati-

ons of the multistable tensegrity structure (see Fi-

gure 5a)). However, ﬁnally the support reactions have

to be checked. The y-components of those reactions

have to be positive. Otherwise, the contact between

the node and the ground get lost and a tilting sequence

is initiated. Therefore, and in order to take the given

contact stiffness into account, a dynamical relaxation

of both equilibrium conﬁgurations of the system using

(10) with a = 0 and µ

= µ = 0 is evaluated. The ﬁnal

state ~q after the compliance of the break-off-criteria

~q| < 10

−8

m/s and |

~q| < 10

−8

m/s

) is declared as

. Indeed, beside the resulting stable equilibrium

state I as consequence of a tilting sequence the stable

equilibrium state II (contact nodes 2 and 4) occurs.

This issue conﬁrmes the idea that changing the equili-

brium state of the tensegrity structure initiates a tilting

sequence of the entire motion system. The resulting

equilibrium conﬁgurations I and II of the motion sy-

stem are illustrated in Figure 5b).

Dynamical

Relaxation

Dynamical

Relaxation

! Tilting

Figure 5: Stable equilibrium states of multistable tensegrity

structure - a) as result of the mechanical model shown in

Figure 4, b) as result of dynamical relaxation.

This approach was repeated starting from (12) for

other combinations of contact nodes (2 and 4, 1 and

3, 2 and 3). Because of the symmetric topology of

the structure and the selected parameter values equi-

valent results occur. As consequence of the approxi-

mation by static supports two valid stable equilibrium

states are determined. Evaluating a dynamical relax-

ation one of these states yields to a tilting sequence

and the occuring ﬁnal states ~q

are equivalent to the

states I and II shown in Figure 5b). Without loss of

generality, for the following investigations the state I

corresponds to the contact nodes 1 and 4 (state II cor-

responds to the contact nodes 2 and 4).

3.2 Simulation of the Motion Behavior

The nonlinear system of equations of motion of the

entire motion system is solved numerically using a

RUNGE-KUTTA-METHOD 4

ORDER with an appro-

priate step size (∆t = 10

−4

s). As initial condition the

conﬁguration I or II is assumed an the entire system

is supposed to be at rest (

~q(t = 0) =

0). The motion

of the system is simulated for 1100 actuation periods.

However, only the steady state solution which is as-

sumed after 1000 actuation periods is evaluated. As

amplitude the value a = 10

−4

m is chosen. Moreo-

ver, the motion is evaluated for different friction pro-

perties. The motion of the system is illustrated ex-

emplarily on Figure 6 to present the qualitative mo-

tion behavior. Moreover, for the considered actuation

frequency and friction properties the different initial

conditions yield to opposite directions of motion.

t [s]

[m]

10 10.2 10.4 10.6 10.8 11

970

980

990

t [s]

[m]

10 10.2 10.4 10.6 10.8 11

-1000

-990

-980

Figure 6: Motion behavior for f = 10 Hz, µ

= µ = 0.1 and

- a) state I as initial condition, b) state II as initial condition.

However, as consequence of the transient dyn-

amics a change into another equilibrium state III

occurs for several actuation frequencies. For this state

a collision between the compressed member 2 and 3

appears. Moreover, a reverse change into the state I

or II seems to be difﬁcult because of the low potential

energy at this critical state. Therefore, this conﬁgura-

tion should be avoided. This conﬁguration is shown

in Figure 7 with the nodes 1 and 5 as contact points.

Because of the symmetry the same conﬁguration will

occur with the contact nodes 2 and 5.

Figure 7: Critical equilibrium state III of the crawling mo-

tion system with nodes 1 and 5 as contact nodes.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

126

As indicator of the motion behavior the steady

state velocity v of the system is evaluated. This pa-

rameter can be calculated considering the velocity of

the node i (i = 1, 2,3,4, 5) for an actuation period du-

ring the steady state motion. This formula is given in

(14). The parameter t

is an arbitrary time instance.

v = f

+1/ f

(t)dt (14)

The results of the steady state velocity for the equili-

brium states I and II as initial condition with different

friction properties are illustrated in Figure 8. The grey

areas represent the frequency ranges which lead to a

change into the critical equilibrium state III as conse-

quence of the transient dynamics.

f [Hz]

v [mm=s]

0 2 4 6 8 10 12 14 16 18 20

-20

-10

initial state: I initial state: II

f [Hz]

v [mm=s]

0 2 4 6 8 10 12 14 16 18 20

-30

-20

-10

f [Hz]

v [mm=s]

0 2 4 6 8 10 12 14 16 18 20

-20

-10

Figure 8: Steady state velocity of the crawling motion

system with the different equilibrium conﬁgurations as

initial conditions and - a) µ

= µ = 0.1, b) µ

= µ = 0.2,

c) µ

= µ = 0.5.

These results show that for low actuation frequen-

cies ( f < 8 Hz) the motion can be considered as in-

efﬁcient (v < 1 mm/s). For the following frequency

range (8 Hz < f < 9.8 Hz) the critical conﬁguration

occurs as result of the transient dynamics. However,

for actuation frequencies above 10 Hz the results con-

ﬁrm the basic idea of this approach. A motion of the

entire system appears as consequence of small oscil-

lations around the stable state I or II. Indeed, the di-

rection of motion can be varied by changing the equi-

librium conﬁguration at the initial state. For the inves-

tigated parameters the use of state I as initial condi-

tion yields to a positive motion (v > 0 mm/s). Assu-

ming the state II as initial condition a negative motion

(v < 0 mm/s) occurs. Therefore, the results conﬁrm

that the multistability of the tensegrity structure can

be utilized to control the direction of motion of a cra-

wling motion system.

The inﬂuence of the chosen equilibrium state on

the direction of motion becomes obvious regarding

the corresponding vibration mode of the crawling mo-

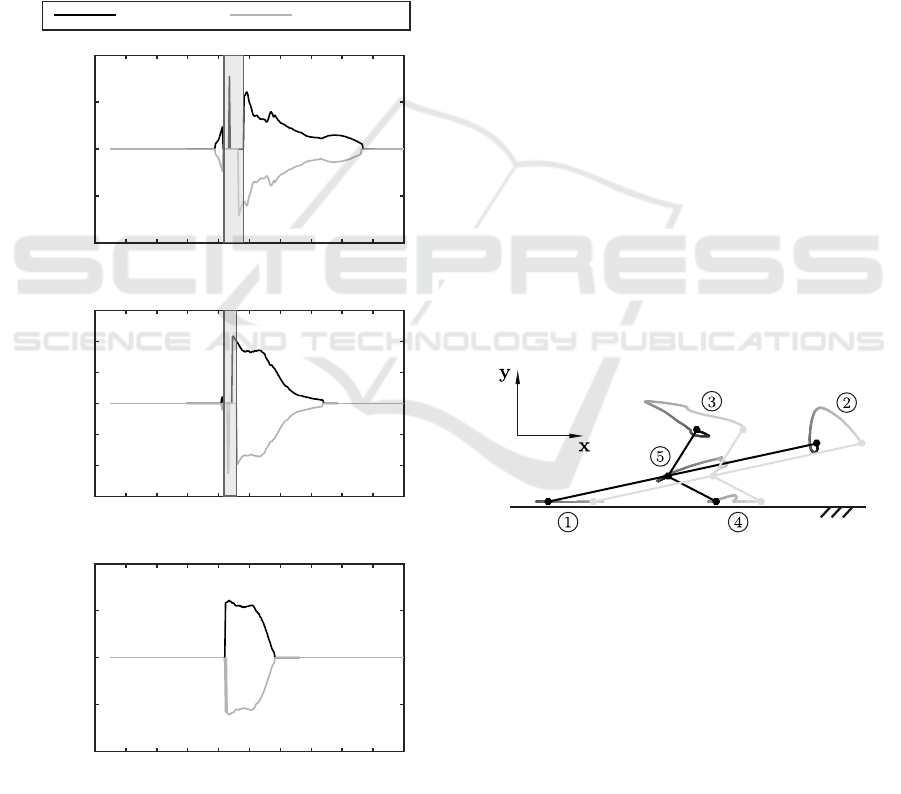
tion system. In Figure 9 the scaled trajectories of the

nodes are exemplarily illustrated. Focusing on the

acting contact points, a partial lifting of node 4 can

be recognized whereas node 1 is permanent in contact

with the horizontal ground. This issue as well as the

different contact forces yield to occurrence of friction

effects which are essential for the motion. Changing

the equilibrium state, a similar effect results. Howe-

ver, the arrangement of the contact nodes is different

which affects the direction of motion.

Figure 9: Scaled trajectories of nodes during one actuation

period (dark → bright) for state I as initial state, f = 10 Hz

and µ

= µ = 0.2 - scale: |x|

∗

= 10|x|, |y|

∗

= 2|y|.

3.3 Change of the Equilibrium State

The previous results show that a uniaxial bidirectio-

nal motion of the considered system is possible using

only one actuator. However, the change between the

equilibrium state I and II has not be considered yet.

Of course, different methods and strategies of actuati-

ons are possible to realize the mentioned switch be-

tween these states. But the following investigation

only show that it this change of equilibrium states

is possible for a chosen parameter set. Therefore, as

actuation strategy of the tensioned member 8 a half-

Dynamical Investigation of Crawling Motion System based on a Multistable Tensegrity Structure

127

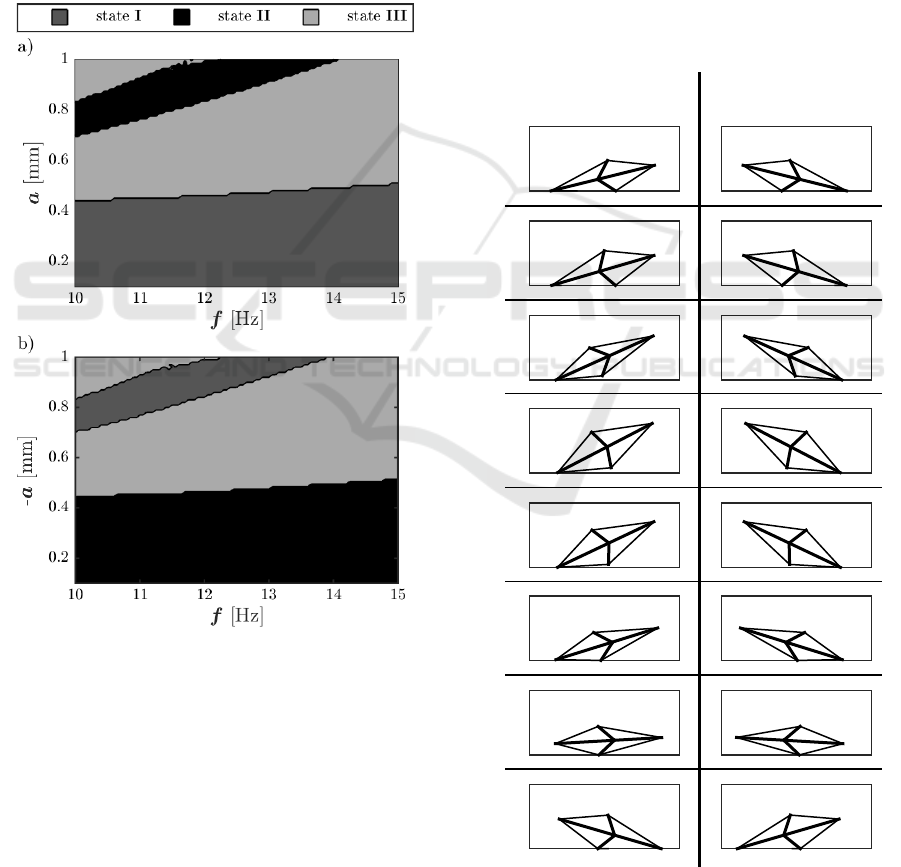
wave of a sine is selected. The resulting excitation

function u(t) is given in (15).

u(t) =

(

asin(2π f t) if t mod 1/ f ≤ π

0 else

(15)

The resulting actuation force can be calculated by (6)

using u(t) instead of s(t). For the change from state

I into state II the frequency is varied from 10 Hz to

15 Hz and the amplitude from 10

−4

m to 10

−3

m. For

the reverse change of states, the same frequency range

is considered. However the excitation amplitude is

supposed to be in a range from −10

−3

m to −10

−4

The according results are shown in Figure 10.

Figure 10: Dynamical investigation of the change of

the equilibrium state for a chosen actuation strategy with

= µ = 0.1 and - a) state I as initial state, b) state II as

initial state.

These results conﬁrm that a change of the equi-

librium states is possible for the selected actuation

strategy. Therefore, for example the use of only

one actuator with an actuation frequency of 10 Hz

enables a uniaxial forward and backward motion as

well as a change of the equilibrium state (I → II and

II → I) utilizing the emphasized multistability of the

tensegrity structure.

However, these results show that for a signiﬁcant

parameter range a change into the critical equilibrium

state III occurs. As mentioned in the previous section

a reverse change into another equilibrium state seems

to be difﬁcult. Hence, the occurrence of the critical

state prevents a further use of the motion system. The-

refore, for the construction of a prototype safeguards

which prohibit a change into the critical equilibrium

state III should be taken into account (e.g. mechan-

cial stops).

In order to illustrate the dynamics during the

change of the equilibrium states corresponding con-

ﬁgurations at different time instances are displayed

exemplarily in Figure 11. This ﬁgure shows that as

consequence of the change of the equilibrium state of

the tensegrity structure a tilting sequence of the entire

locomotion system occurs as supposed in Figure 1.

0 s

I ! II

0:025 s

0:05 s

0:075 s

0:1 s

0:125 s

0:15 s

0:175 s

II ! I

Figure 11: States during the change of the conﬁgurations for

= µ = 0.1 and f = 10 Hz a = 0.8 mm, b) a = −0.8 mm.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

128

4 CONCLUSIONS

This paper deals with the use of a multistable compli-

ant tensegrity structure for the application in a craw-

ling motion system. Most of the known crawling mo-

tion system allow only a one-way motion or requires

advanced demands to the operating actuator in order

to realize a bidirectional uniaxial motion. In this pa-

per a crawling motion system basing on a multistable

tensegrity structure is modeled. The tensegrity struc-

ture enables multiple stable equilibrium conﬁgurati-

ons and is in contact to horizontal plane due to gravity.

As consequence of the acting gravitational forces the

application of certain equilibrium states initiates a til-

ting sequence. Hence, the mode of the entire motion

system is changing. Moreover, total different dynami-

cal properties result for the identical actuation of the

system. Transient simulations are evaluated for se-

lected parameter values of the tensegrity structure and

the steady state solution which assumed after 1000

actuation periods is considered. The motion behavior

which is characterized by the steady state velocity is

analyzed for the different equilibrium conﬁgurations

as initial state and diverse friction properties. The re-

sults conﬁrm that a feasible control of the direction

of motion occurs utilizing the given multistability of

the tensegrity structure. At total, these investigations

show that, indeed, a bidirectional uniaxial motion can

be realized by the use of only one actuator with a se-

lected excitation frequency.

However, for a signiﬁcant parameter range a

change into an additional equilibrium state occurs.

Because of the corresponding low potential energy,

a reverse change into another equilibrium state seems

to be difﬁcult. Hence, after the occurrence of this cri-

tical state the motion system cannot be used anymore.

Therefore, a prototype should be equipped with safe-

guards like mechanical stops which prohibt a change

into that critical equilibrium state.

Moreover, the authors target the development of a

prototype as well as the experimental validation of the

theoretical results shown in this paper.

ACKNOWLEDGEMENTS

This work is supported by the Deutsche Forschungs-

gemeinschaft (DFG project BO4114/2-1).

REFERENCES

ohm, V., Sumi, S., Kaufhold, T., et al. (2017). Compli-

ant multistable tensegrity structures. Mechanism and

Machine Theory, 115:130 – 148.

ohm, V., Zeidis, I., and Zimmermann, K. (2013). Dyn-

amic analysis of a simple planar tensegrity structure

for the use in vibration driven locomotion systems. In

12th Conference on Dynamical Systems - Theory and

Applications, pages 341–352.

ohm, V., Zeidis, I., and Zimmermann, K. (2015). An ap-

proach to the dynamics and control of a planar ten-

segrity structure with application in locomotion sys-

tems. International Journal of Dynamics and Control,

3(1):41–49.

ohm, V. and Zimmermann, K. (2013). Vibration-driven

mobile robots based on single actuated tensegrity

structures. In 2013 IEEE International Conference on

Robotics and Automation, pages 5475–5480.

Bolotnik, N., Zeidis, I., Zimmermann, K., et al. (2006). Dy-

namics of controlled motion of vibration-driven sys-

tems. Journal of Computer and Systems Sciences In-

ternational, 45(5):831–840.

Chen, L. H., Kim, K., Tang, E., et al. (2017). Soft spherical

tensegrity robot design using rod-centered actuation

and control. Journal of Mechanisms and Robotics,

9(2):025001–025001–9.

Fang, H.-B. and Xu, J. (2011). Dynamic analysis and op-

timization of a three-phase control mode of a mobile

system with an internal mass. Journal of Vibration

and Control, 17(1):19–26.

Fang, H.-B. and Xu, J. (2012). Controlled motion of a

two-module vibration-driven system induced by inter-

nal acceleration-controlled masses. Archive of Applied

Mechanics, 82(4):461–47.

Hustig-Schultz, D., SunSpiral, V., and Teodorescu, M.

(2016). Morphological design for controlled tense-

grity quadruped locomotion. In 2016 IEEE/RSJ In-

ternational Conference on Intelligent Robots and Sys-

tems (IROS), pages 4714–4719.

Khazanov, M., Jocque, J., and Rieffel, J. (2014). Evolution

of locomotion on a physical tensegrity robot. 14th In-

ternational Conference on the Synthesis and Simula-

tion of Living Systems, pages 232–238.

Kim, K., Chen, L. H., Cera, B., et al. (2016). Hopping and

rolling locomotion with spherical tensegrity robots. In

2016 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems (IROS), pages 4369–4376.

Liu, H., Yu, Y., Sun, P., et al. (2016). Motion analysis of the

four-bar tensegrity robot. In 2016 IEEE International

Conference on Mechatronics and Automation, pages

1483–1488.

Rieffel, J. A., Valer-Cuevas, F. J., and Lipson, H. (2010).

Morphological communication: exploiting coupled

dynamics in a complex mechanical structure to

achieve locomotion. Journal of the Royal Society In-

terface, 7(45):613–621.

Sabelhaus, A. P., Bruce, J., Caluwaerts, K., et al. (2015).

System design and locomotion of superball, an untet-

hered tensegrity robot. In 2015 IEEE International

Conference on Robotics and Automation (ICRA), pa-

ges 2867–2873.

Schorr, P., Sumi, S., B

ohm, V., et al. (2017). Dynamical

investigation of a vibration driven locomotion system

Dynamical Investigation of Crawling Motion System based on a Multistable Tensegrity Structure

129

based on a multistable tensegrity structure. In 14th

Conference on Dynamical Systems - Theory and Ap-

plications, pages 485–496.

Steigenberger, J. and Behn, C. (2012). Worm-Like Locomo-

tion Systems. An intermediate theoretical Approach.

De Gruyter Oldenbourg.

Sumi, S., B

ohm, V., and Zimmermann, K. (2017). A mul-

tistable tensegrity structure with a gripper application.

Mechanism and Machine Theory, 114:204 – 217.

Tietz, B. R., Carnahan, R. W., Bachmann, R. J., et al.

(2013). Tetraspine: Robust terrain handling on a ten-

segrity robot using central pattern generators. In 2013

IEEE/ASME International Conference on Advanced

Intelligent Mechatronics, pages 261–267.

Zimmermann, K., Zeidis, I., and Behn, C. (2009a). Mecha-

nics of Terrestrial Locomotion with a Focus on Non-

pedal Motion Systems. Springer.

Zimmermann, K., Zeidis, I., Bolotnik, N., et al. (2009b).

Dynamics of a two-module vibration-driven system

moving along a rough horizontal plane. Multibody Sy-

stem Dynamics, 22(2):199–219.

Zimmermann, K., Zeidis, I., and Pivovarov, M. (2013). Dy-

namics of two interconnected mass points in a resis-

tive medium. Differential Equations and Dynamical

Systems, 21(1):21–28.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

130