Dynamic Analysis of the Fractional PID Controller

Juliana Tonasso Herdeiro and Renato Aguiar

Dept. of Electrical Engineering, Centro Universit

ario FEI,

Av. Humberto de Alencar Castelo Branco, SBC, Sao Paulo, Brazil

Keywords:

PID Controller, Fractional PID Controller, Fractional Calculus, Data Aquisition, Robustness.

Abstract:

This article presents as main objective the study and application of the fractional PID controller in a positioning

system, a controller that has basis on the fractional calculus theory originated in 1695 and, despite having

generated several paradoxes in the decade, nowadays there are important applications of this theory, as the

one reported in this paper. Initially, the controller will be designed by means of computational simulation for

the nominal model of a plant, using a program in Matlab and optimization algorithms and, then, applying in

a real process using a data acquisition technique in order to analyse its dynamic behavior in the presence of

real external disturbances. Given that the fractional PID is a generalization of the traditional PID, the goal is

to obtain, in practice, the beneﬁts of this one in relation to the another, mainly observing the requirements of

robustness and stability that must be present in the system.

1 INTRODUCTION

The great industrial growth in recent years, along with

the technological advance, produced constant chan-

ges in society as a whole. Increasingly the indus-

trial processes become independent of human being

and industrial automation reﬂects this process, for ex-

ample, in the use of the robotic arm, which allows,

when properly controlled, to perform welding, pain-

ting, displacement of objects, among other applicati-

ons, automatically.

The PID controller (Proportional + Integrative +

Derivative), widely used in industry, is one of the

most traditional controllers in control theory and there

are several methods for obtaining it (Dorf and Bishop,

2009). Result of the combination of three basic con-

trollers, in other words, the combination of propor-

tional, integrative and derivative controllers, its efﬁ-

ciency on making a response of a system display pre-

determined characteristics motivated studies that pro-

vided several methods for tuning this type of control-

ler (Ogata, 1998).

The following transfer function (Dorf and Bishop,

2009) describes that controller which, in this paper,

will be denominated as traditional PID (or classical

PID, as it is also known in academic publications):

PID

trad

(s) = K

+ K

s, (1)

where K

, K

and K

are, respectively, proportional,

integrative and derivative gains of the controller.

Over the years, a new use possibility for the tradi-

tional PID controller has been noticed, which is know

as fractional PID. As it is a generalization of the tradi-

tional PID, it promises to be a model closer to reality,

and provide a more reﬁned control system.

Herewith, it can be thought about implementing

the fractional PID in several industrial applications,

being able to replace the so called traditional PID.

As an example, in (Tepljakov et al., 2011) the aut-

hors comment on the focus given to fractional calcu-

lus in the last years, applied to control systems design

due to more precise modeling and control enhance-

ment possibilities. Already in (Tavazoei, 2012) the

author highlights the use of fractional order dynamics

to obtain more realistic models for real world pheno-

mena and physical processes such as thermal systems

and polarization phenomena. Other practical applica-

tions are also mentioned, such as suppression of chao-

tic oscillations in electrical circuits and compensating

disturbances on the position and velocity servo sys-

tems.

In more recent studies, as in (Sandhya et al.,

2016), examples of the best fractional controller that

can be designed are given, arguing that it overcomes

the best integer order controller even though it is ve-

riﬁed that this latter works comparatively well. One

of these examples considers a fractional controller for

an integer order plant (DC motor with elastic shaft -

a model from Mathworks, 2006), and the optimiza-

Herdeiro, J. and Aguiar, R.

Dynamic Analysis of the Fractional PID Controller.

DOI: 10.5220/0006852904270434

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 427-434

ISBN: 978-989-758-321-6

427

tion algorithms used are ITAE (Integral of Time Mul-

tiplied by Absolute Error) and ISE (Integral of the

Square of the Error). The author emphasizes the use

of software and hardware for the efﬁcient implemen-

tation of these controllers in industrial and robotic ap-

plications. Aspects of the implementation of these sy-

stems are also evaluated in robotic arms, showing that

the robustness - for variable loads of the object and

small disturbances at the reference - is present in the

system.

In the paper (Binazadeh and Youseﬁ, 2017) the

authors consider a cascade control structure with

fractional controllers slave (internal loop) and master

(of external links) and computer simulations exhibits

the good performance of the proposed project.

More recent articles as seen in (Morsali et al.,

2017), (Khubalkar et al., 2016a) and (Khubalkar

et al., 2016b), further reinforce the validity of the

Fractional PID controller study.

Finally, the objective of this research is to evalu-

ate if the fractional PID can be really more useful for

a control system concerning to robustness, stability

and limitation of the control effort. It is organized as

follows: in section 2 a fractional calculus idea is pro-

vided; the methodology adopted in this work is pre-

sented in section 3; in section 4 the controllers are

designed and applied in the mathematical model of

the plant; the same controllers are applied in the real

plant in presence of disturbances and the results are

presented in section 5. Finally, the conclusions are

presented in section 6.

2 AN IDEA OF FRACTIONAL

CALCULUS

The fractional PID has its fundamental basis embed-

ded in the theory of Fractional Calculus (Camargo,

2009). This theory arose in 1695, and from there nu-

merous studies were done to contribute to the deve-

lopment of the fractional calculus, highlighting, Abel

and Liouville, who were the ﬁrst to ﬁnd an application

for this theory. However, among the various deﬁniti-

ons for the fractional order differential and the fractio-

nal order integral, the following deﬁnitions stand out:

• Gr

unwald-Letnikov deﬁnition (GL):

f (t) = lim

h→0

[

t−α

]

∑

j=0

(−1)





f (t − jh). (2)

• Riemann-Liouville deﬁnition (RL):

f (t) =

Γ(m − α)





f (τ)

(t −τ)

α−m+1

dτ,

(3)

for m − 1 < α < m, m ∈ N, where Γ(·) is Euler’s

gamma function.

Therefore, based on the fractional calculus theory,

the denominated fractional PID controller arises, in

which the derivative and integrative terms have fracti-

onal orders. It has the following transfer function (Ta-

vazoei, 2012):

PID

f rac

(s) = K

+ K

, (4)

where λ and β are arbitrary constants, positive and

less than 1.

As can be seen, while in traditional PID the aim is

to ﬁnd the optimal K

, K

and K

gains, in fractional

PID there are ﬁve parameters to be adjusted: K

, K

, λ and β. This, obviously, might allow a more

reﬁned tuning of the PID so that the system produces

a dynamic response as expected. However, in relation

to the traditional PID, it is worth noting that if λ = β =

1, the fractional PID becomes equal to the traditional,

and, therefore, the traditional PID is a particular case

of the fractional PID.

However, among all the existing studies about

fractional PID, some questions are still present: can

the fractional PID produce robustness to the system,

concerning to the rejection of external disturbances?;

the tuning of all fractional PID parameters based on

a single optimization method is more efﬁcient than

merging optimization methods?; the fractional PID

applied on a real plant, with all its nonlinearities, will

maintain the same performance presented for a nomi-

nal plant? These questions will be answered during

this work.

3 METHODOLOGY

The purpose here is to control a position of a servo

system using the traditional PID controller and then

using a fractional PID.

Initially, both controllers were tuned using the

ITAE performance index. ITAE is the most employed

index available as the minimum value of the integral

is easily discernible when the system parameters are

varied. As the absolute error is time weighted, this

criteria has good applicability when a reduction of the

contribution of large errors are necessary and a grea-

ter emphasis is placed on errors that occur later in the

transient response of the system.

The expression that describes this index is (Dorf

and Bishop, 2009):

ITAE =

t |e(t)| dt, (5)

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

428

where, typically, the upper limit T of the integral is de-

ﬁned as the settling time T

, which is the time required

for the response reach and remain within speciﬁed li-

mits (usually 2% to 5% of the ﬁnal value). Therefore,

it is a sufﬁciently large time span that includes tran-

sient and steady state. Thus, a system is considered

optimal when the chosen performance index reaches

an extreme minimum value. In other words, the opti-

mal system to be developed is one that minimizes this

index (Dorf and Bishop, 2009).

In a second case, speciﬁcally for the fractional

PID, the gains were tuned using the Linear Quadra-

tic Regulator method (LQR) (MUKHOPADHYAY,

1978) and the parameters that deﬁne the order of

the derivative and integrative terms were deﬁned by

ITAE. Which means the tuning via Linear Quadratic

Regulator will be used for optimizing the parameters

, K

of the controller to be designed. A com-

parison between this method and ITAE becomes rele-

vant since a more suitable tuning can be obtained and,

consequently, achieving optimal systems.

The method presents precepts of the Modern Con-

trol theory as concepts of state space modeling, with

detriment of the transfer function model complexities,

to develop an equivalent solution to ﬁnd the gains K

, K

of a system, with some advantages that are pro-

perly discussed in (MUKHOPADHYAY, 1978).

The FOMCON toolbox (Tepljakov et al., 2011)

has an optimization tool (which uses an optimize

function) to tune a controller by minimizing the

function given by a predetermined performance in-

dex. The FOMCON was idealized as a reﬂection of

the growth in research and development of the fracti-

onal controller due to the new possibilities generated

through the modeling of this type of system. The

tool is simple to manipulate, provides a graphical user

interface and several resources for system analysis,

which allows fast practical results to be generated (Te-

pljakov et al., 2011).

In all these cases simulations were made for the

mathematical model of the servo system. Finally,

these same controllers were applied to the real system

through the data acquisition technique, which allows

the communication between Matlab and a real plant.

Comparisons with the traditional PID will be

made and a robustness analysis of the fractional PID

will be performed.

The real system used here is a servo system (a

servo positioner) shown in Figure 1.

The nominal transfer function of the servo positi-

oner, obtained by experimental analysis is:

H(s)

servo system

+ 4s

. (6)

Figure 1: Real plant - Servo positioner.

Some components of the real plant are presented

as follows:

• DC Motor: It is a direct current motor that can

reach up to 2500 rpm;

• Tachogenerator (or Tachometer): It is an elec-

tromagnetic device that, when rotated, generates

an output voltage proportional to the speed of its

axis. This property will be used to obtain the

speed feedback of the control system (LJ Techni-

cal Publications Department, 2016);

• Magnetic brake: It consists of a permanent mag-

net attached to a pivoted rod that allows the intro-

duction of a magnetic brake when placed in front

of the aluminum disc. The magnetic brake inser-

tion rod has three positions (0,1 and 2), and the

load intensity can be changed according to this

position selection (LJ Technical Publications De-

partment, 2016).

Some nonlinearities are inherent to this plant, such

as dead zone of the motor and backlash on gears,

which can cause the so-called backlash effect, besi-

des noise. Therefore, it can be noticed that the servo

system used here is a set that meets the intentions of

this work and can enable the achievement of relevant

practical results.

4 DESIGN AND SIMULATION

The ﬁve parameters of the fractional PID controller,

as well as the three parameters of the traditional PID

controller, were tuned using the FOMCON toolbox.

First, K

, K

and K

will be deﬁned by identifying

an entire order model for the plant, and a suitable tu-

ning method.

Then, the parameters λ and β are tuned using the

optimization tool. A performance index was deﬁned

Dynamic Analysis of the Fractional PID Controller

429

(in this case, the ITAE, which considers the absolute

error over time).

A block diagram was developed in Simulink for

the traditional and fractional PID, both applied to the

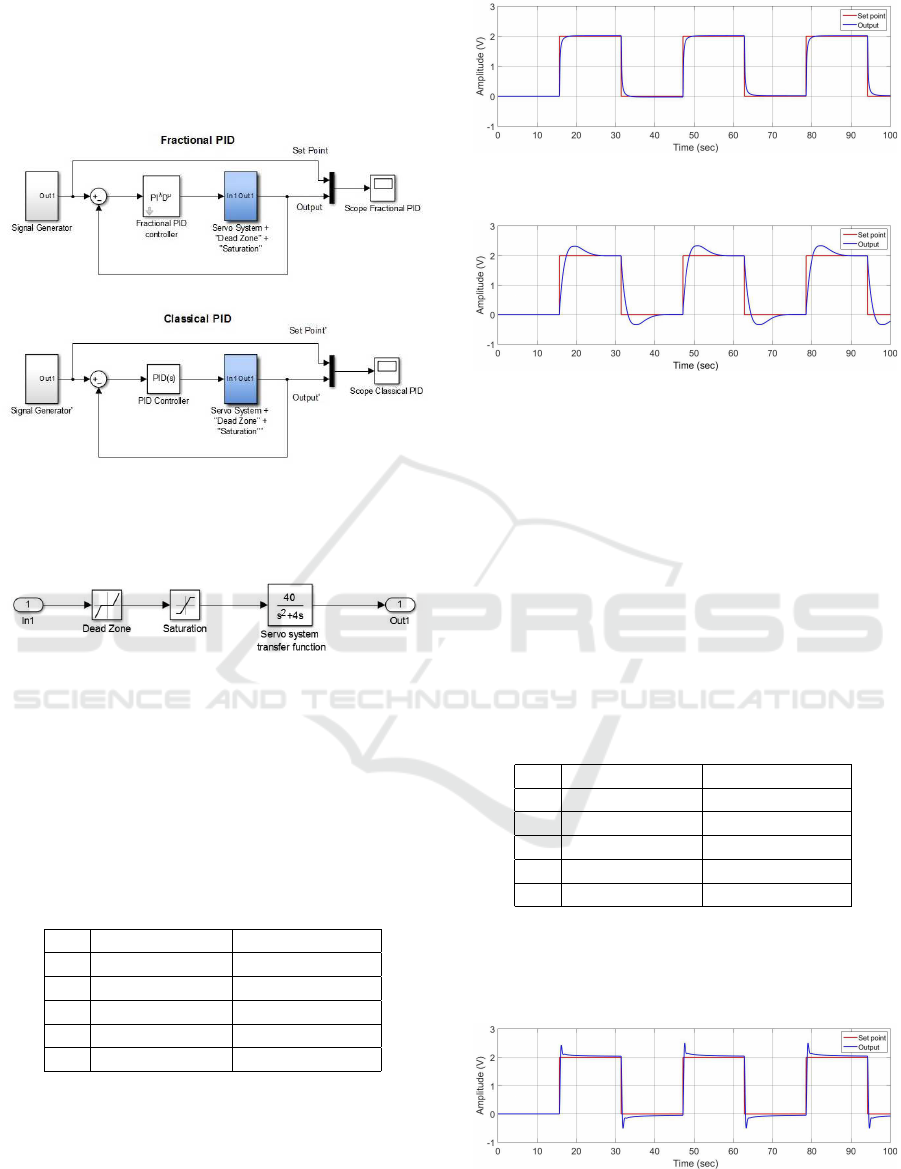
same plant. These diagrams are given in Figure 2.

Figure 2: Block diagrams in Simulink.

Figure 3 shows the contents of the servo system

block.

Figure 3: Contents of the block which represents the servo

system shown in Figure 2.

Firstly, the traditional PID was tuned via ITAE

performance index. Then, the fractional PID para-

meters were obtained via toolbox FOMCON, ﬁxing

, K

and K

, previously found in the traditional PID

tuning, and optimizing λ and β via ITAE. The para-

meters were shown in Table 1.

Table 1: Controller parameters for ITAE tuning.

Fractional PID Traditional PID

5,4115 5,4115

2,0841 2,0841

5,2487 5,2487

λ 0,15918 -

β 0,67146 -

The system responses using the fractional PID tu-

ned and also the traditional PID are presented in ﬁgu-

res 4 and 5 respectively.

As can be seen, the tuning of the fractional PID

provided a faster response without overshoot.

One more tuning of coefﬁcients was performed in

which K

, K

and K

are adjusted by the Linear Qua-

Figure 4: Response for the fractional PID when K

=5,4115;

=2,0841; K

=5,2487;λ=0,15918; β=0,67146.

Figure 5: Response for the traditional PID when

=5,4115; K

=2,0841; K

=5,2487.

dratic Regulator (obtained through a program deve-

loped in Matlab) and λ and β are, then, optimized

through the toolbox FOMCON based on the ITAE

performance index (ﬁxing K

, K

and K

found pre-

viously in the LQR tuning via Matlab and allowing

the toolbox to optimize λ and β). This procedure has

as objective to analyze if the composition of two ad-

justment methods is efﬁcient for tuning the fractional

PID controller. The parameters obtained are shown in

Table 2.

Table 2: Controller parameters for Linear Quadratic Regu-

lator tuning (traditional PID) and for Linear Quadratic Re-

gulator and ITAE tuning (fractional PID).

Fractional PID Traditional PID

1,2551 1,2551

1 1

0,1877 0,1877

λ 0,36832 -

β 0,89995 -

The system responses using the fractional PID tu-

ning and also the traditional PID are shown in ﬁgures

6 and 7 respectively.

Figure 6: Response for the fractional PID when K

=1,2551;

=1; K

=0,1877;λ=0,36832; β=0,89995.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

430

Figure 7: Response for the traditional PID when

=1,2551; K

=1; K

=0,1877.

Both simulations are very similar when observing

the overshoot, but the fractional PID give a more fas-

ter accommodation time response. On the other hand,

the fractional PID controller presents an stationary er-

ror as can be seen in Figure 6, not observed in the

traditional PID simulation (Figure 7).

In the next session, the same controllers will be

applied in the real plant in presence of nonlinearities

and disturbances.

5 APPLICATION OF

FRACTIONAL AND

TRADITIONAL PID IN REAL

PLANT MODEL

After the controllers are tuned and simulated by me-

ans of computational analysis, it is necessary to verify

their functionalities in a real system, the servo positi-

oner, which has several nonlinearities that can com-

promise the desired ﬁnal behavior, such as the dry

friction of the plant of the system, gap in the gears,

dead zone of the motor and saturation of the power

ampliﬁer.

The servo system was powered and connected to

the National Instruments data acquisition interface for

obtaining data.

To establish the transmission and reception of data

between the servo system and Matlab/Simulink, the

National Instruments PCI 6221-37 pin data acquisi-

tion board was used. This board has 16 channels of

analog inputs and 2 channels of analog outputs and

through the CB-37FH connector, it is possible to use

the inputs and outputs of the board to perform the

communication between the PID contained in Matlab

and the real plant.

A block diagram has been developed in Simulink

to integrate virtual and real components. The analog

input block represents the control output (the signal

which comes from the servo positioner), connected

with an adjustable transfer function ﬁlter to elimi-

nate high frequency noise produced by the derivative

action. The analog output block contains the signal

that is inserted into the motor. Besides these compo-

nents, the traditional and fractional PID blocks were

used to simulate the responses.

Therefore, the same procedure performed for the

nominal model of the system was performed in the

real model of the plant. Figure 8 shows the block di-

agram of the control system with the performance of

the traditional PID tuned with ITAE.

Figure 8: Block diagram in Simulink for the traditional PID.

Figures 9 and 11 presents the system response,

using the traditional PID, without external distur-

bance and with external disturbance, respectively. Fi-

gures 10 and 12 presents, respectively, the control

efforts of the controller without external disturbance

and with disturbance. The intent is to verify the ef-

ﬁciency that the controller manages to maintain this

control effort within an acceptable limit.

Figure 9: Response for the traditional PID when

=5,4115; K

=2,0841; K

=5,2487.

Figure 10: Control effort for the traditional PID when

=5,4115; K

=2,0841; K

=5,2487.

The traditional PID tuned via ITAE resulted in a

similar response with the one viewed previously in

computational simulation (Figure 5). The controller

Dynamic Analysis of the Fractional PID Controller

431

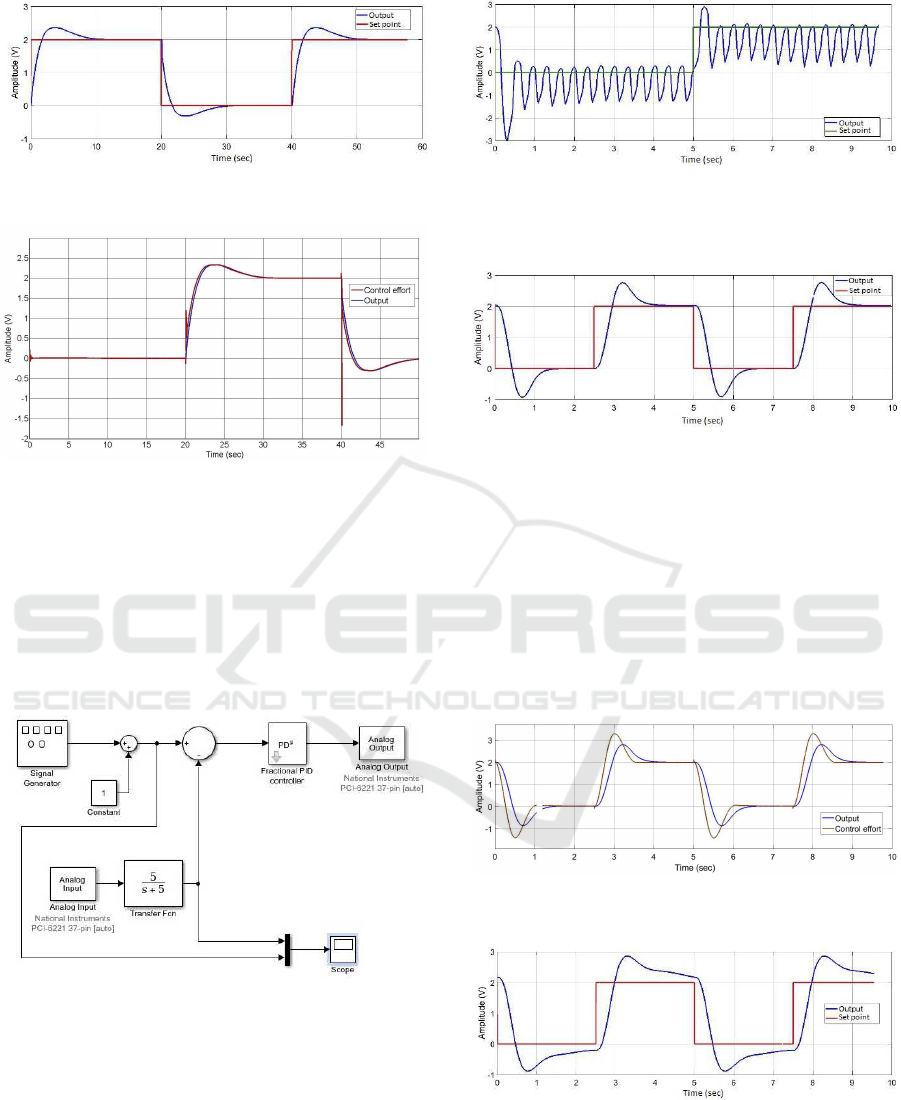
Figure 11: Response for the traditional PID with distur-

bance when K

=5,4115; K

=2,0841; K

=5,2487.

Figure 12: Control effort for the traditional PID with distur-

bance when K

=5,4115; K

=2,0841; K

=5,2487.

managed very well in front of the disturbances, but

when observing the control effort, the peaks may in-

dicate a loss for the system as a great effort needs to

be spent in a very small time.

Figure 13 shows the block diagram of the cont-

rol system with the performance of the fractional PID

tuned with ITAE.

Figure 13: Block diagram in Simulink for the fractional

PID.

As a result, ﬁgure 14 show the system response

for the fractional PID with K

, K

ﬁxed by ITAE

and λ and β optimized singly, also with ITAE.

In this case, it can be noted that the system, dif-

ferent from the computational results, has an unstable

behavior.

As an alternative to this practical case, the fracti-

onal PID controller was tuned using the Linear Qua-

Figure 14: Response for the fractional PID with K

, K

ﬁxed by ITAE and λ and β optimized singly, also with

ITAE. The obtained parameters: K

=5,4115; K

=2,0841;

=5,2487;λ=0,15918; β=0,67146.

Figure 15: Response for the traditional PID when

=1,2551; K

=1; K

=0,1877.

dratic Regulator method (MUKHOPADHYAY, 1978)

and the integrator and derivative orders tuned with

ITAE performance index, as was done in section 4.

But before, the traditional PID was also tuned by the

Linear Quadratic Regulator method. Figures 15 and

17 presents, respectively, the responses using the tra-

ditional PID without and with disturbances and Figu-

res 16 and 18 highlight the control effort present in

the system.

Figure 16: Control effort for the traditional PID when

=1,2551; K

=1; K

=0,1877.

Figure 17: Response for the traditional PID with distur-

bance when K

=1,2551; K

=1; K

=0,1877.

The Linear Quadratic Regulator method increased

the overshoot for the traditional PID and, in face of

the disturbance, also increased the settling time. It is

required more from the controller when comparisons

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

432

Figure 18: Control effort for the traditional PID with distur-

bance when K

=1,2551; K

=1; K

=0,1877.

Figure 19: Response for the fractional PID when

=1,2551; K

=1; K

=0,1877; λ=0,36832; β=0,89995.

of control effort are made with the tuning via ITAE.

Figures 19 and 21, respectively, presents the re-

sponses using fractional PID without and with distur-

bances, and Figures 20 and 22 presents the respective

control efforts.

Figure 20: Control effort for the fractional PID when

=1,2551; K

=1; K

=0,1877; λ=0,36832; β=0,89995.

Figure 21: Response for the fractional PID with distur-

bance when K

=1,2551; K

=1; K

=0,1877; λ=0,36832;

β=0,89995.

Figure 22: Control effort for the fractional PID with dis-

turbance when K

=1,2551; K

=1; K

=0,1877; λ=0,36832;

β=0,89995.

The fractional PID clearly has obtained an efﬁ-

cient tuning with the Linear Quadratic Regulator Met-

hod in detriment of the ITAE tuning with gives an un-

stable behavior (Figure 14). The controller also ma-

nages well to maintain the control effort.

An ﬁne adjustment for the fractional PID has per-

formed in order to achieve the best controller that can

be projected. The idea was to reduce K

and to in-

crement the K

parameter (to reduce the excessive

overshoot).The result is given in ﬁgures 23 and 24

which presents, respectively, the ﬁne adjustment and

the control effort associated.

Figure 23: Fractional PID ﬁne adjustment when

=1,2551; K

=0,85; K

=0,3377; λ=0,36832; β=0,89995.

Figure 24: Control effort for the fractional PID ﬁne adjus-

tment when K

=1,2551; K

=0,85; K

=0,3377; λ=0,36832;

β=0,89995.

The potentialities of the fractional PID were

shown as the ﬁne adjustment generated a response

without overshoot and a satisfactory control effort.

6 CONCLUSIONS

In this work we intended to tune the traditional and

fractional PID in a positioning system. For the PID

tuning, two methods were used: i) the ITAE per-

formance index, ii) the Linear Quadratic Regulator.

The ﬁrst phase consisted in applying the PID in the

nominal model of the plant and, in a second phase,

the same controllers obtained were applied in the real

plant with all its nonlinearities.

By means of the designed controllers, it is obser-

ved that the ITAE index is efﬁcient to tune the tra-

ditional PID and also the fractional PID when app-

lied to the mathematical model of the plant. In this

sense, the superiority of the fractional PID efﬁciency

is remarkable, since the system response has a shorter

settling time and without overshoot. However, when

Dynamic Analysis of the Fractional PID Controller

433

these controllers are applied to a real plant with its

nonlinearities, the system controlled by the fractional

PID starts to present an unstable response.

One solution for this problem was to tune fractio-

nal PID gains using Linear Quadratic Regulator met-

hod and adjust the derivative and integrative orders

using the ITAE performance index. In the mathema-

tical model of the plant, the responses of the system

controlled by the fractional and traditional PID were

very similar. However, when applied in the real plant,

the fractional PID makes the system produce a stable

and faster response when compared to the traditional

PID, even in the presence of disturbances.

Therefore, when applying the controllers in the

mathematical model and in the real plant, it could be

observed that the fractional PID tends to have, in fact,

a greater efﬁciency when compared with the traditio-

nal PID, with respect to the robustness of performance

in the presence of disturbances, speed of response and

reduction of overshoot. However, in a real model, it

is necessary to take care in choosing the optimization

method. The fractional PID proved to be more efﬁ-

cient in a real case when its gains were tuned using the

Linear Quadratic Regulator and the integrator and de-

rivative orders adjusted by the ITAE. Thus, the com-

bination of two optimization methods for fractional

PID tuning has proven to be a promising way to apply

the controller to a real plant.

REFERENCES

Binazadeh, T. and Youseﬁ, M. (2017). Desig-

ning a Cascade-Control Structure Using Fractional-

Order Controllers: Time-Delay Fractional-Order

Proportional-Derivative Controller and Fractional-

Order Sliding-Mode Controller. In Journal of Engi-

neering Mechanics. American Society of Civil Engi-

neers.

Camargo, R. F. (2009). C

alculo Fracion

ario e Aplicac¸

oes.

In Doctoral Thesis. UNICAMP, Sao Paulo.

Dorf, R. C. and Bishop, R. H. (2009). Sistemas de Controle

Modernos. LTC, Rio de Janeiro, 11nd edition.

Khubalkar, S., Chopade, A., Junghare, A., and Aware, M.

(2016a). Design and Tuning of Fractional Order PID

Controller for Speed control of Permanent Magnet

Brushless DC Motor. In IEEE First International

Conference on Control, Measurement and Instrumen-

tation (CMI). IEEE.

Khubalkar, S., Chopade, A., Junghare, A., Aware, M., and

Das, S. (2016b). Design and Realization of Stand-

Alone Digital Fractional Order PID Controller for

Buck Converter Fed DC Motor. In Circuits, Systems,

and Signal Processing. Springer.

LJ Technical Publications Department, L. (2016). Further

analog control of the DC motor training system. In

Curriculum Manual CA03. LJ Technical Systems Inc.,

U.S.A.

Morsali, J., Zare, K., and Hagh, M. T. (2017). Applying

fractional order PID to design TCSC-based damping

controller in coordination with automatic generation

control of interconnected multi-source power system.

In Engineering Science and Technology, an Internati-

onal Journal. Elsevier.

MUKHOPADHYAY, S. (1978). P.I.D. Equivalent of Opti-

mal Regulator. In Electronics Letters. IET.

Ogata, K. (1998). Engenharia de Controle Moderno. Pren-

tice Hall, Rio de Janeiro, 3nd edition.

Sandhya, A., Prameela, M., and Sandhya, R. (2016). An

overview of Fractional order PID Controllers and its

Industrial applications. In International Journal of In-

novations in Engineering and Technology. IJIET.

Tavazoei, M. S. (2012). From Traditional to Fractional PI

Control: A Key for Generalization. In IEEE Industrial

Electronics Magazine. IEEE.

Tepljakov, A., Petlenkov, E., and Belikov, J. (2011). FOM-

CON: Fractional-order modeling and control toolbox

for MATLAB. In Mixed Design of Integrated Circuits

and Systems (MIXDES), Proceedings of the 18th In-

ternational Conference. IEEE.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

434