
Lightweight Attribute-based Encryption Supporting Access Policy
Update for Cloud Assisted IoT
Sana Belguith
1
, Nesrine Kaaniche
2
and Giovanni Russello
1
1
Cyber Security Foundry, University of Auckland, New Zealand
2
SAMOVAR, CNRS, Telecom SudParis, University Paris-Saclay, Paris, France
Keywords:
Constant-size Attribute based Encryption, Access Policy Update, Cloud Assisted IoT, Confidentiality, Access
Control.
Abstract:
Cloud-assisted IoT applications are gaining an expanding interest, such that IoT devices are deployed in dif-
ferent distributed environments to collect and outsource sensed data to remote servers for further processing
and sharing among users. On the one hand, in several applications, collected data are extremely sensitive and
need to be protected before outsourcing. Generally, encryption techniques are applied at the data producer
side to protect data from adversaries as well as curious cloud provider. On the other hand, sharing data among
users requires fine grained access control mechanisms. To ensure both requirements, Attribute Based Encryp-
tion (ABE) has been widely applied to ensure encrypted access control to outsourced data. Although, ABE
ensures fine grained access control and data confidentiality, updates of used access policies after encryption
and outsourcing of data remains an open challenge. In this paper, we design PU-ABE, a new variant of key
policy attribute based encryption supporting efficient access policy update that captures attributes addition
and revocation to access policies. PU-ABE contributions are multifold. First, access policies involved in the
encryption can be updated without requiring sharing secret keys between the cloud server and the data ow-
ners neither re-encrypting data. Second, PU-ABE ensures privacy preserving and fine grained access control
to outsourced data. Third, ciphertexts received by the end-user are constant sized and independent from the
number of attributes used in the access policy which affords low communication and storage costs.
1 INTRODUCTION
Nowadays, IoT applications are widely used in dif-
ferent fields such as smart cities, e-health, intelligent
transport systems, to name a few (Farhan et al., 2018;
Atwady and Hammoudeh, 2017; Coates et al., 2017;
Belguith et al., 2018). Due to their limited storage
and computation capacities, IoT devices are usually
assisted with cloud services to store and process ge-
nerated data (Kaaniche and Laurent, 2017b; Belguith
et al., 2015). IoT devices produce huge amounts of
data which need to be securely collected and shared
among different users (Bacis et al., 2016a; Bacis et al.,
2016b). Consequently, encryption and access control
mechanisms are important to protect data from unaut-
horised access (Belguith et al., 2016).
Attribute based encryption (ABE) ensures encryp-
ted access control to outsourced data while limiting
privacy leakage of data producers and users (Kaani-
che and Laurent, 2017a). ABE consists of encipher-
ing data with respect to an access policy over a set of
attributes where users who have the matching attribu-
tes can recover data. Nowadays, with the emergence
of applications adapted to distributed and dynamic en-
vironments, several settings require adding new users,
strengthening access patterns and/or removing current
users from systems. A naive solution is to re-encrypt
the whole data contents using new access policy by
the data owner and re-outsource them to the cloud
server. However, this solution is extremely expen-
sive in computation and communications costs as it
should be re-executed at every time a user is added
or removed. Proxy re-encryption techniques are used
to update users in outsourced systems. These mecha-
nisms allow a server to re-encrypt stored data without
accessing their content using a re-encryption key (Li-
ang et al., 2015; Ge et al., 2018). Attribute-based
Proxy Re-encryption (AB-PRE) systems have been
applied for access policy update. In AB-PRE, when
the data owner decides to update access policies of
some ciphertexts, she uses her private key to genera-
ted a re-encryption key for each ciphertext to be chan-
ged from an old access policy to a new one. After-
wards, all the generated re-encryption keys are uplo-
Belguith, S., Kaaniche, N. and Russello, G.
Lightweight Attribute-based Encryption Supporting Access Policy Update for Cloud Assisted IoT.
DOI: 10.5220/0006854601350146
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 135-146
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
135

aded to a proxy server to update the ciphertext using
the received keys. Although AB-PRE schemes allow
re-encryption without decrypting ciphertext or acces-
sing the plaintexts, it requires that the data owner ge-
nerates valid re-encryption keys. When the number of
ciphertext rises, it becomes inefficient for a data ow-
ner to generate all the re-encryption keys and upload
them to the proxy. Furthermore, this may also be un-
feasible for limited bandwidths. Therefore, attribute-
based proxy re-encryption schemes may not be effi-
cient when updating a huge the number of ciphertexts.
Key Policy Attribute Based Encryption (KP-ABE)
is widely applied to secure data in several distribu-
ted systems such as Publish and Subscribe systems
(Pub/Sub) (Ion et al., 2012; Esposito and Ciampi,
2015), pay-TV systems (Ogawa et al., 2017), vehicu-
lar networks (Nkenyereye et al., 2016), ..., where rules
on who may read a document must be specified but
it is unable to specify policies on a per-message ba-
sis. Obviously, these dynamic environments usually
require efficiently adding new users and/or revoking
existent users. That is, KP-ABE consists in labeling
user’s key by an access structure that specifies which
type of ciphertext the key can decrypt, while cipher-
text are labeled by a set of attributes. Thus, KP-ABE
are adapted to distributed and decentralized environ-
ments. Instead, Ciphertext Policy Attribute Based En-
cryption (CP-ABE) schemes consists in associating
an access structure to the ciphertext while assigning
a set of credentials to deciphering users. CP-ABE
schemes supporting policy update have been recently
explored by Jiang et al. (Jiang et al., 2016; Jiang
et al., 2017). Indeed, the authors proposed a CP-ABE
scheme where new attributes can be added or current
attributes can be removed efficiently without sharing
re-encryption keys.
This motivates us to introduce the first KP-ABE
scheme supporting adding and/or removing attributes
from the access policy without sharing keys with the
cloud server.
Contributions – In this paper, we propose Policy
Update Attribute Based Encryption (PU-ABE), a
novel key policy attribute based encryption scheme
which supports access policy update. This proposed
scheme is suitable for bandwidth-limited applications
as the size of the ciphertext received by end-users
does not depend on the number of attributes involved
in the access policy. In PU-ABE, the encrypting
entity generates a ciphertext involving encrypted
data together with some extra components used for
supporting the access policy update feature. The
ciphertext is forwarded to the cloud server that can
update the access policy upon demand. Indeed, the
cloud server does not need to be trusted. That is, it
stores and shares ciphertexts among authorised users
and also executes access policy update algorithm as
requested. While executing these functionalities, the
remote server is unable of decrypting any ciphertexts
neither accessing any secret keys. For supporting
the policy update feature, PU-ABE provides two
functions. The first function permits to add new
attributes to the access policy used to encrypt data.
The second function ensures revoking attributes from
the access policy used in the encryption phase. To
prove the security of our proposed constructions, we
present an updated security model to capture security
requirements related to policy updates.
Paper Organisation – The remainder of this work is
as follows: Section 2 highlights security considerati-
ons and design goals. Then, Section 3 reviews related
work and section 4 describes the system and security
models. Section 5 presents the mathematical back-
ground. In Section 6, an overview of PU-ABE is in-
troduced and the detailed construction are presented.
Section 7 presents a rigorous security discussion. Fi-
nally, a theoretical analysis of computational perfor-
mances is presented in Section 8, before concluding
in Section 9.
2 PU-ABE FRAMEWORK
In this section, we first present the network model,
detailing the involved entities and their interactions in
Section 2.1. Then, we detail the security requirements
that the proposed system should fulfill in Section 2.2.
2.1 Architecture
As depicted by Figure 1, our PU-ABE framework
considers a cloud service provider that stores data ge-
nerated by data owners and share them among aut-
horised users. Four different entities are defined as
follows:
• The Central Trusted Authority (CTA), known by
the Attribute authority, is responsible for gene-
rating the global public parameters and issuing
users’ secret keys. CTA is considered as a trus-
ted entity in our model.
• The Cloud Service Provider (CSP) is a remote
cloud server who stores and shares data among
authorised users. CSP is also responsible of exe-
cuting the update algorithm to change the access
policy involved in the ciphertext, w.r.t. the data
owner’s recommendations.
SECRYPT 2018 - International Conference on Security and Cryptography
136

• The data owner (O) is the data producer. She de-
fines access rights and encrypts data with respect
to them before outsourcing to the cloud. In ad-
dition, the data owner generates extra ciphertext
components used by the update algorithm.
• The data users (U) requests access to outsourced
data. She decrypts the received data using his
access rights. A user may be malicious if she tries
to access data without authorisation.
2.2 Security Requirements
To design an efficient attribute based encryption
scheme supporting efficient access policy update, the
following requirements need to be achieved:
• access policy update – our PU-ABE scheme
should ensure adding new attributes and/or remo-
ving attributes from the access policy.
• flexible access control – our proposal should en-
sure flexible security policies among dynamic
groups of users, w.r.t. forward secrecy and bac-
kward secrecy.
– backward secrecy means that a new added user
to a group is unable to decrypt information cre-
ated prior to their introduction.
– forward secrecy means that a compromise of
the secret key does not affect the secrecy of fu-
ture encrypted data.
• data confidentiality – our PU-ABE scheme has
to protect the secrecy of outsourced and encryp-
ted data contents against curious users and curious
cloud service provider.
• low computation overhead and storage cost –
the proposed algorithms should have low proces-
sing complexity and acceptable storage cost to be
adapted to resource-constrained devices and dis-
tributed environments.
3 ATTRIBUTE BASED
ENCRYPTION SCHEMES
Attribute-based Encryption (ABE) has been designed
to ensure encrypted flexible access control for out-
sourced data (Sahai and Waters, 2005). Unlike tradi-
tional public key encryption schemes, ABE consists
in encrypting data for many users. Therefore, decryp-
ting entities’ private keys and encrypted data are la-
beled with a set of attributes or a structure over attri-
butes. A user is able to decrypt a ciphertext if there
is a match between her private key and the cipher-
text (Bethencourt et al., 2007). Attribute based en-
cryption schemes are classified into two categories,
namely: Key-Policy ABE (KP-ABE) and Ciphertext-
Policy ABE (CP-ABE) (Goyal et al., 2006). In KP-
ABE, ciphertexts are labeled with a set of attributes
while users’ private keys are associated with an access
policy which can be any monotonic structure. The
user is able to decrypt the ciphertext if her access po-
licy is satisfied by the attributes embedded in the cip-
hertext. KP-ABE schemes have been widely applied
to secure data in distributed systems such as Internet
of Things, publish and subscribe systems, intelligent
transport systems, etc. (Yao et al., 2015).
Although ABE schemes ensure flexible access
control to encrypted data, the communication and
computation overhead as well as the bandwidth con-
sumption increase exponentially with the number of
attributes required in the access policies. To save the
storage cost of ciphertext and processing overhead of
encryption, attribute based encryption schemes with
constant ciphertext size have been introduced (Her-
ranz et al., 2010; Ge et al., 2012; Attrapadung et al.,
2012; Wang and Luo, 2012). In these schemes, the
size of the generated ciphertext does not depend on
the number of attributes used on the threshold access
policies, which presents an interesting feature mainly
for resource-constrained devices. Herranz et al. (Her-
ranz et al., 2010) have proposed the first constant size
threshold ciphertext-policy attribute based encryption
scheme. Indeed, the ciphertext size is constant and
does not depend on the number of attributes invol-
ved in the threshold access policies. Afterwards, se-
veral CP-ABE schemes with constant cipheretxt size
have been proposed (Ge et al., 2012; Belguith et al.,
2017; Li et al., 2017). Due to the construction of CP-
ABE schemes, monotone access policies based sche-
mes can not be extended to ensure a constant cipher-
text size. For instance, these schemes consist in only
using threshold or conjunctive access policies which
do not provide the desired expressiveness.
Several expressive Key policy attribute based en-
cryption schemes with constant ciphertext size have
been designed (Attrapadung et al., 2012; Wang and
Luo, 2012; Emura et al., 2009). Wang et al. (Wang
and Luo, 2012) have proposed a KP-ABE scheme
with constant ciphertext size. This scheme relies on
a monotone access policy to express the users’ attri-
butes.
Although, these schemes ensure reduced commu-
nication and computation costs, they still present a
major limitation which is their incapacity of changing
access policies of ciphertexts. In dynamic environ-
ments, users may be often added or removed, then
Lightweight Attribute-based Encryption Supporting Access Policy Update for Cloud Assisted IoT
137
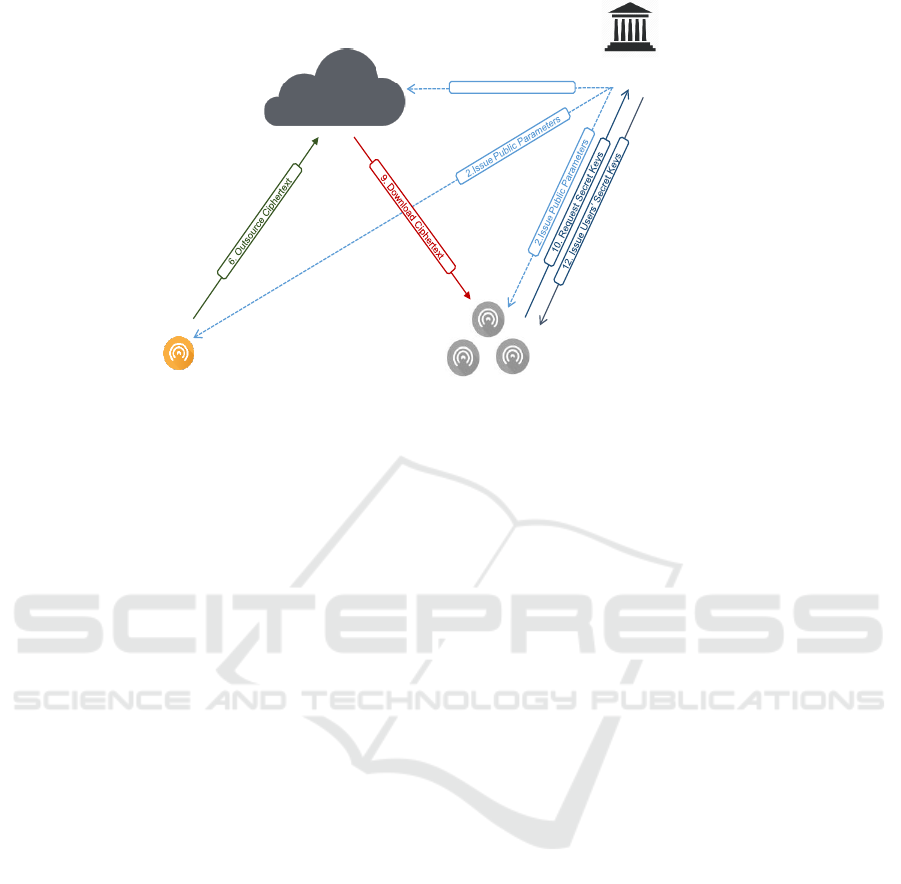
Central Trusted Authority
Cloud Service Provider
2.Issue Public Parameters
Data UsersData Owner
3. Define access policy
4. Encrypt data w.r.t to access policy
5. Generate ciphertext components
for access policy updates
7. Store ciphertexts
8. Update access policy
13. Decrypt cipherext
1. Generate public
parameters
11. Generate users’ secret
keys
Figure 1: PU-ABE involved entities and their interaction.
access policies should be updated to support these
changes. Recently, the first CP-ABE with policy up-
date has been proposed by Jiang et al. (Jiang et al.,
2016; Jiang et al., 2017). The authors introduced
a new variant of CP-ABE supporting access policy
update that captures the functionalities of attribute
addition and revocation from access policies. They
provide two CP-ABE schemes supporting AND-gate
access policies with constant-size ciphertexts. In key
policy attribute based encryption schemes, policy up-
date is still not supported. This motivates us to ad-
dress the problem of constructing the first key policy
attribute based encryption scheme with policy update.
4 MODEL DESCRIPTION
In this section, we first present the system model of
our PU-ABE scheme (subsection 4.1). Then, we de-
tail our security model (subsection 4.2).
4.1 System Model
Our policy-update key-policy attribute based encryp-
tion scheme consists of five randomized algorithms:
setup, encrypt, update, keygen and decrypt, defined
as follows:
setup(ξ) → (pp,msk) – the setup algorithm is per-
formed by a central trusted authority, known by the
attribute authority. It takes as input a security para-
meter ξ and outputs the public parameters pp and the
secret master key msk.
encrypt(pp,S,M) → CT – the encryption algo-
rithm is performed by an enciphering entity E. It ta-
kes as inputs the public parameters pp, the set of the
encryption attributes S and the message M. This al-
gorithm outputs the encrypted message, referred to as
CT .
update(pp,CT, ind,U) → CT
0
– the update algo-
rithm is executed by a cloud server. It takes as inputs
the public parameters pp, a ciphertext CT that con-
tains the set of enciphering attributes S = {a
i
}
i=1..m
such that |S | = m, an operation indicator ind where
ind = add or ind = revoke and a set of attributes U
with U ∩ S =
/
0 if ind = add or U ⊂ S if ind = revoke.
It outputs a new ciphertext CT
0
for the new encrypting
set of attributes S
0
such as S
0
= S ∪ U or S
0
= S \ U
w.r.t. ind value.
keygen(pp,msk,Ψ) → sk – this randomized algo-
rithm is executed by the attribute authority to derive
the secret keys of a decrypting entity D. Given the pu-
blic parameters pp, an access policy Ψ of the user D
and the secret master key msk. The algorithm outputs
the user’s secret key sk w.r.t. Ψ.
decrypt(pp,sk,CT
0
) → M – the decryption
algorithm is executed by the decrypting entity D. It
takes as inputs the public parameters pp, the user’s
secret key sk and the ciphertext CT
0
. The algorithm
returns the message M if D has correctly obtained
the secret key related to the required set of attributes
for deciphering the encrypted message. Otherwise,
the algorithm outputs a reject symbol ⊥.
Our PU-ABE scheme has to satisfy the correct-
ness property. The correctness property requires
SECRYPT 2018 - International Conference on Security and Cryptography
138

that for all security parameter ξ, all attribute uni-
verse descriptions U, all (pp,msk) ∈ setup(ξ), all
(S,U) ⊆ U (i.e; U is the attribute universe), all sk ∈
keygen(pp,msk,Ψ), all M ∈ M (i.e; M is the mes-
sage universe), all Ψ ∈ G (G is the access policy
space), all CT ∈ encrypt(pp,S , M), and all CT
0
∈
(pp,CT, ind,U) if the decrypting user has correctly
obtained the secret key sk related to the Ψ required
access policy S
0
for deciphering the encrypted mes-
sage, the derypt(pp,sk,CT
0
) outputs M.
4.2 Security Model
For designing a secure policy-update attribute based
encryption scheme, we consider the case of malicious
adversaries with respect to the indistinguishability
property. The indistinguishability property means
that if an adversary has some information about the
plaintext, he should not learn about the ciphertext.
This security notion requires the computational
impossibility to distinguish between two messages
chosen by the adversary with a probability greater
than a half.
To design the most suitable security model consi-
dering the confidentiality requirement, we adopt
an updated security model to capture security re-
quirements related to policy updates (Jiang et al.,
2017). PU-ABE is said to be indistinguishable
against non-adaptive chosen ciphertext attacks if
there is no probabilistic polynomial time (PPT)
adversary that can win the Exp
con f
security game
with non-negligible advantage. The Exp
con f
game
is formally defined, between an adversary A and a
challenger C as follows:
INITIALISATION – A selects a set of encryption
attributes S
∗
(i.e; S
∗
corresponds to the set of attri-
butes specified for the encryption) to be used for en-
crypting the challenge ciphertext, as a set of attributes
S
∗
= {a
i
}
i=1..m
where |S
∗
| = m. A sends S
∗
to C.
SETUP – the challenger C runs the setup(ξ) algo-
rithm, sends the public parameters pp to the adversary
A and keeps secret the master key msk.
QUERY PHASE 1 – the adversary A queries, for
each session i, an access policy Ψ
A,i
. The challenger
C answers by running the keygen(pp,msk, Ψ
A,i
) al-
gorithm and sends the resulting secret key sk
A,i
to the
adversary A. Note that the access policy Ψ
A,i
does
not satisfy the encryption attribute set S
∗
.
CHALLENGE PHASE – during the challenge
phase, A picks two equal length cleartexts M
0
∗
and
M
1
∗
as well as an attribute set U
∗
with |U
∗
| = t
U
∗
∩ S
∗
=
/
0 if ind = add or U
∗
⊂ S
∗
if ind = revoke.
The challenger C chooses a random bit b from {0, 1}
with S
0
∗
= S
∗
\ U
∗
for ind = add or S
0
∗
= S
∗
∩ U
∗
for ind = revoke and computes the challenge encryp-
ted message CT
b
∗
= encrypt(pp,S
∗
,M
b
∗
). It gives
CT
b
∗
to the adversary if U =
/
0, otherwise CT
0∗
b
=
update(pp,CT
b
∗
,ind,U
∗
).
QUERY PHASE 2 – in this phase, the adversary A
can query a polynomially bounded number of queries
as in QUERY PHASE 1, except that A cannot query
secret keys related to a set of attributes S
∗
.
GUESS – A tries to guess which message M
i
,
where i ∈ {0, 1} corresponds to the enciphered data
CT
b
∗
. Thus, A outputs a bit b
0
of b and wins the
game if b = b
0
. The advantage of the adversary A in
the above game is defined as Adv
A
[Exp
Con f
(1
ξ
)] =
|Pr[b = b
0
] −
1
2
|.
5 MATHEMATICAL
BACKGROUND
In this section, we first introduce the access structure
in section 5.1. Then, in section 5.2, we present the
bilinear maps. Finally, we introduce some security
assumptions.
5.1 Access Policies
Access policies can be represented as a boolean
functions of attributes or a Linear Secret Sharing
Scheme (LSSS) matrix.
Access Structure – Let P = {P
1
,·· · , P
n
} be a set of
parties. A collection A ⊆ 2
{P
1
,···,P
n
}
is monotone if
∀B,C if B ∈ A and B ⊆ C then C ∈ A.
An access structure is a collection A of non-empty
subsets of {P
1
,·· · , P
n
}, such as A ⊆ 2
{P
1
,···,P
n
}
\
/
0.
Note that any access structure can be converted
into a boolean function. Boolean functions can be
defined as an access tree, where the leaves present the
attributes while the intermediate and the root nodes
are the logical operators AND (∧) and OR (∨).
Linear Secret Sharing Schemes (LSSS) – Let P be a
set of parties, A be l ×n matrix, and ρ : {1, 2, ··· ,l} →
P be a function that maps a row to a party for labeling.
A secret sharing scheme for access structure Ψ over
a set of parties P is a linear secret sharing scheme
(LSSS) in Z
p
and is represented by (A, ρ) if it consists
of two efficient algorithms:
• Share((A,ρ),s): The share algorithm takes as in-
put s ∈ Z
p
which is to be shared. It randomly
chooses β
1
,·· · , β
n
∈ Z
p
, and defines β = (β
1
=
Lightweight Attribute-based Encryption Supporting Access Policy Update for Cloud Assisted IoT
139

s,β
2
,·· · , β
k
)
T
. It outputs M.β as the vectors of l
shares. The share λ
i
=< A
i
,β
T
> belongs to party
ρ(i), where A
i
is the i − th of A.
• Recon((A, ρ),S): The reconstruction algorithm
takes as input an access set S ∈ A. Let I =
{i|ρ(i) ∈ S}. It outputs a set of constants {µ
i
}
i∈I
such that
∑
i∈I
µ
i
· λ
i
= β
1
= s.
5.2 Bilinear Maps
Let G
1
, G
2
and G
T
be three multiplicative groups of
a finite field having the same order p. An admissi-
ble asymmetric pairing function ˆe from G
1
× G
2
in
G
T
has to be bilinear, non degenerate and efficiently
computable.
5.3 The General Diffie-Hellman
Exponent Assumption
In our PU-ABE construction, we make use of the
generalisation of the Diffie-Hellman exponent as-
sumption, formally defined by Boneh et al. in (Boneh
et al., 2005). The authors have introduced a class of
assumptions that appeared with the use of pairing-
based schemes namely Decisional DiffieHellman
assumption (DDH), Bilinear Diffie-Hellman (BDH),
and q-Bilinear Diffie Hellman Exponent (qBDHE)
assumptions, detailed hereafter.
Let B = (p,G
1
,G
2
,G, ˆe : G
1
×G
2
→ G) be a bilinear
map group such that G
1
= G
2
= G. Let g
0
be a
generator of G and set g = ˆe(g
0
,g
0
) ∈ G. Let s
and n be positive integers and P,Q ∈ F
p
[X
1
,·· · , X
n
]
s
be two s-tuples of n-variate polynomials over F
p
where P = (p
1
,·· · , p
s
) and Q = (q
1
,·· · , q
s
) and
p
1
= q
1
= 1. For any function h : F
p
→ Ω and any
vector (x
1
,·· · , x
n
) ∈ F
n
p
, h(P(x
1
,·· · , x
n
)) stands
for (h(p
1
(x
1
,·· · , x
n
)),·· · ,h(p
s
(x
1
,·· · , x
n
))) ∈
Ω
s
and h(Q(x
1
,·· · , x
n
)) stands for
(h(q
1
(x
1
,·· · , x
n
)),·· · ,h(q
s
(x
1
,·· · , x
n
))) ∈ Ω
s
.
Let f ∈ F
p
[X
1
,·· · , X
n
], it is said that f depends on
(P,Q), which we denote by f ∈ P,Q, when there is a
linear decomposition
f =
∑
1≤i, j≤s
a
i, j
· p
i
· p
j
+
∑
1≤i≤s
b
i
· q
I
, a
i, j
,b
i
∈ Z
p
Let P,Q be as above and f ∈ F
p
[X
1
,·· · , X
n
]. The
(P,Q, f )-General Diffie- Hellman Exponent problems
are defined as follows.
Definition 1: (P,Q, f )-GDHE. Given a tuple
H(x
1
,·· · , x
n
) = (g
P(x
1
,···,x
n
)
0
,g
Q(x
1
,···,x
n
)
) ∈ G
s
1
× G
s
,
compute g
f (x
1
,···,x
n
)
.
Definition 2: (P,Q, f )-GDDHE. Given
H(x
1
,·· · , x
n
) ∈ G
s
1
× G
s
, compute g
f (x
1
,···,x
n
)
as
above, decide whether T = g
f (x
1
,···,x
n
)
.
We refer to (Boneh et al., 2005) for a proof that
(P,Q, f )-GDHE and (P,Q, f )-GDDHE have generic
security when f /∈ < P,Q >.
6 A NOVEL KEY POLICY
ATTRIBUTE BASED
ENCRYPTION SUPPORTING
POLICY UPDATE
In this section, we first give an overview of our propo-
sed constant size PU-ABE scheme (subsection 6.1).
Then, we detail the scheme construction.
6.1 Overview
In this paper, we develop a novel key-policy attribute
based encryption scheme that supports access policy
update. Our contribution extends Wang et al.’s key
policy attribute based encryption scheme (Wang and
Luo, 2012) to support adding new attributes or revo-
king others from the encryption access policy. In-
deed, the cloud server is able to change a ciphertext
encrypted with respect to an access policy S to a cip-
hertext encrypted with respect to a new access policy
S
0
such that S
0
corresponds to S ∪ U in case of attri-
butes’ addition and S \ U in case of attributes’ revo-
cation. This update does not need any re-encryption
key neither the data owner to be online. It is only ba-
sed on some extra ciphertext components as detailed
in Section 6.2) which are used by the cloud server in
the update algorithm. Indeed, while encrypting data
contents, E generates additional elements in the cip-
hertext which point out attributes that can be added
or removed later. When an access policy update is
required, the cloud server uses the ciphertext’s com-
ponents to generate a new ciphertext suitable for the
new access policy then forwards it to the decrypting
entity.
6.2 Concrete Construction
Our PU-ABE construction, supporting both attribu-
tes’ addition and revocation, is based on five algo-
rithms defined as follows:
• setup – given the security parameter ξ, the attri-
bute authority chooses three cyclic groups G
1
, G
2
and G
T
of prime order p and defines a bilinear
SECRYPT 2018 - International Conference on Security and Cryptography
140

pairing ˆe : G
1
× G
2
→ G
T
. It also randomly se-
lects two generators g ∈ G
1
and h ∈ G
2
as well
as a secret random value α ∈ Z
∗
p
. In addition, the
attribute authority sets v = ˆe(g,h), {h
α
i
}
i=1···k
and
{u
i
= g
α
i
}
i=1···k
where k = |U| is the cardinal of
the attributes universes U. Finally, it chooses a
cryptographic hash function H : {0,1}
∗
⇒ Z
∗
p
and
outputs the public parameters pp as follows:
pp = (G
1
,G
2
,G
T
,v = ˆe(g,h), h,{h
α
i
}
i=1···k
,
{u
i
= g
α
i
}
i=1···k
)
The master secret key is defined as msk = (g,α).
• encrypt – let S be the set of the encryption
attributes S = {a
i
}
m
i=1
. This algorithm, executed
by the encrypting entity E takes an extra input
which is a maximum revocation number r ≤ m.
The data owner chooses s ∈ Z
∗
p
and computes the
ciphertext CT as follows:
E
0
= h
s·
∏
a
i
∈S
(α+H (a
i
))
E
1
= E
α
0
,·· · , E
k−m
= E
α
k−m−1
C
1
= u
−s
1
=,·· · ,C
r+1
= u
−s
r+1
C
M
= M · ˆe(g,h)
s
• update – the update algorithm first checks the
operation indicator ind. Then, if ind = add,
it proceeds as (i), otherwise if ind = revoke it
executes (ii):
(i) – given a ciphertext CT encrypted w.r.t. a set
of attributes S and U = {a
0
1
,·· · , a
0
t
} a new set of
attributes where U ∩ S =
/
0, the server has to add
elements of U to the set of encrypting attributes
S of the ciphertext CT . To do so, it proceeds as
follows:
Let F(x) be the polynomial in x defined as F(x) =
∏
a
i
∈U
(x + H (a
i
)) = f
t
x
t
+ f
t−1
x
t−1
+ · · · + f
0
Then, the algorithm computes E
0
0
= E
F(α)
0
=
∏
t
i=0
E
f
i
i
. The new ciphertext is then defined
as CT
0
= (E
0
0
,C
1
,C
M
) w.r.t. S
0
, the new set of
encrypting attributes defined as S
0
= S ∪ U.
(ii) – given a ciphertext CT encrypted w.r.t. a set
of attributes S and a revocation attribute set U =
{a
0
1
,·· · , a
0
t
} ⊆ S where t ≤ r, the server updates
the ciphertext CT as follows:
Let F(x) be the polynomial in x as F(x) =
1
∏
a
i
∈U
H (a
i
)
∏
a
i
∈U
(x + H (a
i
)) = f
t
x
t
+ f
t−1
x
t−1
+
··· + f
0
Then, the algorithm computes CT
0
as follows:
E
0
0
= E
1
∏
a
i
∈U
H (a
i
)
0
= h
s·
∏
a
i
∈S\U
(α+H (a
i
))F(α)
C
0
1
=
∏
t+1
t=1
C
f
i−1
i
= g
−αs
∑
t+1
i=1
α
i−1
f
i−1
= u
−sF(α)
1
C
0
M
= C
M
ˆe(
∏
t
i=1
C
− f
i
i
,h) = M ˆe(g,h)
s
∑
t
i=0
f
i
α
i
= Mv
sF(α)
• keygen – it computes the private key associated
to an access structure Ψ w.r.t. an LSSS scheme
(A,ρ) such that A is the corresponding l × n ma-
trix. First, the keygen algorithm generates shares
of 1 relying on the LSSS schema w.r.t. (A,ρ), as
detailed in section 5. Namely, it chooses a column
vector β = (β
1
,β
2
,·· · , β
n
)
T
, while β
1
= s = 1 and
β
2
,·· · , β
n
∈ Z
p
. Then for each i = 1 to l, it calcu-
lates λ
i
=< A
i
,β
T
>, and sets sk as follows:
sk = {D
i
,(K
i, j
)
n
j=0
}
l
i=0
= {g
λ
i
α+H (ρ(i))
,(h
λ
i
α
j
)
n
j=0
}
l
i=0
• decrypt – the cipherext CT
0
is encrypted un-
der the set of attributes S
0
= S ∪ U = {a
t+m
i=1
}.
The decrypting entity D having a secret key
sk
(A,ρ)
first sets I = i|ρ(i) ∈ S
0
, and calcu-
lates the reconstruction of constants µ
i∈I
=
Recon((A,ρ),S ). The decryption key correspon-
ding to the LSSS scheme w.r.t. (A, ρ) is parsed
as sk = {D
i
,(K
i, j
)
n
j=0
}
l
i=0
. Then, D computes the
polynomial on the variable α with degree m+t −1
as follows:
P
i,A(α)
=
λ
i
α
(
∏
j=1, j6=i
(α+H (a
j
))−
∏
j=1, j6=i
H (a
j
)))
D calculates h
P
i,A(α)
according to his secret key
component (K
i, j
)
n
j=0
. Afterwards, she computes
Y
i
which can be retrieved based on two cases w.r.t.
the ind operator value, such that:
– Case 1: if attributes have been added to the
access policy:
Y
i
= ( ˆe(C
1
,h
P
i,A(α)
) · ˆe(D
i
,C
2
))
1
∏
j=1, j6=i
H (a
i
))
= ˆe(g,h)
sλ
i
Finally, D computes Y =
∏
i∈I
Y
µ
i
i
= ˆe(g,h)
s
and retrieves M = C
M
/Y . Note that if no chan-
ges have been made to the access policy and the
corresponding ciphertext, the decryption pro-
cess follows Case 1.
– Case 2: if attributes have been revoked from
the access policy:
Y
i
= ( ˆe(C
0
1
,h
P
i,A(α)
) · e(D
i
,E
0
0
))
1
∏
j=1, j6=i
H (a
i
))
= ˆe(g,h)
sF(α)λ
i
Lightweight Attribute-based Encryption Supporting Access Policy Update for Cloud Assisted IoT
141

Finally, D computes Y =
∏
i∈I
Y
µ
i
i
= ˆe(g,h)
s
and retrieves M = C
0
M
/Y .
7 SECURITY ANALYSIS
In this section, we first prove the correctness of our
PU-ABE construction, with respect to the data de-
cryption algorithms proposed in the previous con-
struction, in section 7.1. Then, we prove the security
of our proposal, with respect to the indistinguishabi-
lity property in Section 7.2.
7.1 Correctness
In the following, we prove the correctness of the PU-
ABE proposed construction w.r.t. the attributes’ ad-
dition and revocation. A decrypting entity D who
possesses a set of attributes expressed with respect to
an access structure Ψ, satisfying S
0
first sets P
i,A(α)
=
λ
i
α
(
∏
j=1, j6=i
(α + H (a
j
)) −
∏
j=1, j6=i
H (a
j
))). Then,
D uses his secret keys to compute Y
i
with respect to
the two following cases:
• Case 1: if ind = add and S
0
= S ∪ U, then Y
i
is
computed as:
Y
i
= [ ˆe(C
0
1
,h
P
i,A(α)
) · ˆe(D
i
,E
0
0
)]
1
∏
j=1, j6=i
H (a
j
))
= [ ˆe(g
−αs
,h
P
i,A(α)
) · ˆe(g
λ
i
α+H (ρ(i))
,E
F(α)
0
)]
1
∏
j=1, j6=i
H (a
j
))
= [ ˆe(g
−αs
,h
P
i,A(α)
)
· ˆe(g
λ
i
α+H (ρ(i))
,h
s·
∏
a
j
∈A
(α+H (a
j
))F(α)
)]
1
∏
j=1, j6=i
H (a
j
))
= [ ˆe(g,h)
−αsP
i,A(α)
· ˆe(g,h)
sλ
i
F(α)·
∏
j=1, j6=i
(α+H (a
j
))
)]
1
∏
j=1, j6=i
H (a
j
))
= [ ˆe(g,h)
−sλ
i
(
∏
j=1, j6=i
(α+H (a
j
))
ˆe(g,h)
sλ
i
∏
j=1, j6=i
H (a
j
)
· ˆe(g,h)
sλ
i
F(α)·
∏
j=1, j6=i
(α+H (a
j
))
]
1
∏
j=1, j6=i
H (a
j
)
= [ ˆe(g,h)
sλ
i
∏
j=1, j6=i
H (a
j
)
]
1
∏
j=1, j6=i
H (a
j
)
= ˆe(g,h)
sλ
i
Afterwards, the decrypting entity D computes:
Y =
∏
i∈I
Y
µ
i
i
=
∏
i∈I
ˆe(g,h)
sλ
i
µ
i
= ˆe(g,h)
s
∑
i∈I
λ
i
µ
i
= ˆe(g,h)
s
Recall that the constants mu
i∈I
are
the reconstruction of the LSSS matrix
µ
i∈I
= Recon((A,ρ),A). Therefore, the user
retrieves Y using the following equation
< λ,µ >=
∑
i∈I
λ
i
µ
i
=
∑
i∈I
β
1
=
∑
i∈I
1 = 1
Finally, D retrieves M such as:
M =
C
M
Y
=
C
M
ˆe(g,h)
s
=
M ˆe(g,h)
s
ˆe(g,h)
s
• Case 2: if ind = revoke and S
0
= S \ U, Y
i
is com-
puted as follows:
Y
i
= [ ˆe(C
0
1
,h
P
i,A(α)
) · ˆe(D
i
,E
0
0
)]
1
∏
j=1, j6=i
H (a
j
))
= [ ˆe(u
−sF(α)
1
,h
P
i,A(α)
) · ˆe(g
λ
i
α+H (ρ( j))
,
h
s·
∏
a
j
∈A\U
(α+H (a
j
))F(α)
)]
1
∏
j=1, j6=i
H (a
j
))
= [ ˆe(g,h)
−sλ
i
F(α)(
∏
j=1, j6=i
(α+H (a
i
))−
∏
j=1, j6=i
H (a
i
)))
·
ˆe(g,h)
sλ
i
·
∏
j=1, j6=i
(α+H (a
j
))F(α)
)]
1
∏
j=1, j6=i
H (a
j
))
= [ ˆe(g,h)
−sλ
i
F(α)(
∏
j=1, j6=i
(α+H (a
i
))
· ˆe(g, h)
sλ
i
F(α)
∏
j=1, j6=i
H (a
i
)))
· ˆe(g, h)
sλ
i
F(α)·
∏
j=1, j6=i
(α+H (a
j
)))
]
1
∏
j=1, j6=i
H (a
j
))
= ˆe(g, h)
sλ
i
F(α))
∏
j=1, j6=i
H (a
i
)
∏
j=1, j6=i
H (a
j
)
= ˆe(g, h)
sF(α)λ
i
Afterwards, the decrypting entity computes:
Y =
∏
i∈I
Y
µ
i
i
=
∏
i∈I
ˆe(g,h)
sF(α)λ
i
µ
i
= ˆe(g,h)
sF(α)
∑
i∈I
λ
i
µ
i
= ˆe(g,h)
sF(α)
Finally, D retrieves M such as:
M =
C
0
M
Y
=
C
0
M
ˆe(g,h)
sF(α)
=
M ˆe(g,h)
sF(α)
ˆe(g,h)
sF(α)
7.2 Confidentiality
In the following proof, we prove that our PU-ABE
scheme is CPA-Secure against non-adaptive Chosen
Ciphertext Attacks with respect to Theorem 1.
Theorem 1. For any adversary A, against CPA-
Secure against non-adaptive chosen ciphertext, our
PU-ABE scheme is indistinguishable according to
Definition 4.2 with respect to the hardness of the Ge-
neral Diffie-Hellman Exponent (GDHE) assumption (
Definition 5.3)
SECRYPT 2018 - International Conference on Security and Cryptography
142

Proof. To decrypt a ciphertext CT’ associated with an
updated access policy S
0
, A must recover ˆe(g,h)
s
, in
case of attributes’ addition and ˆe(g,h)
s
∑
t
i=0
f
i
α
i
, in case
of attributes’ revocation, where the secret sharing key
s is embedded in the ciphertext. For this purpose, A
has to retrieve the corresponding
˜
C
M
and the related
private key.
To prove that our scheme is secure against
selective non-adaptive chosen ciphertext attacks,
we first consider that A is running the Exp
con f
experiment with an entity B. This latter is running
the Exp
B
. Wang et al. security game (Wang and
Luo, 2012), with C. The objective of this proof is to
show that the advantage of A to win the G
S−CPA
(1
κ
)
security game is equivalent to the advantage of Exp
B
to win the Wang et al. security game (Wang and Luo,
2012). Hereafter, A and B proceed as follows:
INITIALISATION – in this phase, the adversary A
gives the algorithm C a challenge set of attributes S
∗
.
SETUP – the challenger C runs the
setup(ξ) algorithm, sends the public parameters
pp = (G
1
,G
2
,G
T
,v = ˆe(g,h),g
α
,h,h
α
,·· · , h
α
k
,{u
i
=
g
α
i
}
i=1···k
) to B and keeps secret msk. Consequently,
B sends pp to A.
QUERY PHASE 1 – B sets an empty table T and
repeatedly queries an access policy Ψ
A,i
, for each ses-
sion i. That is, B uses C to derive and send the
queried secret keys to A. The challenger C ans-
wers by running the keygen(pp,msk, Ψ
A,i
) algorithm.
The challenger C generates shares of 1 relying on
the LSSS schema w.r.t. (A,ρ). It chooses a co-
lumn vector β = (β
1
,β
2
,·· · , β
n
)
T
, while β
1
= s = 1
and β
2
,·· · , β
n
∈ Z
p
. Then for each i = 1 to l, it
calculates λ
i
=< A
i
,β
T
>, and sets sk as sk
A,i
=
{g
λ
i
α+H (ρ(i))
,(h
λ
i
α
j
)
n
j=0
}
l
i=0
.
Note that the access policy Ψ
A,i
does not satisfy
the encryption attribute set S
∗
. The private keys
sk
A,i
= {g
λ
i
α+H (ρ(i))
,(h
λ
i
α
j
)
n
j=0
}
l
i=0
are returned to B.
Subsequently, B sets a new entry with the private key
and returns sk
A,i
= {g
λ
i
α+H (ρ(i))
,(h
λ
i
α
j
)
n
j=0
}
l
i=0
to A.
CHALLENGE PHASE – during the challenge
phase, A picks two equal length cleartexts M
0
∗
and
M
1
∗
as well as an attribute set U
∗
with |U
∗
| = t
U
∗
∩ S
∗
=
/
0 if ind = add or U
∗
⊂ S
∗
if ind = revoke.
Subsequently, B selects S
B
such that S
B
⊆ S
0
∗
, such
as S
0
∗
= S
∗
\ U
∗
for ind = add or S
0
∗
= S
∗
∩ U
∗
for
ind = revoke.
Afterwards, B sends the access structure S
B
and the
two equal length messages M
0
and M
1
, defined by
A to the challenger C . The challenger C chooses
a random bit b from {0,1} with S
0
B
= S
B
\ U
∗
for ind = add or S
0
B
= S
B
∩ U
∗
for ind = revoke
and computes the challenge encrypted message
CT
b
∗
= encrypt(pp,S
0
B
,M
b
∗
).
E
0
= h
s·
∏
a
i
∈S
0
B
(α+H (a
i
))
E
1
= E
α
0
,·· · , E
p−m
= E
p−m−1
C
1
= u
−s
1
=,·· · ,C
r+1
= u
−s
r+1
C
M
= M ·v
s
= M · ˆe(g,h)
s
The challenger C gives CT
b
∗
to the adversary if
U =
/
0, otherwise CT
0∗
b
= up date(pp,CT
b
∗
,ind,U
∗
).
QUERY PHASE 2 – in this phase, the adversary A
can query a polynomially bounded number of queries
as in QUERY PHASE 1, except that A cannot query
secret keys related to a set of attributes S
∗
.
Hereafter, two cases are considered w.r.t. the ind
operator value, randomly selected by C in order to
encrypt the challenging message such that:
• Case 1 – the first case corresponds to attributes’
addition, such that C sets S
0
B
= S
B
∪ U
∗
and
outputs an encrypted message CT
0
b
, as defined in
section 6.2. In this case, we first show that how a
challenge ciphertext should be produced. In fact,
given a ciphertext CT encrypted w.r.t. a set of at-
tributes S
B
and U
∗
= {a
0
1
,·· · , a
0
t
} a new set of at-
tributes where U ∩ S =
/
0, C has to add elements
of U
∗
to the set of encrypting attributes S
B
of the
ciphertext CT
0
b
. To do so, it proceeds as follows:
Let F(x) be the polynomial in x defined as F(x) =
∏
a
i
∈U
∗
(x + H (a
0
i
)) = f
t
x
t
+ f
t−1
x
t−1
+ ··· + f
0
Then, the algorithm computes E
0∗
0
= E
∗
F(α)
0
=
∏
t
i=0
E
f
i
i
. The new ciphertext is then defined as
CT
0
b
= (E
0∗
0
,C
1
,C
M
) w.r.t. S
0
, the new set of en-
crypting attributes defined as S
0
B
= S
B
∪ U
∗
.
• Case 2 – the second case corresponds to attribu-
tes’ revocation, such that C defines S
0
B
= S
B
\U
∗
and outputs an encrypted message CT
0
b
, as de-
tailed in section 6.2. That is, given a ciphertext
CT encrypted w.r.t. a set of attributes S
0
B
and a
revocation attribute set U
∗
= {a
0
1
,·· · , a
0
t
} ⊆ S
0
B
where t ≤ r, the server updates the ciphertext
CT
0
b
as follows: Let F(x) be the polynomial in x
as F(x) =
1
∏
a
0
i
∈U
∗
H (a
0
i
)
∏
a
0
i
∈U
(x +H (a
0
i
)) = f
t
x
t
+
f
t−1
x
t−1
+ ··· + f
0
. Similarly, the new ciphertext
is then defined as CT
0
b
= (E
0∗
0
,C
0∗
1
,C
0∗
M
) w.r.t.
S
0
, the new set of encrypting attributes defined as
S
0
B
= S
B
\ U
∗
.
Lightweight Attribute-based Encryption Supporting Access Policy Update for Cloud Assisted IoT
143

Without loss of generality, the distribution of the
received challenge ciphertext does not depend on the
attributes’ addition and revocation. More precisely,
the distribution of the challenge enciphered message
is quite similar in both cases. Thus, the resistance of
PU-ABE scheme against CPA, follows (Wang and
Luo, 2012) construction, w.r.t. to B, that is proven
secure under the GDDHE assumption. Thus, the
view of B is indistinguishable from the view of A,
considering a randomly selected enciphered message
w.r.t. S
0
B
referring to the updated access policy.
As such, we prove that our PU-ABE construction
is secure against selective non-adaptive chosen cip-
hertexts attacks in the standard model, under the GD-
DHE assumption, with respect to Exp
con f
security ex-
periment.
8 PERFORMANCES ANALYSIS
In this section, we present the computation and
the storage complexities of our proposed PU-ABE
scheme. In our analysis, we are interested in the com-
putations performed to execute the encrypt, update
and the decrypt algorithms as well as the size of the
generated encrypted message and the size of the se-
cret keys as introduced in Table 1.
8.1 Storage Complexities
Emura et al. (Emura et al., 2009) introduced a KP-
ABE scheme requiring only 2 keys per user indepen-
dent of the users’ attributes. In addition, this scheme
generates a ciphertext composed only of 3 elements.
Herranz et al. (Herranz et al., 2010) have proposed the
first CP-ABE scheme generating a ciphertext whose
size does not depend on the number of attributes used
in the threshold access policy. In this scheme, the de-
crypting entity needs k + n secret keys’ where k is the
cardinal of the attributes universes and n is the num-
ber of the users’ attributes.
In (Ge et al., 2012), the authors proposes a CP-ABE
scheme with constant ciphertext size. However, this
schemes requires the use of 3k − 2 + n secret keys.
Similarly, the authors in (Wang and Luo, 2012) pro-
posed a KP-ABE scheme which produces only 3 ele-
ments in the ciphertext. The users’ secret keys are
equal to k(n + 1). This size of secret keys is due to
the use of LSSS monotone access policies which ma-
kes the scheme more expressive than the aforementi-
oned schemes.
Although, the above schemes ensure low storage
and communication costs, they do not support access
policy updates. Indeed, if the access rights change
with the addition or the revocation of some attributes,
outsourceddata need to be re-encrypted.
Jiang et al. (Jiang et al., 2017), have proposed
a threshold CP-ABE scheme supporting access po-
licy update. The authors proposed two different con-
struction. The first construction ensures the addition
of attributes to the access policy. This incurs the gene-
ration of a ciphertext whose size is equal to 3 + k − m
to be forwarded to the cloud server however the final
user only receives 3 elements of the ciphertext no mat-
ter how many attributes are used in the access policy.
The second construction provides the ability to revoke
attributes from the access policy. Therefore, the gene-
rated access policy depends on the maximum number
of attributes in an attribute revocation list. Like the
first construction, the user only needs three elements
to decrypt data. Both the proposed construction re-
quire n + 1 secret keys for every user.
In our PU-ABE scheme, we apply a compact po-
licy update technique to ensure adding and/or remo-
ving attributes from access policies in KP-ABE sche-
mes. Therefore, the proposed construction genera-
tes a ciphertext size equal to 3 + k + r − m. Users
receives a constant ciphertext size independent from
the number of attributes involved in the access po-
licy and from the applied update procedures. PU-
ABE relies in using monotone access policies, then
the users secret keys are equal to n+k elements. The-
refore, the proposed PU-ABE scheme ensures expres-
siveness and policy updates while introducing compa-
rative storage with similar ABE schemes.
8.2 Computation Complexities
The proposed schemes in (Emura et al., 2009), (Her-
ranz et al., 2010) and (Wang and Luo, 2012) introduce
an encryption algorithm which requires two exponen-
tiations in G
1
and one exponentiation in G. Ge et
al.’s scheme (Ge et al., 2012) introduces an encryp-
tion algorithm requiring 5 exponentiations in G
1
and
one exponentiation in G.
In Emura et al.’ scheme (Emura et al., 2009), the de-
crypting entity needs to perform two pairing operati-
ons and 3 exponentiations in G
1
. Herranz et al. (Her-
ranz et al., 2010) decryption algorithm requires n + 1
exponentiations in G
1
, 5 pairing functions and one ex-
ponentiation in G. In (Ge et al., 2012) scheme, the
users executes 4 pairing operations and 2(k − n) ex-
ponentiations in G
1
. Wang et al. proposed a KP-ABE
scheme (Wang and Luo, 2012) where the decryption
algorithm performs n + 1 exponentiations in G, one
exponentiation in G
1
and two pairing operations.
The aforementioned schemes do not ensure access
SECRYPT 2018 - International Conference on Security and Cryptography
144

Table 1: Features and Functionality Comparison of Attribute Based Encryption Schemes.
Scheme Policy Update Access Policy Type Key size Ciphertext size Encryption Cost Update Cost Decryption Cost
(Emura et al., 2009) 7 AND-Gates CP-ABE 2 3 2E
1
+ E – 2τ
p
+ 3E
1
(Herranz et al., 2010) 7 Monotone KP-ABE k+n 3 2E
1
+ E – (n + 1)E
1
+ 5τ
p
+ E
(Ge et al., 2012) 7 Threshold CP-ABE 3k − 2 + n 4 5E
1
+ E – 4τ
p
+ 2E
1
(k − n)
(Wang and Luo, 2012) 7 Monotone KP-ABE k(n + 1) 3 2E
1
+ E – (n + 1)E +E
1
+ 2τ
p
(Jiang et al., 2017)
X Threshold CP-ABE n + 1 3 + k − m / 3 (k − m + 2)E
1
+ E tE
1
nE
1
+ 2τ
p
X Threshold CP-ABE n + 1 r + 3 / 3 (r + 2)E
1
+ E (2t + 2)E
1
+ τ
p
nE
1
+ 2τ
p
PU-ABE X Monotone KP-ABE (n+ 1)k 3 + k − m + r/3 (k − m + 2 + r)E
1
+ E tE
1
/(2t + 2)E
1
+ τ
p
2τ
p
+ E
1
+ (n + 1)E
We denote by E
1
the exponentiation cost in G
1
, E the exponentiation cost in G and τ
P
the computation cost of a
pairing function ˆe. n is the number of attributes of a user. k is the cardinal of the universe of attributes U. m is
the number of attributes used in an access policy for encryption. t is the number of attributes (t = |U|) added or
removed from an access policy and r is the maximum number of attributes supported by the revocation list.
policies update. Jiang et al.’s scheme is the first
CP-ABE scheme supporting policy updates. In this
scheme, the encryption algorithm related to the at-
tributes addition construction require k − m + 2 ex-
ponentiations in G
1
and only one exponentiation in
G. In addition, the attribute revocation encryption
algorithms requires r + 2 exponentiations in G
1
and
only one exponentiation in G. This proposal con-
sists in executing an update algorithm by the cloud
server to update the used access policy used in the
encryption. Therefore, it requires t exponentiations
in G
1
to add attributes and 2t + 2 exponentiations in
G
1
and one pairing operation to revoke attributes. In
(Jiang et al., 2017), the decryption algorithm incurs
2τ
p
+ nE
1
overhead.
PU-ABE scheme requires the execution of (k −
m + 2 + r) exponentiations in G
1
and only one expo-
nentiation in G. The proposed scheme requires the
execution of two update functions to add attributes or
revoke attributes from the access policy. To add new
attributes, it requires t exponentiations in G
1
while
revoking t attributes needs to an overhead equal to
(2t + 2)E
1
+ τ
p
, where t is the number of attributes
to be added or removed. Our PU-ABE scheme requi-
res 2τ
p
+ E
1
+ (n + 1)E as a decryption overhead due
to the use of monotone access policies.
Above all, our proposed PU-ABE scheme pre-
sents quite similar to the computation costs of the re-
lated attribute based encryption schemes while provi-
ding more practical features mainly related to expres-
siveness and policy update.
9 CONCLUSIONS
Attribute based encryption is often used to ensure en-
crypted access control to outsourced data for multi-
user settings. That is, in several applications, users
are removed and/or added, thus, it require an efficient
update of users’ access rights.
In this paper, we propose PU-ABE, a novel key
policy attribute based encryption technique, with
short size ciphertexts that supports access policy up-
date. Indeed, a cloud server can add and/or remove
attributes from the encryption access policy without
requiring data re-encryption. The proposed PU-ABE
scheme is proved to be secure against chosen cipher-
texts attacks in the standard model. Finally, a detailed
performances analysis showed that PU-ABE cipher-
texts are short-sized and independent from the num-
ber of attributes used in the access policy which af-
fords low communication and storage costs, compa-
red to most-closely related schemes.
ACKNOWLEDGEMENTS
This research is supported by STRATUS (Security
Technologies Returning Accountability, Trust and
User-Centric Services in the Cloud), a project funded
by the Ministry of Business, Innovation and Employ-
ment (MBIE), New Zealand.
REFERENCES
Attrapadung, N., Herranz, J., Laguillaumie, F., Libert, B.,
De Panafieu, E., and R
`
afols, C. (2012). Attribute-
based encryption schemes with constant-size cipher-
texts. Theoretical Computer Science, 422:15–38.
Atwady, Y. and Hammoudeh, M. (2017). A survey on au-
thentication techniques for the internet of things. In
Proceedings of the International Conference on Fu-
ture Networks and Distributed Systems, page 8. ACM.
Bacis, E., De Capitani di Vimercati, S., Foresti, S., Pa-
raboschi, S., Rosa, M., and Samarati, P. (2016a).
Mix&slice: Efficient access revocation in the cloud. In
Proceedings of the 2016 ACM SIGSAC Conference on
Computer and Communications Security, pages 217–
228. ACM.
Bacis, E., di Vimercati, S. D. C., Foresti, S., Paraboschi, S.,
Rosa, M., and Samarati, P. (2016b). Access control
management for secure cloud storage. In Internatio-
nal Conference on Security and Privacy in Communi-
cation Systems, pages 353–372. Springer.
Lightweight Attribute-based Encryption Supporting Access Policy Update for Cloud Assisted IoT
145

Belguith, S., Jemai, A., and Attia, R. (2015). Enhancing
data security in cloud computing using a lightweight
cryptographic algorithm. In ICAS 2015 : The Eleventh
International Conference on Autonomic and Autono-
mous Systems, pages 98–103. IARIA.
Belguith, S., Kaaniche, N., Jemai, A., Laurent, M., and
Attia, R. (2016). Pabac: a privacy preserving attri-
bute based framework for fine grained access control
in clouds. In 13th IEEE International Conference on
Security and Cryptography(Secrypt).
Belguith, S., Kaaniche, N., Laurent, M., Jemai, A., and At-
tia, R. (2017). Constant-size threshold attribute ba-
sed signcryption for cloud applications. In SECRYPT
2017: 14th International Conference on Security and
Cryptography, volume 6, pages 212–225.
Belguith, S., Kaaniche, N., Laurent, M., Jemai, A., and
Attia, R. (2018). Phoabe: Securely outsourcing
multi-authority attribute based encryption with policy
hidden for cloud assisted iot. Computer Networks,
133:141–156.
Bethencourt, J., Sahai, A., and Waters, B. (2007).
Ciphertext-policy attribute-based encryption. In IEEE
Symposium on Security and Privacy.
Boneh, D., Boyen, X., and Goh, E.-J. (2005). Hierarchical
identity based encryption with constant size cipher-
text. In Annual International Conference on the The-
ory and Applications of Cryptographic Techniques,
pages 440–456. Springer.
Coates, A., Hammoudeh, M., and Holmes, K. G. (2017). In-
ternet of things for buildings monitoring: Experiences
and challenges. In Proceedings of the International
Conference on Future Networks and Distributed Sys-
tems, page 38. ACM.
Emura, K., Miyaji, A., Nomura, A., Omote, K., and
Soshi, M. (2009). A ciphertext-policy attribute-based
encryption scheme with constant ciphertext length.
In International Conference on Information Security
Practice and Experience, pages 13–23. Springer.
Esposito, C. and Ciampi, M. (2015). On security in pu-
blish/subscribe services: a survey. IEEE Communica-
tions Surveys & Tutorials, 17(2):966–997.
Farhan, M., Jabbar, S., Aslam, M., Hammoudeh, M.,
Ahmad, M., Khalid, S., Khan, M., and Han, K.
(2018). Iot-based students interaction framework
using attention-scoring assessment in elearning. Fu-
ture Generation Computer Systems, 79:909–919.
Ge, A., Zhang, R., Chen, C., Ma, C., and Zhang, Z. (2012).
Threshold ciphertext policy attribute-based encryption
with constant size ciphertexts. In Australasian Con-
ference on Information Security and Privacy, pages
336–349. Springer.
Ge, C., Susilo, W., Fang, L., Wang, J., and Shi, Y.
(2018). A cca-secure key-policy attribute-based proxy
re-encryption in the adaptive corruption model for
dropbox data sharing system. Designs, Codes and
Cryptography, pages 1–17.
Goyal, V., Pandey, O., Sahai, A., and Waters, B. (2006).
Attribute-based encryption for fine-grained access
control of encrypted data. In The 13th ACM confe-
rence on Computer and communications security.
Herranz, J., Laguillaumie, F., and R
`
afols, C. (2010). Con-
stant size ciphertexts in threshold attribute-based en-
cryption. In International Workshop on Public Key
Cryptography, pages 19–34. Springer.
Ion, M., Russello, G., and Crispo, B. (2012). Design and
implementation of a confidentiality and access cont-
rol solution for publish/subscribe systems. Computer
networks, 56(7):2014–2037.
Jiang, Y., Susilo, W., Mu, Y., and Guo, F. (2016).
Ciphertext-policy attribute based encryption suppor-
ting access policy update. In International Conference
on Provable Security, pages 39–60. Springer.
Jiang, Y., Susilo, W., Mu, Y., and Guo, F. (2017).
Ciphertext-policy attribute-based encryption suppor-
ting access policy update and its extension with pre-
served attributes. International Journal of Information
Security, pages 1–16.
Kaaniche, N. and Laurent, M. (2017a). Attribute based en-
cryption for multi-level access control policies. In SE-
CRYPT 2017: 14th International Conference on Secu-
rity and Cryptography, volume 6, pages 67–78. Scite-
press.
Kaaniche, N. and Laurent, M. (2017b). Data security and
privacy preservation in cloud storage environments
based on cryptographic mechanisms. Computer Com-
munications, 111:120–141.
Li, J., Sha, F., Zhang, Y., Huang, X., and Shen, J. (2017).
Verifiable outsourced decryption of attribute-based
encryption with constant ciphertext length. Security
and Communication Networks, 2017.
Liang, K., Au, M. H., Liu, J. K., Susilo, W., Wong, D. S.,
Yang, G., Yu, Y., and Yang, A. (2015). A secure
and efficient ciphertext-policy attribute-based proxy
re-encryption for cloud data sharing. Future Gene-
ration Computer Systems, 52:95–108.
Nkenyereye, L., Park, Y., and Rhee, K. H. (2016). A
secure billing protocol over attribute-based encryp-
tion in vehicular cloud computing. EURASIP Jour-
nal on Wireless Communications and Networking,
2016(1):196.
Ogawa, K., Tamura, S., and Hanaoka, G. (2017). Key mana-
gement for versatile pay-tv services. In International
Workshop on Security and Trust Management, pages
3–18. Springer.
Sahai, A. and Waters, B. (2005). Fuzzy identity-based en-
cryption. In EUROCRYPT 2005.
Wang, C.-J. and Luo, J.-F. (2012). A key-policy attribute-
based encryption scheme with constant size cipher-
text. In Computational Intelligence and Security
(CIS), 2012 Eighth International Conference on, pa-
ges 447–451. IEEE.
Yao, X., Chen, Z., and Tian, Y. (2015). A lightweight
attribute-based encryption scheme for the internet
of things. Future Generation Computer Systems,
49:104–112.
SECRYPT 2018 - International Conference on Security and Cryptography
146
