An Efficient Privacy-preserving Recommender System for e-Healthcare
Systems
Danilo Verhaert, Majid Nateghizad and Zekeriya Erkin
Cyber Security Group, Department of Intelligent Systems, Delft University of Technology, The Netherlands
Keywords:
Recommender System, Privacy-preserving, Homomorphic Encryption, Multi-party Computation,
Comparison Protocol.
Abstract:
The significant growth of medical data has necessitated the development of secure health-care recommender
systems to assist people with their health-being effectively. Unfortunately, there is still a considerable gap
between the performance of secure recommender systems and normal versions. In this work, we develop
a privacy-preserving health-care recommendation algorithm to reduce that gap. The main strength of our
contribution lies in providing a highly efficient solution, while the sensitive medical data are kept confidential.
Our studies show that the runtime of our protocol is 81,5% faster than the existing implementation for small
bit-lengths, and even more so for large bit-lengths.
1 INTRODUCTION
Deploying advanced information technology in the
healthcare field has resulted in the migration of med-
ical records from paper-based to Electronic Health
Records (EHRs). This migration has facilitated shar-
ing of medical data to healthcare organizations and
research institutions, to provide high-quality health-
care services faster and more convenient (Longo and
Drazen, 2016). This concerns health services includ-
ing but not limited to storing, managing, analyzing,
and sharing of EHRs (Baroody and Hansen, 2012;
Tiggle, 2012). Having a large amount of EHRs along-
side other health information can be very beneficial
for people who are seeking for medical information.
In fact, this amount of medical information is chang-
ing the behavior of patients to become more edu-
cated and self-caring (Gavgani, 2010). Recent stud-
ies (Kivits, 2006; McMullan, 2006) show that well-
informed patients are more involved in their treat-
ment, and their behavior in the patient-physician re-
lationship changes.
However, the vast amount and irrelevancy of med-
ical information are great challenges for patients, hin-
dering them from drawing a conclusion on their health
status and taking proper actions (Sommerhalder et al.,
2009). As a solution to this challenge, Recommender
Systems (RSs) can collect the information from dif-
ferent resources and generate recommendations based
on the preferences of patients for a set of condi-
tions such as age, gender, and symptoms (Lu et al.,
2015). RSs allow patients to get preliminary advice
on specific symptoms, choose proper physicians in
their vicinity who are experts in the particular field,
or build a community of patients who have the simi-
lar diseases.
Although RSs can benefit patients in many ways,
using RSs, especially in the medical domain, raises
privacy concerns (Ramakrishnan et al., 2001; Fiza
et al., 2016). Patients’ preferences and medical in-
formation are highly privacy-sensitive. Medical in-
formation may include types of diseases and symp-
toms, personal data, and financial information, which
are the potential targets for attackers (Chhanabhai
and Holt, 2007; Alem
´
an et al., 2013). The privacy
challenges in RSs arises doubts in patients, making
them less willing to share their sensitive medical data
RSs. Data encryption is a well-known approach to
address the privacy concerns in RSs, since it provides
data confidentiality, while the data can be still uti-
lized for generating recommendations without loss of
accuracy (Katzenbeisser and Petkovic, 2008; Hoens
et al., 2013). However, applying data encryption
to any system introduces significant overheads both
computation- and communication-wise. This chal-
lenge is what causes a huge performance gap between
the performance of a system when operations are per-
formed over clear data and the secure version of the
same system. Many researchers have been focusing
on improving cryptographic building-blocks recently
188
Verhaert, D., Nateghizad, M. and Erkin, Z.
An Efficient Privacy-preserving Recommender System for e-Healthcare Systems.
DOI: 10.5220/0006858501880199
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 188-199
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Nateghizad et al., 2016; Schoenmakers and Tuyls,
2006).
In this work, we improve the performance of
(Hoens et al., 2013) through using state-of-the-
art cryptographic building blocks and algorithmic
changes. In (Hoens et al., 2013), a framework is intro-
duced that enables patients to receive recommenda-
tions to choose the best physicians based on their pref-
erence and conditions in a privacy-preserving form.
The system also allows patients to rate their physi-
cians, which later helps to rank these physicians based
on their reputation and thereby generate more accu-
rate recommendations. However, the low efficiency
of the system makes it challenging to use it in large-
scale applications.
2 RELATED WORK
The importance of protecting users’ private data in
RSs has made researchers introduce different ap-
proaches to achieve secure RSs. Among these ap-
proaches, data perturbation (Agrawal and Srikant,
2000) and cryptography (Lindell and Pinkas, 2000)
have as of late been investigated further in the litera-
ture. To statistically protect private data, Polat and Du
in (Polat and Du, 2005) proposed a secure RS by us-
ing randomized perturbation techniques in (Agrawal
and Srikant, 2000). Later, Zhang et al. (Zhang et al.,
2006) proved that original private data can be de-
rived from the disguised data by employing two tech-
niques: k-means clustering and singular value decom-
position. To achieve a trade-off between privacy and
accuracy, Shokri et al. (Shokri et al., 2009) introduced
an RS that is built on a distributed communication
and aggregation to hide private data. McSherry and
Mironov (McSherry and Mironov, 2009) proposed
an RSs that provides differential privacy, surveyed
by Dwork (Dwork, 2007), with the same trade-off
between security and privacy. Cissee and Albayrak
(Ciss
´
ee and Albayrak, 2007) developed a privacy-
preserving RS based on multi-agent system technol-
ogy demanding a secure environment and trusted soft-
ware. Canny (Canny, 2002) introduced a secure RS
to aggregate data securely, allowing users to generate
recommendations from their preference data.
Katzenbeisser and Petkovic (Katzenbeisser and
Petkovic, 2008) proposed a secure RS for consumer
healthcare using cryptographic private profile match-
ing techniques. Erkin el al. (Erkin et al., 2011; Erkin
et al., 2012) developed more efficient RSs built on
multi-party computation and homomorphic encryp-
tion. Although using cryptographic techniques guar-
antees preventing private data leakage, it introduces
computational and communicational overheads and
requires the presence of a semi-trusted third party in
the protocols. Hoens et al. (Hoens et al., 2013) de-
veloped a framework built upon cryptographic tools
that enables patients to find proper physicians based
on their preference data. Their system allows patients
to contribute their rating for physicians in the sys-
tem. However, (Hoens et al., 2013) introduces sig-
nificant overhead, computation- and communication-
wise. Using inefficient building blocks and converting
encrypted decimal values to binary form are among
the main reasons that make the recommendation sys-
tem in (Hoens et al., 2013) impractical in large-scale
databases.
3 PRELIMINARIES
In this section, we describe several preliminaries re-
quired for understanding the protocol. We first ex-
plain the cryptographic primitives and follow up by
describing the building blocks in the protocol. Here-
after the framework and architecture of the system are
elaborated on.
3.1 Cryptographic Primitives
3.1.1 Homomorphic Encryption
Homomorphic encryption is a type of encryption
where performing certain operations on encrypted
data results in operations on the underlying data. In
this work, we rely on an additively homomorphic
cryptosystem, Paillier (Paillier, 1999). Given two
encrypted messages E
pk
(m
1
) and E
pk
(m
2
), a new
ciphertext whose decryption yields the sum of the
plaintext messages m
1
and m
2
can be obtained by
performing a certain operation over the ciphertexts:
D
sk
(E
pk
(m
1
)∗E
pk
(m
2
)) = m
1
+m
2
. Consequently, an
exponentiation of a ciphertext with any public value
yields the encrypted product of the original plaintext
and exponent: D
sk
(E
pk
(m)
e
) = m ∗ e.
3.1.2 Secret Sharing
The concept of secret sharing refers to methods for
distributing a secret s amongst a group of participants,
each of whom is allocated a part of the secret. The se-
cret can be reconstructed only when a sufficient num-
ber of shares are combined together. We use the secret
sharing scheme of A. Shamir (Shamir, 1979), which
assumes n parties share a secret s in a way that each
party owns the function value f
s
(i) of a polynomial f
s
with a degree of at most t and s = f
s
(0). Note that in
An Efficient Privacy-preserving Recommender System for e-Healthcare Systems
189

Table 1: Symbols and their descriptions.
Symbol Description Symbol Description
a,b Secret inputs n Number of servers
E Encryption function t threshold
D Decryption function s
jk
Score for physician j on condition k
m Plaintext r
jk
Rating for physician j on condition k
c Ciphertext w
jk
Weight for physician j on condition k
s Secret v Weight for certain health conditions
l Bit length of secret inputs b Experience factor
i Patient q Thresholds for the experience factor
j Physician m thresholds for the experience factor
k Health condition ∈
R
X A random number in X
[a] Encrypted value of a / Integer division
[a]
lB
Encryption of l least significant bits of a f
jk
Non-zero flag
Z
n
Paillier message space δ Difference in experience factors
the remainder of this paper, computational servers are
used as parties for this scheme.
3.1.3 Secure Multi-party Computation
The goal of secure multi-party computation is to eval-
uate a certain function based on the secrets of multiple
parties. This work makes use of two secure multi-
party computations (MPC). The first MPC is sharing
a value additively amongst several parties, and the
second MPC is threshold decryption which enables a
group of k out of n parties to securely decrypt a value
without leaking any information about the private key
as studied by Damg
˚
ard and Jurik (Damg
˚
ard and Ju-
rik, 2001). This relies on the secret sharing scheme
mentioned above.
3.2 Building Blocks
In this section, we describe four building blocks used
in existing (Hoens et al., 2013) and our proposal. In
what follows, [a] is used to denote an encrypted value
of a. Furthermore, [a]
lB
denotes encryption of l least
significant bits a, i.e., [a]
lB
= h[a
0
],...,[a
l−1
]i, where
a
i
∈ {0,1} for i = 0,...,l − 1 and a =
∑
l−1
i=0
a
i
2
i
.
MULT A protocol that on input [a] and [b] produces
[a ∗ b].
BITS A protocol that on input [a] and l, produces en-
cryption of at least l least significant bits of the
underlying plaintext of [a], i.e. [a]
lB
.
BIT-LE A protocol that, given [a
1
]
lB
and [a
2
]
lB
out-
puts an encrypted bit [b], where b = 1 if a
1
≤ a
2
.
COMP A protocol that takes two encrypted inputs
[a] and [b] and generates [1] if a > b, and [0] oth-
erwise.
The way in which these building blocks function is as
follows.
3.2.1 MULT
Secure multiplication is a well-researched problem
with a large number of available solutions. Since
multiplication of the underlying values using only en-
crypted values is impossible in the Paillier cryptosys-
tem, one of the values to be multiplied has to be de-
crypted, and consequently an exponentiation can be
done to obtain the product of the two encrypted val-
ues. The MULT building block in this instance starts
additive sharing, where an encrypted value is addi-
tively split among a number of server. Given input [a]
and [b] where the product [a · b] is desired. We choose
to additively split the value [b] among n servers. Each
server i for i = 1,....n − 1 chooses a random number
r
i
∈ Z
N
, encrypts and broadcasts this encryption [r
i
] .
Each server now possesses [b], [r
1
],.... [r
n−1
] and lo-
cally computes [b
0
] = [b−
∑
n−1
i=1
[r
i
] = [b]
∏
∑
n−1
i=1
r
i
]
−1
.
Then all participants (or at least t) jointly decrypt
[b
0
] for party n using threshold decryption as for ex-
ample in (Damg
˚
ard and Jurik, 2001). Note that ev-
ery server now has a share, of which the sum is
b
0
+ r
1
+ .... + r
n
= b. Each server can then use the
homomorphic property of the encryption scheme to
compute [a]
b
i
= [a · b
i
], after which all the servers as-
semble their values to obtain [a · (b
0
+ r
1
+ ... + r
n
)] =
[a · b],
3.2.2 BITS
Schoenmakers et al. (Schoenmakers and Tuyls, 2006)
describe gates to produce an encryption of the l least
significant bits of the underlying plaintext of [a].
Three different gates are described: LSB, LSBs, and
BITREP. LSB only encrypts the least significant bit,
LSBs a number l of least significant bits and BITREP
the entire binary number. Since we require the l least
significant bits of [a], we use the LSBs gate which
SECRYPT 2018 - International Conference on Security and Cryptography
190

produces these on input [a]. To do so, the n par-
ties should first jointly generate l random bits and
encrypt these to jointly obtain the bits [r
0
],...,[r
l−1
].
Next, all parties generate their own random num-
ber r
∗,i
∈
R
{0,...,2
l+κ−1
− 1} and broadcast it so that
r
∗
=
∑
n
i=1
r
∗,i
can be publicly computed. Here κ is
a security parameter which when increased leads to
better security but more computation time.
The value y is then computed in the following
manner:
y = a −

l−1
∑
j=0
r
j
2
j
+
n
∑
i=1
r
∗,i
· 2
l

mod n (1)
Note that the values of r are encrypted, so this re-
sults in these actual computations:
[y] = [a] ∗

l−1
∏
j=0
[r
j
]
2
j
∗
n
∏
i=1
[r
∗,i
]
2
l

−1
mod n
2
(2)
Now y is jointly decrypted using the thresh-
old scheme and converted to its binary notation
y
0
,...,y
l−1
. Since a = y+r, if both y and r were avail-
able in plaintext a would be trivial to obtain using an
addition circuit:
a
i
= y
i
+ r
i
+ c
i−1
− 2c
i
c
i
= y
i
r
i
+ y
i
c
i−1
+ r
i
c
i−1
− 2y
i
r
i
c
i−1
, c
−1
= 0
(3)
Where 0 ≤ i ≤ l −1 and c is the so-called ’carry’
bit used for intermediate computation. However, de-
crypting r is not an option since that would reveal the
plaintext value of a and remove the point of this en-
tire building block. Instead, this addition circuit can
be implemented in the encrypted domain as follows:
If y
i
= 0:
[a
i
] = [r
i
] · [c
i−1
] · ([c
i
]
2
)
−1
[c
i
] = MULT ([r
i
],[c
i−1
]), c
−1
= 0
(4)
If y
i
= 1:
[a
i
] = [y
i
] · [r
i
] · [c
i−1
] · ([c
i
]
2
)
−1
[c
i
] = [r
i
] · [c
i−1
] · MULT ([r
i
],[c
i−1
])
−1
, c
−1
= 0
(5)
Notice that first, since y
i
can take the value of ei-
ther 0 or 1, and unfortunately the number 0 is not
in mod n, we have to make different cases for y = 0
and y = 1 (this does save computation time though).
Next, we are dealing with a multiplication of two en-
crypted numbers, where we use the previously in-
troduced MULT block. Finally, note that the [...]
−1
stands for a modulo inverse operation. The output of
the protocol now is l encrypted output bits [a
i
] (the fi-
nal carry bit is ignored, hence computing modulo 2
m
),
which is the desired output.
3.2.3 BIT-LE
Bunn and Ostrovsky (Bunn and Ostrovsky, 2007) de-
scribe a protocol to find the minimum of two numbers.
The existing realization builds upon this protocol in
the encrypted domain by making use of additive ho-
momorphism. Let X = c
1
c
2
...c
M
and Y = d
1
d
2
...d
m
(so that c
1
and d
1
are the MSBs). This building block
returns an output of L = 0 if X ≤ Y and L = 1 if X > Y :
L = (c
1
⊕ d
1
)c
1
+ (c
1
⊕ d
1
⊕ 1)(c
2
⊕ d
2
)c
2
+(c
1
⊕ d
1
⊕ 1)(c
2
⊕ d
2
⊕ 1)(c
3
⊕ d
3
)c
3
+ ...+
+(c
1
⊕ d
1
⊕ 1)...(c
M−1
⊕ d
M−1
⊕ 1)(c
M
⊕ d
M
)c
M
(6)
Where ⊕ signifies an XOR operation which can
be rewritten to:
c ⊕ d = c + d − 2cd (7)
Since all input bits are delivered in the encrypted do-
main, an encrypted XOR can be computed in the fol-
lowing manner:
[c] ⊕ [d] = [c] ⊕ [d] ⊕ (MULT ([c],[d])
2
)
−1
(8)
Rewriting the entire building block in this manner
then gives an encrypted bit [L] as an output where
L = 1 if X > Y . Since we want L = 1 if X ≤ Y , we
simply swap the inputs in out protocol to obtain our
desired value.
3.3 Framework
It is important to choose a base framework, containing
the essential structure of a system and is a good guide-
line for defining one. In light of a fair comparison of
efficiency with Hoens et al. (Hoens et al., 2013) the
same framework is used, based on several functional,
privacy and reliability requirements. These require-
ments exist to maintain both the privacy of the patient
and the integrity of the system.
3.3.1 Functional Requirements
A suitable framework allows patients to rate their
physicians according to the patients’ satisfaction. Pa-
tients i can submit a rating for a physician j concern-
ing health condition k. This rating, denoted as r
i jk
,
is selected from a pre-defined range [1,n], where 1 is
the lowest score and n the highest. The submission
of these ratings by a multitude of patients leads to the
physician receiving an aggregate score relating to a
certain health condition denoted by s
jk
. It is computed
by any function of the sum of individual ratings and
An Efficient Privacy-preserving Recommender System for e-Healthcare Systems
191

the number of patients who have submitted a rating
w
jk
, e.g., r
jk
/w
jk
.
Additionally, the framework should allow the ex-
istence of this score to be available for new patients,
enabling them to find a physician relating to their
health condition. It should also allow a patient to find
a physician for a combination of conditions.
3.3.2 Privacy and Reliability Requirements
As previously discussed, a vital aspect of a recom-
mender system in the medical domain should be its
privacy. Both the inquiries a patient makes and the
existing data of the RS should be inaccessible to
the public, and even when somehow partially leaked
should not be traceable to a patient. Another essential
property of an RS framework is that it should be re-
liable. Patients should be able to get honest ratings,
which cannot be manipulated by parties like small
groups of unreasonable users or dishonest competi-
tors. This effect should be either prevented or de-
tected and compensated for.
3.4 Architecture
The next step in constructing an RS is to ensure all the
requirements of the framework are met by construct-
ing a suitable architecture. Hoens et al. (Hoens et al.,
2013) propose an architecture called SPA (Secure
Processing Architecture), which we use and elabo-
rate on in this section. In this architecture data is al-
ready encrypted at the patient’s side before sending,
suggesting the computation of all recommendations
is performed over encrypted data.
3.4.1 Computing Recommendations
Each computational server maintains the encrypted
sum of all the ratings for a certain physician j and
health condition k, [r
jk
], and the encrypted total num-
ber of submitted ratings for those also called the
weight [w
jk
]. When a patient submits a new rating
[r
i jk
], she includes a weight [w
i jk
], being equal to 1
for health conditions the patient wants to submit a rat-
ing for and 0 for all others. The sum of ratings is
then updated as [r
jk
]∗ [r
i jk
] = r
jk
+r
i jk
and the weight
[w
jk
] ∗ [w
i jk
] = w
jk
+ w
i jk
by utilizing the property of
the Paillier cryptosystem (Section 3.1.1).
A straightforward way to compute the physicians’
scores s
jk
is used: dividing r
jk
by w
jk
, thereby com-
puting the average rating. How this division is done
in the encrypted domain using the properties of the
homomorphic cryptosystem is explained in Section
3.4.3.
3.4.2 Bonus Factor
It might be beneficial to add a factor to let experienced
physicians with a large number of patients have some
advantage compared to physicians who have treated
a small number of patients for a certain health condi-
tion k. For this reason a bonus factor b
jk
is proposed,
so that s
jk
= r
jk
/w
jk
+ b
jk
. Here r
jk
/w
jk
∈ [1, n] and
b
jk
∈ [1,m], for a n and m free of choice. To determine
b
jk
, we check how many patients w
jk
a certain physi-
cian j has treated concerning health condition k, com-
pare this w
jk
with certain bucket values (t
1
,t
2
,...,t
q
),
and assign a factor (b
1
,b
2
,...,b
q
) accordingly, i.e. for
i = 1,2,....,q we set b
jk
= b
i
if the value of w
jk
is be-
tween thresholds t
i
and t
i+1
. The values of t
i
and b
i
are picked beforehand as desired, with the constraint
that they are increasing and b
i
≤ m.
For example, we can choose n = 10, m = 5,
b = (1,2, 3,4, 5) and q = (0,3,5, 10,20). The sys-
tem allows a patient to give ratings in the range of
[1,10], giving a bonus b
jk
of 1 to physicians j who
have treated more than 0 patients concerning a cer-
tain health condition k, a bonus of 2 when they have
treated more than three patients, etcetera. Using a
non-linear scale like this ensures physicians can’t be
the top recommended ones after having been rated
just once or twice but also doesn’t give a too unfair
advantage over a physician who has treated for exam-
ple 12 patients versus a physician who has treated 31
patients (just one point).
3.4.3 Comparing Scores
Computing two scores can then be done by computing
the following for two different physicians:
s
j
1
k
= r
j
1
k
/w
j
1
k
+ b
j
1
k
vs s
j
2
k
= r
j
2
k
/w
j
2
k
+ b
j
2
k
(9)
Since a division over the plaintext like this is im-
possible without decryption, s
jk
is instead stored as
a numerator-denominator pair ([s
0
jk
],[w
jk
]) = ([r
jk
+
b
jk
w
jk
],[w
jk
]). This allows us to compare two physi-
cians j
1
and j
2
by comparing s
0
j
1
k
w
j
2
k
to s
0
j
2
k
w
j
1
k
, de-
livering the same results as one would get by compar-
ing the two scores in 9.
A technical difficulty arising with this is that the
comparison might be incorrect if a physician j has no
ratings. That is, both w
j
k
and s
0
j
k
will be 0. To ensure
the result is always correct, a flag f
jk
is added which
indicates whether w
jk
is non-zero. The comparison
will then be between s
0
j
1
k
w
j
2
k
+ non-zero(w
j
1
k
) and
s
0
j
2
k
w
j
1
k
+ non-zero (w
j
2
k
) (note that this still always
delivers a correct comparison). To compute this non-
zero property we use an OR-function over the en-
SECRYPT 2018 - International Conference on Security and Cryptography
192

crypted bits, which is realized by a number of secure
additions and a bitwise comparison and gives an en-
crypted bit as an output (the output is one if the OR
over the plaintext bits is 1).
3.4.4 Privacy Requirements
The public-key cryptosystem Paillier is used, where it
is assumed that the public key necessary for data en-
cryption is known to all parties. However, in this case,
we choose to make the private key unavailable to any
single entity; accordingly a decryption can only be
done using threshold decryption as mentioned in Sec-
tion 3.1.3. This concept is relied on to let a number of
computational servers collect data from patients and
jointly compute recommendations. The earlier de-
fined privacy requirement stated that when part of the
data was leaked, it should not in any way reveal infor-
mation regarding a patient. To comply to this require-
ment, the computational servers should be maintained
by mutually distrustful parties, such that any t of them
are unlikely to conspire. It is essential that in no way
any party finds out anything about the patient. Even
if a patient encrypts the data before sending it if she
only sends a rating for a particular physician j and
health condition k it is quite apparent to learn what
kind of condition the patient has. The easiest way to
hide the actual information sent is to let the patient
submit weights for not just one but every physician
j and condition k. In that case, only one (or possi-
bly more if the patient was treated more) submitted
rating has the actual rating and carries a weight of 1,
while the other submitted values will have a rating
and weight 0. The servers are then able to compute
the scores or recommendations for all physicians and
conditions without learning anything about which rat-
ing the patient wanted to send.
Note that the computational servers can’t just re-
veal the scores s
jk
: given these scores, when a patient
would then submit a rating and a weight for a spe-
cific physician j and condition k, it would be trivial
to find out what value and for which condition and
physician this patient submitted a rating. While de-
signing a specific system, it is important to realize
that there is a continuous trade-off between high pri-
vacy and low computational overhead. For example, a
consideration would be to do reveal the scores s
jk
but
only periodically update them, having the benefit of a
patient being instantly able to see which physician is
recommended for which condition and therefore sav-
ing both the hassle of communication and computing.
However, in doing this, with low volumes of recom-
mendations, a malicious server might be able to deci-
pher what an individual patient submitted. Depending
on the size of the user base, this might become an at-
tractive option, but for now, we choose not to reveal
the scores.
4 PRIVACY-PRESERVING
RECOMMENDER SYSTEM
Where the previous section contained an explanation
of the existing protocol, in this section, we propose
an improved version of this protocol. Since the most
time-consuming steps of the protocol are the building
blocks, for our proposal we started by looking care-
fully at these building blocks, and for possible ways
how to improve them.
Inspecting the performance (elaborately done later
in 6) shows us that the runtime of the current proto-
col is dominated by the execution time of the BITS
and BIT-LE building blocks. The function of these
building blocks is to convert an encrypted number to
an encrypted bitwise representation and do a compar-
ison over these encrypted bits respectively.
The combined goal of these two building blocks
is to find out if a > b for given a and b without dis-
closing them, which is a common multi-party com-
putation problem known as a secure comparison. In
addition to it being the first multi-party (two-party)
computation problem to be ever considered (By Yao
et al. (Yao, 1982) under the name of the millionaire’s
problem), it is a fundamental primitive in a consid-
erable amount of applications. The setting for most
applications is that neither the inputs nor the output
are revealed to any of the parties, which is also the
setting of this application.
We use the state-of-the-art two-party comparison
protocol by Nateghizad et al. (Nateghizad et al.,
2016) to construct a multi-party comparison protocol
for use in the current application. Since this proto-
col takes two encrypted bits as an input and returns
an encrypted bit with the comparison result as an out-
put, it does the same as the two combined building
blocks. We, therefore, denote this improved secure
comparison as a building block COMP and proceed
by explaining it.
4.1 Improved Protocol
Using the new building block COMP, the improved
protocol can be realized. Besides the different build-
ing block, we perform the protocol in the same way
except for one detail. Recall a non-zero flag f
jk
was
used to make sure the comparisons are not between
zero’s. We choose to initialize w
jk
to 1, making it so
that this value will never be zero (and raise the thresh-
olds accordingly). As a result, comparing two physi-
An Efficient Privacy-preserving Recommender System for e-Healthcare Systems
193

cians while one has no ratings will still be no problem
at all.
We are now ready to present an improved version
of the protocol.
1. The computational server compute for every
physician j in parallel:
(a) set [c
1
] = [1] and execute [c
i
] ←
COMP([t
i
],[w
jk
]) for i = 2, ...,q.
(b) locally compute [b
jk
] = [
∑
m
i=1
c
i
δ
i
] =
∏
m
i=1
[c
i
]
δ
i
(c) execute [d] ← MULT ([b
jk
],[w
jk
]) and locally
set [s
0
jk
] = [r
jk
+ d] = [s
jk
] · [d].
2. The servers sort all tuples ([s
0
jk
],[w
jk
],[ f
jk
]) for
all physicians j using a suitable sorting algo-
rithm and output the result, where each com-
parison is performed on ([s
0
xk
],[w
xk
],[ f
xk
]) and
([s
0
yk
],[w
yk
],[ f
yk
]) as follows:
(a) execute [v
x
] ← MULT([s
0
xk
],[w
yk
]) and [v
y
] ←
MULT ([s
0
yk
],[w
xk
])
(b) locally compute [v
0
x
] = [v
x
]·[ f
xk
] = [v
x
+ f
xk
] and
[v
0
y
] = [v
y
] · [ f
yk
] = [v
y
+ f
yk
]
(c) execute [z] ← COMP([v
x
],[v
y
]) and open the
value of z.
5 SECURITY ANALYSIS
In this section, we provide proof to show that health-
care recommender system (HCRS) is simulation se-
cure in the semi-honest security model. We use the
simulatability paradigm (Lindell, 2017) in our proofs,
where security is defined as a comparison of compu-
tation work-flow in “real world” and “ideal world”.
In real world, each party in the protocol executes
its part of the computation. Let us denote π as the
health-care recommender system; we can split π into
two parts: π = π
CS
and π
KM
, CS refers to the compu-
tation server and KM is the key manager. Assuming
CS is corrupted by an adversary A, then A has access
to its inputs, and the given messages from KM. Simi-
larly, when KM is corrupted, the adversary has access
to the intermediate computation results.
In an ideal world, it is assumed that the corrupted
party uses a simulator to generate the outputs of the
other parties. This setting is similar to the condition,
where all the computations are performed with only
one corrupted party. In an ideal world, an adversary
´
A has only access to the inputs of the corrupted party
and the randomly generated outputs from the simula-
tors. The goal is to show that A can learn equal or
negligibly more than
´
A, meaning that they are com-
putationally indistinguishable, then we can claim that
HCRS is a simulation secure protocol.
Definition 5.1. Let a ∈ {0,1}
∗
represents the parties’
inputs, n ∈ N to be a security parameter, and X =
{X(a,n)}
a∈{0,1}
∗
;n∈N
and Y = {Y (a, n)}
a∈{0,1}
∗
;n∈N
,
two infinite sequences of random variables, are prob-
ability ensembles. Then, X and Y are computation-
ally indistinguishable, denoted as X
c
≡ Y , if there is
a polynomial p(.) for every non-uniform polynomial-
time probabilistic algorithm (nuPPT) D such that:
|Pr[D(X (a, n)) = 1] − Pr[D(Y (a,n)) = 1]| < 1/p(n)
(10)
5.1 Security of HCRS
The inputs of CS for generating recommendations is
[r
jK
], [w
jk
], [t
i
], [b
i
], and δ
i
, where j and k refer to the
physician and condition, respectively. Note that KM
has no private input that is denoted by φ. To show that
the process of generating recommendation is simula-
tion secure, we need to prove that parties are unable to
infer any private information about the patient’s pref-
erence and physicians private data.
Let denote the computation of c
i
as (CS ◦ KM)
f
1
,
b
jk
as CS
f
1
, d as (CS ◦ KM)
f
2
, and ´s
jk
as CS
f
2
,
◦ refers to multi-party computation. Let f =
((CS ◦ KM)
f
,CS
f
), where (CS ◦ KM)
f
= ((CS ◦
KM)
f
1
,(CS ◦ KM)
f
2
) and CS
f
= (CS
f
1
,CS
f
2
), and
f to be the functionality that computes the health-
care recommendation. The view of the i
th
party
i ∈ {CS,KM} for generating recommendation on
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n) = (w,r
i
;m
i
1
,··· , m
i
z
), where
w ∈ {[r
jK
],[w
jk
],[t
i
],[b
i
],φ} based on the value of i,
r
i
are the i
th
party internal random numbers, and
m
i
z
represents the z
th
message that is received by
i
th
party. out put
HCRS
i
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n) repre-
sents the output of each party in HCRS. To represent
the joint output of both parties, we denote
out put
HCRS
= (out put
HCRS
1
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n),
out put
HCRS
2
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n)).
(11)
Definition 5.2. HCRS securely computes f =
(CS
f
,KM
f
) in the semi-honest security setting if there
exits PPT algorithms Sim
CA
and Sim
KM
such that:
{(Sim
CS
(1
n
,[r
jK
],[w
jk
],[t
i
],[b
i
],CS
f
, f ))}
c
≡ {(view
f
CS
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n),
out put
f
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n))}
(12)
and
{(Sim
KM
(1
n
,φ,KM
f
, f ))}
c
≡
{(view
f
KM
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n),
out put
f
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n))}
(13)
SECRYPT 2018 - International Conference on Security and Cryptography
194

Theorem 1. HCRS securely computes the function-
ality f , when CS is corrupted by adversary A in the
presence of semi-honest adversaries.
Proof. We need to show that A cannot computation-
ally distinguish between the random generated out-
puts of S
2
and truly generated ones from KM. CS
receives outputs from KM in performing the opera-
tions COMP and MULT . By using S
2
instead of KM,
CS receives encryption of randomly generated values;
however, because A has not access to the private key
and a semantically secure encryption scheme is used
in the protocol, A is unable to distinguish between
garbage outputs from S
2
and real generated outputs
from KM. Therefore, we can claim that HCRS is
simulation secure when CS is corrupted if the used
building-blocks in HCRS, COMP (Nateghizad et al.,
2016) and MULT (Nateghizad et al., 2016), are se-
cure (Canetti, 2001).
Theorem 2. HCRS securely computes the function-
ality f , when KM is corrupted by adversary A in the
presence of semi-honest adversaries.
Proof. Unlike the CS, KM has access to the private
key and can decrypt the outputs of the CS. Thus, we
need to show the A cannot infer any private informa-
tion about the encrypted inputs of CS during the pro-
cess of generating recommendation. Given S
1
as the
simulator of CS and security parameter 1
n
, KM works
for every physician j as follows:
1. S
1
generates q − 1 pair of random numbers ˆr
i
and
´r
i
, and run the (CS ◦ KM)
f
1
for i ∈ {2,· ·· ,q}.
2. S
1
generates two random numbers r
1
and r
2
, then
performs (CS ◦ KM)
f
2
.
The only collaboration between two parties CS and
KM happen for the computation of [c
i
] and [d], and
the rest of the operations are performed locally in CS.
Therefore, if A cannot learn any private information
by performing (CS ◦ KM)
f
1
and (CS ◦ KM)
f
2
, then
HCRS is simulation secure when KM is corrupted.
The security proof of COMP and MULT are already
provided in (Nateghizad et al., 2016) and (Canetti,
2001), respectively. Thus,
{(Sim
KM
(1
n
,φ,KM
f
, f ))}
c
≡
{(view
f
KM
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n),
out put
f
([r
jK
],[w
jk
],[t
i
],[b
i
];φ; n))}
(14)
6 COMPUTATIONAL
COMPLEXITY
Clearly, the protocol we propose has less steps than
the original protocol proposed by Hoens et al (Hoens
et al., 2013). However, we still need to confirm that
the protocol is actually more efficient. We do this by
checking the exact computational complexity for both
protocols. We do this in terms of computational oper-
ations, and summarize the results in a table.
6.1 Building Blocks
The computational complexity formalizes a difficult
problem by quantifying the amount of resources
needed to solve it. Usually a rough approximation
like the ”big O” notation is used, but we choose
to compute the exact computational complexity by
checking the exact number of computations done.
A computation on a plaintext value is incredibly
cheap in comparison to an operation on an encrypted
value. For instance, a simple operation as 2
3
in the
plaintext domain is very easy to compute whereas [2]
3
involves possibly taking the third power of a 1024-bit
number when using a relatively small 1024-bit Pail-
lier key. Since operations on encrypted values heav-
ily dominate the runtime only these are listed for the
computational complexity. Since we are using addi-
tive homomorphism, in this case in the form of the
Paillier cryptosystem, these operations can be split up
in two general categories:
• A multiplication of encrypted values [a] · [b], re-
sulting in an addition of the underlying plaintext
values a + b.
• An exponentiation of an encrypted value by a
plaintext value [a]
b
, resulting in a multiplication
of the underlying plaintext values a · b.
A multiplication of encrypted values always takes
around the same amount of time, since the encrypted
numbers are of the same order of size. However, an
exponentiation of encrypted values can vary greatly:
[2]
2
is much easier to compute than [2]
1024
. We ac-
cordingly use slightly different notations for the two
of these: 1 exponentiation for the former and 1
1024
exponentiation for the latter.
The computational complexity of the protocol for
both the existing and the proposed protocol are dom-
inated by the building blocks. Hence, we express the
computational complexity of all these building blocks
and use this as a measure to check the improved ef-
ficiency. Recall that n is the amount of servers, l the
length of the greatest number in bits and t out of n
An Efficient Privacy-preserving Recommender System for e-Healthcare Systems
195

servers are needed to perform the threshold decryp-
tion.
6.1.1 MULT
We start by computing [b]
∏
∑
n−1
i=1
[r
i
]
−1
, which is
equal to n − 1 multiplications. Then, the threshold
decryption scheme is ran, which has 2t − 1 exponen-
tiations on encrypted numbers. Finally each server
has to ompute an exponent [a]
b
i
, resulting in n expo-
nentiations.
The MULT scheme therefore has in total n − 1
multiplications and n + 2t − 1 exponentiations.
6.1.2 BITS
We start by looking at computing the value of y. 2
shows us l − 1 multiplications from the first prod-
uct and n − 1 multiplications from the second prod-
uct, with one multiplication between these two for
l +n − 1 multiplications. Next are the exp operations.
A number of l exponentiations are done in the first
summation, one in the second summation, and one
over the total product in the brackets for a total of
l + 2 exp operations. Finally one final multiplication
is done to compute y. Next is the addition circuit, as
shown in equations 4 and 5. Since y
i
can take the val-
ues of both 0 and 1 and the computation varies for
both situations, the complexity differs:
y
i
= 0 : Two multiplications, one exp(−1), one
exp(2) and one MULT.
y
i
= 1 : Five multiplications, one exp(−1), one
exp(2) and one MULT.
Therefore we take the average of these two situa-
tions as the complexity, being 3.5 multiplications, one
exp(−1), one exp(2) and one MULT. This results in
a total of l + n + 3.5 multiplications, l
2
1
,...,2
l
+ 1
2
l
+ 3
exponentiations and one MULT for the entire BITS
building block.
6.1.3 BIT-LE
Since the complexity of the BIT-LE building block
varies heavily depending on the number of bits and is
not easily readable, we compute the complexity for a
few cases and deduce the actual complexity by check-
ing the pattern.
Therefore we can conlude that for BIT-LE the
complexity of multiplications increases with (3l −
1)n, whereas the complexity of exponentiations in-
creases with (3l − 1)n
w
i
+ (2l − 1)
−1
.
6.1.4 COMP
Alice starts by doing 3 multiplications and 1 exponen-
tiation.
Bob performs a threshold decryption. Next to
this he only performs operations on plaintext and en-
crypts, so this is not very computationally intensive.
Hereafter Alice does l multiplications and l expo-
nentiations. Bob continues by doing l threshold de-
cryptions. Finally, Alice computes the result using
three multiplications and two exponentiations.
In total, this comes down to l + 6 multiplications,
l +3 exponentiations and l + 1 threshold decryptions.
6.2 Total Computational Complexity
Summarizing the previously found results leads to
the total computational complexity for each building
block as shown in 2.
Table 2: Computational complexity for the building blocks
used in both protocols, where the MULT building block is
shown as an operation.
[a + b] exp
MULT n − 1 n
BITS l + n + 3.5 l
2
1
,...2
l
+ 1
2
l
+ 3
BIT-LE 3l − 1 2l − 1
COMP 6 + l l + 3
Since the number of operations required for the
MULT and threshold decryption d
t
operations is
known, we can further reduce our table. The amount
of operations for a threshold decryptions are 2t − 1
exponentiations. By doing this and working out the
products we obtain 3.
Table 3: Computational complexity for the building blocks
of the protocol introduced in (Hoens et al., 2013).
[a + b] exp
MULT n − 1 n + 2t − 1
BITS l + 2n + 2.5 l
2
1
,...2
l
+ 1
2
l
+ 2 + n + 2t
BIT-LE 3ln − n 6lt + 3ln − 3l − n + 1
COMP 6 + l 2lt + 2t + 2
From this we can clearly see the difference in
complexity and the significant improvement made by
the new protocol. Especially for large numbers l, note
that the complexity of exponentiations of BITS and
BIT-LE increase a lot in comparison to the complex-
ity of COMP. This is logical, because BITS has to
output a great number of bits and BIT-LE will have to
perform a comparison on each of these.
SECRYPT 2018 - International Conference on Security and Cryptography
196

The notion that the new protocol is faster is fur-
ther confirmed by the implementation results in the
following section.
7 IMPLEMENTATION
For the sake of analyzing the performance, the exist-
ing and improved realizations were implemented us-
ing Java using Paillier encryption with a 1024-bit key.
Java was chosen to both follow suit with the exist-
ing implementation and due to its ease of implement-
ing distributed algorithms. First, the old protocol was
implemented, consisting of the three building blocks
MULT, BITS and BIT-LE, the paillier and threshold
decryption scheme, some other small functions like
OR and XOR and of course the main protocol for exe-
cution. After this the new protocol was implemented,
which basically changes the BITS and BIT-LE build-
ing blocks to one COMP building block.Because we
were mainly interested in the computational complex-
ity involved we tested the protocol on one desktop,
having an Intel Core i7-7700 HQ CPU with 2.80 GHz
and 4 cores and a total of 16 GB of memory (RAM).
To make the tests more general and since the main
focus of this work is to show the improved compu-
tational performance of the building blocks only step
1 of the protocol was implemented. Note that the ta-
ble with execution times shown in Hoens et al (Hoens
et al., 2013) also only mention a table with the execu-
tion times of step 1.
The three values that mostly impact the perfor-
mance are 1)Amount of physicians j, 2) Amount of
bucket thresholds t
i
, and 3) Bit length of the thresh-
olds l.
In order to vary these three metrics, various sce-
narios of thresholds which might be applicable to
practice were devised, enabling an overview in which
the time can be seen by putting the number of physi-
cians against several scenarios:
1. (0,1,3) - bit length = 2
2. (0,3,5, 10,20) - bit length = 5
3. (10,50,100, 500,1000) - bit length = 10
4. (1000,5000,10000, 50000,100000) - bit length =
20
5. (0,10,50, 100,500, 1000,5000, 10000,50000
100000) - bit length = 20
The number of servers n was chosen to be 5, of
which 3 are required to do threshold decryption. The
results of the existing implementation are presented in
4, whereas the results of the proposed implementation
are found in 5. In both tables, the execution time of
Table 4: Execution times (seconds) for step 1 of the protocol
using the the existing realization. No.P refers to the number
of physicians.
No.P
Thresholds scenario used
s
1
s
2
s
3
s
4
s
5
5 141 505 1186 2337 4029
10 281 1010 2290 4985 7970
20 532 2134 4638 9650 16394
50 1284 5005 10970 26384 40772
Table 5: Execution times (seconds) for step 1 of the protocol
using the the proposed realization.
No.P
Thresholds scenario used
s
1
s
2
s
3
s
4
s
5
5 26 72 120 222 396
10 52 134 245 455 775
20 101 270 504 933 1527
50 251 716 1208 1938 4013
step 1 of the protocol is shown, where the number of
physicians is presented vertically, and the threshold
scenario is used horizontally.
To give the reader a graphical overview, the exe-
cution times for scenario 2 and scenario 5 have been
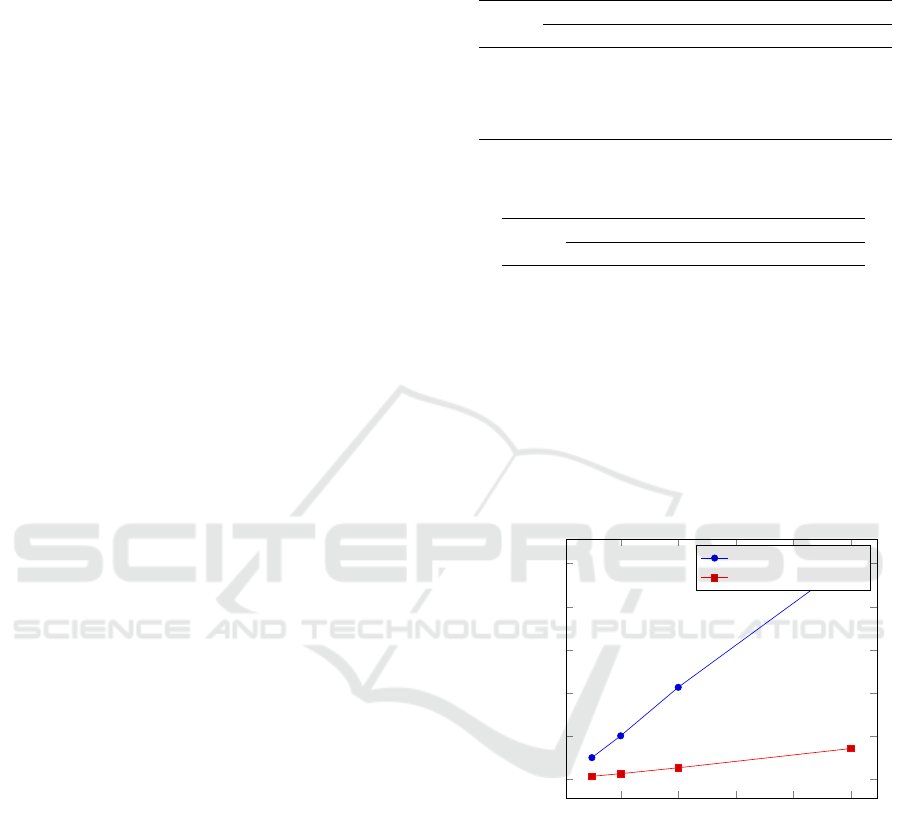
plotted in Figure 1 and Figure 2 respectively.
10 20 30 40
50
0
1,000
2,000
3,000
4,000
5,000
Number of physicians
Execution time (s)
Existing realization
Proposed realization
Figure 1: Timing results of scenario 2 for the existing and
proposed realization.
The proposed realization is much faster. For sce-
nario 1, a speedup of approximately 81,5% is already
achieved, while for scenario five a speedup of approx-
imately 90% is achieved. This relative difference in
speedups can be explained by the fact that the com-
plexity of the old building blocks is much more de-
pendent on the bit length l in comparison to the new
building block. The execution time of the proposed
implementation is dominated mostly by the use of
threshold decryptions; therefore, this time could be
even further reduced by employing a technique called
data packing. Essentially, the main idea of this is to
An Efficient Privacy-preserving Recommender System for e-Healthcare Systems
197

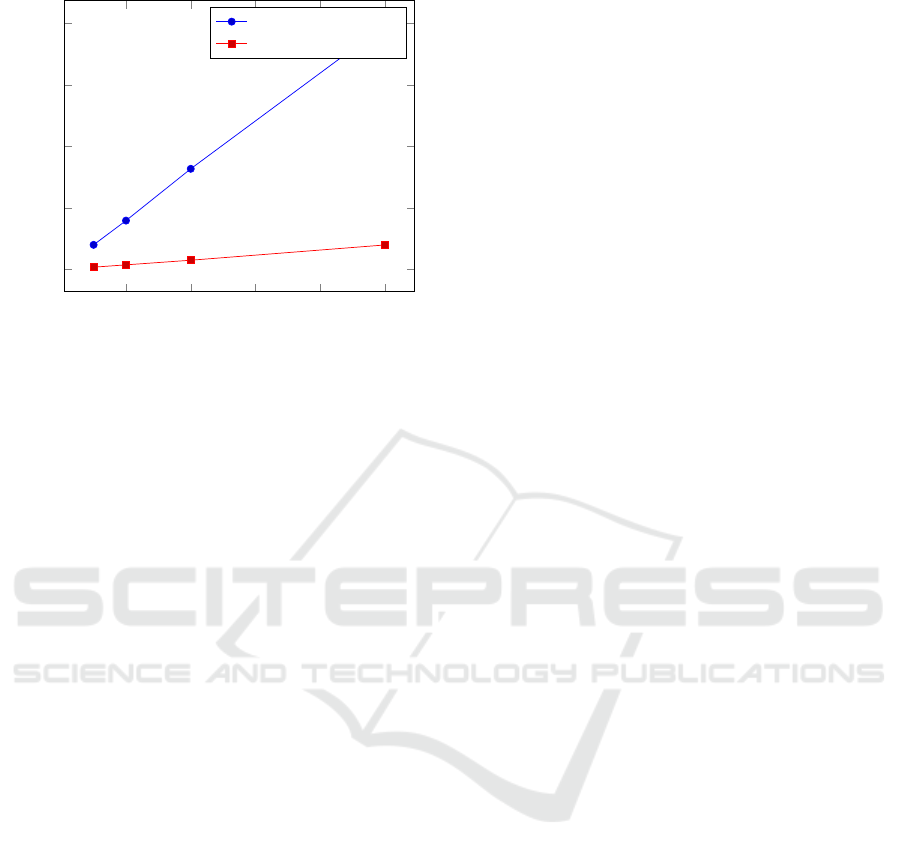
10 20 30 40
50
0
1
2
3
4
·10
4
Number of physicians
Execution time (s)
Existing realization
Proposed realization
Figure 2: Timing results of scenario 5 for the existing and
proposed realization.
use the message space of the Paillier cryptosystem
that is much larger than the values to be compared,
so that multiple values can be stored in one encrypted
variable.
8 CONCLUSION
This work presents a reliable medical privacy pre-
serving recommender system, building on an exist-
ing framework by Hoens et al. (Hoens et al., 2013).
Since medical information is considered private in-
formation, an architecture is provided satisfying the
requirements of this framework, relying on secure
(encrypted) data and secure multi-party techniques to
perform operations on this data. Unfortunately, the
secure architecture of the existing realization is com-
putationally expensive, hindering the deployment of
the protocol in practice. In this paper, we investigated
the performance of the existing realization and signif-
icantly improved upon this by changing several parts
of the protocol without laying a hand on the underly-
ing framework or architecture. Especially the propo-
sition of a protocol executing secure comparison de-
livered a significant speedup. More precisely, the run-
time of the existing protocol is reduced by 81,5% for
small bit-lengths, and it is reduced even further for
larger bit lengths. This improvement leads to a more
efficient and practical reliable medical privacy pre-
serving recommender system.
ACKNOWLEDGMENTS
We would like to thank T. R. Hoens and M. Blanton
for their help in understanding their ideas and provid-
ing the implementation of their work.
REFERENCES
Agrawal, R. and Srikant, R. (2000). Privacy-preserving data
mining. In Proceedings of the 2000 ACM SIGMOD
International Conference on Management of Data,
May 16-18, 2000, Dallas, Texas, USA., pages 439–
450.
Alem
´
an, J. L. F., Se
˜
nor, I. C., Lozoya, P.
´
A. O., and Toval,
A. (2013). Security and privacy in electronic health
records: A systematic literature review. Journal of
Biomedical Informatics, 46(3):541–562.
Baroody, A. J. and Hansen, S. W. (2012). Changing per-
spectives: Institutional logics of adoption and use
of health information technology. In Proceedings of
the International Conference on Information Systems,
ICIS 2012, Orlando, Florida, USA, December 16-19,
2012.
Bunn, P. and Ostrovsky, R. (2007). Secure two-party k-
means clustering. In Proceedings of the 14th ACM
conference on Computer and communications secu-
rity, pages 486–497. ACM.
Canetti, R. (2001). Universally composable security: A
new paradigm for cryptographic protocols. In 42nd
Annual Symposium on Foundations of Computer Sci-
ence, FOCS 2001, 14-17 October 2001, Las Vegas,
Nevada, USA, pages 136–145.
Canny, J. F. (2002). Collaborative filtering with privacy.
In 2002 IEEE Symposium on Security and Privacy,
Berkeley, California, USA, May 12-15, 2002, pages
45–57.
Chhanabhai, P. and Holt, A. (2007). Consumers are ready
to accept the transition to online and electronic records
if they can be assured of the security measures. Med-
scape General Medicine, 9(1):8.
Ciss
´
ee, R. and Albayrak, S. (2007). An agent-based ap-
proach for privacy-preserving recommender systems.
In 6th International Joint Conference on Autonomous
Agents and Multiagent Systems (AAMAS 2007), Hon-
olulu, Hawaii, USA, May 14-18, 2007, page 182.
Damg
˚
ard, I. and Jurik, M. (2001). A generalisation, a sim-
plification and some applications of paillier’s proba-
bilistic public-key system. In Public Key Cryptogra-
phy, 4th International Workshop on Practice and The-
ory in Public Key Cryptography, PKC 2001, Cheju
Island, Korea, February 13-15, 2001, Proceedings,
pages 119–136.
Dwork, C. (2007). An ad omnia approach to defining and
achieving private data analysis. In Privacy, Security,
and Trust in KDD, First ACM SIGKDD International
Workshop, PinKDD 2007, San Jose, CA, USA, August
12, 2007, Revised Selected Papers, pages 1–13.
Erkin, Z., Beye, M., Veugen, T., and Lagendijk, R. L.
(2011). Efficiently computing private recommenda-
tions. In Proceedings of the IEEE International Con-
ference on Acoustics, Speech, and Signal Processing,
SECRYPT 2018 - International Conference on Security and Cryptography
198

ICASSP 2011, May 22-27, 2011, Prague Congress
Center, Prague, Czech Republic, pages 5864–5867.
Erkin, Z., Veugen, T., Toft, T., and Lagendijk, R. L.
(2012). Generating private recommendations effi-
ciently using homomorphic encryption and data pack-
ing. IEEE Trans. Information Forensics and Security,
7(3):1053–1066.
Fiza, A. R., Lizawati, S., Zuraini, I., and Narayana, S. G.
(2016). Safety and privacy issues of electronic med-
ical records. Indian Journal of Science and Technol-
ogy, 9(42).
Gavgani, V. Z. (2010). Health information need and seek-
ing behavior of patients in developing countries’ con-
text; an iranian experience. In ACM International
Health Informatics Symposium, IHI 2010, Arlington,
VA, USA, November 11 - 12, 2010, Proceedings, pages
575–579.
Hoens, T. R., Blanton, M., Steele, A., and Chawla, N. V.
(2013). Reliable medical recommendation systems
with patient privacy. ACM TIST, 4(4):67:1–67:31.
Katzenbeisser, S. and Petkovic, M. (2008). Privacy-
preserving recommendation systems for consumer
healthcare services. In Proceedings of the The Third
International Conference on Availability, Reliability
and Security, ARES 2008, March 4-7, 2008, Techni-
cal University of Catalonia, Barcelona , Spain, pages
889–895.
Kivits, J. (2006). Informed patients and the internet: a medi-
ated context for consultations with health profession-
als. Journal of health psychology, 11(2):269–282.
Lindell, Y. (2017). How to simulate it - A tutorial on the
simulation proof technique. In Tutorials on the Foun-
dations of Cryptography., pages 277–346.
Lindell, Y. and Pinkas, B. (2000). Privacy preserving
data mining. In Advances in Cryptology - CRYPTO
2000, 20th Annual International Cryptology Confer-
ence, Santa Barbara, California, USA, August 20-24,
2000, Proceedings, pages 36–54.
Longo, D. L. and Drazen, J. M. (2016). Data sharing. New
England Journal of Medicine, 374(3):276–277.
Lu, J., Wu, D., Mao, M., Wang, W., and Zhang, G. (2015).
Recommender system application developments: A
survey. Decision Support Systems, 74:12–32.
McMullan, M. (2006). Patients using the internet to obtain
health information: how this affects the patient–health
professional relationship. Patient education and coun-
seling, 63(1):24–28.
McSherry, F. and Mironov, I. (2009). Differentially pri-
vate recommender systems: Building privacy into the
netflix prize contenders. In Proceedings of the 15th
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, Paris, France, June
28 - July 1, 2009, pages 627–636.
Nateghizad, M., Erkin, Z., and Lagendijk, R. L. (2016).
An efficient privacy-preserving comparison protocol
in smart metering systems. EURASIP J. Information
Security, 2016:11.
Paillier, P. (1999). Public-key cryptosystems based on com-
posite degree residuosity classes. In Advances in
Cryptology - EUROCRYPT ’99, International Confer-
ence on the Theory and Application of Cryptographic
Techniques, Prague, Czech Republic, May 2-6, 1999,
Proceeding, pages 223–238.
Polat, H. and Du, W. (2005). Svd-based collaborative fil-
tering with privacy. In Proceedings of the 2005 ACM
Symposium on Applied Computing (SAC), Santa Fe,
New Mexico, USA, March 13-17, 2005, pages 791–
795.
Ramakrishnan, N., Keller, B. J., Mirza, B. J., Grama, A.,
and Karypis, G. (2001). Privacy risks in recommender
systems. IEEE Internet Computing, 5(6):54–62.
Schoenmakers, B. and Tuyls, P. (2006). Efficient binary
conversion for paillier encrypted values. In Advances
in Cryptology - EUROCRYPT 2006, 25th Annual In-
ternational Conference on the Theory and Applica-
tions of Cryptographic Techniques, St. Petersburg,
Russia, May 28 - June 1, 2006, Proceedings, pages
522–537.
Shamir, A. (1979). How to share a secret. Commun. ACM,
22(11):612–613.
Shokri, R., Pedarsani, P., Theodorakopoulos, G., and
Hubaux, J. (2009). Preserving privacy in collabora-
tive filtering through distributed aggregation of offline
profiles. In Proceedings of the 2009 ACM Conference
on Recommender Systems, RecSys 2009, New York,
NY, USA, October 23-25, 2009, pages 157–164.
Sommerhalder, K., Abraham, A., Zufferey, M. C., Barth, J.,
and Abel, T. (2009). Internet information and medical
consultations: experiences from patients and physi-
cians perspectives. Patient education and counseling,
77(2):266–271.
Tiggle, M. (2012). Urban Alabama physicians and the elec-
tronic medical record: A qualitative study. PhD thesis.
Yao, A. C. (1982). Protocols for secure computations. In
Foundations of Computer Science, 1982. SFCS’08.
23rd Annual Symposium on, pages 160–164. IEEE.
Zhang, S., Ford, J., and Makedon, F. (2006). Deriving pri-
vate information from randomly perturbed ratings. In
Proceedings of the Sixth SIAM International Confer-
ence on Data Mining, April 20-22, 2006, Bethesda,
MD, USA, pages 59–69.
An Efficient Privacy-preserving Recommender System for e-Healthcare Systems
199