Anonymous Data Collection Scheme from Short Group Signatures

Jan Hajny

, Petr Dzurenda

, Lukas Malina

and Sara Ricci

Department of Telecommunications, Brno University of Technology, Technicka 12, Brno, Czech Republic

Department of Mathematics and Computer Science, Universitat Rovira i Virgili, Avda. Paisos Catalans 26,

Tarragona, Spain

Keywords:

Group Signatures, Anonymity, Privacy, Revocation, Identiﬁcation, Efﬁciency.

Abstract:

Data collection schemes are used for secure and reliable data transfer from multiple remote nodes to a central

unit. With the increasing importance of smart meters in energy distribution, smart house installations and

various sensor networks, the need for secure data collection schemes becomes very urgent. Such schemes

must provide standard security features, such as conﬁdentiality and authenticity of transferred data, as well

as novel features, such as the strong protection of user’s privacy and identiﬁcation of malicious users. In

this paper, we provide the full cryptographic speciﬁcation of a novel scheme for secure privacy-friendly data

collection that is designed for computationally restricted user devices and supports all the security, privacy-

protection and inspection features. Using the scheme, data can be anonymously collected from almost all types

of devices, including simple sensors and smart meters. On the other side, malicious users can be efﬁciently

identiﬁed and revoked. Furthermore, we provide the practical results of our implementation of the scheme on

embedded devices, smart phones, smart cards, smart watches, computers and servers so that the efﬁciency can

be thoroughly evaluated on various platforms.

1 INTRODUCTION

Currently, there are proven cryptographic mecha-

nisms that are able to guarantee the basic security

properties in classical computer networks containing

mostly PCs and servers. However, the structure of

communication networks is changing in recent years

and the infrastructures are becoming more and more

heterogeneous, comprising industrial devices, small

personal wearable devices, sensors, microcontrolers,

etc. These devices are often very computationally

constrained, which prevents the usage of standard

cryptographic techniques for securing the communi-

cation. Lightweight cryptography mechanisms are

being sought for the deployment on such devices. On

the other side, the number of such personal devices

is huge and quickly rising with the expansion of IoT

networks, smart grids, cyber physical systems, etc. In

some scenarios, millions of constrained devices com-

municate with one another and with central nodes.

That is the case of sensor networks, in particular smart

metering systems. In such applications, millions of

relatively simple devices produce data that are col-

lected by central nodes. Providing security in such

environment is difﬁcult, as the constrained devices are

very limited in computational power and memory on

one side and the central nodes must securely collect a

very high number of messages from various sources

on the other side.

In addition to the traditional requirements on con-

ﬁdentiality and authenticity, new demands on privacy

protection are being imposed, mostly by EU regula-

tions, but also by some U.S. strategic plans (NST,

2011). That leads to the design of technologies that

limit any disclosure of private information that is not

necessary for the system functionality. However, such

privacy-enhancing features are often extremely costly

regarding computational resources.

In this paper, we propose a cryptographic scheme

based on group signatures that is designed to address

the challenges identiﬁed above. Our anonymous data

collection scheme allows constrained devices to efﬁ-

ciently generate group signatures on their data. There-

fore, the collectors can be assured that data are col-

lected from trusted sources and were not modiﬁed

during a transfer. The signatures are fully anony-

mous, untraceable and unlinkable, thus supporting the

full set of privacy-enhancing features. The collec-

tor learns that the signature was created by a trusted

group member, but the concrete identity stays undis-

closed. As an additional key feature, our scheme also

provides efﬁcient revocation, i.e., a practical mecha-

200

Hajny, J., Dzurenda, P., Malina, L. and Ricci, S.

Anonymous Data Collection Scheme from Short Group Signatures.

DOI: 10.5220/0006858602000209

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 200-209

ISBN: 978-989-758-319-3

nism to identify and invalidate malicious users.

We present the full cryptographic description of

all protocols of the scheme, show the efﬁciency anal-

ysis and the results of our implementation on devices

with diverse computational power, from smart cards,

microcontrollers to standard PCs. By showing also

practical results, we prove the readiness of the scheme

for a real-world use. Besides the straightforward use

in data collection systems, we also note other applica-

tions, such as e-ticketing, transportation and e-IDs.

1.1 State of the Art

The work on anonymous data collection schemes be-

came intensive only very recently, with the deploy-

ment of smart metering technologies into practical in-

stallations. However, the cryptographic primitives,

that are the main building blocks of these schemes,

are known for more than a decade. The core build-

ing blocks are the group signatures, allowing users to

create signatures using their private keys and veriﬁers

to verify the signatures using a common public key.

The research into group signatures was started by the

seminal work of Chaum and van Heyst in (Chaum

and Van Heyst, 1991). A large number of group

signatures has been proposed, e.g., in (Camenisch

and Lysyanskaya, 2003; Boneh et al., 2004; Del-

erabl

ee and Pointcheval, 2006; Hwang et al., 2011;

Boneh and Shacham, 2004; Ferrara et al., 2009; Kim

et al., 2011). In particular, the scheme called BBS

(Boneh et al., 2004) serves as a fundamental build-

ing block for many security solutions (e.g., (Lin et al.,

2007) and (Zhang et al., 2008)). Recently, short ran-

domizable signatures were proposed (Pointcheval and

Sanders, 2016) that allow efﬁcient proofs of signature

knowledge and creating group signatures by signing

the individual users’ private keys by the manager’s

private key. For the veriﬁcation, only the manager’s

public key is necessary. We take the same approach

in our scheme.

Furthermore, some privacy preserving solutions

based on pseudonyms have been proposed, e.g., in

(Finster and Baumgart, 2013; Rottondi et al., 2015;

Raya and Hubaux, 2007; Rottondi et al., 2015; Raya

and Hubaux, 2007). However, the solutions based

on pseudonyms are usually inefﬁcient as they require

users to switch between many (pseudo)identities, thus

need extensive cryptographic material and multiple

keys.

Both the group signature schemes and the

pseudonymous schemes mostly lack efﬁcient revoca-

tion mechanisms that are scalable enough for large ap-

plications with millions of constrained user devices.

Either the revocation function needs very expensive

computations (such as bilinear pairings) or is rather

tailored for authentication and access control schemes

(such as (Camenisch et al., 2016; Hajny and Malina,

2013)).

As a result, we lack a practical data collection

scheme that is provably secure, with short and fast

signatures, with efﬁcient revocation mechanisms and

providing all privacy-enhancing features.

1.2 Our Contribution

We propose a novel cryptographic scheme that we call

an anonymous data collection scheme that is instan-

tiated using the wBB signature (Boneh and Boyen,

2008) and the efﬁcient proofs of their knowledge (Ca-

menisch et al., 2016). On a general level, we take the

approach of (Pointcheval and Sanders, 2016), i.e., we

let the manager sign all users’ private keys. The users

then prove the knowledge of such a signature and the

veriﬁer checks the proof using the manager’s public

key. Our scheme is unique in the following proper-

ties:

• provides all privacy-enhancing features:

anonymity, unlinkability, untraceability,

• the signatures are small and constant: the size is

below 169 B using a strong 224 b curve,

• the signature generation is fast: requires no bilin-

ear pairing and only 5 exponentiations,

• the signature veriﬁcation including revocation

check is efﬁcient: requires only 2 pairings and

O(|RL|

) exponentiations,

• the scheme is built using primitives with formal

security proofs.

Besides the cryptographic design, we also pro-

vide the complete implementation results and bench-

marks on a wide spectrum of devices, i.e. smart cards,

micro-controllers and PCs. The practical results cer-

tify the usability in practice using contemporary cryp-

tographic parameters recommended by NIST (Barker,

2016).

2 PRELIMINARIES

2.1 Notation

We describe the proof of knowledge protocols (PK)

using the efﬁcient notation introduced by Camenisch

and Stadler (Camenisch and Stadler, 1997). The pro-

tocol for proving the knowledge of discrete logarithm

Revocation List

Anonymous Data Collection Scheme from Short Group Signatures

201

Prover Veriﬁer

c,g, p,q

w ∈ Z

r ←

¯c = g

¯c

−−−−−−−−−−−−−−−−−−−−−−→

e ←

←−−−−−−−−−−−−−−−−−−−−−

z = (r − ew) mod q

−−−−−−−−−−−−−−−−−−−−−−→

¯c

= g

Accept/Re ject

−−−−−−−−−−→

Figure 1: Schnorr’s proof of knowledge of discrete loga-

rithm PK{w : c = g

} in Z

∗

of c with respect to g is denoted as PK{α : c = g

The symbol “:” means “such that” and “|x|” is the

bitlength of x. We write a ←

A when a is sampled

uniformly at random from A. A secure hash function

is denoted as H .

2.2 Proofs of Knowledge

The statements about discrete logarithms in prime or-

der groups can be easily proven using the Σ-protocols

(Camenisch and Stadler, 1997).

A simple yet very useful protocol for proving the

discrete logarithm knowledge is based on the Schnorr

signature scheme (Schnorr, 1991). Using this proto-

col, the prover proves his knowledge of a discrete log-

arithm with respect to public parameters c, g, p,q, i.e.,

he proves the knowledge of w : c = g

mod p, where

p is prime modulus, q is group order and g is Z

∗

gen-

erator. The protocol is depicted in Fig. 1.

The proof of discrete logarithm knowledge is a

simple 3-way protocol where the prover commits to a

random number r in the ﬁrst step, receives a challenge

e in the second step and responds by z to the challenge

in the third step. The protocol is Honest Veriﬁer Zero-

Knowledge (HVZK).The protocol can be easily mod-

iﬁed to the proof of knowledge signature (SPK) by

computing the challenge e as e = H (e,m).

2.3 Bilinear Pairing

Let G

, G

, and G

be groups of prime order q. A

bilinear map e : G

× G

→ G

must satisfy bilin-

earity, i.e., e(g

) = e(g

)

for all x,y ∈ Z

;

non-degeneracy, i.e., for all generators g

∈ G

and

∈ G

, e(g

) generates G

; and efﬁciency, i.e.,

there exists an efﬁcient algorithm G(1

) that outputs

the bilinear group (q,G

,e,g

2.4 Weak Boneh-Boyen Signature

The weak Boneh-Boyen (wBB) signature scheme

(Boneh and Boyen, 2008) can be used to efﬁciently

sign (blocks of) messages. Furthermore, the sig-

nature scheme can be easily integrated with the

zero-knowledge proofs so that the knowledge of

signed messages (and signatures themselves) can be

proven anonymously, unlinkably and utraceably. We

recall the signing and veriﬁcation algorithms below,

the efﬁcient proofs of knowledge are described, e.g.,

in (Camenisch et al., 2016).

Setup: On input security parameter k, generate

a bilinear group (q,G

,e,g

) ← G(1

Take sk ←

, compute pk = g

, and output sk as

private key and pk = (q,G

,e, pk) as

public key.

Sign: On input message m ∈ Z

and secret key

sk, output σ = g

sk+m

Verify: On input the signature σ, mes-

sage m, and public key pk, output 1 iff

e(σ, pk) · e(σ

) = e(g

) holds.

Showing the constant signature σ multiple times

would make the protocol linkable. All user ses-

sions would be linkable to a single proﬁle, which

would make the resulting scheme very privacy un-

friendly. To avoid linkability of signatures, users can

only prove the knowledge of a valid signature by us-

ing the proof deﬁned in (Camenisch et al., 2016). In

this proof, the user chooses a random value r ←

and computes randomized auxiliary values σ

= σ

and

σ = σ

−m

. Then, the knowledge of a signa-

ture is proven by constructing the zero-knowledge

proof π = PK{(m,r) :

σ = σ

−m

} and verifying

σ,g

) = e(σ

, pk). The veriﬁer is convinced, that

the user indeed knows a valid signature on a known

message, although the proof does not release any of

these values.

The wBB signatures were proven existentially un-

forgeable against a weak (non-adaptive) chosen mes-

sage attack under the q-SDH assumption (Boneh and

Boyen, 2008).

2.5 Group Signatures from

Randomizable Proofs of Signatures

Group signatures (Chaum and Van Heyst, 1991) al-

low users to sign messages using their private keys

without being identiﬁable or traceable, as the signa-

tures are veriﬁed using a single, general public key.

SECRYPT 2018 - International Conference on Security and Cryptography

202

There are many proposals for group signatures, fo-

cusing on size, speed of construction, security or ad-

vanced features. For our data collection scheme, we

adopt the approach used in (Pointcheval and Sanders,

2016), i.e., we let the manager to sign the private keys

of users (sk

) using a signature scheme σ (wBB in

our case) that allows efﬁcient randomizable proofs

of the signature knowledge, resulting in signature

σ(sk

). Proving the manager’s signature knowledge

using SPK (Signature Proof of Knowledge) then al-

lows the construction of user’s group signatures on

messages (SPK{sk

: σ(sk

)}(m)). Using such a con-

struction, each user has his own private key but the

signatures are veriﬁed using a common manager’s

key. Furthermore, all signatures are anonymous, un-

traceable and unlinkable.

3 CRYPTOGRAPHIC DESIGN

3.1 General Architecture

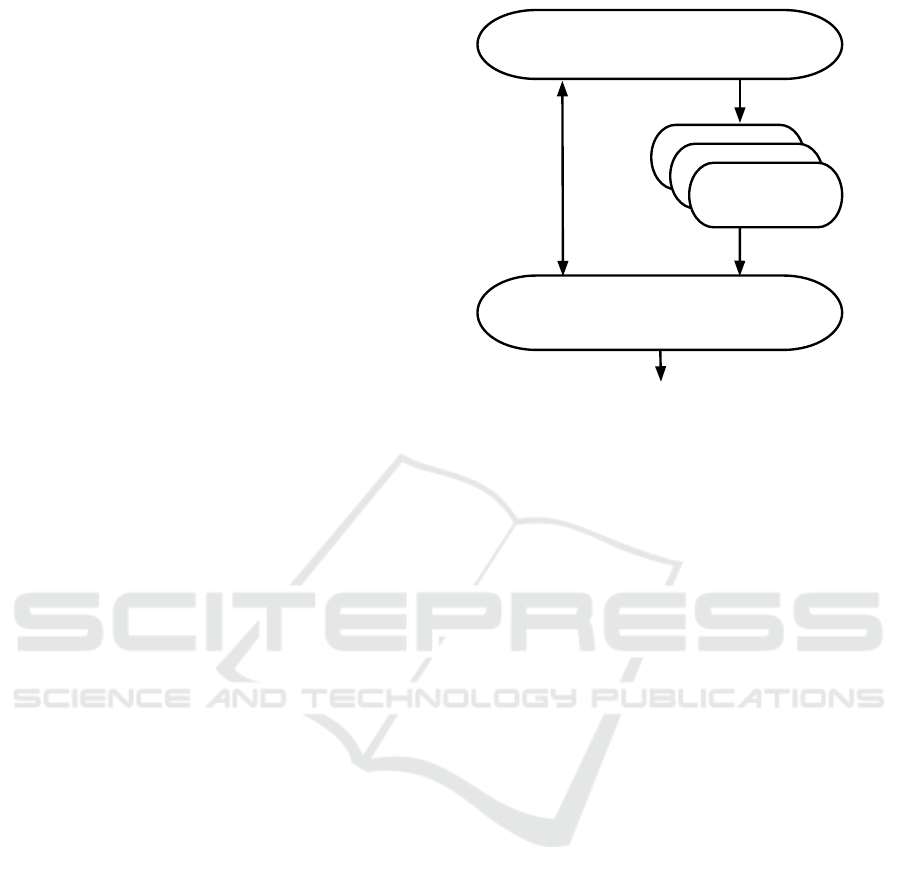
Three types of entities interact in our data collection

scheme: a manager, a user and a collector.

• Manager: the manager generates cryptographic

parameters and keys. It also enrolls new users (de-

vices) and revokes invalid ones.

• User: the user is represented by its device, such as

a smart meter, sensor or some wearable device. It

is the source of data that are signed and transferred

to the central device (collector).

• Collector: the collector represents the central

node that collects all data from users and veriﬁes

the group signatures.

The entities interact in the following cryptographic al-

gorithms and protocols.

• (pk,sk

, par) ← Setup ← 1

: on the input of

security parameter K , the algorithm generates the

public systems parameters par (implicit input of

all other algorithms), the public key shared by all

users pk and the private key of the manager sk

The Setup algorithm is run by the manager.

• (sk

,rd) ← Register ← (id

,sk

): on the input

of the manager’s private key sk

and the user iden-

tiﬁer id

, the register protocol outputs the user’s

private key sk

and updates the manager’s revo-

cation database rd. The Register algorithm is

run as an interactive protocol between the man-

ager and the user.

• sig(sk

,m) ← Sign ← (m, id

,sk

): on the input

of the message m, user’s identiﬁer id

and its pri-

vate key sk

, the algorithm outputs the signature

Manager

User

Collector

RegisterRevoke

Sign/Verify

Setup

0/1

User

Figure 2: Architecture of the scheme proposed.

on the message sig(sk

,m). The algorithm is run

by the user.

• 0/1 ← Verify ← (sig(sk

,data),m, pk): on the

input of the message m, signature sig(sk

,m) and

the public key pk, the algorithm returns 1 iff the

signature is valid and 0 otherwise. The algorithm

is run by the collector.

• id

← Revoke ← (rd,sig(sk

,data)): on the in-

put of the manager’s revocation database rd and

a signature sig(sk

,m), the algorithm outputs the

identiﬁer id

of the signer.

The algorithms and protocols must fulﬁll the fol-

lowing security properties of group signatures deﬁned

by Bellare et al. (Bellare et al., 2005). The manager

is trusted not to impersonate signers.

• Correctness: signatures are veriﬁed correctly iff

generated by valid and honest users.

• Anonymity: all signatures are anonymous, un-

traceable and unlinkable to all entities except the

manager.

• Traceability: the manager can de-anonymize, link

and trace signatures.

The privacy-enhanced data collection scheme is

presented in Fig. 2.

3.2 Instantiation using wBB Signatures

We instantiate the algorithms and protocols of the data

collection scheme presented in the previous section

using the wBB signature (Boneh and Boyen, 2008)

and its efﬁcient proof of knowledge (Camenisch et al.,

Anonymous Data Collection Scheme from Short Group Signatures

203

Manager User i

←

←−−−−−−−−−−−−−−−−

= g

+id

−−−−−−−−−−−−−−−−→

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Collector

r ←

= g

= sk

−id

π = SPK{(id

,r) :

= sk

−id

∧ g

= g

}(m)

,sk

,π

−−−−−−−−−−−−−−−−−−−−−−→

Check π

)

= e(sk

, pk)

Revocation Check:

= sk

0−id

i∈RL

Figure 3: Register, Sign and Verify algorithms.

2016). On a high level, we let the user to obtain

a wBB signature on his private identiﬁer from the

manager. Then, the user proves the knowledge of

such a signature anonymously and efﬁciently using

the Schnorr-like zero-knowledge protocol for prov-

ing the knowledge of a discrete logarithm (Camenisch

and Stadler, 1997). For the conversion from the proof

of knowledge to the signature, we use the Fiat-Shamir

heuristics (Fiat and Shamir, 1987).

We present the concrete algorithm and protocol in-

stantiations below.

3.2.1 Setup

(pk, sk

, par) ← Setup ← 1

: the algorithm inputs

the security parameter K and generates the bilinear

group with parameters par = (q,G

,e,g ∈

∈ G

) satisfying |q| = K . It also generates

the manager’s private key sk

←

and computes

the public key pk = g

. It outputs the (pk, par) as

a public output and the sk

as the manager’s private

output.

3.2.2 Register

(sk

,rd) ← Register ← (id

,sk

): the protocol is

distributed between the user and the manager. The

manager inputs his private key sk

and the user in-

puts his private identiﬁer id

. The protocol outputs

the wBB signature sk

= g

+id

to the user over a

secure channel and updates the manager’s revocation

database rd by storing id

3.2.3 Sign

sig(sk

,m) ← Sign ← (m,id

,sk

): the algorithm

inputs the user’s private identiﬁer id

, his private

key sk

and the message to be signed. It outputs the

signature sig(sk

,m) that consists of the following

elements (g

,sk

,π):

• g

= g

: the generator raised to a randomly chosen

randomizer r ←

• sk

= sk

: the users’s private key raised to the ran-

domizer.

•

= sk

−id

: the randomized private key raised to

the user identiﬁer.

• π = SPK{(id

,r) :

= sk

−id

∧ g

= g

}(m):

proof of knowledge of r and id

signing the mes-

sage m.

3.2.4 Verify

0/1 ← Verify ← (sig(sk

,m),m, pk, bl): the algo-

rithm inputs the massage m, its signature (sig(sk

,m),

a blacklist bl and the public key pk. It checks the

proof of knowledge signature π and checks that the

signature is valid with respect to the manager’s public

key using the equation e(

)

= e(sk

, pk). The

collector also performs the revocation check

0−id

for all id

values stored on the blacklist bl. If

the revocation check equation holds for any value on

the blacklist, the signature is rejected. Otherwise, the

signature is accepted if all other checks pass.

SECRYPT 2018 - International Conference on Security and Cryptography

204

3.2.5 Revoke

bl ← Revoke ← (rd, sig(sk

,m)): the algorithm in-

puts a signature sig(sk

,m) and a revocation database

rd. It checks

= sk

0−id

for all id

s in rd. The id

that holds in the equation is put on a public blacklist

bl.

The Register, Sign and Verify algorithms are

presented in CS notation in Fig 3.

4 SECURITY ANALYSIS

We imply the security of our scheme from the se-

curity of the building blocks. The wBB signature

scheme used for signing the private keys is unforge-

able against a non-adaptive chosen message attack un-

der the q-SDH assumption (Boneh and Boyen, 2008).

The group signature is an efﬁcient proof of knowledge

based on the standard zero-knowledge proofs (Ca-

menisch and Stadler, 1997) that are complete, sound

and zero-knowledge in the random oracle model.

4.1 Correctness

The proof π is always accepted for valid signatures,

due to the completeness of the proof of knowledge

protocol. The proof π is always reject for the invalid

signatures, due to the soundness property of the proof

of knowledge protocol.

The pairings are always accepted if a valid man-

ager’s key is used in the signature:

) = e(sk

, pk) (1)

e(sk

−id

) = e(sk

) (2)

e(g

−id

+id

) = e(sk

) (3)

e(g

r+id

r−id

+id

) = e(sk

) (4)

e(sk

) = e(sk

) (5)

e(sk

)

= e(sk

)

(6)

4.2 Anonymity

The proof π is always anonymous, untraceabe and un-

linkable due to the zero-knowledge property of the

proof of knowledge protocol.

Distribution of g

,sk

is random and uniform

in Z

as r is selected randomly and uniformly from

. Thus, the values disclosed are indistinguishable

from random elements.

4.3 Traceability

Provided the user’s private identiﬁer id

, the signa-

tures are linkable by

= sk

0−id

5 IMPLEMENTATION RESULTS

We present the computational and communication

complexity analysis in this section. Furthermore, we

present the results of our practical implementation on

several types of devices, including constrained de-

vices and wearables here.

The user’s device has to compute only 5 exponen-

tiations to construct the proof. On the other side, the

veriﬁer has to perform 2 bilinear pairings and 3 expo-

nentiations to verify the proof. The revocation check

time is linear to the number of revoked users and,

therefore, requires O(|RL|) exponentiations, where

|RL| is the number of revoked users. The computa-

tional and communication costs of our scheme is con-

siderably reduced due to the use of EC cryptography

which requires smaller keys compared to traditional

protocols on a similar security level. Our signatures

contain only 3 elements of G

, and 3 elements of Z

Therefore, using a strong 224 b elliptic curve, only

255 B need to be sent as a signature. In case that

EC point compression is used, we can reduce the sig-

nature size to less than 169 B (1347 b). Hence, the

size of Z

remains 224 b and the size of each ele-

ment of G

is 225 b rather than 448 b. This is espe-

cially signiﬁcant in smart card communication scenar-

ios, where the payload size of APDU message is re-

stricted to 255 B if T=0 transmission protocol is used.

We implemented the Sign and Verify protocols,

the full description of our algorithms is in Fig. 4.

5.1 Performance

Our proposal is particularly suitable for data col-

lections systems, such as smart metering. In these

systems, the data are anonymously collected by a

central collector from the remote nodes. Further-

more, due to the fast signature generation speed and

size efﬁciency, our scheme can by used in a wide

range of other applications, such as e-ticketing and

transportation e-IDs. For this reason, we performed

the measurements on different kinds of devices,

both constrained (wearables, embedded devices)

and powerful (PC, server) ones. We considered the

following test scenarios:

Smart Metering: smart houses are equipped with

different types of sensors, e.g., for gas, water, or elec-

Anonymous Data Collection Scheme from Short Group Signatures

205

User i Collector

,sk

r,ρ

,ρ

← Z

= g

= sk

−id

t = sk

e = H (g

,sk

,t, m)

= ρ

− er

= ρ

+ eid

,sk

,e,s

−−−−−−−−−−−−−−−−−→

t = (

)

= H (g

,sk

t,m)

)

= e(sk

, pk)

Revocation Check:

= sk

0−id

i∈RL

Figure 4: Implementation of Sign and Verify algorithms.

tricity consumption detection. The collected data are

sent to an energy supplier (collector) who performs

statistical evaluations on the consumption in a given

area. The consumption proﬁle of a concrete user

must remain anonymous, thus the application cannot

be used directly for billing purposes. However, if

a non-standard household consumption is detected,

the energy supplier can request the identity of the

”malicious“ user from a trusted third party. In this

scenario, the smart house sensors can be represented

Raspberry Pi devices, while PC and server can act as

a collector.

E-ticketing: wearable devices, such as smart cards,

smart phones and smart watch, can be used for stor-

ing tickets. Validity of a ticket can be checked by a

terminal, e.g. installed in a vehicle. In this scenario,

Raspberry Pi device represents a terminal and a wear-

able acts as a user’s device. The veriﬁcation can be

performed locally on the terminal or remotely on the

powerful central server.

We performed the measurement on all devices

mentioned above. The detailed HW and SW speci-

ﬁcations are described in Tab. 1.

The performance tests required the implementa-

tion of the proposed scheme on different platforms

and operation systems. In case of the smart card ap-

plication, only standard MultOS API and free pub-

lic development environment (Eclipse IDE for C/C++

Developers, SmartDeck 3.0.1, MUtil 2.8) were used.

Table 1: Speciﬁcation of tested devices.

Device CPU/MCU OS RAM

Card – Multos 4.2 2 KB

Phone 1 Kirin 655 Android 7.0 3 GB

Phone 2 Krait 400 Android 5.1 2 GB

Watch 1 ARM Cortex-A7 Android 6.0 512 MB

Watch 2 ARM Cortex-A7 Android 7.0 768 MB

Pi 3 ARM Cortex-A53 Raspbian 9.3 1 GB

Pi 2 ARM Cortex-A7 Raspbian 9.3 1 GB

Pi ARM1176JZF-S Raspbian 9.3 512 MB

PC Intel i7-7700 Debian 8.6 16 GB

Server Intel Xeon 2.27 Debian 8.6 32 GB

Card – Smart card, Phone 1 – HUAWEI P9 Lite 2017, Phone 2 – SONY

Experia Z1 Compact, Pi 3 – Raspberry Pi 3 Model B, Pi 2 – Raspberry Pi

2 Model B, Pi – Raspberry Pi Model B+, Watch 1 - Sony SmartWatch 3

SWR50, Watch 2 – HUAWEI Watch 2.

Table 2: Performance of Sign and Verify protocols for

different elliptic curves on various user devices.

Signing time [ms] Veriﬁcation time [s]

Curve d159 d201 d224 d159 d201 d224

SC 362 415 442 – – –

Phone 1 180 253 336 2.1 2.5 3.1

Phone 2 665 705 943 10.9 11.6 12.7

Watch 1 1252 2215 2889 26.2 31.0 38.0

Watch 2 1019 1139 1637 13.6 15.8 19.2

Pi 3 18 24 30 0.082 0.115 0.138

Pi 2 32 42 53 0.144 0.197 0.236

Pi 67 89 110 0.266 0.372 0.434

PC 3 4 5 0.007 0.009 0.011

The application is written in MULTOS assembly code

and C language. Smart phones and smart watches run

an Android application written in Java language. In

particular, we used Android Studio 3.0.1 as the of-

ﬁcial IDE for Android app development along with

Android SDK depending on the speciﬁc device, and

jPBC-2.0.0 library which allows performing opera-

tions over elliptic curves (point addition, scalar multi-

plication and bilinear pairing). The rest of the devices

run OS Linux and, therefore, the scheme was imple-

mented in C, where PBC-0.5.14 library was used for

the elliptic curve operations. The scheme was devel-

oped in NetBeans IDE 8.2 development environment.

The code was remotely build and executed on the tar-

geted device, i.e., Raspberry Pi/2/3, PC and server.

The Sign and Verify algorithms were imple-

mented using pairing-friendly elliptic curves. Since

our scheme requires asymmetric bilinear pairing, we

considered the elliptic curves of D types from the

PBC library, namely d159, d201, and d224. The per-

formance tests were run 10 times on each device, and

the arithmetic mean of the measured values was cal-

culated. The computation time of Sign and Verify

algorithms is provided in Tab. 2. At the ﬁrst sight,

the effectiveness of Sign protocol is obvious. Using

the 224 b elliptic curve, which is of 112 b security

strength, the Sign protocol takes only 442 ms on a

SECRYPT 2018 - International Conference on Security and Cryptography

206

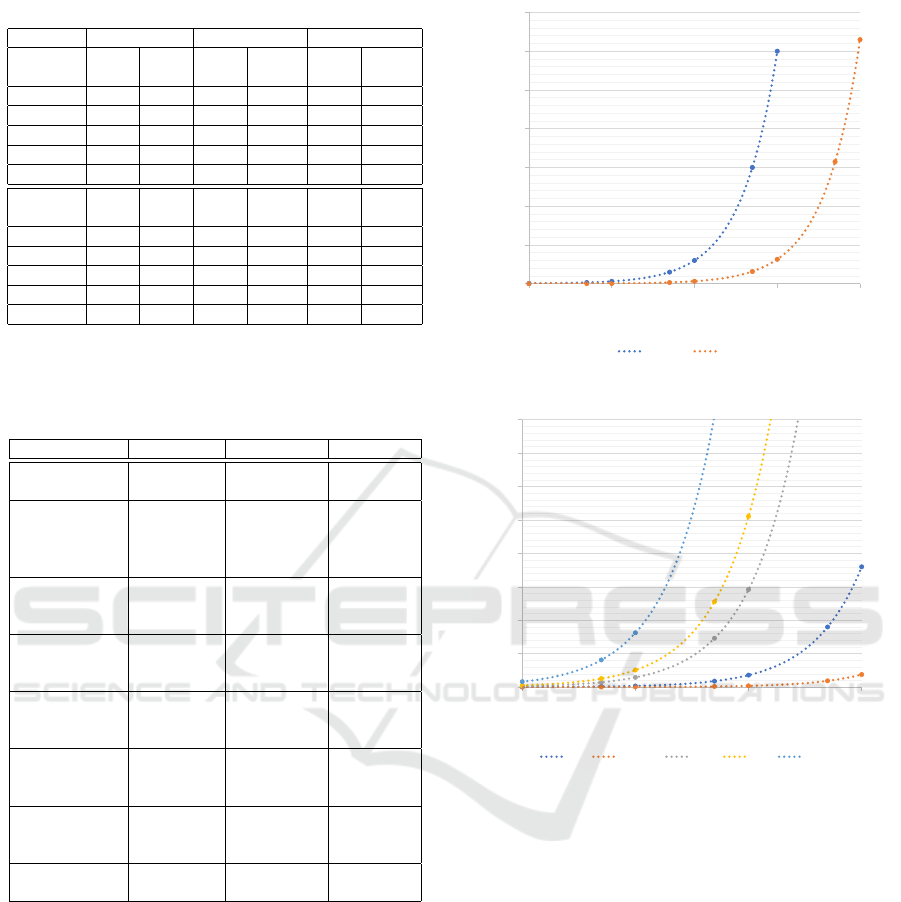
Table 3: Benchmarks of primitive operations.

Curve d159 d201 d224

EC op. E

P E

[ms] [s] [ms] [s] [ms] [s]

SC 40 – 44 – 50 –

Phone 1 38 1.0 48 1.2 65 1.4

Phone 2 153 5.4 161 5.7 187 6.7

Watch 1 350 12.4 457 14.7 548 18.5

Watch 2 196 6.5 246 7.5 325 9.1

EC op. E

P E

[ms] [ms] [ms] [ms] [ms] [ms]

Pi 3 3.3 31.6 4.7 45.3 5.8 55.2

Pi 2 6.0 54.8 7.9 77.4 10.2 94.5

Pi 12.8 97.9 17.2 140.1 21.1 167.6

PC 0.4 2.1 0.5 2.9 0.7 3.6

Server 0.2 1.9 – – 0.3 3.3

EC op. – operation over elliptic curve, E

– EC scalar multiplication in G

P – bilinear paring, P : G

× G

→ G

Table 4: Comparison with current short group signature

schemes.

Scheme Sign Cost Verify Cost Sign Size

BBS (Boneh

et al., 2004)

+3E

1P+8E

+3E

+6Z

(1545 b)

DP (Deler-

abl

ee and

Pointcheval,

2006)

+3E

1P+7E

+3E

+5Z

(1559 b)

HLCCN

(Hwang et al.,

2011)

+5E

1P+5E

+4E

+5Z

(1375 b)

ACJT (Ate-

niese et al.,

2000)

12E

∗

10E

∗

+1Z

(7328 b)

CG (Ca-

menisch and

Groth, 2004)

10E

∗

10E

∗

+1Z

(8352 b)

IMSTY (Is-

shiki et al.,

2006)

∗

+5Z

(6155 b)

HM GS (Ha-

jny et al.,

2013)

∗

10E

∗

+1Z

(7328 b)

Our Scheme 5E

2P+3E

+3Z

(1035 b)

– EC scalar multiplication in G

, similarly E

and E

, P – bilinear

pairing.

smart card. On the other hand, the Android devices

are slow in EC operations, in particular in bilinear

pairing. In fact, Tab. 3, which provides the bench-

marks of the crucial elliptic curve primitive operations

on the tested devices, shows that Watch 1 and Watch

2 are slower than smart cards although they are much

more powerful. This is due to the use of the jPBC li-

brary, which is a library written in Java rather than in

C. Furthermore, HW acceleration of EC operations is

employed on smart cards.

The Fig. 5 and Fig. 6 show the time needed to

complete the malicious user identiﬁcation and revo-

cation check procedure. The user identiﬁcation pro-

0,5

1,5

2,5

3,5

1 10 100 1000 10000

time [min]

System users [-]

Thousands 

PC Server

Figure 5: Time needed to identify a malicious user.

0,5

1,5

2,5

3,5

10 100 1000 10000

time [s]

Revoked users [-]

PC Server Pi 3 Pi 2 Phone 1

Figure 6: Time needed to check the black list.

cedure requires to perform scalar multiplications on

the considered device (the cost of this operation is de-

picted in Tab. 3). In case of the de-anonymisation

procedure, the number of scalar multiplications is

equal to the number of users. We stress, that the de-

anonymisation procedure is expected to be performed

on powerful devices and can be parallelized on their

processors and cores (CPU/Cores). For instance, our

PC (1/4), and server (2/8) are able go through the list

of thousands of users and ﬁnd the identity of a user in

less than 4 min, see Fig. 5.

In the revocation check procedure, the PC (1/4)

and server (2/8) are able to search the blacklist in less

than 0.5 s, see Fig. 6.

5.2 Comparison

In this section, we provide the comparison of our

scheme with the state-of-the-art group signature

Anonymous Data Collection Scheme from Short Group Signatures

207

schemes. We considered the efﬁcient group signature

schemes identiﬁed in (Malina et al., 2018). Tab. 3

shows the comparison of our scheme with these pair-

ing and non-pairing based group signature schemes.

Bilinear pairing and exponentiation operations are de-

noted as P and E, respectively. The execution time of

each operation depends on the bitlength of the ele-

ments in respective groups and ﬁelds. In the pairing-

based schemes, G

, G

, Z

denote different

groups with the following bitlengths: |G

| = 175 b,

| = 175 b and |G

| = 1050 b computed as k · |G

where k is the embedding degree (e.g. k = 6). |Z

= 170 b denotes the ﬁeld size of an elliptic curve. In

the non-pairing schemes, |G

∗

| = 1024 b denotes the

multiplicative RSA group with exponents from |Z

| =

160 b. The total length of signatures depends on the

security level chosen.

6 CONCLUSIONS

We presented a novel data collection scheme which

is more efﬁcient than comparable state-of-the-art

schemes as shown in the comparative complexity

analysis. The proposed scheme is built using primi-

tives with formal security proofs and the security of

the proposed scheme itself was proven.

Our proposal is particularly suitable for data col-

lections systems, such as smart metering. However,

our scheme can be also used in other areas of IoT,

such as smart grids, Industry 4.0, e-ticketing, trans-

portation e-IDs, due to the signature generation speed

and short size.

Moreover, we provided the full implementation

results from a wide range of devices, including IoT

devices, to show the efﬁciency of our solution. A sig-

nature on the 112 b security level can be generated

in 442 ms on a standard smart card, in 336 ms on a

current smart phone and in 18 ms on the Raspberry Pi

3. Furthermore, our scheme provides fast revocation

checks, the blacklisted user can be identiﬁed in less

than 2 s.

ACKNOWLEDGEMENTS

Research described in this paper was ﬁnanced by

the Ministry of Industry and Trade grant # FV20354

and the National Sustainability Program under grant

LO1401. For the research, infrastructure of the SIX

Center was used.

REFERENCES

(2011). National strategy for trusted identities in

cyberspace. http://www.whitehouse.gov/sites/de-

fault/ﬁles/rss viewer/NSTICstrategy 041511.pdf.

Ateniese, G., Camenisch, J., Joye, M., and Tsudik, G.

(2000). A practical and provably secure coalition-

resistant group signature scheme. In Annual In-

ternational Cryptology Conference, pages 255–270.

Springer.

Barker, E. (2016). Recommendation for key management

part 1: General (revision 4). NIST Special Publication

Part 1, 800(57):1–147.

Bellare, M., Shi, H., and Zhang, C. (2005). Foundations

of group signatures: The case of dynamic groups. In

Menezes, A., editor, Topics in Cryptology – CT-RSA

2005, pages 136–153, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Boneh, D. and Boyen, X. (2008). Short signatures without

random oracles and the SDH assumption in bilinear

groups. Journal of Cryptology, 21(2):149–177.

Boneh, D., Boyen, X., and Shacham, H. (2004). Short

group signatures. In Advances in Cryptology -

CRYPTO’04.

Boneh, D. and Shacham, H. (2004). Group signatures with

veriﬁer-local revocation. In Proceedings of the 11th

ACM conference on Computer and communications

security, CCS ’04, pages 168–177, New York, NY,

USA. ACM.

Camenisch, J., Drijvers, M., and Hajny, J. (2016). Scalable

revocation scheme for anonymous credentials based

on n-times unlinkable proofs. In Proceedings of the

2016 ACM on Workshop on Privacy in the Electronic

Society, WPES ’16, pages 123–133, New York, NY,

USA. ACM.

Camenisch, J. and Groth, J. (2004). Group signatures: Bet-

ter efﬁciency and new theoretical aspects. In Interna-

tional Conference on Security in Communication Net-

works, pages 120–133. Springer.

Camenisch, J. and Lysyanskaya, A. (2003). A signature

scheme with efﬁcient protocols. In Proceedings of the

3rd international conference on Security in commu-

nication networks, SCN’02, pages 268–289, Berlin,

Heidelberg. Springer-Verlag.

Camenisch, J. and Stadler, M. (1997). Efﬁcient group sig-

nature schemes for large groups. In Kaliski, B., edi-

tor, Advances in Cryptology - CRYPTO ’97, volume

1294 of Lecture Notes in Computer Science, pages

410–424. Springer Berlin / Heidelberg.

Chaum, D. and Van Heyst, E. (1991). Group signatures. In

Proceedings of the 10th annual international confer-

ence on Theory and application of cryptographic tech-

niques, EUROCRYPT’91, pages 257–265, Berlin,

Heidelberg. Springer-Verlag.

Delerabl

ee, C. and Pointcheval, D. (2006). Dynamic

fully anonymous short group signatures. In Progress

in Cryptology-VIETCRYPT 2006, pages 193–210.

Springer.

Ferrara, A. L., Green, M., Hohenberger, S., and Pedersen,

M. Ø. (2009). Practical short signature batch veriﬁca-

SECRYPT 2018 - International Conference on Security and Cryptography

208

tion. In Topics in Cryptology - The Cryptographers’

Track at the RSA Conference, volume 5473, pages

309–324. Springer.

Fiat, A. and Shamir, A. (1987). How to prove your-

self: Practical solutions to identiﬁcation and signature

problems. In Odlyzko, A. M., editor, Advances in

Cryptology — CRYPTO’ 86, pages 186–194, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Finster, S. and Baumgart, I. (2013). Pseudonymous smart

metering without a trusted third party. In Trust, Secu-

rity and Privacy in Computing and Communications

(TrustCom), 2013 12th IEEE International Confer-

ence on, pages 1723–1728.

Hajny, J. and Malina, L. (2013). Unlinkable attribute-based

credentials with practical revocation on smart-cards.

In Mangard, S., editor, Smart Card Research and Ad-

vanced Applications - CARDIS 2012, volume 7771

of Lecture Notes in Computer Science, pages 62–76.

Springer Berlin Heidelberg.

Hajny, J., Malina, L., Martinasek, Z., and Zeman, V. (2013).

Privacy-preserving svanets: Privacy-preserving sim-

ple vehicular ad-hoc networks. In Security and Cryp-

tography (SECRYPT), 2013 International Conference

on, pages 1–8. IEEE.

Hwang, J. Y., Lee, S., Chung, B.-H., Cho, H. S., and Nyang,

D. (2011). Short group signatures with controllable

linkability. In Lightweight Security & Privacy: De-

vices, Protocols and Applications (LightSec), 2011

Workshop on, pages 44–52. IEEE.

Isshiki, T., Mori, K., Sako, K., Teranishi, I., and Yonezawa,

S. (2006). Using group signatures for identity man-

agement and its implementation. In Proceedings of

the second ACM workshop on Digital identity man-

agement, pages 73–78. ACM.

Kim, K., Yie, I., Lim, S., and Nyang, D. (2011). Batch

veriﬁcation and ﬁnding invalid signatures in a group

signature scheme. IJ Network Security, 13(2):61–70.

Lin, X., Sun, X., han Ho, P., and Shen, X. (2007). Gsis: A

secure and privacy preserving protocol for vehicular

communications. In IEEE Transactions on Vehicular

Technology, volume 56, pages 3442–3456.

Malina, L., Dzurenda, P., and Hajny, J. (2018). Eval-

uation of anonymous digital signatures for privacy-

enhancing mobile applications. In Int. J. Security and

Networks, Vol. 13, No. 1, pages 27–41. IEEE.

Pointcheval, D. and Sanders, O. (2016). Short Random-

izable Signatures, pages 111–126. Springer Interna-

tional Publishing, Cham.

Raya, M. and Hubaux, J.-P. (2007). Securing vehicular ad

hoc networks. J. Comput. Secur., 15:39–68.

Rottondi, C., Mauri, G., and Verticale, G. (2015). A pro-

tocol for metering data pseudonymization in smart

grids. Transactions on Emerging Telecommunications

Technologies, 26(5):876–892.

Schnorr, C. P. (1991). Efﬁcient signature generation by

smart cards. Journal of Cryptology, 4:161–174.

Zhang, C., Lu, R., Lin, X., Ho, P.-H., and Shen, X. (2008).

An efﬁcient identity-based batch veriﬁcation scheme

for vehicular sensor networks. In INFOCOM, pages

246–250. IEEE.

Anonymous Data Collection Scheme from Short Group Signatures

209