Clustering Big Data

Michele Ianni

, Elio Masciari

, Giuseppe M. Mazzeo

and Carlo Zaniolo

DIMES, University of Calabria, Rende (CS), Italy

ICAR-CNR, Rende (CS), Italy

Facebook, Menlo Park, U.S.A.

UCLA, Los Angeles, U.S.A.

Keywords:

Clustering, Big Data, Spark.

Abstract:

The need to support advanced analytics on Big Data is driving data scientist’ interest toward massively parallel

distributed systems and software platforms, such as Map-Reduce and Spark, that make possible their scalable

utilization. However, when complex data mining algorithms are required, their fully scalable deployment

on such platforms faces a number of technical challenges that grow with the complexity of the algorithms

involved. Thus algorithms, that were originally designed for a sequential nature, must often be redesigned in

order to effectively use the distributed computational resources. In this paper, we explore these problems, and

then propose a solution which has proven to be very effective on the complex hierarchical clustering algorithm

CLUBS+. By using four stages of successive reﬁnements, CLUBS+ delivers high-quality clusters of data

grouped around their centroids, working in a totally unsupervised fashion. Experimental results conﬁrm the

accuracy and scalability of CLUBS+ on Map-Reduce platforms.

1 INTRODUCTION

The current era of Big Data (Nature, 2008) has forced

both researchers and industries to rethink the compu-

tational solutions for analyzing massive data. In fact,

a great deal of attention has been devoted to the design

of new algorithms for analyzing information available

from Twitter, Google, Facebook, and Wikipedia, just

to cite a few of the main big data producers. Although

this massive volume of data can be quite useful for

people and companies, it makes analytical and re-

trieval operations really time consuming due to their

high computational cost. A possible solution relies

upon the opportunity to cluster big data in a com-

pact but still informative version of the entire data set.

Obviously, such clustering techniques should produce

clusters (or summaries) having high accuracy. Clus-

tering algorithms could be beneﬁcial in several appli-

cation scenarios such as cybersecurity, user proﬁling

and recommendation systems, to cite a few. Although

all textbooks describe clustering as the quintessential

“unsupervised learning task” all the major algorithms

proposed so far require signiﬁcant guidance from the

user, such as the number of clusters to be derived for

k-means++ and the termination condition for hier-

archical clustering. In (Mazzeo et al., 2017) the au-

thors proposed CLUBS

, a clustering algorithm that

manages to be very effective without any user guid-

ance by (i) operating in multiple stages whereby the

techniques used at one stage compensate for the short-

comings of the previous stages, and by (ii) applying

carefully selected and well-tuned criteria to assure the

quality of the results produced at each stage. In par-

ticular, the beneﬁt of (i), is illustrated by the fact that

while over-splitting represents a very difﬁcult issue

for most divisive algorithms, it is much less of con-

cern here, because a certain degree of over-splitting

can be tolerated since it will be undone in the succes-

sive stages that include an agglomerative step.

In this paper we present a parallel version of

CLUBS

, which we call CLUBS-P. Like CLUBS

CLUBS-P, scales linearly w.r.t. the size of the data

set. Furthermore, experiments show that the speed-up

increases almost linearly as more machines for run-

ning the algorithm are available. These two features

make CLUBS-P a very effective algorithm for cluster-

ing large amount of data. Finally, a nice feature of

CLUBS-P is that once the data set to be clustered has

been distributed across the available machines, there

is no need to move data, as CLUBS-P requires the ma-

chines to exchange only summary information.

We provided a new implementation of our parallel

276

Ianni, M., Masciari, E., Mazzeo, G. and Zaniolo, C.

Clustering Big Data.

DOI: 10.5220/0006858702760282

In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 276-282

ISBN: 978-989-758-318-6

clustering algorithm, based on the widely used Big

Data framework Apache Spark (Zaharia et al., 2010).

The implementation of a distributed algorithm

calls for suitable solution to some crucial problem in

a distributed programming environment such as: load

balancing and fault tolerance. A very popular solution

proposed in recent years for implementing parallel al-

gorithms tailored for Big Data is Apache Spark

. In-

deed, it offers very useful functions which relieves the

programmers from the explicit management of pro-

cess assignment and memory management. In this re-

spect, we implemented our CLUBS-P algorithm based

on Spark. This paper is organized as follows. In

Section 2 we provide an overview of CLUBS

, while

in Section 3 we ﬁrst discuss the crucial points of

CLUBS

with a view to its parallelization, that lead

to devising CLUBS-P, for which we present a new im-

plementation based on Apache Spark (Section 4). In

Section 5 we present the experimental results and, ﬁ-

nally, in Section 6 we draw our conclusions.

2 AN OVERVIEW OF CLUBS

In (Mazzeo et al., 2017) the authors introduced

CLUBS

. It is a parameter-free around-centroid clus-

tering algorithm based on a fast hierarchical ap-

proach, that combines the beneﬁts of the divisive and

agglomerative approaches. The ﬁrst operation per-

formed by CLUBS

is the deﬁnition of a binary space

partition of the domain of the dataset D, which yields

set of coarse clusters that are then reﬁned. The next

operation is an agglomerative procedure performed

over the previously reﬁned clusters, which is followed

by a ﬁnal reﬁnement phase. In the reﬁnement phases,

outliers are identiﬁed and the remaining points are

assigned to the nearest cluster. In our running ex-

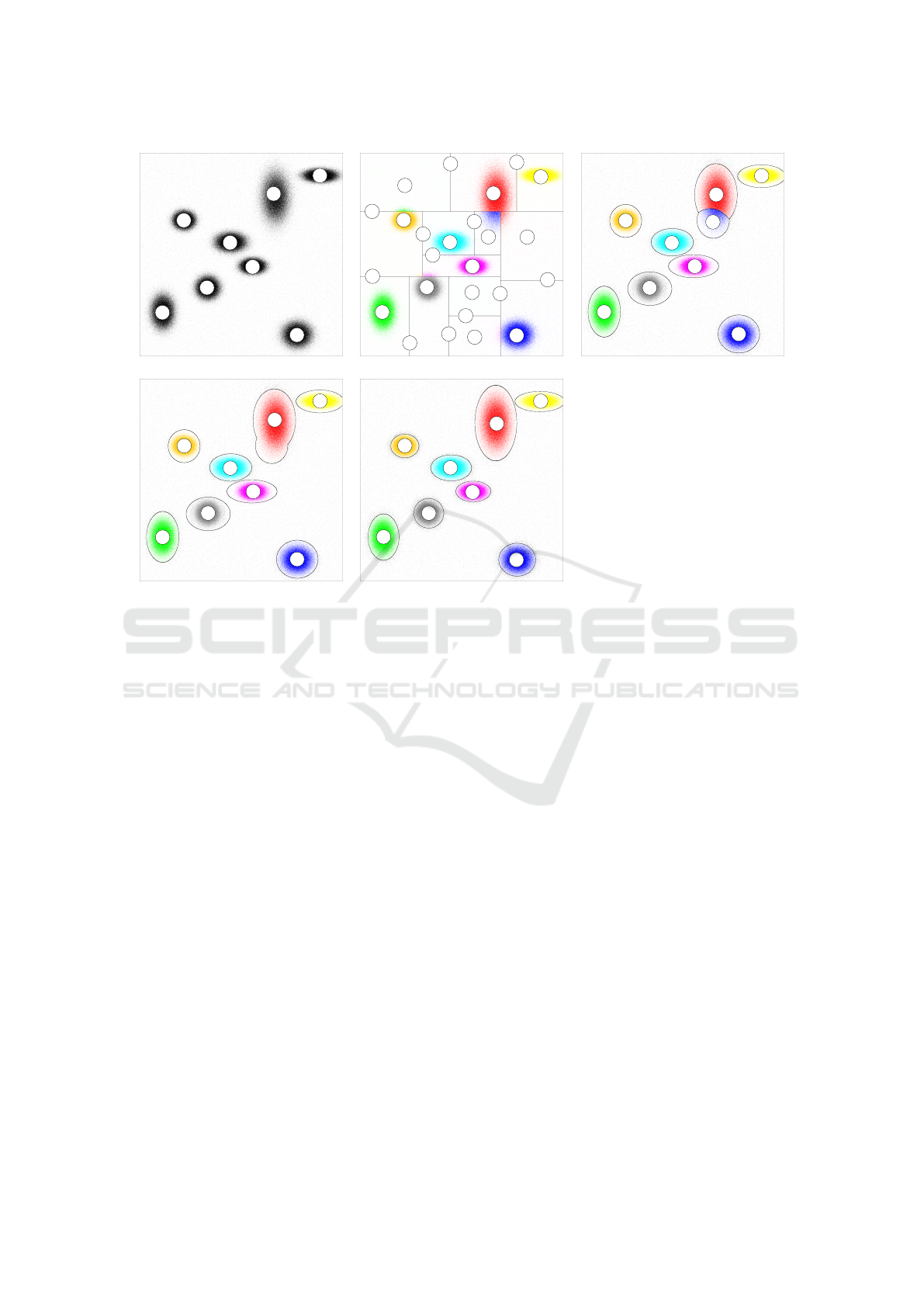
ample of Fig. 1, we show how the successive steps

of CLUBS

applied to the two-dimensional data dis-

tribution of Fig. 1(a), produce the results shown in

Fig. 1(b–e). In order to make this paper-self con-

tained, in the following we provide some details about

the four steps of CLUBS

allowing a full comprehen-

sion of the parallel algorithm implemented in this pa-

per, while a more exhaustive description of the algo-

rithm phases can be found in (Mazzeo et al., 2017).

The divisive step of CLUBS

performs a top-down

binary partitioning of the data set to isolate hyper-

rectangular blocks whose points are as much as pos-

sible close to each other: this is equivalent to mini-

mizing the within clusters sum of squares (WCSS) of

the blocks, an objective also pursued by k-means and

http://spark.apache.org/

many other algorithms.

Since ﬁnding the partitioning which minimizes

a measure such as the WCSS is NP-hard even for

two-dimensional points (Muthukrishnan et al., 1999),

CLUBS

uses a greedy approach where the splitting

hyperplanes are orthogonal to the dimension axes,

and the blocks are recursively split into pairs of clus-

ters that optimize speciﬁc clustering criteria that will

be discussed later. Given a input dataset, the algo-

rithm begins with a single cluster S corresponding to

the whole data set. S is entered into a priority queue,

Q. Q contains blocks of the partition that is iteratively

build over the dataset. While Q is not empty, a block

B is removed and split into a pair of blocks. If the

split is effective, the pairs of blocks replace B in Q,

otherwise B becomes a ‘ﬁnal’ block for this phase.

In order to efﬁciently ﬁnd the best split for a block,

the marginal distributions of the block must be com-

puted. In particular, for each dimension i of a d-

dimensional block B we must compute the functions

: R → N and LS

: R → R

, deﬁned as follows

(x) =

p ∈ B ∧ p[i] = x

(1)

(x) =

∑

p∈B∧p[i]=x

p (2)

where p[i] is the i-th coordinate of the point p.

These functions can be represented as maps, or, as-

suming that the coordinates of the points are integers,

as arrays. In (Mazzeo et al., 2017) the authors showed

that the split that minimizes the WCSS can be found

through a linear scan of these maps/arrays. The au-

thors conducted an extensive evaluation of the effec-

tiveness of criteria proposed in the literature for esti-

mating the quality and naturalness of a cluster set (Ar-

belaitz et al., 2013), and they concluded that the

Calinski-Harabasz index, CH-index for short, is the

most suitable to their needs (Calinski and Harabasz,

1974). Brieﬂy, after each step, we compute the new

CH-index, and if it is increased by the split, then we

consider the split effective and continue the divisive

phase. Otherwise, we check a “local” criterion, based

on the presence of a ‘valley’ in the marginal distribu-

tion. In fact, even though a split could not decrease

the overall CH-index, a very large local discontinuity

could justify the split of a block anyway.

When the divisive phase is completed, the overall

space is partitioned into (a) blocks containing clus-

ters, and (b) blocks that only contain noise points. In

this intermediate reﬁnement phase CLUBS

seeks to

achieve the objectives of (I) separating the blocks that

contain clusters from those that do not, and (II) gener-

ating well-rounded clusters for the blocks in the pre-

vious group.

Clustering Big Data

277

(a) (b) (c)

(d) (e)

Figure 1: A two-dimensional data set with 8 clusters (a), its partitioning after the divisive step (b), the intermediate reﬁnement

(c), the agglomerative step (d), and the ﬁnal reﬁnement (e).

Task (I) is performed by using the observation that

(a) the density of blocks containing only noise is low,

and (b) the density of such blocks is rather uniform

because of the random nature of noise.

For instance, these tests applied to our running ex-

ample in Fig. 1(b) have classiﬁed blocks “J”, “K”, “L”

and “M” as outlier-blocks.

Once, the cluster-blocks have been found, we can

now proceed with task (II).

This step produces well-rounded clusters that re-

store the natural clusters that might have been shaved-

off by rigid partitioning scheme leveraged in the

divisive step. For instance, the block of data in

Fig. 1(b), which contains the points of the cluster “E”

in Fig. 1(a), contains also some points of the original

cluster “F” which is now reassembled about its cen-

troid.

In the agglomerative step, the clusters produced

by the previous step are merged whenever this im-

proves the overall clustering quality. The process of

merging is symmetric to that of splitting: at each step

we ﬁnd the pair of clusters whose merge produces

the least increase of WCSS and, if CH-index resulting

from their merge increases, the merge is actually per-

formed by replacing the two clusters by their union. If

we determine that merging these two clusters will de-

crease the CH-index, the merge is not performed and

the whole agglomerative phase ends, since no merg-

ing of other cluster pair can improve CH-index.

Fig. 1(d) shows that the the cluster “B” is obtained

as the merge of the clusters “B” and “I” of Fig. 1(c).

The agglomerative step is a very fast step, as does

not require to access data, since it is based only on

previously computed summary information.

The agglomerative step often produces clusters of

slightly irregular shapes due to the approximate and

greedy criteria used in the previous steps. For in-

stance, Fig. 1(d) shows that cluster “B” has been ob-

tained by merging clusters “B” and “I” of Fig. 1(c).

The evident asymmetry is due to the fact that the

block “K” of Fig. 1(b) has been considered an outlier-

block during the intermediate reﬁnement, and the

points at its upper-left corner have been asymmetri-

cally adsorbed (due to their different position and ra-

dius) by blocks “B” and “I”.

The ﬁnal reﬁnement step improves the quality of

clusters and also identiﬁes the ﬁnal outlier points.

The algorithm used to perform ﬁnal reﬁnement is

basically the same as the one used for task (II) of the

intermediate reﬁnement (see (Mazzeo et al., 2017)

for further details).

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

278

3 CLUBS-P: THE

PARALLELIZATION OF CLUBS

We now analyze the steps of CLUBS

with the aim of

pointing out the issues to be tackled in order to paral-

lelize its execution.

We assume that n workers (i.e., different ma-

chines) with equivalent hardware features are avail-

able. The workers are coordinated by a master ma-

chine. The dataset is distributed over the worker

nodes that store locally a portion of the dataset, which

can be, for instance stored, in a distributed ﬁle system,

or even previously split over the local ﬁle systems of

the machines.

It is quite intuitive that the critical operations that

can beneﬁt from the availability of multiple workers

are those requiring to access the original data: 1) com-

putation of the marginal distributions during the divi-

sive phase; 2) computation of the local density of out-

lier blocks candidates during the intermediate reﬁne-

ment; 3) assignment of points to the closest centroid

during the reﬁnement phases;

The parallelization of the operations above is dis-

cussed in the following. The other operations, which

involves computations on summary information, in-

stead, can be handled by the master, using the same

approach as in the original version of CLUBS

3.1 Parallel Computation of the

Marginal Distributions

As remarked in previous section, the computation of

the marginal distributions, more speciﬁcally of the

vectors C and LS, is the only operation that requires

to access the data during the divisive step. This opera-

tion can be efﬁciently performed in parallel thanks to

the associativity and commutativity of the sum and

count operations, which are the only mathematical

operations involved in the computation. Therefore,

given a block partition of the data B, {B

,...B

those vectors can be independently computed on each

(thus in parallel) and the vector for the whole block

B can be obtained by simply summing the vectors ob-

tained on all the B

. According to the Map-Reduce

paradigm, each block B

is mapped to a set of pairs

of vectors, representing its C and LS for each dimen-

sion, and these vectors are subsequently reduced by

summing vectors of the same dimension.

3.2 Parallel Computation of the Local

Density of the Blocks

The local density of blocks has to be computed in or-

der to evaluate the criterion used for Task II of the

intermediate reﬁnement. After the master has the list

of the blocks resulting from the divisive phase, it also

has their ranges and their global density. In order to

check if the local density around the centroid of each

block is signiﬁcantly higher than the global density, it

computes the boundaries of a small range around the

centroid (i.e., a range of size 1/10 of the whole block

range), and then coordinates the parallel computation

of the count of the points falling in each of these ‘re-

stricted’ ranges. Even in this case, the only mathe-

matical operation involved in the computation is sum,

thus the operation is perfectly parallelizable. In fact,

for each portion of data of a block, it is possible to in-

dependently compute the count of points laying in the

restricted range, and then the overall count is simply

given by the sum of the partial counts. This count al-

lows the master to compute the local density, and thus

apply the criterion described above.

3.3 Parallel Assignment of the Points to

the Clusters

The assigment of the points to the clusters, or their

classiﬁcation as outliers, is an operation performed

in both the reﬁnement steps. Each worker can per-

form this operation independently on the others. The

master, which has the summary information about the

clusters, needs to send to every worker the informa-

tion needed to compute the distance between points

and clusters. After the computation, the same infor-

mation must be updated by the master, since the clus-

ter assignment of some points is likely to change. To

this end, each node can compute the summary infor-

mation for its data, and then, again, the master can

simply obtain the global values of the new centroids,

number of points per cluster, and cluster radius, after

summing up all the values obtained from the workers.

We presented the general ideas on which our ‘ab-

stract’ algorithm CLUBS-P is based for the paral-

lelization of CLUBS. In the following, we propose

a new implementation of this algorithm, using the

Apache Spark. The implementation is available as

open source software

4 CLUBS-P MEETS SPARK: CLUBS

The implementation of a distributed algorithm re-

quires a lot of effort for solving speciﬁc issues related

to the problem, but also general issues for distributed

computing, such as load balancing and fault toler-

ance. Nowadays, a very popular framework for im-

https://github.com/gmmazzeo/clubspark

Clustering Big Data

279

plementing parallel algorithms tailored for Big Data

is Apache Spark

. As a matter of fact, it offers

very useful functions which relieves the programmers

from the burden of handling the general issues of dis-

tributed computing.

For sake of brevity, we will mention here only the

Spark’s features that are relevant to our scope. The

main data structure used by Spark is Resilient Dis-

tributed Dataset (RDD). An RDD is a read-only, par-

titioned collection of records. Spark’s API allows the

deﬁnition of custom functions in order to manipulate

RDD when implementing our algorithm.

Two of the core Spark’s functions, working on an

RDD according to the the map-reduce paradigm, are

the following: a) mapPartitions: RDD returned by

mapPartitions is obtained by transforming each parti-

tion of the source RDD as speciﬁed by a user-deﬁned

function; b) reduce: RDDs are aggregated in pairs by

using a user-deﬁned function that must be commuta-

tive and associative in order to perform the reduction

step in parallel.

As described in Section 3, the operations that

CLUBS-P performs on data are commutative and as-

sociative, therefore we can safely adopt Spark for im-

plementing our algorithm, that we call CLUBS

Since the computation of marginal distributions is

the most expensive operation and the most interest-

ing, from a technical point of view, in the following

we provide in Algorithm 1 the details of its imple-

mentation using Spark.

Algorithm 1: Marginal Distribution Computation.

Input: D: RDDhPointi representing points in a block B.

Output: Marginal distribution for B.

1: RDDhMaphDouble, Integeri[]i mc ←

D.mapPartitions(new CMapper());

2: MaphDouble, Integeri[] C ← ms. reduce(new

CReducer());

3: RDDhMaphDouble, Double[]i[]i mls ←

data.mapPartitions(new LSMapper());

4: MaphDouble, Double[]i[] LS ← mls. reduce(new

LSReducer());

5: return C, LS;

Lines 1–2 compute the C function over the in-

put data, for every dimension. More speciﬁcally,

line 1, computes this function for the data of each

worker, through our object CMapper, which simply

scans the data of the worker, updating a counter for

each possible coordinate of each dimension. Then,

line 2 aggregates the partial counts, using the object

CReducer. The computation of LS functions is per-

formed by lines 3–4. The object LSMapper is similar

http://spark.apache.org/

to CMapper, but instead of updating counters, it up-

dates arrays representing the sum of points. The same

holds for the object LSReducer.

In the following, we report a simple example that

clariﬁes how map-reduce paradigm is applied by the

algorithm.

Example 1. Consider a toy dataset consisting of 9

points partitioned over 2 nodes as follows::

part

= {(4,4),(5,7),(5, 8),(5, 4),(6,4)}

and

part

= {(2,7),(2,5),(3, 6),(5, 7)}

The results of the mapping operations (lines 1 and

3) for each node and each dimension are reported in

Table 1.

Table 1: Results of the map operations.

part

dim 1

coord 4 5 6

mc 1 3 1

mls (4, 4) (15, 19) (6, 4)

dim 2

coord 4 7 8

mc 3 1 1

mls (15, 12) (5, 7) (5, 8)

part

dim 1

coord 2 3 5

mc 2 1 1

mls (4, 12) (3, 6) (5, 7)

dim 2

coord 5 6 7

mc 1 1 2

mls (2, 5) (3, 6) (7, 14)

For instance, the points in partition 1 that have

coordinate of dimension 2 equal to 4 are the fol-

lowing: (4,4), (5,4), and (6, 4). Therefore, for the

dimension 2 and coordinate 4 mc is 3, and mls is

(4,4)+(5,4) + (6,4) = (15,12).

The results of the reducing operations (lines 2 and

4) for each dimension are reported in Table 2.

Table 2: Results of the reduce operations.

dim 1

coord 2 3 4 5 6

C 2 1 1 4 1

LS (4, 12) (3, 6) (4, 4) (20, 26) (6, 4)

dim 2

coord 4 5 6 7 8

C 3 1 1 3 1

LS (15, 12) (5, 2) (3, 6) (12, 21) (5, 8)

For instance, consider the coordinate 5 of dimen-

sion 1. C is obtained as 3 + 1 = 4, and LS as

(15,19)+(5,7) = (20, 26).

5 EXPERIMENTAL RESULTS

As mentioned above, CLUBS-P shares the ideas of

CLUBS

. Since the clustering obtained by CLUBS-

P for a given data set is the same that obtained by

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

280

400

1 2 4 8 16

Execution time (s)

N. of workers

CLUBS* Sensitivity to dataset size

400

1 2 4 8 16

Execution time (s)

N. of workers

CLUBS* Sensitivity to dimensionality

(a) (b)

400

1 2 4 8 16

Execution time (s)

N. of workers

CLUBS* Senstivity to number of clusters

400

1 2 4 8 16

Execution time (s)

N. of workers

CLUBS* Sensitivity to noise

0.01

0.05

0.1

Figure 2: CLUBS

Execution Times vs number of workers varying dataset size (a), data dimensionality (b), number of

clusters (c), and noise ratio (d).

CLUBS, we can say that the accuracy of CLUBS-P is

the same as that of CLUBS. The latter has been proven

to be better than that of existing algorithms (CLUBS,

), and, thus, we do not report accuracy results here,

for space limitation and because our goal is rather

to prove the effectiveness of the parallelization of

CLUBS

in order to apply it in the Big Data scenario.

We tested our parallel implementation on several syn-

thetic datasets obtained by means of an open source

synthetic data generator

, which generates data distri-

butions where each cluster follows a possibly differ-

ent gaussian distribution, while noise points are ran-

domly added. We generated datasets with 10

, 10

and 10

points. For each dataset size, we varied the

dimensionality in the range [2..16] and the number of

clusters in the range [2..32]. Finally, in order to test

the robustness of our algorithm w.r.t. noise, we added

a number of randomly distributed points ranging be-

tween 0 and 0.1 times the total number of points. Ex-

periments were executed on a cluster having 16 com-

puting machines (100GB RAM available each). As

previously said, our implementations, according to

Reproducible Research (RR) policy are publicly avail-

able

. We studied the running times obtained using 1,

https://github.com/gmmazzeo/clugen

https://github.com/gmmazzeo/clubspark

2, 4, 8, or 16 workers

, varying one data parameter

at a time, while maintaining constant the other ones.

The non-varying parameters, in each experiment were

set as 10

points, 16 dimensions, 32 clusters, and 0.1

noise ratio.

In the following, we report the results obtained us-

ing CLUBS

5.1 Evaluating CLUBS

In this section, we report the performances obtained

using CLUBS

in the same experimental setting,

which are depicted in Figure 2. We found that the per-

formances obtained by using the Spark-based imple-

mentation are less stable than expected, this is proba-

bly due to the fact that Spark uses some random shuf-

ﬂing of data which we can not control. Furthermore,

with Spark assigning a given portion of the data set to

each node is not achievable as the actual physical dis-

tribution of data among workers can not be controlled.

In general, we found a good speedup for 2 and 4 work-

ers, while the speedup is reduced when the number of

workers is further increased. This is probably due to

We ran one worker per different machine of the cluster,

thus, the number of workers and machines here are the

same.

Clustering Big Data

281

the overhead introduced by the Spark framework. In

terms of sensitivity to the data parameters, from the

experimental results we can observe that the speedup

of CLUBS

is not affected by the data dimensional-

ity and noise ratio (the absolute running time, instead,

is affected by dimensionality, as expected). For the

sensitivity to the number of clusters, the speedup is re-

duced when the number of clusters increases, because

the divisive phase is the phase requiring the most net-

work communication, and its duration increases with

the number of clusters.

6 CONCLUSIONS

In this paper we discussed CLUBS-P, an algorithm for

around-centroid clustering for Big Data. We evalu-

ated a new implementation of CLUBS-P, in order to

perform a kind of feasibility analysis w.r.t. the big

data setting. The results obtained show a very good

scalability of the algorithm.

REFERENCES

Arbelaitz, O., Gurrutxaga, I., Muguerza, J., P

eRez, J. M.,

and Perona, I. n. (2013). An extensive comparative

study of cluster validity indices. Pattern Recognition,

46(1):243–256.

Calinski, T. and Harabasz, J. (1974). A dendrite method

for cluster analysis. Communications in Statistics -

Theory and Methods, 3(1):1–27.

CLUBS. Clubs+ website. http://yellowstone.cs.ucla.edu/

clubs/. Accessed: 2016-03-25.

Mazzeo, G. M., Masciari, E., and Zaniolo, C. (2017). A

fast and accurate algorithm for unsupervisedclustering

around centroids. Information Sciences, 400.

Muthukrishnan, S., Poosala, V., and Suel, T. (1999). On

rectangular partitionings in two dimensions: Algo-

rithms, complexity, and applications. In ICDT, pages

236–256.

Nature (2008). Big data. Nature.

Zaharia, M., Chowdhury, M., Franklin, M. J., Shenker,

S., and Stoica, I. (2010). Spark: Cluster comput-

ing with working sets. In Proceedings of the 2Nd

USENIX Conference on Hot Topics in Cloud Comput-

ing, HotCloud’10, pages 10–10, Berkeley, CA, USA.

USENIX Association.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

282