
Combining Prediction Methods for Hardware Asset Management
Alexander Wurl
1
, Andreas Falkner
1
, Alois Haselb
¨
ock
1
, Alexandra Mazak
2,∗
and Simon Sperl
1
1
Siemens AG
¨
Osterreich, Corporate Technology, Vienna, Austria
2
TU Wien, Business Informatics Group, Vienna, Austria
Keywords:
Predictive Asset Management, Obsolescence Management, Partial Least Squares Regression, Data Analytics.
Abstract:
As wrong estimations in hardware asset management may cause serious cost issues for industrial systems,
a precise and efficient method for asset prediction is required. We present two complementary methods for
forecasting the number of assets needed for systems with long lifetimes: (i) iteratively learning a well-fitted
statistical model from installed systems to predict assets for planned systems, and - using this regression model
- (ii) providing a stochastic model to estimate the number of asset replacements needed in the next years for
existing and planned systems. Both methods were validated by experiments in the domain of rail automation.
1 INTRODUCTION
A crucial task in Hardware Asset Management
1
is the
prediction of (i) the numbers of assets of various types
for planned systems, and (ii) the numbers of assets in
installed systems needed for replacement, either due
to end of lifetime (preventive maintenance) or due
to failure (corrective maintenance). This is especi-
ally important for companies that develop, engineer,
and sell industrial and infrastructural systems with a
long lifetime (e.g., in the range of decades) like power
plants, factory equipment, or railway interlocking and
safety systems.
Predicting the number of assets for future projects
is important for sales departments to estimate the po-
tential income for the next years and for bid groups
to estimate the expected system costs. Simple linear
regression models achieve only sub-optimal results
when heterogeneous data sources, faulty data ware-
house entries, or non-standard conditions in installed
systems are involved. Therefore, we combine Partial
Least Square Regression with an iterative algorithm
that removes anomalies introduced by non-standard
conditions and faulty data so that the learned model
can provide optimal prediction results for future pro-
jects.
∗
Alexandra Mazak is affiliated with the CDL-MINT at TU
Wien.
1
Please note, that in this article we use the term ”asset” in
the sense of physical components such as hardware modu-
les or computers but not in the sense of financial instru-
ments.
Usually, service contracts oblige a vendor to gua-
rantee the functioning of the system for a given time
period with a failure rate or system down-time lower
than a specified value. This implies that all failing har-
dware assets (and often also those expected to fail in
near future) must be replaced without delay in order
to ensure continuous service. A precise prediction of
the number of asset types needed in the next n years
is essential for the company to calculate service pri-
ces and to fulfill the service obligations for replacing
faulty components. Often, such predictions are made
by experts relying on their experiences and instinct,
including a certain safety margin. A more informed
prediction is based on expectation values: Add the
number of assets in existing systems and the expec-
tation values for the numbers of assets for planned
systems to get a basis for calculating the expectation
values of asset replacements. This kind of prediction
is simple, but it cannot provide information about the
confidence interval of the prediction. A prediction far
below the actual need may cause that assets are not
available in time with all the annoying consequences
for the vendor such as penitent fees and a bad repu-
tation. A prediction far beyond the actual need will
bind costs in unnecessary asset stocks. We provide
a predictive model for the asset replacements, taking
into account all necessary data from installed systems,
project predictions and renewal necessities. The re-
sult is a probability function representing not only the
predicted number of assets but also the uncertainty of
the prediction.
Summarizing our approach, in the first step, we
Wurl, A., Falkner, A., Haselböck, A., Mazak, A. and Sperl, S.
Combining Prediction Methods for Hardware Asset Management.
DOI: 10.5220/0006859100130023
In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 13-23
ISBN: 978-989-758-318-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
13

calculate a regression model capable to predict the
number of assets for planned systems. Using this re-
gression model, the second step provides a predictive
model for the number of new assets and asset repla-
cements needed in the next n years for installed and
planned systems.
This paper is organized as follows: Section 2 pre-
sents the asset regression model for computing the as-
sets of a planned system. Section 3 presents the asset
prediction model for estimating the overall number of
assets needed in the next n years, including assets for
planned systems and renewal assets. Section 4 pre-
sents related work and Section 5 concludes the paper.
2 ASSET REGRESSION MODEL
In this section, we present an iterative learning met-
hod for predicting the number of assets of a given type
needed for a planned system. This model is learned
from the relation between feature and asset numbers
in installed systems (in previous projects). Features
are properties of a system or project that can be coun-
ted or measured by domain experts. For instance, in
the domain of rail automation, features are the num-
bers of track switches, of signals of various types, of
railway crossings, etc. In large systems, there are
hundreds of different features and asset types, whe-
reas the number of installed systems may be lower
than hundred. In order to reduce efforts for the pla-
ners of future projects who need to supply the feature
numbers, we need to find a minimal subset of features
that still can predict the number of assets of a given
type with sufficient accuracy.
The problem to find a model that predicts assets
from a given amount of features relates to multivariate
data analysis (MVA). One method amongst others in
MVA that addresses similar complex settings is Par-
tial Least Squares Regression (PLSR) (Wold et al.,
2001). PLSR is a technique for collinear data that re-
duces the input variables (i.e., the features) to a smal-
ler set of uncorrelated components and performs least
squares regression on these components. This techni-
que is especially useful when features are highly col-
linear, or when the data set reveals more features than
observations (i.e., installed systems in previous pro-
jects). Furthermore, unlike ordinary multiple regres-
sion, PLSR does not suppose that the set of input fe-
atures is resolved from ambiguities in data. Since
PLSR performs least squares regression on compo-
nents instead of original data, the original data can be
measured with ambiguities. This makes the technique
more robust to measurement uncertainty.
The main two reasons why standard linear regres-
sion does not perform well in our setting are the large
number of input variables compared to the number
of observations, and the fact that some observations
(i.e., some previous projects) contain non-standard
data disrupting the learned model.
2.1 Overview of PLSR
Now we give a brief overview of the PLSR approach
(see, e.g., (Wold, 1980)). The input data set is availa-
ble in the form of the following data matrix:
D =
x
1,1
··· x
1,p
y
1,1
··· y
1,d
x
2,1
··· x
2,p
y
2,1
··· y
2,d
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x
n,1
··· x
n,p
y
n,1
··· y
n,d
(1)
Each observation i (1 ≤ i ≤ n) in D corresponds to an
existing system and consists of input variable values
x
i,1
, . . . , x
i,p
(features) and related output variable va-
lues y
i,1
, . . . , y
i,d
(assets). The task is to exploit the co-
variance relationship between input and output varia-
bles, to estimate the assets for planned systems where
only the features are known. PLSR takes into account
the underlying relationship, i.e., the latent structure,
of features and assets. The matrices X and Y are de-
composed into latent structures in an iterative process.
The latent structure corresponding to the most varia-
tion of Y is extracted and explained by a latent struc-
ture of X that explains it the best.
The model of the population of D consists of
a p-dimensional input variable vector X and a d-
dimensional output variable vector Y. Instead of cal-
culating the parameters β in the linear model
y
i
= x
>
i
β + ε
i
in PLSR, we estimate the parameters γ in the so-called
latent variable model
y
i
= t
>
i
γ + ε
i
(2)
where the new coefficients γ are of dimension q ≤ p,
ε is an error (noise) term, i.e., the residuals, and the
values t
i
of the variables are put together in a (n × q)
score matrix T . According to (Wold, 1980), the ob-
jective of PLSR is to estimate the scores T . Due to the
dimension reduction, the regression of y on T should
be more stable. The construction of T is sequentially
performed for k = 1, 2, . . . , q through the PLS criteria
a
k
= argmax
a
Cov(y, Xa)
under the constraints ka
k
k = 1 and Cov(Xa
k
, Xa
j
) = 0
for 1 ≤ j < k. The vectors a
k
with k = 1, 2, . . . , q are
called loadings, and they are collected in the columns
of the matrix A. The resulting score matrix is then
T = XA.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
14

Once the loadings are computed, the regression model
of (2) can be used as predictive regression model for
assets.
2.2 Application of PLSR
One of the major challenges in our problem domain
comes from potential outliers of asset quantities in
the data set. Since the input data originate from he-
terogeneous data sources, anomalies may occur due
to the complexity of merging data structures and due
to non-standard conditions in some projects. Even if
high data quality during the process of data integra-
tion is achieved by approaches such as described in
(Wurl et al., 2017), anomaly detection including mo-
del validation is required during the training phase of
the prediction model.
In model validation, the most common methods
for training regression models are Cross-Validation
(CV) and Bootstrapping. In our setting, CV is pre-
ferred because it tends to be less biased than Boots-
trapping when selecting the model and it provides a
realistic measurement of the prediction accuracy.
To ensure a stable prediction model, we make use
of a double cross-validation strategy which is a pro-
cess of two nested cross-validation loops. The inner
loop is responsible for validating a stable prediction
model, the outer loop measures the performance of
prediction. This strategy is applied to similar approa-
ches that have been described for optimizing the com-
plexity of regression models in chemometrics (Filz-
moser et al., 2009), for a binary classification problem
in proteomics (Smit et al., 2008), and for a discrimi-
nation of human sweat samples (Dixon et al., 2007).
Our approach is a formal, partly new combination of
known procedures and methods, and has been imple-
mented in a function for the programming environ-
ment R
2
, as illustrated in Figure 1.
In the internal cross-validation loop CV1, we train
our model with 80% of the data, using 10-fold cross-
validation. In the external cross-validation CV2, we
test our trained model with the 20% rest of the full
data set.
2.2.1 Training
Our regression model potentially uses all input vari-
ables of all observations to predict a selected output
variable. For each row i = 1..n of the training set as
subset of data matrix D (see Equation 1), the asset a
(a ∈ {1 . . . q}) is estimated by a function f
a
on the in-
put variables. The predicted values
ˆy
i,a
= f
a
(x
i,1
, x
i,2
, . . . , x
i,d
)
2
www.r-project.org
Figure 1: Double Cross-Validation: First, learn a model on
training data set CV1. Second, test the model with the opti-
mal number of components c
opt
on test data set CV2.
should be as close as possible to the real asset values.
”As close as possible” is achieved by an iterative pro-
cess of improving the prediction model step by step,
which is computed by means of PLSR in combination
with CV.
In the inner CV loop, we employ 10-fold CV
to train the model. By training, we aim at finding
the number of components which adequately explains
both predictors and response variances. This is calcu-
lated by the Root Mean Squared Error of Prediction
(RMSEP) for asset a:
RMSEP =
v
u
u
u
t
1
n
n
∑
i=1
(y
i,a
− ˆy
i,a
)
2
| {z }
quadratic error
The differences y
i,a
− ˆy
i,a
are called residuals. RM-
SEP calculates the residual variation as a function of
the number of components. The result presents for
each component the estimated cross validation error
and the cumulative percentage of variance explained.
Aiming for an optimal number of components, the
goal is to find the component with the lowest cross
validation error. The minimum indicates the number
of components with minimal prediction error and an
optimum rank of the cumulative percentage of vari-
ance explained.
While calculating RMSEP, the estimated CV error
usually decreases with an increasing number of com-
ponents. In case of an error increase, it is likely that:
1. Dependent and independent variables are not line-
arly related enough to each other.
2. The data set contains insufficient number of ob-
servations to reveal the relationship between input
and output variables.
Combining Prediction Methods for Hardware Asset Management
15

3. There is only one component needed to model the
data.
In the outer loop, in addition to RMSEP we use
the significance indicator R
2
. R
2
is defined by
R
2
= 1 −
∑
(y
i,a
− ˆy
i,a
)
2
∑
(y
i,a
− y
a
)
2
(3)
R
2
is a value between 0 and 1 and measures how close
the test data are to the values predicted by the regres-
sion model. A low R
2
value (e.g., R
2
< 0.9) indicates
that there are still outliers in the observations we used
for training the model. These outliers in the data de-
graded the quality of our model, so we remove them
and train a new model without them.
Algorithm 1 sketches the iterative process of trai-
ning a model for asset prediction. Firstly, the data set
is shuffled to obtain a fair distribution of observations.
Secondly, a PLSR regression model is trained and
validated through RMSEP. As a result, the model is
trained again with the optimal number of components
c
opt
. Thirdly, this model is applied to the test data set
and R
2
is computed. We use two criteria to decide
whether our model is already good enough or not:
(i) the RMSEP must monotonically decrease with the
number of components used, and (ii) according to lon-
gitudinal studies R
2
must be at least 0.9 (Mooi et al.,
2018). If the model is not yet good enough, we re-
move all observations from the data set that we cate-
gorized as outliers. After some experiments, the follo-
wing outlier classification has turned out to be useful:
Outliers are observations with residuals that are larger
than 25% of the maximum asset value in the data set.
After removing the noisy observations, learning starts
again. We proceed with this learning cycle until our
model meets the above mentioned quality criteria or
no improvement could be achieved.
In the last step of Algorithm 1, the features that
significantly contribute to a prediction are extracted
according to their weights. Currently, this selection is
done by a domain expert based on the weights of the
features that dominate the prediction model.
2.3 Prediction
Our trained model is now
ˆy
a
= f
a
(X
0
) (4)
where X
0
⊆ {x
1
, . . . , x
d
} is the set of significant fea-
tures used for predicting assets of type a based on a
Algorithm 1: Calculate Asset Regression Model.
1. Shuffle rows in the data set to obtain a fair dis-
tribution of observations.
2. Train a PSLR regression model
(a) Apply a 10-fold cross-validation to the trai-
ning data set.
(b) Compute RMSEP and evaluate optimal
numbers of components c
opt
.
(c) Apply a 10-fold cross-validation to the trai-
ning data set using c
opt
.
3. Test model on test data set by computing R
2
.
If RMSEP does not monotonically decrease
with the number of components,
or if R
2
< 0.9
(a) Identify outliers in observations and remove
them.
(b) Go to step 2.
4. Extract significant features to select the final
prediction model.
model f
a
. Applying this model to concrete feature
values
¯
X
0
of features X
0
for a planned system will
provide an expectation value for the number of as-
sets a. In this sense, the output variable ˆy
a
could be
seen as a random variable with a normal distribution
- ˆy
a
∼ N (µ, σ
2
) - where the mean value µ is f
a
(
¯
X
0
)
and σ is the above described mean square error RM-
SEP. Therefore, a 95% confidence interval is given by
y
a
= ˆy
a
± 2 ∗ RMSEP (Friedman et al., 2001). In the
next subsection, we demonstrate this on an example.
2.4 Example and Experimental Results
We tested validity of our method on a data set from the
railway safety domain with data collected over about
a decade. Our data set contained ca. 140 features
(input variables), ca. 300 assets (potential output va-
riables), and ca. 70 observations (installed systems).
We chose the concrete asset type A41 - a hardware
module that controls track switches - to demonstrate
training of the regression model and prediction. We
implemented this example and the regression training
algorithm in R, making use of the plsr() function in
the pls library
3
.
Before starting any calculation, we preprocessed
the data set by removing all assets except A41 and
shuffled the data set in order to have a fair distribution
of the training data set and the test data set. Following
Algorithm 1, we built the model by specifying A41 as
the output variable and all features as input variables,
and performed 10-fold cross-validation based on the
NIPALS algorithm (Wold, 1966; Wold, 1980).
3
http://mevik.net/work/software/pls.html
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
16
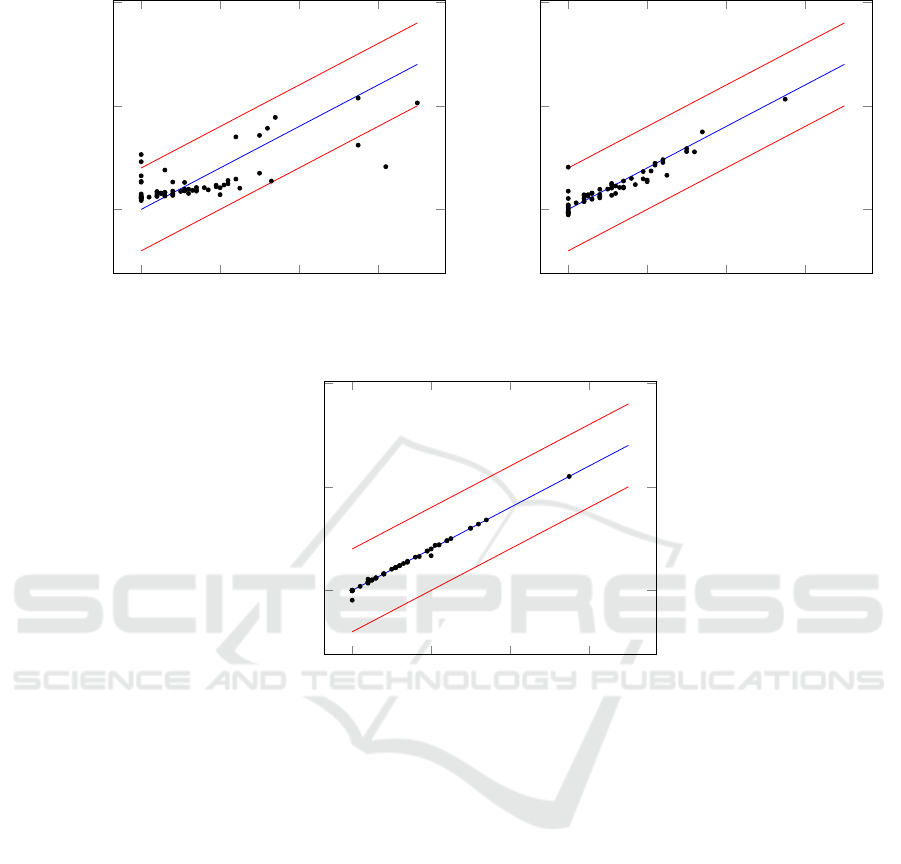
0 20 40
60
0
50
100
measured
predicted
(a) Cycle 1: RMSEP=14.11, R
2
=0.35
0 20 40
60
0
50
100
measured
predicted
(b) Cycle 2: RMSEP=2.77, R
2
=0.87
0 20 40
60
0
50
100
measured
predicted
(c) Cycle 3: RMSEP=1.74, R
2
=0.94
Figure 2: Three cycles for training a regression model for asset A41.
Figure 2 shows the three training cycles for A41.
After the first cycle, four observations were identified
as outliers and removed from the training set. After
the second cycle, another two observations were re-
moved. After the third cycle we ended up in a regres-
sion model of high precision.
The features are the input variables of the regres-
sion model. Their values must be provided by domain
experts. To compute/count/measure these feature va-
lues (e.g., counting the signals of various types in a
railway station, or measuring the distances between
signals on the tracks) is often a time-consuming and
expensive task. The reduction of the feature set to a
small subset of significant ones with satisfying pre-
dictive power will save time and costs, especially in
the usually very stressful phase of proposal prepara-
tion.
Therefore we identified the most significant input
variables by analyzing the coefficients of the input va-
riables in the model. Figure 3 shows the first 10 posi-
tive coefficients sorted by their values. It can easily be
seen that feature F31 (corresponding to the number of
track switches of the railway station) and feature F32
(corresponding to the number of track key-locks) have
much more impact on asset A41 than all the other fe-
atures. We learned a final model based on these two
input variables only. This final model, as shown in
Figure 4, is used for predicting the asset values in the
test data set and does not show noticeable differences
to the results of the last iteration (see Figure 2 (c)),
although it is based on two features only.
We tested the described method on other asset ty-
pes, e.g. on hardware modules for controlling track-
side signals, and it shows a similar behavior – after a
few cycles of outlier removal the learned regression
models have high prediction quality.
Combining Prediction Methods for Hardware Asset Management
17
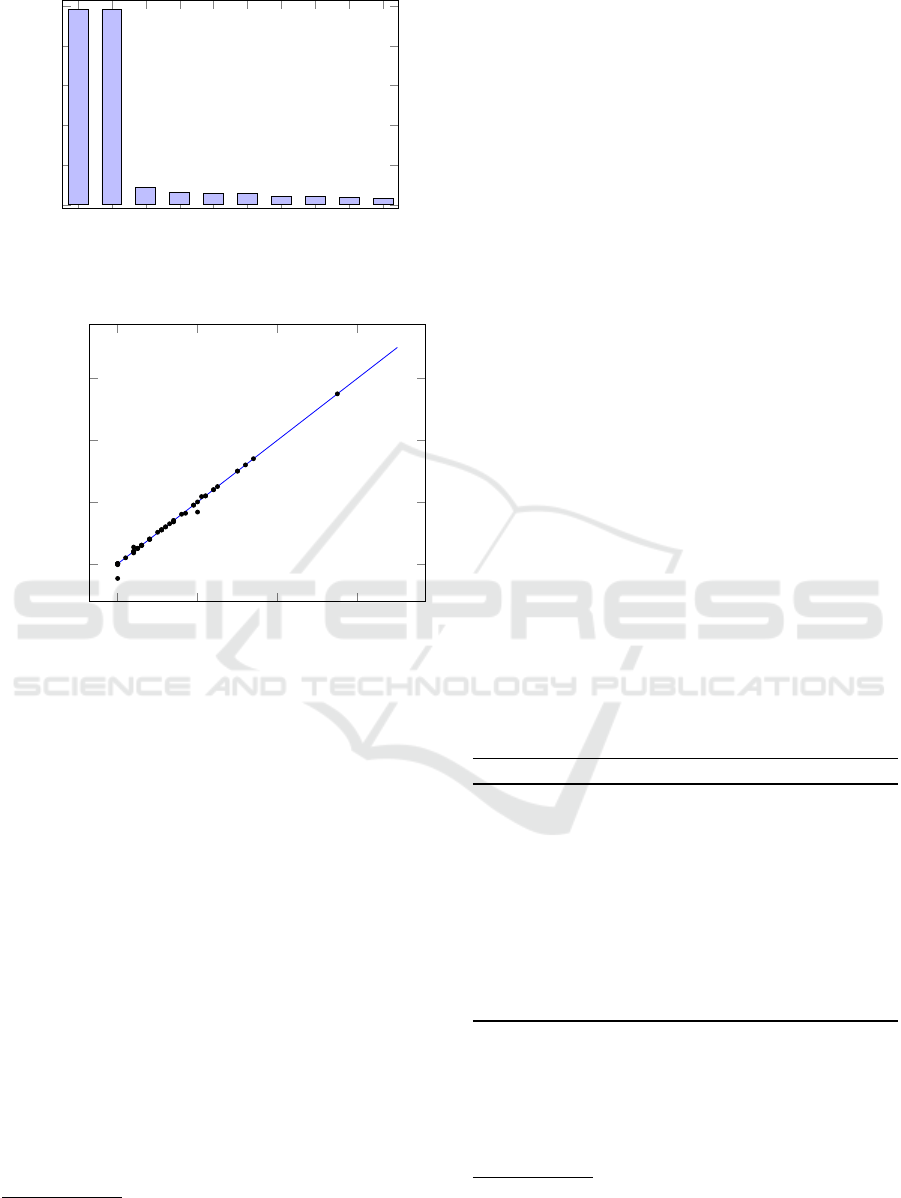
F31
F32
F14
F22
F8
F7
F94
F42
F111
F6
0
0.2
0.4
0.6
0.8
1
Features
Figure 3: Importance Analysis of Features.
0 20 40
60
0
20
40
60
measured
predicted
Figure 4: Final linear regression model for asset A41 based
on features F31 and F32 only.
3 ASSET PREDICTION MODEL
Building upon the regression model of the previous
section, in this section we present a stochastic model
for answering the following question: How many as-
sets of type A are needed in the next n years? The
input parameters of this problem are:
• An asset type A. Associated with an asset type is
a failure rate, like MTBF (mean time between fai-
lure). MTBF is the expected time between failures
of the asset. We only consider failures that cause
the replacement of the asset.
4
The failures can be
seen as random samples of a non-repairable popu-
lation and the failure times follow a distribution
with some probability density function (PDF).
• A scope S = {s
1
, . . . , s
n
} is a set of asset groups.
Basically, each asset group corresponds to all as-
sets of type A of an installed or planned system
4
A detailed differentiation of MTBF and MTTF (Mean
Time To Failure) is beyond the scope of this paper.
that must be taken into account for the forecast.
Each member of an asset group must have the
same installation date. As we will see later, this is
important for computing the renewal numbers (ol-
der assets are more likely to fail than newer ones).
Therefore, an installed system may be represen-
ted by more than one asset group: one group for
all assets initially installed and still alive, and the
other groups for the already necessary asset repla-
cements.
Each s ∈ S has the following properties:
– M
s
is a random variable representing the num-
ber of assets in the asset group s ∈ S; Pr(M
s
=
n), n ∈ N, is the probability that s contains n
elements.
– tbos
s
: Begin of service time of all assets in s ∈
S. At this point in time the assets has been or
will be installed in the field.
5
– teos
s
: End of service time of all assets in s ∈
S. This is the time where the service contract
ends. After this point in time the assets need no
longer be replaced when failed.
– A probability q
s
∈ [0, 1] representing the like-
lihood that the system containing s ∈ S will be
ordered. Trivially, for already installed assets
q
s
= 1.
• A point in time t
target
∈ N up till that the prediction
should be made. All assets in the scope whose
service times overlap the period [t
now
,t
target
] are to
be taken into account. The service time of interest
for each asset group s ∈ S is then
τ
s
= min(teos
s
,t
target
) −tbos
s
.
Algorithm 2: Total Asset Prediction.
1. Input: (i) asset type A (ii) scope (iii) target time
t
target
2. Collect asset groups of given asset type and gi-
ven scope: S = {s
1
, . . . , s
n
}
(a) Existing assets from installed systems
(b) Asset predictions for planned systems
3. Perform renewal asset analysis:
ˆ
R
s
4. Compute estimator for each asset group:
ˆ
N
s
5. Sum up asset group estimators:
ˆ
N
total
=
∑
s∈S
ˆ
N
s
Please note that the computation of the forecast
model is always done for assets of a given type A, so
for the sake of simplifying the notation we omit to
subscript all variables with A in this section.
The prediction of needed assets must take into ac-
count both renewal of already installed assets in case
5
We use a simple representation of time: years started from
some absolute zero time point. This simplifies arithmetic
operations on time variables.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
18

of non-repairable failures and new assets needed for
planned systems. We will present a stochastic model
that combines both cases. Algorithm 2 summarizes
the steps how to compute such a prediction model. In
step 1, the user has to provide an asset type, a scope,
and a target point in time. In step 2, the asset groups
from the installed base (existing projects) and the sa-
les database (future projects) are collected. Then a
stochastic model that represents needed renewal as-
sets is computed based on failure rates/failure distri-
butions of the assets and the service time periods of
the asset groups. In step 4, an estimator is computed
for each asset group using project order probability,
the probability of the number of assets in the group,
and the renewal model. Finally, all these estimators
are summed up to an overall asset estimator
ˆ
N
total
.
We present the details in the next subsections.
3.1 Renewal Processes
To estimate the number of assets needed for replace-
ment of failing assets we resort to the theory of re-
newal processes, see, e.g., (Grimmett and Stirzaker,
2001; Randomservices.org, 2017). In this subsection,
we recap the main definitions of renewal processes
and show how we apply it to predict the number of
assets that must be replaced because of failures. A re-
newal process is a stochastic model for renewal events
that occur randomly in time. Let X
1
be the random
variable representing the time between 0 and the first
necessary renewal of an asset. The random variables
X
2
, X
3
, . . . are the subsequent renewals. These varia-
bles X
i
are called inter-arrival times. In our case, their
distribution is directly connected to the failure rates
or MTBF of the asset type. So (X
1
, X
2
, X
3
, . . .) is a se-
quence of independent, identically distributed random
variables representing the time periods between rene-
wals. X
i
takes values from [0, ∞), and Pr(X
i
> 0) > 0.
Let f
X
(t) be the PDF and F
X
(t) = Pr(X ≤ t) be the
distribution function of the variables X
i
.
The random variable T
n
for some number n ∈ N
represents the so-called arrival time; F
T
n
(t) = Pr(T
n
≤
t) represents the probability of n renewals up to time
t. T
n
is simply the sum of the inter-arrival variables
X
i
:
T
n
=
n
∑
i=1
X
i
The PDF of T
n
is therefore the convolution of its con-
stituents:
f
T
n
= f
∗n
X
= f
X
∗ f
X
∗ . . . ∗ f
X
Remark. To add two random variables one has to
apply the convolution operator on the their PDFs. The
convolution operator ∗ for two functions f and g is
defined as
( f ∗ g)(t) =
Z
f (t
0
)g(t − t
0
)dt
0
, continuous case
( f ∗ g)(n) =
∞
∑
m=−∞
f (m)g(n − m) , discrete case
The expression f
∗n
stands for applying the convo-
lution operator on a function f n times. For many
probability distribution families, summing up two
random variables and therefore computing the con-
volution of their PDFs is easy. For instance, the sum
of two Poisson distributed variables with parameters
λ
1
and λ
2
is: Poi[λ
1
] + Poi[λ
2
] = Poi[λ
1
+ λ2]. (End
of remark.)
In the renewal process, the arrival time variables
T
n
are used to create a random variable N
t
that counts
the number of expected renewals in the time period
[0,t]. It is defined in the following way:
N
t
= |{n ∈ N : T
n
≤ t}| for t ≥ 0
The arrival time process T
n
and the counting pro-
cess N
t
are kind of inverse to each other, where the
probability distribution of N
t
can be derived from the
probability distribution of T
n
. Thus, the theory of re-
newal processes gives us a tool for deriving the coun-
ting variable N
t
from a given failure distribution X
of an asset. For complicated distributions of X, the
derivation of N
t
could get elaborate and could rea-
sonably be done by numeric methods only, but it is
straight-forward for some prominent distribution fa-
milies. The most important case is the Poisson pro-
cess, where X has an exponential distribution with pa-
rameter λ. In this case, the n-th arrival time variable
T
n
has a Gamma distribution with shape parameter n
and rate parameter λ, and the counting variable N
t
has
a Poisson distribution with parameter λt.
3.2 Prediction Model
In this subsection we describe how to combine the
number of assets in each asset group M
s
(s ∈ S), the
above described renewal counting variable N
τ
s
, and
the probability q
s
representing the likelihood that the
assets will be ordered to an estimator, i.e., a proba-
bility mass function
6
(PMF), reflecting the number of
needed assets in a given time period.
Definition 1 (Renewal Estimator
ˆ
R
s
). Let M
s
be a
random variable representing the number of assets in
the asset group s ∈ S. Let N
τ
s
be the renewal coun-
ter for the service time period τ
s
of asset group s.The
renewal estimator
ˆ
R
s
is a random variable, where
6
A probability mass function (PMF) is the discrete counter-
part of a probability distribution function (PDF). A PMF
f (n) corresponding to a random variable X is Pr(X =
n), n ∈ N.
Combining Prediction Methods for Hardware Asset Management
19

Pr(
ˆ
R
s
= n), n ∈ N, is the probability that exactly n
renewal assets are needed in total for the asset group
s ∈ S. It’s PMF f
ˆ
R
s
is defined in the following way:
f
ˆ
R
s
(n) :=
∞
∑
k=0
f
M
s
(k) f
∗k
N
τ
s
(n) (5)
Definition 2 (Asset Group Estimator
ˆ
N
s
). Let M
s
be
a random variable representing the number of assets
in the asset group s ∈ S. Let q
s
be the probability
that the project containing the assets of s are orde-
red at all. Let
ˆ
R
s
be the renewal estimator as defined
above.
ˆ
N
s
is a random variable with Pr(
ˆ
N
s
= n), n ∈ N,
representing the probability that the number of assets
needed for s is exactly n. It is the sum of the number of
assets and the number of renewals scaled by the order
probability. Its PMF is:
f
ˆ
N
s
(n) := q
s
( f
M
s
(n) ∗ f
ˆ
R
s
(n)) + (1 − q
s
)δ
0
(n) (6)
Remark. The delta function δ
k
(x) (also called unit
impulse) is 1 at x = k and otherwise 0. We use the
delta function here to express certainty of zero assets
in the case that the project will not be ordered. As we
use later, the convolution with the delta function can
be used for shifting: f (x) ∗ δ
k
(x) = f (x − k). (End of
remark.)
Definition 3 (Total Asset Estimator
ˆ
N
total
). The to-
tal asset estimator
ˆ
N
total
is a random variable with
Pr(
ˆ
N
total
= n),n ∈ N, representing the probability that
the total number of assets needed for all asset groups
s ∈ S until t
target
is exactly n. It is the sum of the asset
group estimators
ˆ
N
s
.
ˆ
N
total
:=
n
∑
s∈S
ˆ
N
s
(7)
Its PMF is the convolution of the PMFs of the asset
group estimators
ˆ
N
s
:
f
ˆ
N
total
(n) :=
∗
s∈S
f
ˆ
N
s
(n) (8)
The probability distribution f
ˆ
N
total
can now be
used for calculating its expectation value, its variance
or standard deviation, but also the number of needed
assets with a guaranteed probability that the number
will be high enough, i.e., compute the smallest n with
Pr(
ˆ
N
total
<= n) is greater or equal some given pro-
bability, like 0.75 or 0.95, depending on the certainty
the forecast should provide.
The design of the variables in this framework is
both suited for installed and planned systems. For a
planned system, the probability that the system will be
ordered is an information provided by sales experts.
The estimation of how many assets will be needed
can be predicted by the regression model described in
Section 2. In this case, the estimator M
s
corresponds
to a random variable derived from the regression mo-
del ˆy = f ( ¯x), where ¯x is the feature vector of the plan-
ned system. See Equation 4 in Section 2.3.
For asset groups of installed systems, the order
probability q
s
is simply 1, and the estimator variable
M
s
for the asset count is the delta function δ
k
(n) with
k being the actual number of installed assets. In this
case the asset group estimator
ˆ
N
s
is simply the shifted
renewal estimator
ˆ
R
s
with PDF f
ˆ
R
s
(n − k). It should
be noted that
ˆ
N
total
not only contains predicted assets,
but also all already installed assets. These could be
simply subtracted from
ˆ
N
total
, if only the number of
assets to be ordered in the future are needed.
3.3 Example
Figure 5 shows a small example that shall demon-
strate the combination of statistical methods of our
asset prediction framework.
Figure 5: Example of an asset prediction problem, contai-
ning 3 asset groups of existing projects (s
1
, s
2
, s
3
) and 2 fu-
ture projects with asset groups s
4
and s
5
.
We use an exponential distribution of the failure
rates of the assets with λ = 0.125 (i.e., 0.125 failu-
res per year expected), corresponding to a MTBF of 8
years. So the renewal counting variables N
τ
are Pois-
son distributed: N
τ
∼ Poi(λτ). The number of assets
of the existing systems 1 to 3 are 6, 4, and 15, so
M
s
1
∼ δ
6
, M
s
2
∼ δ
4
, and M
s
3
∼ δ
15
. The number es-
timators M
s
4
and M
s
5
of the two planned systems are:
M
s
4
: Pr(M = 7) = 0.2, Pr(M = 8) = 0.6, Pr(M = 9) =
0.2; M
s
5
: Pr(M = 8) = 0.05, Pr(M = 9) = 0.1, Pr(M =
10) = 0.7, Pr(M=11)=0.1, Pr(M = 12) = 0.05. The
resulting asset group estimators and the total asset
estimator are depicted in Fig. 6. Some interesting
results are shown in Table 1. The first row shows
the resulting expectation values of the number of as-
sets. The other rows in Table 1 show the variances
and standard deviations of our estimator probability
functions, along with 3 examples of asset estimati-
ons with specified likelihood, i.e., F
−1
(p) stands for
the number of assets n with Pr(F ≤ n) >= p. While
usually only this expectation value is used for asset
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
20

prediction, our approach provides valuable additional
information, like the standard deviation, and the pos-
sibility to find an asset number estimation with high
reliability, like F
−1
(0.95).
20 40
60
0.100
0.200
0.300
0.400
n
f
ˆ
N
s
(n)
ˆ
N
s
1
ˆ
N
s
2
ˆ
N
s
3
ˆ
N
s
4
ˆ
N
s
5
(a) Asset Group Estimators
ˆ
N
s
60
80 100 120
0.010
0.020
n
f
ˆ
N
total
(n)
(b) Total Asset Estimator
ˆ
N
total
Figure 6: Probability mass functions of predicted assets for
asset groups and total asset estimator for the example sce-
nario depicted in Fig. 5.
900
950
1,000
1,050
0.005
0.010
n
f
ˆ
N
total
(n)
Figure 7: Probability mass function for an estimator of asset
A41. 580 assets are already installed. The total expectation
value
E
is 975 (corresponds to 395 new assets), the standard
deviation σ is 26.30, F
−1
(0.75) = 993 (corresponds to 413
new assets), F
−1
(0.95) = 1018 (corresponds to 438 new
assets).
Figure 7 shows the resulting total asset estimator
of a real world example. We applied our method to the
data set used in Section 2.4 and computed a predictor
for the number of assets of type A41 for the next 10
years. About 40 installed systems with 580 instances
of asset A41 and 7 future systems have been taken into
account. Subtracting the already installed 580 assets,
we get an expectation value of 395 additional assets,
covering the assets for the 7 new systems and asset
renewals. A prediction with 95% likelihood results in
438 new assets.
4 RELATED WORK
In industry, asset management is defined as the ma-
nagement of physical, as opposed to financial, assets
(Amadi-Echendu et al., 2010). Managing assets may
comprise a broad range of different potentially over-
lapping objectives such as planning, manufacturing,
and service. Depending on the scope of asset mana-
gement, the data included determine the possibilities
of predictive data analytics (Li et al., 2015). An es-
sential part of asset management, especially in manu-
facturing, is to estimate the condition (health) of an
asset.
In the last decade, an engineering discipline, cal-
led prognostics, has evolved aiming to predict the re-
maining useful life (RUL), i.e., the time at which a
system or a component (asset) will no longer per-
form its intended function (Vachtsevanos et al., 2006).
Since the reason for non-performance is most often a
failure, data-driven prognostics approaches consist of
modeling the health of assets and learning the RUL
from available data (Mosallam et al., 2015; Mosallam
et al., 2016). (Bagheri et al., 2015) present a stochas-
tic method for data-driven RUL prediction of a com-
plex engineering system. Based on the health value of
assets, logistic regression and the assessment output is
used in a Monte Carlo simulation to estimate the re-
maining useful life of the desired system. (Lee et al.,
2017) calculate the weighted RUL of assets to op-
timize the productivity in cyber-physical manufactu-
ring system by applying Principal Component Analy-
sis (PCA) in combination with Restricted Boltzmann
Machine (RBM).
Other predictive methods aim for predicting the
obsolescence of assets based on sales data. (Sandborn
et al., 2007) propose a data-mining approach inclu-
ding linear regression to estimate when an asset beco-
mes obsolete. Based on this approach, (Ma and Kim,
2017) use time series models instead of linear regres-
sion models and state that prediction over years may
be inaccurate. (Jenab et al., 2014) examine the de-
tection of obsolescence in a railway signaling system
with a Markovian model and mention that forecasting
obsolescence of assets may be inexact. (Thaduri et al.,
Combining Prediction Methods for Hardware Asset Management
21

Table 1: Some resulting probability values for the example scenario depicted in Fig. 5.
s
1
s
2
s
3
s
4
s
5
Total
E
21 9 45 13 11 99
var 14.91 4.97 29.68 47.95 78.47 175.58
σ 3.86 2.23 5.45 6.92 8.86 13.25
F
−1
(0.50) 21 9 45 15 15 99
F
−1
(0.75) 24 10 49 17 18 108
F
−1
(0.95) 28 13 54 21 22 119
2015) draft the potential application of predictive as-
set management in the railway domain by incorpora-
ting heterogeneous data sources such as construction
and sales data. One of the main challenges is pre-
dictive asset management for long-term maintenance
which coincides with our context.
One possible starting point to address the pre-
diction of long-term asset management is formulating
the product life cycle with evolutionary parametric
drivers that describe an asset type whose performance
or characteristics evolve over time (Solomon et al.,
2000). Since evolutionary parametric drivers cannot
be found in our database, procurement life modeling
may be used (Sandborn et al., 2011). The most pro-
minent model of the mean procurement life, which
is analogous to the mean-time-to-failure (MTTF), is
the bathtub curve (Klutke et al., 2003), usually mo-
deled by Weibull distributions. This model represents
three regimes in the lifetime of a hardware module:
the first phase shows high but decreasing failure ra-
tes (”infant mortality”), the main, middle phase shows
low, constant failure rates, and the third phase repre-
sents ”wear out failures” and therefore increasing fai-
lure rates.
A prominent model in preventive maintenance
(see, e.g., (Gertsbakh, 2013)) represents the replace-
ment of an asset after a constant time before the fai-
lure probability gets too high. This can be modeled by
a distribution function F that consists of two parts: the
first part is some ”conventional” distribution function,
but from a defined replacement time t
r
on, the proba-
bility of replacement is just 1.
Our input data is taken from the installed base (da-
tabase of currently installed systems) and the sales da-
tabase containing forecasts of expected future projects
(planned systems). Unlike previous predictive obso-
lescence approaches where the main goal is to esti-
mate the date when particular assets become obsolete,
the combination of our data sets enables us to repre-
sent not only the numbers of renewal assets needed
for n years but also the uncertainty of the estimation
for long-term maintenance.
5 CONCLUSION AND FUTURE
WORK
In this paper, we proposed a predictive asset manage-
ment method for hardware assets. The proposed met-
hod consists of two phases: In the first phase, a regres-
sion model is learned from installed systems to pre-
dict assets for planned systems. In the second phase,
a stochastic model is used for summing up all assets
needed in the next n years for existing and also future
projects, taking renewals of failing components into
account. In experiments we validated our method in
the domain of railway safety systems.
There are several ideas for future work: Currently,
when calculating an asset regression model we ap-
ply PLSR in an iterative way. In future work, we
aim at a broader evaluation by comparing additional
methods such as Sparse partial robust M-regression
(Hoffmann et al., 2015), or Robust and sparse estima-
tion methods for high dimensional linear and logistic
regression (Kurnaz et al., 2017).
In our approach we train the model for each asset
type separately. This means that the set of features
for each regression model is minimized for each asset
separately. An important problem for future work is
to find a minimal subset of features that is significant
for predicting all assets. Furthermore, it would be in-
teresting to take costs of feature measurement into ac-
count. E.g., in the railway domain it is easier to count
signals and track switches than insulated rail joints of
a railroad region. An optimal subset of features is one
with minimal total measurement costs.
Presently, we use a given MTBF per asset type
in our method. We assume that prediction accuracy
can be further improved by applying advanced prog-
nostics techniques for customizing the MTBF to the
respective system context.
Although we tested our method only on data from
rail automation, we suppose that applying it to har-
dware components in other domains will produce si-
milar results of prediction. This needs to be evaluated
in future work.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
22

ACKNOWLEDGEMENTS
This work is funded by the Austrian Research Promo-
tion Agency (FFG) under grant 852658 (CODA). We
thank Walter Obenaus (Siemens Rail Automation) for
supplying us with test data.
REFERENCES
Amadi-Echendu, J. E., Willett, R., Brown, K., Hope, T.,
Lee, J., Mathew, J., Vyas, N., and Yang, B.-S. (2010).
What Is Engineering Asset Management?, pages 3–
16. Springer London, London.
Bagheri, B., Siegel, D., Zhao, W., and Lee, J. (2015).
A Stochastic Asset Life Prediction Method for
Large Fleet Datasets in Big Data Environment. In
ASME 2015 International Mechanical Engineering
Congress and Exposition, pages V014T06A010–
V014T06A010. American Society of Mechanical En-
gineers.
Dixon, S. J., Xu, Y., Brereton, R. G., Soini, H. A., Novotny,
M. V., Oberzaucher, E., Grammer, K., and Penn, D. J.
(2007). Pattern recognition of gas chromatography
mass spectrometry of human volatiles in sweat to dis-
tinguish the sex of subjects and determine potential
discriminatory marker peaks. Chemometrics and In-
telligent Laboratory Systems, 87(2):161–172.
Filzmoser, P., Liebmann, B., and Varmuza, K. (2009). Re-
peated double cross validation. Journal of Chemome-
trics, 23(4):160–171.
Friedman, J., Hastie, T., and Tibshirani, R. (2001). The
elements of statistical learning, volume 1. Springer
series in statistics New York.
Gertsbakh, I. (2013). Reliability theory: with applications
to preventive maintenance. Springer.
Grimmett, G. and Stirzaker, D. (2001). Probability and
random processes. Oxford university press.
Hoffmann, I., Serneels, S., Filzmoser, P., and Croux, C.
(2015). Sparse partial robust M regression. Chemome-
trics and Intelligent Laboratory Systems, 149:50–59.
Jenab, K., Noori, K., and Weinsier, P. D. (2014). Obsoles-
cence management in rail signalling systems: concept
and markovian modelling. International Journal of
Productivity and Quality Management, 14(1):21–35.
Klutke, G., Kiessler, P. C., and Wortman, M. A. (2003). A
critical look at the bathtub curve. IEEE Trans. Relia-
bility, 52(1):125–129.
Kurnaz, F. S., Hoffmann, I., and Filzmoser, P. (2017).
Robust and sparse estimation methods for high-
dimensional linear and logistic regression. Chemome-
trics and Intelligent Laboratory Systems.
Lee, J., Jin, C., and Bagheri, B. (2017). Cyber physical
systems for predictive production systems. Production
Engineering, 11(2):155–165.
Li, J., Tao, F., Cheng, Y., and Zhao, L. (2015). Big data
in product lifecycle management. The Internatio-
nal Journal of Advanced Manufacturing Technology,
81(1-4):667–684.
Ma, J. and Kim, N. (2017). Electronic part obsolescence fo-
recasting based on time series modeling. International
Journal of Precision Engineering and Manufacturing,
18(5):771–777.
Mooi, E., Sarstedt, M., and Mooi-Reci, I. (2018). Market
Research. Springer.
Mosallam, A., Medjaher, K., and Zerhouni, N. (2015).
Component based data-driven prognostics for com-
plex systems: Methodology and applications. In Re-
liability Systems Engineering (ICRSE), 2015 First In-
ternational Conference on, pages 1–7. IEEE.
Mosallam, A., Medjaher, K., and Zerhouni, N. (2016).
Data-driven prognostic method based on bayesian ap-
proaches for direct remaining useful life prediction.
Journal of Intelligent Manufacturing, 27(5):1037–
1048.
Randomservices.org (2017). Renewal processes. http://
www.randomservices.org/random/renewal/index.html
[Online; accessed 3-February-2018].
Sandborn, P., Prabhakar, V., and Ahmad, O. (2011). Fore-
casting electronic part procurement lifetimes to enable
the management of DMSMS obsolescence. Microe-
lectronics Reliability, 51(2):392–399.
Sandborn, P. A., Mauro, F., and Knox, R. (2007). A data
mining based approach to electronic part obsolescence
forecasting. IEEE Transactions on Components and
Packaging Technologies, 30(3):397–401.
Smit, S., Hoefsloot, H. C., and Smilde, A. K. (2008). Sta-
tistical data processing in clinical proteomics. Journal
of Chromatography B, 866(1-2):77–88.
Solomon, R., Sandborn, P. A., and Pecht, M. G. (2000).
Electronic part life cycle concepts and obsolescence
forecasting. IEEE Transactions on Components and
Packaging Technologies, 23(4):707–717.
Thaduri, A., Galar, D., and Kumar, U. (2015). Railway
assets: A potential domain for big data analytics. Pro-
cedia Computer Science, 53:457–467.
Vachtsevanos, G. J., Lewis, F., Hess, A., and Wu, B. (2006).
Intelligent fault diagnosis and prognosis for engineer-
ing systems. Wiley Online Library.
Wold, H. (1966). Nonlinear Estimation by Iterative Least
Squares Procedures in: David, FN (Hrsg.), Festschrift
for J. Neyman: Research Papers in Statistics, London.
Wold, H. (1980). Model construction and evaluation when
theoretical knowledge is scarce: Theory and applica-
tion of partial least squares. In Evaluation of econo-
metric models, pages 47–74. Elsevier.
Wold, S., Sj
¨
ostr
¨
om, M., and Eriksson, L. (2001). Pls-
regression: a basic tool of chemometrics. Chemo-
metrics and intelligent laboratory systems, 58(2):109–
130.
Wurl, A., Falkner, A., Haselb
¨
ock, A., and Mazak, A.
(2017). Using signifiers for data integration in rail
automation. In Proceedings of the 6th International
Conference on Data Science, Technology and Appli-
cations, volume 1, pages 172–179.
Combining Prediction Methods for Hardware Asset Management
23
