PAPEETE: Private, Authorized, and Fast Personal Genomic Testing
Angelo Massimo Perillo
1
and Emiliano De Cristofaro
2
1
Universit
`
a di Salerno, Fisciano (SA), Italy
2
University College London, London, U.K.
Keywords:
Genomic Privacy, Privacy-preserving Technologies, Homomorphic Encryption.
Abstract:
Over the past few years, the increased affordability of genome sequencing and the ensuing availability of ge-
netic data have propelled important progress in precision medicine and enabled a market for personal genomic
testing. This yields exciting new opportunities for faster and more accurate diagnosis, personalized treatments,
and genetically tailored wellness plans. At the same time, however, it also creates important security and pri-
vacy threats. In this paper, we present a new cryptographic protocol, PAPEETE (Private, Authorized, fast
PErsonal gEnomic TEsting) suitable for running different types of tests on users’ genetic data—specifically,
SNPs. The protocol, which builds on additively homomorphic encryption, provides privacy for both users and
test facilities, and it guarantees that the test is authorized by an appropriate authority like the FDA. Finally, we
present a prototype implementation of PAPEETE, and an experimental evaluation that attests to the real-world
practicality of our techniques.
1 INTRODUCTION
Over the past few years, progress in DNA sequencing
and genomics has paved the way for a not-so-distant
future where large chunks of the population in devel-
oped countries will have access to genetic testing. Se-
quencing is not the only way to analyze the genome,
as in-vitro techniques have long been used to look for
known genetic differences using biomarkers. How-
ever, the availability of affordable sequencing makes
it possible to perform genetic testing via computer al-
gorithms, more easily and at a lower cost. Individuals
will soon be able to get their genome fully sequenced
once, then, all tests can be done in computation over
digitized copies of the genomes.
This progress is also fostering a new “direct-to-
consumer” (DTC) personal genomic market, with
companies offering genetic testing for a few hundred
US dollars or less. Most DTC companies require in-
dividuals to provide a saliva sample via mail, and then
perform either genotyping or whole exome sequenc-
ing to extract relevant genetic information and pro-
vide their customers with access to personalized re-
ports related to health (i.e., the individual’s suscepti-
bility to Parkinson’s disease), carrier status, wellness
(i.e., how well they metabolize caffeine), and ances-
try/genealogy, which reveal the ethnic heritage of the
individual.
Moreover, well-known efforts aimed to recruit
participants to voluntarily make their genome avail-
able for research purposes (e.g., the 100K Genomes
Project in the UK (Genomics England, 2013), the
Precision Medicine initiative in the US (US National
Institute of Health, 2016), or the Personal Genome
Project (PGP Global Network, 2005)). Also, pun-
dits and policymakers have also begun to advocate
that we completely replace in-vitro testing with se-
quencing, motivated by a possible reduction in life-
time costs (Roberts, 2017).
Alas, widespread availability of genomic data
prompts ethical, security, and privacy concerns. A
full genome sequence not only identifies its owner,
but also contains information related to ethnic her-
itage, disease predispositions, and many other phe-
notypic traits (Fowler et al., 2011). Furthermore, due
to its hereditary nature, access to one’s genome also
implies access to close relatives’ genomes. Therefore,
disclosing genomic data of a single individual might
put at risk the privacy of more people and for a long
period, since genomes do not change much over time
and across generations (Humbert et al., 2013).
1.1 Private & Authorized Personal
Genomic Testing
In this paper, we focus on personal genomic tests:
these are somewhat similar to those performed by
484
Perillo, A. and Cristofaro, E.
PAPEETE: Private, Authorized, and Fast Personal Genomic Testing.
DOI: 10.5220/0006859704840489
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 484-489
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

DTC companies and essentially work by analyzing an
individual’s set of SNPs (Single Nucleotide Polymor-
phisms). SNPs are the most common DNA variations
across individuals, occurring in 1% or more of a pop-
ulation (NIH, 2018). They constitute the genetic fea-
ture that is most commonly studied, and are used in
the majority of applications of genetic testing (Welter
et al., 2013).
We assume that users undergo sequencing/geno-
typing and obtain the list of the SNPs they carry; users
can then allow doctors and testing facilities to per-
form genomic tests for a variety of reasons, including
personalized medicine (Personalized Medicine Coali-
tion, 2003) as well as any kinds of test depending
on their SNPs. Consider, for instance, the following
products already offered today:
• Personalized nutrition plans by the company Nu-
trigenomix, which tests 45 genetic SNPs (Nu-
trigenomix, 2012);
• Analysis and personalization of diet, lifestyle, ex-
ercise, cardiovascular and mental activities by
GeneSNP, testing 61 SNPs (Gene SNP, 2015);
• Genetic health risks and carrier status by
23andMe, testing a few hundred SNPs (23andMe,
2006);
• Assessment of drug response and disease suscep-
tibility at GenePlanet (GenePlanet, 2016).
Overall, we focus on tests that can be expressed as a
weighted average computed over the SNPs and some
importance factors (or weights). Specifically, the re-
sult R to test X is computed as:
R(X) =
∑
i
w
i
· Pr[X |SNP
i
]
∑
i
w
i
(1)
where, for each of SNP
i
, w
i
is the weight
and Pr[X|SNP
i
∈ {0,1,2}] a SNP-dependent weight.
{0,1, 2} represents, respectively, the presence of the
SNP in no, one, or both chromosomes.
Privacy. Our goal is to support testing in such a way
that the only information revealed is the outcome of
the test. No other information is leaked, for both
the user and the test owner. This is crucial for both
parties: the former so that testing can be performed
on their genomic data without having to expose the
whole genome; the latter as test specifics might need
to be kept confidential, as they likely constitute valu-
able intellectual property.
Authorization. Furthermore, we argue that the test
itself – specifically, the weights in Eq. 1 as well
as their position – needs to be authorized by an
appropriate authority, such as the FDA. This is just
as important as privacy in order to guarantee the user
Certification
Authority
User
Testing
Facility
Authorize
Weights
Test
Figure 1: PAPEETE Architecture.
that, while the test specifics are concealed for confi-
dentiality reasons, the test has actually been verified
by an appropriate authority so that the testing facility
cannot dishonestly learn SNPs information from the
user. As discussed below, this is a crucial issue that
has been overlooked in previous work (Ayday et al.,
2013; Danezis and De Cristofaro, 2014).
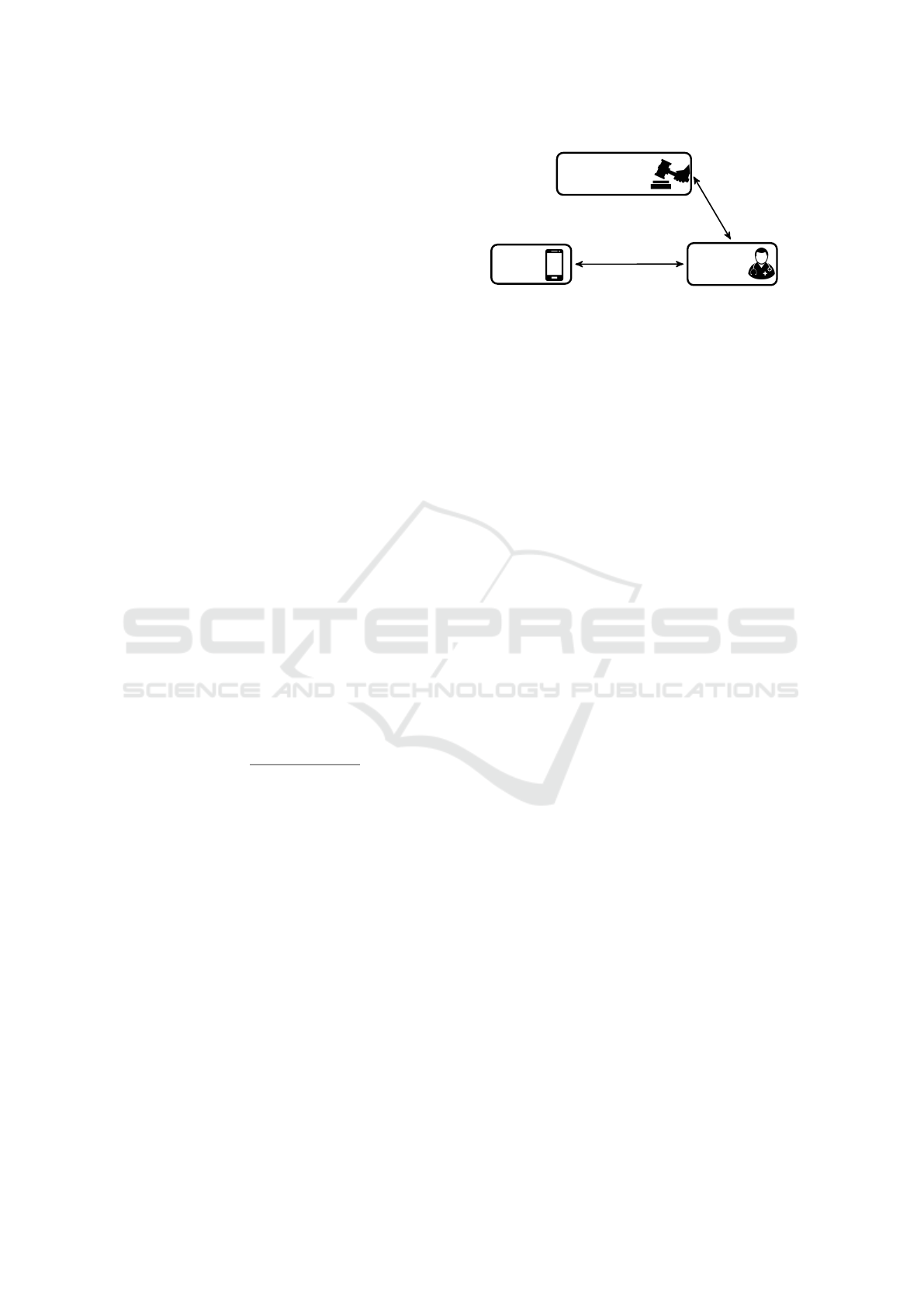
PAPEETE. With this motivation in mind, we present
PAPEETE (Private, Authorized, fast PErsonal gE-
nomic TEsting). As illustrated in Fig. 1, the pro-
tocol involves three entities: (1) a Testing Facility,
which wants to run a test on user’s genomic data with-
out revealing which positions are being tested and the
weights associated to them; (2) a User, who allows the
Testing Facility to run the test, if authorized, without
revealing her SNPs; and (3) a Certification Author-
ity, which is trusted to authorize the Testing Facility’s
test, specifically, the weights and their positions.
The protocol is formed by two main blocks, one
for the authorization and one for the actual test, built
on top of Additively Homomorphic Elliptic Curve El-
Gamal, both incurring complexity linear in the num-
ber of the SNP dictionary. We also implement a pro-
tocol prototype, demonstrating that our authorization
mechanism introduces a negligible overhead com-
pared to related work yielding non-authorized proto-
cols (Danezis and De Cristofaro, 2014).
1.2 Related Work
Our work aims to support personal genomic test-
ing, expressed as a weighted average computed over
SNPs, while simultaneously guaranteeing privacy, au-
thenticity, and efficiency. To the best of our knowl-
edge, prior work has not produced any solution that
simultaneously achieves all of our requirements.
(Baldi et al., 2011) introduce a protocol for pri-
vate personalized medicine testing, guaranteeing au-
thorization and privacy; they only support testing for
the presence of some SNPs in the user’s genome, but
not more complex operations like weighted average.
Their protocol relies on Authorized Private Set Inter-
section (De Cristofaro and Tsudik, 2010) and can op-
PAPEETE: Private, Authorized, and Fast Personal Genomic Testing
485

Table 1: Comparison to previous work.
Work Privacy Authorization Efficiency Weighted Avg
(Baldi et al., 2011) ! ! ! %
(Ayday et al., 2013) ! % % !
(Danezis and De Cristofaro, 2014) ! % ! !
PAPEETE ! ! ! !
erate on full genomes, but can achieve efficiency by
means of offline pre-computation.
(Ayday et al., 2013) introduce Private Disease
Susceptibility (PDS) testing which, similar to our
work, aims to perform a weighted average over a pa-
tient’s SNPs. They use Paillier (Paillier et al., 1999)
to privately compute the weighted average and rely on
a semi-trusted authority (Storage & Processing Unit,
or SPU) to store and retrieve the user’s encrypted
SNPs. Their protocol is relatively slow when consid-
ering hundreds of thousand/million SNPs and, more
importantly, does not provide any mechanism for au-
thorizing the weights.
(Danezis and De Cristofaro, 2014) present an im-
provement over (Ayday et al., 2013), introducing a
different encoding allowing them to replace Paillier
with Additively Homomorphic El-Gamal cryptosys-
tem (ElGamal, 1985), reducing computational and
communication complexities. Their protocol does not
support authorization either.
The difference between PAPEETE and previous
work is also summarized in Table 1.
Finally, (Naveed et al., 2014) introduce a primi-
tive called Controlled Functional Encryption (C-FE)
and use it to let individuals authorize use of their ge-
netic data for specific research purposes. C-FE is used
to encrypt the user’s genome under a public key is-
sued by a central authority; then, testing facilities can
run tests using a one-time function key, obtained by
the authority, which corresponds to a specific func-
tion. In other words, the authorization mechanism de-
termines whether or not a function can be executed,
without any control on the data being tested or the
weights used. Also, (Djatmiko et al., 2014) proposed
a secure evaluation algorithm to compute genomic
tests that are based on a linear combination of test-
specific genome components and coefficients defined
by the test. Their scheme is based on the use of par-
tially homomorphic Paillier encryption and private in-
formation retrieval (PIR). Additional related work in-
clude (De Cristofaro et al., 2012; De Cristofaro et al.,
2013).
2 PRELIMINARIES
We now review relevant cryptography background.
Elliptic Curve Discrete Logarithm Problem
(ECDLP). Let E be an elliptic curve of order q
with generator g. Informally, given points P, Q ∈ E,
such that Q ∈ hPi, the ECDLP assumption states
that determining k s.t. Q = P
k
is computationally
unfeasible.
Decisional Diffie-Hellman assumption (DDH). Let
E be an elliptic curve of order q with generator g.
Informally, the DDH assumption states that, given
g
a
and g
b
for uniformly and independently chosen
a,b ∈ Z
q
, the value g
ab
is indistinguishable from a
random element in E.
Additively Homomorphic Elliptic Curve based El-
Gamal (AH-ECC). The AH-ECC cryptosystem (El-
Gamal, 1985) involves three algorithms:
1. KeyGen(1
λ
): On input a security parameter λ,
select an appropriate elliptic curve E of order q
and public generator g. Choose random private
key x ∈ Z
q
, define the public key as pk = g
x
, and
output public parameters (E,g,pk).
2. Encrypt(m,pk): The message m is encrypted by
drawing a random element k ∈ Z
q
and comput-
ing two EC-points as (A,B) = (g
k
,pk
k
·g
m
). The
output ciphertext is (A,B).
3. Decrypt(A,B,x): Compute the element g
m
=
B · A
−x
. A pre-computed table of discrete log-
arithms may then be used to recover m from g
m
(which is practical for small ranges of m).
The cryptosystem is additively homomorphic,
as (A
1
,B
1
) · (A
2
,B
2
) = (A
1
· A
2
,B
1
· B
2
) =
(g
k
1
+k
2
,pk
k
1
+k
2
· g
m
1
+m
2
). Thus, m
1
+ m
2
is en-
crypted under k
1
+ k
2
.
3 THE PAPEETE PROTOCOL
We now present the PAPEETE (Private, Authorized,
fast PErsonal gEnomic TEsting) protocol.
Entities. PAPEETE involves the following parties:
SECRYPT 2018 - International Conference on Security and Cryptography
486

• Common input: E, q, G,n
• T’s input: {w
1
,··· ,w
n
}
1. CA chooses following values and keeps them se-
cret:
d ← Z
q
and e = 1/d (mod q)
2. T - CA: {w
1
,··· ,w
n
}
3. CA:
∀i = 1,··· ,n, compute: W
i
= G
i·e
· G
w
i
·e
· G
e
4. CA - T: {W
1
,··· ,W
n
}
5. T:
Pick: x ← Z
q
and, ∀i, k
i
← Z
q
∀i, compute: ct
i
= (A
i
,B
i
) = (G
k
i
,G
x·k
i
·W
i
)
Figure 2: Authorization (offline).
• T’s input: x,{ct
1
,··· ,ct
n
}
• U’s input: SNP
1
,··· ,SNP
n
• CA’s input: d
1. T - U: {ct
1
,··· ,ct
n
}
2. U sets ct
res
, p
res
and s
res
to 0, and, in a streaming
manner, computes:
ct
res
= ct
res
+ (ct
i
· SNP
i
)
p
res
= p
res
+ (i · SNP
i
)
s
res
= s
res
+ SNP
i
3. U - CA: ct
res
, p
res
,s
res
4. CA computes:
(ct
res
)
d
= [(A
res
)
d
,(B
res
)
d
], G
−p
res
, , G
−s
res
and
Res = [(A
res
)
d
,(B
res
)
d
· G
−p
res
· G
−s
res
]
5. CA - T: Res
6. T decrypts Res as: G
∑
w
j
= B
d
res
· G
−p
res
· G
−s
res
·
A
−x·d
res
OUTPUT: G
∑
w
j
Figure 3: Test (online).
• User (U), on input their genomic data
{SNP
1
,. .., SNP
n
}, stored on their device
and encoded as 3-bit binary vectors – e.g., if
SNP
i
= 1, it is encoded as 010;
• Testing Unity (T), on input weights, w
1
,. .., w
n
,
to be assigned to each SNP; and
• Certification Authority (CA).
Authorization. As illustrated in Fig. 2, T needs to
obtain, from the CA, the authorization to use weights
{w
1
,. .., w
n
} to conduct personal genomic testing on
users. Public parameters include an elliptic curve E
of order q, a generator G, as well as the number of
SNPs n. We also assume that T and CA can establish a
secure and authenticated channel, using standard net-
work security techniques.
CA generates a keypair (e,d) s.t. e = 1/d
(mod q), and keeps both values secret. Granting au-
thorization to use weight w
i
at position i essentially
corresponds to CA performing an exponentiation, us-
ing her exponent e, over w
i
and i. Note that CA needs
to authorize the test only once (independently from
the number of users), hence, we consider this to be
part of an “offline” phase. Also, T can pre-compute
the encryption of the (authorized) weights to speed
up the online phase presented next.
Test. Fig. 3 shows how to execute a private and au-
thorized test on U’s SNPs. T sends each encrypted
and authorized weight, ct
i
, to U, which, in a stream-
ing fashion, computes the encrypted result of the test
(ct
res
). U also computes the sum of the positions of the
SNPs (p
res
) and the sum of all the SNPs (s
res
), and
sends it, together with ct
res
, to CA. The latter needs
to unmask the result before sending it back to T, in
order to make the decryption possible. Finally, Tcan
decrypt the result.
Correctness. It is easy to observe that the protocol is
correct. Let s be the total sum of the SNPs, then:
Res = B
d
res
· G
−p
res
· G
−s
res
· A
−x·d
res
= G
d·x·
∑
k
j
· G
d·e·
∑
i
j
· G
d·e·
∑
w
j
· G
d·e·s
·G
−p
res
· G
−s
res
· G
−d·x·
∑
k
j
= G
∑
i
j
· G
∑
w
j
· G
s
· G
−p
res
· G
−s
res
If
∑
i
j
= p
res
and s = s
res
, the equation above will be
equal to G
∑
w
j

Security. To ease presentation, we do not include a
complete security proof of the protocol, as it actually
stems straightforwardly from ECDLP and DDH as-
sumptions, respectively, for the authorization step and
the underlying encryption scheme. As for the former,
note that even if T could somehow calculate both G
d
and G
e
in some way, it would still not be able to sign
weights, or remove the authorization exponent e from
previously signed weights or results.
4 EVALUATION AND
IMPLEMENTATION
In this section, we present an empirical evaluation
of the performance of the PAPEETE protocol. We
also compare it against prior work not providing au-
thorization, specifically, the protocol by (Danezis and
De Cristofaro, 2014). First, we take a look at time,
space, and communication complexities for both the
PAPEETE: Private, Authorized, and Fast Personal Genomic Testing
487

Table 2: Execution times and bandwidth consumption.
SNPs Offline Online Bandwidth
PAPEETE (Danezis and De Cristofaro, 2014) PAPEETE (Danezis and De Cristofaro, 2014)
1,000 3.88s 3.85ms 0.83s 0.82s 64.51KB
10,000 37.77s 37.40s 7.04s 7.03s 645.12KB
100,000 6.27m 6.22m 1.31m 1.31m 6.3MB
1,000,000 62.77m 62.21m 18.89m 18.88m 63MB
parts of which the protocol is composed (offline au-
thorization and online test). Then, we give some de-
tail about the setup used in our experiments. Finally,
we show the results of our tests and comparison.
Offline Operations. We start by analyzing the com-
plexity of the authorization phase (Fig. 2), which is
linear in the number of SNPs considered. CA needs
to perform n exponentiations to authorize n weights
(step (3)), while T performs O(n) exponentiations to
encrypt the authorized weights (5). Note that T can
reuse the same values (ct
i
) for multiple tests. Commu-
nication complexity is also linear, as in steps (2) and
(4), O(n) values are transferred between T and CA. Fi-
nally, we observe that all operations can be pipelined,
which means that, unless T and CA are connected via
a very slow link, authorizing the test (3) does not in-
troduce a significant overhead on top of the weight
encryption (5).
Online Test. Next, we analyze the complexity of the
online test (Fig. 3). Both computation and communi-
cation complexities are linear in the number of SNPs,
and the steps involving CA (3)–(5) only requires the
transmission of a constant number of ciphertexts and
the computation of a constant number of exponentia-
tions. Once again steps (1)–(2) can be pipelined.
Experimental Setting. We have implemented our
protocols and performed 1,000 runs to evaluate real-
world running times and bandwidth consumption.
Both T and CA run on an Apple MacBook Pro (OSX
10.11) equipped with an Intel Core i5 2.4 GHz proces-
sor and 8GB of RAM memory, while U on a Google
Nexus 5 (Android 6.0.1), with a Qualcomm Snap-
dragon 800 2.3 GHz CPU and 2GB of RAM memory,
all connected over a WiFi network (40Mbps) using
TCP sockets. Our code base, available upon request,
is written in Java, using the Spongy Castle crypto-
graphic library for Android (Spongy Castle, 2012)
and the Bouncy Castle library for Mac (The Legion
of the Bouncy Castle, 2000).
1
Experimental Results. To speed up operations, we
have used the following encoding in step (2) in the
1
Somewhat unexpectedly, we find that, if we encode el-
liptic curve points in byte arrays before transferring them,
we get a significant performance slow down. Thus, we en-
code and send each coordinate of the points individually.
online test protocol (Fig. 3): if SNP
i
= 0, we jump to
the next value, while if SNP
i
= 1, we execute the two
computations as described; otherwise (SNP
i
= 2), we
sum the ciphertext ct
i
twice. In Table 2, we report the
running times as well as bandwidth consumption in-
curred by the PAPEETE protocol, and compare them
against prior work that does not support authorization.
More specifically, we have re-implemented and run
the protocol in (Danezis and De Cristofaro, 2014) us-
ing the same experimental settings discussed above.
Note that (Danezis and De Cristofaro, 2014) also has
an “offline” step where weights can be pre-encrypted.
We vary the number of SNPs considered, assuming
that, on average, 20% of them is non-zero, as advised
by colleagues in UCL’s Genetics Department.
We note that in all cases, complexities grow linear
in the number of SNPs. Above few hundred thousand
SNPs, we also observe a small “penalty” on the mo-
bile device that is introduced by Android’s garbage
collector, which is executed more often, thus occupy-
ing a non-negligible CPU time. With 1 million SNPs,
the time required to authorize and encrypt the weights
is approximately 1 hour, and anyway this operation
needs to be performed only once. The same values
can be used to run any number of tests on user’s SNPs,
taking only an average time of less than 19 minutes.
As for the bandwidth, with 1 million SNPs, 35MB are
exchanged during the offline and 63MB during the
online parts. We also measure the space required to
store the SNPs on U’s smartphone, and for the autho-
rized and encrypted weights on T’s computer. With 1
million SNPs, we need 418.5KB on the smartphone
and 63MB on the laptop. Overall, our experiments
demonstrate that (1) the overhead incurred by the au-
thorization is negligible, when compared to state of
the art (Danezis and De Cristofaro, 2014) (running
times are only 1% slower), and (2) our protocol is very
efficient and can already be used in the real world.
Finally, we perform another experiment aiming to
evaluate the impact of non-zero SNPs on the user’s
genome. To this end, in Fig. 4, we plot the total
running time for the execution of a test using 10,000
SNPs, varying the percentage of non-zero SNPs from
20 (as in the previous experiments) to 50. We ob-
serve that performance also grows linearly, similarly
to (Danezis and De Cristofaro, 2014), but not to (Ay-
SECRYPT 2018 - International Conference on Security and Cryptography
488

20 30 40
50
7
10
14
17
% of non-zero SNPs
Running Time (s)
Figure 4: Running time for different % of non-zero SNPs.
day et al., 2013), where exponentiations are executed
on all the SNPs, even the zero ones.
5 CONCLUSION
In this short paper, we presented PAPEETE, a novel
protocol supporting Private, Authorized, fast PEr-
sonal gEnomic TEsting. We implemented a proto-
type of the protocol and evaluated experimentally,
also comparing it against prior work that does not sup-
port authorization (Danezis and De Cristofaro, 2014).
Our experiments attested to the real-world practical-
ity of the protocol, which makes us confident that we
will soon be able to deploy it in pilot applications in
collaboration with geneticists and doctors.
As part of future work, we plan to develop a full-
blown graphical user interface and perform user stud-
ies to assess the usability and acceptability of our
techniques.
ACKNOWLEDGEMENTS
This research has been supported by a Google Faculty
Award grant and the EU Project H2020-MSCA-ITN
“Privacy & Us” (Grant No. 675730).
REFERENCES
23andMe (2006). https://www.23andme.com.
Ayday, E., Raisaro, J. L., Hubaux, J.-P., and Rougemont,
J. (2013). Protecting and evaluating genomic privacy
in medical tests and personalized medicine. In ACM
WPES.
Baldi, P., Baronio, R., De Cristofaro, E., Gasti, P., and
Tsudik, G. (2011). Countering gattaca: Efficient and
secure testing of fully-sequenced human genomes. In
ACM CCS.
Danezis, G. and De Cristofaro, E. (2014). Fast and private
genomic testing for disease susceptibility. In ACM
WPES.
De Cristofaro, E., Faber, S., Gasti, P., and Tsudik, G.
(2012). Genodroid: Are Privacy-Preserving Genomic
Tests Ready for Prime Time? In ACM WPES.
De Cristofaro, E., Faber, S., and Tsudik, G. (2013). Se-
cure Genomic Testing With Size-and Position-Hiding
Private Substring Matching. In ACM WPES, pages
107–118.
De Cristofaro, E. and Tsudik, G. (2010). Practical private
set intersection protocols with linear complexity. In
Financial Cryptography.
Djatmiko, M., Friedman, A., Boreli, R., Lawrence, F.,
Thorne, B., and Hardy, S. (2014). Secure evaluation
protocol for personalized medicine. In ACM WPES.
ElGamal, T. (1985). A public key cryptosystem and a signa-
ture scheme based on discrete logarithms. IEEE trans-
actions on information theory, 31(4).
Fowler, J. H., Settle, J. E., and Christakis, N. A. (2011).
Correlated genotypes in friendship networks. Pro-
ceedings of the National Academy of Sciences, 108(5).
Gene SNP (2015). http://www.genesnp.com.
GenePlanet (2016). https://www.geneplanet.com.
Genomics England (2013). The 100,000 Genomes
Project. https://www.genomicsengland.co.uk/the-
100000-genomes-project/.
Humbert, M., Ayday, E., p. Hubaux, J., and Telenti, A.
(2013). Addressing the concerns of the lacks familiy:
Quantification of kin genomic privacy. In ACM CCS.
Naveed, M., Agrawal, S., Prabhakaran, M., Wang, X., Ay-
day, E., p. Hubaux, J., and Gunter, C. A. (2014). Con-
trolled functional encryption. In ACM CCS.
NIH (2018). What are single nucleotide polymorphisms
(SNPs)? https://ghr.nlm.nih.gov/primer/genomic re-
search/snp.
Nutrigenomix (2012). https://www.nutrigenomix.com.
Paillier, P. et al. (1999). Public-key cryptosystems based on
composite degree residuosity classes. In Eurocrypt.
Personalized Medicine Coalition (2003). http://www. per-
sona lizedmedicinecoalition.org.
PGP Global Network (2005). Personal Genomes Project.
http://www.personalgenomes.org/.
Roberts, M. (2017). Chief medical officer calls for gene
testing revolution. http://www.bbc.co.uk/news/health-
40479533.
Spongy Castle (2012). https://rtyley.github.io/spongycastle/.
The Legion of the Bouncy Castle (2000). http://www. boun-
cycastle.org.
US National Institute of Health (2016). All of Us Research
Program. https://allofus.nih.gov/.
Welter, D., MacArthur, J., Morales, J., Burdett, T., Hall, P.,
Junkins, H., Klemm, A., Flicek, P., Manolio, T., Hin-
dorff, L., et al. (2013). The NHGRI GWAS Catalog, a
Curated Resource of SNP-Trait Associations. Nucleic
Acids Research, 42.
PAPEETE: Private, Authorized, and Fast Personal Genomic Testing
489