
Internal Simulation for Autonomous Robot Exploration of Lava Tubes
Ra
´
ul Dom
´
ınguez, Sascha Arnold, Christoph Hertzberg and Arne B
¨
ockmann
German Research Center for Artificial Intelligence – Robotics Innovation Center,
Robert-Hooke-Str. 1, 28359 Bremen, Germany
Keywords:
Autonomous Navigation, Robotics Simulation, Path Planning, SLAM, Exploration.
Abstract:
Space Exploration stands as one of the most challenging endeavors of our time. Extraterrestrial caves in
particular have been identified by the scientific community as of great interest. They could be suitable for
allocating astronaut planetary stations, but little is known about them. In this paper, we describe and analyze
robotic cave exploration using internal simulation and SLAM technologies and provide experimental results.
The experiments were performed in a lava tube selected due to its representativeness as space analog. Expen-
sive mission costs, communication constraints and navigational challenges in space missions demand highly
developed degrees of autonomy and safety on the robots. For this reason, our solution incorporates methods
for the validation of paths based on on-board, internal simulation. The methods provide the means to increase
the confidence of successful executions by simulating using physics models the planned path. A highly realis-
tic model of the robot and an on-line generated model of the environment are required. Assuming the demands
of the space robotics scenario, all software runs on-board.
1 INTRODUCTION
Caves are an important cornerstone of human space
exploration (Wynne, 2016). They can provide a na-
tural shelter from radiation, extreme temperature cy-
cles and small meteoroids, allowing the deployment
of light-weight habitats and reducing the overall costs.
Caves might also provide access to water ice deposits
and protected underground environments that can re-
veal information about geological processes and po-
tential extraterrestrial life. Lava tubes have been iden-
tified in Moon and although they have not yet been
confirmed in Mars, there is significant evidence of
their existence (Daga et al., 2009). In fact, many
cave-like features have been identified on Mars and
on Moon in the recent years.
To reduce the risks and to ensure the suitability
of a cave for allocating astronauts or any other possi-
ble usage, robotic platforms can be used to generate
maps and analyze the state of the tubes. When going
underground, robotic systems must maintain a cons-
tant data-link to the surface, usually done by a wire
(Nesnas et al., 2012), or be able to explore the cave
autonomously. Although a wire link can be benefi-
cial to reach the entrance, it will easily get entangled
and limits the exploration range in the tube. In this
paper we focus on the internal simulation as a key el-
ement that enables a robot equipped with a LiDAR to
Figure 1: The Asguard V4 rover. A four leg-wheel hybrid
robot designed for difficult outdoor environments, equipped
with an embedded quad core i7 CPU, a Velodyne LiDAR,
Xsens IMU and a 360 degree camera. Additionally the
rover can carry payloads of up to 5 kg (e.g. a spectroscope
or sampling drill) Image: Robbie Shone, ESA.
autonomous explore, map and find it’s way back in a
cave.
For performing the experiments and to analyse
our software and hardware, we selected the lava tube
Cueva del Viento in Icod de los Vinos (Spain). Cueva
del Viento is the largest lava tube in Europe. It is lo-
cated at the volcanic island of Tenerife, an exceptional
location for planetary analog environments (Preston
144
Domínguez, R., Arnold, S., Hertzberg, C. and Böckmann, A.
Internal Simulation for Autonomous Robot Exploration of Lava Tubes.
DOI: 10.5220/0006860701440155
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 144-155
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

et al., 2012). For the exploration mission, a 240 m
long section of the tube was selected which is pre-
served without any human modification and where the
risks of collapse were very low. As platform for our
experiments we utilized the Asguard V4 rover shown
in Fig. 1.
The entrance to the cave is located in a cavity of
the floor, with a height of around 0.5 m and a width
of approximately 0.75 m. After the entrance through
the small opening, follows an inclined and muddy sur-
face. In a real mission, this first section would have to
be traversed by the robot with the help of some rope
or cable. In a multi-robot mission this objective could
be achieved.
Nowadays, planetary robotic missions rely hea-
vily on the operations center at earth for navigation.
The paths that the robot executes are designed on
earth with human experts in the loop, based on the
data acquired in the previous days. This approach is
safe, but makes planetary exploration very slow. Fur-
thermore, in the case of long caves, like the one des-
cribed in the experimental part, communication with
earth for each path execution implies entering and
leaving the cave constantly. Thus, in order to explore
the cave in depth, an autonomous system which pro-
vides larger exploration ranges is preferable. The pro-
posed solution does not require human intervention
for the safe navigation and mapping of the cave.
One of the most important features of space
robotic systems is safety. In order to address this
issue, our solution incorporates an on-board simu-
lator. The internal simulator enables the system to
predict what the consequences of the potential path
plan executions would be. The concept is based on
ideas from the Simulation Cognition Theory (Hess-
low, 2012). (Marques and Holland, 2009) propose
a framework which includes the minimal require-
ments, components, a taxonomy of architectures and
examples of these. The internal simulator has been
previously identified as a useful approach for deci-
sion taking and path planning in space robotics in
(Roßmann et al., 2014; Dom
´
ınguez et al., 2015) and
for planning and navigation in indoor environments
(Rockel et al., 2014; Rockel et al., 2015; Chella and
Macaluso, 2009).
As opposed to other works, our internal simula-
tor runs on-board and uses a simulated environment
which was generated online by the rover from its col-
lected sensor data. To achieve this, our SLAM and
our Simulator have been designed to share and work
on the same environment representation using the li-
brary Envire (Hidalgo Carri
´
o et al., 2016).
Environment representation and navigation in
cave missions impose additional path planning and
Figure 2: Approach for the Autonomous Cave Exploration:
Explorer chooses a goal pose in a travesable area close to
an unknown region. Internal Simulator executes the path
planning on-board. If the result is successful, the planning
in the real environment is executed. Feedback is given to
the Explorer.
mapping requirements with respect to other space
robotics cases. In particular, lava tubes can form 3
dimensional pathways which are not found in open
areas. At this point, traditional 2 dimensional grid-
based path planning algorithms become insufficient.
Our environment representation, path planner and ex-
ploration components are able to represent, explore
and find motion plans in such environments. This is
achieved by incorporating a third dimension on the
grid map and by building a bi-directional graph of
connected traversable areas from it.
The proposed SLAM, Path Planning, Exploration
and Internal Simulation methodology are presented in
Section 2. The result of its evaluation with experi-
mental cases is presented in Section 3. Conclusions
are presented in Section 4 along with the next research
goals.
2 METHODOLOGY
Our overall approach is shown in Fig. 2. The Ex-
ploration Behavior is in charge of selecting the next
target pose based on the known Multi-Level Sur-
face (MLS) map, the current pose and feedback from
the internal simulator regarding previously attempted
goal poses. SLAM is responsible for the localization
and for the construction and maintenance of the En-
vironment Representation in its different forms: MLS
Maps for planning and Polymeshes for internal sim-
ulation. The Internal Simulator replicates the path
planning components and its execution to identify
whether the traverse to a goal pose is feasible. Finally,
the Path Planner executes the motion plan in the real
environment if the result of the prediction is a success.
Although the Exploration Behavior is the direct-
Internal Simulation for Autonomous Robot Exploration of Lava Tubes
145

ing component, it highly depends on the inputs from
the other modules. Thus, SLAM, Path Planning and
the Internal Simulator are explained first.
2.1 SLAM
The SLAM solution used in this work is a graph
SLAM approach in which odometry, LiDAR and in-
clination based constraints are online modeled and
optimized. The state space consists of the robot poses,
each associated with a 360 degree LiDAR scan and a
bias state modeling the IMU to LiDAR rotation error.
The LiDAR has a vertical resolution of 1.25
◦
cover-
ing the range from −30
◦
to 10
◦
and a horizontal res-
olution of 0.18
◦
. In order to model the inclination
of the IMU and the relative transformations between
the LiDAR scans together, the pose of the IMU with
respect to the LiDAR needs to be calibrated. Model-
ing the bias allows to associate this calibration with
an uncertainty and therefore avoids that the optimiza-
tion becomes overconfident. In case of a low accu-
racy calibration it also allows refining the calibration
by starting with a higher uncertainty.
In order to perform the graph optimization in real-
time we reduce the amount of constraints by model-
ing only the result of the ICP algorithm based align-
ment between two LiDAR scans as a constraint. The
technique relies on the Generalized-ICP (GICP) from
(Segal et al., 2009). As odometry constraint we ap-
ply the wheel rotation rates and the orientation pro-
vided by the IMU to a skid-steer kinematics model of
the robot. Modeling the IMU based inclination con-
strains the error in roll and pitch and therefore reduces
the error in altitude.
Since we consider a 360 degree LiDAR scan with
an acquisition time of 0.1 seconds to be a static mea-
surement of the environment we have to convert the
single measurements into the same frame. We apply
interpolated odometry based transformations to each
of the 64K measurements in order to convert them
into the acquisition time of the first measurement.
This allows us to deal with motion distortions inside
a full scan resulting from fast (particularly roll/pitch)
motion of the robot, due to the stiff and unstructured
surfaces usually found in lava tubes.
Each state x
t
∈ SE(3) is associated with a point
cloud measurement of the surrounding environment.
New states are added to the graph based on the change
in rotation and translation of the robot. The ICP based
measurement is defined as
z
l,t, j
= C
−1
x
j
C
x
t
ε
l,t
(1)
where C
x
t
is the transformation matrix of the state
x
t
∈ SE(3). ICP based constraints are added for each
state x
t
to the j states within the closest Euclidean
distance. ε
l
is a Gaussian random variable modeling
the ICP measurement noise with zero mean and a co-
variance Q
l
. The constraint of the ICP based edges is
modeled as
(z
l,t, j
C
−1
x
j
C
x
t
)
>
Q
−1
l,t
(z
l,t, j
C
−1
x
j
C
x
t
) (2)
where z
l,t, j
∈ SE(3) is the result of point cloud align-
ment of the ICP algorithm. The operator adds
a local perturbation ε ∈ R
3
to a manifold element
x ∈ SE(3): ε 7→ x ε and is the corresponding re-
verse operator : SE(3) × SE(3) → R
3
. For more
mathematical details we refer the reader to (Hertzberg
et al., 2013).
The odometry measurement is defined as
z
o,t
= C
−1
x
t−1
C
x
t
ε
o,t
(3)
where ε
o
is a Gaussian random variable modeling the
odometry measurement noise with zero mean and a
covariance Q
o
. Odometry based constrains are only
added between successive states x
t−1
to x
t
. The con-
straint of the odometry based edges is modeled as
(z
o,t
C
−1
x
t−1
C
x
t
)
>
Q
−1
o,t
(z
o,t
C
−1
x
t−1
C
x
t
) (4)
where z
o,t
∈ SE(3) is the measurement of the skid-
steer kinematics model from t − 1 to t.
The measurement of the inclination is defined as
z
h,t
= R
−1
b
R
−1
x
t
ˆ
k ε
h,t
(5)
where R
x
t
is the rotation matrix of the state x
t
, R
b
is the rotation matrix of the bias state b and
ˆ
k is the
unit vector [0, 0, 1]
>
. The bias b ∈ SO(3) describes
the error in the IMU to LiDAR rotation. ε
h
is a Gaus-
sian random variable modeling the inclination mea-
surement noise with zero mean and a covariance Q
h
.
The constraint of the inclination edges is modeled as
(z
h,t
R
−1
b
R
−1
x
t
ˆ
k)
>
Q
−1
h
(z
h,t
R
−1
b
R
−1
x
t
ˆ
k) (6)
where z
h,t
∈ S
2
is the measurement of inclination from
an IMU.
The graph optimization minimizes the squared
error of all constraints given all measurements
(z
l,1:t
, z
o,1:t
, z
h,1:t
) to find the best solution for the
states x
1:t
and b.
argmax
x
1:t
,b
p(x
1:t
, b|z
l,1:t
, z
o,1:t
, z
h,1:t
) (7)
We use the g2o framework (K
¨
ummerle et al., 2011)
as back-end in order to model and optimize the graph.
The result of the SLAM are the aligned poses of
the robot and their associated LiDAR scans. As a next
step the scans are projected into map formats in order
to fulfill the requirements of the planning and the in-
ternal simulation. The planning needs to distinguish
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
146

Figure 3: Left: Multi-Level Surface map of a section of the
cave with a cell size of 10 cm. Right: Polygon mesh of the
same scene. The color indicates the change in altitude, one
meter equals one color cycle.
between traversable and non-traversable regions, re-
quires fast access to the local height information and
the ability to represent multiple levels. While the in-
ternal simulation requires a very accurate representa-
tion of the surfaces.
Fig. 3 shows the two map types that are created on
request of the path planning and the internal simula-
tion. The planning uses a Multi-Level Surface (MLS)
(Triebel et al., 2006) map since it allows to represent
multiple levels while accurately encoding height in-
formation and uncertainty. It is a 2D grid managing a
list of entries providing height, occupancy and uncer-
tainty information for each cell.
In order to create an accurate representation of the
surface of the environment for the simulation we ex-
tract a polygon mesh from an intermediate map for-
mat. The intermediate map format is a voxel grid
holding the estimated truncated signed distance to the
closest surface and uncertainty in each cell. Modeling
truncated signed distance functions (TSDF) (Curless
and Levoy, 1996) with the goal of accurate surface re-
construction have been recently used especially in the
context of RBGD-camera based SLAM (Newcombe
et al., 2011). We show that it can also be applied suc-
cessfully on LiDAR based SLAM. Each measurement
is ray-traced on the line from the sensor origin to the
measurement in the range [−δ, +δ] around the mea-
surement (δ is the truncation parameter). The CPU
based ray tracing is implemented based on the work
from (Amanatides et al., 1987). In order to extract the
surface from the TSDF volume we use the Marching
Cubes algorithm (Lorensen and Cline, 1987).
The generation of those maps from the LiDAR
measurements is expensive and not real time capable,
therefore they are created on demand by the Internal
Simulator. Usually, after the robot has reached the
goal position and a new trajectory needs to be planned
and evaluated.
2.2 Path Planning
Caves are complex and unpredictable environments
that may contain multiple overlapping levels. We ap-
proach path planning in such environments by devel-
oping a robust algorithm able to cope with multiple
2D levels embedded in a 3D world. Our multi level
path planner assumes that the target scenario does not
incorporate dynamic obstacles. A reasonable assump-
tion in exploration of extraterrestrial caves.
Path planning in unstructured environments has
been thoroughly explored and several solutions have
been proposed, e. g., (Daily et al., 1988; Lacroix et al.,
2002; Howard and Kelly, 2007; Rekleitis et al., 2013).
However, those solution are in general limited to 2D
or 2.5D planning and are not suitable for multi path
level planning.
Multi level solutions have been proposed in
(K
¨
ummerle et al., 2009) and in (B. Rusu et al., 2009).
The solution of (K
¨
ummerle et al., 2009) is probably
the closest to our implementation. Their solution is
also based on MLS maps and uses motion primitives.
However they employ a two-steps planning approach
where the first step returns a coarse result that is im-
proved by a local planning step, whereas we imple-
mented a one-step solution that yields good results.
In order to plan efficiently, the MLS map pro-
vided by the SLAM is converted into a traversabil-
ity map (TravMap). Our TravMap encodes knowl-
edge about the local traversability using four different
patch types: traversable, obstacle, unknown and ex-
plorable.
A patch is marked traversable if enough support
exists in the region for the robot to stand on and there
are no obstacles that would hinder the robots traversal.
Thus to asses if a patch is traversable, first a surface
analysis is performed and second an obstacle check.
In the surface analysis the overall slope of the sup-
port plane must not exceed a predefined slope limit
and there must not exist steps within the plane that ex-
ceed the maximum step height of the robot. If these
two requirements are met, the patch is initially con-
sidered traversable and obstacle check is performed.
A 3D obstacle check is performed against the
MLS using a robot model-based bounding box which
ignores the orientation of the system. Thus, patches
where the robot won’t collide with obstacles when
standing in at least one orientation are marked as
traversable. This approach pursues to find any pos-
sible path on the TravMap, by marking as obstacle
patches only those that are guaranteed to be non-
traversable in all robot orientations.
The obstacle check improves performance during
the posterior planning steps by performing and initial
prune of the search space. Nevertheless, during path
planning a more detailed obstacle check is done that
incorporates the orientation of the robot.
The local support plane is calculated using
Internal Simulation for Autonomous Robot Exploration of Lava Tubes
147

RANSAC (Fischler and Bolles, 1981) plane fitting.
Patches are marked as unknown in case insufficient
data is available to find such a plane (i. e., less than 5
inliers support the plane). Such places usually indi-
cate a lack of data in the map and are natural targets
for further exploration. However since critical knowl-
edge is missing in order to assess the traversability of
unknown patches, they cannot be the target of a plan-
ning process. Therefore, we select traversable patches
nearby and mark them explorable. The robot should
be able to attain more information of the environment
by driving onto these patches.
Generating the TravMap is a computationally ex-
pensive process that was not compatible with stop-
free navigation on our system. Thus, it is performed
as less as possible, i. e., only when the robot has
reached a goal position while waiting for the next tar-
get pose. Due to the static nature of the target envi-
ronment map re-generation of the TravMap is in our
case seldom needed.
(a) MLS map (b) Traversability map
Figure 4: For exploration and path planning, the
Traversabilty Map (b) is generated from the Multi-Level
Surface map (a). The coordinates axis describe the current
pose of the robot, the background grid has a resolution of
1 m, the resolution of the MLS and the traversability map
are 0.1 m. In (b): Green cells represent traversable surfaces,
red ones obstacles, magenta are unknown and blue are ex-
plorable areas. Yellow arrows mark the target candidates
for the path planning.
An MLS map and the TravMap that was generated
from it are presented in Fig. 4. The map is created by
growing from the current robot position. Expansion
stops at patches marked as unknown or border, result-
ing in a 3D representation of all the places that the
robot can reach from its current position. Each patch
in the map is linked to its neighbors. Thus, it is equi-
valent to a double connected graph structure that can
be searched efficiently for traversable paths.
Path planning is done using SBPL (Cohen et al.,
2010; Likhachev et al., ) and the ARA* algorithm
(Likhachev et al., 2004). ARA* was chosen due to
it’s anytime characteristics. It can provide a subop-
timal solution quickly and refine it until an optimal
solution is found.
In the TravMap, x and y are the coordinates of the
patch the robot is standing on and z is the patches
height. The state space is discretized and consists of
(x, y, z, θ) where x, y and θ are discretized while z re-
mains continuous.
To keep the number of possible state transitions
low, two-dimensional spline based motion primitives
are used to model the robot motions. For distance cal-
culation the primitives are projected onto the 3D sur-
face the robot is driving on. Because the primitives
are distorted when projected on a non-flat surface, the
final trajectory may contain motions that slightly de-
viate from the motion primitives.
The time it would take the robot to follow the
shortest path on the TravMap is used as heuristic. The
cost function consists of the actual time it would take
the robot to follow the selected motion primitive as
projected onto the 3D surface. Optionally, a term rep-
resenting the closeness to obstacles can be factored in
to favor trajectories that stay well clear of obstacles.
The robot’s forward, backward and turning speeds
can be configured separately and are used to calculate
the travel time.
While searching, only collision free motion prim-
itives are considered. To achieve this, a 3D bound-
ing box check against the MLS is computed for ev-
ery discretized pose that can occur on a given prim-
itive. These checks are the most CPU intensive part
of the path planning algorithm. Thus, the overall per-
formance depends largely on the number of motion
primitives that need to be checked at each step. How-
ever, the obstacle checks can be parallelized, i. e., for
a given state all possible successors can be found at
the same time as long as enough processing time is
available. For this reason, we are able to use a very
detailed set of motion primitives and yield good re-
sults without any further optimization.
2.3 Internal Simulator
The internal simulation has in this context the task of
predicting the probability of a path traverse execution
to be successful. Ideally, the accuracy of the predic-
tion is well known. This accuracy is dependent of
many factors: Some can be grouped into biases from
the simulation (e.g. wrong surface friction estimation,
errors in the robot model), others related to the path’s
complexity (e.g. length, curves, orientation changes)
and others due to a certain level of intrisic indetermin-
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
148

ism in the simulated and in the real execution.
The internal simulator incorporates running
clones of the components from which the results we
intend to validate and of the ones they depend on,
except for the sensor drivers. The sensor drivers
are replaced in this copy of the components network
by modules that produce analog data based on the
robotics physics engine, or in the case of the cameras,
by the graphical engine used to render it. In this case,
the cloned components are the path planning, the ex-
ecution layer and all subcomponents on which they
depend, except for the SLAM which is connected to
both the original components and their clones. Nev-
ertheless, the SLAM has a different role in the inter-
nal simulator: It provides the surfaces of the environ-
ment. The surfaces are required to compute physical
interactions with the robot model. SLAM is not used
for localization of the cloned components interacting
with the simulated environment and it does not main-
tain any environment representation based on simu-
lated sensor data.
The cloned components and their interactions take
place on the same Robotic Control Operating System
than the original components and on-board the sys-
tem. Thus, their interactions and resulting behavior
are highly similar. We consider this an important fea-
ture because delays in the communication layer be-
tween components can have consequences more diffi-
cult to predict outside the system itself.
The validation process of a goal position in the
internal simulation is the following: (1) The internal
simulation requests to the SLAM module a polygon
mesh. The mesh is generated from the aligned point
cloud that SLAM maintains and it has a resolution
of 5 cm. (2) With the mesh, the simulated environ-
ment, in which the physical model of the robot is also
placed according to its estimated pose, is updated. (3)
A TravMap is generated based on the MLS map of the
environment which is also provided by the SLAM. (4)
The path planning uses the TravMap to plan a path.
(5) The plan execution is simulated on-board. (6)
If the target is reached, the goal pose is considered
validated and the goal pose is passed to the executive
layer. Otherwise, feedback is provided to the Explo-
ration Module, so that another target pose is selected.
The internal simulation is complex and requires
high computational costs. Thus, it must be carefully
decided in which situations it should be used. Fur-
thermore, depending on the hardware available, its in-
tegration might be unfeasible or only possible after a
careful adaptation of the different process priorities.
In fact, this is the first application know to the authors
where the robotics simulator runs on-board along with
the rest of the components. A requirement for scena-
rios where access to external computational resources
is not possible like the one targeted.
In order to minimize the computational costs and
increase the reliability of the approach, a new envi-
ronment representation library (Hidalgo Carri
´
o et al.,
2016) has been developed. The library lies both at the
core of SLAM and the Internal Simulation. Using the
same environment representation in both components
has at least two advantages: (1) It reduces the number
of dependencies of the software and (2) minimizes the
conversions between representation models. To the
best of the authors knowledge, this is the first case
of a robotic setup in which the simulated scenes are
generated on-board based on the environment repre-
sentation that the system itself constructs, instead of
using pre-designed simulated scenes with little or no
change.
Another tool shared by different components is
the Flexible Collision Library from (Lee et al., 2017),
which is used in the collision check of the path plan-
ning and to determine the collisions between the robot
model and the simulated surfaces.
2.4 Exploration
Relying on the previously described components, the
following exploration behavior has been implemented
and tested: First, each explorable patch on the map is
evaluated based on its proximity to the current robot
pose, number of unexplored patches nearby and pro-
ximity to a specified target position.
A path is planned to the most promising patch. If
no path could be found or its simulation execution de-
termines a failure, the next candidates are analyzed
until a safe path is found.
Once a path has been found, the robot starts fol-
lowing the Trajectory and once the target position
is reached, the current MLS is updated and a new
TravMap map is generated. The process repeats until
the desired area has been explored or another criteria
(e. g., a time limit or low battery condition) is fulfilled,
at which point the robot returns to its starting pose.
The return is relevant for cave scenarios because the
system needs to recharge and establish communica-
tion after the exploration.
Terrain conditions inside the cave are unknown
and most likely complex. The robot might get stuck,
slip or skid at random locations. Thus the robot might
deviate from the planned trajectory while moving. To
avoid leaving the traversable map and running into
obstacles we continuously monitor the current robot
position and stop the motion if the robot is about to
leave the traversable part of the map. If this happens
the maps are updated and the exploration process re-
Internal Simulation for Autonomous Robot Exploration of Lava Tubes
149

Figure 5: A map of the cave with some geo-referenced
points on it (crosses). These points were marked with ma-
genta spheres when taking the data logs in order to use them
as ground truth to estimate the accuracy of our localization
and mapping. Image: Courtesy of Geodata air S.A.
peats.
In certain situations, borders of the currently
explored map cannot be distinguished from actual
down-hill cliffs, e. g., if the LiDAR is not able to see
any surface after the cliff. This would result in the
exploration strategy repeatedly trying to explore al-
ready visited places. To avoid this, we implemented
a simple coverage map, which accumulates the areas
around the robot positions. Patches which are covered
by this map, will not be considered as candidates for
exploration.
3 RESULTS
In this section we summarize experiments performed
to test the different modules and its interactions in an
analog scenario to a Martian or Lunar lava tube. The
experiments were conducted with the Asguard V4
rover in a 240 meter long section of the Cueva del
Viento lava tube in November of 2017. The cove-
red section starts at the entrance Breveritas and goes
to the South. In Fig. 5 a cartographic representation
of the cave produced by a topographic company is
shown. It represents the different elevations and some
geo-referenced positions which were used as ground
truth.
The rover is equipped with a Xsens IMU, a Velo-
dyne HDL-32E LiDAR and two cameras with super
fish eye lenses. Each camera has a horizontal opening
angle of 220°, fully covering 360° around the rover.
3.1 Cave Mapping
In this section we show that the accuracy of the pose
graph of our SLAM solution is within a mean position
difference of 0.4 m to the ground truth.
In order to evaluate the accuracy of our SLAM
solution eleven globally referenced landmarks in the
240 m long subsection of the lava tube were used as
ground truth. Prior to our experiments those survey
markers (≈ 5 mm metal pins) had been located within
Figure 6: Shows an artificial landmark (magenta colored
sphere) placed on a position for which ground truth infor-
mation was available. The Apriltag in the background was
used to distinguish between different landmarks.
an independent geodetic survey. The ground truth po-
sitions are associated with an uncertainty of 0.05 m.
In order to later identify the landmarks in the cam-
era images, we placed magenta colored spheres with
a diameter of 8 cm on top of the survey markers. The
landmarks were not integrated in the SLAM to im-
prove the positioning or map construction, we only
compared the expected position of the landmarks in
the SLAM with their known ground truth positions.
The positions of the spheres in the camera images
were detected by applying a HSV (Hue, Saturation,
Value) based color segmentation followed by a cir-
cle Hough Transformation. Since the only source of
light inside of the cave were the lights of the rover, the
detection was prone to strongly changing light con-
ditions, reflections on the surface of the spheres and
outliers (Fig. 6). Therefore, especially the detected
size of the sphere in the image needed to be associ-
ated with a higher uncertainty.
For collecting this data set the rover was first ma-
nually driven, from a starting point above one of the
landmarks, 240 m into the cave and then back to the
starting point. Fig. 7 shows the trajectory (blue line)
of the robot during the mission in North/East and
North/Altitude direction. The starting point is at the
origin of the local coordinate frame. The red crosses
show the known positions of the landmarks in the lo-
cal frame and the green crosses show their expected
positions in the SLAM.
Since the ground truth information is only avai-
lable when spheres are detected in the camera im-
ages, the difference to the ground truth can only be
observed for the corresponding robot poses at those
times. We assume that the error grows approximately
linear during the time between observing different
landmarks.
To compute the mean position difference we ap-
plied a bundle adjustment of the expected positions
of the landmarks to the ground truth. As a result the
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
150

Figure 7: Top: North-East trajectory of the robot. Bottom:
North-Altitude trajectory of the robot. The red crosses show
the globally referenced landmarks used as ground truth and
the green crosses show the mean of their expected position.
Figure 8: Blue: Position difference from ground truth and
associated standard deviation for each landmark. Red: Dif-
ference in altitude from ground truth and associated stan-
dard deviation.
mean position difference to the ground truth is within
0.4 m over the whole trajectory. The mean difference
in altitude direction is within 0.17 m, due to modeling
the IMU based inclination constraints in the SLAM
(Eq. 6).
Fig. 8 shows the mean position difference to the
ground truth and associated standard deviation for
each single landmark. The landmarks are arranged
Figure 9: Polygon mesh of the cave, generated from a TSDF
voxel grid with a resolution of 5 cm. The cave diameter at
this section is approx. 4 m.
Figure 10: Path planning test in a simulated oversized park-
ing garage.
from ID 1 at the origin of the mission up to ID 11 at
the furthest area inside the cave. The diversity and
magnitude of deviations is due to the challenges in
the sphere detection. The amount of measurements to
compute the means and standard deviations variates
between 7 (ID 6) and 41 (ID 5, ID 11) with a mean of
24 observations per landmark. It can be seen that the
position difference is higher in the North/East direc-
tion since we are able to reduce the error in altitude
direction by modeling the inclination constraints.
Fig. 9 shows the polygon mesh generated from the
LiDAR measurements projected into a TSDF voxel
grid with a resolution of 5 cm.
3.2 Path Planning
We tested several simulated as well as real scenarios
to benchmark the path planner. All tests were done on
an Intel Core i7-6700 using all available cores. The
set of motion primitives used for all tests consists of
850 primitives. In order to reduce the friction of the
wheels and the chances of damage on the rough lava
tube surfaces, point turns where not included in the
motion primitives.
The multi level planning capability is first shown
in a simulated parking garage as the accessible part
of the cave on Tenerife does not have multiple le-
vels. The TravMap of the garage consists of 128478
patches covering 1284.78 m
2
at a grid resolution of
0.1 m while the TravMap of the cave consists of
59083 patches covering 590.83 m
2
.
Planning of a trajectory from lowest to the high-
est level of the garage as seen in Fig. 10 took 80.39 s
of CPU time or 40.13 s of real time. Fig. 11 rep-
resents a standard case: planning of a trajectory of
43.48 m length in the cave. Planning took 426.78 s
of CPU time and 65.88 s of real time. A more com-
plex case is shown in Fig. 12. Here the impact of
lots of obstacles can be observed. Two trajectories
were computed, the optimal solution took 2276.87 s
of CPU time or 343.6 s of real time while a subop-
timal solution was found in 102.21 s of CPU time or
Internal Simulation for Autonomous Robot Exploration of Lava Tubes
151
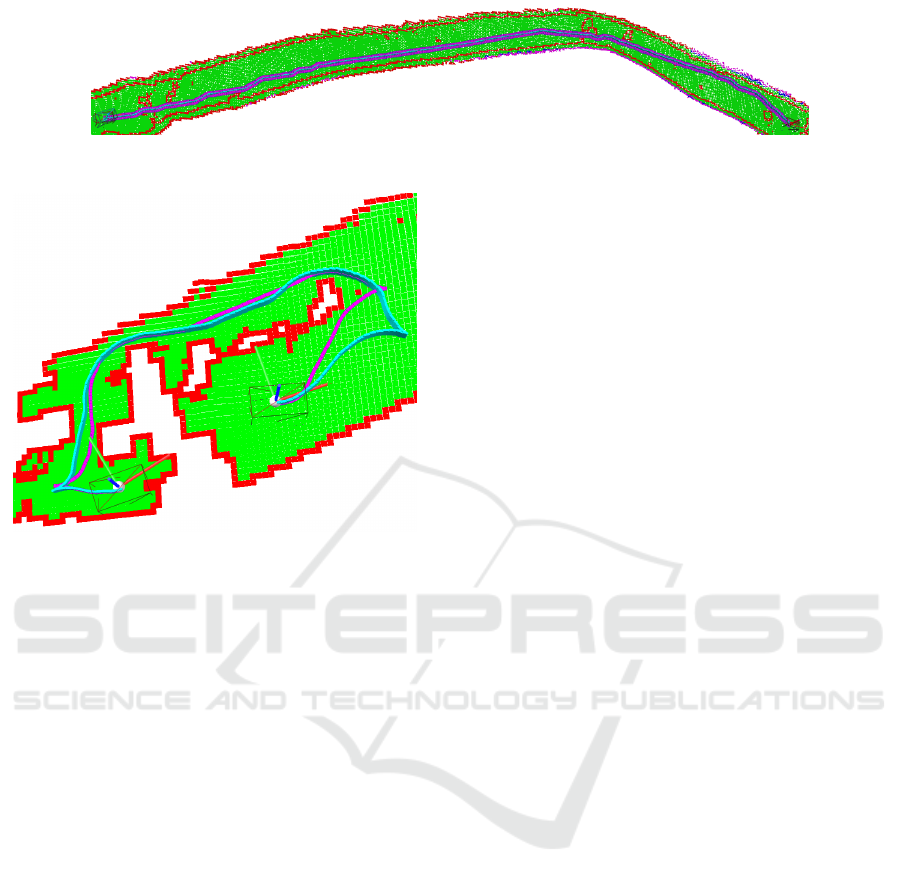
Figure 11: Planning a trajectory of 43.48m length in a cave.
Figure 12: Path planning test in the cave with a lot of ob-
stacles. The cyan trajectory is optimal, the magenta trajec-
tory is a suboptimal solution. The wireframe boxes show
the robot’s bounding box. The coordinate systems show the
start and end pose of the robot.
27.365 s of real time. The trajectories are 12.12 m and
11.62 m long respectively. This case especially shows
the value of using the ARA* algorithm, which can be
parametrized whether to decide to wait for the opti-
mal path or just use a suboptimal one to get on with
the task as soon as possible.
3.3 Internal Simulation
Among all the navigation experiments performed in
the cave, we have selected one trajectory to analyze
the accuracy of the internal simulation. The initial and
target position of the robot and the traversed paths are
shown in Fig. 13, along with the correspondent visu-
alization of the generated simulation. The path has
two sections, the first one is a straight trajectory and
the second a curve started after a direction change.
Our path planning has been configured to avoid point
turns in the rough surfaces of the lava tube. In other
surfaces, a point turn and a straight trajectory would
have been more efficient.
We analyzed the distance between the most accu-
rate estimation of the position that was available for
the robot and the positions in the simulated execu-
tion. The poses from the simulation are directly pro-
vided by the physical engine. While the estimation
of the real poses of robot were obtained offline after
an expensive ICP-based pose graph relaxation on the
collected pointclouds.
In order to analyze how different the real path and
the simulated path are, a distance function is defined.
The distance function must take into account the posi-
tions where the robot went as well as the time relative
to the beginning of the path traverse. We compare the
positions of the robot and the simulated robot at the
same time stamps relative to the time stamp when the
movement starts.
Fig. 14 shows the distances measured between
poses at same relative time stamps since the begin-
ning of the motion. The SLAM-based pose estima-
tion updates are less frequent than the simulation pose
updates. Thus, in order to apply the error estimation
function, first a sub-sampling of the pose samples of
the simulation was done.
In Fig. 15 the error is shown with respect to time.
The average of the Root Mean Squared Error (RMSE)
between simulated and real poses was 0.419 m for this
path execution. During the first section of the trajec-
tory execution, positions do not accumulate a large
error, but the error increases during the turn. Finally,
when both reach the end of the trajectory the error de-
creases again. One of the main causes of the error in
the second section of the trajectory is that the robot
reaches the goal position already at 14th second in
simulation while the real one takes 4 seconds more.
The delay in the real execution is caused by a lack of
accuracy in the surface friction model as well as in the
robot model (e.g. simulated motors).
Another insight that we found interesting when
analyzing the results is shown in Fig. 16. Due to
the lower frequency at which ICP can run on the sys-
tem with respect to the wheel odometry, errors in the
position estimation generated by the wheel odome-
try can be identified as spikes in the on-board pose
estimation. We have identified the possibility of cor-
recting online the pose estimation by using the poses
from the internal simulated path execution. Espe-
cially, if higher accuracy is achieved through better
parametrization and modeling of the simulation.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
152

(a) Internally simulated trajectory execution
(b) Trajectory performed by the real robot
Figure 13: The internal simulation (a) is produced from sensor data taken by the real robot. It can run on-board the system
and has been used for path execution validation before real execution (b) is done.
Figure 14: Measurement of the error between the two path
executions, points from the simulation path are sub-sampled
according to the time stamps at which the poses of the real
execution are available.
0 5 10 15
Time (s)
0.0
0.2
0.4
0.6
0.8
RMSE (m)
Figure 15: Error between real position estimation and sim-
ulated position during internal simulation and posterior ex-
ecution of the trajectory. Error increases during a turn and
because the final position is reached faster in the simulation.
3.4 Exploration
In Fig. 17 we show an example how the cave gets
explored successively. Targets near the current robot
pose are preferred, as long as they are expected to re-
sult in newly observed areas. We did not put much
effort into refining or optimizing the exploration be-
havior, as our ad-hoc implementation gave sufficient
results for our purposes.
Figure 16: The poses of the executed trajectory in simula-
tion and real execution are displayed together. In this case,
the simulation predicts a successful path execution.
4 CONCLUSIONS
A novel approach for safe autonomous exploration of
lava tubes in a space scenario composed of SLAM,
Internal Simulation, Path Planning and Exploration
modules has been described. This methodology is
based on a graph-SLAM. Models with associated un-
certainty for both planning (the MLS map) and Inter-
nal Simulation (an accurate polygon mesh) are gener-
ated on demand.
The experiment performed in the lava tube shows
an accuracy of position in average of 0.6 m. The
ground truth was calculated by identifying geo-
referenced markers and performing bundle adjust-
ment of the collected sensor data with the correct po-
sition of the markers.
The proposed Path Planning uses specific robot
motion primitives to efficiently search in the space
of solutions offered by the graph of connected
traversable patches which was generated from the
MLS map. The planner is different from previous
approaches since it only uses one path for the com-
plete traverse achieving successful results and it is
able to find solutions in environments with multi-
Internal Simulation for Autonomous Robot Exploration of Lava Tubes
153

Figure 17: Sequence of traversability maps, showing the exploration behavior
ple unstructured traversable surfaces. In the cave
experiments our path planning was able to provide
traversable paths of 12.12 m in highly unstructured
areas in 27.365 s. In areas of the tube with less ob-
stacles, planning of a long trajectory is achieved in
65.88 s for 43.48 m.
The first on-board robotic simulator which relies
on the environment representation of the robot to up-
date the simulated environment was presented. It is
used to accurately replicate the path planning and exe-
cution modules of the robot for validation of potential
goal poses. In the experimental section, a procedure
to analyze the error in the trajectory execution was
presented. The methodology is useful to better esti-
mate the prediction horizon in which the simulation
can be considered realistic. While error in the pre-
diction of straight trajectories is low, turns are more
difficult to predict accurately. Further executions of
the simulated and the real path executions are envi-
sioned to provide more statistical significant results
in the future. It has as well been identified that the
results of the simulated executions could be useful as
a correcting vector for the pose estimation.
The exploration behavior allows for the mapping
of unknown regions. It selects traversable goal poses
for which navigation from the current pose has been
predicted as successful by the internal simulator.
ACKNOWLEDGMENT
The presented work was developed in the Entern
project (grant No. 50RA1406, 50RA1407) which is
funded by the German Federal Ministry of Economics
and Technology (BMWi).
We greatly acknowledge Museos de Tenerife and
Cueva del Viento for giving us access to the lava tube
and for providing us with local support in many ways.
REFERENCES
Amanatides, J., Woo, A., et al. (1987). A fast voxel traversal
algorithm for ray tracing. In Eurographics, volume 87,
pages 3–10.
B. Rusu, R., Sundaresan, A., Morisset, B., Hauser,
K., Agrawal, M., Latombe, J., and Beetz, M.
(2009). Leaving flatland: Efficient real-time three-
dimensional perception and motion planning. J. Field
Robot., 26(10):841–862.
Chella, A. and Macaluso, I. (2009). The perception loop in
CiceRobot, a museum guide robot. Neurocomputing,
72(4-6):760–766.
Cohen, B. J., Chitta, S., and Likhachev, M. (2010). Search-
based planning for manipulation with motion prim-
itives. In 2010 IEEE International Conference on
Robotics and Automation, pages 2902–2908.
Curless, B. and Levoy, M. (1996). A volumetric method for
building complex models from range images. In Pro-
ceedings of the 23rd annual conference on Computer
graphics and interactive techniques, pages 303–312.
ACM.
Daga, A. W., Allen, C., Battler, M. M., Burke, J. D., Craw-
ford, I. A., L
´
eveill
´
e, R. J., Simon, S. B., and Tan, L. T.
(2009). Lunar and martian lava tube exploration as
part of an overall scientific survey. In Annual Meet-
ing of the Lunar Exploration Analysis Group, volume
1515, page 15.
Daily, M., Harris, J., Keirsey, D., Olin, D., Payton, D.,
Reiser, K., Rosenblatt, J., Tseng, D., and Wong, V.
(1988). Autonomous cross-country navigation with
the ALV. In [No source information available], vol-
ume 2, pages 718 – 726.
Dom
´
ınguez, R., Schwendner, J., and Kirchner, F. (2015).
On-board simulator for autonomy enhancement in
robotic space missions. In In Symposium on Advanced
Space Technologies in Robotics and Automation (AS-
TRA).
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: A paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Commun. ACM, 24(6):381–395.
Hertzberg, C., Wagner, R., Frese, U., and Schr
¨
oder, L.
(2013). Integrating generic sensor fusion algorithms
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
154

with sound state representations through encapsula-
tion of manifolds. Information Fusion, 14(1):57–77.
Hesslow, G. (2012). The current status of the simulation
theory of cognition. Brain research, 1428:71–9.
Hidalgo Carri
´
o, J., Arnold, S., B
¨
ockmann, A., Born, A.,
Dom
´
ınguez, R., Hennes, D., Hertzberg, C., Ma-
chowinski, J., Schwendner, J., Yoo, Y., and Kirchner,
F. (2016). EnviRe - environment representation for
long-term autonomy.
Howard, T. M. and Kelly, A. (2007). Optimal rough ter-
rain trajectory generation for wheeled mobile robots.
The International Journal of Robotics Research,
26(2):141–166.
K
¨
ummerle, R., Grisetti, G., Strasdat, H., Konolige, K.,
and Burgard, W. (2011). g
2
o: A general framework
for graph optimization. In Robotics and Automa-
tion (ICRA), 2011 IEEE International Conference on,
pages 3607–3613. IEEE.
K
¨
ummerle, R., Hahnel, D., Dolgov, D., Thrun, S., and Bur-
gard, W. (2009). Autonomous driving in a multi-level
parking structure. In 2009 IEEE International Confer-
ence on Robotics and Automation, pages 3395–3400.
Lacroix, S., Mallet, A., Bonnafous, D., Bauzil, G., Fleury,
S., Herrb, M., and Chatila, R. (2002). Autonomous
rover navigation on unknown terrains: Functions and
integration. The International Journal of Robotics Re-
search, 21(10-11):917–942.
Lee, J. et al. (2017). Flexible collision library.
https://github.com/flexible-collision-library/fcl.
Likhachev, M. et al. Search-based planning lab.
http://www.sbpl.net.
Likhachev, M., Gordon, G. J., and T., S. (2004). ARA*:
Anytime A* with provable bounds on sub-optimality.
In Thrun, S., Saul, L. K., and Sch
¨
olkopf, B., editors,
Advances in Neural Information Processing Systems
16, pages 767–774. MIT Press.
Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:
A high resolution 3d surface construction algorithm.
In ACM siggraph computer graphics, volume 21,
pages 163–169. ACM.
Marques, H. G. and Holland, O. (2009). Architectures
for functional imagination. Neurocomputing, 72(4-
6):743–759.
Nesnas, I. A. D., Matthews, J. B., Abad-Manterola, P., Bur-
dick, J. W., Edlund, J. A., Morrison, J. C., Peters,
R. D., Tanner, M. M., Miyake, R. N., Solish, B. S., and
Anderson, R. C. (2012). Axel and duaxel rovers for
the sustainable exploration of extreme terrains. Jour-
nal of Field Robotics, 29(4):663–685.
Newcombe, R. A., Izadi, S., Hilliges, O., Molyneaux, D.,
Kim, D., Davison, A. J., Kohi, P., Shotton, J., Hodges,
S., and Fitzgibbon, A. (2011). KinectFusion: Real-
time dense surface mapping and tracking. In Mixed
and augmented reality (ISMAR), 2011 10th IEEE in-
ternational symposium on, pages 127–136. IEEE.
Preston, L., Barber, S., and Grady, M. (2012). Concepts for
activities in the field of exploration (cafe). tn2: The
cataloge of planetary analogues.
Rekleitis, I., Bedwani, J., Dupuis, E., Lamarche, T., and Al-
lard, P. (2013). Autonomous over-the-horizon naviga-
tion using LIDAR data. Autonomous Robots, 34(1):1–
18.
Rockel, S., Klimentjew, D., Zhang, L., and Zhang, J.
(2014). An hyperreality imagination based reasoning
and evaluation system (HIRES). In 2014 IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pages 5705–5711.
Rockel, S., Kone
ˇ
cn
´
y,
ˇ
S.and Stock, S., Hertzberg, J., Pecora,
F., and Zhang, J. (2015). Integrating physics-based
prediction with semantic plan execution monitoring.
In 2015 IEEE/RSJ International Conference on Intel-
ligent Robots and Systems (IROS), pages 2883–2888.
Roßmann, J., Guiffo Kaigom, E., Atorf, L., Rast, M., Grin-
shpun, G., and Schlette, C. (2014). Mental models
for intelligent systems: eRobotics enables new ap-
proaches to simulation-based AI. KI - K
¨
unstliche In-
telligenz, 28(2):101–110.
Segal, A., Haehnel, D., and Thrun, S. (2009). Generalized-
ICP. In Robotics: Science and Systems, volume 2,
page 435.
Triebel, R., Pfaff, P., and Burgard, W. (2006). Multi-
level surface maps for outdoor terrain mapping and
loop closing. In Intelligent Robots and Systems, 2006
IEEE/RSJ International Conference on, pages 2276–
2282. IEEE.
Wynne, J. J. (2016). The scientific importance of caves in
our solar system: Highlights of the 2nd international
planetary caves conference, Flagstaff, Arizona. NSS
NewS, page 5.
Internal Simulation for Autonomous Robot Exploration of Lava Tubes
155
