
Forecasting the Class of Daily Clearness Index for PV Applications
Giuseppe Nunnari
Dipartimento di Ingegneria Elettrica, Elettronica e Informatica, Universit
´
a degli Studi di Catania,
Viale A. Doria, 6, 95125 Catania, Italy
Keywords:
Clearness Index, Hidden Markov Models, Neural Network Models, Naive-Bayes Models, Surrogate Models,
Persistent Model.
Abstract:
This paper deals with the problem of forecasting the class of the daily clearness index which can be relevant
for PV applications. A large number of solar stations, publicly available, was processed by using five different
approaches, namely, the feed-forward neural networks, the Hidden Markov models, the Naive-Bayes models,
the Surrogate models and the Persistent models. Experimental results show that one-day ahead forecasting of
the class of daily clearness can be reliable performed in a 2-class framework and with less accuracy in a 3-class
framework. Furthermore, for this purpose, the HMM approach is recommended among the considered ones.
The global performance of the class prediction models, evaluated by calculating the average confusion rate
(CR), showed that using HMM models provide C R ≤ 0.3 for 2-class clustering classes, while, for the 3-class
framework it rises to 0.35.
1 INTRODUCTION
Solar energy is a source of clean energy of ever in-
creasing interest, with the feature of being floating
at all-time scales. As the weight of the photovoltaic
plants (PV) becomes more consistent over the whole
electricity production grid, it is obvious that the prob-
lem of energy fluctuations becomes increasingly im-
portant for the purposes of the grid stability. The in-
termittent and stochastic character of solar radiation
has been studied for instance by (Notton and Voyant,
2018). A recent review paper who tries to identify-
ing methods that may be used to forecast PV power
fluctuations is given by (Barbieri et al., 2017). One of
the approaches to reduce the impact of fluctuations
is prediction. Indeed, this allows managers to bal-
ance the production of electrical energy by using con-
ventional sources (Antonanzas et al., 2016). A huge
literature referring with the problem of solar radia-
tion forecast, demonstrates that statistical approaches,
mainly of autoregressive kinds, are able to predict so-
lar energy at very-short term only, as clearly stated in
(Voyant et al., 2017). Indeed, in the very short time
domain, referred to as Now-casting (0 -3 h), the fore-
cast is usually based on extrapolations of real-time
measurements, while for Short-Term Forecasting (3
- 6 h), real-time measurements or satellite data are
coupled with Numerical Weather Prediction (NWP)
models.
A huge plethora of approaches for short-term predic-
tion of solar radiation time series have been proposed
which include, Artificial Neural Networks (ANN)
(Raza et al., 2018), Adaptive Neuro-Fuzzy Infer-
ence Systems (ANFIS) (Piri and Kisi, 2015), Par-
ticle Swarm Optimization and Evolutionary algo-
rithms (Nian et al., 2013), Generalized Autoregres-
sive with Conditional Heteroskedasticity (ARMA-
GARCH) models (Sun et al., 2015), Bayesian sta-
tistical models (Lauret et al., 2013), Fuzzy coupled
with Genetic Algorithms models (Kisi, 2014), just to
mention a few. Furthermore, statistical approaches
based on decomposition of the original time series
have been studied in (Prema and Rao, 2015). How-
ever, regardless of the considered approach, statistical
(autoregressive) models, since are based on the natu-
ral autocorrelation of measures performed at a point,
cannot reliably forecast the exact value of solar ra-
diation at daily scale, i.e. 1-day ahead. To partially
overcome this shortcoming, we propose in this paper
to modify the target of forecasting from true to class
values. In other words, we propose to associating to
the original solar radiation time series, a time series of
classes c(t), i.e. a sequence of integer values, which
will become the forecasting target. It is trivial to un-
derstand that this kind of forecasting problem is as
much hard as large is the number of classes associ-
172
Nunnari, G.
Forecasting the Class of Daily Clearness Index for PV Applications.
DOI: 10.5220/0006860801720179
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 172-179
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
ated to the original time series. For this reason, in this
paper we will consider clustering into 2 or 3 classes.
Furthermore, in order to avoid dealing directly with
the amount of solar radiation, we consider the clear-
ness index, a dimensionless measure of the solar radi-
ation at ground level, defined as (1).
k
t
=
I
t
I
clr
t
(1)
In expression (1), I
t
is the solar radiation irradiance
measured at ground level and I
clr
t
is the modeled clear
sky irradiance. Computing the clearness index, we fil-
ter the deterministic fluctuation of solar radiation due
to the natural Earth’s rotation and spinning, thus leav-
ing the random component generated by weather con-
ditions and in particular by the clouds cover. Among
several clear sky models proposed in literature to
compute the I
clr
t
term, we have considered the Ine-
ichen and Perez model for global horizontal irradi-
ance, as presented in (Ineichen and Perez, 2002) and
(Perez, 2002). The Matlab code that implement this
model was belongs to the SNL PVLib Toolbox, is-
sued by the Sandia National Labs PV Modeling Col-
laborative (PVMC) platform. This paper is organized
as follows. In section 2 we will report some results
concerning the analysis of daily k
t
time series with the
aim of showing that they represent a hard task for au-
toregressive models, since they are based on the nat-
ural autocorrelation. In section 3 we will give a brief
description of the machine learning approaches con-
sidered to perform forecasting. Section 4 is devoted
to describe numerical results and, finally, in section 5
we draw some conclusions.
2 ANALYSIS OF DAILY
CLEARNESS TIME SERIES
In order to objectively characterize the behavior of
daily k
t
time series, several analyzes were carried out
on a representative set of solar radiation recording sta-
tions.
2.1 Data and Sites
To make reproducible the results described in this pa-
per, public available data was considered. Indeed,
the data set consists of hourly average time series
recorded at hundreds stations stored in the National
Solar Radiation Database managed by the NREL (Na-
tional Renewable Energy Laboratory). Data of this
database was recorded from 1991 to 2005. It is rather
difficult to give a precise idea of the variability of this
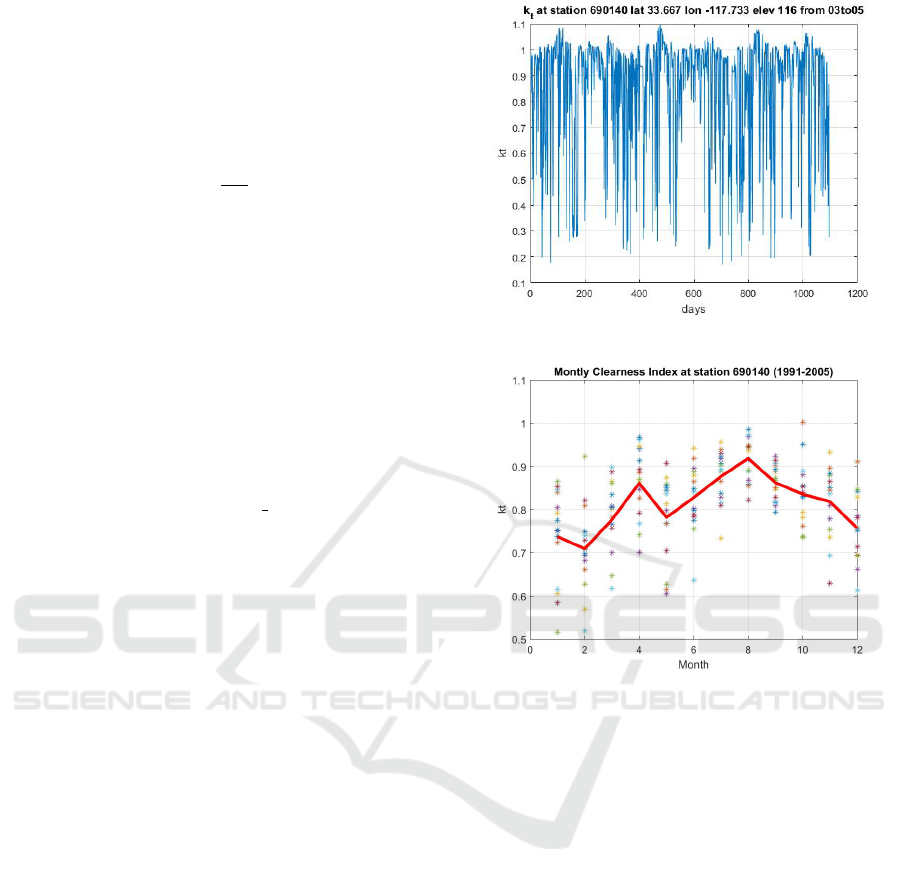
Figure 1: k
t
daily values computed at the station ID690140.
Figure 2: Fluctuations of the monthly k
t
index the station
ID690140 during 1991 to 2015.
type of time series as it depends very much on the ge-
ographical location, and particularly on the latitude.
However, just to familiarize, we report in Figure 1
daily values of k
t
measured at the station ID690140
from 2003 to 2005. It can be seen that there is a
high variability of this index at daily time scale, with
the feature that during summer months the range of
variability is lower with respect to the others months.
However, large k
t
fluctuations occurs from month to
month and for each month, as shown in Figure 2.
The dots represent the monthly k
t
values, averaged
for each month of the year from 1991 to 2005, while
the thick red curve is obtained averaging over each
month.
2.2 Slope of the k
t
Power Density
Spectrum
The absolute value of the slope of the power den-
sity spectrum, here indicated as β, is often considered
to characterize the long-term memory of a process.
For instance, a slope equal to zero indicates a white
Forecasting the Class of Daily Clearness Index for PV Applications
173
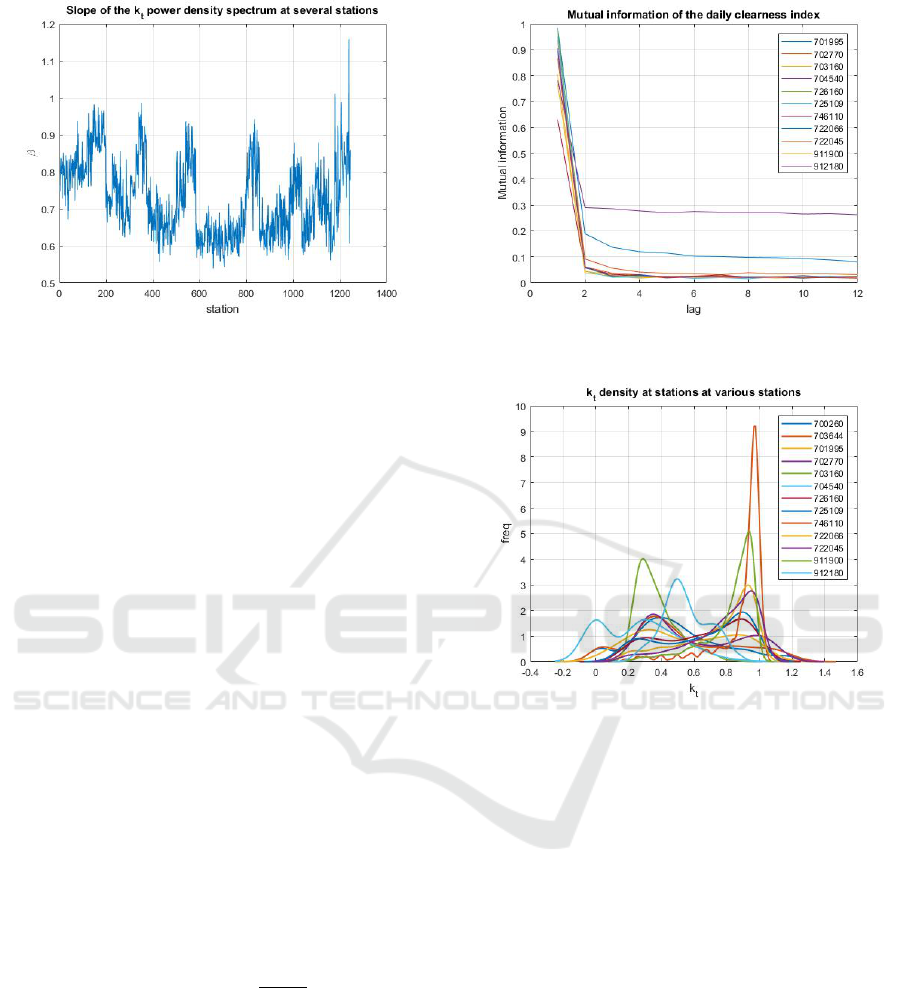
Figure 3: Slope of k
t
daily values power density spectrum
computed for several hundreds stations of the dataset.
noise, i.e. a completely uncorrelated time series, due
to the fact that its energy is equally distributed for all
frequencies and thus the power spectrum is flat. In-
stead, a random walk, i.e. a time series in which the
differences between consecutive samples is a white
noise, has β = 2. A slope ranging between β = 0.5
to β = 1.5 is a signature of the so-called 1/ f noise.
Long-memory processes have been observed in sev-
eral fields such as physics, biology, astrophysics, geo-
physics, and sociology, just to mention a few.
We have computed the slope of daily k
t
density spec-
trum for several hundred of stations, as shown in Fig-
ure 3. As it is possible to see, β ranges in [0.5,1.2],
with an average value of about 0.63, thus meaning that
daily k
t
time series can be classified as 1/ f noises.
2.3 Mutual information
Since, dealing with the traditional autocorrelation
function one of the shortcomings is that it is a linear
measure, in this paper, in order to capture the nonlin-
ear correlation of daily k
t
time series, we have com-
puted the so called mutual information I, defined as
(2).
I = −
∑
i, j
p
i j
(k)ln
p
i j
(k)
p
i
p
j
(2)
In this expression, for some partition of the time se-
ries range, p
i
is the probability to find a time series
values in the i
th
interval and p
i j
is the joint probabil-
ity that an observation falls in the i
th
interval and the
observation time k later falls into the j
th
interval.
The Mutual information computed for a selected
number of stations in a wide range of latitudes is
shown in Figure (4). It is possible to see, regard-
less the particular station, that it decays from 1 to
0.1 in approximately one lag, thus meaning that it is
Figure 4: Mutual information of k
t
daily values computed
for selected station operating in a wide range of latitudes.
Figure 5: k
t
densities at 12 station with different latitude in
the range lat ∈ [13.5670,70.2170]. The station in the top of
the legend has lat = 70.2170, while the one at the bottom
has latitude lat = 13.5670. The others station differs each
other about 5 degrees in terms of latitude.
rather difficult to reliably forecast the k
t
index, one-
day ahead, by using Auto-regression models only.
2.4 k
t
Probability Distribution Densities
Functions
The probability distribution densities function (pdf)
of daily k
t
is strictly depending on the geographical
coordinates of the measuring station and in particular
on the latitude, as shown in Figure 5. Roughly speak-
ing, it is possible to say that solar stations located at
high latitudes exhibit pdf density functions with peaks
at low k
t
value. Furthermore, stations with latitude in
a narrow interval, exhibits densities with peaks in a
narrow k
t
interval, as shown in Figure 6.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
174
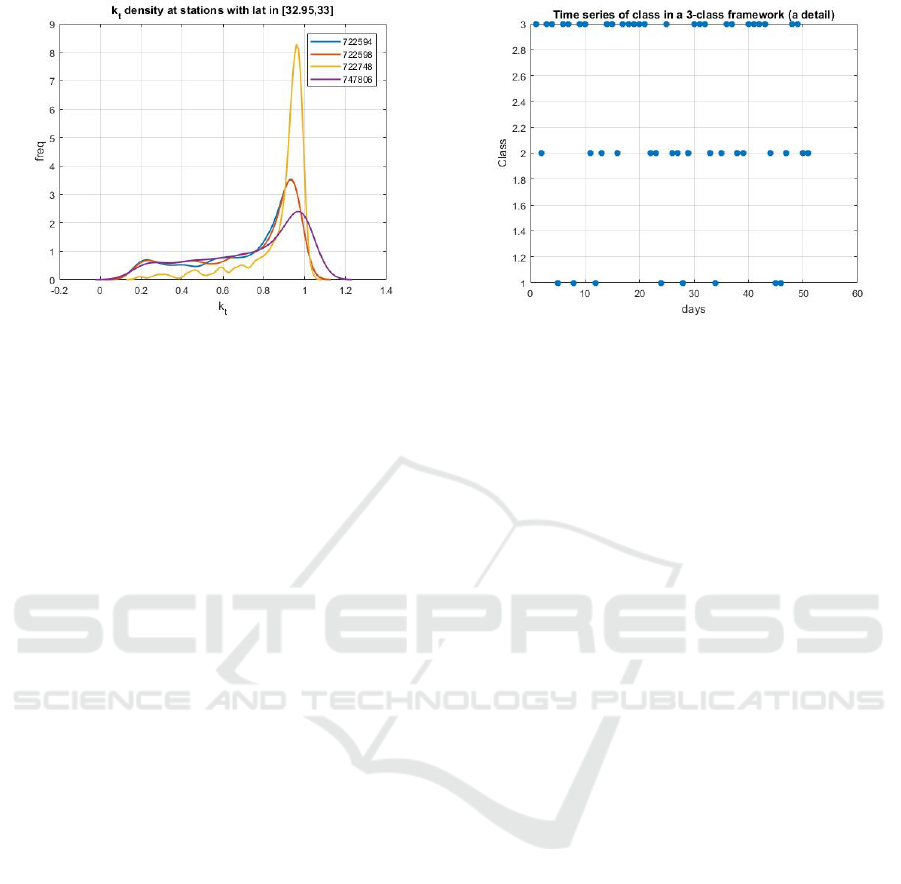
Figure 6: k
t
densities at four station with latitude in a narrow
range ∈ [32.95,33].
3 FORECASTING THE CLASS OF
DAILY CLEARNESS
Predicting the class of k
t
does require the replacement
of the original time series with an integer time se-
ries c(t), referred to as a time series of classes. Of
course, the prediction problem is as difficult as larger
the number of considered classes.
3.1 Associating a Time Series of Classes
to Daily Clearness
Among several criteria available to associate a time
series of classes to daily k
t
, we have considered in this
paper a simple threshold based approach. In more de-
tail we set a threshold equal to 0.70 for clustering into
two classes and the thresholds [0.6,0.8] when we in-
tend to cluster into three classes. These values were
experimental computed in order to roughly balance
the number of elements in each class. Probably, this
criterion is too simplistic for solar stations operating
in a wide range of latitudes. However, since this is a
preliminary study of and we aim to have a rough idea
of predictability of the k
t
class, we believe that this
choice is acceptable. Clustering into two and three
classes k
t
time series, will be referred in the paper as
2-class and 3-class framework, respectively. An ex-
ample of time series of the class in a 3-class frame-
work is shown in Figure 7.
3.2 Machine Learning Approaches
We have considered three popular machine learn-
ing approaches, namely the Hidden Markov Model
(HMM), the Non-linear Autoregressive (NAR) model
and the Naive Bayesian model (NBM) in order to
Figure 7: Time series of classes associated to k
t
daily time
series, recorded at the station 690140 (a detail).
solve the stated forecasting problem. Furthermore,
we have inter-compared the performances with two
different kinds of low reference models, namely the
persistent and the surrogate model. These models are
shortly described in the following sections.
3.3 Predicting the Class by using HMM
Models
A HMM (Rabiner, 1989) is a modeling approach in
which we observe a sequence of emissions, but we
do not know the sequence of states the model went
through to generate the emissions. Thus, in general
a HMM model is characterized by two matrices, re-
ferred to as the transition and the emission matrices,
respectively. In our schematization, we consider the
true time-series of classes c(t) associated to k
t
, as the
sequence of states and the sequence of classes ob-
served for tomorrow, i.e. c(t + 1), as the sequence
of emissions. Based on these assumptions, we train
a HMM model to forecast ˆc(t + 1). To transform
the transition and emission matrices, computed dur-
ing the training process, into the sequence of classes
ˆc(t + 1), we have considered the Viterbi algorithm
(Viterbi, 1967).
3.4 Predicting the Class by using NAR
Models
The NAR-based model consists of two main steps.
1. In the first step, one-day ahead k
t
predictions are
performed by using a non-linear regression model
of the form (3).
k
t
(t + 1) = f (k
t
(t), k
t
(t − 1),..., k
t
(t − (d − 1))
(3)
Forecasting the Class of Daily Clearness Index for PV Applications
175
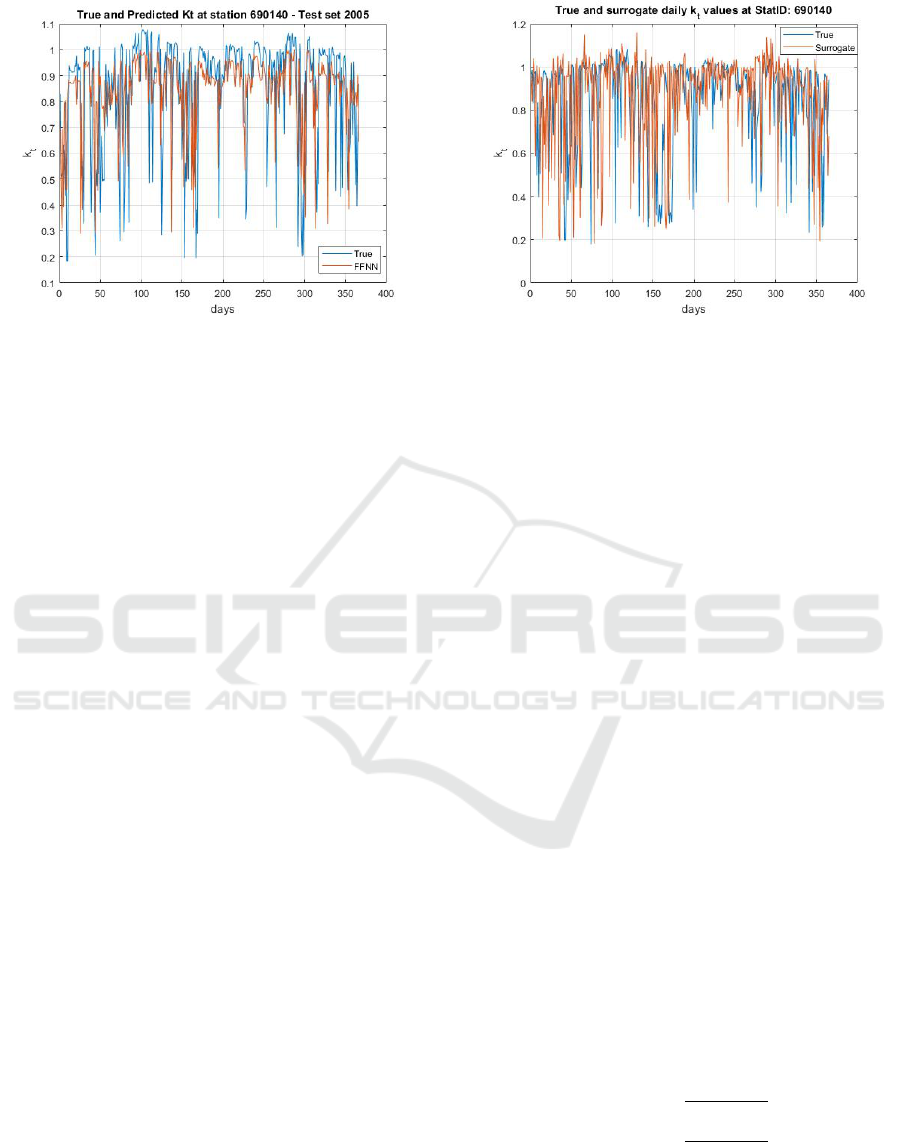
Figure 8: True-Predicted k
t
at the station 690140.
2. In the second step, the predicted class ˆc(t + 1) is
obtained by associating a class to the predicted
ˆ
k
t
(t + 1), as described in section 3.1.
In this paper, step 1 was performed by training a feed-
forward neural network (FFNN), to approximate the
unknown non linear function f . The number of delays
d in expression (3) was set to 2, due to the scarce auto-
correlation of the daily k
t
clearness index, as pointed
out in section 2.3. The FFNN was trained by using k
t
values, recorded during 2003-2014, while the test was
performed considering the year 2005. As an example,
the true and predicted values at the station ID690140
are shown in Figure 8. For all trials the number of
neurons of the FFNN in a unique hidden layer was set
to 20.
3.5 Predicting the Class by using Naive
Bayes Classifier
Naive Bayes classifiers are probabilistic classifiers
based on the Bayes theorem, with a strong (naive)
independence assumption between the features. In
more detail, indicating as f (x) a classifier that maps
the input features x ∈ X to the output class label
y ∈ {1,...,n
c
}, a Naive Bayes classifier is character-
ized by expression (4).
f (x) = ˆy(x) = argmax
y
p(y|x) (4)
where p(y|x) is the class posterior probability density
which is computed by applying the Bayes rule.
3.6 Predicting the Class by using Low
Level Reference Models
In this paper, we consider two low reference models
to predict the class of k
t
, namely the persistent model
and the surrogate models.
Figure 9: True and surrogate daily k
t
values at the station
690140.
3.6.1 The Persistent Model
The persistent model forecasts the class by using the
equation ˆc(t + 1) = c(t).
3.6.2 The Surrogate Model
With the term surrogate model we refer one which
generates
ˆ
k
t
(t) by using a kernel function trough the
following steps:
• let p
k
t
the probability density function (pdf) of k
t
computed by using a kernel function;
• generate a time series
ˆ
k
t
(t) of random number
having p
k
t
as pdf, which will be considered as
forecast;
• associate a time series of class to
ˆ
k
t
(t).
In this paper, in order to generate more realistic sur-
rogate time series, instead of using a unique p
k
t
pdf
function, we have identified, for each individual sta-
tion, 12 different functions, one for each month of the
year. An example of true and surrogate k
t
time series
is shown in Figure 9.
3.7 Performance Indices
In order to objectively asses to what extent a predicted
time series of classes is close to the true one, we have
considered the T PR (True Predicted Rate) and the
T NR (True Negative Rate), defined as follows:
T PR(i) =
T P(i)
T P(i)+FN(i)
(5)
T NR(i) =
T N(i)
T N(i)+FP(i)
(6)
where T P(i) and FN(i) is the number of true posi-
tive and false positive patterns, respectively, attributed
by the model to the class C
i
and i is the class in-
dex. The sum P(i) = T P(i) + FN(i) is, of course,
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
176
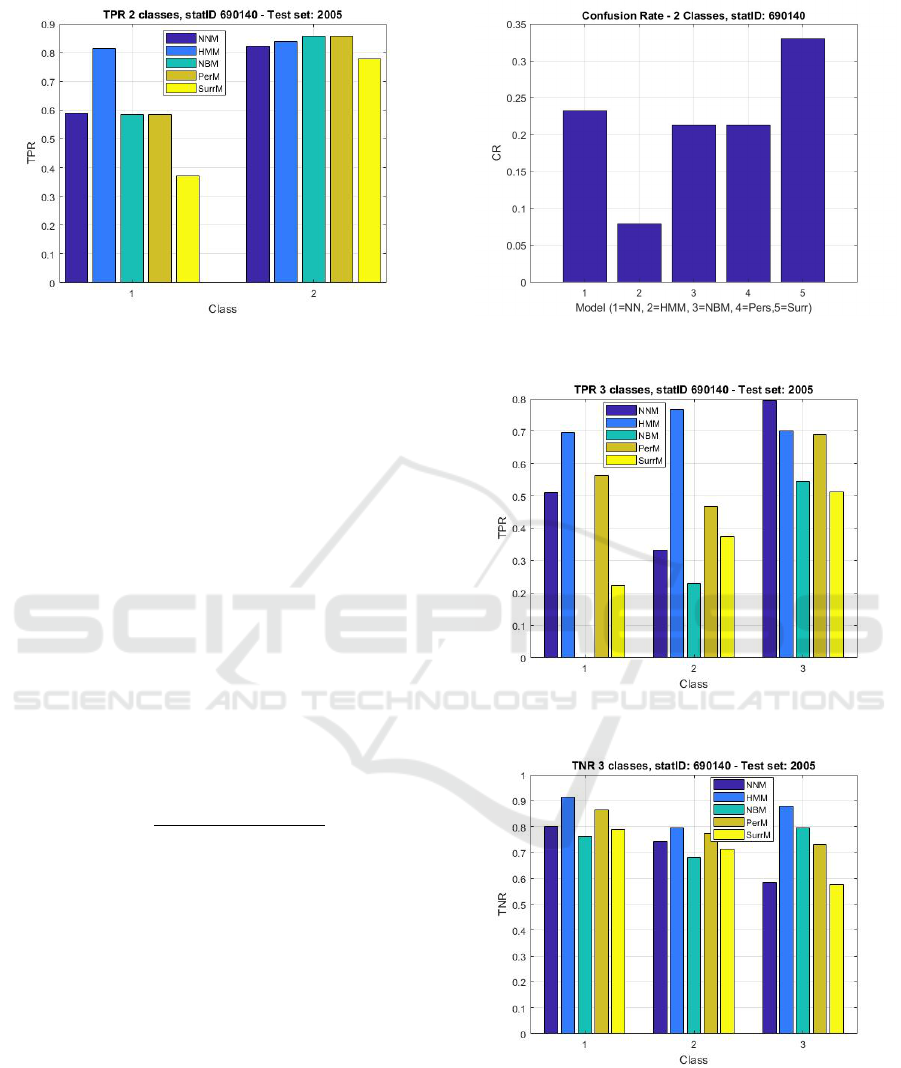
Figure 10: TPR for the 2-class framework at the station
ID690140.
the total number of patterns attributed by the model
to the class C
i
. Similarly, T N(i) is the number of pat-
terns which are correctly identified as not belonging
to the class C
i
and FP(i) is the number of false posi-
tives attributed by the model to the class C
i
. The sum
N(i) = T N(i) + FP(i) is the total number of patterns
recognized by the model as not belonging to the class
C
i
. Clearly, a good predictor would be characterized
by values of TPR and TNR both close to 1. Further-
more, it is to bearing in mind that for a 2-class frame-
work equations (7) hold.
T NR(1) = T PR(2) (7)
T NR(2) = T PR(1) (8)
As a global index, to measure the classifier perfor-
mances, we have computed the so-called confusion
rate index CR, defined as (9):
CR =
FP + FN
T P + T N + FP + FN
(9)
Of course CR ∈ [0,1] and lower values of c
r
are best.
4 NUMERICAL RESULTS
Results described in this section was obtained by us-
ing, for each station, time series, recorded from 2003
to 2005. Two years of data (2003 and 2004) was con-
sidered to identify the models, while the remaining for
the test. As an example, referring to a 2-class frame-
work, the performances of the five inter-compared
models, in terms of TPR and CR, are shown in Figure
10 and 11, respectively. As it is possible to see, the
HMM model outperform the others, since exhibits a
TPR better than 0.8 for both the classes and a confu-
sion rate better than 0.1. Similarly, clustering into
three classes, the performances of the inter-compared
Figure 11: CR for the 2-class framework at the station
ID690140.
Figure 12: TPR in a 3-class clustering at the station
ID690140.
Figure 13: TNR in a 3-class clustering at the station
ID690140.
approaches are shown in Figure 12,13 and 14 respec-
tively. As it is possible to see, even if the HMM
approach is not the best in terms of TPR for all the
classes, since for instance for the class C
3
the NNM
model outperform the others (Figure 12), it is the one
Forecasting the Class of Daily Clearness Index for PV Applications
177
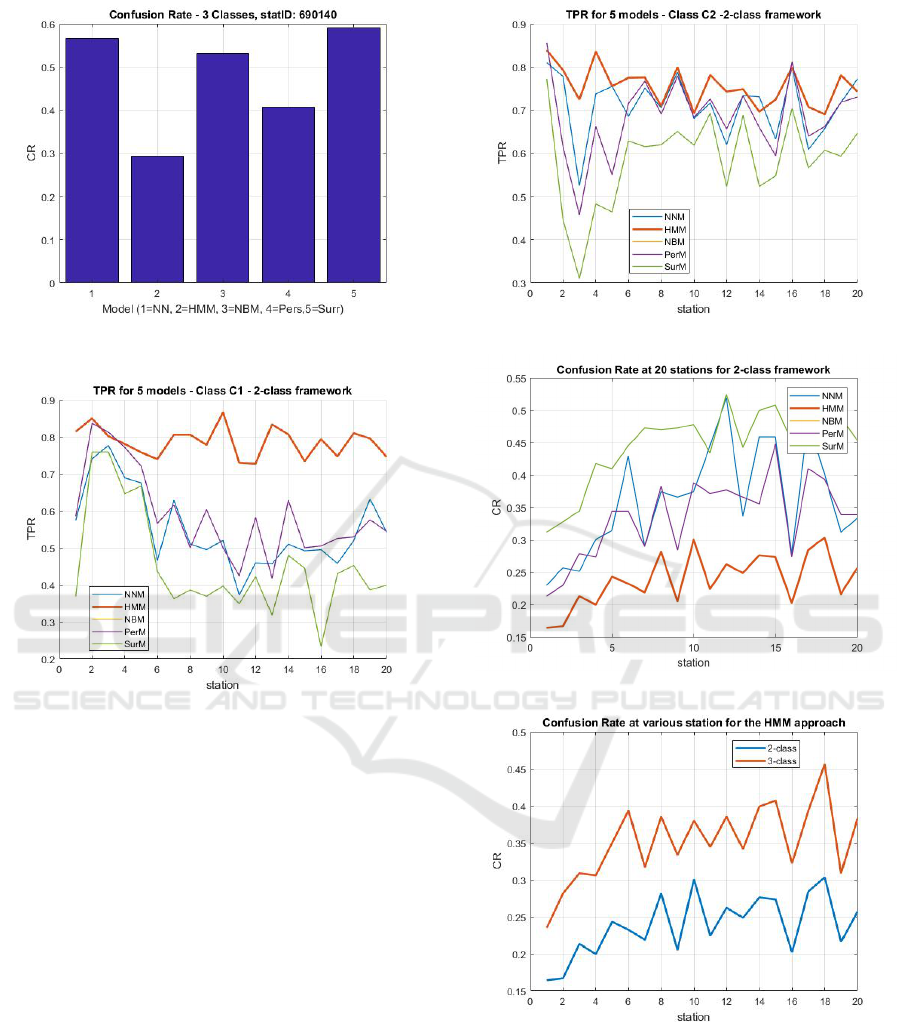
Figure 14: CR in a 3-class framework, at the station
ID690140.
Figure 15: TPR at 20 stations, for the class C1.
which exhibits the lowest CR, that, for this station, is
lower than 0.3 (see Figure 14).
As we are aware that results obtained for an indi-
vidual station do not allow to draw general conclu-
sions, we have repeated the calculations for several
stations of the NOAA database. In Figure 15, 16
and 17, we report the results, in terms of TPR and
CR, for 20 stations selected in a wide range of lati-
tudes, for a 2-class framework. To simplify the Fig-
ures, the selected stations are indicated by integers
from 1 to 20. As it is possible to see, the HMM
model exhibits, with rare exceptions, the best TPR,
as shown in Figure 15 and 16 for the classes C
1
and C
2
, respectively. Furthermore, the HMM ap-
proach exhibits the lowest CR (see Figure 17). In
more detail, for the 2-class framework, we have com-
puted, averaging among the 20 stations, that the mean
confusion rates are: 0.3607,0.2385,0.3350,0.3350,
and 0.44567 for the NNM, HMM, NBM, PerM and
SurM models, respectively. Thus, the HMM is the
best, among the five inter-compared models, in terms
of CR, while the SurM is the worst. As obvious,
Figure 16: TPR at 20 stations, for the class C2.
Figure 17: CR at 20 stations, for the 2-class framework.
Figure 18: CR comparison, for the 2-class and 3-class
frameworks, at 20 stations.
the CR increases when we try to forecast in a 3-
class framework, as shown in Figure 18. For the
3-class framework, we have computed, averaging
among the 20 stations, the following confusion rates:
0.5116,0.3515, 0.4820,0.4613, 0.5708, for the NNM,
HMM, NBM,PersM and SurrM, respectively. Thus,
it is confirmed that also in this case the HMM model
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
178

outperforms the others. However, as expected, the
mean confusion rate rises to 0.3515, while, as de-
scribed above, for the 2-class framework it is 0.2385.
5 CONCLUSIONS
This work was motivated by the awareness that one-
day ahead forecasting of k
t
time series cannot be re-
liably performed by using autoregressive models, due
to the lack of autocorrelation at daily scale, as pointed
out in section 2. To overcome this drawback, we tried
to perform 1-step ahead forecasting of the k
t
class.
To this purpose, we have implemented five different
forecasting models. One of them is still a nonlinear
autoregressive model (NNM), while two are proba-
bilistic (the HMM and the NMB). Finally, the two re-
maining are the well-known persistent model (PersM)
and the surrogate model (SurM), based on the genera-
tion of random sequences with predefined probability
density functions. Results, obtained processing time
series of a significant number of recording stations,
point out that forecasting 1-step ahead the class of
daily k
t
in a 2-class framework can be done with rel-
ative high accuracy. In other terms, we can forecast if
the daily k
t
for tomorrow, will be lower or higher than
the threshold value, that in this paper was assumed to
be equal to 0.70, for all the stations. For this purpose,
based on our experience, we recommend the HMM
approach which gives CR ≤ 0.3, for all the stations,
with an average value of about 0.25. Forecasting in
a 3-class framework is still possible but with lower
accuracy, since the CR is, on average, of about 0.35.
However, we believe that improvements are possible
by incorporating into the models some peculiar fea-
tures of the individual stations (e.g. the latitude), an
aspect that in this work has not been taken into ac-
count. Indeed, as we have seen in section 2.4, k
t
prob-
ability density functions are strictly related to latitude
and therefore a classification with fixed thresholds, as
done in this work, can not guarantee the best results.
Work is in progress to this end.
REFERENCES
Antonanzas, J., Osorio, N., Escobar, R., Urraca, R., de Pi-
son, F. M., and Antonanzas-Torres, F. (2016). Re-
view of photovoltaic power forecasting. Solar Energy,
136:78 – 111.
Barbieri, F., Rajakaruna, S., and Ghosh, A. (2017). Very
short-term photovoltaic power forecasting with cloud
modeling: A review. Renewable and Sustainable En-
ergy Reviews, 75:242 – 263.
Ineichen, P. and Perez, R. (2002). A new airmass inde-
pendent formulation for the linke turbidity coefficient.
Physica A, 73:151–157.
Kisi, O. (2014). Modeling solar radiation of mediterranean
region in turkey by using fuzzy genetic approach. En-
ergy Conversion and Management, 64:429–436.
Lauret, P., Boland, J., and Ridley, B. (2013). Bayesian sta-
tistical analysis applied to solar radiation modelling.
Renewable Energy, 49:124–127.
Nian, Z., Behera, P., and Williams, C. (2013). Solar ra-
diation prediction based on particle swarm optimiza-
tion and evolutionary algorithm using recurrent neu-
ral networks. IEEE International Systems Conference
(SysCon) 2013.
Notton, G. and Voyant, C. (2018). Chapter 3 - forecasting
of intermittent solar energy resource. In Yahyaoui, I.,
editor, Advances in Renewable Energies and Power
Technologies, pages 77 – 114. Elsevier.
Perez, R. (2002). A new operational model for satellite-
derived irradiances: Description and validation. Solar
Energy, 73:307–317.
Piri, J. and Kisi, O. (2015). Modelling solar radiation
reached to the earth using anfis, nn-arx, and empirical
models (case studies: Zahedan and bojnurd stations).
Journal of Atmospheric and Solar-Terrestrial Physics,
123:39–47.
Prema, V. and Rao, K. U. (2015). Development of statistical
time series models for solar power prediction. Renew-
able Energy, 83:100–109.
Rabiner, L. R. (1989). A tutorial on hidden markov models
and selected applications in speech recognition. Math-
ematics of Control, Signals, and Systems, 77:257–286.
Raza, M. Q., Mithulananthan, N., and Summerfield, A.
(2018). Solar output power forecast using an ensemble
framework with neural predictors and bayesian adap-
tive combination. Solar Energy, 166:226 – 241.
Sun, H., Yan, D., Zhao, N., and Zhou, J. (2015). Empirical
investigation on modeling solar radiation series with
armagarch models. Energy Conversion and Manage-
ment, 92:385–395.
Viterbi, A. J. (1967). Error bounds for convolutional codes
and an asymptotically optimum decoding algorithm.
IEEE Transactions on Information Theory, 13:260–
269.
Voyant, C., Notton, G., Kalogirou, S., Nivet, M., Paoli, C.,
Motte, F., and Fouilloy, A. (2017). Machine learning
methods for solar radiation forecasting - a review. Re-
newable Energy, 105:569–582.
Forecasting the Class of Daily Clearness Index for PV Applications
179
