Spatially Explicit Coupled Map Lattice Simulation of Malaria
Transmission in the Brazilian Amazon
Anthony E. Kiszewski
1
, Marcia Castro
2
and Sarah McGough
2
1
Natural and Applied Sciences, Bentley University, 175 Forest Street, Waltham, MA, U.S.A.
2
Harvard T.H. Chan School of Public Health, 677 Huntington Avenue, Boston, MA, U.S.A.
Keywords: Malaria, Mosquito, Cellular Automata, Coupled Map Lattice, Spatially Explicit, Individual-based.
Abstract: End stage malaria elimination efforts will require interventions against transmission that is sparse, cryptic and
spotty, situations suited for explicitly spatial simulation. A simulation of mosquito population dynamics and
Plasmodium vivax malaria transmission in the Brazilian Amazon is described combining techniques of
cellular automata and coupled map lattices. Within a 200x200 grid, 64 dispersed communities of 50
households each are represented with larval breeding sites following a random Gaussian distribution. Discrete
representation of individual humans allows examination of the effect of circulation and migration. Continuous
representation of mosquito abundance allows for more realistic scaling over space. Simulations (n=100) reach
equilibrium within 200 daily time steps. Adult mosquito populations range between 230-241,000 individuals.
An average parous rate of 56.5% for stable mosquito populations is consistent with values reported in local
field studies of the primary vector, Anopheles darlingi. Equilibrium prevalence of P. vivax infections averages
3% (1.8-3.9%) and is highly sensitive to treatment seeking behaviour of asymptomatics. This simulation
provides a stable platform that may be useful for investigating the role of human migration and asymptomatic
malaria in perpetuating transmission cycles in this region and interventions supporting malaria elimination
efforts.
1 INTRODUCTION
Plasmodium vivax is currently the dominant species
of malaria in the Brazilian Amazon (Barbosa et al.
2014). While less dangerous than P. falciparum,
infections cause recurrent attacks that impose
enormous impacts on the health and economic
potential of residents (Mendis et al. 2001).
Certain areas of the Amazon have reported
promising declines of both P. falciparum and P. vivax
transmission (Barbosa et al. 2014, Vitor-Silva et al.
2016), However, asymptomatic infections challenge
malaria elimination efforts because there is less
incentive to seek treatment in the absence of
symptoms. Asymptomatic infections can persist and
remain infectious for many months in the absence of
treatment (Tripura et al. 2016).
Anopheles darlingi is the dominant vector of
malaria in the Brazilian Amazon (Castro et al. 2006,
Pimenta et al. 2015). Anthropogenic changes to the
natural landscape have only increased its role in
maintaining malaria transmission cycles (Vittor et al.
2006, 2009) in settlement areas.
Local migration into, from and between (i.e.
circulation) Amazonian communities may serve to
disperse and perpetuate foci of transmission (Martens
and Hall 2000). Residents of Amazonia are highly
mobile, colonizing new areas and circulating on a
daily, seasonal and periodic basis within settled
communities in pursuit of labor and trade (Camargo
et al. 1994; McGreevy et al. 1989).
Such movements have the potential to perpetuate
malaria transmission by repopulating extinct foci
with new parasites from transmission ‘hot spots.’
Thus, these activities also pose a challenge to malaria
elimination efforts.
Individual-based models allow the study of
patchiness and non-random dispersal on the dynamics
of disease transmission (Auger et al. 2008, de Castro
et al. 2011), important factors where transmission is
low and locality-dependent. Thus, we developed an
explicitly spatial simulation that captures key features
of malaria transmission in this region including the
behavior of An. darlingi, human population
distribution and mobility, intraspecific competition
112
Kiszewski, A., Castro, M. and McGough, S.
Spatially Explicit Coupled Map Lattice Simulation of Malaria Transmission in the Brazilian Amazon.
DOI: 10.5220/0006862701120119
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 112-119
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

among larvae and the frequency of asymptomatic
carriage of infectious parasites.
We aimed to create a platform in which to explore
surveillance and intervention strategies to achieve
local elimination of malaria in South America, and to
assess the advantages of a hybrid automata/couple
map lattice approach.
2 METHODS
This simulation was encoded using the J functional
programming language (Jsoftware v. 8.06), a
platform optimized for matrix manipulations.
Simulations were executed on an ASUS Zenbook
laptop (16 GB RAM) running Windows 10.
We combined techniques used in cellular
automata and “coupled map lattices,” an “n”-
dimensional lattice where each site evolves in time
through a map (or recurrence equation) of the form:
X
t+1
= F(X
t
) (1)
X represents all values in the n-dimensional
lattice at time (t) and F(X) represents the set of
functions describing its transition over time. Time (t)
advances in discrete units of 12 hours. Each “k”
(overlay) dimension of the matrix X contains
information about the i,j (row, column) locations of
each variable, including larval mosquito stage, adult
feeding and gonotrophic state, and breeding site
characteristics. Dispersal of adult mosquitoes beyond
their i,j locations occurs over an 8 cell Von Neumann
neighbourhood.
Multiple superimposed and interacting matrices
were used to track variables representing larval
mosquito habitats, human households, and
mosquitoes and humans in various stages of malaria
infection. A hybrid numerical approach was
employed in which humans and disease states were
tracked as discrete integers while mosquito
population dynamics and dispersal were represented
by continuous values representing the number of
mosquitoes per location.
The simulation environment was modeled after
the perennial malaria transmission occurring in and
around Remansinho, a settlement project in southern
Amazonas State near the borders of Acre and
Rondonia. Each cell on the matrix represents an area
of about 100 m
2
for a total simulated area of 4 km
2
.
Bodies of water representing suitable larval
habitats are randomly and Gaussian distributed across
a 200x200 cell matrix. All are assumed to be of equal
depth and surface area and begin with equal nutrient
resources and cycling. For the purposes of the present
simulation such bodies are assumed to be permanent.
The primary mosquito vector, An. darlingi, is
adapted to breeding on the margins of rivers,
particularly in seasons when rivers flood. It has also
been associated with anthropogenic environmental
changes, breeding behind impoundments caused by
road construction through wetland environments
(Rufalco-Moutinho et al. 2016).
Climatic variability is not explicitly depicted.
Thus, temperatures are held constant using the
average temperature at the end of rainy season in
Remansinho (26
o
C www.worldclim.org).
2.1 Human Population
Aerial photos provided a template for the simulation’s
depiction of settlement density. Patterns derived were
used to create a basic unit representing a community
of 50 households along a roadway. These tiles were
tessellated evenly across the matrix, creating a total
of 64 identical ‘communities’ for a total of 3,200
households. Initial household sizes and births
correspond to survey data collected near Remansinho
but constrained to a maximum of eight permanent
residents per household. The maximum population
supported by this layout is thus 25,600 people.
Migration and circulation is simulated by shifting
people between communities. Out-migration and
returns occur on a stochastic basis with outcomes
determined by lottery draw from a uniform
distribution. People who leave a particular household
always return to the same household, although the
duration of their absence can vary. Up to two
household members can be absent at any given time.
Visitors to households are not constrained by the
eight member per household limitation.
2.2 Mosquito Population
2.2.1 Adults
Anopheles darlingi is the sole mosquito vector
species considered in these simulations. Separate
matrices of continuous variables track adult
mosquitoes by stage of gonotrophic cycle (host-
seeking, bloodfed, gravid, ovipositing) and day of
extrinsic incubation, if infected.
Dispersal is weighted towards households when
mosquitoes are in a host-seeking state and towards
larval habitats when they are gravid. Dispersal in the
absence of environmental cues occurs evenly to all
adjoining sites on the matrix. Bloodfed, resting
mosquitoes do not disperse (Hiwat and Bretas 2011).
Spatially Explicit Coupled Map Lattice Simulation of Malaria Transmission in the Brazilian Amazon
113

2.2.2 Subadult Mosquitoes
Larvae only occur on sites where suitable habitats are
present, as indicated by a reference matrix depicting
the locations of such habitats (Figure 1). Oviparous
mosquitoes deposit ova only in such sites.
Figure 1: Distribution of larval mosquito habitats. Bodies
of water (white) supporting mosquito larvae are distributed
randomly via a Gaussian algorithm to 20% of grid sites.
Separate state matrices track larval stages or ‘instars’
by stage of development. Daily mortality rates
derived from life table data (Araujo et al. 2012) are
specific to instar. Larval population dynamics are
constrained by density-dependent intraspecific
interactions (Klomp 1964). Carrying capacity is
dynamic and emergent, deriving from nutrient
limitations in larval habitats.
When nutrients are not limiting, larvae advance in
the optimal period expected at 26
o
C for An. darlingi,
approximately 12 days on average (Bergo et al.
1990). When nutrients are lacking, larval
development is delayed until nutrients become
available (Bar-Zeev 1957, Araújo et al. 2012).
Nutritional content of larval habitats is assumed to
fluctuate in response to utilization by larvae, inflow
from external sources as well as internal inputs
resulting from microbial decomposition or algal
photosynthesis. Each day, there is also a negative
nutrient flux independent of mosquito larval activity
related to uptake by other organisms, sedimentation,
decay or other factors.
Mosquito larvae compete for nutrients with a
precedence favoring older instars. Heuristically, but
based on larval studies (Dahl et al. 1993), 30% of the
available nutriment is assumed to consumed non-
competitively at the rate of 2, 4, 8 and 16% for first
through fourth larval instars respectively. The
remaining nutritive content of the site is then obtained
competitively with priority given to older instars.
2.3 Malaria Transmission
2.3.1 Mosquito to Human
Daily transmission of malaria from mosquitoes to
humans is a function of the number of infected
mosquitoes a person is likely to contact within a
twenty-four hour period. Specifically, the probability
of a person acquiring a malaria infection each day is
governed by the expression:
P
inf(h)
= 1 – (1-i
m
)
nba
(2)
where: i
m
= probability that a single infectious
mosquito bite triggers a patent malaria
infection in a person.
n = number of infectious mosquitoes per
person in a given household.
b = biting success (daily probability that an
infectious mosquito is successful in
obtaining a blood meal from hosts in its
vicinity).
a = anthropophagy (the probability that an
infectious mosquito obtains a blood meal
from a person and not an animal).
Humans are handled as discrete and individual
entities in this simulation with integers representing
infection states. P
inf(h)
is used to determine the
probability of a state transition from uninfected to
infected. This transition is thus executed for only
those individuals for which a random number from a
uniform distribution between 0 and 1 is less than or
equal to the probability of infection. Thereafter,
infections states for each household member change
on a daily basis to represent advancing prepatency.
Risk of acquiring malaria infections is assumed to
be independent of age, as is typical in areas with
seasonal malaria transmission and moderate
prevalence rates (Hay et al. 2004).
2.3.2 Human to Mosquito
The proportion of mosquitoes in a given site
acquiring a malaria infection each day is governed by
the expression:
P
inf(m)
= i
h
pba (3)
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
114

where: i
h
= probability that a mosquito feeding on
an infectious human becomes infected.
p = proportion of humans in a site infectious
with malaria.
b = biting success (daily probability that a
mosquito is successful in obtaining a blood
meal).
a = anthropophagy (the probability that an
infectious mosquito obtains a blood meal
from a person and not an animal).
We assume that all humans bearing patent malaria
infections are equally infectious to mosquitoes and
that asymptomatic infections remain asymptomatic.
Using Moshkovsky’s formula for extrinsic
incubation of P. vivax malaria parasites (Detinova
1962), we assume that infected mosquitoes exposed
to an average ambient outdoor temperature of 26
o
C
would require about 9.13 days (E = 105/T-14.5) to
become infectious.
2.3.3 Intrinsic Incubation
Humans are assigned a discrete integer state
corresponding to their malaria infection status, with 1
representing uninfected individuals, 2-15
representing each day of prepatency for infected
individuals, 16 representing those presenting with
clinical symptoms and 17 representing asymptomatic
individuals. All patent infections are assumed to be
infectious to vectors.
Loss of infection can occur with or without
treatment with infected individuals returning to their
initial state. For this hypoendemic situation, we do
not assume the presence of sufficient immunity to
alter the probability of re-infection. The current
simulation also does not account for superinfection by
parasites in differing developmental stages.
2.4 Sensitivity Analyses
Model parameters, whenever possible, were extracted
from literature appropriate to the area targeted in the
simulation or drawn directly from survey data (Table
1). Simulations using random sets of all input
variables were used to explore the parameter space
and determine the range of outcomes possible,
including human, mosquito and parasite population
dynamics and infection rates. Scatter plots were
generated to track the effect of diverse sets of
randomly sampled model input distributions on each
output variable.
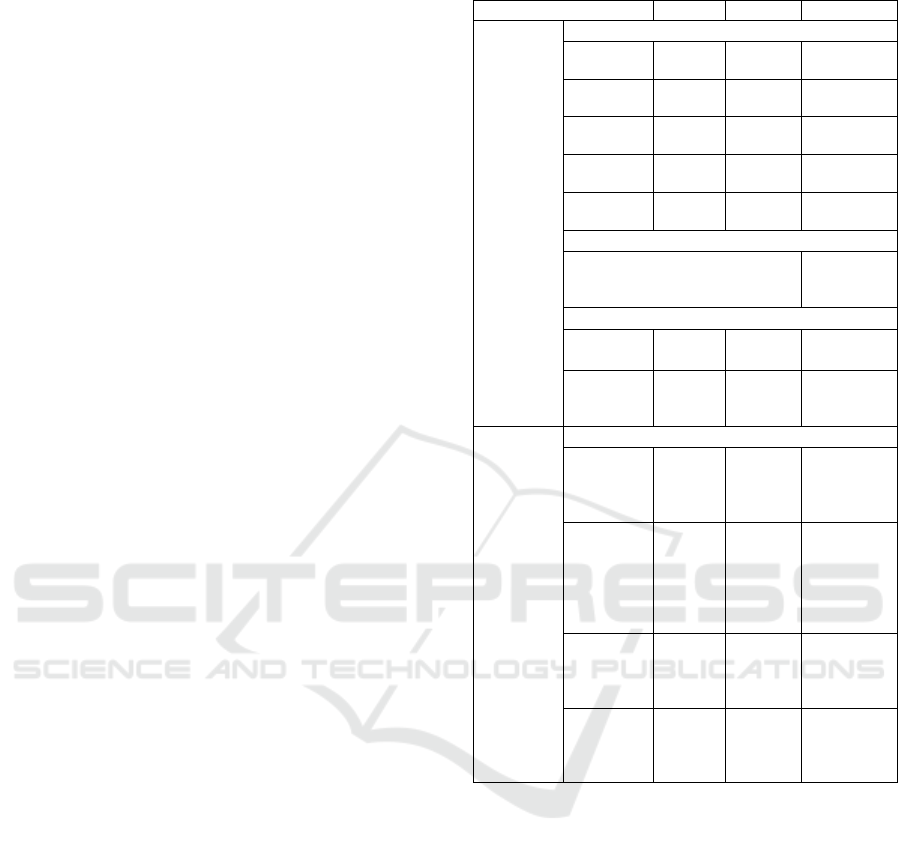
Table 1: Baseline Parameter Assumptions and Sources.
Parameter Value Range Source
Mosquito Immature Survival Rate (daily)
1
s
t
instar 0.80 0.75-
0.85
Araujo et
al. 2012
2
nd
instar 0.90 0.85-
0.95
“
3
rd
instar 0.92 0.85-
0.95
“
4
th
instar 0.95 0.92-
0.98
“
Pupae 0.95 0.92-
0.98
“
Immature Development Period
12 days Gu and
Novak
2006
Mosquito Infection – Extrinsic Incubation
P. vivax 10
days
9-11
days
Paaijmans
et al. 2009
Human
Blood
Index
0.458 0.40-
0.50
Kiszewski
et al. 2004
Trans-
mission
Prob. of
trans. to
human
0.05-
0.13
Krafsur
and
Armstrong
1978
Prob. of
trans. to
mosquito
0.1-0.6 Muirhead-
Thomson
1954,
1957;
Rutledge et
al. 1969
Intrinsic
Incub.
Period
9-12
days
Molineaux
and
Gramiccia
1980
Infectious
period (no
treatment)
18
mos.
12-24
months
Bloland
and
Williams
2002
Elimination did not occur within the range of
natural conditions without external forcing or
intervention. Elimination of parasite populations
occurred in some runs when treatment rates of
asymptomatic carriers were equal or greater than
symptomatics. No parameter sets led to outcomes that
could not be explained by natural interactions. Adult
mosquito survival rate and treatment rate among
asymptomatic humans had the strongest effect on
equilibrium prevalence of infection in humans and
mosquitoes, while variables affecting larval
abundance had the least impact.
3 RESULTS
Parameters selected within reported ranges of natural
values (Table 1) delivered plausible outcomes.
Spatially Explicit Coupled Map Lattice Simulation of Malaria Transmission in the Brazilian Amazon
115

Multiple runs (n=100) showed variable but stable
results between simulations without extreme
variation (Table 2).
Table 2: Mean equilibrium values for primary
outcome variables using default parameters. (n =
100, 1,000 time steps).
Variable Mean/ 95%
CI.
SD Min Max
Human
population
9,416.8
(9402.2,
9431.4)
73.4 9,259 9,593
No. People
infected
279.35
(271.02,
287.68)
41.98 170 365
%
Prevalence
2.97 (2.88,
3.06)
0.45 1.82 3.89
Asympt.
Infections
236.66
(229.68,
243.64)
35.19 143 313
% Asympt. 93.06
(92.76,
93.37)
1.55 89 96
Subadult
Mosquitoe
s (x 10
7
)
1.64 (1.64-
1.65)
0.03 1.58 1.71
Adult
Mosquitoe
s
230,451
(229,595,
231,306)
4,310 220,524 241,256
Infected
Mosquitoe
s
1,394.7
(1,348.6,
1,440.8)
232.2 789 2018.3
Sporozoite
Rate
0.61 (0.59,
0.62)
0.1 0.34 0.88
% Parous 56.51
(56.42,
56.61)
0.48 55.46 57.82
The total population of humans in this simulation
reaches about 9,417 on average, with a minimum of
9,259 and a maximum of 9,593. Adult mosquitoes
reach a mean population size of 230,451 (with a range
of 220,524 to 241,256). These values correspond to a
mosquito/human ratio of about 24:1.
Most outcome variables reach equilibrium in
about 400 time steps. Point prevalence of malaria
infection settles at about 3% on average. Other
measures of transmission stability independent of
infection, such as parous rate, reach equilibrium more
quickly, achieving stable oscillations in about 200
time steps.
Baseline parameters produced lower prevalence
(3%) than reported for P. vivax for Amazonia as a
whole (5.3%) and Rondonia in particular (4.9%,
Arruda et al. 2007), and significantly less than that
reported at Remansinho (9.1%, Barbosa et al. 2014).
An alternative set of parameters employing a
slightly different treatment rate in asymptomatic
humans (0.25% treatment probability per day vs.
0.5%) brought equilibrium prevalence into these
observed ranges (6.2%) while keeping vector
sporozoite rates below 1%.
The number of infected mosquitoes at equilibrium
(Table 2) averages about 1,394 (789-2,018). As one
might expect, there was a strong correlation between
infected mosquitoes and infected humans (R = 0.904,
P<0.001). Abundance of subadult mosquitoes was not
significantly correlated with human malaria
infections (R = 0.19, P=0.059) unlike adult mosquito
abundance (R = 0.26, P=0.008).
Mosquito parous rates do not reach equilibrium,
but rather oscillate stably around a mean of about
54.6% even in runs in excess of one thousand time
steps. This value for parity is slightly higher than the
range observed in natural, stable populations of An.
darlingi (Moreno et al. 2007; Rubio-Palis et al. 2013).
Parity in wild mosquito populations tend to be
observed below 50% except during seasons when
populations are growing after a seasonal interruption.
4 CONCLUSIONS
The baseline parameters of this simulation deliver
outcomes for both human and mosquito malaria
infection dynamics comparable to those observed
within the study areas we are attempting to simulate.
The age structure of mosquito vector populations
as indicated by parous rate is a critical determinant of
vectorial capacity and a sensitive indicator of the
efficacy of anti-vector interventions. Our baseline
value of 56.5% is slightly elevated over empirical
observations of An. darlingi in the region (Moreno et
al. 2007, de Barros et al. 2011). Baseline sporozoite
rates of less than 1% are also consistent with local
observations (Hiwat and Bretas 2011).
While the simulated prevalence rate for P. vivax
malaria infection was significantly less than what was
recently reported from the targeted study area at
Remasinho in southern Amazonas, prevalence values
can differ widely between localities and seasons.
Significant shifts in prevalence have been observed
even in the same areas over the course of a few years
(Barbosa et al. 2014). Modest changes in treatment
rate among asymptomatic people led to simulated
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
116

Figure 2: Distribution of households and malaria cases.
Light blue represents households without malaria. Other
colors (green to red) indicate the presence of malaria in at
least one household member.
prevalence rates within the ranges reported in
surveys.
Malaria surveys in Amazonia suggest that
asymptomatic malaria infections far outnumber
symptomatic infections. While the ratio of
symptomatic to asymptomatic infections produced by
this simulation conforms to these observations, the
ratio we produced (5.54 asymptomatic for every
symptomatic person) is close to the 4-5X range
observed in some empirical studies (Alves et al.
2002).
Prevalence of parasites in humans and vectors was
highly sensitive to the presence of asymptomatic
infections. Such cases may be a critical target for
elimination campaigns because their presence helps
perpetuate transmission and asymptomatic
individuals may be less likely to self-report infections
and seek treatment than those experiencing acute
symptoms of malaria. Active surveillance will be
required to identify these cases.
Other individual or agent-based models have been
successful at reproducing the spatial dynamics of
malaria transmission (Bomblies et al. 2008, Gu and
Novak 2009, Zhou et al. 2010, Eckhoff 2011, Zhu et
al. 2015, Pizzitutti et al. 2015) including some aspects
of human mobility (Zhu et al. 2015, Pizzitutti et al.
2018). The model presented here is distinct from most
prior efforts in its detailed simulation of larval
population dynamics. With few exceptions (Bomblies
et al. 2009), most simulations impose carrying
capacity by increasing mortality or limiting
oviposition in crowded habitats. The present model
allows carrying capacity and larval development rate
to fluctuate in response to crowding. Thus, it captures
the paradoxical effect of enhanced pupal productivity
after ‘thinning’ by insecticidal interventions
(Agudelo-Silva and Spielman et al. 1984), and is thus
well suited for evaluating the impacts of anti-larval
interventions. The mechanism for regulating
mosquito population growth in this simulation was
based on the concept of niche partitioning (Gilbert et
al. 2008) via intraspecific nutrient selectivity by
larval instars (Klomp 1964, Merritt 1987, Dahl et al.
1993).
The current model also allows depiction of
circulation of people to other communities with
overnight stays of variable length with return to their
original households. Prior efforts (Pizzitutti et al.
2018) simulate diurnal activities with daily return to
households of origin. Thus, the influence of
temporary migration in creating new hot-spots and
perpetuating malaria transmission in the face of
elimination campaigns can be assessed. The present
model also depicts differences in treatment-seeking
behavior in symptomatic and asymptomatic humans
which can further facilitate perpetuation of malaria.
One drawback of our modeling approach as
currently formulated is its inflexibility with regards to
simulating climatic variability. Scenarios exploring
climatic changes are possible with this technique, but
require alternative versions to the code for a particular
set of climatic conditions. Because time is discrete
and variables representing infection status represent
specific days of incubation, any changes in extrinsic
incubation period requires changes in the code to
provide additional or fewer classes of incubation
states. As such, the current model is best applied to
shorter time scales where climatic conditions remain
stable.
Other refinements of this model might include
allowing vectors multiple chances to feed over the
course of a single gonotrophic cycle. Such feeding
behavior has been observed with An. darlingi in
natural situations (de Oliveira et al. 2012). The
authors of this work even observed some mosquitoes
feeding more than once in the course of a single day.
Thus, the present study suggests that our
simulation approach provides a stable and relatively
realistic platform for evaluations of malaria
interventions. We hope in particular to exploit the
features of the current model to explore strategies
designed to eliminate transmission in hypo- and
mesoendemic areas, including practices not generally
undertaken or recommended where transmission is
hyperendemic.
Spatially Explicit Coupled Map Lattice Simulation of Malaria Transmission in the Brazilian Amazon
117

Upon incorporating the refinements suggested by
these preliminary evaluations, the simulation will be
applied to several contrasting intervention scenarios.
These will include larval source reductions as part of
a broader strategy of integrated vector management
and mass drug administration in communities. We
also hope to explore in detail the role of human
migration and asymptomatic malaria in perpetuating
transmission cycles in this region towards
maximizing the impact of malaria elimination efforts.
ACKNOWLEDGEMENTS
We thank Dr. Susana Barbosa of the Department of
Parasitology, Institute of Biomedical Sciences,
University of São Paulo, São Paulo, Brazil for her
helpful consultations in developing this model.
REFERENCES
Agudelo-Silva F, Spielman A. 1984. Paradoxical effects of
simulated larviciding on production of adult
mosquitoes. Am J Trop Med Hyg. 33:1267-1269.
Alves FP, Durlacher RR, Menezes MJ, Krieger H, Pereira
da Silva L. 2002. High prevalence of asymptomatic
Plasmodium vivax and Plasmodium falciparum
infections in native Amazonian populations. Am J Trop
Med Hyg. 66:641–648.
Araujo M, Gil L, Silva A. 2012. Larval food quality affects
development time, survival and adult biological traits
that influence the vectorial capacity of Anopheles
darlingi under laboratory conditions. Malaria J. 11:261.
doi:10.1186/1475-2875-11-261.
Arruda ME, Zimmerman RH, Souza RMC, Oliveira-
Ferreira, J. 2007. Prevalence and level of antibodies to
the circumsporozoite protein of human malaria
parasites in five states of the Amazon region of Brazil.
Memórias do Instituto Oswaldo Cruz, 102:367-372.
Auger P, Kouokam E, Sallet G, Tchuente M, Tsanou B.
2008. The Ross-MacDonald model in a patchy
environment. Mathem. Biosci. 216:1232-12131.
Bar-Zeev M. 1957. The effect of density on the larvae of a
mosquito and its influence on fecundity. Bull Res
Council Israel, Sec B. 6:220-228.
Barbosa S, Gozze AB, Lima NF, Batista CL, da Silva
Bastos M, Nicolete VC, Fontoura PS et al. 2014.
Epidemiology of disappearing Plasmodium vivax
malaria: a case study in rural Amazonia. PLoS NTDs.
8:e3109.
Bergo, Eduardo Sterlino, Buralli, Geraldo Magela, Santos,
Jair Licio Ferreira, & Gurgel, Sergio Mello. (1990).
Avaliação do desenvolvimento larval de Anopheles
darlingi criado em laboratório sob diferentes dietas.
Revista de Saúde Pública, 24(2), 95-100.
Bloland PB, Williams HA. 2002. Malaria control during
mass population movements and natural disasters:
Committee on Population (CPOP). National Academies
Press. 184 pp.
Bomblies A, Duchemin J-B, Eltahir EAB. 2009. A
mechanistic approach for accurate simulation of village
scale malaria transmission. Malaria J. 8:223.
doi:10.1186/1475-2875-8-223.
Camargo LMA, Ferreira MU, Krieger H, De Camargo EP,
Da Silva LP. 1994. Unstable hypoendemic malaria in
Rondonia (Western Amazon region, Brazil): epidemic
outbreaks and work-associated incidence in an agro-
industrial rural settlement. Am J Trop Med Hyg. 51:16-
25.
Castro MC, Monte-Mór RL, Sawyer DO, Singer, BH. 2006.
Malaria risk on the Amazon Frontier. PNAS. 103: 2452-
2457.
Charlwood JD, Alecrim WA. 1989. Capture-recapture
studies with the South American malaria vector
Anopheles darlingi, Root. Ann Trop Med Parasitol.
83:569-576.
Dahl C, Sahlen G, Johannisson A, Amneus H. 1993.
Differential particle uptake by larvae of three mosquito
species (Diptera:Culicidae). J. Med Entomol. 30:537-
543.
de Barros FSM, Honorio NA, Arruda ME. 2011.
Survivorship of Anopheles darlingi (Diptera:Culicidae)
in relation with malaria incidence in the Brazilian
Amazon. PLoS One. 6: e22388.
de Castro Medeiros LC, Castilho CAR, Braga C, de Souza
WV, Regis L, Monteiro AMV. 2011. Modeling the
dynamic transmission of dengue fever: investigating
disease persistence. PLoS NTDs. 5:e942.
de Oliveira CD, Tadei WP, Abdalla FC, Paolucci Pimenta
PF, Marinotti O. 2012. Multiple blood meals in
Anopheles darlingi (Diptera:Culicidae). J Vector Ecol.
37:351-8. doi:10.1111/j.1948-7134.2012.00238.x.
Detinova, TS. 1962. Age-grouping methods in Diptera of
medical importance, with special reference to some
vectors of malaria. Geneva : WHO.
Eckhoff PA. 2011. A malaria transmission-directed model
of mosquito life cycle and ecology. Malaria J. 10:303.
Gilbert B, Srivastava DS, Kirby KR. 2008. Niche
partitioning at multiple scales facilitates coexistence
among mosquito larvae. Oikos. 117:944-50.
Gu W, Novak RJ. 2006. Statistical estimation of degree
days of mosquito development under fluctuating
temperatures in the field. J Vec Ecol. 31:107-112.
Gu W, RJ Novak. 2009. Agent-based modelling of
mosquito foraging behaviour for malaria control.
Trans R Soc Trop Med Hyg. 103:1105.
doi:10.1016/j.trstmh.2009.01.006.
Hay SI, Guerra CA, Tatem AJ, Noor AM, Snow RW. 2004.
The global distribution and population at risk of
malaria: past, present, and future. The Lancet,
Infectious Diseases. 4:327-336. doi:10.1016/S1473-
3099(04)01043-6.
Hiwat H, Bretas G. 2011. Ecology of Anopheles darling
Root with respect to vector importance: a review.
Parasit Vectors. 4:177. doi:10.1186/1756-3305-4-177.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
118

Kiszewski AE, Mellinger A, Spielman A, Malaney P, Sachs
SE et al. 2004. A global index representing the stability
of malaria transmission. Am J Trop Med Hyg. 70: 486-
498.
Klomp H. 1964. Intraspecific competition and the
regulation of insect numbers. Ann. Rev. Entomol. 9:17-
40.
Krafsur ES, Armstrong J. 1978. An integrated view of
entomological and parasitological observations on
falciparum malaria in Gambela, western Ethiopian
lowlands. Trans R Soc Trop Med Hyg. 72: 348-356.
Martens P, Hall L. 2000. Malaria on the Move: Human
Population Movement and Malaria Transmission.
Emerg Inf Dis. 6:103-109.
McGreevy PB, Dietze R, Prata A, Hembree SC. 1989.
Effects of immigration on the prevalence of malaria in
rural areas of the Amazon basin of Brazil. Memorias do
Instituto Oswaldo Cruz. 84:485-91.
Mendis K, Sina BJ, Marchesini P, Carter R. 2001. The
neglected burden of Plasmodium vivax malaria. Am J
Trop Med Hyg. 64S:97–106.
Merritt RW. 1987. Do different instars of Aedes triseriatus
feed on particles of the same size? JAMCA. 3:94-96.
Molineaux L, Grammiccia G. 1980. The Garki Project:
research on the epidemiology and control of malaria in
the Sudan savanna of West Africa. Geneva: WHO.
311pp.
Moreno JE, Rubio-Palis Y, Paez E, Perez E. 2007.
Abundance, biting behavior and parous rate of
anopheline mosquito species in relation to malaria
incidence in gold-mining areas of southern Venezuela.
Med Vet Entomol. 21:339-349.
Muirhead-Thomson RC. 1954. Factors determining the true
reservoir of infection of Plasmodium falciparum and
Wuchereria bancrofti in a West African village. Trans
R Soc Trop Med Hyg. 48:208-225.
Muirhead-Thomson RC. 1957. The malarial infectivity of
an African village population to mosquitoes (Anopheles
gambiae). Am J Trop Med Hyg. 6:971-979.
Paaijmans KP, Read AF, Thomas MB. 2009.
Understanding the link between malaria risk and
climate. PNAS. 106:13844-13849.
Pimenta PFP, Orfano AS, Bahia AC, Duarte APM, Rios-
Velasquez CM, Melo FF, Pessoa FAC et al. 2015. An
overview of malaria transmission from the perspective
of Amazon Anopheles vectors. Mem Inst Oswaldo
Cruz, Rio de Janeiro. 110:23-47.
Pizzitutti F, Pan W, Feingold B, Zaitchik B, Alvarez CA,
Mena CF. 2018. Out of the net: an agent-based model
to study human movements influence on local-scale
malaria transmission. PLoS One. 13(3):e0193493.
Doi:10.1371/journal.pone.0193493.
Pizzitutti F, Pan W, Barbieri A, Miranda J, Feingold B,
Guedes GR, Alarcon-Valenzuela J, Mena CF. 2015. A
validated agent-based model to study the spatial and
temporal heterogeneities of malaria incidence in the
rainforest environment. Malaria J. 14:514/
doi:10.1186/s12936-015-1030-7.
Rubio-Palis Y, Bevilaqua M, Medina D, Martinez A. 2013.
Malaria entomological risk factors in relation to land
cover in the Lower Caura River Basin, Venezuela.
Memorias do Instituto Oswaldo Cruz. 108:220-8.
Rufalco-Moutinho P, Schweigmann N, Pimentel
Bergamaschi D, Mureb Sallum MA. 2016. Larval
habitats of Anopheles species in a rural settlement on
the malaria frontier of southwest Amazon, Brazil.
Acta
Tropica. 164:243-258.
Rutledge LC, Gould DJ, Tantichareon B. 1969. Factors
affecting the infection of anophelines with human
malaria in Thailand. Trans R Soc Trop Med Hyg.
63:613-661.
Tripura R, Peto TJ, Chalk J, Lee SJ, Sirithiranont P, Nguon
C, Dhorda M, von Seidlein L, Maude RJ et al. 2016.
Persistent Plasmodium falciparum and Plasmodium
vivax infections in a western Cambodian population:
implications for prevention, treatment and elimination
strategies. Malaria J. 15:181.
Vitor-Silva S, Siqueira AM, de Souza Sampaio V,
Guinovart C, Reyes-Lecca RC, de Melo GC et al. 2016.
Declining malaria transmission in rural Amazon:
changing epidemiology and challenged to achieve
elimination. Malaria J. 15:26.
Vittor AY, Gilman RH, Tielsch J, Glass G, Shields T, et al.
2006. The effect of deforestation on the human biting
rate of Anopheles darlingi, the primary malaria vector
of falciparum malaria in the Peruvian Amazon. Am J
Trop Med Hyg. 74:3-11.
Vittor AY, Pan W, Gilman RH, Tielsch J, Glass G, et al.
2009. Linking deforestation to malaria in the Amazon:
characterization of the breeding habitat of the principal
malaria vector, Anopheles darlingi. Am J Trop Med
Hyg. 81:5-12.
Zhou Y, Arifin SMN, Gentile J, Kurtz SJ, Davis GJ,
Wendelberger BA. 2010. An agent-based model of the
Anopheles gambiae mosquito lifecycle. In summer
simulation mutliconference, Ottawa, Ontario, Canada:
Society for Computer Simulation International. p. 201-
208.
Zhu L, Qualls WA, Marshall JM, Arheart KL, McManus
JW et al. 2015. A spatial individual-based model
predicting a great impact of copious sugar sources and
resting sites on survival of Anopheles gambiae and
malaria parasite transmission. Malaria J. 14:59.
Spatially Explicit Coupled Map Lattice Simulation of Malaria Transmission in the Brazilian Amazon
119