Multi–level Identification of Hammerstein–Wiener (N–L–N)
System in Active Experiment
Marcin Biega
´
nski
Department of Control Systems and Mechatronics, Faculty of Electronics, Wrocaw University of Science and Technology,
Wybrze
˙
ze Wyspia
´
nskiego 27, 50-370 Wrocław, Poland
Keywords:
Hammerstein–Wiener System, Nonlinear System Identification, Nonparametric Identification.
Abstract:
The paper addresses the problem of Hammerstein–Wiener (N–L–N) system identification. The proposed strat-
egy embraces two-experiment approach to the system identification, in which system is excited with random
process in passive experiment and with binary process in active experiment. The proposed approach uses both
parametric (least squares) and nonparametric (kernel estimates) identification tools. It consists of four consec-
utive stages, where linear dynamic and nonlinear static parts of the system are identified separately. Output
nonlinearity estimation is executed under active experiment. The consistency of the estimate is analyzed and
simple simulation example is presented.
1 INTRODUCTION
Hammerstein and Wiener systems are the most pop-
ular structures in a class of so-called block-oriented
nonlinear systems (BONL) (Giri and Bai, 2010) – the
systems that consist of the interaction of linear time-
invariant dynamic subsystems and static nonlinear el-
ements. The scope of applications of these models
is relatively wide and expands on signal processing
(Hasiewicz et al., 2005), biocybernetics, automatic
control (Giannakis and Serpedin, 2001), medicine, ar-
tificial neural networks (Rubio and Yu, 2007), physi-
cal, biological, chemical processes (G
´
omez and Jutan,
2003) and so on. Despite the fact, that Hammerstein
and Wiener systems have high flexibility and pro-
vide remarkable ability to capture large class of com-
plex and nonlinear systems, there are still processes
that need more complex structures with higher mod-
elling capabilities. And that is why scientists started
working on a series combination of Hammerstein and
Wiener models (Bai, 1998), (Sj
¨
oberg et al., 2012),
(Wills et al., 2013).
The paper addresses the problem of SISO
Hammerstein–Wiener system identification, that is,
identification of object being a cascade connection of
two nonlinear static characteristics sandwiched by dy-
namic linear block (Figure 1). Hammerstein–Wiener
system is more convenient, when both actuator and
sensor nonlinearities are present, but it has been also
successfully applied to modelling several physical
processes, such as polymerase reactors (Lee et al.,
2004), pH processes (Kalafatis et al., 2005), mag-
netospheric dynamics, among many others. Unfor-
tunately, despite such extensive interest, the problem
of Hammerstein–Wiener system identification still re-
mains completely open. The fundamental difficulty in
identification is caused by the presence of Wiener part
in which dynamic linear block precedes static nonlin-
earity. Hence, the input of nonlinearity is inaccessible
for measurement and correlated. All in all, the state of
the art in Wiener and Hammerstein–Wiener systems
identification is still not satisfying.
The main goal of the paper is to propose the
algorithm for Hammerstein–Wiener system identifi-
cation that would adapt itself both to Hammerstein
and Wiener systems separately without any additional
knowledge about the examined system. The proposed
procedure is performed in two-experiment approach.
In a passive experiment the system is excited and dis-
turbed by ordinary random processes, whereas in an
active experiment input signal takes shape of a binary
process.
The paper is organized as follows. In Section 2
the identification problem is introduced and formally
described. In Section 3 the proposed steps of the al-
gorithm are described and estimates of the separate
blocks are presented. In Section 4 the consistency
of the output nonlinearity estimate is discussed and
proved. Simple simulation example is presented in
Section 5, and in Section 6 final remarks and conclu-
sions are given.
Biega
´
nski, M.
Multi–level Identification of Hammerstein–Wiener (N–L–N) System in Active Experiment.
DOI: 10.5220/0006863703550361
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 355-361
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
355

2 PROBLEM STATEMENT
We consider a SISO Hammerstein–Wiener system,
i.e. a block-oriented sandwich structure shown in Fig-
ure 1, where u
k
and y
k
are measurable input and out-
put signals at time k, respectively and z
k
is a random
noise. Signals w
k
, x
k
and v
k
are inaccessible for direct
measurement.
Figure 1: Hammerstein–Wiener system.
Functions µ() and η() denote the unknown input
and output nonlinear characteristics, whereas {γ
∗
j
}
q
j=0
are the true and unknown parameters of the finite im-
pulse response of the linear dynamic block. The sys-
tem is described by the following input-output equa-
tion:
y
k
= η
q
∑
j=0

γ
∗
j
µ(u
k− j
)

!
+ z
k
. (1)
The output of the whole system is a sum of output
of second nonlinearity and additive noise.
Regarding the system we assume that:
A. Input and output characteristics of the static
blocks are described by the linear combinations
of known base functions f and g:
µ(u) = µ(u, a
∗
) = a
∗
T
f (u), (2)
a
∗
= (a
∗
1
, a
∗
2
, . .. , a
∗
m
)
T
, a
∗
∈ R
m
,
f (u) = ( f
1
(u), f
2
(u), . . . , f
m
(u))
T
,
η(x) = η(x, b
∗
) = b
∗
T
g(x), (3)
b
∗
= (b
∗
1
, b
∗
2
, . . . , b
∗
n
)
T
, b
∗
∈ R
n
,
g(x) = (g
1
(x), g
2
(x), . . . , g
n
(x))
T
.
Dimensions of the parameters vectors a
∗
and b
∗
are fixed and known. Moreover it is assumed
that static nonlinear characteristics are both Lips-
chitz functions, i.e. are uniformly continuous with
bounded first derivatives. Characteristics are two
times differentiable in arbitrarily small neighbour-
hoods of some points u
0
and x
0
= µ(u
0
)
∑
q
j=0
γ
∗
j
and µ
0
(u
0
) 6= 0, η
0
(x
0
) 6= 0. For ease of presenta-
tion let us assume u
0
= 0, though the method can
be generalized for u
0
6= 0. Additionally, output
characteristic is strictly monotonous.
B. The dynamic subsystem has the impulse response
{γ
∗
j
}
q
j=0
, where q – the length of the system mem-
ory – is assumed to be finite and known:
γ
∗
=

γ
∗
0
, γ
∗
1
, . . . , γ
∗
q

, γ
∗
∈ R
q+1
.
The above assumptions state that a priori knowl-
edge about the system is purely parametric, as the sys-
tem is described by n+m +q+1 parameters. Our fur-
ther assumptions concern input and noise signals and
are given below:
C. System is excited in two separate experiments,
with two different types of signals. The input u
(1)
k
is an i.i.d. random process with Lipschitz prob-
ability density function ν(u) and ν(0) 6= 0. The
input u
(2)
k
is a random binary process.
D. The signals u
k
and z
k
are mutually independent
and have finite variances σ
2
u
< ∞ and σ
2
z
< ∞, re-
spectively. Furthermore E[z
k
] = 0.
Moreover, input characteristic µ(u
(2)
k
) is presumed
as follows: µ(0) = 0, µ(1) 6= 0. The steady-state gain
of the linear dynamic block is not identifiable regard-
less of the identification method, since the internal
signals w
k
and x
k
cannot be measured. Hence, for
clarity of presentation and without any loss of gener-
ality we assume G
∗
=
∑
q
j=0
γ
∗
j
= 1 and µ(1) = 1.
The aim is to estimate the unknown character-
istic of the output nonlinearity η() only on a ba-
sis of the input–output measurements of the whole
Hammerstein–Wiener system {u
k
, y
k
}
N
k=1
.
3 IDENTIFICATION
ALGORITHM
Similarly to (Mzyk and Wachel, 2017) and (Mzyk
et al., 2017), the identification algorithm estimates
linear and nonlinear parts of the Hammerstein–
Wiener system separately. Hence the identification
procedure is divided into four stages:
• direct identification of the impulse response pa-
rameters γ
∗
of linear dynamic block in the pres-
ence of random input and random noise with the
use of least squares method censored by the box
kernel selector (Section 3.1),
• recovery of parameters b
∗
of output nonlinearity
in active experiment by kernel-based estimate on
the grid of deterministic points determined by the
binary excitation (Section 3.2),
• output process filtration in order to generate ad-
ditional signal r
k
with exactly the same expected
value as non-measureable signal x
k
(Section 3.3),
• identification of parameters a
∗
of input nonlinear-
ity analogously to the simpler Hammerstein sys-
tem identification method (Hasiewicz and Mzyk,
2004) (Section 3.4).
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
356

Every single stage of the identification algorithm
must be executed in a specific order as further stages
benefit from the results of former ones.
As system parameters are extracted only from the
measurement data
{
(u
k
, y
k
)
}
N
k=1
, the purpose of the
algorithm is to minimize the following mean squared
criterion Q

ˆ
γ, ˆa,
ˆ
b

= E(y
k
− ˆy
k
)
2
→ min
ˆ
γ, ˆa,
ˆ
b
, where y
k
=
y
k
(γ
∗
, a
∗
, b
∗
) is the system output and ˆy
k
= ˆy
k
(
ˆ
γ, ˆa,
ˆ
b)
is the model output dependent on estimated parame-
ters
ˆ
γ, ˆa and
ˆ
b.
3.1 Identification of Impulse Response
Consider the regression vector that consists of q + 1
consecutive inputs of a system excited with random
process
φ
k
=

u
(1)
k
, u
(1)
k−1
, . . . , u
(1)
k−q

T
.
Assuming linear local behaviour of the system around
point u
0
= 0 and using the following form of the box
kernel selector:
K (v) =
(
1, if
|
v
|
≤ 1
0, otherwise
(4)
we propose the following least squares based esti-
mate of the impulse response parameters γ
∗
(cf. (Bai,
2010), (Mzyk et al., 2017)):
ˆ
γ =
N
∑
k=1
φ
k
φ
T
k
K

∆
k
h

!
−1
N
∑
k=1
φ
k
y
k
K

∆
k
h

!
,
(5)
where ∆
k
is the infinity norm of the regression vector:
∆
k
=
k
φ
k
k
∞
= max
j=0,1,...,q



u
(1)
k− j



.
We assume persistent excitation of the input process
u
(1)
k
for the matrix
∑
N
k=1
φ
k
φ
T
k
K

∆
k
h

to be invertible
(see (S
¨
oderstr
¨
om and Stoica, 1988)). For selecting
bandwidth parameter h there exist dedicated meth-
ods such as cross-validation method (Wand and Jones,
1994), that establish a good trade-off between the bias
and the variance of the estimate.
3.2 Estimation of Output Nonlinearity
Second stage of the algorithm is performed under ac-
tive experiment, where system is excited with binary
random process u
(2)
k
. This active experiment blinds
the input nonlinearity so the signal w
k
also takes shape
of binary process.
Let us introduce the binary representation of all
possibilities of the regression vector φ
k
:
ϕ
1
= (1, 0, . . . , 0)
T
,
ϕ
2
= (0, 1, . . . , 0)
T
,
.
.
.
ϕ
N
0
= (1, 1, . . . , 1)
T
.
There are N
0
such vectors, where N
0
= 2
q+1
. With this
representation and the knowledge about parameters γ
∗
of the impulse response of the linear dynamic block
we are able to form the grid of deterministic points
x
[i]
= ϕ
T
i
γ
∗
, i = 1, 2, . . . , N
0
(6)
that represent all possible realizations of non-
measurable signal x
k
. In these points we can estimate
output nonlinearity with the proposed kernel-based
estimate:
ˆ
η

x
[i]

=
∑
N
k=1
y
k
δ(φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)
, (7)
where
δ(φ
k
, ϕ
i
) =
(
1, if φ
k
= ϕ
i
0, otherwise
(8)
is the kernel-like selector (the regression vector must
exactly match one of the vectors ϕ
i
) and with
0
0
un-
derstood as 0. Denominator in the proposed estimator
averages measurements in local clusters. In general
denominator may be equal to 0, so with the introduc-
tion of denotement of all output measurements, that
have been selected by the kernel technique for given
estimation point x
[i]
: y
(1)
, y
(2)
, . . . , y
(L)
where L is a
random number of measurements, the estimate takes
the following form:
S

x
[i]

=
{
y
k
: φ
k
= ϕ
i
}
, (9)
ˆ
η

x
[i]

= Avg

S

x
[i]

=
(
1
L
∑
L
l=1
y
(l)
, if L > 0
0, otherwise.
(10)
Probability of the perfect match (φ
k
= ϕ
i
) is constant
and equals
P
{
δ(φ
k
, ϕ
i
) = 1
}
=
1
N
0
=
1
2
q+1
.
The result of this step is given by the set of N
0
pairs

x
[i]
,
ˆ
η

x
[i]

N
0
i=1
. (11)
Using this set of pairs, we can easily find the best
fitting parameters by the least squares method:
ˆ
b =

Ψ
T
Ψ

−1
Ψ
T
ζ, (12)
Multi–level Identification of Hammerstein–Wiener (N–L–N) System in Active Experiment
357

where Ψ and ζ are respectively (for g(x) see (3) in
Section 2) :
Ψ =

g(x
[1]
), g(x
[2]
), . . . , g(x
[N
0
]
)

,
ζ =

ˆ
η

x
[1]

,
ˆ
η

x
[2]

, . . . ,
ˆ
η

x
[N
0
]

.
Invertibility of the matrix Ψ
T
Ψ (as well as matrix
Λ
T
N
Λ
N
in (19)) depends on the excitation, input proba-
bility density function and the shape of nonlinear base
functions (S
¨
oderstr
¨
om and Stoica, 1988). Formula-
tion of sufficient general conditions for invertibility
still remains open, and only some special cases can
be given, at the present state of research.
Additionally there is a byproduct of this stage of
the identification procedure. For every single estima-
tion point x
[i]
we obtain a set of output measurements
and its variety depends solely on the presence of the
disturbance process z
k
. So probability density func-
tion of the noise signal can be estimated based on the
value of deviation from the average value
ˆ
η

x
[i]

e.g.
with the kernel-based method (with L > 0):
ˆ
f (z) =
1
Lh
z
L
∑
l=1
K

z
(l)
− z
h
z

(13)
and it can be done N
0
times.
3.3 Output Signal Filtration
After extraction of parameters b
∗
of output nonlinear-
ity parameters a
∗
of the first nonlinear block still re-
main unidentified. If we could identify input nonlin-
earity first, there would be no problem with identifica-
tion of the second nonlinear static block. But the other
way around, our idea is to estimate signal x
k
so we can
identify parameters of first nonlinearity in the way it is
done with simpler Hammerstein system. Asssuming
strict monotonicity of the output nonlinear character-
istic we obtain reversible function that can be used to
recover x
k
process. The proposed approach is shown
in Figure 2.
Figure 2: Reverse flow of output nonlinear block.
Estimation is described by the following equations
y
k
= η(x
k
) + z
k
, (14)
x
k
= η
−1
(y
k
− z
k
). (15)
The problem of non-accessible input noise is known
in the literature as the error-in problem (Chen and
Zhao, 2014). But with the knowledge of probability
density function of the disturbance process f (z) we
can form additional function ς() (Figure 3):
ς(y) = E
{
x
k
|y
k
= y
}
=
Z
∞
−∞
η
−1
(y − z) f (z)dz. (16)
Figure 3: Output signal filtration.
With ς(y) we can generate additional signal r
k
with the same expected value as x
k
i.e.
Er
k
= Eς(y
k
) = E

Z
∞
−∞
η
−1
(y
k
− z) f (z)dz

=
= E

Z
∞
−∞
η
−1
(η(x
k
)) f (z)dz

=
= E

x
k
·
Z
∞
−∞
f (z)dz

= Ex
k
.
(17)
3.4 Identification of Input Nonlinearity
In the final section, due to multistage approach and
with r
k
signal generated, identification of the first non-
linear block is reduced to the Hammerstein system
identification problem (Hasiewicz and Mzyk, 2004).
Signal x
k
can be presented as
x
k
= λ
T
k
θ
∗
, (18)
where
λ
k
=

f
1
(u
(1)
k
), . . . , f
m
(u
(1)
k
), . . . ,
f
1
(u
(1)
k−q
), . . . , f
m
(u
(1)
k−q
)

T
is the regression vector and
θ
∗
=

γ
∗
0
a
∗
1
, . . . , γ
∗
0
a
∗
m
, . . . , γ
∗
q
a
∗
1
, . . . , γ
∗
q
a
∗
m

is the vector of mixed products. After introducing
generic vectors Λ
N
=

λ
T
1
, λ
T
2
, . . . , λ
T
N

T
and R
N
=
(r
1
, r
2
, . . . , r
N
)
T
, mixed products estimate
ˆ
θ can be
represented with the use of signal r
k
:
ˆ
θ =

Λ
T
N
Λ
N

−1
Λ
T
N
R
N
. (19)
With the knowledge about impulse response parame-
ters (Section 3.1) we can benefit from singular value
decomposition to extract parameters ˆa (for details see
(Kincaid and Cheney, 1991)).
With parameters ˆa extracted, the estimate of the
input nonlinearity takes the following shape:
ˆµ(u) = ˆµ(u, ˆa) = ˆa
T
f (u), (20)
where
ˆa = ( ˆa
1
, ˆa
2
, . . . , ˆa
m
)
T
.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
358

4 STATISTICAL PROPERTIES
Theorem 1. Let assumptions A. — D. be in force.
Then, for the Hammerstein–Wiener system and
h ∼ N
−α
, where α ∈

0,
1
d

and d = q + 3, it holds
that
ˆ
γ
j
→ γ
∗
j
, j = 0, 1, . . . , q (21)
in probability as N → ∞, provided that
c = µ
0
(u
0
)η
0
(x
0
) 6= 0.
Sketch of the proof. Under Assumption A. let’s take
Taylor series expansion and apply it to input and out-
put nonlinearities around points u
0
and x
0
:
µ(u
k
) = µ(u
0
) + c
1
(u
k
− u
0
) + ρ(u
k
), (22)
η(x
k
) = η(x
0
) + c
2
(x
k
− x
0
) + ξ(x
k
). (23)
Parameters c
1
and c
2
are non-zero constants and
are equal to first derivatives of functions µ() and
η() in points u
0
and x
0
. Observing that
|
ρ(u
k
)
|
=
o(h) and
|
ξ(x
k
)
|
= o(h), the theorem can be proved
analogously to Theorem 3 in (Mzyk and Wachel,
2017).
Theorem 2. Under Assumptions A. — D., it holds
that
E

η

x
[i]

−
ˆ
η

x
[i]

2
→ 0, as N → ∞, (24)
in each estimation point x
[i]
= ϕ
T
i
γ
∗
, i = 1, 2, . . . , N
0
,
such that x
[i]
∈ cont(η(), g()), where cont(η(), g()) is
a set of all points of continuity of η() and g().
Proof. For each estimation point x
[i]
we have
E
h
ˆ
η(x
[i]
)
i
= E
"
∑
N
k=1
y
k
δ(φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)
#
=
= E
"
∑
N
k=1
(v
k
+ z
k
) · δ(φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)
#
=
= E


∑
N
k=1
η

x
[i]

· δ(φ
k
, ϕ
i
) + z
k
· δ(φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)


=
= E
"
η

x
[i]

+
∑
N
k=1
z
k
· δ(φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)
#
=
= η

x
[i]

+ E
"
∑
N
k=1
z
k
· δ(φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)
#
.
(25)
Let y
(1)
, y
(2)
, . . . , y
(L)
be the output measurements se-
lected in (9). The number of measurements L is ran-
dom, but its expected value tends to infinity with in-
creasing number of measurements:
EL = P (φ
k
= ϕ
i
) · N =
1
N
0
· N =
N
2
q+1
, (26)
so
P(L = 0) → 0, as N → ∞. (27)
As a result, using Wald identity, bias of the estimate
asymptotically tends to zero:
E

∑
N
k=1
z
k
· δ (φ
k
, ϕ
i
)
∑
N
k=1
δ(φ
k
, ϕ
i
)

=
E
h
∑
L
k(l)=1
z
k(l)
i
EL
=
=
EL · Ez
1
EL
= 0.
(28)
The variance of the output measurement depends
solely on the variance of noise signal and equals
var

y
(l)

= var

η

x
[i]

+ z
(l)

=
= var

η

x
[i]

+ var

z
(l)

= σ
2
z
.
(29)
Assuming that the random number of measurement
is greater than zero, the conditional variance of the
estimate takes the following form:
var
h
ˆ
η

x
[i]
i
=
N
∑
k=1
P(L = k) · var
"
1
k
k
∑
l=1
y
(l)
#
=
=
N
∑
k=1
P(L = k) ·
var
h
y
(l)
i
k
=
=
N
∑
k=1
P(L = k) ·
σ
2
z
k
=
=
N
0
· σ
2
z
N
= c ·
1
N
∼ N
−1
.
(30)
Finally, from (28) and (4), the asymptotical con-
vergence of the estimate is proven (cf. (Mzyk, 2007)
or (Mzyk and Wachel, 2017)).
5 NUMERICAL EXAMPLE
In this section we describe a simple and intuitive sim-
ulation example that illustrates the first two stages of
the proposed algorithm. In the experiment, we sim-
ulated Hammerstein–Wiener system with nonlinear
static characteristics chosen as:
µ(u, a
∗
) = a
∗
1
u + a
∗
2
u
2
, a
∗
= (a
∗
1
, a
∗
2
)
T
= (0.8, 0.2)
T
,
η(x, b
∗
) = b
∗
1
x + b
∗
2
x
2
, b
∗
= (b
∗
1
, b
∗
2
)
T
= (0.7, 0.4)
T
,
and with the following impulse response of the dy-
namic filter:
γ
∗
= (0.6, 0.3, 0.1)
T
.
The system was excited by two types of random pro-
cesses. The first one used in the passive experi-
ment was chosen as uniformly distributed random
Multi–level Identification of Hammerstein–Wiener (N–L–N) System in Active Experiment
359

process u
(1)
k
∼ U(−1, 1). The second one used in
the active experiment

u
(2)
k

was a random binary
process with equal probabilities of 0 and 1. More-
over, the system was disturbed by random process
z
k
∼ U(−0.5, 0.5) (50% noise with respect to exci-
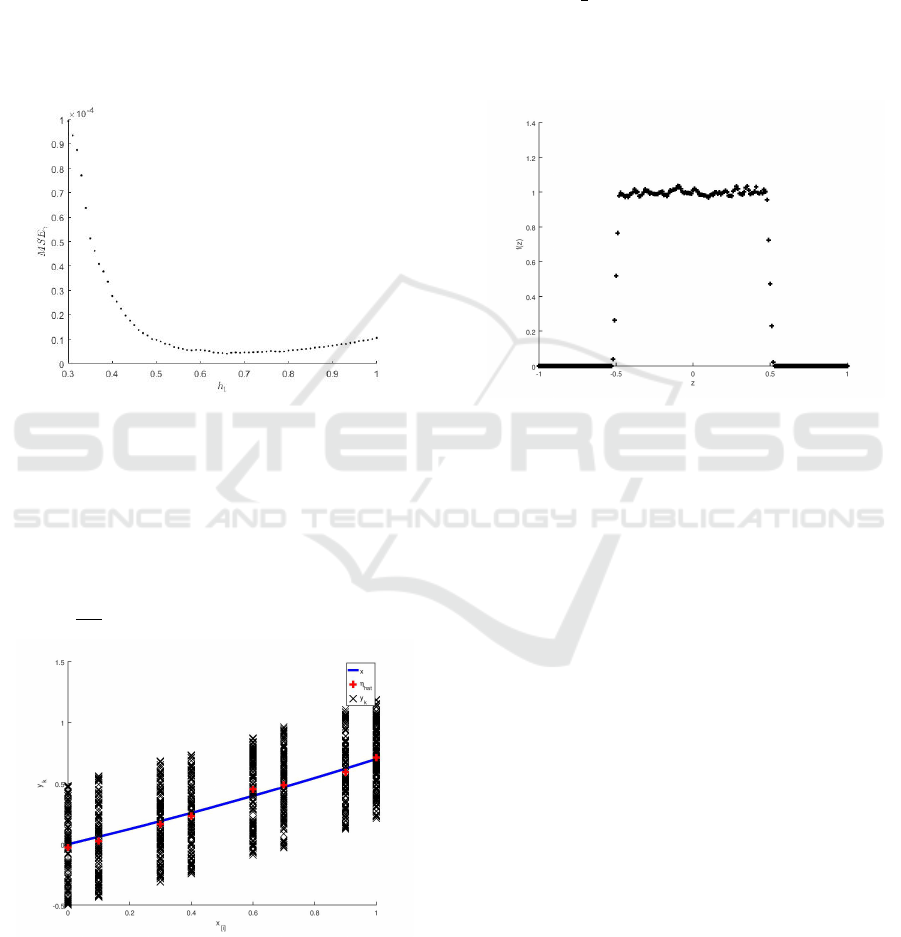
tation signal). Bandwidth parameter h was selected
with the cross-validation method (see Figure 4) and
set to 0.66. To illustrate the asymptotic (i.e. for
N → ∞) behaviour of the proposed method, the pa-
rameters were recovered based on N = 10
5
input–
output measurement pairs {(u
k
, y
k
))}
N
k=1
.
Figure 4: Cross-validation method for bandwidth parameter
h.
As a result of the first stage, kernel-censored
least squares estimate recovered the following pa-
rameters of the finite impulse response (all param-
eters are rounded to the third decimal place):
ˆ
γ =
(0.613, 0.302, 0.085)
T
, so the mean square error be-
tween real and estimated parameters was equal to
MSE
γ
=
1
q+1
∑
q
i=0
(γ
∗
i
−
ˆ
γ
i
)
2
= 1.38 · 10
−4
.
Figure 5: The nonparametric estimates of output nonlinear-
ity (crosses) compared to real characterisic η(x) (line). Out-
put measurements presented in the background (X marks).
In the second stage, the output nonlinearity was
estimated on the grid of deterministic points {x
[i]
}
N
0
i=1
,
where N
0
= 2
q+1
= 8. In these points, output
nonlinearity was estimated with the use of kernel-
based method. In the Figure 5 we can see the out-
put measurements grouped in clusters and results of
the estimate compared to the real output nonlinear-
ity. Finally, we recovered the following parame-
ters
ˆ
b = (0.699, 0.401)
T
with the mean squared er-
ror MSE
b
=
1
2
∑
2
i=1

b
∗
i
−
ˆ
b
i

2
= 1.1 · 10
−6
. Further-
more, as a byproduct of this step we could estimate
the probability density function of the noise signal in
each estimation point x
[i]
. Results of this estimation
are presented in Figure 6.
Figure 6: Kernel-based identification of probability density
function f (z).
The next step of the algorithm – creation of addi-
tional signal r
k
as a covolution of inversion of output
nonlinearity and probability density function of the
disturbance process – can be processed simulatively
with the following methods: fast Fourier transform,
numerical integration with Riemann sum or Monte
Carlo method. Lastly, the input nonlinearity can be
recovered as in simpler Hammerstein system.
6 CONCLUSIONS
In the paper, a new method of identification of the the
Hammerstein–Wiener (N–L–N) system has been pro-
posed and analyzed under assumptions presented at
the beginning of the article. The idea of identification
routine consists of both parametric (least squares) and
nonparametric (kernel estimate) techniques, and is di-
vided into separate identification of linear dynamic,
and nonlinear static parts of the system. Identification
of the output nonlinearity is done under active exper-
iment, with random binary excitation. The system is
identifiable and the solution is unique for the impulse
response fulfilling the given assumptions and for out-
put nonlinearity satisfying Haar condition. Dividing
the problem into four separate stages significantly re-
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
360

duces dimensionality of the problem. Effectiveness
of the method is strictly dependent on the length of
the impulse response which is specific for the whole
class of Wiener-type systems, where linear dynamic
block is followed by static nonlinearity (”course of
dimensionality”). In consequence, proposed strategy
is rather recommended for short memory dynamic fil-
ters, but the class of admissible nonlinearities is rel-
atively broad. More general cases are remained for
further research.
ACKNOWLEDGEMENTS
The work was supported by the National Science Cen-
tre, Poland, Grant No. 2016/21/B/ST7/02284.
REFERENCES
Bai, E.-W. (1998). An optimal two-stage identification al-
gorithm for Hammerstein-Wiener nonlinear systems.
Automatica, 34(3):333–338.
Bai, E.-W. (2010). Non-parametric nonlinear system identi-
fication: An asymptotic minimum mean squared error
estimator. IEEE Transactions on Automatic Control,
55(7):1615–1626.
Chen, H. and Zhao, W. (2014). Recursive Identification and
Parameter Estimation. CRC Press.
Giannakis, G. B. and Serpedin, E. (2001). A bibliography
on nonlinear system identification. Signal Processing,
81(3):533 – 580. Special section on Digital Signal
Processing for Multimedia.
Giri, F. and Bai, E. (2010). Block-oriented Nonlinear Sys-
tem Identification. Springer-Verlag London, London.
G
´
omez, J. C. and Jutan, A. (2003). Identification and model
predictive control of a pH neutralization process based
on linear and Wiener models. IFAC Proceedings Vol-
umes, 36(16):1507 – 1512. 13th IFAC Symposium on
System Identification (SYSID 2003), Rotterdam, The
Netherlands, 27-29 August, 2003.
Hasiewicz, Z. and Mzyk, G. (2004). Combined parametric-
nonparametric identification of Hammerstein sys-
tems. IEEE Transactions on Automatic Control,
49(8):1370–1375.
Hasiewicz, Z., Pawlak, M., and
´
Sliwinski, P. (2005). Non-
parametric identification of nonlinearities in block-
oriented systems by orthogonal wavelets with com-
pact support. IEEE Transactions on Circuits and Sys-
tems I: Regular Papers, 52(2):427–442.
Kalafatis, A. D., Wang, L., and Cluett, W. R. (2005). Identi-
fication of time-varying pH processes using sinusoidal
signals. Automatica, 41(4):685 – 691.
Kincaid, D. and Cheney, W. (1991). Numerical Analysis:
Mathematics of Scientific Computing. Brooks/Cole
Publishing Co., Pacific Grove, CA, USA.
Lee, Y. J., Sung, S. W., Park, S., and Park, S. (2004). Input
test signal design and parameter estimation method
for the Hammerstein-Wiener processes. Industrial &
Engineering Chemistry Research, 43(23):7521–7530.
Mzyk, G. (2007). A censored sample mean approach
to nonparametric identification of nonlinearities in
Wiener systems. IEEE Transactions on Circuits and
Systems II: Express Briefs, 54(10):897–901.
Mzyk, G., Biega
´
nski, M., and Kozdra
´
s, B. (2017). Multi-
stage identification of an N-L-N Hammerstein-Wiener
system. In 2017 22nd International Conference on
Methods and Models in Automation and Robotics
(MMAR), pages 343–346.
Mzyk, G. and Wachel, P. (2017). Kernel-based identifi-
cation of Wiener-Hammerstein system. Automatica,
83:275 – 281.
Rubio, J. and Yu, W. (2007). Stability analysis of nonlin-
ear system identification via delayed neural networks.
IEEE Transactions on Circuits and Systems II: Ex-
press Briefs, 54(2):161–165.
Sj
¨
oberg, J., Lauwers, L., and Schoukens, J. (2012). Iden-
tification of Wiener-Hammerstein models: Two algo-
rithms based on the best split of a linear model ap-
plied to the SYSID’09 benchmark problem. Control
Engineering Practice, 20(11):1119 – 1125. Special
Section: Wiener-Hammerstein System Identification
Benchmark.
S
¨
oderstr
¨
om, T. and Stoica, P., editors (1988). System Identi-
fication. Prentice-Hall, Inc., Upper Saddle River, NJ,
USA.
Wand, M. and Jones, M. (1994). Kernel Smoothing. Chap-
man & Hall/CRC Monographs on Statistics & Ap-
plied Probability. Taylor & Francis.
Wills, A., Sch
¨
on, T. B., Ljung, L., and Ninness, B. (2013).
Identification of Hammerstein-Wiener models. Auto-
matica, 49(1):70–81.
Multi–level Identification of Hammerstein–Wiener (N–L–N) System in Active Experiment
361