Improved Discrete RRT for Coordinated Multi-robot Planning

Jakub Hv

ezda

1,2

, Miroslav Kulich

and Libor P

reu

cil

Czech Institute of Informatics, Robotics, and Cybernetics, Czech Technical University in Prague, Prague, Czech Republic

Department of Cybernetics, Faculty of Electrical Engineering, Czech Technical University in Prague, Czech Republic

Keywords:

Multi-robot Systems, Trajectory Planning, Coordination, Rapidly-Exploring Random Tree.

Abstract:

This paper addresses the problem of coordination of a ﬂeet of mobile robots – the problem of ﬁnding an optimal

set of collision-free trajectories for individual robots in the ﬂeet. Many approaches have been introduced

during last decades, but a minority of them is practically applicable, i.e. fast, producing near-optimal solutions,

and complete. We propose a novel probabilistic approach based on the Rapidly Exploring Random Tree

algorithm (RRT) by signiﬁcantly improving its multi-robot variant for discrete environments. The presented

experimental results show that the proposed approach is fast enough to solve problems with tens of robots in

seconds. Although the solutions generated by the approach are slightly worse than one of the best state-of-

the-art algorithms presented in (ter Mors et al., 2010), it solves problems where ter Mors’s algorithm fails.

1 INTRODUCTION

Recent advances in mobile robotics and increased de-

ployment of robotic systems in many practical appli-

cations lead to intensive research of multi-robot sys-

tems. One of the most important problems is the coor-

dination of trajectories of individual robots/agents in

such systems: given starting and destination positions

of the robots, we are interested in ﬁnding their tra-

jectories that do not collide with each other, and the

overall cost is minimized. An optimization criterion

can be a sum of lengths of the individual trajectories

or the time the last robot reaches its destination posi-

tion.

Several ﬁelds of the industry such as airports are

nowadays faced with a higher increase in trafﬁc than

the actual capacity. This leads to reliance on path opti-

mizations to increase their throughput. Another typi-

cal application where multi-robot coordination plays

an important role might be planning in an automa-

ted warehouse, see Fig. 1, where autonomous robots

effectively deliver desired goods from/to given positi-

ons.

Multi-robot path planning and motion coordina-

tion has been studied since the 1980s, and many

techniques have been developed during this period,

see (Parker, 2009) for a nice overview. This pro-

blem (formulated as the warehouseman’s problem)

was proved to be PSPACE-complete (Hopcroft et al.,

1984). For the case where robots move on a predeﬁ-

Figure 1: Automated warehouse: G-COM system by Gren-

zebach (https://www.grenzebach.com) in a costumer appli-

cation.

ned graph complexity of the problem can be reduced,

nevertheless, it is still NP-hard (Goldreich, 2011),

which means that optimal solutions cannot generally

be found in a reasonable time for non-trivial instances

(e.g., for a number of robots in order of tens).

Solutions to the problem consider either cou-

pled or decoupled approaches. Centralized (cou-

pled) approaches consider the multi-robot team as

a multi-body robot for which classical single-robot

path planning can be applied in composite conﬁgu-

ration space. Traditional centralized methods are ba-

sed on complete (i.e., the algorithm ﬁnds a solution if

it exists or reports that no solution exists otherwise)

and optimal classical algorithms and provide optimal

solutions (Latombe, 1991), (Lavalle, 1998), (Ryan,

ezda, J., Kulich, M. and P

reu

cil, L.

Improved Discrete RRT for Coordinated Multi-robot Planning.

DOI: 10.5220/0006865901710179

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 171-179

ISBN: 978-989-758-321-6

171

2008). However, these approaches require computati-

onal time exponential in the dimension of the com-

posite conﬁguration space, so they are appropriate

for small-sized problems only. This drawback leads

to the development of methods that prune the search

space. For instance, Berg et al. (van den Berg et al.,

2009) decompose any instance of the problem into

a sequence of sub-problems where each subproblem

can be solved independently from the others. The Bi-

ased Cost Pathﬁnding (Geramifard et al., 2006) em-

ploys generalized central decision maker that resol-

ves collision points on paths that were pre-computed

independently per unit, by replanning colliding units

around the highest priority unit. Another approach is

to design an algorithm based on a speciﬁc topology

describing the environment. (Peasgood et al., 2008)

present a multi-phase approach with linear time com-

plexity based on searching a minimum spanning tree

of the graph, while an approach for grid-like environ-

ments is introduced in (Wang and Botea, 2008). A

ﬂow-annotated search graph inspired by two-way ro-

ads is built to avoid head-to-head collisions and to re-

duce the branching factor in search. Nevertheless, the

computational complexity is still high (e.g., (van den

Berg et al., 2009) solves a problem with 40 robots in

12 minutes, (Wang and Botea, 2008) needs approx.

30 seconds for 400 robots).

On the contrary, decoupled methods present a

coordination phase separated from the path planning

phase. These approaches provide solutions typically

in orders of magnitude faster times than coupled plan-

ners, but these solutions are sub-optimal. Moreover,

the decoupled methods are often not complete as they

may suffer from deadlocks. These approaches are di-

vided into two categories: path coordination techni-

ques and prioritized planning. Path coordination con-

siders tuning the velocities of robots along the pre-

computed trajectories to avoid collisions (LaValle and

Hutchinson, 1998), (Simeon et al., 2002), while pri-

oritized planning computes trajectories sequentially

for the particular robots based on the robots’ priori-

ties. Robots with already determined trajectories are

considered as moving obstacles to be avoided by ro-

bots with lower priorities (van den Berg and Over-

mars, 2005), (Bennewitz et al., 2001), (Cap et al.,

2015). A similar idea was presented in (ter Mors

et al., 2010), where adaptation of the A* algorithm

is sequentially planning on a graph augmented by in-

formation in which time intervals the particular nodes

are occupied by already processed robots.

Several computationally efﬁcient heuristics have

been introduced recently enabling to solve problems

for tens of robots in seconds. Windowed Hierarchical

Cooperative A* algorithm (WHCA*) employs heu-

ristic search in a space-time domain based on hier-

archical A* limited to a ﬁxed depth (Silver, 2005).

Chiew (Chiew, 2010) proposes an algorithm for n

vehicles on a n × n mesh topology of path network

allowing simultaneous movement of vehicles in a cor-

ridor in opposite directions with computational com-

plexity O(n

). Luna and Bekros (Luna and Bekris,

2011) present a complete heuristics for general pro-

blems with at most n − 2 robots in a graph with n

vertices based on the combination of two primitives

- “push” forces robots towards a speciﬁc path, while

“swap” switches positions of two robots if they are to

be colliding. An extension which divides the graph

into subgraphs within which it is possible for agents

to reach any position of the subgraph, and then uses

“push”, “swap”, and “rotate” operations is presen-

ted in (DeWilde et al., 2014). Finally, Wang and

Wooi (Wang and Goh, 2015) formulate multi-robot

path planning as an optimization problem and approx-

imate the objective function by adopting a maximum

entropy function, which is minimized by a probabilis-

tic iterative algorithm.

Although many of the approaches mentioned

above have nice theoretical properties, the most

practically usable algorithm is probably Context-

Aware Route Planning (CARP) presented in (ter Mors

et al., 2010) as it is fast, produces solutions of high

quality, and although it is not complete, it ﬁnds a so-

lution for a large number of practical setups.

(Kiril Solovey, 2014) presented MRdRRT algo-

rithm, which is a probabilistic approach for path

planning on predeﬁned structures for relatively small

number of robots inspired by RRT algorithm (Lavalle,

1998). (Dobson et al., 2017) improves upon MR-

dRRT by presenting its optimal variant.

In this paper, we present a probabilistic appro-

ach which extends and improves a discrete version

of Rapidly-Exploring Random Tree (RRT) for mul-

tiple robots (Kiril Solovey, 2014). Our approach fo-

cuses mainly on scalability with increasing number

of agents as well as improving the quality of solu-

tion compared to (Dobson et al., 2017) that presents

the optimal version of the dRRT algorithm but keeps

the number of robots relatively low. We show that

the proposed extensions allow solving problems with

tens of robots in times comparable to CARP with a

slightly worse quality of results. On the other hand,

the proposed algorithm ﬁnds solutions also for setups

where CARP fails.

The rest of the paper is organized as follows. The

multi-agent path-ﬁnding problem is presented as well

as the used terms are deﬁned in Section 2. The multi-

robot discrete RRT algorithm and the proposed im-

provements are described in Section 3, while perfor-

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

172

med experiments, their evaluation, and discussion are

presented in Section 4. Finally, Section 5 is dedicated

to concluding remarks.

2 PROBLEM DEFINITION

Multi-agent pathﬁnding/coordination is a problem

that is concerned about ﬁnding paths for multiple

agents from their given start locations to their target

locations without colliding with each other or obsta-

cles in the environment while also optimizing a global

cost function.

To specify the problem more precisely, assume:

• A set of k homogenous agents each labeled

, a

, ..., a

• A graph G(V, E) where |V | = N. The vertices V of

the graph are all possible agent’s locations, while

E represents a set of all possible agent’s transiti-

ons between the locations.

• A start location s

∈ V and a target location t

∈ V

of each agent.

The aim is to ﬁnd a set of collision-free trajecto-

ries on G(V, E) each of them specifying locations of

an individual agent at all time moments so that agents

are at their start locations initially and at their goal lo-

cations ﬁnally. Note that the time is discretized into

time moments to simplify the problem.

The following paragraphs explain key used terms

and specify additional constraints to the generated tra-

jectories.

2.1 Actions

Every agent can perform two types of action at each

time point: It can either move into one of the neighbo-

ring nodes, or it can wait at its current location. Every

algorithm can make different assumptions regarding

the cost of these actions, but we assume that staying

idle has zero cost of distance traveled, but costs time.

Furthermore, once an agent reaches its target location,

it waits at this location for other agents to ﬁnish.

2.2 Constraints

The main constraints on agent movement assumed in

this paper are:

• No two agents a

and a

can occupy the same ver-

tex v ∈ V at the same time.

• Assume two agents a

, a

located in two neighbo-

ring nodes v

, v

∈V respectively, they can not tra-

vel along the same edge (v

, v

) at the same time

in opposite directions. In other words, two neig-

hboring agents cannot swap positions. However,

it is possible for agents to follow one another as-

suming that they do not share the same vertex or

edge concurrently. For example, if the agent a

moves from v

∈ V to v

∈ V then the agent a

can move from v

∈ V to v

∈ V at the same time.

2.3 Composite Conﬁguration Space

The composite conﬁguration space G = (V , E) is a

graph that is deﬁned as follows. The vertices V are all

combinations of collision-free placements of m agents

on the original graph G. These vertices can also be

viewed as m agent conﬁgurations C = (v

, v

, ..., v

where an agent a

is located at a vertex v

∈ G and

the agents do not collide with each other. The edges

of G can be created using either Cartesian product or

Tensor product. For the purposes of this paper the

Tensor product is used because is allows simultaneous

movement movement of multiple agents and thus for

two m agent conﬁgurations C = (v

, v

, ..., v

), C

, v

, ..., v

) the edge (C,C

) exists if (v

, v

) ∈ E

for

every i and no two agents collide with each other du-

ring the traversal of their respective edges.

The distance between two neighboring nodes C

, v

, ..., v

) and C

= (v

, v

, ..., v

) in a com-

posite roadmap is calculated as the sum of Euclidean

distances d between the corresponding nodes:

δ(C

) =

∑

i=0

d(v

, v

)

3 PROPOSED ALGORITHM

3.1 Discrete RRT

A discrete multi-robot rapidly-exploring random tree

(MRdRRT)(Kiril Solovey, 2014) is a modiﬁcation of

the RRT algorithm for pathﬁnding in an implicitly

given graphs embedded in a high-dimensional Euc-

lidean space.

Just like RRT, the MRdRRT grows a tree T rooted

in the vertex s representing start positions of the ro-

bots in a composite conﬁguration space R

by iterati-

vely adding new points to the tree while also trying to

connect to the goal conﬁguration t without violating

any constraints, e.g. collision with the environment.

The growth is achieved by randomly sampling a point

u in the composite conﬁguration space and then ex-

tending the tree towards this sample. Note that verti-

ces newly added to the tree are taken from G: given

a sample u and the node v ∈ V nearest to it, the best

Improved Discrete RRT for Coordinated Multi-robot Planning

173

neighbor v

∈ V has to be found. To generate neig-

hbor nodes of already visited nodes MRdRRT uses

a technique called oracle. Without loss of generality

consider that G is embedded in [0, 1]

. For two points

v, v

∈ [0, 1]

the ρ (v, v

) denotes a ray that begins in

v and goes through v

. ∠

, v

) given three points

v, v

, v

∈ [0, 1]

denotes the (smaller) angle between

ρ(v, v

) and ρ(v, v

). The way the oracle is used is

given sample point u it returns the neighbor v

of v

such that the angle between rays ρ(u, v

) and ρ(v, v

)

is minimized. This can be deﬁned as

(v, u) := argmin

∈V



∠



u, v





v, v



∈ E



It is possible that the tree will if given sufﬁcient

time, eventually reach t during the expansion phase.

However it is unlikely for larger problems. MRdRRT,

therefore, attempts to connect the newly added node

with t employing so-called local connector which is

successful for restricted problems only, but fast, so it

can be run often.

3.2 Proposed Improvements

Although the original MRdRRT can solve path-

ﬁnding problems for several robots, the realization of

its particular steps is inefﬁcient, which disqualiﬁes it

to deal with complex scenarios containing tens of ro-

bots. The authors of MRdRRT present experimen-

tal results with up to 10 robots and mention that their

algorithm is unable to solve problems with a signiﬁ-

cantly larger number of robots. We, therefore, intro-

duce several improvements to the original version.

The original expansion phase generates random

samples from a bounding box of G which is inefﬁ-

cient in maps with tight spaces as it would not allow

robots to stand still as their next action and would not

ﬁnd a solution in situations where standing still was

required for one of the robots. Moreover, the majo-

rity of generated points is far from a solution leading

to a relatively huge growth of the tree over the con-

ﬁguration space and thus to the high computational

complexity of the algorithm. Instead of generating a

point from R

, we ﬁnd shortest paths for every robot

separately in the preprocessing phase and after that

we compose a sample only from points q for which

dist(s

, q) + dist(q, t

) ≤ dist(s

) + ∆, where dist is

a distance of two points, s

and t

are start and goal

positions of i-th robot, and ∆ > 0 is a deﬁned constant

threshold.

The original oracle generates a sample and checks

it for collisions, which is inefﬁcient as many samples

are discarded. Our version iterates over positions of

all robots v

and tries to generate a new step v

for each

of them towards the sample point u

while avoiding

collisions and also minimizing the angle (u

, v

) by

keeping a list of collision conﬁgurations that need to

be avoided.

Another proposed improvement is the use of the

CARP algorithm (ter Mors et al., 2010) as a local con-

nector as well as a random shufﬂing of the order in

which CARP attempts to plan trajectories of indivi-

dual agents to their desired locations. This algorithm

creates a free time window graph on which agents ﬁnd

the shortest paths one by one while updating the free

time window graph with their paths so that collisions

are avoided.

Algorithm 1: Improved MRdRRT algorithm.

1: T .init (s)

2: loop

3: EXPAND (T )

4: REW IRE (T , v

)

5: P ← CONNECT

TO TARGET (T , t)

6: if not empty(P) then return

RETRIEV E PATH (T , P )

The last set of modiﬁcations to the algorithm is the

addition of steps inspired by RRT* algorithm (Kara-

man and Frazzoli, 2010) which include the new re-

wiring step and modiﬁcation of expansion step, see

Alg. 1. At the start of the algorithm, the tree is initia-

lized with the node that contains the initial conﬁgura-

tion of agents (line 1). The main loop of the algorithm

then starts with the newly modiﬁed expansion phase

(line 3). After a new node is added the rewiring step

is called (line 4) that attempts to revise the structure

of the tree to improve path length to the root. The al-

gorithm ﬁnally tries to connect the newly added node

with the goal conﬁguration. If it succeeds the algo-

rithm returns the found path.

The change to the expansion phase, Alg. 2, con-

sists of connecting the new node v

to a node alre-

ady in the tree T that minimizes the distance traveled

from the initial conﬁguration s. The additional step

of the expansion phase in the original RRT* consists

of checking nodes in the radius around the new node

for the best predecessor and then connecting v

it. However, in the multi-agent discrete scenario (Alg.

2) the computational requirements to perform a simi-

lar task are much higher because it would require to

run a local connector method on each node in the ra-

dius and then perform the distance to root check. The

expansion phase was thus modiﬁed so that it employs

nearest neighbor search instead of radius (line 2). The

key difference is that in the ﬁrst step of expansion the

random sample u (line 1) is generated, but after that

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

174

the new node v

is not created from the nearest neig-

hbor of u. Instead, N nearest neighbors of u are ite-

rated over (lines 6-11) and a new node v

is generated

from each of them using the oracle O

, but not added

into the tree. Each v

is checked for the distance tra-

veled through the tree T towards the root s and only

a node that minimizes this distance is connected to its

corresponding predecessor.

Algorithm 2: Improved MRdRRT EXPAND(T , r).

1: u ← RANDOM SAMPLE ()

2: NNs ← getNearestNeighbours(u)

3: v

pred

= −1

4: d

best

= ∞

5: v

best

6: for c ∈ NNs do

7: v

← O

(c, u)

8: if l

) < d

best

then

9: d

best

= l

)

10: v

pred

= c

11: v

best

= v

12: T .add

vertex



best



13: T .add edge



pred

, v

best



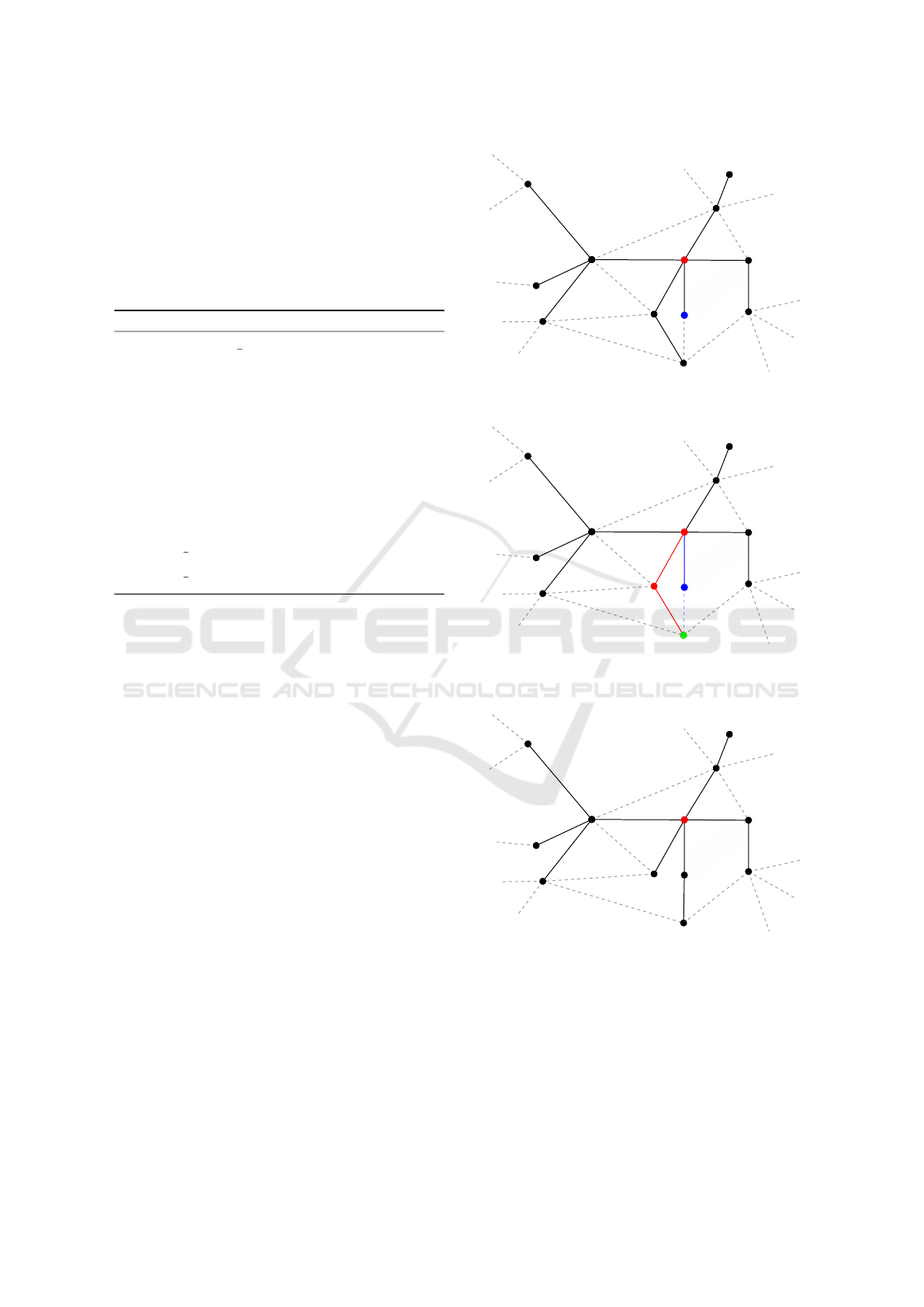
The rewiring step of RRT* locally revises a struc-

ture of T by checking whether nodes within the radius

r around a newly added node v

have the distance tra-

veled towards the root node shorter when they had v

as their predecessor. This step was modiﬁed for the

use in a multi-agent discrete case (Alg. 3) by omitting

the radius and iterating over N nearest neighbors of v

instead. Because these neighboring conﬁgurations c

might not be direct neighbors of v

in the composite

graph G, the local connector is used to obtain a path

between these two nodes (line 3). If the local connec-

tor fails to ﬁnd the path, the neighbor is immediately

skipped (lines 4-5). In the case the local connectors

successes in ﬁnding a path p between v

and c it is

checked whether the length of the path from the root

to v

concatenated with the path p and the node c is

shorter than the distance traveled through T from the

root to c(lines 5-7). If it is shorter, then all nodes of

p are added to T . The ﬁrst node of p is connected as

the successor of v

and the last node of p is chosen as

a new predecessor of c. An example of the rewiring

step is displayed in Fig. 2.

4 EXPERIMENTS

Performance of the proposed method has been evalu-

ated, and comparison with the CARP algorithm (ter

(a) Initial state of the tree. The root node is coloured red,

while the newly added node v

is coloured blue.

(b) The path through the newly added node v

(blue) to one

of its nearest neighbors (green) is shorter than the current

path to this node (red).

Figure 2: Example of the rewiring procedure.

Mors et al., 2010) has been done. The experiments

were performed on two sets of artiﬁcially created

maps and assignments with the aim to compare the

quality of obtained results and runtime as well as the

reliability of both algorithms.

This ﬁrst set of maps was created to demonstrate

how both algorithms perform depending on the den-

Improved Discrete RRT for Coordinated Multi-robot Planning

175

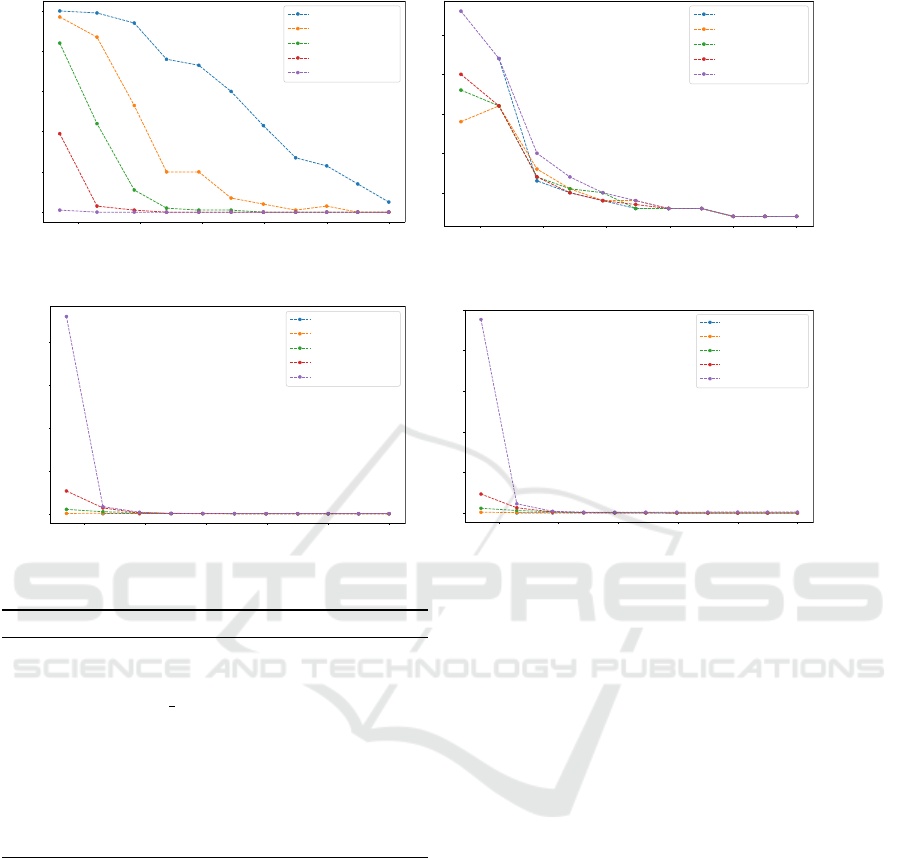
(a) Number of failed assignments

100 0 110 0 120 0 130 0 140 0 150 0

Num ber of edges in graph

100

# failed assignm ent s

CARP lim it 1

CARP lim it 1 0

CARP lim it 1 0 0

CARP lim it 1 0 0 0

dRRT

(b) Median number of plan steps

1000 1100 1200 1300 1400 1500

Num ber of edges in graph

Plan steps

CARP lim it 1

CARP lim it 1 0

CARP lim it 1 00

CARP lim it 1 000

dRRT

1000 1100 1200 1300 1400 1500

Num ber of edges in graph

500

1000

1500

2000

It erat ions

CARP lim it 1

CARP lim it 10

CARP lim it 100

CARP lim it 1000

dRRT

(d) Median time to plan

1000 1100 1200 1300 1400 1500

Num ber of edges in graph

2000

4000

6000

8000

10000

Median t [m s]

CARP lim it 1

CARP lim it 10

CARP lim it 100

CARP lim it 1000

dRRT

Figure 3: Comparison of the proposed approach (dRRT) with CARP.

Algorithm 3: REWIRE(T , v

1: NNs ← getNearestNeighbours(v

)

2: for c ∈ NNs do

3: p ← LOCAL CONNECT OR(v

, c)

4: if p ←

0 then

5: Continue

6: n ← LastNode (p)

7: if l

) + l (p) +δ(n, c) < l

8: T .add(p)

9: c.predecessor = n

sity of the given graph and the number of cycles in it.

The set was created by generating a random spanning

tree of a 20 × 20 grid map followed by the creation of

additional maps by iteratively adding a ﬁxed number

of original edges into the spanning tree. The experi-

ments were thus carried out on the set consisting of

11 maps ranging from a spanning tree to the full grid.

Furthermore, 100 different assignments for a ﬂeet of

100 robots were created by randomly sampling start

and goal nodes for each agent and each such assig-

nment was tested on all of these maps. The CARP

algorithm was tested by giving it the limit of 1, 10,

100, 1000 attempts to ﬁnd a solution where the order

in which agents were planned was randomly shufﬂed

for each attempt.

The results of this experiment can be seen in

Fig. 3. The ﬁrst thing to notice in Fig. 3a is that the

proposed approach shows a much higher success rate

even on the spanning tree, where it had its single fai-

lure. Contrary, CARP had 100% failure rate on the

spanning tree when given only 1 attempt and 39%

when given 1000 attempts. It can be seen in Fig. 3c

and Fig. 3d that once the number of edges in the graph

reaches 1090, the algorithms behave very similarly in

terms of runtime and the needed number of iterati-

ons to ﬁnd the plan. The proposed method provides

a slightly higher median of a number of steps of the

resulting plan as can be seen in Fig. 3b. This can be at-

tributed to the fact that the median is calculated from a

higher number of successful plans compared to CARP

algorithm.

The second set of maps was created speciﬁcally

together with assignments so that the problems would

be impossible to solve for the CARP algorithm. The

maps and assignments were randomly generated by

the following process:

1. Create a basic problem that is impossible to solve

for the CARP algorithm depicted in Fig. 4a. Ar-

rows indicate the starting and goal positions of ro-

bots A and B on the graph. CARP fails because the

agents need to swap their positions while having

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

176

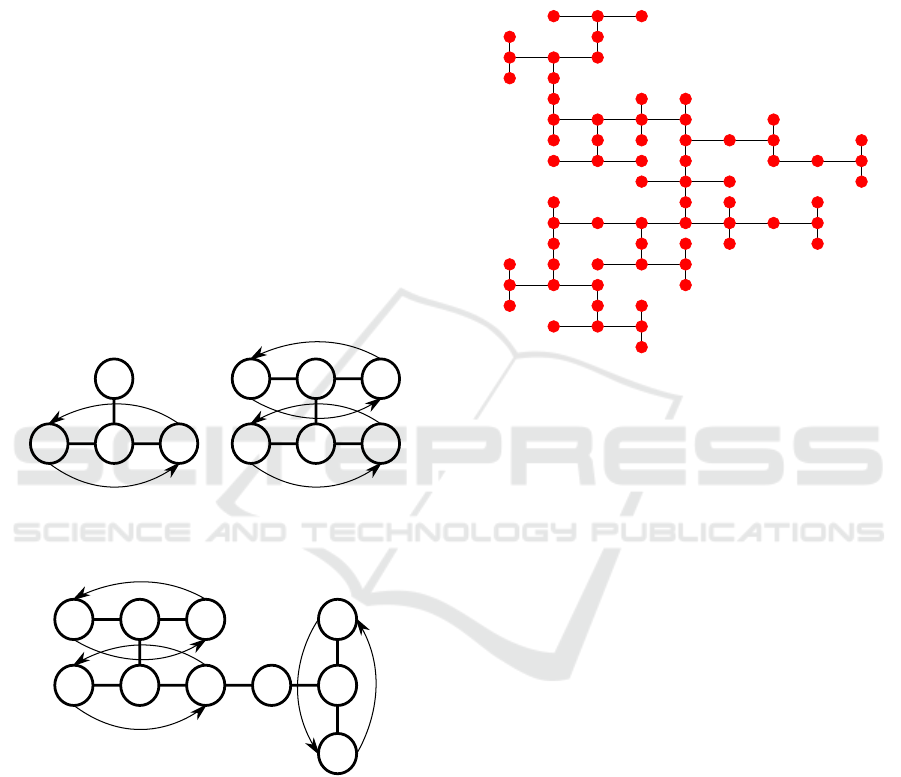
the same distance to the only node they can use

to avoid each other. Because CARP plans agents

sequentially one by one while ignoring the sub-

sequent agents, no ordering of these agents can

solve this issue.

2. Pick random node that has only one edge associa-

ted with it.

3. Either add 2 nodes A and B to either side of this

node if possible along with corresponding assign-

ment of 2 agents – The ﬁrst agent going from A to

B and the second one from B to A. The example

of this step can be seen in Fig. 4b. The alternative

method to expand the map is to connect the same

structure to it as in the Step 1 together with the

same type of assignment, the example of which

can be seen in Fig. 4c.

4. Repeat Steps 2 and 3 until the map of a required

size is generated.

The example of a fully generated map following

the previous steps can be seen in Fig. 5.

A B

(a) Base problem.

A B

(b) First type of map

expansion

A B

C D

Figure 4: Map generation procedure.

The second set of experiments was carried out on

the second set of maps with the aim to illustrate the

behavior of the proposed algorithm on assignments

that CARP algorithm can not solve. The total of 400

different combinations of a map and assignment were

generated: 100 each for 10, 20, 30 and 40 agents.

The results of this experiment can be seen in Fig. 6.

The setup numbers 1 to 4 correspond to the number

of agents 10 to 40 respectively.

For up to 30 agents the success rate is 100% while

it is decreased to 95% for 40 robots. Regarding the

computational time results, the algorithm takes ap-

proximately 1 second to calculate the paths for each

agent in assignments that are impossible to solve for

CARP algorithm for up to 30 agents even with relati-

vely complicated assignments.

Figure 5: Example of a generated map.

5 CONCLUSION

In this paper, we presented a novel algorithm for coor-

dination of a ﬂeet of robots on a graph. The algorithm

is based on a discrete version of RRT for multiple ro-

bots (MRdRRT), but it signiﬁcantly improves particu-

lar steps of this algorithm which allows it to solve pro-

blems assuming tens of robots in few seconds. This is

in contrast to the original MRdRRT which can solve

problems up to ten robots in tens of seconds. The ex-

perimental comparison moreover shows that the pro-

posed approach can solve problems unsolvable for

CARP which is one of the best practical algorithms

nowadays. Finally, our approach is comparable to

CARP in computational time and quality of the ge-

nerated solutions for problems with up to 100 robots

which are solvable by CARP. The main drawback is

that the computational complexity with respect to the

number of robots is still exponential.

The ideas of RRT* showed promise in bringing

the obtained solution closer to optimum, but for the

cost of increased execution time. For this reason, the

future work should focus on improvement of the pro-

posed algorithm in terms of reducing the number of

required iterations to ﬁnd the ﬁrst solution. This could

be done for example by reducing the dimensionality

of the problem by planning smaller groups of agents

Improved Discrete RRT for Coordinated Multi-robot Planning

177

Figure 6: Results of the proposed approach on assignments which CARP is unable to solve.

in batches and then considering them as obsta-

cles moving in time for the subsequent groups.

ACKNOWLEDGEMENTS

This work has been supported by the European

Union’s Horizon 2020 research and innovation

programme under grant agreement No 688117,

by the Technology Agency of the Czech Repu-

blic under the project no. TE01020197 “Centre

for Applied Cybernetics”, the project Rob4Ind4.0

CZ.02.1.01/0.0/0.0/15 003/0000470 and the Euro-

pean Regional Development Fund. The work of Ja-

kub Hv

ezda was also supported by the Grant Agency

of the Czech Technical University in Prague, grant

No. SGS18/206/OHK3/3T/37.

REFERENCES

Bennewitz, M., Burgard, W., and Thrun, S. (2001). Optimi-

zing schedules for prioritized path planning of multi-

robot systems. In Robotics and Automation, 2001.

Proceedings 2001 ICRA. IEEE International Confe-

rence on, pages 271 – 276 vol.1.

Cap, M., Novak, P., Kleiner, A., Selecky, M., and Pechou-

cek, M. (2015). Prioritized Planning Algorithms for

Trajectory Coordination of Multiple Mobile Robots.

IEEE Transactions on Automation Science and Engi-

neering, Special Is.

Chiew, K. (2010). Scheduling and routing of autonomous

moving objects on a mesh topology. Operational Re-

search, 12(3):385–397.

DeWilde, B., Ter Mors, A., and Witteveen, C. (2014). Push

and Rotate: A complete Multi-agent Pathﬁnding al-

gorithm. Journal of Artiﬁcial Intelligence Research,

51:443–492.

Dobson, A., Solovey, K., Shome, R., Halperin, D., and Be-

kris, K. E. (2017). Scalable asymptotically-optimal

multi-robot motion planning. In 2017 International

Symposium on Multi-Robot and Multi-Agent Systems

(MRS), pages 120–127.

Geramifard, A., Chubak, P., and Bulitko, V. (2006). Biased

Cost Pathﬁnding. In AAAI Conference on Artiﬁcial In-

telligence and Interactive Digital Entertainment, pa-

ges 112–114.

Goldreich, O. (2011). Finding the Shortest Move-Sequence

in the Graph-Generalized 15-Puzzle Is NP-Hard. In

Goldreich, O., editor, Studies in Complexity and Cryp-

tography. Miscellanea on the Interplay between Rand-

omness and Computation - In Collaboration with Li-

dor Avigad, Mihir Bellare, Zvika Brakerski, Shaﬁ

Goldwasser, Shai Halevi, Tali Kaufman, Leonid Le-

vin, Noam Nisan, Dana Ron,, volume 6650 of Lecture

Notes in Computer Science, pages 1–5. Springer.

Hopcroft, J., Schwartz, J., and Sharir, M. (1984). On the

Complexity of Motion Planning for Multiple Indepen-

dent Objects; PSPACE- Hardness of the ”Warehouse-

man’s Problem”. The International Journal of Robo-

tics Research, 3(4):76–88.

Karaman, S. and Frazzoli, E. (2010). Incremental sampling-

based algorithms for optimal motion planning. CoRR,

abs/1005.0416.

Kiril Solovey, Oren Salzman, D. H. (2014). Finding a

needle in an exponential haystack: Discrete rrt for ex-

ploration of implicit roadmaps in multi-robot motion

planning. Algorithmic Foundations of Robotics XI, pa-

ges 591–607.

Latombe, J.-C. (1991). Robot Motion Planning. Kluwer

Academic Publishers, Norwell, MA, USA.

LaValle, S. and Hutchinson, S. (1998). Optimal motion

planning for multiple robots having independent go-

als. IEEE Transactions on Robotics and Automation,

14(6):912–925.

Lavalle, S. M. (1998). Rapidly-Exploring Random Trees: A

New Tool for Path Planning. Technical Report (Com-

puter Science Deptartment, Iowa State University),

11.

Luna, R. and Bekris, K. E. (2011). Efﬁcient and com-

plete centralized multi-robot path planning. In 2011

IEEE/RSJ International Conference on Intelligent Ro-

bots and Systems, pages 3268–3275. IEEE.

Parker, L. E. (2009). Path Planning and Motion Coordina-

tion in Multiple Mobile Robot Teams. Encyclopedia

of Complexity and System Science.

Peasgood, M., Clark, C. M., and McPhee, J. (2008).

A Complete and Scalable Strategy for Coordinating

Multiple Robots Within Roadmaps. Robotics, IEEE

Transactions on, 24(2):283–292.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

178

Ryan, M. R. (2008). Exploiting Subgraph Structure in

Multi-Robot Path Planning. Journal of Artiﬁcial In-

telligence Research, pages 497–542.

Silver, D. (2005). Cooperative Pathﬁnding. In The 1st con-

ference on Artiﬁcial Intelligence and Interactive Digi-

tal Entertainment, pages 117–122.

Simeon, T., Leroy, S., and Lauumond, J.-P. (2002). Path

coordination for multiple mobile robots: a resolution-

complete algorithm. IEEE Transactions on Robotics

and Automation, 18(1):42–49.

ter Mors, A. W., Witteveen, C., Zutt, J., and Kuipers, F. A.

(2010). Context-aware route planning. In Dix, J.

and Witteveen, C., editors, Multiagent System Techno-

logies, pages 138–149, Berlin, Heidelberg. Springer

Berlin Heidelberg.

van den Berg, J. and Overmars, M. (2005). Prioritized mo-

tion planning for multiple robots. In 2005 IEEE/RSJ

International Conference on Intelligent Robots and

Systems, pages 430–435. IEEE.

van den Berg, J., Snoeyink, J., Lin, M. C., and Manocha, D.

(2009). Centralized path planning for multiple robots:

Optimal decoupling into sequential plans. In Trinkle,

J., Matsuoka, Y., and Castellanos, J. A., editors, Ro-

botics: Science and Systems V, University of Washing-

ton, Seattle, USA, June 28 - July 1, 2009. The {MIT}

Press.

Wang, K.-H. C. and Botea, A. (2008). Fast and Memory-

Efﬁcient Multi-Agent Pathﬁnding. In ICAPS, pages

380–387.

Wang, W. and Goh, W. B. (2015). A stochastic algorithm

for makespan minimized multi-agent path planning in

discrete space. Applied Soft Computing, 30:287–304.

Improved Discrete RRT for Coordinated Multi-robot Planning

179