
Multi-Objective Approach for Support Vector Machine Parameter
Optimization and Variable Selection in Cardiovascular Predictive
Modeling
Christina Brester
1,3
, Ivan Ryzhikov
1,3
, Tomi-Pekka Tuomainen
2
, Ari Voutilainen
2
,
Eugene Semenkin
3
and Mikko Kolehmainen
1
1
Department of Environmental and Biological Sciences, University of Eastern Finland, Kuopio, Finland
2
Institute of Public Health and Clinical Nutrition, University of Eastern Finland, Kuopio, Finland
3
Institute of Computer Sciences and Telecommunication, Reshetnev Siberian State University of Science and Technology,
Krasnoyarsk, Russia
Keywords: Support Vector Machine, Cardiovascular Predictive Modeling, Multi-objective Evolutionary Algorithm,
Parameter Optimization, Variable Selection.
Abstract: We present a heuristic-based approach for Support Vector Machine (SVM) parameter optimization and
variable selection using a real-valued cooperative Multi-Objective Evolutionary Algorithm (MOEA). Due to
the possibility to optimize several criteria simultaneously, we aim to maximize the SVM performance as
well as minimize the number of input variables. The second criterion is important especially if obtaining
new observations for the training data is expensive. In the field of epidemiology, additional model inputs
mean more clinical tests and higher costs. Moreover, variable selection should lead to performance
improvement of the model used. Therefore, to train an accurate model predicting cardiovascular diseases,
we decided to take a SVM model, optimize its meta and kernel function parameters on a true population
cohort variable set. The proposed approach was tested on the Kuopio Ischemic Heart Disease database,
which is one of the most extensively characterized epidemiological databases. In our experiment, we made
predictions on incidents of cardiovascular diseases with the prediction horizon of 7–9 years and found that
use of MOEA improved model performance from 66.8% to 70.5% and reduced the number of inputs from
81 to about 58, as compared to the SVM model with default parameter values on the full set of variables.
1 INTRODUCTION
Cardiovascular diseases (CVDs) are one of the most
frequent causes of people’s deaths around the world
for today. Stress, unhealthy diet, physical inactivity,
harmful use of tobacco and alcohol increase the risk
of CVDs significantly. Nowadays, even young
people suffer from CVDs. According to the report of
the World Health Organization, in 2015 about 17.7
million people died from CVDs (it was 31% of all
global deaths) (World Health Organization, 2017).
Early detection of a high CVD risk for a patient is
considered to be the main issue for doctors to
undertake appropriate measures in time and prevent
non-fatal or fatal incidents of CVDs.
In this paper, we develop a predictive system
based on a Support Vector Machine (SVM) and a
Multi-Objective Evolutionary Algorithm (MOEA),
which is applied to tune SVM meta and kernel
function parameters and select a proper set of input
variables. There are many comparative studies in
which SVMs outperform other predictive models on
different problems, including medical diagnostics
(Bellazzi and Zupan, 2008; Yu et al., 2005).
Moreover, this model copes successfully with a
high-dimensional set of input variables (Ghaddar
and Naoum-Sawaya, 2018), which is important for
our study because the data used contains 81
variables.
A number of successful studies are devoted to
optimizing SVM parameters by various heuristic
approaches. In most cases, however, only one-
criterion optimization algorithms are used (Ren and
Bai, 2010; Liao et al., 2015). In our study, we
Brester, C., Ryzhikov, I., Tuomainen, T-P., Voutilainen, A., Semenkin, E. and Kolehmainen, M.
Multi-Objective Approach for Support Vector Machine Parameter Optimization and Variable Selection in Cardiovascular Predictive Modeling.
DOI: 10.5220/0006866001990205
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 199-205
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
199

employ a real-valued cooperative MOEA to
optimize two criteria at once: the model predictive
ability and the number of input variables (Cho and
Hoang, 2017; Zhao et al., 2011). In epidemiology,
reducing the number of input variables is quite
important because it leads to fewer clinical tests and
lower costs for patients.
In medical data mining studies, researches often
compare their proposals with conventional models
on several test problems from repositories (Brameier
and Banzhaf, 2001; Cheng et al., 2006; Tu et al.,
2009). However, our goal is not to compare different
models but to take the first step in building a
predictive model based on real “raw” high-
dimensional data. The presented model has been
trained and tested on the Kuopio Ischemic Heart
Disease (KIHD) dataset, which is one of the most
properly characterized epidemiological study
populations with a huge variety of variables:
biomedical, psychosocial, behavioral, clinical and
other. Previously, some of these variables have been
pre-selected and used in risk factor analysis. In our
approach, we do not involve experts to pre-select
explanatory variables but perform variable selection
algorithmically.
The next sections describe the approach
proposed in detail, experimental results, conclusions,
and future plans.
2 PREDICTIVE MODELING
SVM models are widely used in machine learning to
solve classification and regression problems from
various practical areas (Boser et al., 1992).
Generally, training SVM models is performed by
minimizing the error function (1):
min,
2
1
1
→
⋅+⋅
=
N
i
i
T
ξCww
(1)
which is subject to the constraints:
i
i
T
i
by ξ−≥+⋅ 1)( xw
and
,0≥
ξ
i
Ni ,...,1=
,
where C is an adjustable parameter of regularization,
i
ξ expresses an error
,0max( ))(1 b
i
T
i
y +⋅⋅− xw
on training examples
),,(
ii
yx ,1±∈
i
y
Ni ,...,1=
,
N is the number of training examples.
These models are more complex in comparison
with a linear regression and allow reflecting non-
linear dependencies due to the ‘kernel trick’, i.e.
kernel functions map points into a higher
dimensional space, where a linear separation is
applicable. In this work, we use a Radial Basis
Function as a kernel (2):
)exp(),(
2
i2i1i2i1
K xxxx −⋅σ−= . (2)
SVMs have a strong theoretical background and,
in general, training these models is reduced to
solving a dual quadratic programming problem with
one global optimum.
By this time, a number of effective approaches to
solve this quadratic programming problem have
been proposed, for example, Sequential Minimal
Optimization (SMO) (Platt, 1998). However, there
are still some parameters which require proper
tuning. They are meta (C) and kernel function
parameters ( σ ) and, as can be found in other studies
(Liao et al., 2015; Syarif et al., 2016), an arbitrary
choice of their values may lead to a significant
deterioration in the solution quality. The easiest way
to tune these parameters is to use a grid search, but it
requires quite a lot of computational time to check a
good amount of values. As an alternative, heuristic
optimization methods might be applied to find a
pseudo-optimal combination of parameter values.
Evolutionary Algorithms (EA) operate with a set
of candidate-solutions, which allows investigating a
search space in a parallel way. One of important
benefits of using EAs in optimizing SVM
parameters is a possibility to incorporate variable
selection into parameter tuning. This leads not only
to finding proper values of SVM meta and kernel
function parameters but also to determination of an
effective input variable set corresponding to these
particular SVM parameters. In our study, we
propose to apply a MOEA to optimize two criteria
simultaneously (3). The first criterion reflects the
model predictive ability and the second one
expresses the number of selected variables
selected
N :
.min
min;_1
2
1
→=
→−=
selected
Nf
scoreFf
(3)
In the first criterion, we estimate the F-score
metric (Goutte and Gaussier, 2005), specifically the
F
1
-measure with equally weighted precision and
recall.
To solve this two-criterion optimization problem
(3), we have developed a real-valued cooperative
modification of the Strength Pareto Evolutionary
Algorithm 2 (SPEA2) (Zitzler et al., 2002). In this
algorithm, a chromosome consists of real-valued
genes which code SVM parameters C, σ , and input
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
200

Figure 1: SVM training with a cooperative SPEA2.
variables. To evaluate criteria f
1
and f
2
for each
chromosome, it should be decoded in the following
way:
;
1
geneC = ;
2
gene=σ
<
≥
=
+
+
5.0if,selectednot
,5.0ifselected,
2j
2j
j
gene
gene
x
. (4)
Then, for each pair (C,
σ
) with a certain set of
selected variables, the SVM model is trained using
the SMO algorithm. The F-score metric is estimated
in the 3-fold cross-validation procedure on the
training data.
The modified SPEA2 is based on an island
model cooperation (Whitley et al., 1997), which
allows us to reduce computational time because a
number of populations evolve in a parallel way. In
addition to that, cooperative modifications of EAs
demonstrate higher performance in comparison with
their original versions (Brester et al., 2018).
Available resources are divided among
subpopulations (islands) equally:
L
M
M
isl
= , where
M
is the total number of individuals,
L
is the
number of subpopulations. One crucial concern in
the island cooperation is a migration process, which
implies that in some
r
m iterations (generations)
islands exchange the best
c
m individuals. In the
proposed modification, the migration set replaces
individuals with the worst fitness values in each
island population. Thus, we have implemented a
fully connected topology: each island sends its best
solutions to all the other ones and, as a response, it
receives solutions from other islands. The final
solution is obtained by merging all the populations
and archives, and, then, selecting the best solution
based on the f
1
criterion (Figure 1).
Originally, SPEA2 operates with binary strings,
however, for real-valued optimization problems a
number of genetic operators have been developed.
To select effective solutions for the offspring
generation, we apply binary tournament selection.
As a crossover operator, we use intermediate
recombination. In a mutation operator, we
implement the next scheme (Liu et al., 2009):
,
1yprobabilitwith,
yprobabilitwith),(
'
−
−⋅γ+
=
mj
mjjjj
j
px
pabx
x
(5)
with
=
+η
+η
⋅−−
<−⋅
γ
otherwise,)22(1
5.0if,1)2(
1
1
1
1
rand
randrand
j
, (6)
where rand is a uniformly random number [0, 1].
There are two control parameters: the mutation rate
n
p
m
1
=
, where n is the chromosome length, and the
distribution index
η
is equal to 1.0 (6).
j
a and
j
b
are the lower and the upper bounds of the
j-th
variable in the chromosome (5).
3 DATABASE DESCRIPTION
The epidemiologic ongoing cohort study, KIHD
(Kuopio Ischemic Heart Disease), was started in
1984 to investigate risk factors of CVDs and some
other diseases in the population of Eastern Finland,
where one of the highest rate of coronary heart
disease (CHD) was recorded (Salonen, 1988).
Multi-Objective Approach for Support Vector Machine Parameter Optimization and Variable Selection in Cardiovascular Predictive
Modeling
201

Table 1: The KIHD data description.
Examinations Period Participants Variables
Baseline 1984-1989 Men 8000
4-year 1991-1993 Men 5000
11-year 1998-1999 Men, women 3000
20-year 2006-2008 Men, women 750
In Table 1, we present a timeline of the KIHD
study, which currently consists of four examination
periods. At the baseline time point (1984–1989),
2,682 middle aged (42, 48, 54, 60 years) recruited
men from the city of Kuopio and its surrounding
communities of Eastern Finland were randomly
chosen for participation in the KIHD study. Later, in
1998-2001, 920 ageing recruited women joined this
follow-up study.
This dataset is one of the most thoroughly
characterized epidemiologic study populations in the
world, with thousands of biomedical, psychosocial,
behavioural, clinical, and other variables in its
dataset. The KIHD study, as a valuable source for
epidemiologic research, has attracted many
scientists, which has yielded in more than 500
original peer reviewed articles in international
scientific journals over the past 30 years. However,
there are no studies yet that would try to use this
unique database for predicting the appearance of
CVDs without any variable pre-selection.
In spite of the fact that, originally, the main focus
in the KIHD study was on CVDs, and especially on
ischemic heart disease, other health outcomes such
as cancer, diabetes, and dementia, have been also
investigated (Kurl
et al., 2015; Tolmunen et al.,
2014, Virtanen
et al., 2016; Brester et al., 2016).
In our predictive modeling, we engage the 20-
year examination data with a representative subset of
variables preselected by an experienced
epidemiologist. This data contains information about
incidents and fatal events of various diseases by
2015. In this work, we consider only CVD-related
outcomes (stroke, CHD, acute myocardial infarction
(AMI), etc.) All the subjects were labelled as
‘healthy’ (none of CVDs occurred) and ‘unhealthy’
(any incident of CVDs or fatal CVD event
occurred).
Moreover, we applied the following pre-
processing:
1) Subjects who had any CVD in their
anamnesis at the 20-year examination were
excluded so that we got state vectors (vectors
of variables) for people who were healthy at
the beginning of the observation period;
2) Subjects with more than 50% of missing
values in the state vector and, then, variables
with more than 30% of gaps were removed.
The rest of missing values were filled with a
nearest neighbour method (Beretta and
Santaniello, 2016).
Thus, all these pre-processing steps led to the
dataset with 778 subjects and 81 variables: 360 sick
subjects and 418 healthy subjects. In the next
section, we present the experimental results of our
modeling aimed at making accurate predictions for
the subjects about CVDs by 2015 bases on their state
vectors recorded in 2006–2008.
4 EXPERIMENTS AND RESULTS
Before training predictive models on the KIHD data,
we checked if there were outliers or not. Data was
collected from different sources, some variables
were measured, others were recorded from
questionnaires. It is clear that there might be
mistakes. Moreover, there might be even wrong
labels because people do not always go to the
hospital if they have some CVD symptoms.
Therefore, firstly, we decided to estimate Cook’s
distance, which is used in Regression Analysis to
find the most influential points in the sample (Cook,
1977). Cook’s distance for the
i-th sample point is
calculated based on the difference between a linear
regression trained on the whole dataset and a
regression model trained on the dataset after
removing the
i-th sample point. The higher Cook’s
distance is, the more influential point we have.
In Figure 2 and 3, we demonstrate Cook’s
distance values for KIHD subjects and Cook’s
distance distribution in a form of a histogram.
Figure 2: Cook’s distances for KIHD subjects.
Figure 3: Cook’s distance distribution estimation.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
202
In theory, there is no strict rule how to choose a
threshold to determine outliers. After a number of
experiments, we decided to remove KIHD subjects
with Cook’s distance which is higher than 0.0025, so
that to keep 85% of the sample.
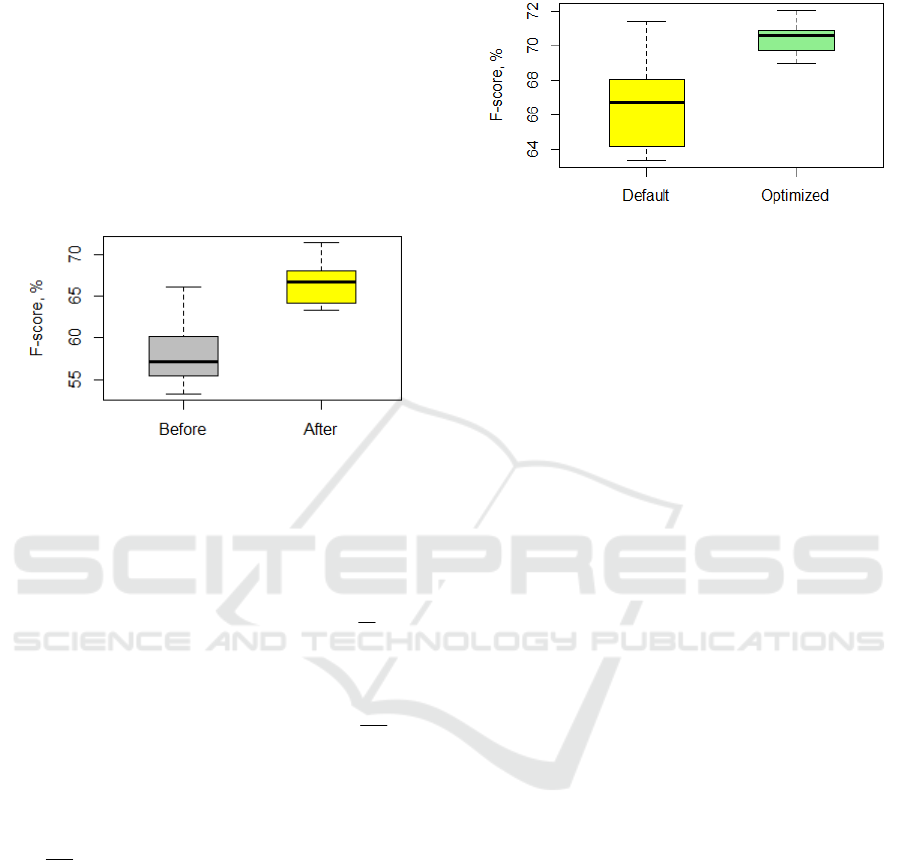
The SVM model performance was assessed in
the 5-fold cross-validation procedure. In Figure 4,
we compare F-score values before and after
removing the most influential points. In this
experiment, default values of
C and σ were 1.0 and
0.01, correspondingly (these values are used in
WEKA package (Hall
et al., 2009)).
Figure 4: SVM performance with default parameters
before and after removing outliers.
In the next experiment, we applied the modified
SPEA2 to optimize SVM parameters and perform
variable selection. The algorithm parameters were
assigned as follows:
18=
isl
M , 20=T (the number
of generations),
,3=L
4=
r
m , 2=
c
m , 5=
isl
M
(the archive size),
1.0
1
=a , 10
1
=b (bounds of
possible C values),
001.0
2
=a , 1.0
2
=b (bounds of
possible σ values),
0=
j
a
,
1=
j
b
,
nj ,3=
. To
start the search from larger variable sets and prevent
the algorithm from premature convergence to
solutions with very few selected variables, in the
initial population we generated the
j-th gene
( nj ,3= ) based on the rule (7):
=
8.0ofyprobabilitwith),1;5.0(
2.0ofyprobabilitwith),5.0;0(
rand
rand
gene
j
.
(7)
For each fold in the cross-validation procedure,
we obtained the following optimized parameter
(
C, σ ) values: 1 – (5.6876, 0.0541), 2 – (6.0277,
0.0536), 3 – (7.5469, 0.0387), 4 – (6.2696, 0.0380),
5 – (4.8698, 0.0771). The number of selected
variables was equal to 57.8 averaged over 5 folds. In
Figure 5, we compare F-score values achieved by
SVM models with default and optimized parameters,
on the full and reduced variable sets.
Figure 5: SVM performance with default parameters on
the full dataset and optimized parameters on the selected
variable set.
Thus, in this experiment we increased the
average F-score value from 66.8 % up to 70.5% with
the MOEA use.
At this point, we chose one best solution from all
variants returned by MOEA islands. Indeed, we
offer to return populations and archives with non-
dominated individuals, as can be seen in Figure 1,
because this allows us to choose not only one but
also a number of good solutions which might be
included in the ensemble of SVM models. This idea
should be taken into account as a possible way to
improve the achieved performance.
5 CONCLUSION
In this study, we introduced the effective approach
aimed at training SVM models with optimized
parameters and performing variable selection at
once. Simultaneous optimization of two criteria
became possible owing to the MOEA use, namely
the real-valued cooperative SPEA2. The island
model cooperation allowed us not only to reduce
computational time but also to increase the
performance of the original SPEA2.
Practically, our proposal was applied to
cardiovascular predictive modeling: we investigated
its effectiveness on the thoroughly characterized
epidemiological data containing many different
subjects and variables. Typically, CVDs are
predicted by using a few pre-selected, already
known, explanatory variables. Our approach
diminishes the need for pre-selection and,
simultaneously, may reveal novel previously
unknown explanatory variables. On average, we
managed to achieve 70.5% of F-score, which,
definitely, should be improved later. However,
applying the MOEA we could obtain 5.5% of the
Multi-Objective Approach for Support Vector Machine Parameter Optimization and Variable Selection in Cardiovascular Predictive
Modeling
203

relative improvement in F-score and accomplish
variable selection. All in all, this study combines for
the first time the real world epidemiological data, the
advanced EA-based optimization and database pre-
processing using Cook’s distance.
Currently, we have predicted CVDs for the next
7-9 years with one time point predictors, whereas, in
the future we plan to test the presented approach in
multiple time point predictor data (baseline, 4-year,
11-year examinations) and make predictions for
longer periods.
Moreover, at the next step, we should take
advantage of the MOEA distinctive feature to return
a number of non-dominated points, which might be
involved in the ensemble of SVM models.
REFERENCES
Bellazzi, R., Zupan, B., 2008. Predictive data mining in
clinical medicine: Current issues and guidelines.
International Journal of Medical Informatics, vol. 77,
issue 2, pp. 81-97.
Beretta, L., Santaniello, A., 2016. Nearest neighbour
imputation algorithms: a critical evaluation. BMC Med
Inform Decis Mak, 16 Suppl 3: 74. doi:
10.1186/s12911-016-0318-z.
Boser, B.E., Guyon, I.M., Vapnik, V.N, 1992. A training
algorithm for optimal margin classifiers. Proceedings
of the fifth annual workshop on Computational
learning theory – COLT '92, pp. 144-52.
Brameier, M., Banzhaf, W., 2001. A Comparison of
Linear Genetic Programming and Neural Networks in
Medical Data Mining. IEEE Transactions on Evolu-
tionary Computation IEEE, vol. 5, no. 1, pp. 1-10.
Brester, Ch., Kauhanen, J., Tuomainen, T. P., Semenkin,
E., Kolehmainen, M., 2016. Comparison of Two-
Criterion Evolutionary Filtering Techniques in
Cardiovascular Predictive Modelling. Proceedings of
the 13th International Conference on Informatics in
Control, Automation and Robotics (ICINCO), vol. 1,
pp. 140-145.
Brester, Ch., Ryzhikov, I., Semenkin, E., Kolehmainen,
M., 2018. On Island Model Performance for
Cooperative Real-Valued Multi-Objective Genetic
Algorithms. Advances in Swarm and Computational
Intelligence. In press
Cheng, T-H., Wei, Ch-P., Tseng V.S., 2006. Feature
Selection for Medical Data Mining: Comparisons of
Expert Judgment and Automatic Approaches. IEEE
proc of 19th IEEE Symposium on Computer-Based
Medical Systems (CBMS‘06), pp. 165-170.
Cho, M. Y., Hoang,
T. T., 2017. Feature Selection and
Parameters Optimization of SVM Using Particle
Swarm Optimization for Fault Classification in Power
Distribution Systems. Comput Intell Neurosci.
DOI: 10.1155/2017/4135465.
Cook, R.D., 1977. Deletion of influential observation in
linear regression. Techno-metrics, 19, pp. 15-18.
Ghaddar, B., Naoum-Sawaya, J., 2018. High dimensional
data classification and feature selection using support
vector machines. European Journal of Operational
Research, vol. 265, issue 3, pp. 993-1004.
Goutte, C., Gaussier, E., 2005. A probabilistic
interpretation of precision, recall and F-score, with
implication for evaluation. ECIR'05 Proceedings of
the 27th European conference on Advances in
Information Retrieval Research, pp. 345–359.
Hall, M., Frank, E., Holmes, G., Pfahringer, B.,
Reutemann, P., Witten, I. H., 2009. The WEKA Data
Mining Software: An Update. SIGKDD Explorations,
Volume 11, Issue 1.
Kurl, S, Jae, SY, Kauhanen, J, Ronkainen, K, Laukkanen,
JA, 2015. Impaired pulmonary function is a risk
predictor for sudden cardiac death in men. Ann Med,
47(5), pp. 381–385.
Liao P., Zhang X., Li, K., 2015. Parameter Optimization
for Support Vector Machine Based on Nested Genetic
Algorithms. Journal of Automation and Control
Engineering, vol. 3, no. 6, pp. 507-511.
Liu, M., Zou, X., Chen, Y., Wu, Z., 2009. Performance
assessment of DMOEA-DD with CEC 2009 MOEA
competition test instances. 2009 IEEE Congress on
Evolutionary Computation. DOI: 10.1109/CEC.2009.
4983309.
Platt, J., 1999. Fast Training of Support Vector Machines
using Sequential Minimal Optimization. Advances in
Kernel Methods, pp. 185-208.
Ren, Y., Bai, G., 2010. Determination of Optimal SVM
Parameters by Using GA/PSO. Journal of computers,
vol. 5, no. 8, pp. 1160-1168.
Salonen, J. T., 1988. Is there a continuing need for
longitudinal epidemiologic research? The Kuopio
Ischaemic Heart Disease Risk Factor Study. Ann Clin
Res, 20(1-2), pp. 46-50.
Syarif, I., Prugel-Bennett, A., Wills, G., 2016. SVM
Parameter Optimization Using Grid Search and
Genetic Algorithm to Improve Classification Perfor-
mance. Telkomnika, vol. 14, no. 4, pp. 1502- 1509.
Tolmunen, T, Lehto, S. M., Julkunen, J., Hintikka, J.,
Kauhanen, J., 2014. Trait anxiety and somatic
concerns associate with increased mortality risk: a 23-
year follow-up in aging men. Ann Epidemiol, 24(6),
pp. 463-468.
Tu, M. C., Shin, D., Shin, D. K., 2009. A Comparative
Study of Medical Data Classification Methods Based
on Decision Tree and Bagging Algorithms. IEEE proc
of Eighth International Conference on Dependable
Autonomic and Secure Computing, pp. 183-187.
Virtanen, J. K, Mursu, J, Virtanen, H. E., Fogelholm, M.,
Salonen, J. T., Koskinen, T. T., Voutilainen, S.,
Tuomainen, T. P., 2016. Associations of egg and
cholesterol intakes with carotid intima-media
thickness and risk of incident coronary artery disease
according to apolipoprotein E phenotype in men: the
Kuopio Ischemic Heart Disease Risk Factor Study. Am
J Clin Nutr, 103(3), pp. 895-901.
World Health Organization: fact sheet ‘Cardiovascular
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
204

diseases (CVDs)’, 2017. URL: http://www.
who.int/mediacentre/factsheets/fs317/en/. Accessed
30.03.2018.
Whitley, D., Rana, S., and Heckendorn, R., 1997. Island
model genetic algorithms and linearly separable
problems. Proceedings of AISB Workshop on Evolu-
tionary Computation, vol.1305 of LNCS: pp. 109-125.
Yu, J. S., Ongarello, S., Fiedler, R., Chen, X. W., Toffolo,
G., Cobelli, C., Trajanoski, Z., 2005. Ovarian
cancer identification based on dimensionality
reduction for high-throughput mass spectrometry data.
Bioinformatics, 21, pp. 2200-2209
Zhao, M., Fu, Ch., Ji, L., Tang, K., Zhou. M., 2011.
Feature selection and parameter optimization for
support vector machines: A new approach based on
genetic algorithm with feature chromosomes. Expert
Systems with Applications, 38(5): pp. 5197-5204.
Zitzler, E., Laumanns, M., Thiele, L., 2002. SPEA2:
Improving the Strength Pareto Evolutionary Algorithm
for Multiobjective Optimization. Evolutionary
Methods for Design Optimisation and Control with
Application to Industrial Problems EUROGEN 2001
3242 (103): pp. 95-100.
Multi-Objective Approach for Support Vector Machine Parameter Optimization and Variable Selection in Cardiovascular Predictive
Modeling
205
