State Space Identification Algorithm based on Multivariable Impulse
Response
Mateus Giesbrecht, Gilmar Barreto and Celso Pascoli Bottura
School of Electrical and Computer Engineering FEEC, University of Campinas UNICAMP, Campinas, SP, Brazil
Keywords:
Identification Algorithms, Least-squares Identification, Parameter Identification, System Identification, Linear
Multivariable Systems, State-space Realization, Impulse Responses, Markov Parameters.
Abstract:
In this paper the definitions of multivariable discrete impulse and multivariable discrete impulse response are
clearly stated and explored. From these definitions, two methods to determine the Markov parameters of a
multivariable linear system from input and output data are described. Combining any of the methods to a
known method to determine the state space model matrices from the Markov parameters, a practical algorithm
to determine state space models from input and output data is obtained. The algorithm is then implemented and
compared to a known subspace identification algorithm. The main contributions of this paper are the explicit
definitions of multivariable discrete impulse and multivariable discrete impulse response, the discussion of
these concepts and the application of them to solve the multivariable linear system identification problem.
1 INTRODUCTION
It is possible to characterize a time invariant discrete
causal linear system from its infinite sequence of dis-
crete impulse response. For Single Input-Single Out-
put (SISO) systems, which in this paper are referred
as monovariable systems, the discrete impulse and the
discrete impulse response are well defined concepts
that are discussed in many standard textbooks such as
(Oppenheim and Schafer, 2010) and (Bottura, 1982).
For Multiple Input-Multiple Output (MIMO) sys-
tems, referred in this paper as multivariable systems,
the multivariable discrete impulse and the multivaria-
ble discrete impulse response are tricky concepts that
are worth of some more discussions and attention. In
this paper it is clearly stated that the multivariable dis-
crete impulse is in fact a set of signals and the multi-
variable discrete impulse response is actually the con-
catenation of the system responses to each one of the
signals in that set. The impulse response is also de-
fined as an infinite set of Markov parameters. Obvi-
ously, those parameters are scalars for monovariable
systems and matrices for multivariable systems.
Although an infinite set of Markov parameters
characterizes a linear system, it is not usual to use this
set to that end because of at least three reasons: The
first one is that, even if just the significant elements of
the infinite set are used, a compact representation of
the system is difficult to achieve. The second one is
that, if this representation is used to simulate the re-
sponse of the system to a given input, the necessary
number of operations is greater than the number of
operations that would be used if the system was des-
cribed by more compact forms. The third is that, with
this representation, it is not possible to determine the
values of the system internal states.
There are many ways to compact the discrete re-
presentation of a system, such as the use of the diffe-
rence equations, the discrete transfer functions or the
discrete state space equations, as proposed in (Kal-
man, 1963). The state space representation is ex-
tremely useful because it provides an efficient algo-
rithm to evaluate the system states and the outputs, as
described in (Kalman, 1960). For this reason, many
methods were developed to determine matrices of the
state space representation of a linear system, given by
the following equations:

X(k + 1) = AX(k) + BU(k)
Y(k) = CX(k) + DU(k)
(1)
in which X(k) ∈ R
n
is the state vector, U(k) ∈ R
m
is
the input and Y(k) ∈ R
l
is the system output. A ∈
R
n×n
, B ∈ R
n×m
, C ∈ R
l×n
e D ∈ R
l×m
are the matri-
ces to be determined.
There are at least two approaches to deal with the
problem of finding a discrete state space representa-
tion of a linear system. The first one is the solution
of the minimal partial realization problem and the se-
466
Giesbrecht, M., Barreto, G. and Bottura, C.
State Space Identification Algorithm based on Multivariable Impulse Response.
DOI: 10.5220/0006866204660473
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 466-473
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

cond one is the use of subspace identification algo-
rithms.
In the first approach, a finite set of Markov para-
meters is assumed to be known, and the state space
matrices are evaluated from this set using a singular
value decomposition (SVD). This approach is explo-
red in the references (Ho and Kalman, 1966), (Tether,
1970), (Inouye, 1983). The problem that this appro-
ach solves is defined as the minimal partial realization
problem, since it aims to find a mathematical realiza-
tion of the system with the minimal possible number
of states and is based on a finite set of Markov para-
meters, that is a partial information from the infinite
set of Markov parameters that in fact represents the
system.
Usually the papers that discuss the minimal partial
realization problem do not detail how to determine the
set of Markov parameters from the system input and
output data. One of the contributions of this paper
is to explore the determination of the set of Markov
parameters from the input and output data, demon-
strating that a practical identification algorithm can
be obtained from this.
The second approach to deal with the problem of
finding a discrete state space representation of a li-
near system is based on organizing the system input
and output data in matrices with a special structure,
that can be used to determine the state space model
matrices. The algorithms that apply this approach are
known as the subspace methods for identification, and
there are at least three of them, as discussed in the se-
quence:
The first algorithm, known as Multivariable Out-
put Error State Space (MOESP), was proposed in
(Verhaegen and Dewilde, 1992a), (Verhaegen and De-
wilde, 1992b). In this algorithm, the system matrices
are obtained from the decomposition of special ma-
trices, assembled with system input and output data.
In the second algorithm, the system states are obtai-
ned from decompositions of a special structure of
data matrices and, after that, the system matrices are
obtained with a simple application of the least squa-
res methods. This approach is used in the Numeri-
cal Algorithm for Subspace Identification (N4SID),
introduced in (Overschee and de Moor, 1994). The
third algorithm is an extension of the application of
the Canonical Correlation Analysis (CCA) to the time
series realization problem considering exogenous in-
puts. The application of the CCA to the time series re-
alization problems was introduced in (Akaike, 1974)
and (Akaike, 1975). This consists on finding an opti-
mal predictor to the future data based on projections
on the subspace spanned by the past data. The ex-
tension of this algorithm for systems with exogenous
inputs was introduced in (Katayama and Picci, 1999)
and is based on finding the projection of the future
outputs on the space of past inputs, outputs and future
inputs.
In this article, an algorithm for multivariable dis-
crete system state space identification is discussed.
The algorithm is based on the determination of the
Markov parameters from the input and output data
and then on the solution of the minimal partial rea-
lization problem by the method proposed in (Ho and
Kalman, 1966). To develop that, the explicit defini-
tion of the multivariable impulse response is explo-
red in section 2. In the same section a procedure to
identify the Markov parameters from discrete impulse
input is also shown. Then, in section 3, a practical
method to find the Markov parameters from input and
output data mentioned in (Katayama, 2005) is descri-
bed. The section 4 is devoted to explain how to solve
the minimal partial realization problem. The combi-
nation of the procedures described in sections 2 or 3
with the one described in section 4 is referred in this
paper as the Multivariable Discrete Impulse Response
Identification (MDIRI) algorithm. In section 5 the re-
sults of an identification problem with the MOESP
and with the MDIRI are shown. Finally, in section 6
the conclusions are presented.
2 DETERMINATION OF
IMPULSE RESPONSE
MATRICES FROM THE
MULTIVARIABLE DISCRETE
IMPULSE
In this section, the determination of the impulse re-
sponse matrices of a linear multivariable system using
the multivariable discrete impulse is developed. Initi-
ally, the noiseless case is discussed and then, the ana-
lysis for an output corrupted by noise is presented.
Let m be the number of inputs and l the number
of outputs of a multivariable time invariant discrete
causal linear system. There is a set of l × m matrices
that relate the l-dimensional system output at the in-
stant k to the m-dimensional inputs on that time and
on the past. Those parameters are denoted as G(k),
k = 0 ...∞. With this definition, denoting the l × 1
output vector at the instant k as:
Y(k) =

y
1
(k) y
2
(k) ·· · y
l
(k)

T
(2)
and the m × 1 input vector at instant k as:
U(k) =

u
1
(k) u
2
(k) ·· · u
m
(k)

T
(3)
State Space Identification Algorithm based on Multivariable Impulse Response
467

the following relation is valid:
Y(k) =
∞
∑
i=0
G(i)U(k − i) (4)
where:
G(k) =




g
11
(k) g
12
(k) . . . g
1m
(k)
g
21
(k) g
22
(k) . . . g
2m
(k)
.
.
.
.
.
.
.
.
.
.
.
.
g
l1
(k) g
l2
(k) ... g
lm
(k)




(5)
Thus, if all elements g
i j
(k), i = 1 .. .l, j = 1 . ..m,
k = 0 ... ∞ are determined, it will be a realization of
the multivariable system.
For stable systems, just a finite set of matrices
G(k) is significant. If the number of significant ma-
trices G(k) is denoted as n
IR
and if the initial state of
the system is assumed zero, the equation (4) can be
rewritten as:
Y(k) =
min(k,n
IR
)
∑
i=0
G(i)U(k − i) (6)
where min(α,β) denotes the smaller number between
α and β.
One of the ways to determine the elements of the
n
IR
significant matrices G(k) is to perform m expe-
riments. In each one of those experiments, the sy-
stem response for an input sequence with u
j
(0) = 1,
j = 1...m, and all other elements null, is observed.
The set of m input signals used in those experiments
is defined in this paper as the multivariable discrete
impulse.
It is important to notice that, differently from the
monovariable case, it is not possible to define only
one input signal as the multivariable discrete impulse.
Because of that, the definition of multivariable dis-
crete impulse is used simply as an analogous to the
monovariable case, and not as a definition of only one
signal.
As an example, let j = 1. In this experiment the
following input will be applied to the system:
U(k) =

[
1 0 ... 0
]
T
k = 0
0
m
k 6= 0
(7)
in which 0
m
is the null vector at R
m
. Consequently,
from (6), the outputs will be:
y
i
(k) = g
i1
(k), i = 1 ... l
(8)
thus, applying the input defined in (7), it is possible
to determine the first column of the matrices G(k),
k = 0 · ·· n
ir
.
Figure 1: Hypothetical multivariable discrete impulse app-
lied to a system.
With a similar procedure, it is possible to notice
that in each one of the m experiments, one of the co-
lumns of the matrices G(k) will be determined, and
by the end of those experiments, there will be an al-
gebraic model that is a realization of the system under
study. Since the matrices G(k) are the system res-
ponses to the multivariable discrete impulse, they are
defined as the system multivariable discrete impulse
response. Those matrices are also defined as the Mar-
kov parameters of the deterministic system. In the
figure 1, a representation of the application of the m
inputs to the system, resulting into the determination
of its multivariable impulse response, is shown.
Now consider the case where the system outputs
are corrupted by an arbitrary Gaussian colored noise
with dimension l denoted by:
V(k) =

v
1
(k) v
2
(k) ·· · v
l
(k)

T
(9)
From the partial stochastic realization theory (Akaike,
1974), (Faurre, 1976), (Giesbrecht and Bottura,
2016), it is known that any Gaussian noise can be
generated as the output of a filter that has as input a
zero mean uncorrelated multivariable Gaussian white
noise E(k) with dimension p given by:
E(k) =

e
1
(k) e
2
(k) ·· · e
p
(k)

T
(10)
In (Giesbrecht and Bottura, 2017) more details about
the white noise can be found.
Thus, considering the system initial state null, it is
possible to find a set of matrices H(k) ∈ R
l×p
such as:
V(k) =
min(k,n
c
)
∑
i=0
H(i)E(k − i) (11)
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
468

in which n
c
is the number of significant matrices
H(k).
Consequently, the output of a multivariable sy-
stem subjected to an arbitrary colored noise V(k) will
be given by the following expression:
Y(k) =
min(k,n
IR
)
∑
i=0
G(i)U(k − i) +
min(k,n
c
)
∑
i=0
H(i)E(k − i)
(12)
If the multivariable discrete impulse is applied to the
system corrupted by noise, the outputs of the m ex-
periments will not be exactly the columns of the ma-
trices G(k). In fact, returning to the example where
j = 1, in which the input is defined in (7) and the noi-
seless output is given by (8), from (12) a noisy output
will be given by:
y
I
(k) = g
I 1
(k) +
min(k,n
c
)
∑
i=0
p
∑
j=1
h
I j
(i)e
j
(i) (13)
I = 1 ·· · l
Besides the corrupted outputs, it is still possible to
determine the Markov parameters by the multivaria-
ble impulse if a considerable great number N of tests
is performed for each one of the m inputs. Since by
the white noise definition:
E[e
j
(k)] = lim
N →∞
1
N
N
∑
i=1
e
j
(k) = 0 ∀ j,k, (14)
Consequently, the expected value of the outputs after
a considerably great number of experiments will be
the desired Markov parameters.
3 DETERMINATION OF
IMPULSE RESPONSES FROM
OTHER INPUTS
In practical problems, it might be difficult to apply a
set of multivariable discrete impulses to a system and
observe the outputs. To solve this issue, in this section
it is shown that it is possible to determine the impulse
response matrices of a multivariable system from any
persistent exciting input with a simple application of
the least squares method.
The equation (4) can be rewritten as:
Y(k) = G(0)U(k) + G(1)U(k − 1) + ···
Y(k + 1) = G(0)U(k + 1) + G(1)U(k) + ·· ·
Y(k + 2) = G(0)U(k + 2) + G(1)U(k + 1) + · ··
.
.
.
(15)
The transposition of both sides of the equation above
results in:
Y(k)
T
= U(k)
T
G(0)
T
+ U(k − 1)
T
G(1)
T
+ · · ·
Y(k + 1)
T
= U(k + 1)
T
G(0)
T
+ U(k)
T
G(1)
T
+ · · ·
Y(k + 2)
T
= U(k + 2)
T
G(0)
T
+ U(k + 1)
T
G(1)
T
+ · · ·
.
.
.
(16)
which can be rewritten as:
Y
bl
T
= U
bl
T
G
bl
T
(17)
in which Y
bl
and G
bl
are the following block matri-
ces:
Y
bl
=

Y(k) Y(k + 1) Y(k + 2) ·· ·

(18)
G
bl
=

G(0) G(1) G(2) · · ·

(19)
and U
bl
T
is the following Toeplitz block matrix:
U
bl
T
=





U(k)
T
U(k − 1)
T
·· ·
U(k + 1)
T
U(k)
T
·· ·
U(k + 2)
T
U(k + 1)
T
·· ·
.
.
.
.
.
.
.
.
.





(20)
From the relations above, if a finite persistent ex-
citing input is applied to the system, the output will
be finite and it will be possible to determine a finite
number of system impulse response matrices with the
following expression, that is a direct application of the
least-squares method:
G
bl
= (U
bl
T †
Y
bl
T
)
T
(21)
in which U
bl
T †
is the pseudo-inverse of the matrix
U
bl
T
.
For practical problems, the number of blocks of
G
bl
can be limited to n
IR
, that as previously defined,
is the number of significant impulse responses of the
system. To obtain the desired number of Markov pa-
rameters, the sizes of the data matrices U
bl
and Y
bl
must be adequate. Obviously, for greater n
IR
, bigger
data matrices will be needed.
If the output is corrupted by noise, it is possible
to demonstrate from the optimal properties of the le-
ast squares solution that (21) gives an estimate of G
bl
that minimizes the quadratic error between the system
outputs and the model outputs for the same input.
State Space Identification Algorithm based on Multivariable Impulse Response
469

4 DETERMINATION OF SYSTEM
MATRICES FROM IMPULSE
RESPONSE MATRICES
Once the multivariable impulse response matrices are
determined either by the method described in the
section 3 or by the one described in the section 2,
the state space model matrices can be determined by
the method introduced in (Ho and Kalman, 1966) and
summarized in this section:
From (1) it is possible to demonstrate that the fol-
lowing relation between the impulse responses and
the state space model matrices is valid:
G(k) =

D k = 0
CA
k−1
B k 6= 0
(22)
Supposing that the impulse response matrices are
known, the following finite Hankel matrix can be
built:
H =




G(1) G(2) ... G(k3)
G(2) G(3) ... G(k3 + 1)
.
.
.
.
.
.
.
.
.
.
.
.
G(k3) G(k3 + 1) · · · G(2k3 − 1)




(23)
in which k3 is the number of line blocks of the matrix
H. To solve the partial realization problem, this num-
ber must be chosen such as 2k3 − 1 = n
IR
, where n
IR
is the number of significant impulse responses.
Defining the observability matrix O and the rea-
chability matrix C as:
O =

C
T
(CA)
T
(CA
2
)
T

T
(24)
C =

B AB A
2
B . . .

(25)
and using (22) and (23), it is possible to write:
H = OC (26)
so, to determine the matrices O and C , a singular va-
lue decomposition of H can be made, as indicated be-
low:
OC = UΣV
T
=

U
1
U
2


Σ
11
0
0 0

V
T
1
V
T
2

(27)
So it is possible to define:
O = U
1
Σ
1/2
11
C = Σ
1/2
11
V
T
1
(28)
Let, by definition H
↑
be the matrix H with one line
block shifted upwards and a new line block, following
the structure presented in (23), added to its end. It is
possible to notice that H
↑
= OAC . Thus, if H, O and
C are known, it is possible to determine A as indicated
below:
H
↑
= OAC ⇒ A = O
†
H
↑
C
†
(29)
From the first column block of H, denoted as H(:
,1), it is possible to determine the matrix B with the
following expression:
H(:,1) = OB ⇒ B = O
†
H(:,1)
(30)
In the same way, from the first line block of H, deno-
ted as H(1,:), it is possible to obtain C:
H(1,:) = CC ⇒ C = H(1,:)C
†
(31)
and the matrix D is obtained from (22) as the impulse
response at k = 0.
As shown above, it is possible to determine the
matrices A, B, C and D from the system Markov pa-
rameters, that can be determined either by the method
described in the section 2 or by the described in the
section 3. The combination of the methods is defined
as the MDIRI algorithm. The results of that algorithm
are presented in the next section
5 IDENTIFICATION RESULTS
To evaluate the performance of the algorithms, ex-
periments were executed using the software Matlab
running on a desktop computer equipped with a pro-
cessor Intel Core i3-4160T CPU @ 3.10GHz, 8GB
RAM.
The benchmark to be identified is the following
state space model:
X(k+1) =

0.0002 −0.5
1 −1

X(k)+

−2 1
1 1

U(k)
(32)
Y(k) =

1 3
1 2

X(k) +

1 3
1 1

U(k) + E(k)
(33)
In each experiment, the response of the bench-
mark to random inputs with N = 100 samples was
collected and the set of inputs and outputs was used
in the identification algorithms to be tested.
5.1 MOESP Algorithm Results
To test the MOESP algorithm (Verhaegen and De-
wilde, 1992a), (Verhaegen and Dewilde, 1992b), the
number of line blocks in data matrices, denoted as k
1
,
was varied from 2 to 20 in steps of 1. This limits were
adopted because it was observed that for the number
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
470

of samples used, if k
1
> 20, the LQ decomposition
seldom succeeded, and the identified model was not
stable. For each k
1
, at least 10000 experiments were
tested. The instability problems also happened for
some experiments in the range adopted for the number
of line blocks in data matrices. The results of those
were not taken into account and the experiments were
repeated until 10000 of them resulted in stable sys-
tems. To avoid infinite loops, a limit of 4x the desired
number of experiments was defined. If after this limit
the desired number of successful experiments was not
reached, it was considered that it was not possible to
determine the results with the MOESP for that k
1
.
In each experiment, a new input with N = 100
samples was generated with a bi-dimensional Gaus-
sian distribution with zero mean and variance equal
to the identity. The input was applied to the bench-
mark defined in (32) and (33) and the outputs were
summed to a noise E(k) with the same statistical cha-
racteristics presented by the input, what means that
the noise presents the same order of magnitude that
the true signal does, which represents a challenging
identification problem. The resultant signal was con-
sidered as the output of the system to be identified.
For each one of the 10000 valid experiments for
each k1, the MOESP algorithm was applied to iden-
tify the matrices A, B, C and D from the input and out-
put data. After the identification, the input signal of
the experiment was applied to the model determined
with the MOESP algorithm and the quadratic error E
q
defined as:
E
q
=
1
N
N
∑
k=1
q
(Y(k) − Y
est
(k))
T
(Y(k) − Y
est
(k))
(34)
was calculated, where Y(k) is the benchmark output
calculated with (33) and Y
est
(k) is the output of the
model determined with the MOESP algorithm. The
times taken to determine the state space model matri-
ces and the the Markov parameters were also measu-
red for each one of the experiments. After that, for
each k1, the average error and the average execution
times were calculated.
Table 1: MOESP algorithm results for k1 = 20.
Average Time to obtain Time to obtain
error Markov parameters state space matrices
0.0412676 0.012461 s 0.012449 s
The average errors of the application of the
MOESP algorithm to the 10000 experiments for each
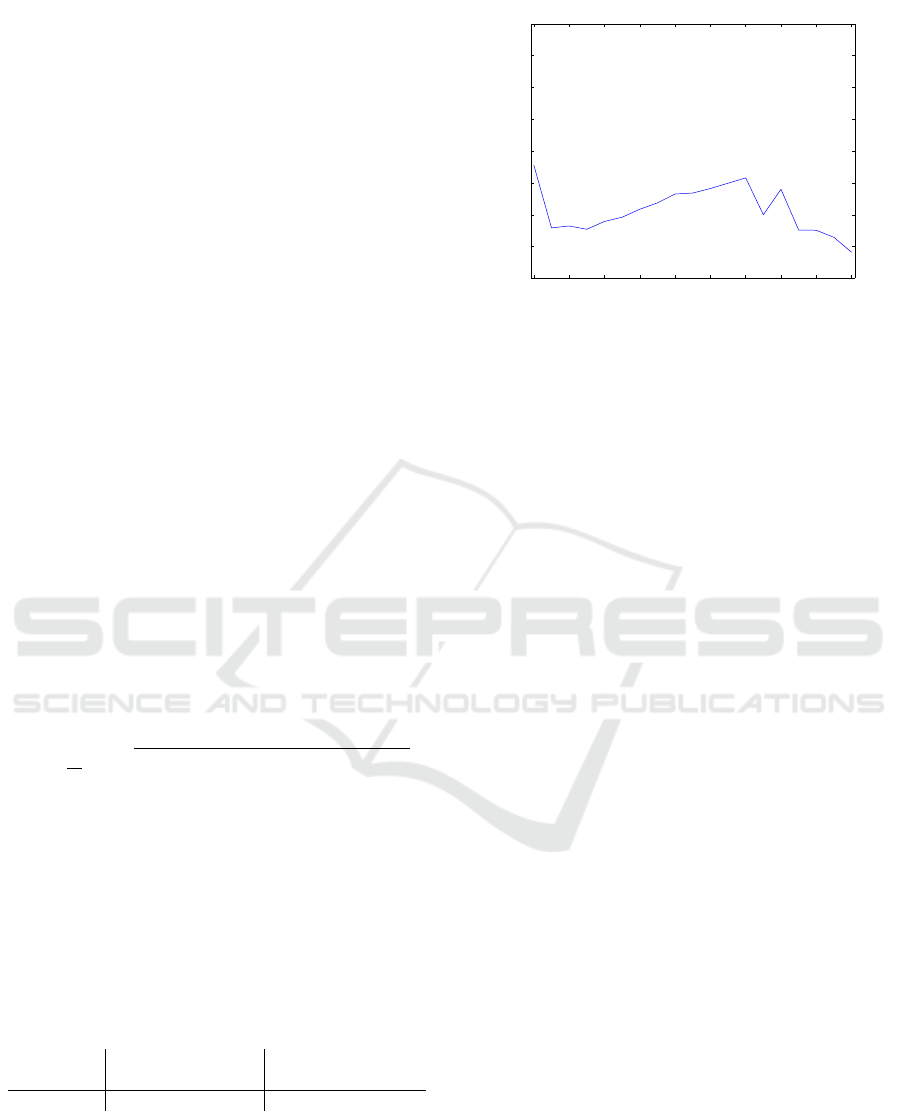
k1 are shown in the figure 2 and the average execution
times in the figure 3. From the figure 2 it is possible
to see that the variation of the average error is not sig-
nificant. The worst result is obtained for k1 = 2, what
2 4 6 8 10 12 14 16 18 20
0.05
0.1
0.15
0.2
0.25
0.3
0.35
k1
Average error X k1
Error
Figure 2: Average errors for the MOESP algorithm as
function of k1.
can be explained by the small number of line blocks
in the data matrices. A small increase in k1 decreases
the error significantly, probably because the data ma-
trix to be decomposed is better conditioned than the
one obtained for k1 = 2. The smallest error is measu-
red for k1 = 20. The results for that k1 are summari-
zed in the table 1.
From the figure 3 it is possible to notice that as
k1 increases, the execution time also increases. This
happens because this variable is related to the dimen-
sion of the matrices that will be decomposed in the
algorithm. From that figure it is also possible to no-
tice that the differences of times to obtain the state
space matrices and to obtain the Markov parameters
are relatively small. This happens because the deter-
mination of the Markov parameters from the system
matrices involves just products between matrices with
relatively small dimensions.
5.2 MDIRI Algorithm Results
The MDIRI algorithm was tested with a similar pro-
cedure. For n
IR
varying from 5 to 49 in steps of 2,
the identification experiments with the MDIRI were
repeated until 10000 of them resulted in stable sys-
tems. For each n
IR
the average values of errors and
the execution times were calculated.
In the figure 4 the average errors found for each
n
IR
adopted are shown. From the figure it is possi-
ble to see that, for n
IR
< 20, the error is considera-
bly below 0.05, that is approximately the best value
found with the MOESP algorithm. It is also possible
to notice that, if the number of impulse responses to
be considered increases until n
IR
= 32, the error also
increases. This is expected since if n
IR
increases, the
number of block lines in the matrix U
bl
T
decreases,
and less data is available to estimate the Markov para-
meters with (21). For n
IR
> 32 the average error sur-
State Space Identification Algorithm based on Multivariable Impulse Response
471

2 4 6 8 10 12 14 16 18 20
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
k1
Execution times − MOESP method
Time (s)
ABCD matrices calculation
G matrices calculation
Figure 3: Average execution times to obtain the state space
matrices and the Markov Parameters with the MOESP al-
gorithm.
10 15 20 25 30 35 40 45
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
n
IR
Average error X n
IR
Error
Figure 4: Average errors for the MDIRI algorithm as
function of n
IR
.
prisingly decreases. Probably this happens because
for that n
IR
, the input data is closer to a square matrix,
what makes the estimation of the G
bl
more accurate
since the linear system (21) is better conditioned. The
smallest error for the MDIRI algorithm was found for
n
IR
= 11. The results for this case are summarized in
the table 2.
Table 2: MDIRI algorithm results for n
IR
= 11.
Average Time to obtain Time to obtain
error Markov parameters state space matrices
0.021473 0.002038 s 0.002625 s
In the figure 5 the average times to find the
Markov parameters and the state space matrices are
shown. Since in this algorithm the first step is to
determine the Markov parameters from the equation
(21) and then to apply the procedure described in the
section 4 to determine the state space model matrices,
the time to obtain the first values is considerably smal-
ler than the time to obtain the second values. From
5 10 15 20 25 30 35 40 45 50
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
n
IR
Execution times − MDIRI method
Time (s)
ABCD matrices calculation
G matrices calculation
Figure 5: Average execution times to obtain the state space
matrices and the Markov Parameters with the MDIRI algo-
rithm.
the same figure it is noticed that as n
IR
increases, the
difference between the time to obtain the state space
model matrices and the time to obtain the Markov pa-
rameters gets bigger. This is explained by the increase
in the computational costs to perform the decomposi-
tions presented in the section 4.
Making a general comparison between the figu-
res 2, 3, 4 and 5 it is possible to notice that accurate
results were obtained with both algorithms within a
reasonable time. By comparing the results presen-
ted in the tables 1 and 2 it is possible to notice that,
specifically for the benchmark studied in this paper,
the MDIRI algorithm resulted in a estimation with al-
most half of the average error obtained with the best
MOESP solution in a execution time that was almost
6 times smaller. This indicates that the algorithm that
is based on the multivariable impulse response may be
advantageous to solve practical problems with higher
accuracy and smaller execution time.
6 CONCLUSIONS
In this paper the definitions of multivariable discrete
impulse and the multivariable discrete impulse re-
sponse were clearly stated and explored. From those
definitions, two methods to determine the system
Markov parameters from input and output data were
described. Combining the described methods to a
known method to determine the state space model ma-
trices from the Markov parameters, a practical algo-
rithm to determine state space models from input and
output data was explored.
The results of the implementation of the MDIRI
algorithm showed that accurate models could be
obtained in a reasonable amount of time. Those re-
sults were compared to the ones obtained with the
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
472

MOESP algorithm and the conclusion was that, for
the tested benchmark, the algorithm described in this
paper is faster and more accurate.
A future research is to compare the MDIRI algo-
rithm to N4SID and CCA concerning the execution
time and average error. Another future direction is to
test the MDIRI performance if the number of samples
get smaller and compare to the performance of other
algorithms. This kind of analysis is important for the
development of future algorithms to identify multiva-
riable discrete time variant systems based on windo-
wed data, such as the one proposed in (Tamariz. et al.,
2005), or to initialize evolutionary algorithms for on-
line time variant system identification, such as the one
proposed in (Giesbrecht and Bottura, 2015).
ACKNOWLEDGEMENTS
The authors would like to thank FAEPEX-UNICAMP
for the financial support.
REFERENCES
Akaike, H. (1974). Stochastic theory of minimal realization.
Automatic Control, IEEE Transactions on, 19(6):667–
674.
Akaike, H. (1975). Markovian representation of stochastic
processes by canonical variables. SIAM Journal on
Control, 13(1):162–173.
Bottura, C. P. (1982). An
´
alise linear de sistemas. Ed. Gua-
nabara Dois.
Faurre, P. L. (1976). Stochastic realization algorithms. In
Mehra, R. and Lainiotis, D., editors, System Identifi-
cation: Advances and Case Studies, pages 1–25.
Giesbrecht, M. and Bottura, C. P. (2015). Recursive
immuno-inspired algorithm for time variant discrete
multivariable dynamic system state space identifica-
tion. International Journal of Natural Computing Re-
search, 5(2):69–100.
Giesbrecht, M. and Bottura, C. P. (2016). An immuno in-
spired proposal to solve the time series realization pro-
blem. In IEEE World Congress on Computational In-
telligence.
Giesbrecht, M. and Bottura, C. P. (2017). Finite length
white noise generation with an immuno inspired al-
gorithm. Expert Systems with Applications, 69:189 –
200.
Ho, B. L. and Kalman, R. E. (1966). Effective con-
struction of linear state-variable models from input-
output functions. Regelungstechnik - zeitschrift f
¨
ur
steuern, regeln und automatisieren, pages 545–548.
Inouye, Y. (1983). Approximation of multivariable linear
systems with impulse response and autocorrelation se-
quences. Automatica, 19(3):265–277.
Kalman, R. E. (1960). A new approach to linear filtering
and prediction problems. Transactions of the ASME-
Journal of Basic Engineering.
Kalman, R. E. (1963). Mathematical description of linear
dynamical systems. Journal of the Society for In-
dustrial and Applied Mathematics Series A Control,
1(2):152–192.
Katayama, T. (2005). Subspace Methods for System Iden-
tification: a Realization Approach. Springer Verlag,
Leipzig.
Katayama, T. and Picci, G. (1999). Realization of stochastic
systems with exogenous inputs and subspace identifi-
cation methods. Automatica, 35:1635–1652.
Oppenheim, A. V. and Schafer, R. W. (2010). Discrete-
time signal processing. Pearson Education Ltd., 3rd
edition.
Overschee, P. V. and de Moor, B. (1994). N4sid: Sub-
space algorithms for the identification of combi-
ned deterministic-stochastic systems. Automatica,
30(1):75–93.
Tamariz., A. D. R., Bottura, C. P., and Barreto, G. (2005).
Iterative moesp type algorithm for discrete time vari-
ant system identification. Proceedings of the 13th Me-
diterranean Conference on Control and Automation
(MED 2005).
Tether, A. (1970). Construction of minimal linear state-
variable models from finite input-output data. IEEE
Transactions on Automatic Control, 15(4):427–436.
Verhaegen, M. and Dewilde, P. (1992a). Subspace model
identification - part 2 : Analysis of the elementary
output-error state-space model identification algo-
rithms. International Journal of Control, 56(5):1211–
1241.
Verhaegen, M. and Dewilde, P. (1992b). Subspace model
identification - part i : The output-error state-space
model identification class of algorithms. International
Journal of Control, 56(5):1187–1210.
State Space Identification Algorithm based on Multivariable Impulse Response
473