Speed Estimation for Control of an Unmanned Ground Vehicle using

Extremely Low Resolution Sensors

an del Pino, Miguel

A. Mu

noz-Ba

on, Miguel

A. Contreras, Sa

ul Cova-Rocamora,

Francisco A. Candelas and Fernando Torres

Group of Automation, Robotics and Computer Vision (AUROVA),

University of Alicante, San Vicente del Raspeig S/N, Alicante, Spain

Keywords:

Kalman Filter, SDKF, Speed Estimation, Speed Control, Incremental Rotary Encoder, Low-resolution,

Low-cost, Mobile Robotics.

Abstract:

In mobile robotics, the low-level control is a key component that translates the desires of the high-level system

into actual voltages and currents to drive the motors. PID controllers have been extensively used for speed con-

trol, but their performance depend heavily on the quality of the process variable (PV) estimation. In fact, noise

and outliers –if not properly ﬁltered– might lead to system instability. In this work, we present a speed esti-

mation strategy that enables us to develop an inexpensive, accurate and easy-to-install speed control solution.

The proposed system relies on a Hall effect sensor and a Single-Dimensional Kalman Filter and its suitability

is demonstrated through a number of real experiments controlling the speed of an Unmanned Ground Vehi-

cle. We detail the design, implementation and validation processes and provide a GitHub repository with the

developed software and CAD designs.

1 INTRODUCTION

To achieve fully autonomous navigation, mobile

robots need to perform different tasks, such as local-

ization, path planning, and trajectory following (Sieg-

wart et al., 2011). In ground robotics, the ﬁnal out-

put of the whole system is usually the desired driv-

ing and steering velocities to control car-like ma-

chines (De Luca et al., 1998), or speciﬁc velocities

for each wheel in differential drive robots (Indiveri

et al., 2007). In this way, a smooth, agile and reliable

low-level control is key for any application, since it

has the responsibility of translating the desires of the

high-level system into real voltages and currents to

drive the motors. PID controllers –and their variants–

are widely used in industrial processes (Jin and Liu,

2014) and are also common for speed control in au-

tonomous vehicles (Thrun et al., 2006; Park et al.,

2015), but they require a correct estimation of the pro-

cess variable (PV) to work properly. In the speed

control case, the PV is the linear velocity of a ve-

hicle and can be calculated from the rotation of the

traction axle. A well known method to estimate the

rotational velocity of an axle is the use of incremen-

tal rotary encoders attached to the motor (Borenstein

et al., 1997). This approach provides rich informa-

Figure 1: BLUE is a UGV designed to support research in

localization and autonomous navigation. Its low-level speed

control is based on a Hall effect and a Single-Dimensional

Kalman Filter.

tion because the encoder resolution gets multiplied by

an –usually high– reduction ratio, needed to generate

206

Pino, I., Muñoz-Bañón, M., Contreras, M., Cova-Rocamora, S., Candelas, F. and Torres, F.

Speed Estimation for Control of an Unmanned Ground Vehicle using Extremely Low Resolution Sensors.

DOI: 10.5220/0006867202060213

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 206-213

ISBN: 978-989-758-321-6

the torque required to move the vehicle at the desired

speed. Using this conﬁguration it is possible to obtain

sub-millimeter linear displacement information using

low-cost hardware (Carnegie et al., 2004). However,

it is not always possible to have access to the motor

driving shaft and then the problem gets more com-

plicated. The present work is being developed in the

context of the BLUE project (roBot for Localization

in Unstructured Environments, see Fig.1). This robot

is adapted from a commercially available electric cart

and it results impossible –at reasonable costs– to in-

stall a high-resolution rotary encoder in the driving

shaft. Instead, the chosen alternative is to install a

collar with magnets in the traction axle using a Hall

effect sensor to measure the rotation. This approach is

robust, inexpensive and easy to implement, but the ob-

tained resolution is extremely low, in our case as low

as 24 pulses per revolution (one pulse every ﬁfteen

degrees), which translates into a signiﬁcant quantiﬁ-

cation noise that is proportional to the sampling fre-

quency (Petrella et al., 2007). One common approach

to deal with noisy sensors is to use low-pass ﬁlters

agglund, 2012) but, despite being computationally

efﬁcient, this approach makes the controller less sen-

sitive to changes. The proposed solution is to imple-

ment a single-dimensional Kalman ﬁlter (SDKF) us-

ing the controller output to feed the prediction stage of

the ﬁlter. The single-dimensional state vector makes

possible to lighten the computational load, avoiding

the matrix inversions required when more complex

dynamic models are used. Our architecture permits

to generate control signals at the desired rate while

the sensor can be queried with larger sampling times,

thus reducing the quantiﬁcation noise. The present

work comprises the design, implementation and ex-

perimental validation of a low-cost speed control sys-

tem that overcomes its limitations thanks to the use

of a Single Dimensional Kalman Filter. It is open-

source, ROS-integrated and can be implemented with

a 3D printer, some magnets, a Hall effect sensor and

an Arduino. We provide a GitHub repository (AU-

ROVA, 2018) to make available the source codes and

the hardware designs.

The rest of this paper is structured as follows: in

section 2 we review different approaches for speed es-

timation using rotary encoders; section 3 is dedicated

to describe the robot used to test the control system;

section 4 details the proposed method; in section 5

we describe the experiments used to adjust the sys-

tem and to evaluate its performance; ﬁnally in section

6 we discuss the results and give some future works.

2 RELATED WORK

As indicated in (Petrella et al., 2007), algorithms that

use incremental rotary encoders to measure speed

can be roughly divided in direct methods and esti-

mation methods. In (Briz et al., 1994) two alterna-

tive direct methods are discussed: one of them counts

the number of encoder pulses in a sampling time,

while the other measures the period between con-

secutive encoder pulses with a high-frequency clock.

These approaches are simple but their performance

depends heavily on the magnitude of the rotational

velocity and present quantiﬁcation and synchroniza-

tion problems. On the estimation side, Kalman ﬁlters

are frequently chosen since they have been success-

fully used in a wide variety of automatic control ap-

plications (Troncoso and Su

arez, 2017; Santamaria-

Navarro et al., 2017). Examples of speed estima-

tion using Kalman Filters and rotary encoders can be

seen in (Kim and Sul, 1996) where the authors use

a computationally intensive multi-dimensional dy-

namic model. In a more recent work (Shaowei and

Shanming, 2012) a single-dimensional Kalman ﬁl-

ter is used for speed estimation with an optical en-

coder of 2500 lines, the authors use a constant veloc-

ity model adjusting the process noise Q dynamically

to take into account that the model is more accurate

at higher speeds. In our case, as we have much lower

resolution and lower velocities, we choose to model

the effect of the control signal in the system to im-

prove the Kalman Filter prediction step.

3 PLATFORM DESCRIPTION

Our research platform BLUE is based on a commer-

cial vehicle from Zallys, speciﬁcally the electric cart

Jespi Z105 (see Fig.1). This cart, which is designed

originally to be operated manually, has been modiﬁed

to run in an autonomous way.

The cart has a length of 1.60m, a distance between

axes of 1.05m, a width of 0.797m, and a weight about

140Kg including the batteries. The maximum pay-

load is about 600Kg, which can be transported on

slopes of up to 30 degrees. It is a four-wheeled ve-

hicle, with robust tires of 16 and 13 inches of diam-

eter for the traction and steering wheels respectively.

The traction wheels are moved by a differential trans-

mission and an electric DC motor of approximately

2.400W, which allows to reach a speed of up to 5Km/h

forward or backward. The traction system also in-

cludes a simple electric brake that ensures that the

vehicle remains immobile when it is stopped. The

steering wheels are operated like in usual cars, and

Speed Estimation for Control of an Unmanned Ground Vehicle using Extremely Low Resolution Sensors

207

Figure 2: Proposed control loop. It permits a high control rate based on the Kalman ﬁlter prediction while extending the pulse

integration time, thus reducing the Hall effect sensor quantiﬁcation noise.

they allow a turning radius of 4m. Thus, this vehicle

ﬁts very well with the Ackermann model. For BLUE,

we have replaced the original arm for manual driving

by a servomotor which allows to control the steering

wheels with precision. The power is provided by two

lead-acid batteries of 12V and 73Ah which provides

a powerful 24V supply and very high range. In addi-

tion, since the cart is intended for hard work, it is built

in steel and is very robust. We have also added a steel

platform bolted at the top of the chassis to facilitate

the installation and accommodation of the equipment

and possible loads.

4 PROPOSED APPROACH

A block diagram of the proposed control system can

be seen in Fig. 2. It shows two loops, each one oper-

ates at different rates: A fast Kalman prediction loop

that uses a dynamic model to relate the derivative of

the control signal with the system acceleration, and a

slower correction loop that uses the Hall effect sen-

sor. Moreover, the system is prepared to receive asyn-

chronous updates of the Kalman ﬁlter using a high-

level sensor fusion system through the ROS interface.

Next, we describe the more relevant elements of the

proposed system.

4.1 PID Control

Inspired by (Thrun et al., 2006) we choose a PID

structure to implement our speed controller. Our sys-

tem provides a ROS interface to adjust the parameters

–including the PID gains– dynamically from the on-

board computer using rosserial. All input and output

signals are published in ROS topics, what enables us

to use rosbags for off-line analysis. In our implemen-

tation, the controller set point can be adjusted using

either the ROS interface or by means of a remote con-

troller (DJI DT7). This RC can also be used to con-

trol directly the output voltage (bypassing the PID) to

study the differences between human and automated

control.

To ease the tuning process, the PID controller

works internally with normalized values, so a pro-

cess of saturation/scaling is applied to the inputs and

the output. To avoid unexpected behaviors, the inte-

gral term is also saturated when it reaches the maxi-

mum output value. The maximum and minimum val-

ues used for normalization are set in a speciﬁc header

ﬁle which describes the hardware components of the

robot. In that way, using the developed control sys-

tem in other robots, or changing some hardware com-

ponent, are straightforward steps.

As the micro-controller loop time may have slight

variations –depending on the interruptions– the ∆t

used for the computation of the integral and deriva-

tive terms is assumed variable and calculated at each

iteration. Finally, when the set-point is zero (within

a small tolerance) the output signal is set to zero and

the PID is reset.

4.2 Hall Effect Sensor

As stated before, it was not possible to install a rotary

encoder in the driving shaft of our traction motor, so

we decided to use a target with magnets attached to

the rear axle of the vehicle. To sense these magnets a

Hall effect proximity sensor was considered the best

option for our application for several reasons: they are

cost-effective, easy-to-use, and resistant to shocks, vi-

brations, extreme temperatures and moisture (Rams-

den, 2011).

A custom mounting bracket for the Hall effect

sensor and a split collar pulse wrap for holding the

magnets were designed using CAD software. They

were both 3D printed and attached to the metal sheet

and the rear axle respectively. The main challenge we

had to face in the design of the pulse wrap was the

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

208

limited space between the metal sheet and the driven

shaft of our robot. It was also intended that the piece

was formed by two identical parts so that they could

be easily replaced. Finally and after several iterations,

a collar of 84.50 mm in diameter and 20 mm in depth

was made. In each of its halves, there were housed six

circular magnets with 10 mm diameter. Thus, once

the piece was assembled in the vehicle we had a total

of 12 magnets, each one with a separation of 15 de-

grees. This angular resolution allows us to calculate

the minimum observable linear distance.

∆x

min

= ∆ω

πD

(1)

Where N

is the number of pulses per revolution,

and D is the diameter of the wheel

, in our case

∆x

min

≈ 0.05 m. On the other hand, the minimum ob-

servable speed, which constitutes our quantiﬁcation

step, depends on sample time ∆t

as follows:

step

∆x

min

∆t

(2)

Our sensor gives measurements that are integer mul-

tiples (N) of the quantiﬁcation step v

meas

= N × v

step

Finally, the number of steps M

depends directly on

sample time:

max

step

max

∆x

min

∆t

(3)

Where v

max

is the vehicle maximum speed. We ob-

serve in (3) that M

is proportional to ∆t

, therefore

the quantiﬁcation noise is proportional to the sam-

pling frequency. With our extremely-low resolution

sensor of 24 pulses per revolution, using a refresh

time of just 100 ms we obtain a v

step

≈ 0.5 m/s. Tak-

ing into account that the maximum velocity of our

robot is about 5 Km/h or v

max

≈ 1.5 m/s, the quantiﬁ-

cation noise results too high to use directly the sensor

measurements to implement the control algorithm, as

we will discuss in section 5.2.

Finally, as the rear axle of our vehicle is differ-

ential, the measured speed corresponds to one of the

wheels and depends on steering angle. We apply a

correction to compute the speed of a virtual center

wheel, to use the bicycle kinematic model, and name

it v

sensor

, because it will be the value used for the

Kalman Filter correction step.

sensor

= b



b −

tanθ



−1

meas

(4)

We obtain this value experimentally, comparing the

sensor measurements with the DGNSS ground truth, and

tuning the diameter value to obtain a zero mean error.

Figure 3: Assembly of a mounting bracket for the Hall ef-

fect sensor and the split collar pulse wrap attached to the

rear axle.

Where b is the wheelbase, c is the rear axle track

and θ is the steering angle of the virtual front wheel

of the bicycle model.

4.3 Single Dimensional Kalman Filter

It is well known that the Kalman ﬁlter is an optimal

estimator for linear systems under Gaussian uncer-

tainty (Andrade-Cetto, 2002). To analyze the present

problem we conducted a number of experiments, de-

tailed in the next section, that conﬁrmed the system

linearity (see Fig.4) and the Gaussianity of the sensor

noise (see Fig.8). One drawback of the Kalman ﬁl-

ter is the need of computing matrix inversions to esti-

mate multidimensional state vectors, this can prevent

the implementation of this kind of ﬁlters in microcon-

trollers that have limited processing power and need

to run complex programs that include communication

tasks and a great volume of interruptions for encoder

pulse counting. One option to reduce the computa-

tional burden when using a Kalman ﬁlter is to reduce

the system model to only one variable (Shaowei and

Shanming, 2012), using this approach the matrices

are reduced to scalars and matrix inversions become

just divisions.

4.3.1 Kalman Filter Equations

One way to write the general Kalman ﬁlter equations

is as follows:

Prediction step:

x ← Fx + Bu (5)

P ← FPF

+ Q (6)

Correction step:

z = y −Hx (7)

Speed Estimation for Control of an Unmanned Ground Vehicle using Extremely Low Resolution Sensors

209

Z = HPH

+ R (8)

K = PH

−1

(9)

x ← x +Kz (10)

P ← P −KZK

(11)

Where ← represents a time update.

4.3.2 Proposed Model

Observing the linear relationship between voltage and

velocity (see Fig.4), and taking into account that we

have direct access to the control signal, we decided to

express the dynamic evolution of the system as a lin-

ear combination of the previous state and the deriva-

tive of the control input, as follows:

First, we assume that the acceleration is propor-

tional to the derivative of the control voltage. Ex-

pressing it in discrete time:

a = G

∆V

∆t

(12)

where G has units of

−1

Our state propagation equation results:

v ← v +G∆V (13)

Since the ∆t is canceled out when integrating the ac-

celeration to calculate the velocity increment.

Observing the presented equations is easy to derive

that:

F = 1 (14)

B = G∆t (15)

u = (V

−V

k−1

)/∆t (16)

Q = σ

model

(17)

H = 1 (18)

R = σ

sensor

(19)

Finally, we can rearrange the original equations

obtaining:

Prediction step:

v ← v +G∆V (20)

← σ

+ σ

model

(21)

Correction step

z = v

sensor

− v (22)

= σ

+ σ

sensor

(23)

k = σ

−1

(24)

v ← v +kz (25)

← σ

− σ

(26)

We make use of the predicted variance to reject outliers

by means of an innovation threshold, so we compute the

correction step only when |z| < 3σ

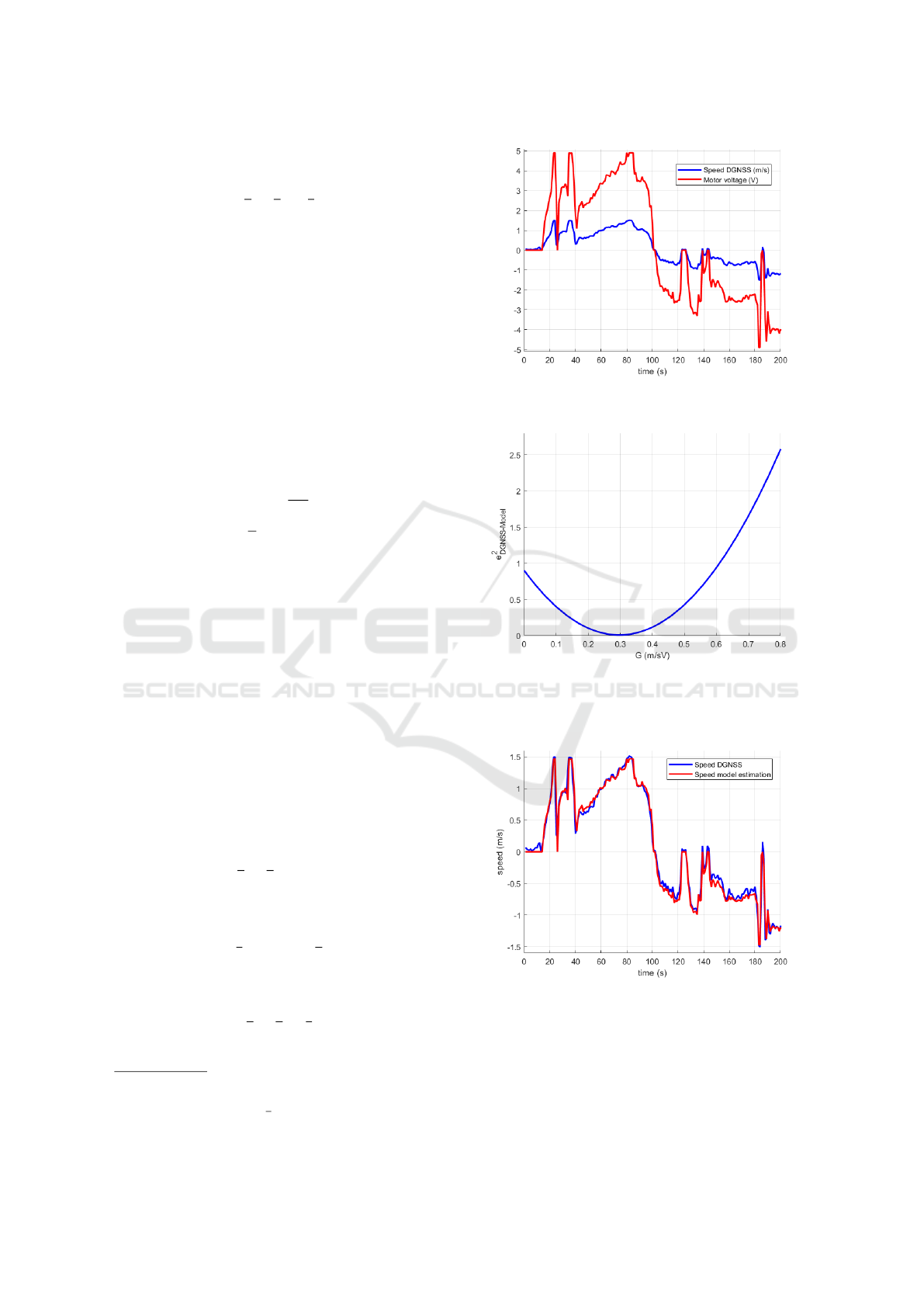
Figure 4: This ﬁgure illustrates the linear relationship be-

tween speed and motor voltage in ﬂat terrain.

Figure 5: We want to ﬁnd the value of G that minimizes

the mean squared error between the ground truth and the

dynamic model predictions. Using the dataset recorded in

ﬂat terrain, we obtain an optimal gain of G

∗

= 0.3.

Figure 6: Training set: Comparison between speed pre-

diction using the proposed dynamic model tuned with the

optimal gain G

∗

, and speed measured by DGNSS (ground

truth). In ﬂat terrain the linear relation between speed and

voltage is constant, for this reason, the prediction ﬁts very

well the ground truth.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

210

5 EXPERIMENTAL RESULTS

In this section we describe the system adjustment and

algorithm validation in our research platform BLUE.

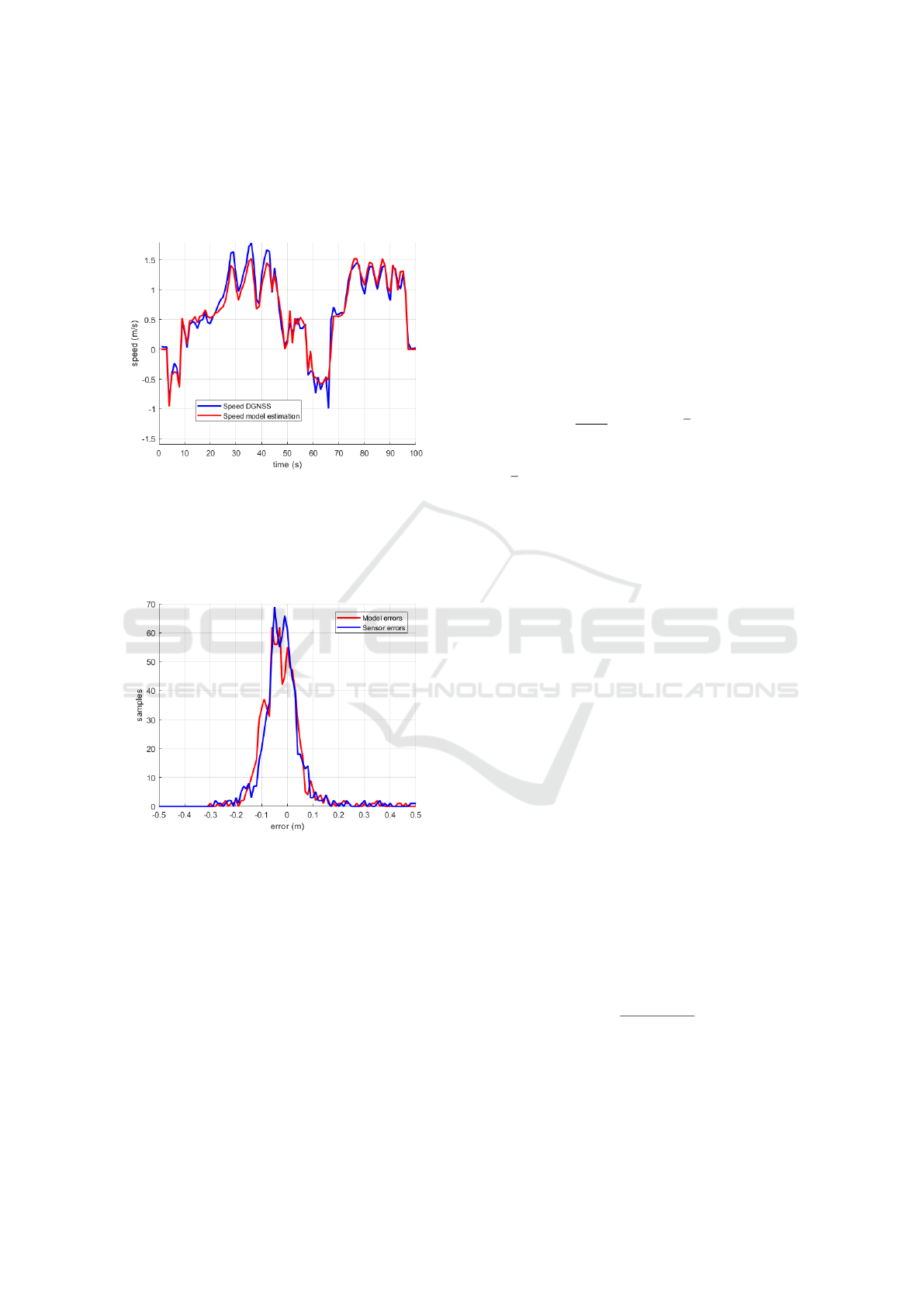
Figure 7: Testing set: Comparison between speed pre-

diction using the training set tuning and speed measured

by DGNSS in terrain with slopes. In the downhills (t =

(25,45)), motor needs less voltage, so the prediction does

not reach the ground truth speed. In the uphills (t =

(75,95)), motor needs more voltage, thus the model ex-

ceeds the ground truth speed.

Figure 8: Prediction and sensor error histograms with re-

spect to the DGNSS ground truth.

5.1 Dynamic Model Adjustment

To implement the SDKF in our proposed control loop,

we need to adjust the parameters G, R, and Q speci-

ﬁed in the model (see section 4.3.2). To obtain these

parameters experimentally, we have conﬁgured our

vehicle without the PID and SDKF blocks shown in

Fig.2, acting directly on the motor through the con-

trol signal (V ) using a remote controller. With this

conﬁguration, we recorded a dataset in free driving

across the campus of the University of Alicante. The

dataset contains: the control signal (V ) published at

10 Hz, the speed measured by the sensor hall (v

sensor

)

also published at 10 Hz, and the speed measured by

the DGNSS (v

), published at 1 Hz, to be used

as ground truth. To analyze jointly the data, as the

publishing rates are different, the control signal is

down-sampled and the measured speed is integrated

to match the sensor output if it were queried one time

per second.

To tune our dynamic model, we deﬁne the optimal

gain G

∗

(see Fig.5) as the one that minimizes the mean

squared error between the ground truth and the state

propagation, without taking into account the sensor

observations:

∗

= arg min

n − 1

∑

i=1

− (v

i−1

+ G∆V ))

(27)

Where v

is the speed measured by DGNSS.

And v is the speed estimated by the model. We cal-

culate this parameter using parts of the dataset that

corresponds to the path in ﬂat terrain. Fig.6 shows an

example of the ﬁt between the model and the ground

truth in ﬂat terrain with the optimal G. On the other

hand, in terrain with slopes, as we show in Fig.7, the

estimated speed does not match the ground truth. In

this case, the constant G that relates the speed to the

voltage is different. These differences between the

model and the ground truth speed are reduced with

the Kalman correction using sensor hall observation.

In order to characterize the process and sensor

noise (see (28) and (29)), we obtained the estima-

tion and observation error histogram. As we show

in Fig.8, the errors obtained indicate uncertainty with

Gaussian probability distribution shape:

q ∼ N(µ

model

,σ

model

) (28)

r ∼ N(µ

sensor

,σ

sensor

) (29)

We observe in Fig.8 a slight bias in the errors that

can be produced because the batch of data is ﬁnite and

the statistics obtained rarely converge to probability

distribution model. We also need to consider that the

ground truth signal is a stochastic function. This in-

dicates that errors obtained are not produced only for

the uncertain of our model. But, in order to simplify

the noise characterization, we considered the DGNSS

speed estimation as a deterministic function.

e =

∑

− v|

(30)

Table 1 shows in a quantitative way the improve-

ments obtained with the use of SDKF solution with

respect to the sensors measurements and the model

predictions. The mean error was calculated using the

expression (30). The prediction error results greater

Speed Estimation for Control of an Unmanned Ground Vehicle using Extremely Low Resolution Sensors

211

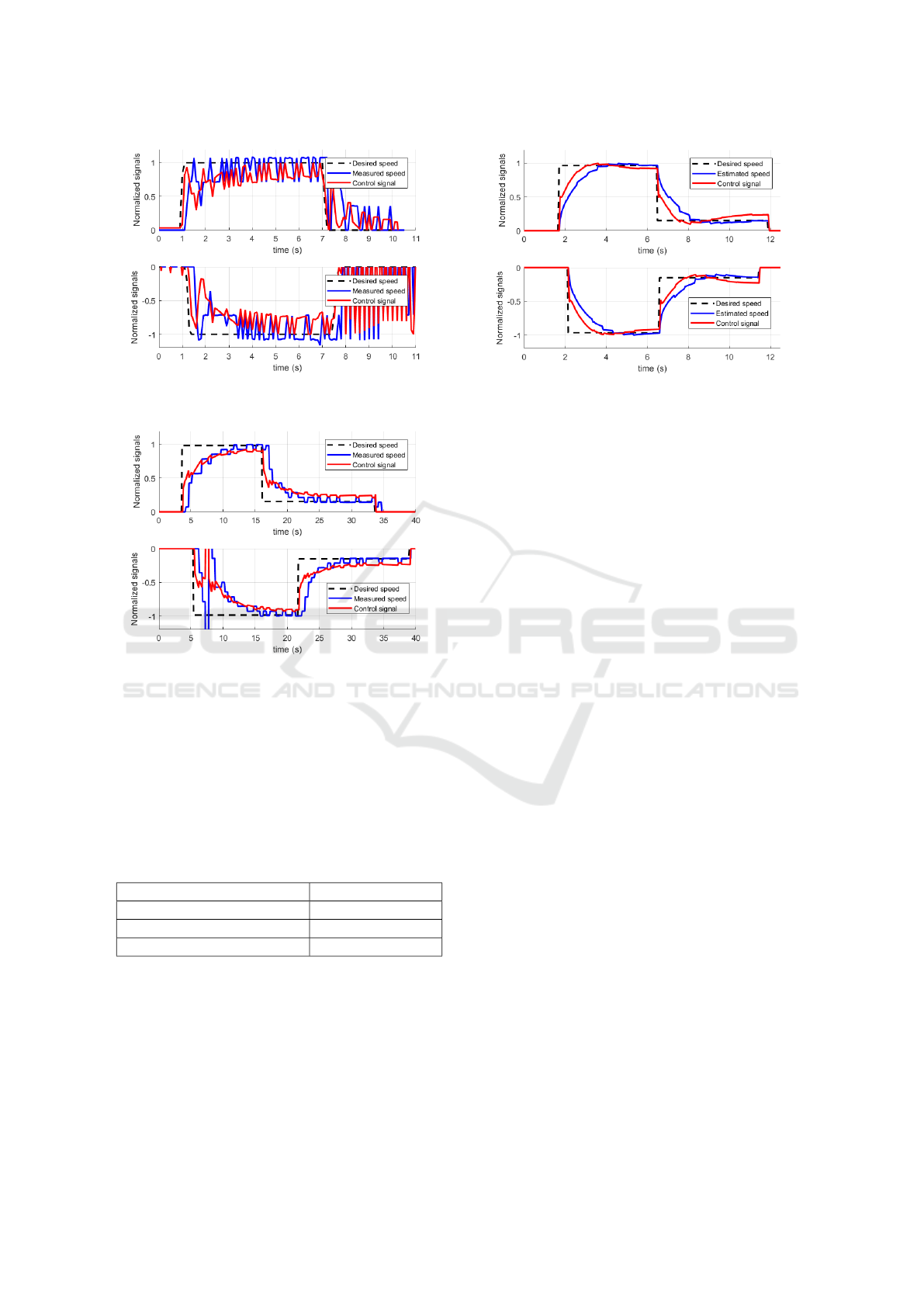
Figure 9: PID control using only the speed measured by the

sensor hall with f

sensor

= 10Hz. The noise makes impossi-

ble to control the speed of the vehicle.

Figure 10: PID control using only the speed measured by

sensor hall with f

sensor

= 2Hz. By increasing the sampling

time, we reduce the noise effect. But this makes the control

too slow for our application.

than the sensor error because the sensor is integrated

at 1 Hz to match the ground truth sampling rate. We

shown in 4.2 that the sensor noise grows linearly with

the frequency, so in a 10 Hz case, we could expect a

mean error of roughly 0.7 meters per second.

Table 1: Errors between velocities calculated with the ex-

periment performed and ground truth speed (DGNSS).

Estimation method @ 1Hz Mean error (m/s)

Sensor hall measurements 0.0677

Model prediction 0.0838

SDKF estimation 0.0585

5.2 PID Tunning Without SDKF

To illustrate the undesirable effect of the low-

resolution sensor noise, we tested the PID controller

without SDKF. The experiments were performed on

a car jack due to the risk of unstable control. We ad-

justed the PID gains in an empirical way, using a step

Figure 11: PID control using the SDFK speed estimation

with f

prediction

= 20 Hz and f

sensor

= 2 Hz. The system is

now free of undesirables oscillations and the control is fast

enough for our application.

function to ﬁx the setpoint, both for positive and neg-

ative speeds.

As shown in Fig.9, we applied the PID control

with sample time T

loop

= T

sensor

= 0.1s. The high

measurement noise produced undesired oscillations

in the control signal. On the other hand, in the case

of the negative step function, when the desired speed

returns to 0, the control signal becomes clearly un-

stable. To reduce the amount of noise, we repeated

the same experiment with T

loop

= T

sensor

= 0.5s. As

shown in Fig.10 the system behavior is better, but too

slow for a good control. Moreover, we can observe

in Fig.10 down, around t = 7.5s, an outlier that pro-

duce an abrupt change in the control signal, this kind

of problem is overcome with the 3σ threshold when

using the SDFK.

5.3 PID Tunning using SDKF

Finally, we describe the tests using our full system

described in Fig.2. The closed loop frequency used

is f

loop

= 20Hz, and the observation is updated at

sensor

= 2Hz.

Firstly we adjusted the PID gains of BLUE over a

car jack to get a ﬁrst approximation of the rigth val-

ues, taking into account that the value of G

∗

was com-

puted with the robot navigating in contact with the

ground. The noise characterization was the described

in subsection 5.1.

Once adjusted the gains, we performed several ex-

periments with BLUE over ﬂat ground. The value of

G, in this case, was the optimal value G

∗

found using

the ﬂat terrain dataset. When we applied the desired

step signals for the setpoint (positive and negative),

we obtained the results shown in Fig.11. We can see

that the estimated signal is now smooth, and there are

no outliers present. The control rate (20 Hz) and the

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

212

time to reach the desired speed (around 2 seconds),

now are suitable to control our vehicle.

6 CONCLUSIONS AND FUTURE

WORK

This paper presented a low cost speed control method

using extremely low resolution sensors under low-

speed conditions. Using a particularization of the

Kalman Filter (SDKF), we were able to increase the

sensor hall sampling time thus reducing considerably

the quantiﬁcation noise while keeping the required

control rate. The proposed solution has been tested in

an Unmanned Ground Vehicle and compared against

a Differential GNSS system, showing that is suitable

to perform an effective speed control. We provide

the developed software and CAD designs through a

GitHub repository.

As future work, we plan to study the possibil-

ity of extending the proposed control method to ac-

celeration and jerk adding a PLL structure to obtain

smoother transients. Moreover, we want to evaluate

the speed control performance using a high-level sen-

sor fusion system to make asynchronous updates of

the Kalman ﬁlter.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish Gov-

erment through grant FPU15/04446 and the research

project DPI2015-68087-R.

REFERENCES

Andrade-Cetto, J. (2002). The kalman ﬁlter. Institut de

Rob

otica i Inform

atica Industrial, UPC-CSIC.

AUROVA (2018). Software and cad repository:

https://github.com/aurova-lab/clear.

Borenstein, J., Everett, H. R., Feng, L., and Wehe, D.

(1997). Mobile robot positioning-sensors and tech-

niques. Technical report, Naval Command Control

and Ocean Surveillance Center RDT and E Div. San

Diego CA.

Briz, F., Cancelas, J., and Diez, A. (1994). Speed mea-

surement using rotary encoders for high performance

ac drives. In Industrial Electronics, Control and In-

strumentation, 1994. IECON’94., 20th International

Conference on, volume 1, pages 538–542. IEEE.

Carnegie, D., Loughnane, D., and Hurd, S. (2004). The

design of a mobile autonomous robot for indoor se-

curity applications. Proceedings of the Institution of

Mechanical Engineers, Part B: Journal of Engineer-

ing Manufacture, 218(5):533–543.

De Luca, A., Oriolo, G., and Samson, C. (1998). Feed-

back control of a nonholonomic car-like robot. In

Robot motion planning and control, pages 171–253.

Springer.

agglund, T. (2012). Signal ﬁltering in pid control. IFAC

Proceedings Volumes, 45(3):1–10.

Indiveri, G., Nuchter, A., and Lingemann, K. (2007). High

speed differential drive mobile robot path following

control with bounded wheel speed commands. In

Robotics and Automation, 2007 IEEE International

Conference on, pages 2202–2207. IEEE.

Jin, Q. B. and Liu, Q. (2014). Imc-pid design based on

model matching approach and closed-loop shaping.

ISA transactions, 53(2):462–473.

Kim, H.-W. and Sul, S.-K. (1996). A new motor speed esti-

mator using kalman ﬁlter in low-speed range. IEEE

Transactions on Industrial Electronics, 43(4):498–

504.

Park, M., Lee, S., and Han, W. (2015). Development of

steering control system for autonomous vehicle using

geometry-based path tracking algorithm. ETRI Jour-

nal, 37(3):617–625.

Petrella, R., Tursini, M., Peretti, L., and Zigliotto, M.

(2007). Speed measurement algorithms for low-

resolution incremental encoder equipped drives: a

comparative analysis. In Electrical Machines and

Power Electronics, 2007. ACEMP’07. International

Aegean Conference on, pages 780–787. IEEE.

Ramsden, E. (2011). Hall-effect sensors: theory and appli-

cation. Elsevier.

Santamaria-Navarro, A., Loianno, G., Sol

a, J., Kumar, V.,

and Andrade-Cetto, J. (2017). Autonomous naviga-

tion of micro aerial vehicles using high-rate and low-

cost sensors. Autonomous Robots, pages 1–18.

Shaowei, W. and Shanming, W. (2012). Velocity and accel-

eration computations by single-dimensional kalman

ﬁlter with adaptive noise variance. Przegld Elek-

trotechniczny, (2), pages 283–287.

Siegwart, R., Nourbakhsh, I. R., and Scaramuzza, D.

(2011). Introduction to autonomous mobile robots.

MIT press.

Thrun, S., Montemerlo, M., Dahlkamp, H., Stavens, D.,

Aron, A., Diebel, J., Fong, P., Gale, J., Halpenny,

M., Hoffmann, G., et al. (2006). Stanley: The robot

that won the darpa grand challenge. Journal of ﬁeld

Robotics, 23(9):661–692.

Troncoso, C. and Su

arez, A. (2017). Control del nivel

de pulpa en un circuito de ﬂotaci

on utilizando una

estrategia de control predictivo. Revista Iberoamer-

icana de Autom

atica e Inform

atica Industrial RIAI,

14(3):234–245.

Speed Estimation for Control of an Unmanned Ground Vehicle using Extremely Low Resolution Sensors

213