Conical Tank Level Supervision using a Fractional Order Model

Reference Adaptive Control Strategy

Hanane Balaska

, Samir Ladaci

and Youcef Zennir

Department of Science and Technology, University Larbi Ben Mhidi, Oum El-Bouaghi, 04000, Algeria

Department of E.E.A., National Polytechnic School of Constantine, BP 75 A, Nouvelle ville Ali Mendjli,

25100 Constantine, Algeria

Department of Petrochemistry, University of Skikda, Route d’Elhadaiek, BP 26, Skikda 21000, Algeria

Keywords:

Model Reference Adaptive Control, Fractional Order System, Fractional Integration, Direct Auto Adjustable

Control, Non Linear System, Robustness, Parametric Variation.

Abstract:

This paper proposes a fractional order model reference adaptive control (FO-MRAC) design in order to com-

mand the level of a conical tank system. The FO-MRAC is based on the choice of a fractional reference model

which speciﬁes the closed loop desired performances. Also, the control strategy adopted introduces fractional

integration in the phase of corrector parameters updating. Model reference adaptive controller of integer or-

der and of fractional order are applied to the non linear system and compared. From the simulation results,

we concluded that FO-MRAC is the controller presenting the best performances, and especially in case of

measurements noise, and parametric variations.

1 INTRODUCTION

Fractional order systems are attracting more and more

researchers in different domains of science and engi-

neering (Mathieu et al., 2003; Ma et al., 2009; El-

sayed and Gaafar, 2003). Fractional order control is a

generalization of the classic control theory of integer

order, its major interest is to improve the control sys-

tem performances using the concepts of non-integer

derivation and fractional order systems. Dynamic

Systems and Fractional Order Controllers, which are

based on the fractional calculation, have gathered the

attention of several researchers. The most known

fractional order control structures are: CRONE con-

troller (Outsaloup, 1991), Fractional PI

controller

(Podlubny, 1999), and fractional adaptive control

(Ladaci et al., 2008).

Adaptive control is one of the popular control tech-

niques applied in industrial applications. This com-

mand consists in adapting the regulator on line with

the variations of the regulated process to ensure a

constant quality of performances. The main reason

which have encouraged researchers to move toward

fractional order adaptive control and essentially to

the fractional order model reference adaptive control

(FO-MRAC) is that The MRAC command is based

on the choice of a reference model that speciﬁes the

desired performances in closed loop, and many re-

search works proved the very good performances of

fractional systems relatively to those of integer order

(Outsaloup, 1995; Ladaci and Bensaﬁa, 2016).

Many fractional order control structure based on

MRAC have been developed in literature (Ladaci and

Charef, 2012). An indirect model reference adaptive

control is used to control a class of fractional order

systems was introduced in (Chen et al., 2016). In

(Vinagre et al., 2002; Ladaci and Charef, 2003), the

authors investigated the use of fractional order pa-

rameter adjustment rule and the employment of frac-

tional order reference model. The use of a fractional

model and the introduction of fractional derivative ﬁl-

ter at the plant output was introduced in (Ladaci and

Charef, 2006).

In this paper, we propose to control a nonlinear

dynamical plant with fractional order model refer-

ence adaptive control to improve the system perfor-

mances. We will deal with the problem of conical

tank level control, which has been widely studied and

several control techniques have been employed, even

with model predictive control (Warier and Venkatesh,

2012) and fractional order PI

controllers(Jauregui

et al., 2016).

This work is organized as follows: Section 2 presents

some theoretical concepts on fractional order systems.

214

Balaska, H., Ladaci, S. and Zennir, Y.

Conical Tank Level Supervision using a Fractional Order Model Reference Adaptive Control Strategy.

DOI: 10.5220/0006869602140221

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 214-221

ISBN: 978-989-758-321-6

The proposed FMRAC strategy is presented in Sec-

tion 3, and the conical tank modelization is given in

Section 4. Section 5 shows the simulation results.

Section 6 is dedicated to the main conclusions and

future researches.

2 FRACTIONAL ORDER

SYSTEMS

Fractional calculus is the domain of analytical math-

ematics which deals with the study and application of

arbitrary order of integrals and derivatives.

2.1 Deﬁnitions

The commonly used deﬁnitions of the fractional or-

der integrals and derivative are the Riemann-Liouville

(R-L) and Gr¨unwald-Letnikov(G-L) deﬁnitions (Old-

ham and Spanier, 1974; Bourouba et al., 2018).

The R-L fractional order integral of order λ > 0 is de-

ﬁned as:

g(t) = D

−λ

g(t) (1)

Γ(λ)

(t −τ)

λ−1

g(τ)d(τ)

and the expression of the R-L fractional order deriva-

tive of order µ > 0 is:

g(t) = D



−ν

g(t)



, µ > 0, (2)

where Γ(.) is the Euler’sgamma function and the inte-

ger m is such that (m−1) < µ < m and ν = m−µ > 0.

The GL fractional order integral of order λ > 0 is

given by:

g(t) = D

−λ

g(t) (3)

= lim

h→0

∑

j=0

(−1)



−λ



g(kh − jh)

Where h is the sampling period and the coefﬁcients

and ω

(−λ)



−λ



the coefﬁcients of the following

binomial:

(1−z)

−λ

∞

∑

j=0

(−λ)

(4)

The GL fractional order derivative of order µ > 0

is also given by

g(t) =

g(t) (5)

= lim

h→0

−µ

∑

j=0

(−1)





g(kh − jh)

where h is the sampling period and the coefﬁcients

(µ)





Γ(µ+1)

Γ( j+1)Γ(µ−j+1)

with ω

(µ)





= 1,

are those of the polynomial:

(1−z)

∞

∑

j=0

(−1)





∞

∑

j=0

(µ)

(6)

2.2 Linear Approximation of Fractional

Order Transfer Functions

For the purpose of our approach we need to use an in-

teger order model approximation of the fractional or-

der model reference in order to implement the adapta-

tion algorithm. For this aim, we use the so-called sin-

gularity function method proposed by (Charef et al.,

1992), and precisely for fractional ﬁrst order system

of the form:

H(s) =

(1+ s p

)

(7)

with β a positive real number such that 0 < β < 1.

The approximation is given by:

H(s) ≈

∏

L−1

v=0





∏

v=0





(8)

Where the singularities are given by:



= (ab)

v = 1,2, 3,..., L−1

= (ab)

v = 1,2, 3,..., L−1

(9)

with,

= p

20β

(10)

a = 10

10(1−β)

b = 10

10β

β =

log(a)

log(ab)

ε is the tolerated error in dβ. L + 1 is the total num-

ber of singularities that can be determined by the fre-

quency band of the system.

2.3 Numerical Approximation of

Riemann Fractional Integral

In our work, we need to use a numerical approxima-

tion for the analytical formulas of the fractional order

Conical Tank Level Supervision using a Fractional Order Model Reference Adaptive Control Strategy

215

Process

Adjustment

mechanism

Reference

Model

Controller

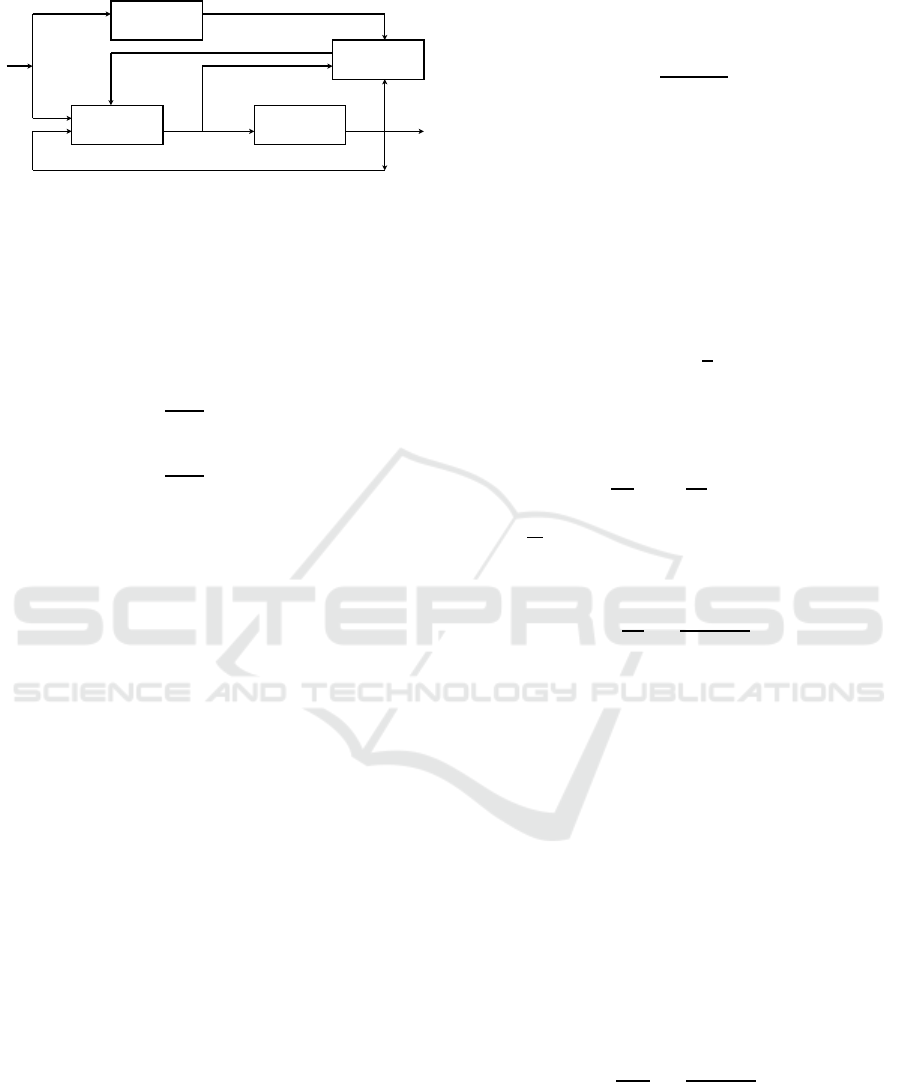
Figure 1: Block Diagram for MRAC approach.

operator and more precisely for the integral of Rie-

mann introduced in (Ladaci and Charef, 2006):

Putting:

t = k∆

Where t is the current time, k an integer, and ∆ sam-

pling period. We obtain:

g(k∆) =

∆

Γ(λ)

k−1

∑

τ=0

(k∆ −τ∆)

λ−1

g(τ∆) (11)

∆

Γ(λ)

k−1

∑

τ=0

(k−τ)

λ−1

g(τ∆)

3 FRACTIONAL ORDER MODEL

REFERENCE ADAPTIVE

CONTROL

3.1 Model Reference Adaptive Control

It’s one of the most used adaptive control approaches,

in which the desired performances are speciﬁed by the

choice of a reference model.

A block diagram representing the principle of this ap-

proach is given in the ﬁgure 1.

The reference model adaptive control system has

an ordinary feedback loop composed of the process

and the regulator and another feedback loop which al-

lows the change of the regulator parameters.

We consider a single input single output system

(SISO) described by the equation:

Ay(t) = Bu(t) (12)

Where u is the control signal and y is the output signal.

A and B represent polynomials functions of either the

differential operator p = d/dt, or the shift operator in

advance q.

The desired closed-loop response is speciﬁed by the

reference model output y

(t) = B

(t) (13)

A general linear regulator can be described by:

Ru(t) = Tu

(t) −Sy(t) (14)

where R, S, and T are polynomials. And we get the

closed-loop system:

y(t) =

AR+ BS

(t) (15)

The mechanism of adjustment of the regulator param-

eters can be obtained using the law of MIT, which is

the original approach for the MRAC.

To represent the MIT law, we consider a closed-loop

system in which the regulator has a vector θ of ad-

justable parameters. Let e be the error between the

output y of the closed loop and that of the reference

model y

. The adjustment of the parameters is done

in such a way as to minimize a cost function deﬁned

J(θ) =

(16)

To minimize J, we have to change the parameters in

the direction of the negative gradient of J, and we

have the famous MIT law:

dθ

= −γ

δJ

δθ

= γϕe (17)

ϕ = −

δe

δθ

, and γ is the adaptation gain.

The following standardized algorithm is less sensitive

to signal levels:

dθ

= γ

ϕe

α+ ϕ

(18)

The control signal is computed using the following

relation:

u = ϕ

θ (19)

Where, ϕ is the regression vector containing the mea-

sured input and output signals u and y and the input

reference signal u

3.2 Fractional approach

In this work we will consider a fractional order refer-

ence model which will be implemented using the sin-

gularity approximation method proposed by (Charef

et al., 1992). Also, in the phase of updating the pa-

rameters of the corrector, we will use the fractional

order parameter adaptation law proposed in (Ladaci

and Charef, 2006) instead of equation (18) given by:

= γ

ϕe

α+ ϕ

(20)

And we will use the numerical Riemann approxima-

tion (11) to obtain fractional order integral of the re-

lation (20).

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

216

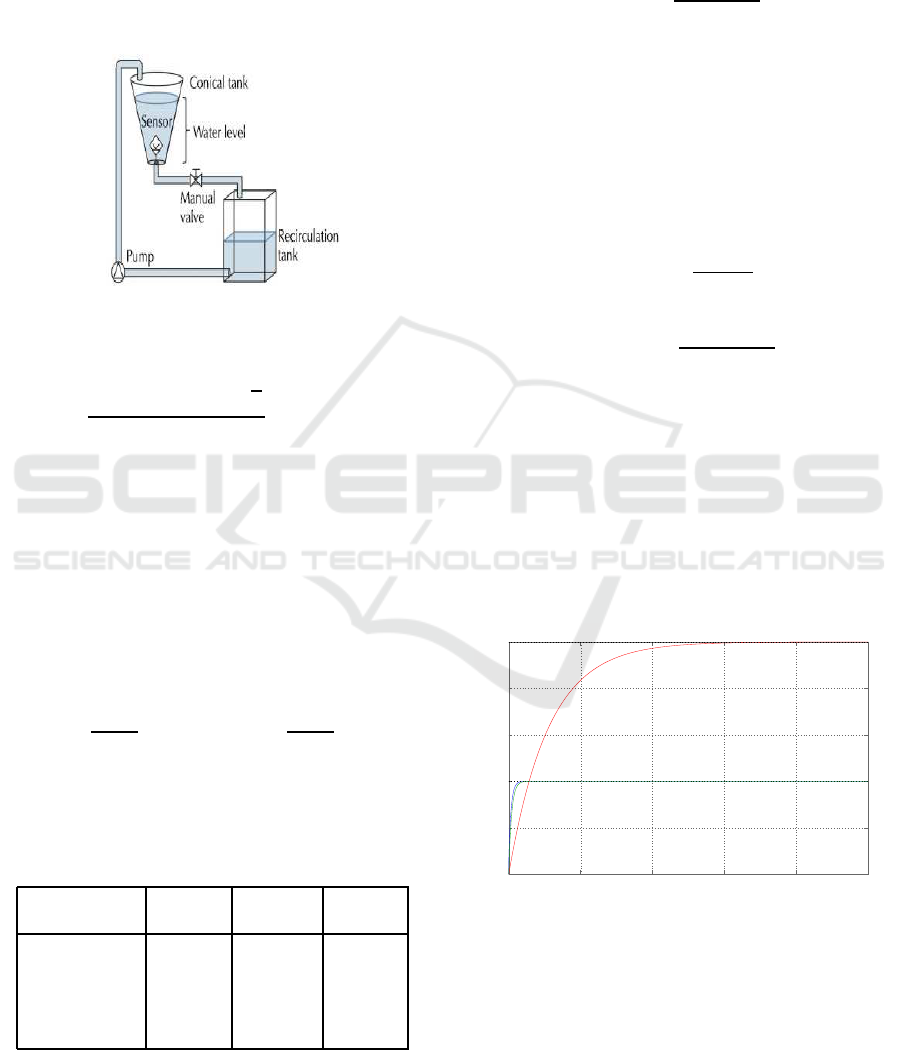
4 CONICAL TANK SYSTEM

The layout of the conical tank system is shown in Fig-

ure 2. The water is pumped from the bottom of the

recirculating tank to the upper part of the conical tank

by means of a pump driven by an induction motor of

variable speed driven by a variable frequency drive.

From (Jauregui et al., 2016), the nonlinear model for

Figure 2: Conical tank conﬁguration.

the conical tank is represented by the following equa-

tion:

h =

5.43f −78.23 + µ

√

0.65h

+ 11.4h + 17.1

= g(h, f) (21)

With µ = −20.63, f is the input and represent the

electrical network frequency expressed in % as a per-

centage of the nominal frequency (50Hz) and ranges

in the interval 0%−100%, h is the output and repre-

sent the water level inside the conical tank expressed

in cm, g(h, f) is a non linear function of these two

variables showing clearly the nonlinearities of the

conical tank system.

The system is linearized around 3 operating points

, f

). These approximations are given by:

h = W(h−h

) + Z( f − f

) (22)

With W =

δg(h, f)

δh



, f

)

and Z =

δg(h, f)

δf



, f

)

To determine the operating points the whole operation

range 15cm−60cm is divided into three segments, as

illustrated in Table 1.

Table 1: Operating points and parameters of linearized

models.

Low Medium High

level level level

Interval (cm) 15-30 30-45 45-60

(cm) 22.5 37.5 52.5

(%) 32.42 37.66 41.92

W -0.0036 -0.0012 -0.0006

Z 0.009 0.004 0.0022

In our work, we try to control the nonlinear sys-

tem around only one operation point (Low level).

So, the linearized system is represented by equation

(22), with W = −0.0036, and Z = 0.009, By posing:

y(t) = h −hop, and u(t) = f − fop, we obtain the

following transfer function (Deghboudj and Ladaci,

2017):

G(s) =

0.009

s+ 0.0036

(23)

5 SIMULATION RESULTS

In this Section, we will apply the proposed fractional

order adaptive control technique to the tank level

control, with the transfer function given in equation

(23).Let us chose reference model transfer functions

of integer order and fractional order respectively:

(s) =

1+ 20s

(24)

and

(s) =

(1+ 20s)

0.6

(25)

is approximated to an integer order model using

the singularity function method (Charef et al., 1992).

The sampling period is ∆ = 0.1sec.

The step response of the fractional order refer-

ence model is compared with that of the integer order

model and with the open loop system step response in

Figure 3.

Figure 4 illustrates the bode plot of the open loop

system, of the integer order reference model, and the

fractional order reference model.

0 500 1000 1500 2000 2500

0.5

1.5

2.5

Step Response

Time (seconds)

Amplitude

Figure 3: Open loop step response of the tank system (red),

step response of the integer order reference model (green),

step response of the fractional order reference model (blue).

From Figure 3, we clearly see that the fractional

order model is faster than the integer order model,

which is conﬁrmed also in Figure 4, where we see

that the fractional reference model has the largest pass

band.

In order to test the effectiveness and the performances

Conical Tank Level Supervision using a Fractional Order Model Reference Adaptive Control Strategy

217

−100

−50

Magnitude (dB)

−4

−3

−2

−1

−90

−45

Phase (deg)

Bode Diagram

Frequency (rad/s)

G_sys

Gm_frac

Gm_entier

Figure 4: Bode plot of G (red), of G

(red), and of G

(blue).

of each controller (MRAC and FO-MRAC), a stan-

dard reference signal u

(t) is applied, consisting of

steps with different amplitudes described in table 2.

Table 2: Reference signal.

t (sec) [0 500] [500 1000] [1000 1500]

r(t) 20 29 15

Also, to evaluate and compare the performances

of each control method, we choose the performance

index given by the sum of the absolute error (SAE) de-

ﬁned in the expression (26), and the sum of the square

input (SSI) deﬁned in (27):

∑

k=0

|e(k∆)| (26)

∑

k=0

u(k∆)

(27)

where N is the samples number, e(k∆) = y(k∆) −

r(k∆).

5.1 Study in the Ideal Case (Without

Disturbances)

Respectively, the real output of the system and the

control signal of the classical MRAC and the FO-

MRAC are shown in Figure 5 and Figure 6.

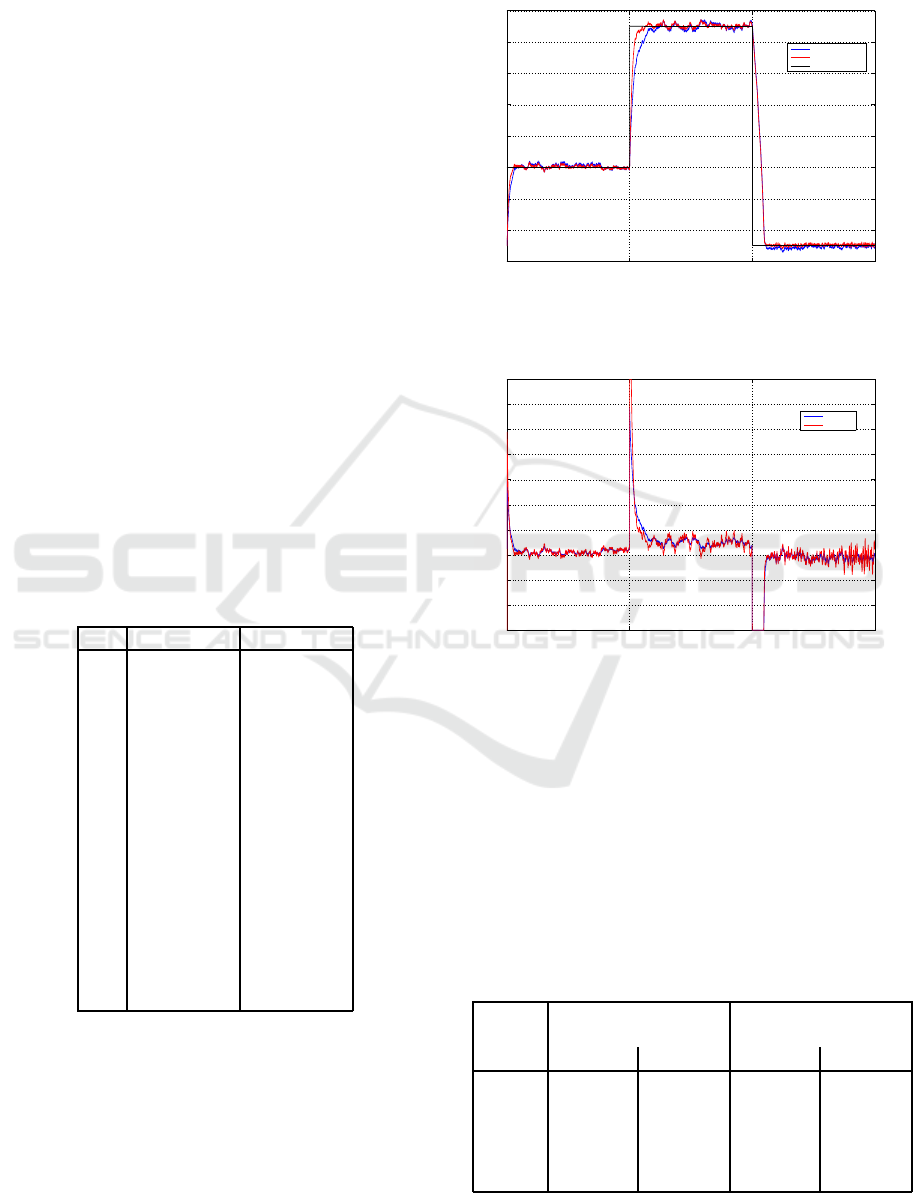
From obtained results, we remark that the output

of the system follows the referential signal, even the

sudden change of the set point signal.

Better results are obtained when using the FO-MRAC

method, where we have the lowest cost function of

error, whereas the MRAC strategy presents the lowest

energy consumption by the control signal. The sys-

tem is faster and more precise with the FO-MRAC

strategy.

In order to study the inﬂuence of the fractional order

0 500 1000 1500

Time (sec)

System output

Classical MRAC

FO−MRAC (m=1.1)

Setpoint signal

Figure 5: The system response with classical MRAC and

with FO-MRAC (m = 1.1).

0 500 1000 1500

100

Time (sec)

Error signal

MRAC

FO−MRAC

Figure 6: The control signal of the classical MRAC and the

FO-MRAC (m = 1.1).

m value on the performance of the control system, we

vary its value from 0.1 to 1.5; the results are grouped

in the following Table 3.

Table 3: Cost functions Versus the fractional order m.

m J

0.1 5.6025 10

1.6313 10

0.2 5.6011 10

1.6313 10

0.3 5.5988 10

1.6313 10

0.4 5.5948 10

1.6314 10

0.5 5.5879 10

1.6315 10

0.6 5.5758 10

1.6318 10

0.7 5.5550 10

1.6322 10

0.8 5.5207 10

1.6331 10

0.9 5.4667 10

1.6346 10

1 5.6484 10

1.6096 10

1.1 5.3649 10

1.6424 10

1.2 5.5223 10

1.6332 10

1.3 5.4757 10

1.6348 10

1.4 5.4264 10

1.6377 10

1.5 5.4376 10

1.6369 10

From the results, the minimum cost of the error is

obtained for m = 1.1, where the control energy con-

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

218

sumption is the greatest. The error cost function is

better for FO-MRAC whereas the criterion J

is better

for integer order MRAC, which means that the frac-

tional order MRAC improves the reference tracking

by mean of a greater input energy effort.

From the Table 3, there exists a trade off between

the control energy consumption and the tracking error

cost. The FO-MRAC strategy allows the resolution of

this trade off by choosing the proper m value.

It is also worthy to notice that the adaptation gain γ is

very small for all fractional orders m (less than 10

−6

)

comparatively to the integer order MRAC (γ = 0.01)

which improves the relative stability of the adaptive

control system.

5.2 Study in the Presence of

Measurement Noises

In order to test the robustness of these controllers in

the case where the measurement is tainted with noise,

we have injected a noise to the output (random signal)

of zero average and standard deviation equal to 0.03.

We study the inﬂuence of the fractional order m value

on the performance of the FO-MRAC system in pres-

ence of measurement noise by varying its value from

0.1 to 1.5, the results are grouped in Table 4.

Table 4: Cost functions Versus the fractional order m in

presence of noises.

m J

0.1 7.0855 10

1.6168 10

0.2 7.0839 10

1.6168 10

0.3 7.0812 10

1.6168 10

0.4 7.0763 10

1.6169 10

0.5 7.0673 10

1.6170 10

0.6 7.0509 10

1.6173 10

0.7 7.0215 10

1.6177 10

0.8 6.9698 10

1.6185 10

0.9 6.8811 10

1.6201 10

1 8.1872 10

1.5961 10

1.1 6.5166 10

1.6305 10

1.2 6.9527 10

1.6186 10

1.3 6.8560 10

1.6202 10

1.4 6.6940 10

1.6235 10

1.5 6.7269 10

1.6226 10

From Table 4, we see that the FO-MRAC is more

robust against noise than the classical MRAC strat-

egy, for the reason that with FO-MRAC, we obtain

always the lowest error cost and that for any value of

the fractional order of integration m. The lowest error

cost is obtained for m = 1.1.

Figure 7 and Figure 8 illustrate respectively the sys-

tem output and the control signal for the two applied

strategies.

0 500 1000 1500

Time (sec)

System output

Classical MRAC

FO−MRAC (m=1.1)

Setpoint signal

Figure 7: The system response with classical MRAC and

with FO-MRAC (m = 1.1) in presence of measurement

noises.

0 500 1000 1500

100

Time (sec)

Control signal

MRAC

FO−MRAC

Figure 8: The control signal of the classical MRAC and the

FO-MRAC (m = 1.1) in presence of measurement noises.

5.3 Study in Case of Model Parametric

Variations

No let us test the robustness of the proposed control

law with respect to model parametric variations. We

consider a set of variation on the parameter values

in equation (23) from the instant 1500 sec. Results

obtained with the classical MRAC and with the FO-

MRAC strategy are exposed in Table 5.

Table 5: Cost functions Versus the parameter variation rate.

Param Classical FO-MRAC

var. MRAC m = 1.1

% J

05 7.0710

1.65 10

5.1310

1.6710

10 7.5510

1.68 10

5.2810

1.7210

20 8.6110

1.76 10

5.6710

1.79 10

40 1.0710

1.92 10

8.4010

1.94 10

60 1.2310

2.10 10

1.0010

2.12 10

Conical Tank Level Supervision using a Fractional Order Model Reference Adaptive Control Strategy

219

The system responses for the two control strate-

gies applied in case of 20% parameter variation and

the control signal of the classical MRAC and the FO-

MRAC controllers are exposed in Figure 9 and Fig-

ure 10.

0 500 1000 1500

Time (sec)

System output

set point signal

Classical MRAC

FO−MRAC (m=1.1)

Figure 9: The system response with classical MRAC and

with FO-MRAC (m = 1.1) in presence of measurement

noises.

0 500 1000 1500

100

Time (sec)

Control signal

MRAC

FO−MRAC

Figure 10: The control signal of the classical MRAC and the

FO-MRAC (m = 1.1) in presence of measurement noises.

From the simulation results, we see that w the sys-

tem is affected by the change of parameter value at

the instant of 1500 sec, after that we observe that the

system tries to follow the consign signal, and at the

end maintains the desired performance. However, it

is also remarkable that with an FO-MRAC strategy,

the error signal has the lower amplitude.

From the Table 5, we see that the FO-MRAC has al-

ways the lowest error cost, even for sudden parameter

variations. So, we conclude that the FO-MRAC is

much more robust than the classical MRAC.

6 CONCLUSIONS

A fractional order model reference adaptive control

has been designed in order to command a conical tank

level with nonlinear dynamics. The reference model

is set to be a fractional model system approximated by

rational transfer function using the singularity func-

tion approach; also a fractional order parameter adap-

tation law is used to update the controller parameters.

Simulation results illustrate the effectiveness of the

proposed control scheme and conﬁrm its robustness

and especially in the presence of measurement noises

and parametric variations.

REFERENCES

Bourouba, B., Ladaci, S., and Chaabi, A. (2018). Re-

duced order model approximation of fractional order

systems using differential evolution algorithm. Jour-

nal of Control, Automation and Electrical Systems,

29(1):32–43.

Charef, A., Sun, H. H., Tsao, Y., and Onaral, B. (1992).

Fractal system as represented by singularity function.

IEEE Transactions on Automatic Control, 37:1465–

1470.

Chen, Y., Cheng, S., Wei, Y., and Wang, Y. (2016). Indirect

model reference adaptive control for a class of linear

fractional order systems. In American Control Con-

ference (ACC), Boston, MA, USA. IEEE.

Deghboudj, I. and Ladaci, S. (2017). Fractional order

model predictive control of conical tank level. In

on Automatic control, Telecommunication and Signals

(ICATS17), Annaba, Algeria, 11–12 December, pages

1–6. IEEE.

El-sayed, A. and Gaafar, F. (2003). Fractional calculus and

some intermediate physical processes. Applied Math-

ematics and Computation, 144:117–126.

Jauregui, C., Duarte-Mermoud, M., Orostica, R., Travieso-

Torres, J., and Beytia, O. (2016). Conical tank level

control using fractional order pid controllers: a sim-

ulated and experimental study. Control Theory Tech,

14(4):369–384.

Ladaci, S. and Bensaﬁa, Y. (2016). Indirect fractional or-

der pole assignment based adaptive control. Engineer-

ing Science and Technology, an International Journal,

19(1):518–530.

Ladaci, S. and Charef, A. (2003). Mit adaptive rule with

fractional integration. In CESA 2003IMACS Multicon-

ference Computational Engineering in Systems Appli-

cations, Lille, France.

Ladaci, S. and Charef, A. (2006). On fractional adaptive

control. Nonlinear Dynamics, 43(4):365–378.

Ladaci, S. and Charef, A. (2012). Fractional adaptive con-

trol: A survey. In Classiﬁcation and Application

of Fractals: New Research Edited by:E.W. Mitchell

and S.R. Murray., pages 261–275. NOVA Publishers,

USA.

Ladaci, S., Loiseau, J., and Charef, A. (2008). Fractional or-

der adaptive high gain controllers for a class of linear

systems. Communications in nonlinear science and

numerical simulations, 13(4):707–714.

Ma, J., Yao, Y., and Liu, D. (2009). Fractional order model

reference adaptive control for hydraulic driven ﬂight

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

220

motion simulator. In SSST 2009, 41st Southeasten

Symposium on System Theory. Tullahoma, TN, USA.

IEEE.

Mathieu, B., Melchior, P., Outsaloup, A., and Ceyral, C.

(2003). Fractional differentiation for edge detection.

Signal Processing, 83:2421–2432.

Oldham, K. and Spanier, J. (1974). The fractional Calculus.

Academic Press, New York.

Outsaloup, A. (1991). La commande CRONE (in French).

Herm`es, Paris.

Outsaloup, A. (1995). La d´erivation non enti`ere (in French).

Herm`es, Paris.

Podlubny, I. (1999). Fractional order systems and pi

controllers. IEEE Transactions on Automatic Control,

44(1):208–214.

Vinagre, B., Petras, I., Podlubny, I., and Chen, Y. (2002).

Using fractional order adjustment rules and fractional

order reference models in model-reference adaptive

control. Nonlinear Dynamics, 29:269–279.

Warier, S. and Venkatesh, S. (2012). Design of controllers

based on mpc for a conical tank system. In Interna-

tional Conference On Advances in Engineering, Sci-

ence and Management, Tamil Nadu, India, pages 309–

313. IEEE.

Conical Tank Level Supervision using a Fractional Order Model Reference Adaptive Control Strategy

221