Efﬁcient Index-based Search Protocols for Encrypted Databases

Majid Nateghizad, Zekeriya Erkin and Reginald L. Lagendijk

Cyber Security Group, Department of Intelligent Systems, Delft University of Technology, The Netherlands

Keywords:

Searching in Encrypted Databases, Homomorphic Encryption, Statistical Query, Indexing, Privacy.

Abstract:

It is astonishing to see more and more services built on user-oriented data, providing numerous tools to improve

ones daily life. Nowadays, data collected from numerous sources is being used to monitor daily activities, i.e.,

monitoring patients. These innovations allow for more cost-efﬁcient and scalable solutions. Nevertheless,

these types of services can pose a threat to the privacy of individuals due to the possibility of leaking highly

privacy-sensitive data. Therefore, it is essential to design such systems in a privacy-preserving manner. In-

spired by a real-life project in the health-care domain, we propose to secure the data using encryption, while

enabling the involved parties to run queries directly on this encrypted data. A vital component of such a sys-

tem is searching for speciﬁc data entries within a large dataset. In this work, we present two cryptographic

protocols that complete such a query by creating an encrypted vector in a simulation secure way. These vectors

consist of a 1 for intended database entry, whereas other items would be represented as a 0. By creating index

tables before the execution of the queries, it has become possible to execute a search query with high perfor-

mance. As we show in our analyses, it takes less than one second to ﬁnd the matching encrypted data-entry

within a database with 100K records. Our proposal is generic, can be applied to several application domains,

and practically compared to similar works.

1 INTRODUCTION

A real-life problem motivates the work presented in

this paper: A hospital wants to monitor its patients us-

ing off-the-shelf smart devices (Treskes et al., 2017)

that measure, among other things, a patient’s weight,

ECG, blood pressure, and blood sugar level. These

devices connect to the smartphone of a patient, who

needs to be monitored on a daily basis. A mobile ap-

plication then sends the measurements to the central

server of the vendor. Afterward, the hospital can use

a web-based application to check the measurements

for any particular patient. The primary reasons to use

such a system are straight-forward: scalability and

cost reduction (Goldschmidt, 2005).

Unfortunately, the whole system relies on the as-

sumption that the vendor is trust-worthy and it has a

secure method to protect against both internal and ex-

ternal attackers. All recent incidents show that this is

not yet the case (Meingast et al., 2006). Currently, it is

possible for a hacker to break into the data servers and

steal privacy-sensitive medical data, such an attacker

can either be a malicious employee or someone who

makes a genuine mistake (Johnson, 2009). It is es-

sential to propose a system where sensitive data are

protected while enabling medical institutions to mon-

itor their patients remotely.

In order to create a secure system with this lay-

out, we propose to encrypt measurements directly on

the smartphone of the user before sending them to the

vendor. We aim to encrypt the data using a homomor-

phic encryption scheme which enables data process-

ing while encrypted, without revealing the content of

data to the vendor or any third party. More precisely,

what is needed for the above system is to identify a

patient, or a group of patients, with speciﬁc condi-

tions, e.g., people with high blood pressure within a

particular time period. Provided that we require se-

mantic security, it is challenging to ﬁnd all the data for

given conditions, since it requires ‘searching through

the encrypted database.’

Searching in encrypted databases has been a chal-

lenge for researchers for many decades. Proposed so-

lutions vary in the cryptographic tools used for en-

crypting data. Examples include: schemes built on

attribute-based encryption (Bethencourt et al., 2007),

homomorphic encryption (Chung et al., 2010) and

special constructions such as Oblivious RAMS (Os-

trovsky, 1990; Goldreich and Ostrovsky, 1996). The

focus has been on improving efﬁciency; the current

state-of-the-art is not as practical as searching within

a plaintext database where different techniques can be

270

Nateghizad, M., Erkin, Z. and Lagendijk, R.

Efﬁcient Index-based Search Protocols for Encrypted Databases.

DOI: 10.5220/0006869802700281

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 270-281

ISBN: 978-989-758-319-3

used to speed up the search function (e.g., creating

hash tables). Therefore, there is a need for further re-

search to achieve higher efﬁciency.

Inspired by the medical application, in this work,

we assume that patients have a smartphone, which

can collect measurements from one or more smart

devices. The data is then sent to the vendor’s stor-

age unit, which can either be a local or cloud-based

database. More interestingly, a patient might utilize

different smart devices from different vendors. The

hospital that wants to monitor a speciﬁc patient, or a

group of patients, should be able to retrieve the related

data without leaking information to any of the ven-

dors. This application setting is challenging for three

reasons: 1) we want to enable hospitals to retrieve

data on sophisticated queries, 2) we also assume

multiple devices from different vendors and 3) the

amount of data collected from the patients is signif-

icantly large. To achieve our goal, we need to identify

the data entries, which are all encrypted, that match

the query provided by the hospital. More precisely,

we assume that there is a global (virtual) database

with encrypted entries from all devices. Given that

database, we want to create an encrypted, binary vec-

tor such that a vector element is 1 for corresponding

database entry and 0, for all other tuples. Given such

an encrypted binary vector, it is possible to build nu-

merous services such as i) generating statistics (i.e.,

counting, averaging), ii) data aggregation, and iii) pri-

vate data retrieval.

To obtain such a vector, we present two crypto-

graphic protocols for secure searching, IBSvI and IB-

SvII. In IBSvI, we propose a computation-wise ef-

ﬁcient searching protocol. In IBSvII, the computa-

tion of generating the encrypted binary vector is per-

formed in one party. However, IBSvII introduces

more computational overhead. These protocols rely

on creating index tables and updating them with each

input received from a device. The index tables are

then used later to execute queries and ﬁnd speciﬁc

database entries at signiﬁcantly lower cost. Our pro-

posal has several advantages over existing works: 1)

our protocols are designed for numerical data, in con-

trast to current work that relies on exact match, 2) our

proposal supports conjunction queries with “AND”,

3) our proposal is simulation secure; it leaks no pri-

vate information including search pattern and access

pattern to the involved entities, and 4) our protocols

enable generating statistics from encrypted data based

on the given conditions.

2 RELATED WORK

Ostrovsky and Goldreich (Ostrovsky, 1990; Goldre-

ich and Ostrovsky, 1996) introduced ORAM where it

is possible to evaluate any query, while the access pat-

tern is kept hidden. ORAM lets users upload their pri-

vate data to a remote storage in encrypted form, and

still have random access to their data in a secure way.

However, ORAM allows users to access only one en-

try at a time with a logarithmic number of commu-

nication rounds for each read. Moreover, in ORAM,

users should know the location of the data that they

are looking for in the database. Later works (Song

et al., 2000; Goh, 2003; Chang and Mitzenmacher,

2005) proposed more efﬁcient ways of searching by

using weaker security models. Song et al. (Song et al.,

2000) introduced a private key based searching that is

communication-wise more efﬁcient than ORAM. The

secure searching in (Song et al., 2000) is based on

generating and storing a two-layer ciphertext in the

remote storage unit. Although the introduced encryp-

tion scheme by Song et al. is proven to be secure, the

searching procedure reveals the access pattern. Simi-

larly, Stefanov et al. (Stefanov et al., 2014) combined

a secure search and ORAM, where the keywords are

kept conﬁdential, but the search protocol still reveals

the access pattern to the remote storage. To improve

the searching performance, as one of the limitations of

Song et al. (Song et al., 2000), Goh (Goh, 2003), and

Chang and Mitzenmacher (Chang and Mitzenmacher,

2005) proposed two new secure searching protocols

with indexing. They constructed an index table along-

side each set of data in the remote storage. The remote

storage uses the index tables to ﬁnd the matching data

instead of checking every single encrypted data. Al-

though (Goh, 2003; Chang and Mitzenmacher, 2005)

are efﬁcient, their proposals leak access pattern to the

untrusted parties.

Curtmola et al. (Curtmola et al., 2011) also pre-

sented a semantically secure search by using asym-

metric data encryption, which is capable of ﬁnding

desired data in sub-linear search time. In (Curtmola

et al., 2011), each user constructs an index, which in-

cludes every possible data that can appear in a query,

then the index table is deterministically encrypted

and outsourced to the remote storage. To perform a

search, a user constructs a query that contains a to-

ken that is a deterministic function of the search data

and sends the token to the remote storage. Then, the

remote storage unit searches for the speciﬁc data in

each set. Although the proposed searching technique

is fast, it has two limitations: 1) users cannot update

the index table of their data unless they generate the

index table again, and 2) the searching technique still

Efﬁcient Index-based Search Protocols for Encrypted Databases

271

reveals the access pattern. To overcome the challenge

of updating index table in (Curtmola et al., 2011), Ka-

mara et al. (Kamara et al., 2012) introduced an im-

provement, which enables updating the index table.

However, the problem of revealing the access pattern

is not addressed in that work. (Ding et al., 2017)

proposes an efﬁcient and secure search that supports

top-k similarity search over encrypted data by using a

random traversal algorithm. However, in (Ding et al.,

2017), users cannot evaluate their queries, but only

the data owner. (Miyoshi et al., 2017) presents an ef-

ﬁcient search technique over encrypted data that uses

Bloom ﬁlter as the indexing technique. Although us-

ing Bloom ﬁlter introduces false-positive results, it

makes the size of the indices very small and indepen-

dent from the security parameter at the cost of leaking

number of matches.

Boneh et al. introduced the ﬁrst Public-key En-

cryption with Keyword Search (PEKS) (Boneh et al.,

2004), which was shown later that it leaks user’s ac-

cess pattern. Furthermore, (Boneh et al., 2004) is in-

secure against ofﬂine keyword guessing attack (Byun

et al., 2006). Boneh et al. proposed another PEKS

(Boneh et al., 2007), which is based on PIR (Chor

et al., 1995) and Bloom ﬁlters, where the aim is to

hide the access pattern. Although (Boneh et al., 2007)

is secure, PIR-based schemes are computationally ex-

pensive. Moreover, in (Boneh et al., 2007) the num-

ber of matches that can be found in the remote stor-

age is ﬁxed beforehand to not leak the number of

matches. To reduce the search overhead, Bellare et al.

(Bellare et al., 2007) introduced an efﬁcient public-

key searchable encryption (ESE), which achieved an

optimal search time. In contrast to PEKS, ESE al-

lows other users to generate tokens and search for data

in the remote storage unit only by having the public

key. However, ESE encryption scheme is determinis-

tic and vulnerable to brute-force attacks.

Sahai and Waters (Sahai and Waters, 2005) in-

troduced a new encryption scheme called Attribute-

Based Encryption (ABE), which is capable of using

an arbitrary string as the public key. In ABE, a cipher-

text is not generated for a particular receiver, but for

whom possess the desired attributes. In later works,

Goyal et al. (Goyal et al., 2006) and Bethencourt et al.

(Bethencourt et al., 2007) revised the ABE and intro-

duced Key-Policy Attribute-Based Encryption (KP-

ABE) and Ciphertext-Policy Attribute-Based Encryp-

tion (CP-ABE). Then, Han et al. (Han et al., 2014)

proposed a new encryption scheme, Attribute-Based

Encryption with Keyword Search (ABEKS), which

enables a multi-user access control based on KP-

ABE. In ABEKS, a token is generated by using user’s

private key, and it consists of the desired data to be

searched in the remote storage unit. However, in (Han

et al., 2014) search is realized through decryption of

ciphertexts in the database, which introduces a signif-

icant computational overhead. Moreover, this tech-

nique requires generating a trapdoor, which necessi-

tates collaboration with data owner. (Zhang et al.,

2016) proposes a privacy-preserving ranked multi-

keyword search in a multi-owner model. This ap-

proach allows each data owner to use his private key

for the encryption. However, this proposal suffers

from the high computational cost of searching. Guo

et al. (Guo et al., 2017) proposed a secure search

that supports multiple data owners setting. (Guo

et al., 2017) also enables rank search based on the

relevance of documents and keyword, and quality of

documents. They also propose an efﬁcient indexing

structure, group keyword balanced binary tree (GBB

tree), to achieve higher efﬁciency in searching. How-

ever, in (Guo et al., 2017), a trusted third proxy is

used to facilitate data outsourcing and query evalua-

tion. Moreover, the improvement over BB-tree leaks

private information regarding access pattern. As it is

stated in (Guo et al., 2017), the GBB-tree may not ac-

cess one or multiple subtrees to reduce computation

overhead, which can reveal access pattern.

Chung et al. (Chung et al., 2010) introduced a se-

cure outsourcing protocol based on Gentry’s fully ho-

momorphic encryption scheme (Gentry, 2009). Al-

though in (Gentry, 2009) conﬁdentiality of data is

preserved, while data processing remains possible, its

computational overhead is still a challenge. Li et al.

(Li et al., 2012) proposed a method to apply homo-

morphic encryption with an overhead linear in the

number of the records. Xiong et al. (Xiong et al.,

2013) introduced a ciphertext-policy-ABE (CP-ABE)

searchable encryption by using homomorphic encryp-

tion, where its search time is proportional to the size

of the dataset. B

osch et al. (B

osch et al., 2012)

proposed a scheme, BTH

, which is a combination

of somewhat homomorphic encryption, and indexing

technique of Chang and Mitzenmacher (Chang and

Mitzenmacher, 2005). In B

osch’s work (B

osch et al.,

2012), only the data owner can perform a search over

the data, since generating trapdoor requires the pos-

session of the private key.

Gentry et al. (Gentry et al., 2015) proposed a se-

cure searching based on ORAM and Somewhat Ho-

momorphic Encryption (SHE) scheme. Although us-

ing ORAM in (Gentry et al., 2015) prevent informa-

tion leakage in searching, it is communication-wise

expensive. Popa et al. (Popa et al., 2012) introduced

one of the most well-known solutions, CryptDB, for

searching over encrypted data. CryptDB uses dif-

ferent encryption schemes depending on the type of

SECRYPT 2018 - International Conference on Security and Cryptography

272

the given query to be evaluated over encrypted data.

However, CryptDB leaks the number of matches to

the untrusted server. Moreover, in (Akin and Sunar,

2015), the authors show that CryptDB is insecure

because it does not provide integrity for the query.

Krell et al (Krell et al., 2017) introduce another se-

cure searching using ORAM, SHE, and Bloom ﬁl-

ter that is signiﬁcantly more efﬁcient. However, they

achieve such efﬁciency at the cost of leaking access

pattern. Moreover, the work in (Krell et al., 2017)

suffers from high storage complexity, where 100K of

records each having four searchable keywords results

in an encrypted index that using 75GB of RAM. An-

other drawback of (Krell et al., 2017) is that it requires

the data owner to be online for searching. Table 1

summarizes the performance and security of the state-

of-the-art searching techniques and our secure search-

ing protocols. In Table 1, we denote multi-reader and

multi-writer setting as M-M, n is the total number of

records, n

is the number of records having the at-

tribute a equal to v, d is the number of data own-

ers, λ is a security parameter, and k stands for top-k

documents as described in (Guo et al., 2017). Note

that, in contrast to the existing works, our proposal

only addresses the problem of ﬁnding the matching

records, not retrieving them. Thus, the current works

and ours are not comparable concerning performance,

communication/computation-wise.

3 SECURE SEARCHING

PROTOCOLS

In this work, there are ﬁve parties: 1) users, 2) data

storage units, 3) query issuer, 4) remote computation

system, and 5) key manager:

i) Key Manager (KM): KM generates a pair of pub-

lic and private keys and shares the public key

with the other parties. KM also collaborates with

RCS to perform two-party computations such as

secure decryption.

ii) Users: They are the owners of private data (pa-

tients) that are stored in remote data storage in

encrypted form. The users send their measure-

ments to the corresponding vendors. The data

is consisting of several attributes, denoted by p

Therefore, the users’ data structure is a tuple

T (id

, p

,id

,v), where id

is the user identity,

is an attribute (e.g., date, time, age, device id,

etc), id

is an unique identity for p

, and v is the

measurement. The users send their encrypted tu-

ples to their data storage units.

iii) Data Storage Unit (DSU): Each data storage unit

collects data from one or multiple users and

sends the data to a remote computation system,

cloud, on a regular basis. In our scenario, DSUs

are the vendors, who are offering smart devices

to people.

iv) Query Issuer (QI): QI is interested in processing

users’ data (i.e., hospital or medical research in-

stitutes). In our work, QI can ask for generating

statistics like counting, averaging, and data ag-

gregating. QI constructs a query that includes

one or multiple attributes as q : {Q

, ´p

}

based on the type of result that QI is interested

in. Q

deﬁnes the type of the query like count-

ing, each ´p

represents the value of an attribute.

To prevent private data leakage, QI encrypts p

values. id

are meta-data that describe ´p

refer-

ring to what type of attribute (i.e., blood pressure

or heart beating rate).

v) Remote Computation System (RCS): RCS is a

considered to be a cloud storage and processing

unit that has sufﬁcient computational and storage

capacity. RCS receives and stores the encrypted

data from all DSUs. RCS also receives encrypted

queries from QI. Henceforward, we denote the

tuple in RCS as T

For our constructions, we use an additively homo-

morphic and semantically secure encryption scheme,

namely Paillier (Paillier, 1999), and a fully homo-

morphic scheme, Fan-Vercanteren (FV) (Fan and Ver-

cauteren, 2012). Our system is designed under the as-

sumption of semi-honest security model (Goldreich,

2004). In our setting, the aim is to protect private

data of users and QI from both KM and RCS, which

are semi-trusted, during the evaluation of the query q

provided by QI. The results of queries are kept hidden

from KM and RCS.

3.1 IBSvI

Searching in IBSvI consists of two phases: First, we

generate indices, which is done before the execution

of the protocol (off-line phase) and second, we in-

voke the searching protocol upon receiving the query

q from QI (on-line phase).

3.1.1 Generating Indices

Indices are constructed in four steps:

1. Users change the measurements of each attribute

, z ∈ {0,··· ,α − 1} to binary form (p

)

, where

i ∈ {0, ·· · , e ≤ ` − 1} and e is the bit-length of

. Then, they assign zero to the rest of bits from

)

to (p

)

`−1

Efﬁcient Index-based Search Protocols for Encrypted Databases

273

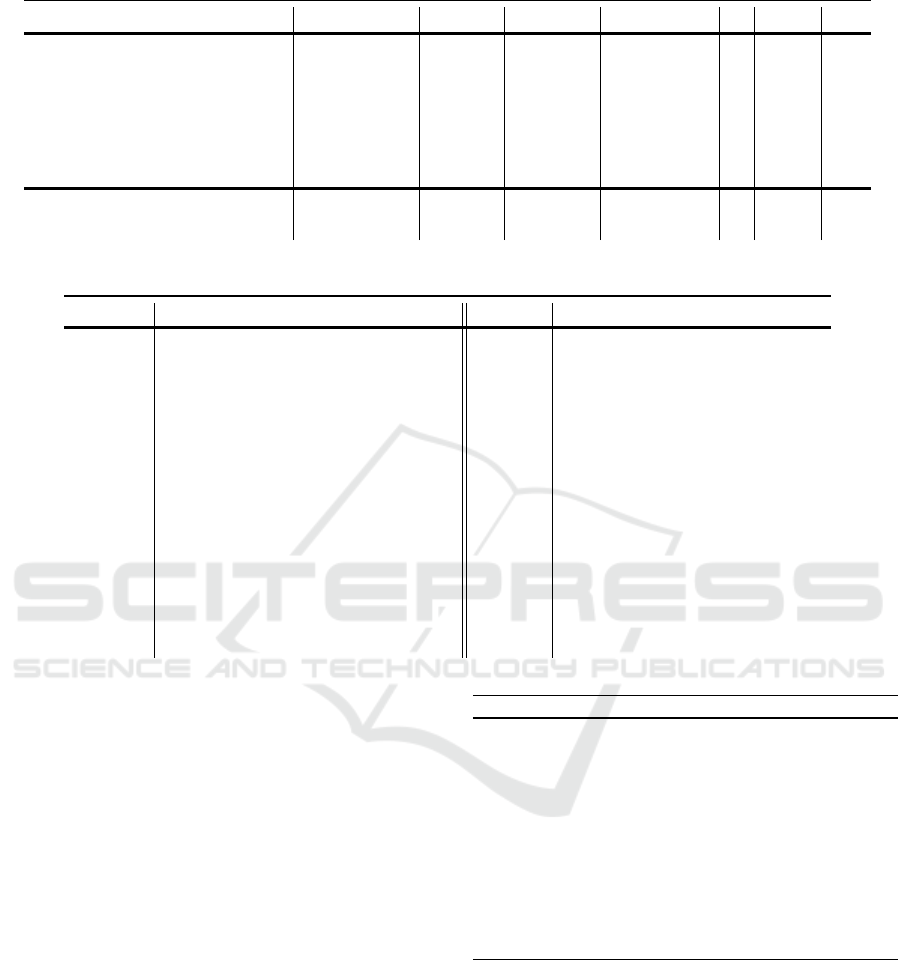
Table 1: Summary of schemes. Communication round is denoted as CR, data transmission as DT, and statistical query as SQ.

Scheme Search CR DT Leakage SQ “AND” M-M

(Goldreich and Ostrovsky, 1996) O(nlog

n) O(logn) O(log

n) no leakage no no no

(Krell et al., 2017) O(logn) O(log

n) O(log

n) access pattern no yes no

(Gentry et al., 2015) O(logn) O(logn) O(n log

n) no leakage no yes no

(Guo et al., 2017) O(n) O(d) O(k) access pattern no yes yes

(Miyoshi et al., 2017) O(log2

+ n

) O(1) O(n

) access pattern no no no

(Kamara et al., 2012) O(n

) O(1) O(λ) access pattern no no no

IBSvI O(mn) O(1) O(n) no leakage yes yes yes

IBSvII O(mn) O(1) O(n) no leakage yes yes yes

Table 2: List of symbols.

Symbol Description Symbol Description

pk/sk public/secret key n encryption modulus

encryption D

decryption

κ security parameter r,r

,θ random number in Z

T tuple of multiple attributes p attribute

α number of attributes in a query bl(p) bit length of p

` maximum bit-length of attributes ϕ false positive rate control

Ans result of query evaluation

ρ package capacity in Paillier

query type id

meta data for p

UnPerm inverse of Perm [x] E

(x)

ρ number of item can be packed in FV index

index tables for p

index

i, j

column and j

row in index

d(a, b) Hamming distance of a and b

value of p

in j

record (T

)

least signiﬁcant bit of T

)

least signiﬁcant bit of p

ω total number of records

Perm permutation function Max

total number of attributes

2. Users multiply each (p

)

by 2

, i ∈ {0, ·· · , e},

encrypts the results as a tuple T

,[id

],[(p

)

] > and send them to their

DSUs, who send the encryptions to RCS later.

3. RCS creates an index for each possible attribute

(there are Max

attributes in total), where each

index has ω rows that is the total number of tuples

collected from DSUs and ` columns.

4. RCS locates each encrypted tuple [(T

)

i, j

] (i

bit

of the j

tuple received from DSUs) in the corre-

sponding generated index, index

]

i, j

← [(T

)

i, j

i ∈ {0, ·· · ,` −1}.

We present values in the binary form to check whether

each encrypted data stored by RCS matches a particu-

lar encrypted data in q without invoking any two-party

protocol. Each value is multiplied by powers of 2

to eliminate false positive results in our construction.

Protocol 1 shows the steps that RCS takes to generate

indices. It indicates that Max

indices are created,

one for each attribute. According to Protocol 1, it

is explicit generating indices in RCS is computation-

free and storage-demanding.

Protocol 1: RCS:GenIndex.

Require: [T

]

Ensure: indices for each p

1: for z = 0 to Max

− 1 do

2: Create index

3: for i = 0 to ` − 1 do

4: for j = 0 to ω − 1 do

5: index

]

i, j

← [(T

)

i, j

]

6: end for

7: end for

8: end for

3.1.2 Secure Searching

Protocol 2 shows the process of evaluating an en-

crypted query [q] over the encrypted databases using

the generated indices.

1. QI

: Once RCS generates the indices, QI con-

structs a query q including e ≤ α attributes ´p

z ∈ {0,· ·· , e−1}, which QI is interested in. Simi-

lar to the process of index generation, QI converts

the values of its attributes to binary form. Then it

SECRYPT 2018 - International Conference on Security and Cryptography

274

Protocol 2: IBSvI.

computes ( ´p

)

← ( ´p

)

∗ (−2

), i ∈ {0, ·· · , e − 1}

and assigns zero to {( ´p

)

,· ·· ,( ´p

)

`−1

2. RCS

: RCS tosses a random coin r for each

pair of (index

i, j

,( ´p

)

) to compute (index

i, j

⊕ (r ∗

),( ´p

)

⊕ (−r ∗ 2

)). Note that the values of

index

i, j

is in encrypted form. Thus, to compute

index

i, j

⊕ (r ∗ 2

), RCS checks whether r = 0,

index

]

i, j

← (r = 0)?(index

]

i, j

) : ([2

] − index

]

i, j

Similarly, to compute ( ´p

)

⊕ (−r ∗ 2

), RCS per-

forms [( ´p

)

] ← (r = 0)?[( ´p

)

] : (−([2

] + [ ´p

)

]).

Afterwards, RCS computes [d

i, j

], which is clearly

zero if |index

i, j

| = |( ´p

)

| that means the i

bit of

index

matches the i

bit of ´p

in q.

3. RCS

: To check if ´p

equals p

of the j

tuple in

the database, RCS checks whether the Hamming

distance d between them is zero, d(index

, ´p

) =

0. To obtain d, RCS computes R

←

∑

`−1

i=0

i, j

4. RCS

: In case of there are multiple ´p

in query

q, RCS checks if the all the ´p

matches the cor-

responding [p

] in each tuple. To do so, RCS can

simply compute [y

] ←

∑

α−1

z=0

], if [y

= 0] then

it means the j

tuple in RCS matches [q]. How-

ever, there is a possibility of obtaining false pos-

itive result. Thus, RCS chooses α uniformly dis-

tributed random number r

, z ∈ {0,··· , α− 1} and

another random number θ. r

values are used in

the protocol to decrease the false positive rate and

θ is used for the security reasons.

5. RCS

: In this step RCS choose ω uniformly ran-

dom numbers ´y

∈ {0,··· ,2

`−1

} and another ran-

dom number ´r. In this step, RCS inserts ω random

numbers, which has ´r zeros, to [y]. This step pre-

vent the KM to learn about the number of matches

and other statistical information from y

values.

6. RCS

: RCS permutes [y

] to not let the KM learn

about the locations of tuples that matched q.

7. KM

: The KM decrypts given [y

], j ∈

{0,· ·· ,2ω − 2}, and checks whether y

= 0.

Then, it creates an array I

, ﬁlled with binary val-

ues such that I

← (y

= 0)?1 : 0.

8. RCS

: RCS reverse permutes [I

] and removes

the dummy encryptions added to [y

] in RCS

Finally, RCS has an encrypted binary array, which

represents the location of matching tuples in the

database. To optimize IBSvI regarding computa-

tion and communication, we also apply data pack-

ing (Erkin et al., 2012; Troncoso-Pastoriza et al.,

2007) on our protocol. Note that we cannot apply

data packing on [I

] because it prevents performing re-

verse permutation and removing dummy encryptions

in RCS

. However, we can skip RCS

, and per-

form RCS

and RCS

on the database itself, where

j = ´r = 0, for evaluation of Q

. This modiﬁcation

allows to pack [I

] and reduces both communication

and computation cost.

3.2 IBSvII

In IBSvII, we achieve a communication cost-free

searching algorithm. Similar to IBSvI, there are two

phases in IBSvII, indexing and searching. The index

tables generation phase is identical to IBSvI except

we do not multiply (p

)

by 2

Protocol 3 shows how IBSvII works. There are

four steps in IBSvII, QI

, RCS

, and RCS

1. QI

: Similar to QI

, QI generates the query

with e ≤ α attributes p

, z ∈ {0,···e − 1}. Then,

QI represents the the values of the attributes

to binary form, encrypts them, and send {[1 −

Efﬁcient Index-based Search Protocols for Encrypted Databases

275

Protocol 3: IBSvII.

)

],· ·· ,[1 − (p

)

`−1

]} to RCS. Afterward, QI

sends Q

plus necessary meta-data to RCS.

2. RCS

: This step computes [d

i, j

] like in RCS

however, [d

i, j

] are binary values. The challenge

in computing [d

i, j

] in RCS

was that it could be

a combination of positive and negative numbers

such that their addition R

becomes zero, which

is considered as a false positive result. In RCS

each [d

i, j

] is squared, which solves the problem of

negative numbers. Recall that (index

i, j

+ ( ´p

)

) ∈

{−1,0, 1}, thus d

i, j

∈ {0, 1} in RCS

3. RCS

: After computation of [d

i, j

], we compute

← R

× d

i, j

. R

remains one if the ´p

in the

query q matches p

of j

record in the database.

4. RCS

: This step apply the “AND” connections

among multiple R

by computing

∏

α−1

z=0

obtain Ans

In IBSvII, we can use batching to reduce the com-

putational overhead. Batching enables not only the

addition of two packed ciphertexts but also supports

multiplication. Thus, all the operations stated in Pro-

tocol 3 can be performed over packed ciphertexts

without collaboration with KM.

4 SECURITY ANALYSES

We consider the semi-honest security model (Goldre-

ich, 2004), where parties are assumed to be honest in

following the protocol description, while they are cu-

rious to obtain more information than they are entitled

to. Given that the only RCS gets is the encrypted out-

put from the protocol, KM should not be able to dis-

tinguish if RCS has a different input and RCS should

not learn more information than the output of the pro-

tocol. We also assume that parties do not collude with

each other.

4.1 Security of IBSvI

Let RCS

= (RCS

,· ·· ,RCS

), KM

= (KM

), and

f = (RCS

,KM

) to be the PPT functionality for IB-

SvI. The view of the ith party (i ∈ {RCS,KM}) during

the execution of IBSvI on (index

,φ) and security

parameter n is denoted by view

IBSvI

(index

,φ, n) =

(w,r

,· ·· ,m

), where w ∈ {index

,φ} based on

the values of i, r

are the ith party internal random

numbers, and m

represents the jth message that

is received by ith party. Note that KM does not

have any initial input, thus its input is denoted as

φ. out put

IBSvI

(index

,φ, n) represents the output of

each party during the execution of IBSvI. To repre-

sent the joint output of both parties, we denote

out put

IBSvI

= (out put

IBSvI

(index

,φ, n),

out put

IBSvI

(index

,φ, n)).

(1)

Deﬁnition 4.1. It can be proven that IBSvI securely

computes f = (RCS

,KM

) in the semi-honest secu-

rity setting if there exits PPT algorithms Sim

RCS

and

Sim

such that:

{(Sim

RCS

,index

,RCS

, f ))}

≡ {(view

RCS

(index

,φ, n),out put

(index

,φ, n))}

(2)

and

{(Sim

,φ, KM

, f ))}

≡ {(view

(index

,φ, n),out put

(index

,φ, n))}

(3)

Theorem 1. The protocol IBSvI is simulation secure

and securely computes the functionality f , when the

party RCS is corrupted by adversary A

RCS

in the pres-

ence of semi-honest adversaries.

Proof. We need to show that RCS cannot computa-

tionally distinguish between generated messages and

outputs from S

and S

, and randomly generated data.

RCS receives an output from S

, [

Ans

], and a mes-

sage from S

, [( ˆp

)

]. Protocol 6 shows the simulators

for KM and QI that are S

and S

, respectively. Note

that because of the space limitation, only the mes-

sage from S

to RCS, [ ˆp

)

], is presented in Protocol

SECRYPT 2018 - International Conference on Security and Cryptography

276

6. Given index

and 1

(security parameters), RCS

works as follow:

1. RCS chooses three uniformly random tapes r, r

and ´r for RCS

2. S

randomly generates u ˆp

∈ N, where u ≤ α,

u random meta data, and a random

. Then,

forms [q] ← {

,[( ˆp

)

]||

}, where i ∈

{0,· ·· ,u ≤ α −1}, ans send [q] to RCS.

3. RCS executes RCS

,i ∈ {1,··· , 5}, and it outputs

[ ˆy

] to S

4. S

tosses j coins

and sends [

] to RCS.

5. RCS performs UnPerm[

], and outputs

[

Ans

] ←Half([

])

The output of the simulation can be writ-

ten as: Sim

RCS

,index

,RCS

, f ) =

(index

,r, r

, ´r; [

],[( ˆp

)

];([

Ans

],φ)]).

The real view of RCS can be pre-

sented as view

RCS

(index

,[( ´p

)

,n]) =

(index

,r, r

, ´r; [I

],[( ´p

)

]). And the output of the

real view is out put

(index

,[( ´p

])

) = ([Ans

],φ).

It can be observed that the encryption pairs

([

],[( ˆp

)

])) and ([I

],[( ´p

)

]) are indistinguish-

able, since the crypto-scheme used in IBSvI is

semantically secure. For the same reason A

RCS

can-

not distinguish between [Ans

] and [

Ans

]. Recalling

that RCS is also given meta-data that describes the

query type and attributes in q, RCS cannot see if

the provided meta-data are corresponding to the

attributes ˆp

in q. Therefore, we can claim that

Sim

RCS

,index

,RCS

, f )

≡ {view

RCS

(index

,[( ´p

)

],n),out put

(index

,[( ´p

)

]).

(4)

Theorem 2. The protocol IBSvI is simulation secure

and securely computes the functionality f , when the

party KM is corrupted by A

in the presence of

semi-honest adversaries.

Proof. The simulation for the case when KM is cor-

rupted is presented in Protocol 7. After receiving 1

KM works as follows:

1. S

chooses a uniformly random number ˆr ∈

{0,· ·· ,2ω − 2}.

2. S

chooses 2ω uniformly random numbers ˆy

∈

{−v,··· , v}, where v = Max

−1)(2

−1), that

contains ˆr zeros.

3. S

encrypts ˆy

and sends the permuted encryptions

[ ˆy

] to KM.

4. KM calls the KM

functionality to obtain encryp-

tions [I

] and send them to S

5. S

performs UnPerm[I

], and outputs

[Ans

] ←Half([I

]).

The simulation and the real view can be written as:

Sim

,φ, KM

, f ) = (φ; [ˆy

];[Ans

]]). (5)

The view and output of KM are

view

(index

,φ, n) = (φ,[y

]) and

out put

(index

,[( ´p

)

]) = (φ,[Ans

]). Since

has the decryption key, we need to show that

cannot distinguish between y

and ˆy

. We need

to consider following points to prove the security

theorem:

1. The values of (index

)

and (p

)

: as it is pre-

sented in Protocol 2, both indices (index

)

and

)

are XORed with uniformly distributed ran-

dom r in RCS

2. The bit-lengths of (index

)

and (p

)

: to hide the

bit-lengths of (index

)

and (p

)

, a ﬁx bit-length

solution is suggested, where (index

)

and (p

)

are ` bits for every entry.

3. Number of attributes α in q: the value of al pha

has a direct effect on the upper and lower bounds

of y

. To prevent A

to learn about the α, as

it is shown in RCS

, RCS multiplies [y]

by the

difference between α and the maximum number

of attributes that QI can put in q, Max

4. Number of zeros in y

: by learning number of ze-

ros from multiple y

, A

might be able to distin-

guish between real y

and ˆy

. RCS

randomizes

the number of zeros by inserting a random number

of zeros to y

Randomizing the stated four properties guarantees

that A

cannot distinguish between y

and ˆy

, thus:

Sim

,φ, KM

, f ) = {view

(index

,φ, n),out put

(index

,[( ´p

)

])}.

(6)

4.2 Security of IBSvII

In IBSvII, computation of Ans

does not require col-

laboration of RCS and KM; thus, RCS can compute

the ﬁnal binary vector Ans

without any communica-

tion. To prove the security of Protocol 3, we need to

show that RCS cannot learn anything from data.

Theorem 3. The protocol IBSvII is simulation secure

and securely computes the functionality f , when the

party RCS is corrupted by adversary A

RCS

in the pres-

ence of semi-honest adversaries.

Efﬁcient Index-based Search Protocols for Encrypted Databases

277

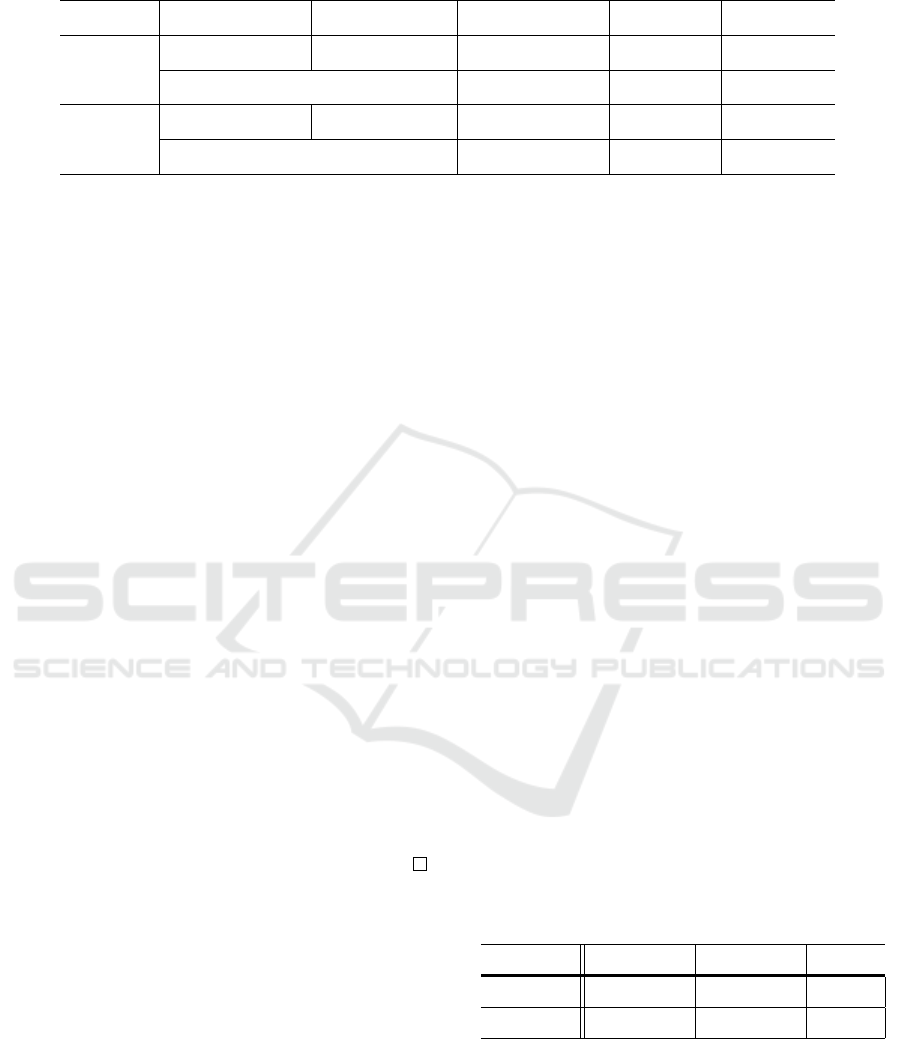
Table 3: Computational complexity of the searching protocols.

Protocols Addition Exponentiation Multiplication Encryption Decryption

IBSvI

(3αω` + αω)/

ρ (αω)

log(θr

)

ρ 0 3ω 2ω/

O(αω`/

ρ) — O(ω) O(ω/

ρ)

IBSvII

(αω`)/

ρ 0 (2αω` +αω)/

ρ 0 0

O(αω`/

ρ) O(αω`/

ρ) — —

Proof. We need to show that RCS is unable to com-

putationally distinguish between the truly generated

messages given from S

, the simulator of QI, and ran-

domly generated data. Given index

and 1

(security

parameters), RCS in IBSvII works as follows:

1. S

randomly generates u ˆp

∈ N, where u ≤ α,

u random meta data, and a random

. Then,

forms [q] ← {

,[( ˆp

)

]||

}, where i ∈

{0,· ·· ,u ≤ α −1}, ans send [q] to RCS.

2. RCS executes RCS

,i ∈ {1, ·· · ,3}, and then out-

puts [Ans

The output of the simulation can be pre-

sented as: Sim

RCS

,index

,RCS

, f ) =

(index

,[( ˆp

)

];[

Ans

],φ). The real view of RCS is

view

RCS

(index

,[( ´p

)

]) = (index

,[( ´p

)

]) and the

real view of the output is out put

(index

,[( ´p

)

]) =

([Ans

],φ). Clearly, the encryptions [( ˆp

)

] and

[( ´p

)

]), and [Ans

] and [

Ans

] are indistinguishable

because of using semantically secure crypto-scheme.

Meta-data in q also does not reveal any information

about the attributes. Therefor, we can claim that

Sim

RCS

,index

,RCS

, f )

≡ {view

RCS

(index

,[( ´p

)

]),out put

(index

,[( ´p

)

]).

(7)

5 PERFORMANCE ANALYSES

5.1 Complexity Analysis

Table 3 shows the computational complexity of our

protocols for searching with multiple attributes (IB-

SvI and IBSvII). In Table 3, we present x number of

exponentiations with y-bit exponents as (x)

. As it

is illustrated in Table 3, the complexity of IBSvI in

terms of the number of additions is linear to the num-

ber of attributes in q, bit-length of attributes, and the

number of records in the database. Moreover, Table 3

shows how applying data packing reduces the num-

ber of homomorphic additions and decryptions. Ta-

ble 3 also shows IBSvII does not require any encryp-

tion and decryption; however, it requires performing

(2αω`+αω)/

ρ homomorphic multiplications, where

ρ is the number of messages that can be packed by de-

ploying batching.

Table 4 summarizes the communicational com-

plexity of the searching protocols in terms of data

transmission, communication round, and storage

complexity. According to Table 4, communication

round for IBSvI is constant, and it is independent of

the bit-length of inputs and the number of attributes

in q. Moreover, Table 4 shows that RCS in IBSvII

computes Ans

without any communication with KM.

Furthermore, data transmission needed is independent

of the number of AND conjunctions used in the query.

Table 4 shows the data transmission needed for the

secure searching protocols per party, RCS, and KM,

where the complexity of IBSvI is O(ω) and indepen-

dent of the number of attributes. Recall that there is

no communication between RCS and KM in IBSvII,

and clearly, no data is transmitted between these two

parties. The batching technique signiﬁcantly reduces

computational costs. Table 4 shows the size of each

protocol’s index table. The value of

ρ depends of bit-

length of `, where smaller ` results in larger

ρ.

Table 4: Communicational and space complexity of the

searching protocols. Data transmission complexity is de-

noted as Data.Trans, communication round as Com.Rond,

and index size as IS.

Protocols Data.Trans Com.Rond IS

IBSvI 4ω/

ρ 1 ω`α/

IBSvII 0 0 ω`α

5.2 Experimental Results

In this section, we present the experimental results

of implementing IBSvI and IBSvII. First, we show

the run-times of the introduced searching protocols

for different α and ϕ values. Then, we compare

SECRYPT 2018 - International Conference on Security and Cryptography

278

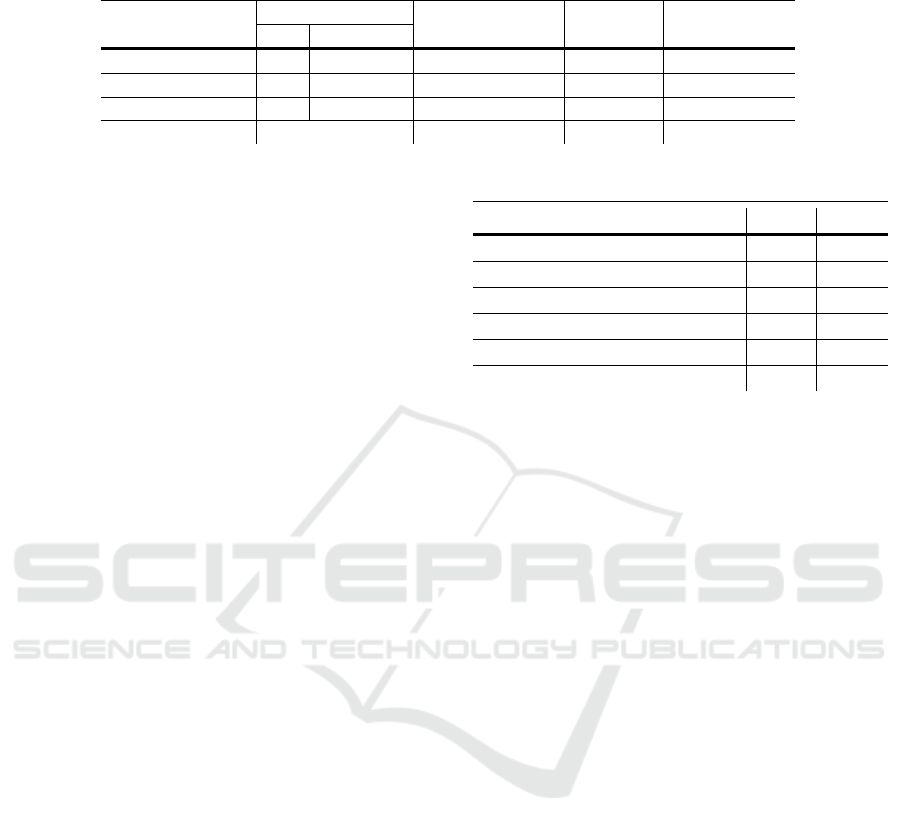
Table 6: Run-times and communication costs of the IBSvI and IBSvII. For (Gentry et al., 2015), we use NA to show that the

work does not report the corresponding value.

Protocols Run-time (second) Data transmission index size communication

RCS KM (megabyte) (megabyte) (round)

IBSvI

Paillier

0.525 5.06 2.19 8.2 1

IBSvI

0.44 0.45 49.45 92.8 1

IBSvII

5.54 0 0 92.8 0

(Krell et al., 2017) 4.0 26 75K NA

their run-times in RCS and KM for different α val-

ues. To obtain the run-times of the protocols, we

use C++ and external libraries: MPIR, Boost, the Se-

cure Computation Library (SeComLib), and SEAL on

a single Linux machine running Ubuntu 14.04 LTS,

with a 64-bit microprocessor and 8 GB of RAM.

We applied a simple parallelization technique in our

implementation (4 threads). The cryptographic key

length of the Paillier is chosen according to NIST

standards (Barker et al., 2007), which are valid un-

til 2030. Table 5 lists the parameters and their values

in our implementation.

Table 6 compares the run-times of the IBSvI, IB-

SvII, and existing works in RCS and KM. To show

the trade-off between computational and communica-

tional costs when using different encryption schemes,

we also provide the run-time of IBSvI when FV is

used, denoted as IBSvI

. Note that Paillier can-

not be used in IBSvII because it does not support

the ciphertext multiplications. Table 6 points out

both IBSvI

Paillier

and IBSvI

demand signiﬁcantly

low computational resources from RCS. These results

show that Paillier equipped with data packing and FV

with enabled batching have the same performance in

performing homomorphic addition. However, there

is a noticeable difference between the run-times of

IBSvI

Paillier

and IBSvI

in RCS, which means the

decryption function in FV is more efﬁcient than Pail-

lier because of being able to pack more messages into

a single ciphertext,

ρ >

ρ. Table 6 presents the run-

time of IBSvII that is roughly similar to the total run-

time of IBSvI

Paillier

. Considering these results, we can

conclude that, contrary to popular belief, using fully

homomorphic crypto-schemes is more efﬁcient than

partially homomorphic ones in certain cases.

Table 6 shows the run-time of secure searching in

(Krell et al., 2017), where only the cost of ﬁnding the

matching records in that work is considered. Accord-

ing to Table 6, the work in (Krell et al., 2017) is also

efﬁcient in ﬁnding the desired records at the costs of

leaking access pattern with an index table size of 75

Gigabytes. Note that the network cost of searching is

not provided separately in (Krell et al., 2017); there-

fore, we put the total network cost (searching and re-

trieving) in Table 6.

Table 5: Parameters and their values.

Parameter Symbol Value

Bit-size of inputs ` 15 bits

Number of records in RCS ω 10

Security parameter κ 112 bits

Number of queries to obtain FPR 10

Capacity of a package (IBSvI)

ρ 89

Capacity of a package (IBSvII)

ρ 2048

6 CONCLUSION

Searching in encrypted databases is a challenging task

due to the complexity introduced by encryption. In

this work, we focus on a medical setting where insti-

tutions would like to use the data collected by smart

wearables from several vendors to analyze them for

the well-being of the patients. In order to make the

system usable in practice, we propose a two-step pro-

cedure: 1) creation of index tables at the time of up-

loading data from vendors to the cloud storage unit,

and 2) executing queries using these tables. Our com-

plexity analysis and experimental results on a large

dataset clearly show the contribution of our work: the

performance of the system is outstanding. It is also

worth mentioning that our idea of creating index ta-

bles can be generalized to other application settings,

introducing a scalable and efﬁcient search mechanism

for encrypted databases where data will later be pro-

cessed under encryption.

REFERENCES

Akin, I. H. and Sunar, B. (2015). On the difﬁculty of secur-

ing web applications using cryptdb. IACR Cryptology

ePrint Archive, 2015:82.

Barker, E., Barker, W., Burr, W., Polk, W., and Smid, M.

(2007). Nist sp800-57: Recommendation for key

management part 1: General (revised). NIST, Tech.

Rep.

Bellare, M., Boldyreva, A., and O’Neill, A. (2007). Deter-

ministic and efﬁciently searchable encryption. In Ad-

vances in Cryptology - CRYPTO 2007, 27th Annual

Efﬁcient Index-based Search Protocols for Encrypted Databases

279

International Cryptology Conference, Santa Barbara,

CA, USA, August 19-23, 2007, Proceedings, pages

535–552.

Bethencourt, J., Sahai, A., and Waters, B. (2007).

Ciphertext-policy attribute-based encryption. In 2007

IEEE Symposium on Security and Privacy (S&P

2007), 20-23 May 2007, Oakland, California, USA,

pages 321–334.

Boneh, D., Crescenzo, G. D., Ostrovsky, R., and Per-

siano, G. (2004). Public key encryption with keyword

search. In Advances in Cryptology - EUROCRYPT

2004, International Conference on the Theory and Ap-

plications of Cryptographic Techniques, Interlaken,

Switzerland, May 2-6, 2004, Proceedings, pages 506–

522.

Boneh, D., Kushilevitz, E., Ostrovsky, R., and III, W. E. S.

(2007). Public key encryption that allows PIR queries.

In Advances in Cryptology - CRYPTO 2007, 27th An-

nual International Cryptology Conference, Santa Bar-

bara, CA, USA, August 19-23, 2007, Proceedings,

pages 50–67.

osch, C., Tang, Q., Hartel, P. H., and Jonker, W. (2012).

Selective document retrieval from encrypted database.

In Information Security - 15th International Confer-

ence, ISC 2012, Passau, Germany, September 19-21,

2012. Proceedings, pages 224–241.

Byun, J. W., Rhee, H. S., Park, H., and Lee, D. H. (2006).

Off-line keyword guessing attacks on recent keyword

search schemes over encrypted data. In Secure Data

Management, Third VLDB Workshop, SDM 2006,

Seoul, Korea, September 10-11, 2006, Proceedings,

pages 75–83.

Chang, Y. and Mitzenmacher, M. (2005). Privacy preserv-

ing keyword searches on remote encrypted data. In

Applied Cryptography and Network Security, Third

International Conference, ACNS 2005, New York, NY,

USA, June 7-10, 2005, Proceedings, pages 442–455.

Chor, B., Goldreich, O., Kushilevitz, E., and Sudan, M.

(1995). Private information retrieval. In 36th Annual

Symposium on Foundations of Computer Science, Mil-

waukee, Wisconsin, 23-25 October 1995, pages 41–

50.

Chung, K., Kalai, Y. T., and Vadhan, S. P. (2010). Im-

proved delegation of computation using fully homo-

morphic encryption. In Advances in Cryptology -

CRYPTO 2010, 30th Annual Cryptology Conference,

Santa Barbara, CA, USA, August 15-19, 2010. Pro-

ceedings, pages 483–501.

Curtmola, R., Garay, J. A., Kamara, S., and Ostrovsky,

R. (2011). Searchable symmetric encryption: Im-

proved deﬁnitions and efﬁcient constructions. Journal

of Computer Security, 19(5):895–934.

Ding, X., Liu, P., and Jin, H. (2017). Privacy-preserving

multi-keyword top-k similarity search over encrypted

data. IEEE Transactions on Dependable and Secure

Computing, PP(99):1–1.

Erkin, Z., Veugen, T., Toft, T., and Lagendijk, R. L.

(2012). Generating private recommendations efﬁ-

ciently using homomorphic encryption and data pack-

ing. IEEE Trans. Information Forensics and Security,

7(3):1053–1066.

Fan, J. and Vercauteren, F. (2012). Somewhat practical fully

homomorphic encryption. IACR Cryptology ePrint

Archive, 2012:144.

Gentry, C. (2009). Fully homomorphic encryption using

ideal lattices. In Proceedings of the 41st Annual ACM

Symposium on Theory of Computing, STOC 2009,

Bethesda, MD, USA, May 31 - June 2, 2009, pages

169–178.

Gentry, C., Halevi, S., Jutla, C. S., and Raykova, M. (2015).

Private database access with he-over-oram architec-

ture. In Applied Cryptography and Network Secu-

rity - 13th International Conference, ACNS 2015, New

York, NY, USA, June 2-5, 2015, Revised Selected Pa-

pers, pages 172–191.

Goh, E. (2003). Secure indexes. IACR Cryptology ePrint

Archive, 2003:216.

Goldreich, O. (2004). The Foundations of Cryptography -

Volume 2, Basic Applications. Cambridge University

Press.

Goldreich, O. and Ostrovsky, R. (1996). Software pro-

tection and simulation on oblivious rams. J. ACM,

43(3):431–473.

Goldschmidt, P. G. (2005). HIT and MIS: implications of

health information technology and medical informa-

tion systems. Commun. ACM, 48(10):68–74.

Goyal, V., Pandey, O., Sahai, A., and Waters, B. (2006).

Attribute-based encryption for ﬁne-grained access

control of encrypted data. In Proceedings of the 13th

ACM Conference on Computer and Communications

Security, CCS 2006, Alexandria, VA, USA, Ioctober

30 - November 3, 2006, pages 89–98.

Guo, Z., Zhang, H., Sun, C., Wen, Q., and Li, W. (2017).

Secure multi-keyword ranked search over encrypted

cloud data for multiple data owners. Journal of Sys-

tems and Software.

Han, F., Qin, J., Zhao, H., and Hu, J. (2014). A general

transformation from KP-ABE to searchable encryp-

tion. Future Generation Comp. Syst., 30:107–115.

Johnson, M. E. (2009). Data hemorrhages in the health-

care sector. In Financial Cryptography and Data Se-

curity, 13th International Conference, FC 2009, Ac-

cra Beach, Barbados, February 23-26, 2009. Revised

Selected Papers, pages 71–89.

Kamara, S., Papamanthou, C., and Roeder, T. (2012). Dy-

namic searchable symmetric encryption. In the ACM

Conference on Computer and Communications Se-

curity, CCS’12, Raleigh, NC, USA, October 16-18,

2012, pages 965–976.

Krell, F., Ciocarlie, G., Gehani, A., and Raykova, M.

(2017). Low-leakage secure search for boolean ex-

pressions. In Topics in Cryptology - CT-RSA 2017

- The Cryptographers’ Track at the RSA Confer-

ence 2017, San Francisco, CA, USA, February 14-17,

2017, Proceedings, pages 397–413.

Li, M., Li, J., and Huang, C. (2012). A credible cloud stor-

age platform based on homomorphic encryption. Net-

info Security, 12(9):35G40.

Meingast, M., Roosta, T., and Sastry, S. (2006). Security

and privacy issues with health care information tech-

nology. In Engineering in Medicine and Biology Soci-

SECRYPT 2018 - International Conference on Security and Cryptography

280

ety, 2006. EMBS’06. 28th Annual International Con-

ference of the IEEE, pages 5453–5458. IEEE.

Miyoshi, R., Yamamoto, H., Fujiwara, H., and Miyazaki,

T. (2017). Practical and secure searchable symmetric

encryption with a small index. In Secure IT Systems -

22nd Nordic Conference, NordSec 2017, Tartu, Esto-

nia, November 8-10, 2017, Proceedings, pages 53–69.

Ostrovsky, R. (1990). Efﬁcient computation on oblivious

rams. In Proceedings of the 22nd Annual ACM Sym-

posium on Theory of Computing, May 13-17, 1990,

Baltimore, Maryland, USA, pages 514–523.

Paillier, P. (1999). Public-key cryptosystems based on com-

posite degree residuosity classes. In Advances in

Cryptology - EUROCRYPT ’99, International Confer-

ence on the Theory and Application of Cryptographic

Techniques, Prague, Czech Republic, May 2-6, 1999,

Proceeding, pages 223–238.

Popa, R. A., Redﬁeld, C. M. S., Zeldovich, N., and Balakr-

ishnan, H. (2012). Cryptdb: processing queries on an

encrypted database. Commun. ACM, 55(9):103–111.

Sahai, A. and Waters, B. (2005). Fuzzy identity-based

encryption. In Advances in Cryptology - EURO-

CRYPT 2005, 24th Annual International Conference

on the Theory and Applications of Cryptographic

Techniques, Aarhus, Denmark, May 22-26, 2005, Pro-

ceedings, pages 457–473.

Song, D. X., Wagner, D., and Perrig, A. (2000). Practical

techniques for searches on encrypted data. In 2000

IEEE Symposium on Security and Privacy, Berkeley,

California, USA, May 14-17, 2000, pages 44–55.

Stefanov, E., Papamanthou, C., and Shi, E. (2014). Practical

dynamic searchable encryption with small leakage. In

21st Annual Network and Distributed System Security

Symposium, NDSS 2014, San Diego, California, USA,

February 23-26, 2014.

Treskes, R. W., van Winden, L. A., van Keulen, N., Atsma,

D. E., van der Velde, E. T., van den Akker-van Marle,

E., Mertens, B., and Schalij, M. J. (2017). Using smart

technology to improve outcomes in myocardial infarc-

tion patients: Rationale and design of a protocol for a

randomized controlled trial, the box. JMIR research

protocols, 6(9).

Troncoso-Pastoriza, J. R., Katzenbeisser, S., Celik, M. U.,

and Lemma, A. N. (2007). A secure multidimensional

point inclusion protocol. In Proceedings of the 9th

workshop on Multimedia & Security, MM&Sec 2007,

Dallas, Texas, USA, September 20-21, 2007, pages

109–120.

Xiong, A.-P., Gan, Q.-X., He, X.-X., and Zhao, Q. (2013).

A searchable encryption of cp-abe scheme in cloud

storage. In Wavelet Active Media Technology and In-

formation Processing (ICCWAMTIP), 2013 10th In-

ternational Computer Conference on, pages 345–349.

IEEE.

Zhang, W., Lin, Y., Xiao, S., Wu, J., and Zhou, S. (2016).

Privacy preserving ranked multi-keyword search for

multiple data owners in cloud computing. IEEE Trans.

Computers, 65(5):1566–1577.

Efﬁcient Index-based Search Protocols for Encrypted Databases

281