A Quantitative Framework to Model Advanced Persistent Threats
∗
Luan Huy Pham
1
, Massimiliano Albanese
1
and Benjamin W. Priest
2
1
Center for Secure Information Systems, George Mason University, 4400 University Drive, Fairfax, VA 22030, U.S.A.
2
Thayer School of Engineering, Dartmouth College, 14 Engineering Drive, Hanover, NH 03755, U.S.A.
Keywords:
Advanced Persistent Threats, Threat Modeling, Steiner Tree.
Abstract:
In recent years, Advanced Persistent Threats (APTs) have emerged as increasingly sophisticated cyber attacks,
often waged by state actors or other hostile organizations against high-profile targets. APT actors employ a
diversified set of sophisticated tools and advanced capabilities to penetrate target systems, evade detection,
and maintain a foothold within compromised systems for extended periods of time. Stealth and persistence
enable APT actors to conduct long-term espionage and sabotage operations. Despite significant efforts to
develop APT detection and mitigation capabilities, the stealthy nature of APTs poses significant challenges,
and defending from such threats is still an open research problem. In particular, quantitative models to capture
how APTs may create and maintain a foothold within a target system are lacking. To address this gap, we
propose a quantitative framework to (i) assess the cost incurred by APT actors to compromise and persist
within a target system; (ii) estimate the value they gain over time by persisting in the system; (iii) simulate
how the footprint of an APT evolves over time when, to maintain stealth, attackers have constraints on the
volume of potentially detectable activity they can engage in. We also propose a preliminary defender model,
and results from the evaluation show that our approach is promising, thus encouraging further research in this
direction.
1 INTRODUCTION
In recent years, we have witnessed the emergence of
Advanced Persistent Threats (APTs), a form of in-
creasingly sophisticated cyber attacks that are often
waged by state actors, organized crime, or other hos-
tile organizations against high-profile targets such as
government agencies and large corporations. APT
actors employ a vast arsenal of diverse and sophisti-
cated tools and possess advanced capabilities to pen-
etrate target systems, evade detection, and maintain
a foothold within compromised systems for extended
periods of times. Stealth and persistence enable well-
resourced and driven APT actors to plan and execute
long-term espionage and sabotage operations. It is not
uncommon to discover and eradicate APTs months or
even years after the initial compromise and after sig-
nificant damage has already occurred. In 2008, an
attack targeted the U.S. Department of Defense and
spread to highly classified networks after an infected
USB flash drive was connected to a computer. For 14
months, the malware periodically exfiltrated informa-
∗
This work was partially supported by the Army Re-
search Office under grant W911NF-13-1-0421.
tion, until Operation Buckshot Yankee finally eradi-
cated it in 2009. In 2011, a successful spear phishing
attack allowed attackers to remotely control over 150
computers in the French Ministry of Economy, and
retrieve documents for over three months before the
attack was discovered.
As shown by countless high-profile incidents, and de-
spite significant efforts to develop APT detection and
mitigation capabilities, the stealthy and sophisticated
nature of APTs still poses significant challenges. In
fact, defending from such threats is still an open re-
search problem. In particular, quantitative models to
capture how an APT actor may create and maintain a
foothold within a target system are lacking, and tradi-
tional approaches rely on unreasonable or inaccurate
assumptions about the attacker’s behavior, which do
not take into account the specific nature of APTs and
their ability to circumvent traditional detection mech-
anisms. For instance, we demonstrate that attackers
do not necessarily need to compromise the most valu-
able nodes within a network in order to maximize
their rewards. APT actors weigh various incentives
and deterrents when considering which nodes to tar-
get and how to move within a network.
282
Pham, L., Albanese, M. and Priest, B.
A Quantitative Framework to Model Advanced Persistent Threats.
DOI: 10.5220/0006872602820293
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 282-293
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

To address current limitations, we propose a quan-
titative framework to (i) assess the cost incurred by
APT actors to compromise and persist within a target
system; (ii) estimate the value they gain by persisting
in the system over time; (iii) simulate how the foot-
print of an APT evolves over time when, to maintain
stealth, attackers have constraints on the volume of
potentially detectable activity they can perform. We
also propose a preliminary defender model, and re-
sults from our evaluation indicate that our approach is
effective in reducing the malware footprint.
The paper is organized as follows. Section 2 dis-
cusses background information on APTs. Section 3
presents the proposed attacker model. Then, Sec-
tion 4 presents a heuristic algorithm for constructing
the malware footprint, and Section 5 reports simula-
tion results. Section 6 presents a preliminary defender
model. Finally, Section 7 discusses related work, and
Section 8 gives some concluding remarks.
2 BACKGROUND
In this section, we discuss the incentives and deter-
rents that APT actors may weigh when evaluating
which nodes to target and how to move within a net-
work. This system of incentives and deterrents is at
the basis of the proposed quantitative framework.
APT Incentives. Of the 66 APTs identified by the
Kaspersky Global Research and Analysis Team, 61
are classified as having the primary function of exfil-
trating data, including credential theft, and cyber espi-
onage (Kaspersky Labs, ). The remaining APTs gen-
erally fall under the category of cyber sabotage, as it is
the case for the renown Stuxnet APT. While perhaps
not a primary function, it has been shown that many
of these threats (e.g., Shamoon) also include some
form of reporting function to transmit data to attacker-
operated command and control (C&C) servers. Even
Stuxnet, known primarily for sabotaging Iranian nu-
clear centrifuges, incorporated extensive features to
transmit system information to the C&C infrastruc-
ture. Thus, we can conclude that the primary in-
centive for malicious actors to deploy APTs is rep-
resented by the ability to stealthily exfiltrate data over
time. To guide the selection of nodes to be compro-
mised and maximize the value gained from exfiltra-
tion campaigns, attackers must be able to map net-
work resources and estimate the value of each such
resource.
Temporal Dynamics. In 2017, the Ponemon Insti-
tute, in a study on organizational data breaches, con-
cluded that organizations which required over 100
days to identify that a breach had occurred faced 36%
higher costs compared to organizations which identi-
fied breaches in under 100 days (pon, 2017). A deeper
analysis (Langner, 2013) of Stuxnet determined that
the malware had the ability to completely destroy the
existing Iranian nuclear refinement capability during
the period the malware was active. However, this
would have almost certainly resulted in its rapid de-
tection and removal. The analysis determined that,
as deployed, Stuxnet had an overall effect of delay-
ing the Iranian nuclear program by 2 years. Thus, the
dwell time of APT malware is critical to determine
the total value it can accrue over time by persisting
within the target network.
Deterrents. APT actors go to great lengths to main-
tain stealth. In particular, they commonly use mul-
tiple zero-day exploits. It is estimated that 50% of
Stuxnet development cost was allocated to stealth-
related features (Langner, 2013). Stuxnet employed
five zero-day exploits. Bounties for the discovery of
vulnerabilities range in the millions of dollars, and
this does not even include the significant cost (Ablon
and Bogart, 2017) associated with developing, testing
and maintaining the exploit code over time. Further-
more, APTs employ a variety of other mechanisms
to maintain stealth and can develop proxy networking
schemes to reduce the overall volume of traffic, espe-
cially outbound traffic, which may otherwise alert net-
work operators. Thus, we can conclude that defensive
mechanisms aimed at increasing the cost of maintain-
ing stealth can potentially deter attackers from com-
promising certain nodes and steer them towards more
cost-effective targets. We capture this logic in our
model, and show that an APT actor can eventually
achieve better long-term benefits by forgoing some
specific targets for the sake of stealth and persistence.
3 ATTACKER MODEL
In this section, we present a model to capture the be-
havior of an APT actor, whose overall goal is to max-
imize the value accrued from gaining and maintaining
a position within the target network, while minimiz-
ing the likelihood of being detected. We first present
some preliminary definitions and discuss our assump-
tions in Section 3.1. Then, in Section 3.2, we present
the proposed cost-reward model in detail.
3.1 Preliminaries and Assumptions
We represent a network as a graph G = (V,E), where
V is a set of network elements – such as routers and
end hosts – and E captures the connectivity between
them. As mentioned earlier, APT actors continue to
A Quantitative Framework to Model Advanced Persistent Threats
283

accrue value as they persist within the target network.
To capture the temporal dynamics of APTs, and with-
out loss of generality, we discretize time as a a finite
sequence of integers T = ht
0
,t
1
,. ..,t
m
i ⊆ N
m
, with
m ∈ N and t
i
< t
i+1
for each i ∈ [1,m]. We then de-
fine reward(t
i
), with i ∈ [1, m], as the value gained by
an APT actor at time t
i
, or, more precisely, during the
time interval ∆t
i
= [t
i−1
,t
i
]. Therefore, the value ac-
crued by the attacker over the entire time horizon T
can be simply defined as Reward =
∑
m
k=1
reward(t
i
).
Due to the sophisticated nature of APTs, the
amount of resources that threat actors invest in re-
searching their targets, and the potential exploitation
of zero-day vulnerabilities, it is reasonable to assume
that APTs are always successful in compromising a
target node. Additionally, we assume a strong adver-
sarial model in which attackers have full knowledge
of the network topology, the location of various assets
– including data items – and their respective value.
3.2 Cost-reward Model
The value an APT actor gains from a target network
during a given time interval depends on the number
and nature of the compromised nodes. We model the
malware footprint within the network as an overlay
tree, rooted at the attacker’s entry point into the net-
work. The choice of using a tree overlay is justified
by the following reasoning. As mentioned previously,
APT actors are highly determined to ensure that their
actions are stealthy in order to maintain persistence
and accrue more value over time. To achieve this
goal, they seek to avoid detection by minimizing the
number of communication channels, as observed in
several instances of existing malware (Symantec Se-
curity Response, 2011; Symantec Security Response,
2015). This behavior can be captured by modeling
communication links as the edges of an overlay tree.
However, there are other means an attacker can use
to minimize detectability. Jafarian et al. introduce
the notion of quantifying detectability by measuring
malware activity during a given time window (Jafar-
ian et al., 2014). Leveraging this concept, we assume
that the need to maintain stealth constrains attackers
to minimize detectability. We model this constraint
as a detectability budget B, representing the attacker’s
level of risk tolerance within any time interval ∆t
i
.
3.2.1 Cost
Attacker interactions with network nodes incur a de-
tectability cost, which quantifies the risk of those in-
teractions being detected. As mentioned earlier, the
cost an attacker is willing to incur during any time
interval ∆t
i
is bounded by B. Detectability costs for
individual nodes can be determined based on several
characteristics of those nodes, as described below.
• Role: Intuitively, nodes with more mission-
critical roles, such as a database server, would un-
dergo more scrutiny and would be more heavily
monitored than typical user workstations. For ex-
ample, staff may routinely check the status of a
critical database, whereas a user workstation may
only be examined when there is an apparent issue.
• Operating System: Newer operating systems in-
herently incorporate additional protection mech-
anisms which render attacks designed for older
systems ineffective. Furthermore, security mon-
itoring options are typically more robust and di-
versified on these operating systems, resulting in
more effective detection of malicious activity. As
a result, newer operating systems generally force
attackers to resort to noisier attacks, which de-
fenders can more readily detect.
• Deployed Defense Mechanisms: Defenders of-
ten deploy additional defense mechanisms to pro-
vide another layer of defense on top of baseline
operating system features. These may include
host-based antivirus software, host-based intru-
sion detection systems, file integrity monitoring
systems, and other similar defenses.
The detectability cost of a node is also affected by
the level of attacker’s effort necessary to compromise
the node and maintain it in the malware footprint. The
attacker’s effort includes activities that can be broadly
classified in the following two categories:
• Compromise and Acquisition: activities per-
formed to establish the attacker’s presence and
control on the target node, including activities
such as scanning and reconnaissance, initial com-
promise, and privilege escalation.
• Operation-on-target and Maintenance: activi-
ties performed to carry out the attacker’s objec-
tives on a compromised node, including activi-
ties such as exfiltrating information, downloading
malware updates, and routing attack traffic.
Another important consideration is that the mal-
ware footprint within a network may not be composed
solely of compromised nodes. An attacker may lever-
age standard network mechanisms to forward mali-
cious traffic through several nodes – such as routers –
without necessarily compromise them. If such nodes
are on the path between two compromised nodes,
they can be considered part of the malware footprint.
Compromising every node within the malware foot-
print is impractical for a variety of reasons. Assuming
SECRYPT 2018 - International Conference on Security and Cryptography
284

that the attacker has the capability to do so, leverag-
ing such capability may not be cost-effective. For in-
stance, compromising a router may give the attacker
additional benefits, but the risk of detection would
also be much higher. In this case, it may be more cost-
effective for the attacker to compromise nodes hosting
sensitive data and use the router to forward exfiltration
traffic originating at the compromised nodes. Intu-
itively, including non-compromised nodes in the mal-
ware footprint enables APT actors to more efficiently
allocate their detectability budget and gain more value
from the target network by using the budget to com-
promise more desirable and cost-effective nodes.
To account for this type of scenario, we con-
sider two classes of nodes in our overlay model,
namely compromised nodes and traffic-forwarding
nodes. The latter are nodes that pass malicious traf-
fic, but are not compromised by the attacker. As these
nodes are only used to passively forward traffic, the
attacker incurs a lower cost to maintain them in the
malware footprint. However, there is still a small risk
associated with these nodes, as malicious traffic pass-
ing through them can be potentially detected. For-
mally, we define the notion of APT Malware Footprint
as follows.
Definition 1 (APT Malware Footprint). The footprint
of an APT malware in a network G = (V,E) is a tree
T = (C ∩ F, root), where
• C ⊆ V is a set of compromised nodes;
• F ⊆ V is a set of non-compromised non-leaf
traffic-forwarding nodes;
• root ∈ C is the root of the tree.
We model detectability as two separate cost func-
tions, namely cost
c
: V ×T → R and cost
f
: V ×T →
R. Specifically, cost
c
(v,t
i
) is the detectability cost in-
curred by the APT malware for compromising node
v and maintaining the compromise at time t
i
. Simi-
larly, cost
f
(v,t
i
) is the detectability cost incurred by
the APT malware for forwarding traffic through node
v at time t
i
. As discussed previously, the detectability
cost of compromising a node is higher than the cost
of forwarding traffic through the same node, therefore
∀v ∈V,∀t
i
∈ T ,cost
c
(v,t
i
) ≥ cost
f
(v,t
i
). Additionally,
∀v ∈ V , cost
c
(v,t
0
) = 0 and cost
f
(v,t
0
) = 0 by defini-
tion. The total cost at time t
i
can be computed as
cost(t
i
) =
∑
v∈C
cost
c
(v,t
i
) +
∑
v∈F
cost
f
(v,t
i
),∀i ∈ [1, m]
It must be noted that, once a node v has been com-
promised at time t
j
, the cost for the attacker to main-
tain v in its footprint during subsequent time intervals
is lower than the cost sustained for the initial compro-
mise. Formally, the cost function cost
c
for a node v
compromised at time t
j
can be defined as
cost
c
(v,t
i
)



= 0 if t
i
< t
j
= c
v
if t
i
= t
j
< c
v
if t
i
> t
j
where c
v
is a constant representing the one-time cost
sustained by the attacker to compromise node v.
3.2.2 Reward
APT malware gains value from information extracted
from target systems. Many prior approaches use the
concept of one or more target nodes (Albanese et al.,
2012; Albanese and Jajodia, 2018), which an attacker
seeks to compromise. In these approaches, target
nodes may represent crown jewels, such as critical
databases or email servers, which would severely im-
pact an organization, if compromised. While these
targets are undoubtedly critical, these approaches do
not account for other valuable information which may
reside on other nodes within the network, nor for the
intrinsic value those nodes may have for an attacker
who seeks to maintain persistence within the network.
An attacker may choose to forgo these targets en-
tirely in favor of more lightly-defended options. This
approach may be especially enticing if the network
defenses are densely concentrated around critical re-
sources and relatively sparse in other regions of the
network. In such a situation, an attacker can compro-
mise a larger proportion of the network without ex-
ceeding its detectability budget. Accruing value in a
more incremental fashion may in fact be a more effec-
tive strategy for an attacker aiming to evade detection.
For example, an attacker may forgo an organization’s
heavily-guarded email server and instead compromise
the organization’s lightly-secured user workstations.
Depending on the organizational security policy, the
attacker may be able to extract not only email mes-
sages that could have been otherwise retrieved from
the server at a much higher risk, but also additional
locally-stored information.
To model the value of nodes throughout the net-
work, we use two separate reward functions, namely
reward
c
: V × T → R and reward
f
: V × T → R.
Specifically, reward
c
(v,t
i
) is the reward gained by
the APT malware for compromising node v or con-
trolling the compromised node at time t
i
. Similarly,
reward
f
(v,t
i
) is the reward gained by the APT mal-
ware for forwarding traffic through node v at time
t
i
. As discussed previously, the reward gained from
a compromised node is higher than the reward from
a non-compromised node used solely for forward-
ing traffic, therefore ∀v ∈ V,∀t
i
∈ T ,reward
c
(v,t
i
) ≥
A Quantitative Framework to Model Advanced Persistent Threats
285

reward
f
(v,t
i
). Additionally, ∀v ∈ V , reward
c
(v,t
0
) =
0 and reward
f
(v,t
0
) = 0 by definition. Finally, the
total reward at time t
i
, with i ∈ [1,m], which was in-
troduced earlier in Section 3.1, can be computed as
reward(t
i
) =
∑
v∈C
reward
c
(v,t
i
) +
∑
v∈F
reward
f
(v,t
i
)
4 TREE FORMATION PROBLEM
The long-term attacker’s objective is to construct an
overlay tree T = (C ∩ F,root) that maximizes total re-
wards over the time horizon T = ht
0
,t
1
,. .. ,t
m
i, sub-
ject to cost constraints.
maximize
T
m
∑
i=1
reward(t
i
)
subject to cost(t
i
) ≤ B,∀i ∈ [1, m]
However, as the above optimization problem
would be unpractical for the attacker to solve, it is
reasonable to assume that a more realistic objective
is to construct, during each time interval ∆t
i
, a partial
tree T
i
= (C
i
∩F
i
,root) that reuses – either partially or
totally – the tree T
i−1
generated during the previous
time interval and maximizes the rewards, subject to
the detectability budget B.
maximize
T
i
∑
v∈C
i
reward
c
(v,t
i
) +
∑
v∈F
i
reward
f
(v,t
i
)
subject to
∑
v∈C
i
cost
c
(v,t
i
) +
∑
v∈F
i
cost
f
(v,t
i
) ≤ B
As formulated, this problem is closely related to
the class of Steiner Tree Problems (Johnson et al.,
2000). In particular, this problem closely models
the Prize-Collecting Steiner Tree Problem (PCST)
and, more specifically, the Node-Weighted Prize-
Collecting Steiner-Tree Problem (NW-PCST), for
which a number of approximation algorithms ex-
ist (Bateni et al., 2013; Sadeghian Sadeghabad, 2013).
These approximation algorithms include rooted vari-
ants, where a specific root node is required to exist in
the tree. These variants would accurately model an
entry or extraction point for the malware. However,
all variants of this problem are generally considered
NP-Hard, and the budgeted variants are shown to be
at least as hard to approximate as the maximum cov-
erage problem (Moss and Rabani, 2007).
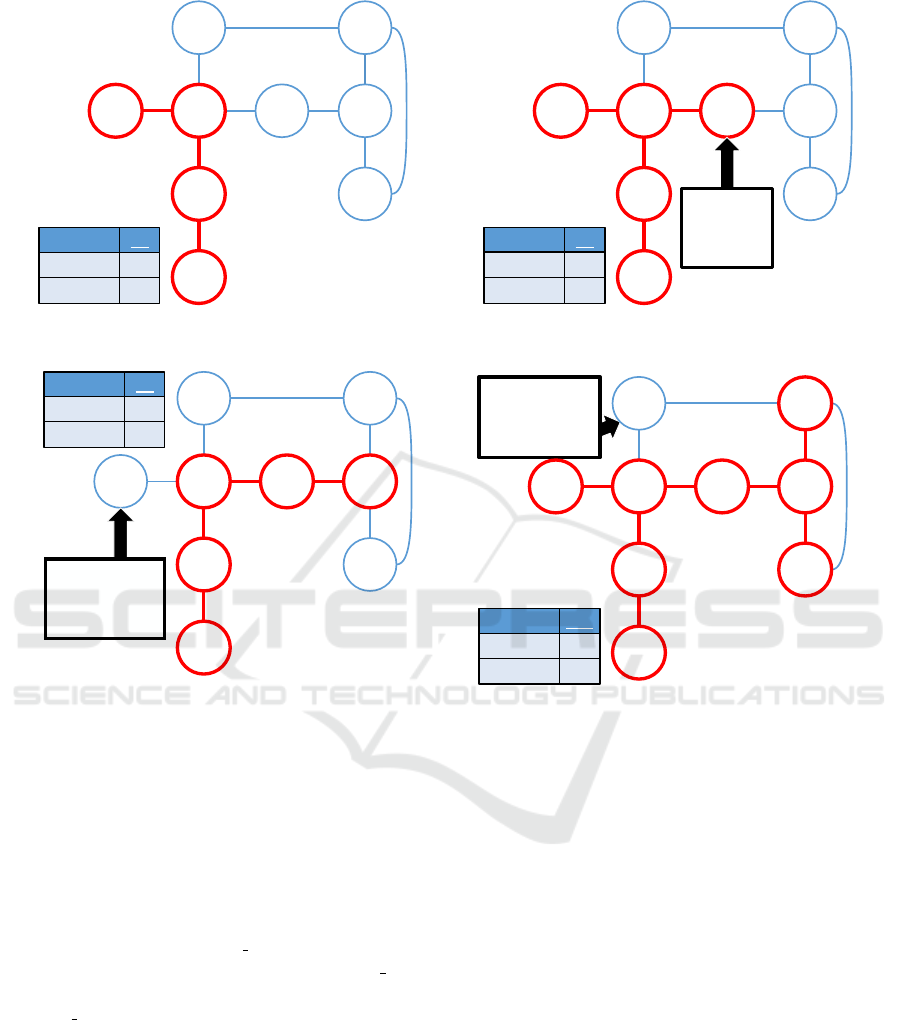
Example 1 (APT Malware Footprint). Figure 1 illus-
trates the concept of APT Malware Footprint using a
simple network and different values, ranging from 40
to 130, for the attacker’s detectability budget. In this
example, we assume that all nodes in the footprint,
marked with a bold red outline, are compromised. In
the figure, which capture a snapshot of the network
at time t
1
, each node v is labeled with its respective
reward r = reward
c
(v,t
1
) and cost c = cost
c
(v,t
1
). In
this example, V
1
is the root node. The figure clearly
shows that an increased detectability budget allows
the attacker to access a larger proportion of the tar-
get network and gain a larger reward. Note that, in
Figures 1(a) and 1(b), the attacker selects V
4
as the
budget does not allow compromising other more re-
warding nodes. However, as shown in Figure 1(c),
with a larger budget, the attacker chooses to forgo V 4
in favor of V
7
, which allows a more efficient use of
the available budget and leads to a larger overall re-
ward. In Figure 1(d), the attacker budget is so large
that nearly the entire network is compromised. How-
ever, it should be noted that the one node which is not
compromised, V
5
, has the single highest value in the
entire graph. However, due to also having the highest
associated cost – indicating the presence of more so-
phisticated defense mechanisms – including this node
would not lead to the largest possible aggregate re-
ward for this budget level. Other threat modeling ap-
proaches focusing on target nodes would likely desig-
nate V
5
as a primary target for the attacker, thus steer-
ing even more defensive resources towards it. This
example demonstrates that an attacker does not nec-
essarily need to compromise nodes with the highest
value in order to maximize the reward.
4.1 Algorithm
In this section we propose an algorithm to model how
an APT actor may build its footprint in the target net-
work. To ensure practical runtimes and to scale to
large networks, we propose an iterative, greedy ap-
proach. At a conceptual level, the algorithm starts
from a root node – which represents the attacker’s en-
try point into the network – and, during each time
interval ∆t
i
, it enumerates routes to potential target
nodes originating from any of the current leaf nodes.
Each route includes a target node, which the attacker
seeks to compromise, and possibly a number of inter-
mediate f orwarding nodes. Note that, for each such
route to be added to the malware footprint, the route’s
terminal node must be compromised for the attacker
to be able to control that route. The length of routes
is controlled by the parameter hop
max
. Each route has
an associate reward and cost, which correspond to the
aggregated reward and cost of all the nodes that com-
prise the route.
When the attacker selects a route, the route is
added to the malware footprint and the attacker may
SECRYPT 2018 - International Conference on Security and Cryptography
286

Budget, B
reward
40
20
V
3
r:0
c:10
V
6
r:10
c:10
V
5
r:90
c:100
V
8
r:40
c:10
V
7
r:50
c:30
V
9
r:20
c:10
V
2
r:0
c:10
V
1
r:0
c:10
V
4
r:20
c:10
cost 40
(a)
Budget, B
reward
50
30
V
3
r:0
c:10
V
5
r:90
c:100
V
4
r:20
c:10
V
6
r:10
c:10
Budget now
allows
including this
node
V
2
r:0
c:10
V
1
r:0
c:10
V
7
r:50
c:30
V
8
r:40
c:10
V
9
r:20
c:10
cost 50
(b)
V
4
r:20
c:10
Budget, B
reward
70
60
At this budget
level, including V
4
does not maximize
reward
V
3
r:0
c:10
V
6
r:10
c:10
V
5
r:90
c:100
V
2
r:0
c:10
V
1
r:0
c:10
V
7
r:50
c:30
V
9
r:20
c:10
V
8
r:40
c:10
cost 70
(c)
Budget, B
reward
130
140
V
5
has the highest
value and it is
within budget, but
does not maximize
reward
V
3
r:0
c:10
V
6
r:10
c:10
V
8
r:40
c:10
V
5
r:90
c:100
V
7
r:50
c:30
V
9
r:20
c:10
V
2
r:0
c:10
V
1
r:0
c:10
V
4
r:20
c:10
cost 100
(d)
Figure 1: Basic example of APT malware footprint for different values of the budget.
enumerate new routes originating from any of the
currently compromised nodes. The attacker selects
routes in this iterative manner until the budget B
is exhausted or there are no more viable routes to
consider. Different strategies may be employed by
the attacker to select a route amongst the available
ones. We have considered three possible route se-
lection strategies: (i) Greatest Reward, which selects
the route that maximizes reward; (ii) Lowest Cost,
which chooses the route that minimizes cost; and
(iii) Cost Effective, which chooses the route that op-
timizes the cost/reward ratio.
We also consider two different tree evolution ap-
proaches. In the conservative approach, the attacker
maintains any node that was compromised during pre-
vious time intervals. In this case, a fraction of the bud-
get B for the current time interval goes toward main-
taining the compromised nodes. As discussed earlier,
the maintenance cost is lower than the cost to com-
promise, so the remaining portion of the budget can
be used to expand the tree. In the dynamic strategy,
the attacker may forgo some of the previously com-
promised nodes and have a larger portion of the bud-
get available to compromise new nodes if this choice
leads to better values of the chosen objective function.
Pseudo-code for the proposed treeConstruction
algorithm and for the auxiliary f indRoutes algorithm
is shown in Algorithm 1 and Algorithm 2 respectively.
Example 2 (Malware Footprint Evolution). To illus-
trate how the malware footprint evolves over time,
consider again the simple example discussed earlier.
In this example, the budget remains constant over time
(B = 55 for each time interval). However, as shown
in Figure 2, during each time interval, the attacker
compromises a larger proportion of the network due
to the cost of maintaining compromised nodes being
lower than the cost of the original compromise. In
this example, node detectability costs are reduced by
50% in the time intervals after initial compromise. By
incorporating the temporal dynamics of detectability
A Quantitative Framework to Model Advanced Persistent Threats
287

Algorithm 1: treeConstruction(G, T,B, hop
max
).
Input: Graph G = (V,E), current tree T = (C ∩ F,root), budget B, and parameter hop
max
.
Output: An updated tree T .
1: // Initialize
2: R ←
/
0
3: runningBudget ← 0
4: r ←
/
0
5: // Bootstrap R with root
6: findRoutes(G, T, r, root, R, runningBudget, 0, B, hop
max
)
7: while R 6=
/
0 do
8: // selectRoute selects route depending on route selection strategy, e.g. Greatest Reward
9: r ← selectRoute(R)
10: // final destination node is compromised, other nodes in the route are traffic-forwarding nodes
11: addRoute(T,r)
12: for all routes ∈ R do
13: // remove invalid routes (routes with the final destination not compromised)
14: // update costs and rewards for remaining routes which share nodes with r
15: end for
16: // Find routes using the newly compromised node
17: findRoutes(G,T, f inalDest,r, R,B, runningBudget, rCost, rReward,hop
max
)
18: end while
19: return T
cost, the threat model reflects the progressive nature
of APT malware behavior, slowly expanding through
the network to avoid detection.
5 SIMULATIONS
In this section, we study the performance of our al-
gorithm for large networks. For each network size,
we generated 30 different network topologies and the
results were averaged over different network settings.
To the best of our knowledge, there are no existing
models that capture the connectivity of an enterprise
network at both layer 2 and layer 3. Therefore, in or-
der to generate different network topologies, we used
scale-free networks and synthesized enterprise net-
work topologies of different sizes. Such networks are
known to accurately capture the connectivity in ISP
networks at the router level (Spring et al., 2002). We
used the NetworkX 2.0 library to generate these net-
works in an incremental fashion, using the Holme and
Kim algorithm, a variant of the Barab
´
asi-Albert (BA)
model. In the BA model, new nodes are added to the
network one at a time and each new node is connected
to one of the existing nodes with a probability that is
proportional to the current degree of that node. There-
fore, a node with a higher degree has a higher prob-
ability of becoming the new node’s neighbor. The
Holme and Kim algorithm tends to generate networks
with more clusters than typical BA networks, which is
intended to more closely model enterprise networks.
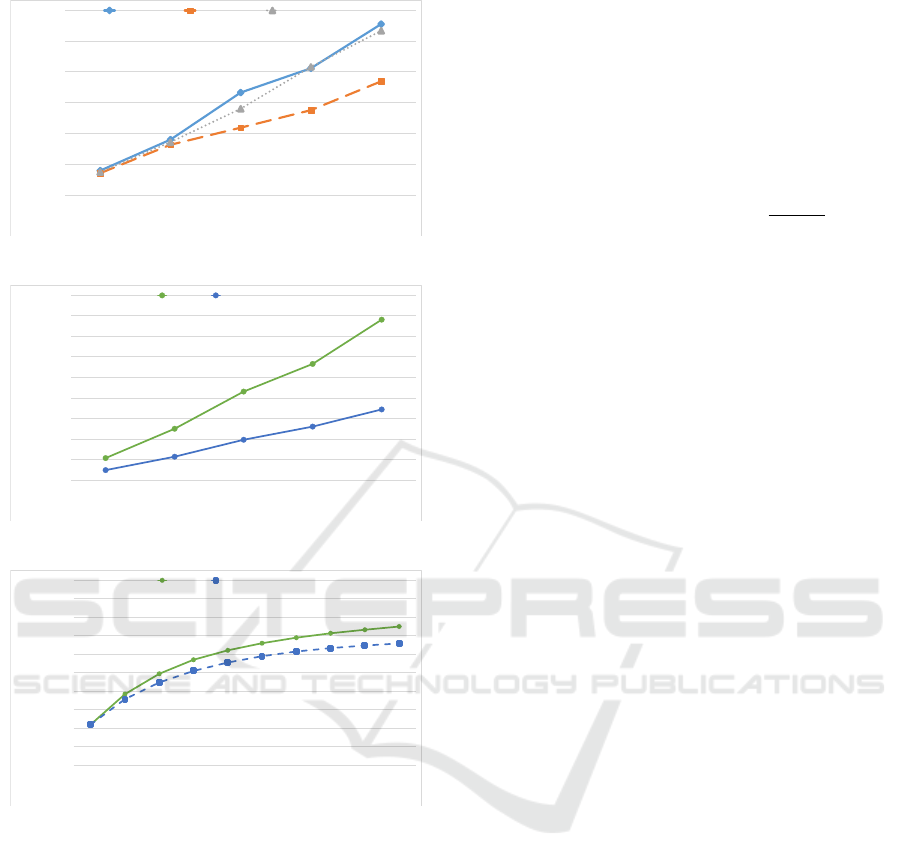
Reward. Figure 3 reports the total reward accrued by
the attacker over a time horizon T = {t
1
,. .. ,t
m
}, with
m = 10, and for all three route selection strategies,
when using the dynamic approach. As expected, the
malware gains greater reward from larger networks,
and the cost-effective strategy yields the best results
among all the strategies considered.
Malware Footprint. Figure 4 reports the percentage
of nodes that are compromised by the malware at time
t
m
, for different network sizes. The Lowest Cost strat-
egy achieves the best results because it tends to com-
promise a large number of low-cost but low-reward
nodes, whereas the Greatest Reward tends to include
high-reward, but also high-cost, nodes, thus exhaust-
ing its budget sooner.
Runtime. Fig. 5 illustrates the average runtime for
different network sizes. It can be seen that the to-
tal runtime increases linearly with the network size.
Instead, Figure 6 compares the runtime of the dy-
namic and conservative approaches for different net-
work sizes. The dynamic approach requires roughly
twice as much time to compute.
Conservative vs. Dynamic Approach. Figure 7 re-
ports the reward accrued by the malware over time as
a percentage of the total value of all network assets.
The chart compares the dynamic and conservative ap-
proaches, and reports values averaged over of all net-
work sizes considered (100,200,300,400,500). Dur-
ing the first time interval, the two approaches yield
the same reward, but then they start to diverge. As
the dynamic approach may reconsider the choice of
target nodes made during previous time intervals, it is
likely to achieve results that are closer to the optimal
solution, as confirmed by the set of charts discussed
in the following paragraph.
SECRYPT 2018 - International Conference on Security and Cryptography
288

Algorithm 2: f indRoutes(G,T, v,r,R,B, runningBudget, rCost, rReward,hop
max
).
Input: Graph G = (V,E), current tree T = (C ∩ F,root), node v, node list r, current set of viable routes R, budget B, runningBudget, rCost, rReward, and
parameter hop
max
Output: The set of viable routes, R, is updated.
1: // Determines if v is suitable for serving as final route destination (compromised node)
2: nodeIn f ectCost ← detectability cost for malware to compromise v
3: if v /∈ C then
4: if runningBudget + rCost + nodeIn f ectCost < B then
5: // Update the r with node data and add to R
6: newRCost ← rCost + nodeIn f ectCost
7: nodeIn f ectReward ← malware reward from the compromise of v
8: newRReward ← rReward + nodeIn f ectReward
9: newRoute ← deep copy of r, v
10: newRouteOption
+
← newRoutw,newRCost,newRReward
11: R
+
← newRouteOption
12: end if
13: end if
14: // Determines if v could be a forwarding node
15: if length(r) < hop
max
then
16: neighbors ← neighbors of n
17: for all neighbor ∈ neighbors do
18: if neighbor /∈ routeOptions then
19: nodeForwardCost ← detectability cost for malware to forward traffic though v
20: if runningBudget + routeCost + nodeForwardCost < B then
21: newRouteCost ← routeCost + nodeForwardCost
22: nodeForwardReward ← any malware reward when forwarding traffic through v
23: newRouteReward ← routeReward + nodeForwardReward
24: newRouteList ← deep copy of routeList,v
25: findRoutes (G,T, neighbor, newRouteList,routeOptions, B,runningBudget, newRouteCost, newRouteReward,hop
max
)
26: end if
27: end if
28: end for
29: end if
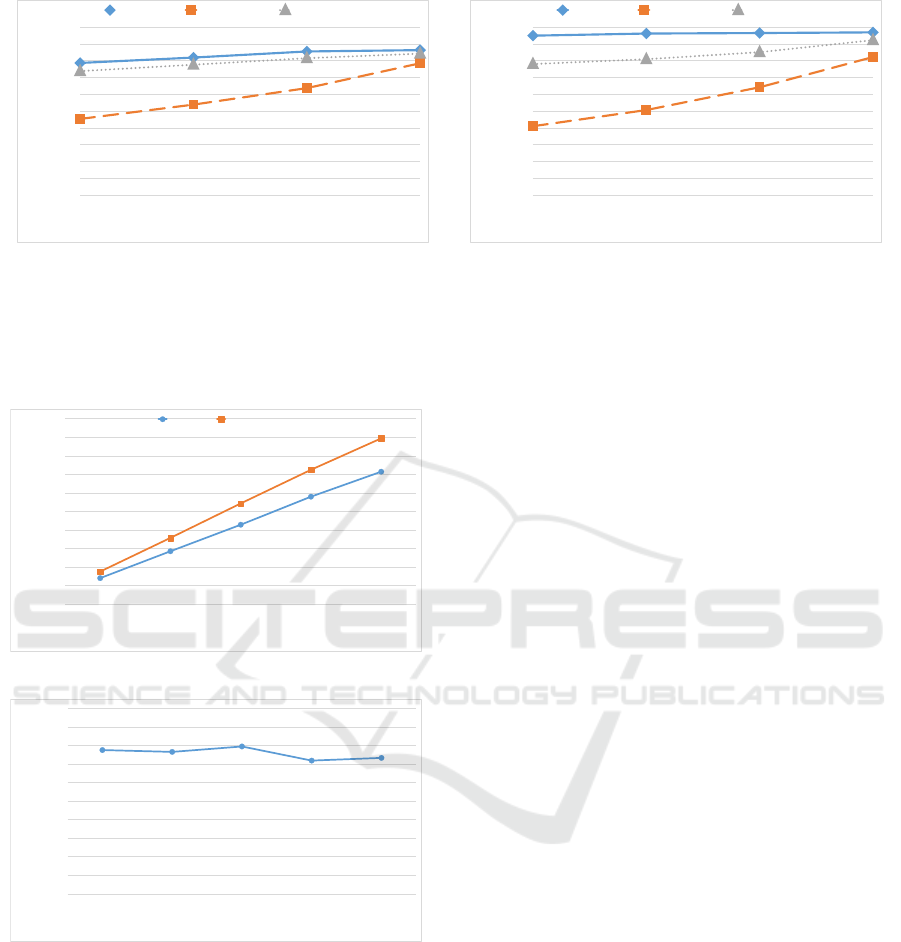
Approximation Ratio. To evaluate the approxima-
tion ratio of the proposed algorithm, we compared
the rewards gained over time using the three route se-
lection strategies with the rewards corresponding to
the optimal solution, which was computed by exhaus-
tively exploring the search space with a brute-force
approach. Figures 8(a) and 8(b) show how the ap-
proximation ratio – for the conservative and the dy-
namic approach respectively – converges to 100% as
the route length increases. As expected, the dynamic
approach converges more rapidly than the conserva-
tive one. Results presented here were generated using
networks of 25 nodes, as computation of the optimal
solution for larger graphs is prohibitive.
6 DEFENDER MODEL
The goal of the defender is to minimize the attacker’s
reward. As the attacker is invested in solving the
rooted tree problem discussed above, and success dur-
ing earlier time intervals implies an increased effec-
tive budget for the current interval, a maximally effec-
tive defender will be one that disrupts the attacker’s
effort to maintain a tree, thus forcing the attacker to
continually compromise new nodes, which results in
inefficient use of the detectability budget.
We assume that the defender has sufficient re-
sources to actively defend k < n nodes, where n = |V |
is the number of network nodes. In real world scenar-
ios, such nodes might receive more frequent security
upgrades or be more heavily monitored. The param-
eter k reflects the organization’s capacity for process-
ing alerts and allocating analyst time. We refer to such
actively defended nodes as watched, and we refer to
the process by which the defender selects a k-subset
S ⊆ V as the defender’s strategy. A watched node’s
cost increases by a multiplicative factor α > 1.
This increase in cost reflects the additional risk an
attacker takes by trying to compromise a node that
is subject to increased monitoring. In each interval
∆t
i
, the defender selects a set S
i
⊆ V according to
one of a family of strategies. Let S
i−1
be the set of
watched nodes from the previous interval. For each
v ∈ S
i
\S
i−1
– the newly watched nodes – cost
c
(v,t
i
) is
increased by a factor of α. For each node v ∈ S
i−1
\S
i
,
A Quantitative Framework to Model Advanced Persistent Threats
289

Budget, B
reward
55
30
Δ 𝑡
1
[0,1]
V
3
r:0
c:10
V
2
r:0
c:10
V
1
r:0
c:10
V
4
r:20
c:10
V
9
r:20
c:10
V
6
r:10
c:10
V
7
r:50
c:30
V
8
r:40
c:10
V
5
r:90
c:100
cost 50
(a)
V
7
r:50
c:30
Budget, B
reward
55
80
Δ 𝑡
2
[1,2]
Maintaining nodes
compromised
during Δ 𝑡
1
incurs
reduced costs
V
7
now in
budget
V
5
r:90
c:100
V
8
r:40
c:10
V
6
r:10
c:5
V
9
r:20
c:10
V
3
r:0
c:5
V
2
r:0
c:5
V
4
r:20
c:5
V
1
r:0
c:5
cost 55
(b)
V
2
r:0
c:5
V
6
r:10
c:5
V
7
r:50
c:15
V
9
r:20
c:10
Budget, B
reward
55
120
Δ 𝑡
3
[2,3]
Note: V
7
now incurs
reduced
costs
V
3
r:0
c:5
V
4
r:20
c:5
V
8
r:40
c:10
V
1
r:0
c:5
V
5
r:90
c:100
cost 50
(c)
V
1
r:0
c:5
V
4
r:20
c:5
Budget, B
reward
55
140
Δ 𝑡
4
[3,4]
V
3
r:0
c:5
V
8
r:40
c:5
V
6
r:10
c:5
V
7
r:50
c:15
V
9
r:20
c:10
V
2
r:0
c:5
V
5
r:90
c:100
cost 55
(d)
Figure 2: Evolution of malware footprint over time.
0
5000
10000
15000
20000
25000
30000
35000
100 200 300 400 500
Reward
Network Size
Cost Effective Greatest Prize Lowest Cost
Figure 3: Reward vs. Network Size.
cost
c
(v,t
i
) is decreased by a factor of α, bringing the
cost back to its normal value. These nodes are no
longer watched. The cost for nodes v ∈ S
i
∪ S
i−1
is
unchanged, as they continue to be watched.
We now discuss several defender strategies. Two
simple strategies are the uniform and the cost-effective
strategy. A defender using the uniform strategy se-
lects a set of k nodes uniformly at random from V dur-
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
100 200 300 400 500
Footprint Size (%)
Network Size
Cost Effective Greatest Reward Lowest Cost
Figure 4: Footprint vs. Network Size.
ing each interval. This is a very simple, low-overhead
strategy that does not consider any structural proper-
ties of the graph, nor any of the node weights.
We define the cost-effectiveness of a node v ∈
V as e(v,t
i
) = reward
c
(v,t
i
)/cost
c
(v,t
i
). Very cost-
effective nodes are those who offer great rewards at
a relatively low cost. A defender adopting the cost-
effective strategy selects a set S
i
⊆ V of k nodes,
SECRYPT 2018 - International Conference on Security and Cryptography
290

0
100
200
300
400
500
600
100 200 300 400 500
Runtime (seconds)
Network Size
Cost Effective Greatest Prize Lowest Cost
Figure 5: Runtime vs. Network Size.
0
200
400
600
800
1000
1200
1400
1600
1800
100 200 300 400 500
Runtime (seconds)
Network Size
Dynamic Conservative
Figure 6: Conservative vs. dynamic approach: runtime.
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1 2 3 4 5 6 7 8 9 10
Reward (%)
Time
Dynamic Conservative
Figure 7: Conservative vs. dynamic approach: reward.
where each node v ∈ S
i
is sampled with probabil-
ity p(v,t
i
) = e(v,t
i
)/
∑
u∈V
e(u,t
i
). The cost-effective
strategy is a generalization of the uniform strategy
that maintains its simplicity. However, the cost-
effective strategy takes more information into ac-
count when deciding the allocation of resources. A
more sophisticated strategy is the betweenness strat-
egy, which is described in the following subsection.
6.1 Betweenness Strategy
Betweenness centrality is a fundamental measure of
a node’s relative importance, and it is well-studied
in network analysis. The betweenness centrality of
a node is defined in terms of the proportion of short-
est paths that pass through it. Thus, a node with high
betweenness is one that connects many other nodes
to one another – such as a boundary node connecting
tightly-clustered subgraphs. This property is a natu-
ral measure of importance in many types of networks,
including power, communication, and disease trans-
mission (Brandes, 2001). For u, v,w ∈ V , suppose that
λ
v,w
is the number of shortest paths from v to w, and
λ
v,w
(u) is the number of such paths that include u.
Then the betweenness centrality of u is calculated as
C(u) =
∑
v,w∈V | u /∈{v,w}∧λ
v,w
6=0
λ
v,w
(u)
λ
v,w
Selecting the nodes with the highest betweenness
centrality may result in a redundant set of nodes when
there is significant overlap among the shortest paths
that contribute to the centrality of two of more se-
lected nodes. To avoid this problem, we can com-
pute the list of top k nodes with respect to between-
ness centrality adaptively, removing all edges inci-
dent to a previously selected node and recomputing
the centrality of the all other nodes before selecting
the next node. We refer to this method of finding
the top k nodes as the adaptive-k betweenness strat-
egy. Fortunately, there exist online polynomial time
algorithms for computing the betweenness centrality
over a graph that is subject to the addition and re-
moval of nodes (Kourtellis et al., 2015). Furthermore,
there exist online approximate adaptive betweenness
centrality algorithms intended to scale to very large
graphs (Yoshida, 2014).
A defender implementing the betweenness strat-
egy interprets the undirected, unweighted graph G =
(V, E) as a directed, weighted graph G
0
= (V,E
0
,w),
where (u,v),(v, u) ∈ E
0
for every (u, v) ∈ E and for
every (u, v) ∈ E
0
, w(u, v) = cost
c
(v)/reward
c
(v). In
this graph, the weight of an edge connecting nodes u
to v is the inverse of the cost-efficiency of v. That is,
the more cost-effective (and therefore attractive to the
attacker) v is, the more likely shortest paths are to go
through it due to the weighting on the nodes. Hence,
the more cost-effective a node, the more likely it is
to have high betweenness centrality. This dispropor-
tionately skews in favor of cost-effective nodes that
have high betweenness centrality in the unweighted
version of the problem. Hence, the defender com-
putes the adaptive betweenness centrality of the graph
G
0
and selects the top k nodes in each time interval.
Figure 9(a) compares the malware footprint be-
fore and after the deployment of a defender’s strat-
egy. In this example, the attacker employs the
cost-effective strategy, whereas the defender selects
k nodes to watch using the adaptive-k betweenness
strategy, where k is set to 10% of the number of nodes
in the network. These nodes increase their cost for
a time interval by a factor α = 10, resulting in a 20%
A Quantitative Framework to Model Advanced Persistent Threats
291

0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1 2 3 4
% of Optimal Reward
Max Hops
Cost Effective Greatest Reward Lowest Cost
(a) Conservative approach
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1 2 3 4
% of Optimal Reward
Max Hops
Cost Effective Greatest Reward Lowest Cost
(b) Dynamic approach
Figure 8: Approximation ratio.
reduction in the number of compromised nodes, and a
15% reduction in attacker’s reward across all network
sizes, as shown in Figure 9(b).
0
50
100
150
200
250
300
350
400
450
500
100 200 300 400 500
Footprint Size (Raw)
Network Size
Defended No Defense
(a) Comparison of number of compromised nodes
0%
2%
4%
6%
8%
10%
12%
14%
16%
18%
20%
100 200 300 400 500
Reward Reduction (%)
Network Size
(b) Reduction in attacker’s reward
Figure 9: Impact of defensive actions on malware.
7 RELATED WORK
Since the emergence of APTs, there has been a sig-
nificant body of research in this field. Earlier work
often examined the failure of existing intrusion de-
tection systems (Chen et al., 2014) and studied the
characteristics of APT malware that allowed attack-
ers to circumvent existing defenses. Later, most re-
search in the field focused on the detection of APT
malware, primarily through various anomaly detec-
tion, network event correlation, flow-based analysis,
and other big data approaches (Marchetti et al., 2016;
Friedberg et al., 2015). These approaches generally
require organizations to devote significant resources
to the collection and processing of event logs. Other
approaches rely on the use of honeypots and honey-
traps to detect APTs (Virvilis et al., 2014).
While these efforts are still ongoing, other mod-
els have recently emerged as more instances of APT
malware have been detected and studied. These ap-
proaches include the use of Petri Nets (Jasiul et al.,
2014), Markov models (Gore et al., 2017), and game-
theoretic models (Fang et al., 2014).
8 CONCLUSIONS
In recent years, Advanced Persistent Threats (APTs)
have emerged as increasingly sophisticated cyber at-
tacks, often waged by state actors or other hostile or-
ganizations against high-profile targets. As discussed,
APT actors have at their disposal a diversified set of
sophisticated tools and advanced capabilities to pen-
etrate target systems, evade detection, and maintain
a foothold within compromised systems for extended
periods of time. Stealth and persistence enable APT
actors to carry on long-term espionage and sabotage
operations. Despite significant efforts to develop APT
detection and mitigation capabilities, the stealthy na-
ture of APTs poses significant challenges, and de-
fending from such threats is still an open research
problem. In particular, quantitative models to capture
how an APT actor may create and maintain a foothold
within a target system are lacking. To address this gap
we have proposed a quantitative framework to (i) as-
sess the cost incurred by APT actors to compromise
and persist within a target system; (ii) estimate the
value they gain over time by persisting in the system;
SECRYPT 2018 - International Conference on Security and Cryptography
292

(iii) simulate how the footprint of an APT evolves
over time when, to maintain stealth, the attackers have
constraints on the amount of potentially detectable ac-
tivity they can engage in. In our model, an attacker
must weigh the value of a given target node against
the probability of detection, which would impair the
attacker’s ability to persist within the target network.
Results from our evaluation have shown that the pro-
posed approach is promising and encourage further
research in this direction.
REFERENCES
(2017). 2017 cost of data breach study. Technical report,
Ponemon Institute.
Ablon, L. and Bogart, A. (2017). Zero days, thousands of
nights: The life and times of zero-day vulnerabilities
and their exploits. Research Reports RR-1751-RC,
RAND Corporation.
Albanese, M. and Jajodia, S. (2018). A graphical model
to assess the impact of multi-step attacks. Journal of
Defense Modeling and Simulation, 15(1):79–93.
Albanese, M., Jajodia, S., and Noel, S. (2012). Time-
efficient and cost-effective network hardening using
attack graphs. In Proc. of the 42nd Annual IEEE/IFIP
Intl. Conf. on Dependable Systems and Networks
(DSN 2012). IEEE.
Bateni, M. H., Hajiaghayi, M. T., and Liaghat, V. (2013).
Improved approximation algorithms for (budgeted)
node-weighted steiner problems. In Proc. of the 40th
Intl. Colloquium on Automata, Languages, and Pro-
gramming (ICALP 2013), pages 81–92. Springer.
Brandes, U. (2001). A faster algorithm for between-
ness centrality. Journal of Mathematical Sociology,
25(2):163–177.
Chen, P., Desmet, L., and Huygens, C. (2014). A study
on advanced persistent threats. In Proc. of the IFIP
Intl. Conf. on Communications and Multimedia Secu-
rity (CMS 2014), pages 63–72. Springer.
Fang, X., Zhai, L., Jia, Z., and Bai, W. (2014). A game
model for predicting the attack path of APT. In Proc.
of the 12th IEEE Intl. Conf. on Dependable, Auto-
nomic and Secure Computing (DASC 2014), pages
491–495. IEEE.
Friedberg, I., Skopik, F., Settanni, G., and Fiedler, R.
(2015). Combating advanced persistent threats: From
network event correlation to incident detection. Com-
puters & Security, 48:35–57.
Gore, R., Padilla, J., and Diallo, S. (2017). Markov chain
modeling of cyber threats. Journal of Defense Model-
ing and Simulation, 14(3):233–244.
Jafarian, J. H., Al-Shaer, E., and Duan, Q. (2014). Spatio-
temporal address mutation for proactive cyber agility
against sophisticated attackers. In Proc. of the 1st
ACM Workshop on Moving Target Defense (MTD
2014), pages 69–78. ACM.
Jasiul, B., Szpyrka, M., and
´
Sliwa, J. (2014). Detection and
modeling of cyber attacks with petri nets. Entropy,
16(12):6602–6623.
Johnson, D. S., Minkoff, M., and Phillips, S. (2000). The
prize collecting steiner tree problem: Theory and
practice. In Proc. of the 11th annual ACM-SIAM Sym-
posium on Discrete Algorithms (SODA 2000), pages
760–769. SIAM.
Kaspersky Labs. Targeted cyberattacks logbook. [Online,
retrieved May 24, 2018].
Kourtellis, N., De Francisci Morales, G., and Bonchi, F.
(2015). Scalable online betweenness centrality in
evolving graphs. IEEE Transactions on Knowledge
and Data Engineering, 27(9):2494–2506.
Langner, R. (2013). To kill a centrifuge: A technical analy-
sis of what stuxnet’s creators tried to achieve. Techni-
cal report, The Langner Group.
Marchetti, M., Pierazzi, F., Colajanni, M., and Guido, A.
(2016). Analysis of high volumes of network traffic
for Advanced Persistent Threat detection. Computer
Networks, 109(2):127–141.
Moss, A. and Rabani, Y. (2007). Approximation algorithms
for constrained node weighted steiner tree problems.
SIAM Journal on Computing, 37(2):460–481.
Sadeghian Sadeghabad, S. (2013). Node-weighted prize
collecting steiner tree and applications. Master’s the-
sis, University of Waterloo, Canada.
Spring, N., Mahajan, R., and Wetherall, D. (2002). Mea-
suring ISP topologies with Rocketfuel. SIGCOMM
Computer Communication Review, 32(4):133–145.
Symantec Security Response (2011). W32.Duqu: The pre-
cursor to the next Stuxnet. Technical report, Symantec
Corporation.
Symantec Security Response (2015). Regin: Top-tier es-
pionage tool enables stealthy surveillance. Technical
report, Symantec Corporation.
Virvilis, N., Vanautgaerden, B., and Serrano, O. S. (2014).
Changing the game: The art of deceiving sophisti-
cated attackers. In Proc. of the 6th Intl. Conf. on Cyber
Conflict (CyCon 2014), pages 87–97. IEEE.
Yoshida, Y. (2014). Almost linear-time algorithms for
adaptive betweenness centrality using hypergraph
sketches. In Proc. of the 20th ACM SIGKDD Intl.
Conf. on Knowledge Discovery and Data Mining
(KDD 2014), pages 1416–1425. ACM.
A Quantitative Framework to Model Advanced Persistent Threats
293