
Application of Hybrid Petri Nets for a Drawing Blood Flow
from Fingertip
Shigenori Togashi
1
, Kei Takenaka
1
, Kenko Uchida
2
, Takashi Irie
3
,
Taku Sakazume
3
and Ryo Miyake
4
1
Hitachi, Ltd., Research & Development Group, 832-2, Horiguchi, Hitachinaka, Ibaraki 312-0034, Japan
2
Hitachi High-Technologies Corporation, Science & Medical Systems Business Group,
24-14, Nishi-shimbashi 1-chome, Minato-ku, Tokyo 105-8717, Japan
3
Hitachi High-Technologies Corporation, Science & Medical Systems Business Group,
882, Ichige, Hitachinaka, Ibaraki 312-8504, Japan
4
The University of Tokyo, Department of Bioengineering, KBIC 212, 7-7, Shin-kawasaki,
Saiwai-ku, Kawasaki, Kanagawa 212-0032, Japan
Keywords: Hybrid Petri Nets, Fluid Dynamic, Elastic Dynamic, Blood Flow, Fingertip.
Abstract: Our objective of this study are to make a fluid dynamical model and to conduct the flow simulation for
obtaining a large amount of drawing blood from a fingertip. The processes of drawing blood are hybrid
systems including both the continuity system of blood flow and the discrete systems of cuff pressing and
puncture. Therefore, we made the modelling of the fingertip drwaing blood process from the analogy of fluid
daynamic tank and pipe systems control using hybrid Petri nets. Using the hybrid Petri nets simulation with
cuff pressing and puncture modeled as discrete and blood flow modeled as continuity, we confirmed that the
simulation results were agreement with the experimental drawing blood data.
1 INTRODUCTION
The concept of a self-managing healthy society is
important for the countries facing the aging
population. To realize a self-managing healthy
society, it is imperative to develop an innovative
system for prophylaxis, diagnosis and treatment that
dramatically reduces hospitalization and visits to the
doctor’s office. Under such a background, the POCT
(Point of Care Testing) using a drawing blood from a
fingertip is one of the preferable technologies to
reduce visits to the doctor’s office (Kumar and
Webster, 2016). That is the reason why the drawing
blood from a fingertip is possible to draw by oneself,
as compared with the drawing blood from an arm by
a nurse at the doctor’s office. Therefore, POCT using
a drawing blood from a fingertip at home and
drugstore has increased in recent years.
The recent POCT using a drawing blood from a
fingertip covers many items of inspection for
lifestyle-related diseases such as high blood pressure,
diabetes, cancers such as stomach, large intestine,
lungs. The self-drawn blood is delivered to the
inspection agency by mail, and the user receives the
inspection results after one week. However, the
problems of the self -drawing blood from a fingertip
are the complicated drawing blood process and too
small amount of blood. In case of check a blood
glucose level, the amount of blood is small such as
under 1 μL, but it is necessary for the above lifestyle-
related diseases and cancers inspection to obtain the
large amount of blood such as over 100 μL. The use
of a cuff band for fastening finger is one of the
preferable methods to obtain the large amount of
blood from a fingertip (Kuramoto, 2007). Based on
the above background, our motivation is to make an
automatic drawing blood machine from fingertip. As
the first step, we think it is very important to
understand the fingertip blood flow.
From the point of simulation around a fingertip,
there are some researches about CFD (Computational
Fluid Dynamics) analysis of the fingertip temperature
and oxygen transport in the human breast tumor under
laser irradiation (He et al., 2006), and about FEM
(Finite Element Method) analysis of the fingertip
contact pressure for developing robot hands (Maeno
et al., 1997). Moreover, from the point of simulation
inside the human body, there are many researches
about CFD analysis of the blood flow in the human
organs (Oshima et al., 2001; Liang et al., 2015).
136
Togashi, S., Takenaka, K., Uchida, K., Irie, T., Sakazume, T. and Miyake, R.
Application of Hybrid Petri Nets for a Drawing Blood Flow from Fingertip.
DOI: 10.5220/0006877701360143
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 136-143
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

Figure 1: Close tank and pipes connection flow modelling of fingertip blood in normal state.
Figure 2: Close tank and pipes connection flow modelling of fingertip blood in congestive state by a cuff band.
However, there is no research for obtaining an
amount of drawing blood from a fingertip. It is for the
reason that the processes of drawing blood are hybrid
systems including both the continuity system of blood
flow and the discrete systems of cuff pressing and
puncture. For the above solution, hybrid Petri nets
(Herajy and Heiner, 2012) is good simulation tool.
Based on the above background, our objective of
this study are to make a fluid dynamical model and to
conduct the flow simulation for obtaining a large
amount of drawing blood from a fingertip using
hybrid Petri nets.
2 MODELLING OF FINGERTIP
BLOOD FLOW
2.1 Fluid Dynamical and Elastic
Dynamical Model
Figure 1(a) shows the normal state with the finger
artery, the capillaries and the finger vein in the
fingertip. Figure 1(b) is corresponding to the fluid
dynamical pipes and close tank connection modelling
of Fig.1(a), that is the finger artery (flow rate : Q
FA
)
and finger vein (flow rate : Q
FV
) are represented as the
pipes, and the capillaries are represented as the
bundled capillaries bulk tank (Volume: V
FC_norm
).
Figure 2(a) shows the congestive state by a cuff
band (Yamakoshi et al., 1982), and Figure 2(b) is
corresponding to the fluid dynamical modelling of
Fig.2 (a). In this case, the pressed finger artery (flow
rate: α
FA
Q
FA
) and the pressed finger vein (flow rate
:α
FV
Q
FV
) by a cuff band are represented as the pipes
with the half-open valves.
Therefore, the increased blood volume (ΔV = V
FC_cong
-V
FC_norm
) in the modelled capillaries bulk tank is
represented as the difference of the flow rate between
the pressed finger artery and vein as shown in Eq. (1).
ΔV = ( α
FA
Q
FA
-α
FV
Q
FV
)Δt,
(1)
where Δt is the valve close time. Moreover, the
increased blood pressure (ΔP = P
FC_cong
-P
FC_norm
) in
the modelled capillaries bulk tank is represented as
(a) Normal state
Finger vein
Finger artery
Finger capillaries
(b) Normal state flow model
Valve-1
(Open)
Capillaries bulk tank
V
FC_norm
Valve-2
(Open)
Q
FA
Q
FV
P
FC_norm
Cuff
(a) Congestive state by a cuff band
(b) Congestive state flow model
Valve-1
(Half-open)
Congestive state
L
FC
Region-1
Capillaries bulk tank
V
FC_cong
Valve-2
(Half-open)
α
FV
Q
FV
α
FA
Q
FA
P
FC_cong
= P
FC_norm
+ΔP
Application of Hybrid Petri Nets for a Drawing Blood Flow from Fingertip
137
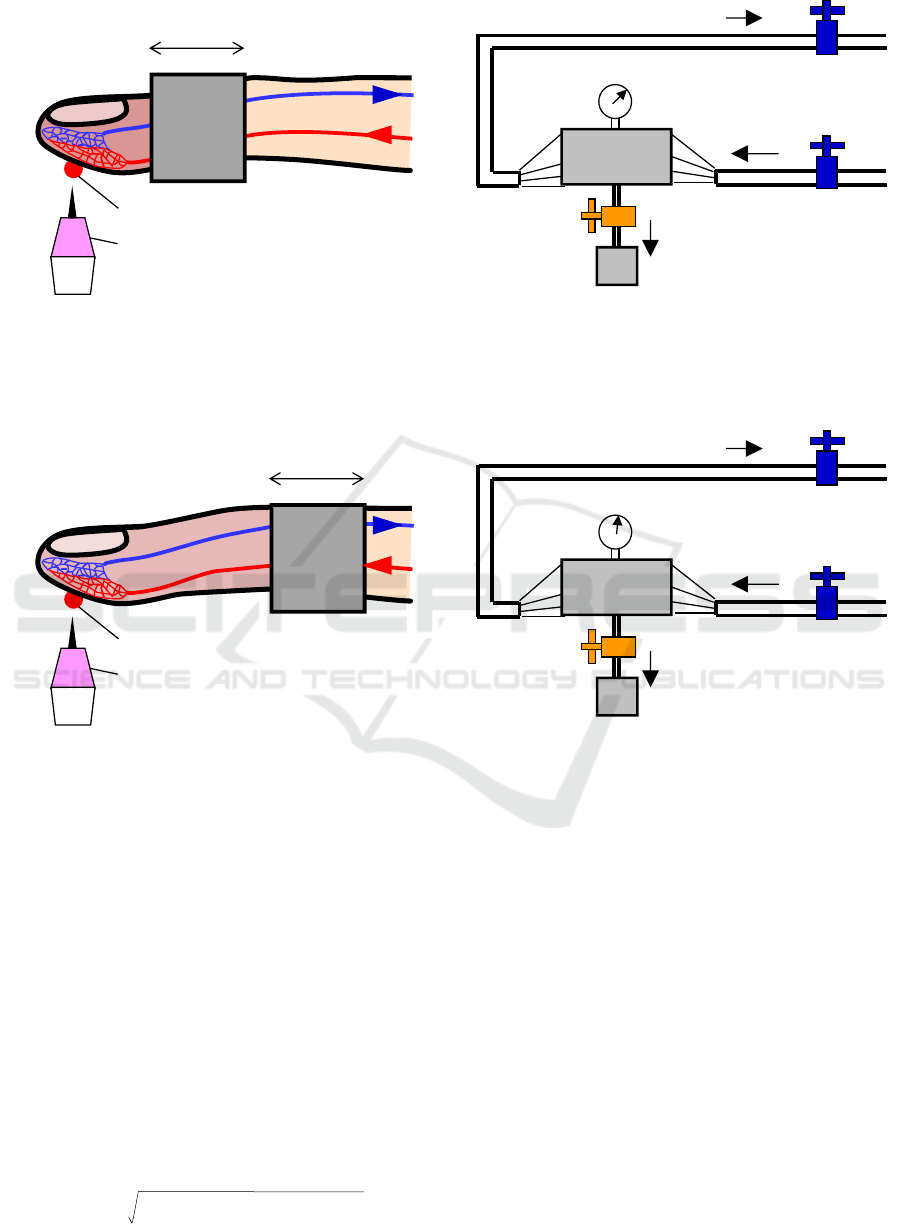
Figure 3: Close tank and pipes connection flow modelling of fingertip blood in drawing blood state with a cuff band on the
region-1 by a puncture device.
Figure 4: Close tank and pipes connection flow modelling of fingertip blood in drawing blood state with a cuff band on the
region-2 by a puncture device.
the elastic dynamic modelling of the blood vessel
wall based on the increased blood volume ΔV as
shown in Eq.(2).
ΔP = { Eh / (2
-
ν ) r } ΔV / V
FC_norm
(2)
where E is the Young’s modulus, ν is the Poisson’s
ratio, h is the thickness, and r is the radius of the blood
vessel wall, respectively.
Figure 3(a) shows the drawing blood state with a
cuff band on the region-1 by a puncture device, and
Figure 3(b) is corresponding to the fluid dynamical
modelling of Fig.3 (a) based on the valve set under
the modelled capillaries bulk tank. The amount of
drawing blood V
BD
is represented as the analogy of
the Venturi effect as shown in Eq.(3).
V
BD
= α
PD
A
FC
2ΔP /ρ ( A
FC
2
/ A
PD
2
-
1 ) Δt
(3)
where A
FC
is the bottom area of the modelled
capillaries bulk tank, A
PD
is the hole area made by the
puncture device, ρ is the blood density, and α
PD
is the
discharge coefficient of puncture hole, respectively.
Figure 4 shows the drawing blood state with a cuff
band on the region-2 by a puncture device, instead of
region-1 as shown in Fig.3.
2.2 Hybrid Petri Nets of
Fluid-Dynamical Model
A Petri net is an algebraic and graphical tool for
modelling phenomena by using three kinds of
elements: “places,” “transitions,” and connecting
“arcs” as shown in Table 1 (Petri, 1962). The hybrid
Petri nets can use both continuous variables (real
numbers) and discrete variables (integers), and for
(a) Drawing blood state by a puncture device
Cuff
Puncture device
Blood drop
(b) Drawing blood state flow model
Region-1
Valve-1
(Half-open)
Valve-3
(Open)
V
FC_cong
Valve-2
(Half-open)
α
FV
Q
FV
α
FA
Q
FA
P
FC_cong
= P
FC_norm
+ΔP
V
BD
α
PD
Q
PD
(a) Drawing blood state by a puncture device
Cuff
Puncture device
Blood drop
(b) Drawing blood state flow model
Region-2
Valve-1
(Half-open)
Valve-3
(Open)
V
FC_cong
Valve-2
(Half-open)
α
FV
Q
FV
α
FA
Q
FA
P
FC_cong
= P
FC_norm
+ΔP
V
BD
α
PD
Q
PD
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
138

execution of the numerical analysis reported here we
used the hybrid Petri nets tool called Visual Object
Net (VON)++ (Peleg et al., 2005).
The basic diagram of the hybrid Petri nets using
VON++ is represented as the combination and the
connection of discrete place, static test arc,
continuous transition, normal arc, continuous place,
inhibitor arc, and discrete transition as shown in Fig.5
(Renganathan and Bhaskar, 2012).
The processes of drawing blood are hybrid
systems including both the continuity system of blood
flow and the discrete systems of cuff pressing and
puncture. Therefore, we made the modelling of the
fingertip drwaing blood process from the analogy of
three-tank reconfiguration control using hybrid Petri
nets (Lunze et al., 2001; Wu et al., 2010; Mendoza et
al., 2012).
Figure 6 shows the modelling of the fingertip
drwaing blood process using hybrid Petri nets based
on the fluid dynamical pipes and close tank
connection modelling as shown in Figs. 1(b), 2(b),
3(b) and 4(b). The cuff band pressing and the
puncture by a lancet device are represented as discrete
variables, and the blood flow is represented as
continuous variables.
Moreover, the fingertip blood flow is assumed as
the Newtonian steady flow, and the blood pulsation is
small enough to be ignored.
Table 1: Basic components of Petri nets model.
Figure 5: Basic diagram of hybrid Petri nets.
Figure 6: Fingertip drawing blood process model using hybrid Petri nets.
Place
Transition
Arc
Discrete
Continuity
Normal arc
Static test arc
Inhibitor arc
Discrete
place
Continuous
place
Discrete
transition
Continuous
transition
Static test arc
Normal arc
Inhibitor arc
Discrete
Discrete
Continuity
FC
Token-C1
Token-C2
Cuff-Open
Cuff-Close
Finger-Artery
Finger-Artery-Cuff
Finger-Vein-Cuff
Finger-Vein
Puncture-ON
Puncture-OFF
Token-P1
Finger-Capillaries
Puncture
Blood-
Drawing
Token-P2
BD
Application of Hybrid Petri Nets for a Drawing Blood Flow from Fingertip
139

2.3 Flow Simulation of Fingertip Blood
Table 2 shows the five simulation cases using hybrid
Petri nets. The Case F1 is the normal state
corresponding the fluid dynamical modelling as
shown in Fig. 1(b). The Case F2 is the congestive
state corresponding the fluid dynamical modelling as
shown in Fig. 1(d). The Case F3 is the drawing blood
state by a puncture device without a cuff band. The
Case F4 is the drawing blood state by a puncture
device with a cuff band on the region-1 corresponding
the fluid dynamical modelling as shown in Fig. 1(f).
Finally, the Case F5 is the drawing blood state by a
puncture device with a cuff band on the region-2.
Table 3 shows the estimation of the blood flow
rate in a finger artery as the initial condition. The
blood velocity U
FA
and the diameter D
FA
of a finger
artery are known as U
FA
=50 mm/s and D
FA
=0.35 mm
(average value from 0.20 to 0.50 mm) (Shore, 2000),
respectively. Therefore, the flow rate Q
FA
( =U
FA
×π
D
F
2
/4 ) is set to 4.8 μL/s.
Table 4 shows the estimation of the blood volume
in finger capillaries as the initial condition. The
velocity U
FC
and the area length L
Fc
as shown in Fig.
1(c) of the finger capillaries are known as U
FC
=0.75
mm/s (average value from 0.5 to 1.0 mm/s) and L
FC
=10 mm (Yamakoshi et al., 1980), respectively.
Therefore, the modelled capillaries bulk tank V
FC
(
=Q
FA
× L
FC
/U
FC
) is set to 64.0 μL. In case of the
congestive state by a cuff band, the area length L
FC
and the modelled capillaries bulk tank V
FC
are
different according to the cuff band position (region-
1 or 2 ).
Table 2: Hybrid Petri nets simulation cases.
Table 3: Estimation of the blood flow rate in a finger artery.
Table 4: Estimation of the blood volume in finger
capillaries.
Table 5: Physical properties for calculation of blood
capillary using Eq.(2).
Table 6: Physical properties for calculation of drawing
blood using Eq.(3).
Table 5 shows the physical properties for
calculation of blood capillary using Eq.(2), and Table
6 shows the physical properties for calculation of
drawing blood using Eq.(3), respectively.
Table 7 shows the five cases initial conditions of
places and transitions. Moreover, the periodical
pressing by a cuff band is 10 s interval, and the
simulation of the each case is conducted to 100 s with
the time increment of 1 s.
2.4 Flow Simulation Results of
Fingertip Blood
Figure 7 shows the simulation results of Case F2. The
results of Case F2 are corresponding to the periodical
congestive state by a cuff band, it is found that the
residential blood volume VFC as shown in Fig.7(a)
and the blood pressure PFC as shown in Fig.7(b) in
the capillaries bulk tank are periodically increased by
a cuff band of 10s interval.
Figure 8 shows the simulation results of Case F3,
Case F4 and Case F5 with the drawing blood by a
puncture device with the periodically congestive state
by a cuff band of 10 s interval. It is found that the
amount of drawing blood from a fingertip VBD
increases in the following order: Case F3 (without a
cuff) < Case F5 (a cuff on region-2) < Case F4 (a cuff
on region-1).
Moreover, the experimental drawing blood data
shown in Table 8 are also plotted with the same
condition as the simulation in Fig.8. The above exper-
Case
Corresponding
fluid dynamical
modelling
Cuff band
Puncture
Region-1 Region-2
F1 Fig.1(b) - - -
F2 Fig.2(b) ○ - -
F3 Fig.1(b) - - ○
F4 Fig.3(b) ○ - ○
F5 Fig.4(b) - ○ ○
UFA (mm/s) DFA (mm) QFA (μL/s)
50 0.35 4.8
U
FC (mm/s
)
LFC (mm) VFC (μL) Cuff
0.75 10.0
64.0 Region-1
128.0 Region-2
E (Pa) ν h (mm)
5.0×10
5
0.45 0.2
α
PD
A
FC
(mm
2
) A
PD
(mm
2
) ρ (kg / m
3
)
0.61 78 0.5 1.05×10
3
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
140

Table 7: Initial conditions of fingertip blood flow model using hybrid Petri nets.
Figure 7: Simulation results of bulk tank volume and
pressure.
iment of the drawing blood from nine volunteers was
approved by the ethics committee of Hitachi group
headquarters. It is found that the simulation results
were agreement with the experimental drawing blood
data of 76 - 86μL and 169 - 231μL with the different
pressing region by a cuff band. Consequently, It is
effective for obtaining a large amount of drawing
blood from a fingertip to the use of a cuff band on the
region-1 with the periodical pressing of 10 s interval.
3 DISCUSSION
The processes of drawing blood are hybrid systems
including both the continuity system of blood flow
and the discrete systems of cuff pressing and
puncture. Therefore, we made the modelling of the
fingertip drwaing blood process from the analogy of
three-tank reconfiguration control using hybrid Petri
nets, and we confirmed the advantages of using
hybrid Petri nets. On the other hand, the scatter of the
experimental data is caused by the individual
difference of the volunteers. Therefore, the modelling
in consideration of the individual difference is
necessary in the future.
In this study, the amount of drawing blood within
90s is proportional to the drawing time as shown in
Fig.8. However, we have to consider the effect of the
blood coagulation in case of more than 180 s and
make the model of non-Newtonian flow.
According to the manuals of some blood
analyzers, the required minimum amount is over 900
Element
Initial conditions and equations
Case F1 Case F2 Case F3 Case F4 Case F5
Discrete
Place
Token-C1
-
1 1 1 1
Token-C2
-
0 0 0 0
Token-P1
- -
1 1 1
Token-P2
- -
0 0 0
Transition
Cuff-Open
-
10 (s) 10 (s) 10 (s) 10 (s)
Cuff-Close
-
10 (s) 10 (s) 10 (s) 10 (s)
Puncture-ON
- -
10 (s) 10 (s) 10 (s)
Puncture-OFF
- -
90 (s) 90 (s) 90 (s)
Continuity
Place
Finger-Capillary FC = 64.0 (μL)
Blood-Drawing BD = 0 (μL)
Transition
Finger-Artery 4.8 (μL)
Finger-Artery-Cuff
-
4.8× α
FA
(μL) with Eq.(2)
Finger-Vein 4.8 (μL)
Finger-Vein-Cuff
-
4.8× α
FA
(μL) with Eq.(2)
Puncture
-
-
Eqs.(3) –(5)
(a) Bulk tank volume under the congestive state
calculated by Eq.(1)
(b) Bulk tank pressure under the congestive state
calculated by Eq.(2)
0
50
100
150
200
250
0
15
30
45
0 20 40 60 80 100
P
FC
(mmHg)
P
FC
(kPa)
t (s)
0
40
80
120
0 20 40 60 80 100
V
FC
(μL)
t (s)
Application of Hybrid Petri Nets for a Drawing Blood Flow from Fingertip
141
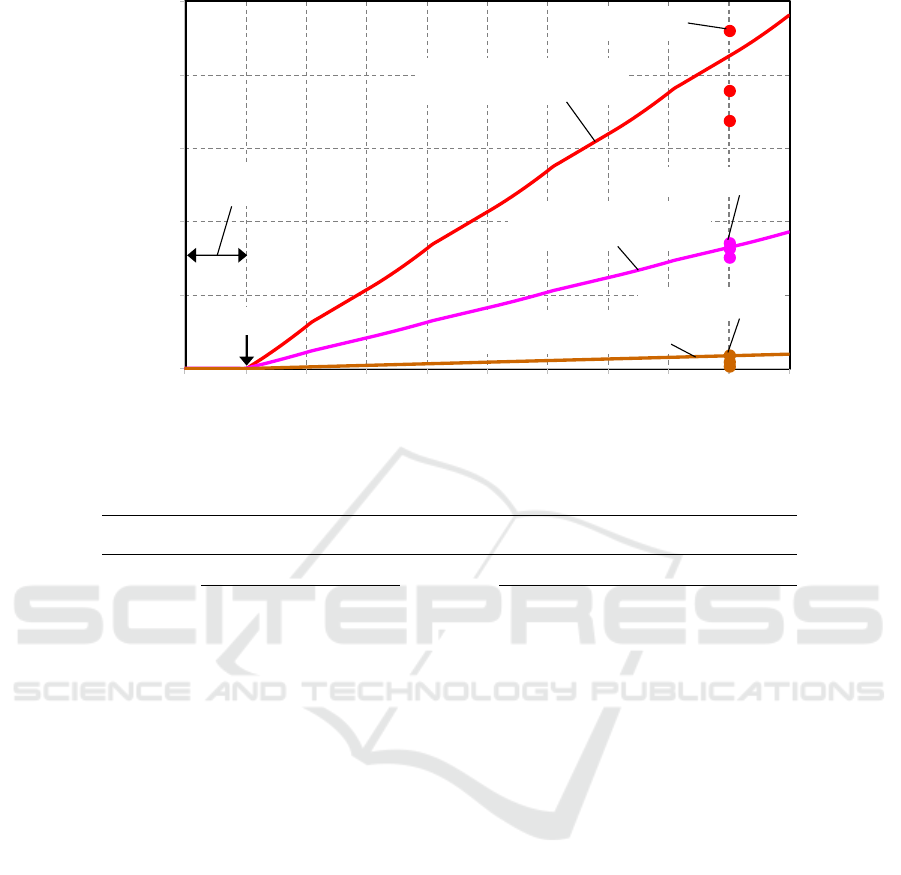
Figure 8: Comparison of the drawing blood between Hybrid Petri nets simulation.
Table 8: Experimental drawing blood data from nine volunteers.
μL for simultaneous biochemical, immune and blood
cell count inspection. It seems be impossible to use
only cuff band for fastening finger. Therefore,we next
try to use the vaccum suction pump concurrently.
4 CONCLUSIONS
Using the hybrid Petri nets simulation with cuff
pressing and puncture modeled as discrete and blood
flow modeled as continuity, we confirmed that the
simulation results were agreement with the
experimental drawing blood data. Consequently, we
confirmed the advantages of using hybrid Petri nets.
Our final target is to make an automatic drawing
blood machine from fingertip. As the next work, we
design the control system of an automatic drawing
blood machine by the optimized simulation results
usung the hybrid Petri nets.
ACKNOWLEDGEMENTS
The part of this study is supported with the research
project of the University of Tokyo COI (Center of
Innovation). The authors would like to thank the
organization of the University of Tokyo COI.
REFERENCES
He, Y. et al., 2006. Computers in Biology and Medicine,
Vol. 36, No.12, pp.1336-1350.
Herajy, M., Heiner, M., 2012. Nonlinear Analysis: Hybrid
Systems, Vol.6, No.4, pp.942–959.
Kumar, V. S., Webster, M., 2016. Clinical Chemistry,
Vol.62, No.5, pp.785-787.
Kuramoto, T., 2007. Comparative Biochemistry and
Physiology, No.148B─3, p.352.
Liang, F. et al., 2015. Journal of Biomechanical
Engineering. Vol.137, No.10, pp.1-12.
Lunze, J. et al., 2001. Control of Complex Cystems. pp. 24-
283.
Maeno, T. et al., 1997. Transactions of the JSME Series C,
Vol.63, No.607, pp.881-888.
Mendoza, G. B. et al., 2012. SIMULATION, Vo.l 88, No.3,
pp.329-347.
Oshima, M. et al., 2001. Computer Methods in Applied
Mechanics and Engineering, Vol.191, No.6, pp.661-671.
Peleg, M. et al., 2005. Journal of the American Medical
informatics Association, Vol.12, No.2, pp.181-199.
Petri, C. A., 1962. Kommunikation mit Automaten. English
Translation, 1966: Communication with Automata,
0
50
100
150
200
250
0 10 20 30 40 50 60 70 80 90 100
V
BD
(μL)
t (s)
Case F4
< Region-1 Cuff Puncture >
Case F5
< Region-2 Cuff Puncture >
Case F3
< Without Cuff Puncture >
Case F4 – Exp.
Case F5 – Exp.
Case F3 – Exp.
Puncture
Increasing
pressure
Age
Sex of nine volunteers
Drawing time
(s)
Classification of nine volunteers
29 - 61
Male Female
90
Case F3 Case F4 Case F5
7 2 3 3 3
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
142

Technical Report RADC-TR-65-377, Rome Air Dev.
Center, New York.
Renganathan, K., Bhaskar, V., 2012. Applied Mathematical
Modelling, Vol. 36, pp. 3941-3947
Shore, A. C., 2000. British Journal of Clinical
Pharmacology, Vol.50, No.6, pp.501-513.
Wu, N. et al., 2010. IEEE Transactions on Systems, Man,
and Cybernetics, Part C (Applications and Reviews),
Vol.40, No.2, pp.159-175.
Yamakoshi, K. et al., 1980. IEEE Transactions on
Biomedical Engineering, Vol.27, pp.150-155.
Yamakoshi, K. et al, 1982, Medical & Biological
Engineering & Computing, Vol.20, pp.307-313.
Application of Hybrid Petri Nets for a Drawing Blood Flow from Fingertip
143
