Indoor Target Tracking using Time Difference of Arrival Measurements
in 3D
Yifan Xie, Seung Hyo Park and Taek Lyul Song
Department of Electronic Systems Engineering, Hanyang University, Ansan, Republic of Korea
Keywords:
TDOA, 3D, Corrleated Measurement Noise, Cholesky, Target Tracking.
Abstract:
Target tracking with time difference of arrival measurements usually encounters the problem of correlated
measurement noises. When the sensor network utilizes the common reference sensor, the covariance matrix
of the correlated measurement noises becomes off-diagonal such that the computational complexity of the
inverse of the covariance matrix as well as the subsequent matrix operations increases proportionally to the
cube of the sensor number. This makes target tracking algorithms inconvenient for practical applications, and
an appropriate measurement noise decorrelation method is required. In multi-sensor environments, the parallel
update and the serial update are applied for exploiting the measurements from different sensors. Although the
two methods deliver the equivalent tracking performances in linear systems, this equivalence does not hold
in nonlinear systems as linearizing the nonlinear functions leads to approximation error. Additionally, the
requirements of the two methods for storage structure and computational resource allocations are different.
This paper presents a target tracking algorithm which integrates the Cholesky decomposition to decorrelate
the measurement noises for the serial update which shows computational efficiency. The tracking performance
is evaluated by estimation accuracy, execution time.
1 INTRODUCTION
With the development of Ultra-wideband (UWB),
indoor target tracking has emerged as a critical
role in civilian and military applications (Taylor,
1994)(Eryildirim and Guldogan, 2016)(Alarifi et al.,
2016). A UWB tracking system consists of multi-
ple spatially distributed sensors and each sensor ex-
ploits the radio signals transmitted from the target to
the sensors independently. The UWB tracking sy-
stems can be classified into different categories ba-
sed on the measurement types: (1) received signal
strength (RSS); (2) time of arrival (TOA); (3) time
difference of arrival (TDOA), etc. The application of
RSS based system is greatly constrained by the sen-
sitivities in channel inconsistency (McCracken et al.,
2013). The TOA based systems though deliver pre-
cise target position estimations, the device mounted
on the target as well as all sensors must be precisely
synchronized that difficult and expensive installations
can be expected (Tuchler et al., 2005). Contrastively
the TDOA based systems perform good accuracy and
only require the reference sensor to be synchronized.
These factors significantly simplifies the installation
requirements and result in its popularity(Alarifi et al.,
2016).
TDOA information is obtained from a wireless
sensor network (WSN) composed of sensors that
collect TOA of target signal. When one sensor is
designated as the common reference sensor in the
WSN, the time difference of arrival measurement
can be obtained by making a difference between two
TOA measurements. Most of the multi-sensor target
tracking algorithm (Hashemipour et al., 1988)(You
et al., 1999)(Gan and Harris, 2001) assume that the
measurement noises from different sensors are uncor-
related as each sensor operates independently. But
due to the common measurement noise of the refe-
rence sensor in the TDOA measurement generation
procedure, the TDOA measurement noises are corre-
lated. The correlated TDOA noise have been discus-
sed in recent literatures (Ho and Chan, 1993)(Kaune
et al., 2011)(Kim et al., 2012). However (Kaune et al.,
2011) mainly addresses the target geolocation pro-
blem, the other problems such as the noise decorre-
lation and the target tracking are not investigated. In
(Kim et al., 2012), the Gram-Charlier orthogonaliza-
tion procedure is applied for noise decorrelation. Ad-
ditionally, (Kim et al., 2012) models the TDOA me-
asurement uncertainty more precisely by approxima-
ting the measurement likelihood to a Gaussian mix-
ture such that better estimation results are achieved
380
Xie, Y., Park, S. and Song, T.
Indoor Target Tracking using Time Difference of Arrival Measurements in 3D.
DOI: 10.5220/0006882903800387
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 380-387
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

at the cost of computational resource and memory
storage.
The algorithms of incorporating measurements
from several sensors for target tracking usually apply
two methods: parallel update and serial update (Bar-
Shalom et al., 2011). These two methods are mathe-
matically equivalent and have the same tracking per-
formances in linear systems when the clutter measure-
ments are not involved (Pao and Frei, 1995)(Pao and
Trailovic, 2000). This equivalence does not hold in
nonlinear systems as linearizing the nonlinear functi-
ons leads to approximation error. The parallel update
stacks all measurements from different sensors into
an augmented measurement vector. The state is up-
dated simultaneously with the stacked vector that all
measurements are utilized at once. The serial update
utilizes the measurement from one sensor at a time.
For nonlinear measurements, the order of updating is
suggested to start from the measurement collected by
the most accurate sensor to reduce the subsequent li-
nearization errors(Duan et al., 2005)(Xie et al., 2016).
In this paper, the Cholesky decomposition (Bar-
Shalom et al., 2004)(Duan et al., 2004)(Duan et al.,
2005) is applied to transform the correlated TDOA
noise into an equivalent one with uncorrelated TDOA
noise. The decomposition matrix is utilized to cre-
ate pseudo measurements and pseudo Jacobian matrix
such that the target tracking can be implemented un-
der uncorrelated noise situation. For computational
efficiency, the serial update operates with pseudo me-
asurements and pseudo Jacobian matrix is proposed
in this paper.
The rest of the paper is organized as follows.
Statements for the state vector formulation and the
TDOA measurement generation are described in
Section 2. Section 3 gives brief descriptions for
the Cholesky decomposition method which is utili-
zed for noise decorrelation. The target tracking met-
hods using decorrelated TDOA measurements for the
parallel update and the serial update are discussed in
Section 4. Simulation study is given in Section 5, fol-
lowed by the concluding remarks in Section 6.
2 PROBLEM STATEMENTS
In this section, state vectors for the target and sensors,
as well as the correlations between TDOA measure-
ments are presented.
2.1 State Vector
The target dynamics are modeled linear Gaussian in
Cartesian coordinates. Under the additive noise as-
sumption, the target kinematic at scan k is defined by
x
k
= F
k
x
k−1
+ ω
k
, (1)
where x
k
= [x
k
y
k
z
k
˙x
k
˙y
k
˙z
k
]
T
is the target state vector
with a position component [x
k
y
k
z
k
]
T
and a velocity
component [ ˙x
k
˙y
k
˙z
k
]
T
, F
k
is the transition matrix, and
ω
k
is the white Gaussian process noise with zero mean
and covariance matrix Q
k
.
In a sensor network with M sensors, the sensors
are stationary with known positions and passively re-
ceive the signal emitted from the target. The state vec-
tor of the i-th sensor is x
i
k
= [x
i
k
y
i
k
z
i
k
0 0 0]
T
. A TDOA
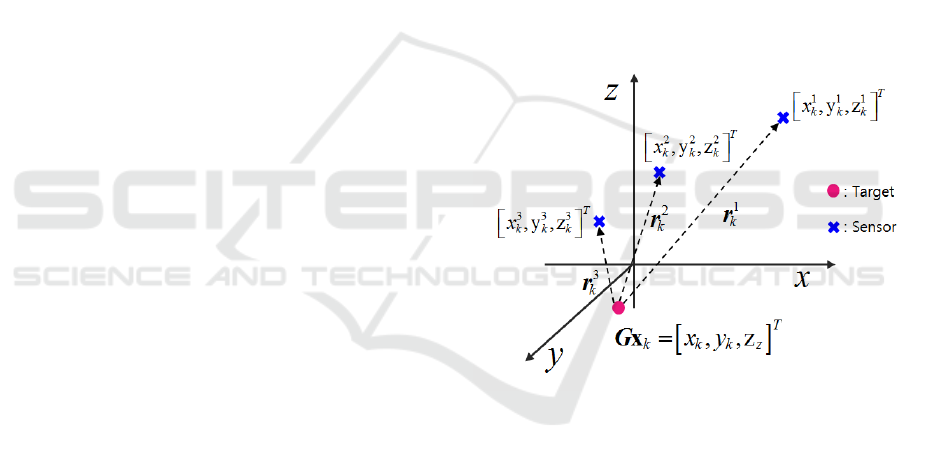
scenario is exemplified in Fig. 1, where
G =

I
3
0
3

(2)
is the position projection matrix, I
n
and 0
n
denote the
n ×n identity and zero matrices respectively. The dis-
tance vector between the target and the i-th sensor is
r
k,i
= Gx
k
−Gx
i
k
, and ||r
k,i
|| is the corresponding Eu-
clidean distance.
Figure 1: A TDOA scenario with 3 sensors.
2.2 TDOA Measurement
Denote sensor s
i
(i = 1,..., M) noise as u
k,i
with stan-
dard deviation σ
i
and sensor s
1
is utilized as reference
sensor. The TDOA measurement in time domain can
be translated into a range difference by multiplying
with the speed of light and is given by
z
k,i
= (||r
k,i
||−||r
k,1
||) + (u
k,i
−u
k,1
) (3)
= h
i
(x
k
) + ν
k,i
, i = 2, 3,...,M (4)
where
h
i
(x
k
) = ||r
k,i
||−||r
k,1
||, (5)
ν
k,i
= u
k,i
−u
k,1
, (6)
ν
k,i
is the TDOA measurement noise, ν
k,i
∼
N (0,σ
2
1,i
) and σ
2
1,i
= σ
2
1
+ σ
2
i
.
Indoor Target Tracking using Time Difference of Arrival Measurements in 3D
381

At each scan k, M −1 TDOA measurements are
generated from M passive sensors, which can be given
in a stack form of
z
k
= [z
k,2
z
k,3
···z
k,M
]
T
. (7)
The measurement equation for z
k
is given by
z
k
= h(x
k
) + ν
k
, (8)
h(x
k
) = [h
2
(x
k
) h
3
(x
k
) ··· h
M
(x
k
)]
T
, (9)
ν
k
= [ν
k,2
ν
k,3
··· ν
k,M
]
T
, (10)
where ν
k
∼N (0,R
k
) and R
k
is the covariance matrix.
Due to the fact that all TDOA measurements are
created under a common reference sensor, the TDOA
measurements are correlated and the relevant cova-
riance matrix becomes off-diagonal (Kaune et al.,
2011). The covariance matrix R
k
is given by
R
k
= E[ν
k
ν
T
k
] =





σ
2
1,2
σ
2
1
··· σ
2
1
σ
2
1
σ
2
1,3
··· σ
2
1
.
.
.
.
.
.
.
.
.
.
.
.
σ
2
1
σ
2
1
··· σ
2
1,M





. (11)
Assume that all sensors are homogeneous with the
same standard deviation of sensor noise σ
u
, then eq
(11) becomes
R
k
= 2σ
2
u




1 0.5 ··· 0.5
0.5 0.5 ··· 0.5
.
.
.
.
.
.
.
.
.
.
.
.
0.5 0.5 ··· 1




, 2σ
2
u
Ω
k
, (12)
where matrix Ω
k
is utilized for the TDOA measure-
ment decorrelation in Section 3.
3 TDOA NOISE
DECORRELATION
The covariance matrix R
k
is off-diagonal and one can
apply a linear transformation to diagonalize it. Since
R
k
is a real-valued symmetric positive-definite matrix,
this transformation can be implemented by Cholesky
decomposition (Bar-Shalom et al., 2004) and yields
R
k
= L
k
Λ
k
L
T
k
, (13)
where L
k
is a unit lower triangular matrix, Λ
k
=
2σ
2
u
I
M−1
and I
n
denotes an n ×n identity matrix. De-
note the (m,n)th elements in Ω
k
and L
k
as Ω
(m,n)
k
and
L
(m,n)
k
, respectively. The decomposition matrix L
k
is
calculated by
L
(m,n)
k
=







q
Ω
(m,n)
k
−
∑
n−1
j=1
(L
(n, j)
k
)
2
, m = n;

Ω
(m,n)
k
−
∑
n−1
j=1
L
(m, j)
k
L
(n, j)
k

/L
(n,n)
k
, m > n;
0, otherwise.
As a consequence, the correlated TDOA measure-
ment noise is transformed into an equivalent pseudo
form with uncorrelated noise.
According to eqs (12) and (13), the covariance
matrix R
k
can be transformed into a form of
R
k
= L
k
E[I
u
I
T
u
]L
T
k
, (14)
together with eq (11) we can get
ν
k
= L
k
I
u
. (15)
The stacked TDOA measurement z
k
in eq (8) can
be rewritten as
z
k
= h(x
k
) + L
k
I
u
. (16)
Multiplying both sides of eq (16) with L
−1
k
, the
pseudo measurement z
p
k
can be obtained by
z
p
k
= L
−1
k
z
k
(17)
= L
−1
k
h(x
k
) + I
u
. (18)
Then I
u
becomes the pseudo measurement noise and
follows
I
u
∼
√
2




N (0,σ
u
)
N (0,σ
u
)
.
.
.
N (0,σ
u
)




. (19)
The covariance matrix of I
u
is equivalent to Λ
k
, which
is diagonal and the pseudo measurement z
p
k
is uncor-
related.
The Jacobian matrix of function h(x
k
) is given by
H
k
=
∂h(x
k
)
∂x
k
. (20)
Similarly, multiplying both sides of eq (20) with L
−1
k
,
the pseudo Jacobian matrix is defined by
H
p
k
= L
−1
k
H
k
. (21)
4 TRACKING WITH
DECORRELATED TDOA
MEASUREMENTS
In this paper, an extend Kalman filter (EKF) is applied
for target tracking with decorrelated TDOA measure-
ments. Before the start of the EKF tracking recursion,
the target should be localized based on the TDOA me-
asurements received at the first scan for track initiali-
zation. After track initialization, the standard EKF
prediction formulae are applied for track propagation.
In the EKF update, the standard measurement and the
Jacobian matrix are replaced by the pseudo ones for
track status update. A flowchart of tracking procedure
is illustrated in Fig. 2.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
382

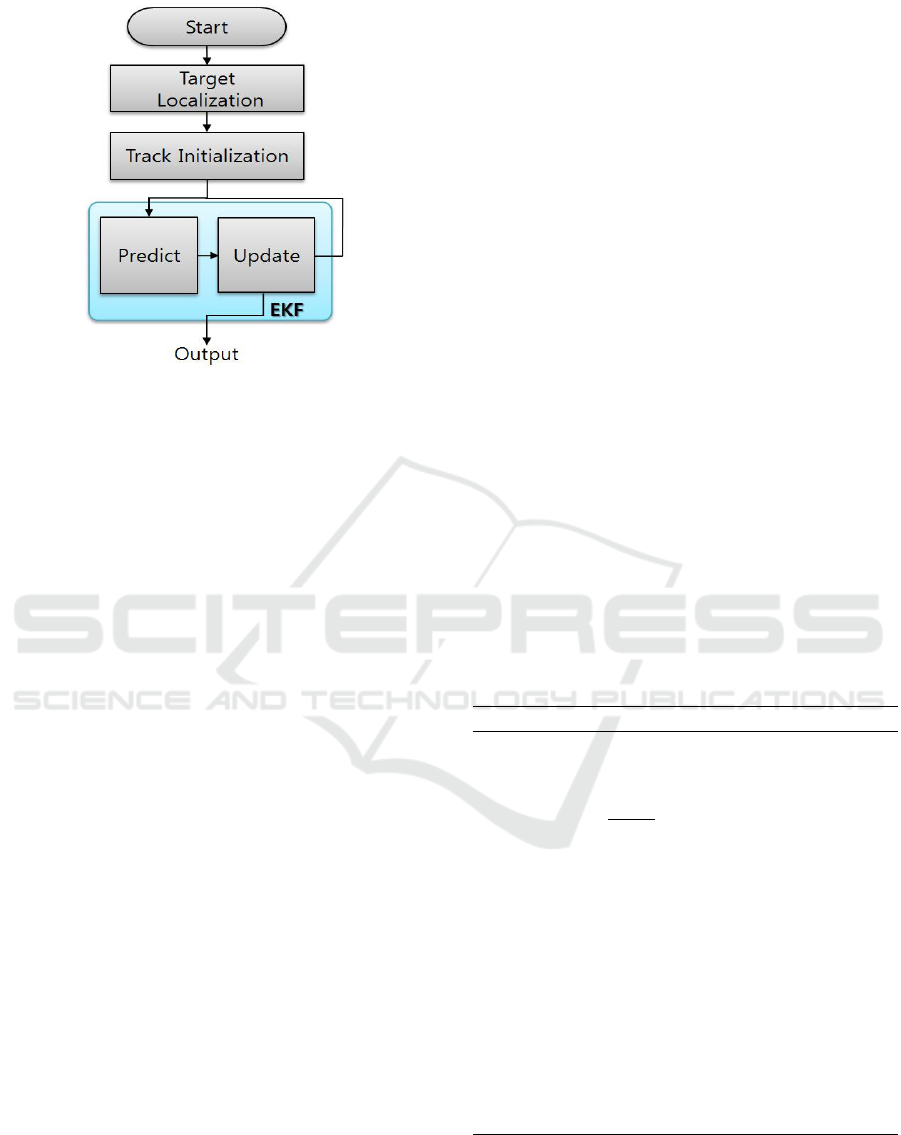
Figure 2: Flowchart of target tracking.
4.1 Track Initialization
The method in (Gillette and Silverman, 2008) of 3D
geo-location using TDOA only measurements, which
claims the initial target position can be localized ef-
fectively when at least 5 sensors are provided, is ap-
plied in this paper. The localized target positions
[ ˆx
0
ˆy
0
ˆz
0
]
T
in three-dimension are further utilized for
one-point track initialization (Challa et al., 2011).
The initial track is parameterized by a initial mean
of the target state x
0
and initial covariance matrix P
0
which are denoted as
x
0
= [ ˆx
0
ˆy
0
ˆz
0
0 0 0]
T
, (22)
P
0
=

2σ
2
u
I
3
0
3
0
3
v
2
max
I
3
/3

, (23)
where v
max
is the maximum target velocity determi-
ned by the designers. The initialized track is used as
an input for the EKF recursion.
4.2 Parallel Update
In the parallel update, the track state is updated si-
multaneously with the stacked measurement z
k
. The
updated state is defined by its mean ˆx
k
and covariance
ˆ
P
k
. The input is a predicted state defined by its mean
¯x
k
and covariance
¯
P
k
:
ˆx
k
= ¯x
k
+ K
k
(z
k
−h(¯x
k
)), (24)
ˆ
P
k
=
¯
P
k
−K
k
H
k
¯
P
k
, (25)
with
S
k
= H
k
¯
P
k
H
T
k
+ R
k
, (26)
K
k
=
¯
P
k
H
T
k
S
−1
k
, (27)
where S
k
is the predicted measurement error covari-
ance with (M −1) ×(M −1) dimension, K
k
is the fil-
ter gain with 6 ×(M −1) dimension.
4.3 Serial Update
Apparently the matrix size in the parallel update in-
creases with the sensor number, which not only com-
plicates the matrix operations but also requires more
memory storages. But in practical applications, the
computational resources in the UWB target tracking
systems may not be able to support large-scale ma-
trix operations especially for inverse and multiplica-
tion. In addition, the oversize matrices such as S
k
and
K
k
also bring heavy storage burden such that practi-
cal implementations can be hardly realized. Contras-
tively the serial update does not operate on the en-
tire stacked pseudo measurement z
p
k
simultaneously,
but update with every element in z
p
k
iteratively. As
a consequence, the reductions in both computational
resource and memory storage can be expected.
In the m-th iteration of serial update, the pseudo
Jacobian matrix, the pseudo measurement and the
predicted measurement are denoted as H
p
k,m
, z
p
k,m
and
¯z
k,m
, respectively. The (m,n)th element in L
−1
k
is de-
noted as L
−1
k
(m,n). The updated track state is de-
fined by mean ˆx
k,m
and covariance
ˆ
P
k,m
, which are
further regarded as the predict mean and covariance
for the next iteration. The iteration proceeds until
the exhaustiveness of pseudo measurements. The
pseudo-code for serial EKF update is shown in Algo-
rithm 1, where matrices S
k,m
and K
k,m
reduce to sizes
of 1 ×1 and 6 ×1 compared to S
k
and K
k
.
Algorithm 1: Serial EKF update.
1: for m = 1 : M −1 do
2: H
p
k,m
= [0 0 0 0 0 0], ¯z
k,m
= 0, z
p
k,m
= 0
3: for n = 1 : m do
4: H
k,n
=
∂h
n
(x
k
)
∂x
k
|
x
k
=¯x
k
5: H
p
k,m
= H
p
k,m
+ L
−1
k
(m,n)H
k,n
6: ¯z
k,m
= ¯z
k,m
+ L
−1
k
(m,n)h
n
(¯x
k
)
7: z
p
k,m
= z
p
k,m
+ L
−1
k
(m,n)z
k,n
8: end for
9: S
k,m
= H
p
k,m
¯
P
k
(H
p
k,m
)
T
+ 2σ
2
u
10: K
k,m
=
¯
P
k
(H
p
k,m
)
T
S
−1
k,m
11: ˆx
k,m
= ¯x
k
+ K
k,m

z
p
k,m
−¯z
k,m

12:
ˆ
P
k,m
=
¯
P
k
−K
k,m
H
p
k,m
¯
P
k
13: ¯x
k
= ˆx
k,m
14:
¯
P
k
=
ˆ
P
k,m
15: end for
4.4 Implementation Issues
The application of the Cholesky decomposition does
not bring complicate matrix operations such as the
Indoor Target Tracking using Time Difference of Arrival Measurements in 3D
383

matrix inverse of L
k
. It is shown that the inverse of
Cholesky decomposition matrix L
k
of the correlated
measurement noise can be predetermined and the ele-
ments L
−1
k
(m,n) of L
−1
k
are invariant as the total sen-
sor number M in one network is fixed. Therefore the
elements L
−1
k
(m,n) can be pre-calculated off-line and
stored in the memory. When L
−1
k
(m,n) is involved
in the calculations of H
p
k,m
, z
p
k,m
and ¯z
k,m
, the rele-
vant data can be read from the memory and utilized
immediately such that computational load is relieved.
Contrastively the parallel update utilizes an augmen-
ted measurement vector which stacks all the available
TDOA measurements for track update. This not only
brings more burden for storage management but also
makes it computationally inefficient since the matrix
operations for high dimensions are much more intrac-
table.
Additionally, the serial update exhibits advantages
in practical implementations. Since the sensor mea-
suring performance can be affected by signal interfe-
rence or glint noise, a part of all sensor measurements
are selected for tracking performance optimality. As
a consequence, the number of validated sensors beco-
mes time variant. The matrix size in parallel update
has to be modified accordingly in time. However, the
only modification in serial update is the iteration num-
ber, which shows more conveniences for practical in-
stallations.
As the computational efficiency is important in
practical applications, the computational load domi-
nates the criterion of update scheme selection while
the tracking performances are similar. The serial up-
date utilizes the measurement from one sensor at a
time that the computations in one iteration can be sig-
nificantly reduced since the high dimensional matrix
operations are avoided. The serial update also enables
to distribute the computations uniformly according to
the TDOA measurement number as shown in Fig. 3.
The iteration number can be flexibly adjusted that a
trade-off between the tracking performance and com-
putational requirements as long as the target observa-
bility is satisfied, i.e., the iteration number should be
at least 3.
5 SIMULATION
In this simulation, the sensor network is composed of
M = 8 homogeneous sensors with 1 ns sensor noise
(σ
u
= 0.3 m). Each sensor receives the signal from
the target periodically with a frequency of f
0
= 30 Hz.
The sensors are divided into two groups (the first layer
and the second layer) and mounted on different altitu-
des for target height estimation. In order to improve
Figure 3: An example of computation distributions of pa-
rallel update and serial update.
target observability condition, the sensors at two lay-
ers are mounted at different positions in x and y axes
as shown in Fig. 4. The length, width and height of
the surveillance region are 25 m, 12 m and 15 m, re-
spectively.
Figure 4: An example of target to sensors geometry in the
UWB target tracking system.
For target tracking using TDOA measurements,
the Cramer-Rao lower bound (CRLB) (Yang and
Scheuing, 2006)(Lui and So, 2009)(Isaacs et al.,
2009) indicates the best theoretical performance of fil-
ters for the root mean squared error (RMSE) metric.
The CRLB value at scan k can be calculated by
CRLB
k
=
q
J
−1
k
(1,1) + J
−1
k
(2,2) + J
−1
k
(3,3), (28)
and J
−1
k
(i, j) indicates the (i, j)th element in the in-
verse of the Fisher information matrix J
k
where
J
k
= H
T
k
R
−1
k
H
k
. (29)
In order to evaluate if the sensors are placed properly,
a CRLB distribution is mapped by a collection of the
CRLB values over all positions. In the CRLB distri-
bution of the scenario, the x −y plane is turned into a
grid with a scale of 0.2 m. The height of the emitter
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
384

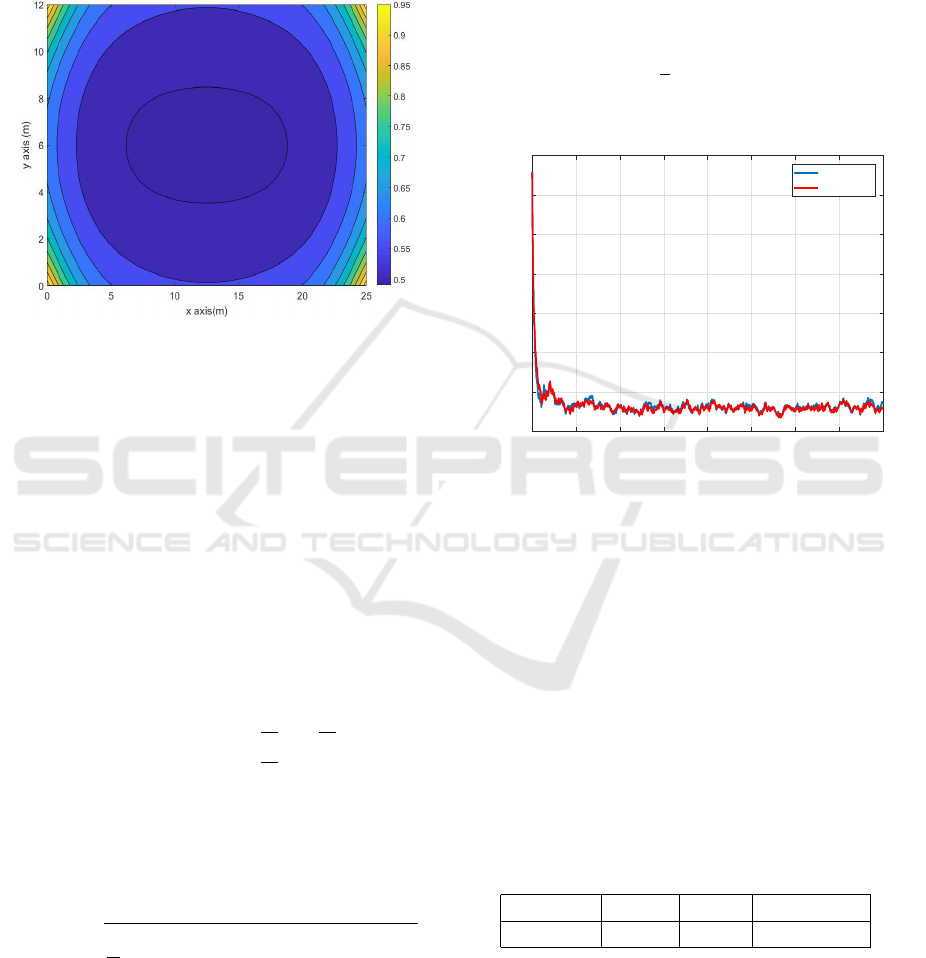
equipped on the target is set to be at 1.4 m. Sensor
s
1
is predefined as the reference sensor. The result
in Fig. 5, in which most of the surveillance area is
shadowed in blue, suggests that the theoretical esti-
mation error is small and the sensors are deployed ap-
propriately.
Figure 5: CRLB of the TDOA scenario.
To validate the effectiveness of the proposed ap-
proach, the EKF for target tracking using decorrelated
TDOA measurements (D-EKF) with different update
schemes are simulated. The simulation results obtai-
ned from the parallel update and the serial update are
denoted as EKF parallel and D-EKF serial, respecti-
vely. The simulation tests N = 100 Monte Carlo runs
and the total simulated time in one run is 40 s. The
sampling time is T
s
= 1/ f
0
. Sensor s
1
performs as
the reference sensor and all the other sensor measure-
ments are assumed to be available in the entire simu-
lated time. The target starts from an initial position
[0 6 -13.6]
T
m and moves with speed [0.5 0 0]
T
m/s
and follows the dynamics of (1) with
F
k
=

I
3
T
s
I
3
0
3
I
3

, Q
k
= σ
2
ω
"
T
4
s
4
I
3
T
3
s
2
I
3
T
3
s
2
I
3
T
2
s
I
3
#
, (30)
where the standard deviation of the process noise is
σ
ω
= 0.707 m/s
2
. The tracking performance is eva-
luated by RMSE, which indicates the accuracy of the
estimated target trajectory. The RMSE in position at
scan k is given by
RMSE
k
=
v
u
u
t
1
N
N
∑
n=1

(x
k
− ˆx
k
)
2
n
+ (y
k
− ˆy
k
)
2
n
+ (z
k
− ˆz
k
)
2
n

.
(31)
As can be seen in Fig. 6, the RMSE curves
for EKF parallel and D-EKF serial indicate that the
tracking performances are similar. The RMSE cur-
ves also demonstrates that the parallel update and the
serial update cannot achieve identical results in non-
linear systems. In the parallel update, H
p
k
is the li-
nearization of the nonlinear function h(x
k
) and is cal-
culated by differentiating w.r.t the predicted state ¯x
k
.
In the serial update, the predicted state ¯x
k
changes
at each iteration, which leads to a different lineariza-
tion error compared with the parallel update. Conse-
quently, the tracking performance of the parallel up-
date becomes different from the serial update. The
averaged RMSE of is around 0.15 m that the TDOA
measurement noise (
√
2σ
u
≈ 0.42 m) is filtered ef-
fectively and the target trajectory is estimated accura-
tely.
0 5 10 15 20 25 30 35 40
Time(sec)
0
0.2
0.4
0.6
0.8
1
1.2
1.4
RMSE(m)
EKF parallel
D-EKF serial
Figure 6: RMSE comparison.
The simulation studies are conducted on a Win-
dows 7 platform (Intel i7-6700 CPU, 16.0 GB RAM)
and run with the MATLAB program. The execu-
tion time comparison in Table 1 reveals that the pa-
rallel update method requires more execution time
(even cannot operate in real-time regarding to T
s
≈
0.0333 sec) compared to the serial update, which ma-
kes it inappropriate for practical installations. By
avoiding the complicate matrix operations in high
matrix dimensions and utilizing the sensor measure-
ments sequentially, the serial update enables to ope-
rate in real-time while distributes the computational
load uniformly.
Table 1: Execution time for one sampling interval (T
s
=
1/ f
0
≈ 0.0333 sec).
Method Parallel Serial One iteration
Time (sec) 0.0534 0.0125 0.0017
6 CONCLUSION
This paper presents an effective method which utili-
zes the serial update and the Cholesky decomposi-
Indoor Target Tracking using Time Difference of Arrival Measurements in 3D
385

tion for target tracking with the multi-sensor TDOA
measurements under the correlated measurement noi-
ses condition. The serial update scheme, which not
only consumes less memory storages but also less
computational resources, is adopted in this paper. To
obtain an equivalent transformation from the parallel
update to the serial update, the inherent correlation
between TDOA measurement noise should be appro-
priately considered. In the proposed D-EKF, the Cho-
lesky decomposition is applied to convert the correla-
ted noise into an pseudo uncorrelated one for the EKF
serial update. The simulation result shows that simi-
lar tracking performances are obtained under different
execution time, which demonstrates the computatio-
nal efficiency of the proposed method.
ACKNOWLEDGEMENT
This work was conducted at High-speed Vehicle Re-
search Center of KAIST with the support of De-
fense Acquisition Program Administration (DAPA)
and Agency for Defense Development (ADD).
REFERENCES
Alarifi, A., Al-Salman, A., Alsaleh, M., Alnafessah, A.,
Al-Hadhrami, S., Al-Ammar, M. A., and Al-Khalifa,
H. S. (2016). Ultra wideband indoor positioning
technologies: Analysis and recent advances. Sensors,
16(5):707.
Bar-Shalom, Y., Li, X. R., and Kirubarajan, T. (2004). Esti-
mation with applications to tracking and navigation:
theory algorithms and software. John Wiley & Sons.
Bar-Shalom, Y., Willett, P. K., and Tian, X. (2011).
Tracking and data fusion. YBS publishing.
Challa, S., Mu
ˇ
sicki, D., Morelande, M. R., and Evans, R. J.
(2011). Fundamentals of object tracking.
Duan, Z., Han, C., and Tao, T. (2004). Optimal multi-
sensor fusion target tracking with correlated measure-
ment noises. In Systems, Man and Cybernetics, 2004
IEEE International Conference on, volume 2, pages
1272–1278. IEEE.
Duan, Z., Li, X. R., Han, C., and Zhu, H. (2005). Sequen-
tial unscented Kalman filter for radar target tracking
with range rate measurements. In Information Fusion,
2005 8th International Conference on, volume 1, pa-
ges 8–pp. IEEE.
Eryildirim, A. and Guldogan, M. B. (2016). A Gaussian
mixture Bernoulli filter for extended target tracking
with application to an ultra-wideband localization sy-
stem. Digital Signal Processing, 57:1–12.
Gan, Q. and Harris, C. J. (2001). Comparison of two measu-
rement fusion methods for Kalman-filter-based multi-
sensor data fusion. IEEE Transactions on Aerospace
and Electronic systems, 37(1):273–279.
Gillette, M. D. and Silverman, H. F. (2008). A linear
closed-form algorithm for source localization from
time-differences of arrival. IEEE Signal Processing
Letters, 15:1–4.
Hashemipour, H. R., Roy, S., and Laub, A. J. (1988). De-
centralized structures for parallel Kalman filtering.
IEEE Transactions on Automatic Control, 33(1):88–
94.
Ho, K. and Chan, Y. (1993). Solution and performance ana-
lysis of geolocation by TDOA. IEEE Transactions on
Aerospace and Electronic Systems, 29(4):1311–1322.
Isaacs, J. T., Klein, D. J., and Hespanha, J. P. (2009). Op-
timal sensor placement for time difference of arri-
val localization. In Decision and Control, 2009 held
jointly with the 2009 28th Chinese Control Confe-
rence. CDC/CCC 2009. Proceedings of the 48th IEEE
Conference on, pages 7878–7884. IEEE.
Kaune, R., H
¨
orst, J., and Koch, W. (2011). Accuracy analy-
sis for TDOA localization in sensor networks. In In-
formation Fusion (FUSION), 2011 Proceedings of the
14th International Conference on, pages 1–8. IEEE.
Kim, W. C., Song, T. L., and Mu
ˇ
sicki, D. (2012). Mo-
bile emitter geolocation and tracking using correlated
time difference of arrival measurements. In Informa-
tion Fusion (FUSION), 2012 15th International Con-
ference on, pages 700–706. IEEE.
Lui, K. W. and So, H.-C. (2009). A study of two-
dimensional sensor placement using time-difference-
of-arrival measurements. Digital Signal Processing,
19(4):650–659.
McCracken, M., Bocca, M., and Patwari, N. (2013). Joint
ultra-wideband and signal strength-based through-
building tracking for tactical operations. In Sensor,
Mesh and Ad Hoc Communications and Networks
(SECON), 2013 10th Annual IEEE Communications
Society Conference on, pages 309–317. IEEE.
Pao, L. Y. and Frei, C. W. (1995). A comparison of pa-
rallel and sequential implementations of a multisensor
multitarget tracking algorithm. In American Control
Conference, Proceedings of the 1995, volume 3, pa-
ges 1683–1687. IEEE.
Pao, L. Y. and Trailovic, L. (2000). The optimal order of
processing sensor information in sequential multisen-
sor fusion algorithms. IEEE Transactions on Automa-
tic Control, 45(8):1532–1536.
Taylor, J. D. (1994). Introduction to ultra-wideband radar
systems. CRC press.
Tuchler, M., Schwarz, V., and Huber, A. (2005). Location
accuracy of an UWB localization system in a multi-
path environment. In Ultra-Wideband, 2005. ICU
2005. 2005 IEEE International Conference on, pages
414–419. IEEE.
Xie, Y., Lee, H., Ahn, M., Lee, B. J., and Song, T. L.
(2016). Joint integrated track splitting for multi-sensor
multi-target tracking in clutter. In Proceedings of
the 13th International Conference on Informatics in
Control, Automation and Robotics, pages 299–307.
SCITEPRESS-Science and Technology Publications,
Lda.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
386

Yang, B. and Scheuing, J. (2006). A theoretical analy-
sis of 2D sensor arrays for TDOA based localization.
In Acoustics, Speech and Signal Processing, 2006.
ICASSP 2006 Proceedings. 2006 IEEE International
Conference on, volume 4, pages 901–904. IEEE.
You, H., Dajin, L., and Yingning, P. (1999). State estimation
for multilevel multisensor data fusion systems. ACTA
ELECTRONICA SINICA, page 08.
Indoor Target Tracking using Time Difference of Arrival Measurements in 3D
387