Investigating the Effect of Software Metrics Aggregation on Software

Fault Prediction

Deepanshu Dixit

and Sandeep Kumar

Department of Computer Science and Engineering, Indian Institute of Technology Roorkee, Roorkee, India

Keywords:

Software Fault Prediction, Aggregation of Software Metrics, Average Absolute Deviation, Interquartile Range.

Abstract:

In inter-releases software fault prediction, the data from the previous version of the software that is used for

training the classiﬁer might not always be of same granularity as that of the testing data. The same scenario

may also happen in the cross project software fault prediction. So, one major issue in it can be the difference

in granularity i.e. training and testing datasets may not have the metrics at the same level. Thus, there is

a need to bring the metrics at the same level. In this paper, aggregation using Average Absolute Deviation

(AAD) and Interquartile Range (IQR) are explored. We propose the method for aggregation of metrics from

class to package level for software fault prediction and validated the approach by performing experimental

analysis. We did the experimental study to analyze the performance of software fault prediction mechanism

when no aggregation technique was used and when the two mentioned aggregation techniques were used.

The experimental study revealed that the aggregation improved the performance and out of AAD and IQR

aggregation techniques, IQR performs relatively better.

1 INTRODUCTION

Software fault prediction mechanism predicts

whether the software module is faulty or not before

applying the testing mechanism. More testing efforts

are made in a module which is predicted as faulty as

compared to the one predicted as non faulty (Rathore

and Kumar, 2017). In many software systems like

banking, ﬁnancial systems, medical systems, satellite

systems, etc., if any bug is left undetected then severe

damages can be caused. Hence, testing is indeed

very important phase in the development of such

software systems (Arar and Ayan, 2016). In cases of

inter-releases software fault prediction, the data from

the previous version of the software that is used for

training the classiﬁer might not always be of same

granularity as that of the testing data, which can be

a major issue. The same scenario may also happen

in the cross project fault prediction. Thus, there is a

need to bring the metrics at the same level. In this

paper, the software metrics available at the class level

are aggregated to package level by computing the

AAD and IQR values of the metrics at the class level.

Generally, the metrics used for the fault pre-

diction mechanism are LOC (Line Of Codes), Mc-

Cabes metrics, Halsteads metrics, Chidamber and Ke-

merer(C&K) metrics, etc. (Honglei et al., 2009)

and the common machine learning techniques used

are naive bayes (Yang et al., 2017), (Turhan et al.,

2013), logistic regression (Arar and Ayan, 2016),

(Zhao et al., 2017), artiﬁcial neural network (Kumar

et al., 2017), (Erturk and Sezer, 2015), support vec-

tor machine (Erturk and Sezer, 2015), decision tree

(Ghotra et al., 2015), random forest (Kamei and Shi-

hab, 2016), etc. In this paper, three machine learn-

ing techniques have been used: logistic regression

(Arar and Ayan, 2016), (Zhao et al., 2017), support

vector machine (Erturk and Sezer, 2015) and deci-

sion tree (Ghotra et al., 2015). Four different perfor-

mance evaluation measures, i.e., accuracy, precision,

recall and F-measure (Arar and Ayan, 2016), (Turhan

et al., 2013), (Kumar et al., 2017), (Kamei and Shi-

hab, 2016) have been used for performance analysis.

Datasets from the publicly available PROMISE data

repository (Menzies et al., 2015) have been used for

experimentation.

Following are the contributions of our work:

• Use of Average Absolute Deviation (AAD) and

Interquartile Range (IQR) based aggregation for the

software metrics are explored. Mostly the aggrega-

tion techniques explored in different works in the ﬁeld

of software fault prediction are sum, mean, median,

maximum, standard deviation, Gini index, Theil in-

dex, Atkinson index and Hoover index, while AAD

304

Dixit, D. and Kumar, S.

Investigating the Effect of Software Metrics Aggregation on Software Fault Prediction.

DOI: 10.5220/0006884003040311

In Proceedings of the 13th International Conference on Software Technologies (ICSOFT 2018), pages 304-311

ISBN: 978-989-758-320-9

and IQR have not yet been explored in this ﬁeld.

• Aggregation of metrics directly from class level

to package level are presented.

• Experimental investigation is done to compare

fault prediction mechanism with and without apply-

ing aggregation technique.

• Performance of learning models, logistic regres-

sion, support vector machine and decision tree are

compared in both the scenarios, with and without ag-

gregation.

Following research questions can be answered

based upon the experimental results obtained in this

work:

RQ1: How does logistic regression, support vec-

tor machine, and decision tree based learning models

perform in without aggregation and with aggregation

scenarios?

RQ2: How does aggregation of metrics affect the

performance of software fault prediction?

RQ3: Out of AAD and IQR, which method of ag-

gregation for metrics produces better results with ref-

erence to software fault prediction ?

Rest of the paper is organized as follows. Section

2 presents the related work. Section 3 presents the

proposed methodology. Section 4 describes the ex-

perimental setup. The results and the corresponding

observations of the experiments conducted in this pa-

per are given in Section 5. Threats to validity are pre-

sented in Section 6, followed by conclusion in Section

2 RELATED WORKS

(Zhang et al., 2017) addressed the problem of differ-

ence in granularity, i.e., the difference in the levels

at which software metrics are collected. They aggre-

gated the data metrics from method level to ﬁle level.

They analyzed eleven aggregation techniques on 255

open source projects. Experiments were conducted

using ten-fold cross validation technique. Four defect

prediction models were dealt with: defect proneness

model, defect rank model, defect count model and ef-

fort aware model. (Zimmermann et al., 2007) worked

on three releases of publicly available eclipse datasets

and mapped the packages and classes to the number

of bugs that were reported before and after the release.

They used version archives and bug tracking systems

to ﬁnd the failed modules in the system. In the soft-

ware fault prediction mechanism, they computed the

metrics at method, class and ﬁle level and aggregated

them to higher levels, i.e., ﬁle and package level us-

ing average, total and maximum values of the metrics.

(Herzig, 2014) used summation, median, mean and

maximum value as the metric aggregation techniques

in software fault prediction mechanism in his work.

(Posnett et al., 2011) used summation while (Koru

and Liu, 2005) used minimum, maximum, summa-

tion and average for the aggregation of metrics in

software fault prediction in their works. According

to (Vasilescu et al., 2011), the software metrics are

generally collected at the micro level such as method,

class and package level. In order to have a view from

the macro level, i.e., system level, these metrics have

to be aggregated. In this paper, the traditional and

econometric aggregation techniques are studied to an-

alyze the correlations amongst them. (Serebrenik and

van den Brand, 2010) were the ﬁrst to apply a fa-

mous econometric measure of inequality, Theil index,

in the ﬁeld of software metric aggregation. Theil in-

dex has been used to get important insights in organ-

isation, software system evolution and in sources of

inequality. (Mordal-Manet et al., 2011) used mean,

(Walter et al., 2016) used mean, standard deviation,

Gini index, Theil index, Atkinson index, Kolm index,

Hoover index and mean logarithmic deviation while

(Ivan et al., 2015) used summation and product for

metric aggregation in software quality model. (Sanz-

Rodriguez et al., 2011) used weighted mean, the Cho-

quet integral and multiple linear regression for the ag-

gregation of metrics to analyze the effect of aggre-

gation in selecting the reusable educational materials

from repositories on the web. (Vasa et al., 2009) ap-

plied Gini index as the aggregation technique to study

the effect on the information the metrics give about

the software system. Most of these available works

present sum, mean, median, maximum, standard de-

viation, Gini index, Theil index, Atkinson index and

Hoover index as the aggregation methods and only a

few of them have used aggregation in software fault

prediction. However, to the best of our knowledge,

AAD and IQR aggregation methods have not been

explored so far for software fault prediction. Also,

most of the works present method to ﬁle level or ﬁle

to package level aggregation. In this paper, efforts

are done to present approach for aggregation of soft-

ware metrics from class to package level for software

fault prediction based on AAD and IQR techniques.

In addition, extensive experimental investigations are

performed using sixteen releases of eight datasets in

inter-releases scenario to analyze the effect of aggre-

gation on the performance of software fault predic-

tion.

Investigating the Effect of Software Metrics Aggregation on Software Fault Prediction

305

3 METHODOLOGY

In software metrics, there are various granularities

such as method level, class level, ﬁle level, package

level, etc. (Zimmermann et al., 2007), (Zimmermann

et al., 2009). In this paper, the metrics in the dataset

are aggregated from the class level to package level.

This section presents some basic terminologies and

the proposed method.

Figure 1: Our approach of fault prediction mechanism.

3.1 Use of Aggregation

In the inter-releases prediction and cross project fault

prediction, the granularity of training and testing

dataset metrics might not always be the same and

when they are needed to be brought at the same level,

then aggregation of the metrics can be used. In a par-

ticular package there exist several classes. The metric

values of all those classes which belong to the same

package are combined together by using aggregation

technique to give one value per metric for every pack-

age. It needs to be done for all the classes and pack-

ages. In this work, we have used the following aggre-

gation methods for analyzing their effect on the soft-

ware fault prediction performance:

3.1.1 Average Absolute Deviation

AAD depicts the average value of the absolute devi-

ations of a given set of values {x

, x

, ....x

} from a

central point. The central point is the average of the

given set of values.

AAD =

∑

i=1

− A(X)| (1)

Where A(X) is the average of the set of values

, x

, ....x

Table 1: Overview of the datasets used.

S.No. Dataset No. of modules (classes)

1 ant 1.6 351

2 ant 1.7 745

3 camel 1.4 872

4 camel 1.6 965

5 ivy 1.4 241

6 ivy 2.0 352

7 poi 2.5 385

8 poi 3.0 442

9 synapse 1.1 222

10 synapse 1.2 256

11 velocity 1.5 214

12 velocity 1.6 229

13 xalan 2.5 803

14 xalan 2.6 885

15 xerces 1.3 453

16 xerces 1.4 588

3.1.2 Interquartile Range

IQR is a measure of statistical dispersion, which is the

difference between the third and the ﬁrst quartile, for

a given set of values.

IQR = Q3 − Q1 (2)

Where Q3 is the third quartile and Q1 is the ﬁrst quar-

tile.

3.2 Approach

Figure 1 shows the work ﬂow of activities in the ap-

proach proposed in this paper. Following steps are

followed in the proposed approach:

Step1: For all the classes that belong to the same

package, the metric values are aggregated using ei-

ther of the two aggregation techniques proposed, i.e.,

AAD and IQR. The aggregation of metrics is done

from the class level to the closest level,i.e., lowest

level package.

Step2: Generally, in every software system, the

number of faulty modules is lesser than the num-

ber of non faulty modules, making the dataset imbal-

ance and thus leading to inaccurate fault prediction.

In order to deal with the class imbalance problem,

SMOTE ( Synthetic Minority Over-sampling Tech-

nique (Chawla et al., 2002)) is used in our work.

Step3: Earlier version of the dataset is used for

training and the later version is used for testing. Eight

pairs of training-testing datasets have been used in our

work.

Step4: Perform fault prediction mechanism using

the training and testing datasets, generated in previous

step.

ICSOFT 2018 - 13th International Conference on Software Technologies

306

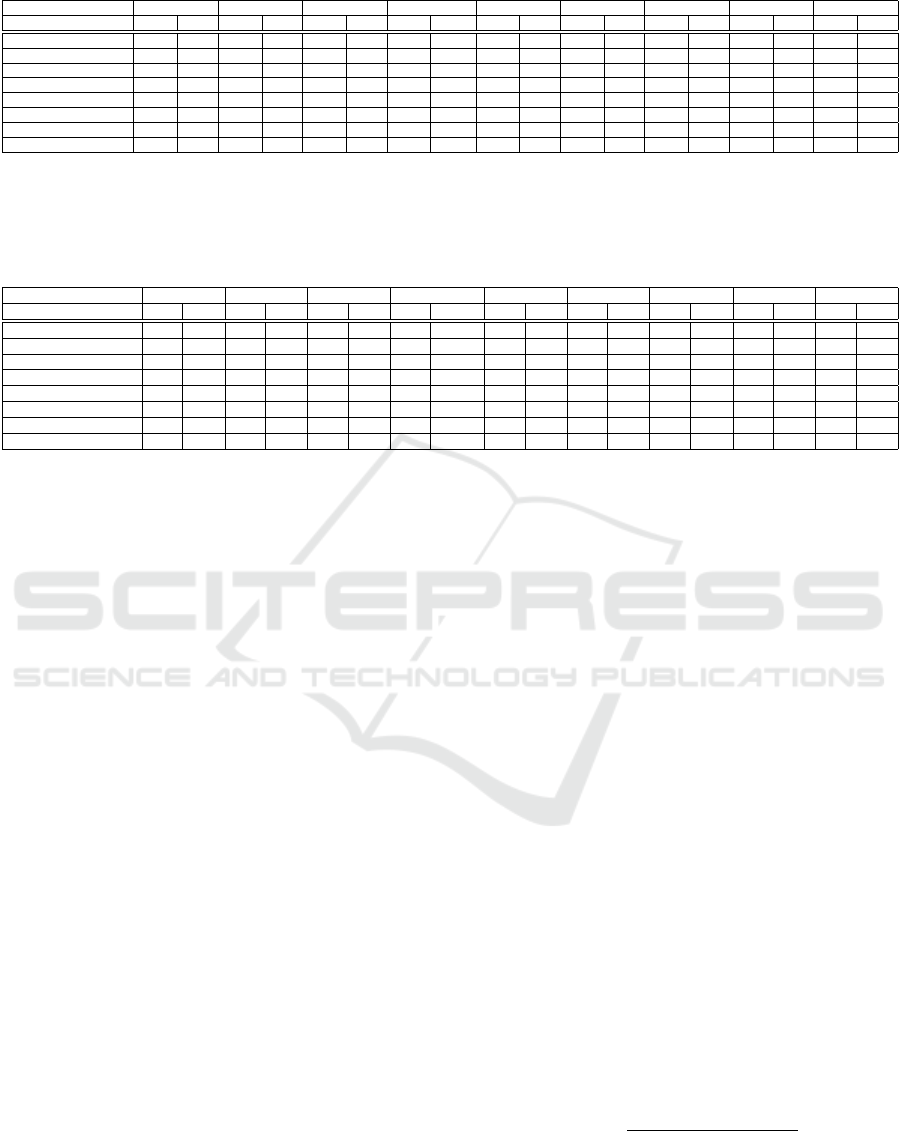
Table 2: Performance in terms of Accuracy % and Precision.

Training-Testing set LR w/o agg. LR AAD LR IQR SVM w/o agg. SVM AAD SVM IQR DT w/o agg. DT AAD DT IQR

Acc. Prec. Acc. Prec. Acc. Prec. Acc. Prec. Acc. Prec. Acc. Prec. Acc. Prec. Acc. Prec. Acc. Prec.

ant1.6-ant1.7 72.21 0.41 46.15 0.46 50 .5 73.69 0.44 70.14 0.63 64.17 0.58 75.57 0.46 67.16 0.63 62.68 0.62

camel1.4-camel1.6 60.62 0.25 85.6 0.69 80.8 0.63 70.56 0.33 87.2 0.73 88 0.74 77.92 0.42 81.6 0.64 84.8 0.72

ivy1.4-ivy2.0 77.27 0.06 73.07 0.61 57.69 0.42 77.55 0.13 61.53 0.45 71.15 0.75 82.67 0.2 59.61 0.41 61.53 0.46

poi2.5-poi3.0 66.28 0.75 80 1 50 1 62.89 0.73 70 0.86 90 1 41.4 0.61 80 0.88 90 1

synapse1.1-synapse1.2 62.89 0.45 57.57 0.66 39.39 0.46 63.28 0.45 57.57 0.63 60.60 0.66 69.53 0.55 54.54 0.61 54.54 0.62

velocity1.5-velocity1.6 61.13 0.45 60 0.77 68 0.88 55.89 0.42 84 0.82 92 0.88 57.2 0.42 88 0.83 80 0.81

xalan2.5-xalan2.6 56.38 0.53 69.04 0.93 61.9 0.95 67.79 0.64 73.8 0.9 69.04 0.93 57.85 0.54 83.33 0.91 80.95 0.91

xerces1.3-xerces1.4 47.61 0.9 60.52 1 63.15 1 50.34 0.91 73.68 1 76.31 1 39.45 0.87 68.42 1 76.31 1

* LR w/o agg.=Logistic Regression without aggregation, LR AAD=Logistic Regression with Average Absolute Deviation, LR IQR=Logistic Regression with Interquartile Range, SVM

w/o agg.=Support Vector Machine without aggregation, SVM AAD=Support Vector Machine with Average Absolute Deviation, SVM IQR=Support Vector Machine with Interquartile

Range, DT w/o agg.=Decision Tree without aggregation, DT AAD=Decision Tree with Average Absolute Deviation, DT IQR=Decision Tree with Interquartile Range, Acc.=Accuracy

,Prec.=Precision.

Table 3: Performance in terms of Recall and F-measure.

Training-Testing set LR w/o agg. LR AAD LR IQR SVM w/o agg. SVM AAD SVM IQR DT w/o agg. DT AAD DT IQR

Rec. F-m. Rec. F-m. Rec. F-m. Rec. F-m. Rec. F-m. Rec. F-m. Rec. F-m. Rec. F-m. Rec. F-m.

ant1.6-ant1.7 0.63 0.5 1 0.63 1 0.66 0.67 0.53 0.83 0.72 0.8 0.67 0.58 0.51 0.67 0.65 0.48 0.54

camel1.4-camel1.6 0.52 0.34 0.85 0.76 0.7 0.66 0.52 0.4 0.82 0.77 0.85 0.79 0.4 0.41 0.7 0.67 0.7 0.71

ivy1.4-ivy2.0 0.07 0.06 0.68 0.65 0.42 0.42 0.17 0.15 0.26 0.33 0.31 0.44 0.17 0.18 0.26 0.32 0.31 0.37

poi2.5-poi3.0 0.69 0.72 0.76 0.86 0.41 0.58 0.64 0.68 0.76 0.81 0.88 0.93 0.21 0.31 0.88 0.88 0.88 0.93

synapse1.1-synapse1.2 0.52 0.48 0.52 0.58 0.31 0.37 0.44 0.44 0.63 0.63 0.63 0.64 0.45 0.5 0.57 0.59 0.52 0.57

velocity1.5-velocity1.6 0.73 0.56 0.46 0.58 0.53 0.66 0.78 0.54 0.93 0.87 1 0.93 0.76 0.55 1 0.9 0.86 0.83

xalan2.5-xalan2.6 0.43 0.48 0.71 0.8 0.6 0.74 0.67 0.66 0.78 0.84 0.71 0.8 0.61 0.57 0.89 0.9 0.86 0.89

xerces1.3-xerces1.4 0.33 0.48 0.51 0.68 0.54 0.7 0.36 0.52 0.67 0.8 0.7 0.83 0.21 0.34 0.61 0.76 0.7 0.83

* LR w/o agg.=Logistic Regression without aggregation, LR AAD=Logistic Regression with Average Absolute Deviation, LR IQR=Logistic Regression with Interquartile Range, SVM

w/o agg.=Support Vector Machine without aggregation, SVM AAD=Support Vector Machine with Average Absolute Deviation, SVM IQR=Support Vector Machine with Interquartile

Range, DT w/o agg.=Decision Tree without aggregation, DT AAD=Decision Tree with Average Absolute Deviation, DT IQR=Decision Tree with Interquartile Range, Rec.=Recall,

F-m.=F-measure.

4 EXPERIMENTAL SETUP

We have used sixteen releases of datasets (8 projects,

each with two releases) from the PROMISE data

repository (Menzies et al., 2015) for experimentation.

The earlier release of a dataset is used for training pur-

pose to predict the fault proneness for the later release

that is used as testing dataset. There are eight pairs of

training-testing datasets in our experiments. Table 1

provides the details of the used datasets.

Various software metrics in the dataset are:

Weighted methods per class (WMC), Depth of In-

heritance Tree (DIT), Number of Children (NOC),

Coupling between object classes (CBO), Response

for a Class (RFC), Lack of cohesion in methods

(LCOM), Lack of cohesion in methods (LCOM3),

Number of Public Methods (NPM), Data Access Met-

ric (DAM), Measure of Aggregation (MOA), Measure

of Functional Abstraction (MFA), Cohesion Among

Methods of Class (CAM), Inheritance Coupling (IC),

Coupling Between Methods (CBM), Average Method

Complexity (AMC), Afferent couplings (Ca), Effer-

ent couplings (Ce), Maximum McCabes cyclomatic

complexity (Max CC), Average McCabes cyclomatic

complexity (Avg CC) and Lines of Code (LOC).

All the implementations in this work have been

done using the R programming language version

3.4.0. It is widely used in data analysis and software

fault predictions.

Three machine learning techniques have been

used for the experimentation: logistic regression

(Arar and Ayan, 2016), (Zhao et al., 2017), support

vector machine (Erturk and Sezer, 2015) and decision

tree (Ghotra et al., 2015).

4.1 Performance Evaluation Measures

Used

In binary classiﬁcation of fault prediction, if in a

package, even a single faulty class is present then that

package is declared to be faulty otherwise non faulty

(Zhao et al., 2017), (Zimmermann et al., 2007), (Zhou

and Leung, 2006). This concept has been used for

calculation of values of performance measures. Four

different performance evaluation measures have been

used as discussed below:

Accuracy: It denotes the percentage of correctly clas-

siﬁed instances to the total number of instances.

Accuracy =

T P + T N

T P + T N + FP + FN

∗ 100 (3)

Precision: It denotes the number of correctly classi-

ﬁed faulty instances amongst the total number of in-

stances classiﬁed as faulty.

Investigating the Effect of Software Metrics Aggregation on Software Fault Prediction

307

Precision =

T P

T P + FP

(4)

Recall: It denotes the number of correctly classiﬁed

faulty instances amongst the total number of instances

which are faulty.

Recall =

T P

T P + FN

(5)

F-measure: It denotes the harmonic mean of the pre-

cision and recall values.

F − measure =

2 ∗ precision ∗ recall

precision + recall

(6)

Where TP represents True Positive, FP represents

False Positive, TN represents True Negative and FN

represents False Negative.

5 EXPERIMENTAL RESULTS

AND ANALYSIS

In this section, ﬁrstly, we have presented the exper-

imental results and then the observations obtained

from the analysis of these results have been presented.

Initially, the experiments are performed using LR,

SVM and DT for inter-releases fault prediction on

class level datasets without applying aggregation.

Then, AAD and IQR aggregation methods are ap-

plied on each of the datasets for metric aggregation

from the class level to package level and LR, SVM,

and DT are used for prediction on the aggregated

datasets. Table 2 shows the performance in terms of

accuracy and precision for these experiments and per-

formance in terms of recall and F-measure is shown

in Table 3. Comparative analysis of performance of

LR, SVM, and DT without using aggregation to corre-

sponding performance on applying aggregation meth-

ods in terms of F-measure are shown in Figure 2, Fig-

ure 3, and Figure 4 respectively.

Following observations are drawn on analyzing

the results:

• From Table 2, it can be seen that DT performs

better than the other two classiﬁers in 50% cases, both

in terms of accuracy and precision when no aggrega-

tion is used. From Table 3, it is observed that SVM

performs better than other two classiﬁers in 75% cases

in terms of recall, while in terms of F-measure, both

SVM and DT came out to be the best, in 37.5% cases,

when no aggregation is used.

• When AAD is used for aggregation, it can be

seen from Table 2 that SVM performs better than

the other two classiﬁers in 50% cases, in terms of

accuracy, while LR performs better than the other

two classiﬁers in 62.5% cases, in terms of precision.

When AAD is used for aggregation, it can be seen

from Table 3 that LR and DT gave the best results ,i.e.,

both in 37.5% cases in terms of recall, while SVM

performs better than the other two classiﬁers in 50%

cases in terms of F-measure.

• When IQR is used for aggregation, it can be seen

from Table 2 that SVM performs better than the other

two classiﬁers in 87.5% and 75%cases in terms of ac-

curacy and precision respectively. It can be seen from

Table 3 that SVM performs better than the other two

classiﬁers in 62.5% and 87.5%cases in terms of recall

and F-measure respectively.

• From Table 2, 3 and Figure 2, 3, 4, it is observed

that for all the learning models, prediction after apply-

ing aggregation shows better performance for most of

the datasets as compared to the case when no aggre-

gation is applied. Out of eight pairs of datasets, in al-

most all the pairs of datasets, either aggregation using

AAD or IQR performs better than the learning models

without applying aggregation in terms of precision,

recall and F-measure for all of the three used classi-

ﬁers. In terms of accuracy, in ﬁve out of eight pairs

of datasets, using either AAD or IQR for aggregation

performs better than the learning models without ap-

plying aggregation for all of the three used classiﬁers.

• From Table 2 and 3 it is observed that aggre-

gation using IQR shows better performance as com-

pared to aggregation using AAD in terms of accuracy,

precision, recall and F-measure, when SVM classi-

ﬁer is used. Aggregation using IQR shows better per-

formance as compared to aggregation using AAD in

terms of accuracy and precision and shows an equiv-

alent performance in terms of F-measure, when DT

classiﬁer is used.

Table 4 shows the comparative analysis of the pre-

sented work with the existing similar works. From

Table 4, it can be seen that the aggregation techniques

AAD and IQR show performance values in the com-

parable and even better range as the other aggregation

techniques explored so far.

Based on the results obtained from the experi-

ments conducted, following research questions can be

answered:

RQ1: How does LR, SVM, and DT based learn-

ing models perform in without aggregation and with

aggregation scenarios?

It is observed that these three learning models per-

form well in both scenarios. However, the perfor-

mance is improved on using the aggregation for all

three learning models.

RQ2: How does aggregation of metrics affect the

performance of software fault prediction?

ICSOFT 2018 - 13th International Conference on Software Technologies

308

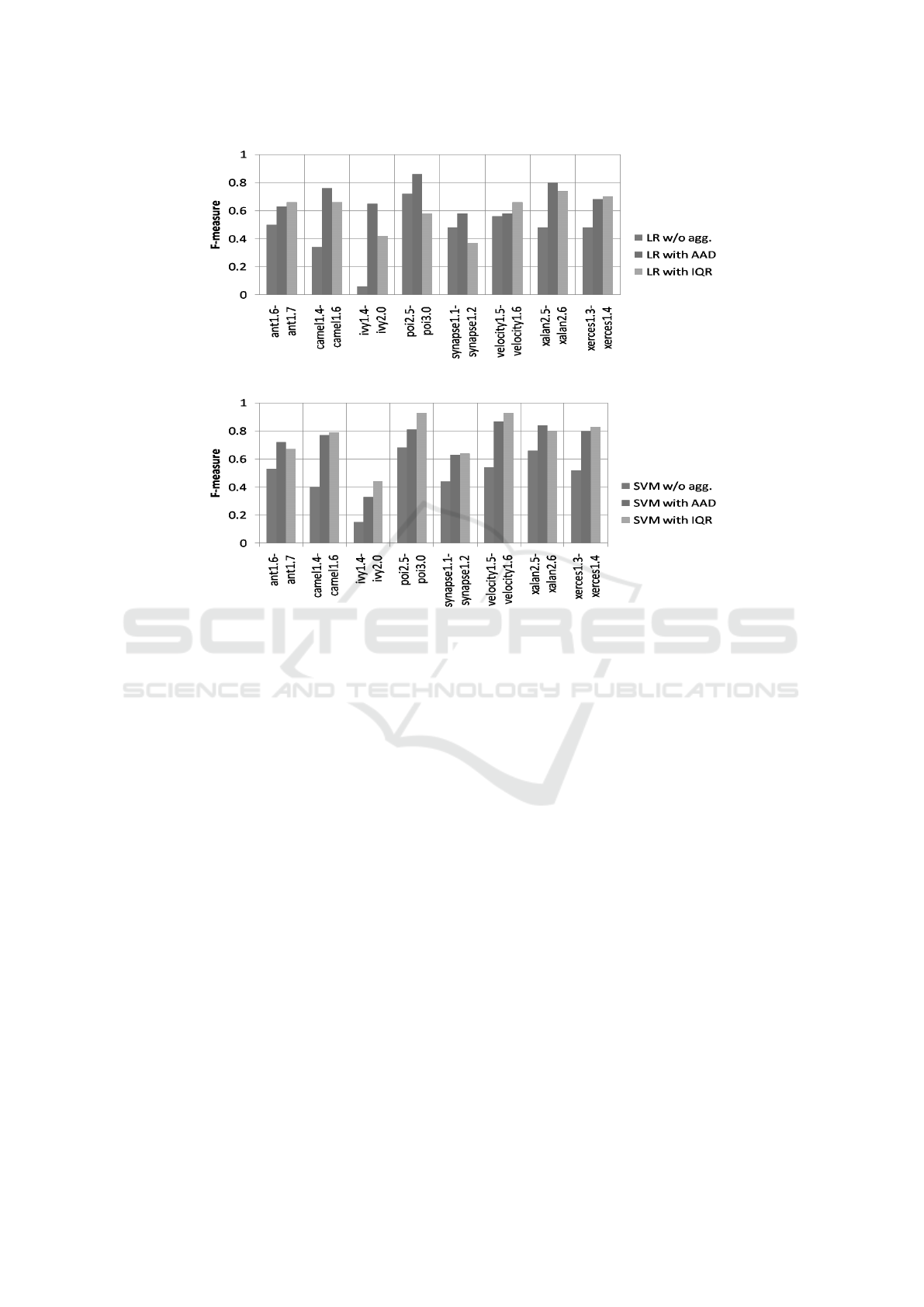
Figure 2: Comparative analysis of performance of LR.

Figure 3: Comparative analysis of performance of SVM.

It is observed from the analysis of experimental

results that the performance of software fault predic-

tion is comparable and even improved in all the sce-

narios under consideration after applying the aggre-

gation of metrics. It shows that if granularity levels

of training datasets and testing datasets are different,

then aggregation can be applied in these datasets to

make them reach same level of granularity and fault

prediction can be performed with acceptable results.

RQ3: Out of AAD and IQR, which method of ag-

gregation for metrics produces better results with ref-

erence to software fault prediction ?

IQR method of aggregation has produced better

results as compared to AAD method of aggregation

in majority of the scenarios under consideration, with

reference to software fault prediction.

6 THREATS TO VALIDITY

In this section, we have presented some possible

threats that may affect the results shown in experi-

mentation.

Internal validity : In this work, we performed

experimentation in inter-releases prediction. Exper-

imentation in different scenario or using different

learning models and different aggregation methods

may produce different results.

External validity : We leveraged different types of

open source software fault datasets of PROMISE data

repository to validate the proposed fault prediction

model using aggregation. The performance might get

affected by some industrial software fault datasets.

Conclusion validity : SMOTE method is used to

balance all imbalanced datasets. Other types of nor-

malization techniques can be used for normalization

of fault datasets and may affect the results.

7 CONCLUSIONS

In this paper, two aggregation methods, Average

Absolute Deviation (AAD) and Interquartile Range

(IQR), for aggregation of software metrics from class

level to package level are investigated for their ef-

fect on the software fault prediction. Aggregation

may need to be performed in inter-releases and cross

project prediction scenarios where the granularity of

the training dataset and the target testing dataset is of

different level. From the experimental analysis, it is

observed that the performance of software fault pre-

diction is comparable or even improved after apply-

Investigating the Effect of Software Metrics Aggregation on Software Fault Prediction

309

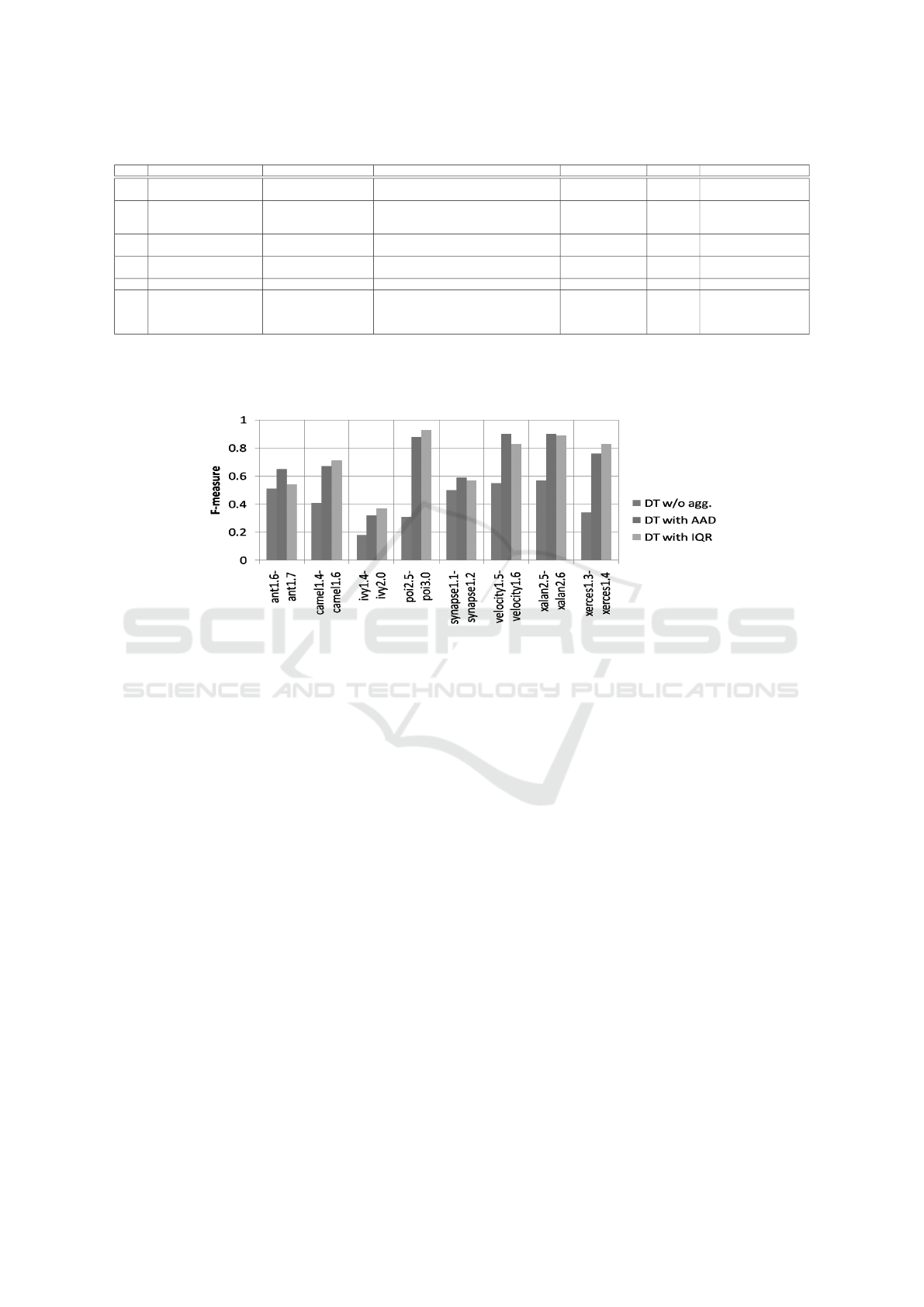
Table 4: A Comparative study of previous similar works with our work.

S.No. Work Reference Classiﬁer(s) Agg. Tech. Agg. Level P.E.M. Range (Min.-Max. value)

1 Zhang et al., (2017) RF

All schemes, Sum,Mean,Median,SD,COV,

Gini,Hoover,Atkinson,Shannon,Entropy,Theil

Method to File AUC 0.55-1 !

2 Zimmermann et al., (2007) LR Average,Sum,Maximum

Method,Class&File

to File&Package

Accuracy

Precision

Recall

61.2-78.9%

0.453-0.785

0.185-0.789

3 Herzig, (2014) MLR,RP,NB,RF,SVM,TP Sum,Maximum,Mean,Median

various levels to

Binary&File level

Precision

Recall

0.29-0.81

0.12-0.70

4 Posnett et al., (2011) LR Sum File to Package

AUC ROC

AUC CE

0.65-1

0.41-0.99

5 Koru and Liu, (2005) DT Minimum,Maximum,Sum,Average Method to Class F-measure 0-0.76

6 Our work LR,SVM,DT AAD,IQR Class to Package

Accuracy

Precision

Recall

F-measure

39.39-92%

0.41-1

0.26-1

0.32-0.93

* Agg.Tech.=Aggregation Technique, Agg. Level=Aggregation Level, P.E.M.=Performance Evaluation Measure, SD=Standard Deviation, COV=Coefﬁcient of Variation, AUC=Area Un-

der Curve,RF=Random Forest, LR=Logistic Regression, MLR=Multinomial Logistic Regression, RP=Recursive Partitioning, NB=Naive Bayes, SVM=Support Vector Machine, TP=Tree

Bagging, DT=Decision Tree, AUC ROC=Area Under Curve Receiver Operating Characteristic, AUC CE=Area Under Curve Cost Effectiveness, AAD=Average Absolute Deviation,

IQR=Interquartile Range.

!: Minimum-Maximum range for best aggregation technique.

Figure 4: Comparative analysis of performance of DT.

ing the aggregation of metrics. Out of AAD and IQR

methods of aggregation, better performance for soft-

ware fault prediction is found for IQR. In future, at-

tempts will be made to design new aggregation meth-

ods to get better prediction results.

ACKNOWLEDGEMENT

This publication is an outcome of the R&D work

undertaken in the project under the Visvesvaraya

PhD Scheme of Ministry of Electronics & Informa-

tion Technology, Government of India, being imple-

mented by Digital India Corporation (formerly Media

Lab Asia).

REFERENCES

Arar,

O. F. and Ayan, K. (2016). Deriving thresholds of

software metrics to predict faults on open source soft-

ware: Replicated case studies. Expert Systems with

Applications, 61:106–121.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: synthetic minority over-

sampling technique. Journal of artiﬁcial intelligence

research, 16:321–357.

Erturk, E. and Sezer, E. A. (2015). A comparison of some

soft computing methods for software fault prediction.

Expert Systems with Applications, 42(4):1872–1879.

Ghotra, B., McIntosh, S., and Hassan, A. E. (2015). Re-

visiting the impact of classiﬁcation techniques on the

performance of defect prediction models. In Proceed-

ings of the 37th International Conference on Software

Engineering-Volume 1, pages 789–800. IEEE Press.

Herzig, K. (2014). Using pre-release test failures to build

early post-release defect prediction models. In 2014

IEEE 25th International Symposium on Software Re-

liability Engineering (ISSRE), pages 300–311. IEEE.

Honglei, T., Wei, S., and Yanan, Z. (2009). The research

on software metrics and software complexity metrics.

In Computer Science-Technology and Applications,

2009. IFCSTA’09. International Forum on, volume 1,

pages 131–136. IEEE.

Ivan, I., Zamﬁroiu, A., Doinea, M., and Despa, M. L.

(2015). Assigning weights for quality software

metrics aggregation. Procedia Computer Science,

55:586–592.

Kamei, Y. and Shihab, E. (2016). Defect prediction: Ac-

complishments and future challenges. In Software

Analysis, Evolution, and Reengineering (SANER),

2016 IEEE 23rd International Conference on, vol-

ume 5, pages 33–45. IEEE.

Koru, A. G. and Liu, H. (2005). Building effective

ICSOFT 2018 - 13th International Conference on Software Technologies

310

defect-prediction models in practice. IEEE software,

22(6):23–29.

Kumar, L., Misra, S., and Rath, S. K. (2017). An empirical

analysis of the effectiveness of software metrics and

fault prediction model for identifying faulty classes.

Computer Standards & Interfaces, 53:1–32.

Menzies, T., Krishna, R., and Pryor, D. (2015). The

promise repository of empirical software engineering

data (2015).

Mordal-Manet, K., Laval, J., Ducasse, S., Anquetil, N., Bal-

mas, F., Bellingard, F., Bouhier, L., Vaillergues, P.,

and McCabe, T. J. (2011). An empirical model for

continuous and weighted metric aggregation. In 2011

15th European Conference on Software Maintenance

and Reengineering (CSMR), pages 141–150. IEEE.

Posnett, D., Filkov, V., and Devanbu, P. (2011). Eco-

logical inference in empirical software engineering.

In Proceedings of the 2011 26th IEEE/ACM Interna-

tional Conference on Automated Software Engineer-

ing, pages 362–371. IEEE Computer Society.

Rathore, S. S. and Kumar, S. (2017). Linear and non-linear

heterogeneous ensemble methods to predict the num-

ber of faults in software systems. Knowledge-Based

Systems, 119:232–256.

Sanz-Rodriguez, J., Dodero, J. M., and Sanchez-Alonso, S.

(2011). Metrics-based evaluation of learning object

reusability. Software Quality Journal, 19(1):121–140.

Serebrenik, A. and van den Brand, M. (2010). Theil index

for aggregation of software metrics values. In Soft-

ware Maintenance (ICSM), 2010 IEEE International

Conference on, pages 1–9. IEEE.

Turhan, B., Mısırlı, A. T., and Bener, A. (2013). Empiri-

cal evaluation of the effects of mixed project data on

learning defect predictors. Information and Software

Technology, 55(6):1101–1118.

Vasa, R., Lumpe, M., Branch, P., and Nierstrasz, O. (2009).

Comparative analysis of evolving software systems

using the gini coefﬁcient. In 2009 IEEE International

Conference on Software Maintenance (ICSM), pages

179–188. IEEE.

Vasilescu, B., Serebrenik, A., and van den Brand, M.

(2011). You can’t control the unfamiliar: A study

on the relations between aggregation techniques for

software metrics. In 2011 27th IEEE International

Conference on Software Maintenance (ICSM), pages

313–322. IEEE.

Walter, B., Wolski, M., Prominski, P., and Kupi

nski, S.

(2016). One metric to combine them all: experimen-

tal comparison of metric aggregation approaches in

software quality models. In Software Measurement

and the International Conference on Software Pro-

cess and Product Measurement (IWSM-MENSURA),

2016 Joint Conference of the International Workshop

on, pages 159–163. IEEE.

Yang, X., Lo, D., Xia, X., and Sun, J. (2017). Tlel: A two-

layer ensemble learning approach for just-in-time de-

fect prediction. Information and Software Technology,

87:206–220.

Zhang, F., Hassan, A. E., McIntosh, S., and Zou, Y. (2017).

The use of summation to aggregate software metrics

hinders the performance of defect prediction mod-

els. IEEE Transactions on Software Engineering,

43(5):476–491.

Zhao, Y., Yang, Y., Lu, H., Liu, J., Leung, H., Wu, Y., Zhou,

Y., and Xu, B. (2017). Understanding the value of

considering client usage context in package cohesion

for fault-proneness prediction. Automated Software

Engineering, 24(2):393–453.

Zhou, Y. and Leung, H. (2006). Empirical analysis of

object-oriented design metrics for predicting high and

low severity faults. IEEE Transactions on software

engineering, 32(10):771–789.

Zimmermann, T., Nagappan, N., Gall, H., Giger, E., and

Murphy, B. (2009). Cross-project defect prediction: a

large scale experiment on data vs. domain vs. process.

In Proceedings of the the 7th joint meeting of the Eu-

ropean software engineering conference and the ACM

SIGSOFT symposium on The foundations of software

engineering, pages 91–100. ACM.

Zimmermann, T., Premraj, R., and Zeller, A. (2007). Pre-

dicting defects for eclipse. In Proceedings of the third

international workshop on predictor models in soft-

ware engineering, page 9. IEEE Computer Society.

Investigating the Effect of Software Metrics Aggregation on Software Fault Prediction

311