Distributed Optimization of Classifier Committee Hyperparameters
Sanzhar Aubakirov
1
, Paulo Trigo
2
and Darhan Ahmed-Zaki
1
1
Department of Computer Science, Al-Farabi Kazakh National University, Almaty, Kazakhstan
2
Instituto Superior de Engenharia de Lisboa, Biosystems and Integrative Sciences Institute
Agent and Systems Modeling, Lisbon, Portugal
Keywords:
Distributed Computing, Text Processing, Machine Learning, Hyperparameters Optimization.
Abstract:
In this paper, we propose an optimization workflow to predict classifiers accuracy based on the exploration
of the space composed of different data features and the configurations of the classification algorithms. The
overall process is described considering the text classification problem. We take three main features that
affect text classification and therefore the accuracy of classifiers. The first feature considers the words that
comprise the inputtext; here we use the N-gram concept with different N values. The second feature considers
the adoption of textual pre-processing steps such as the stop-word filtering and stemming techniques. The
third feature considers the classification algorithms hyperparameters. In this paper, we take the well-known
classifiers K-Nearest Neighbors (KNN) and Naive Bayes (NB) where K (from KNN) and a-priori probabilities
(from NB) are hyperparameters that influence accuracy. As a result, we explore the feature space (correlation
among textual and classifier aspects) and we present an approximation model that is able to predict classifiers
accuracy.
1 INTRODUCTION
The rapid progress on computer–based communica-
tions and information dissemination generates large
amounts of data that are daily available in many do-
mains. The field of machine learning (ML) has seen
unprecedented growth due to a new wealth of data,
to the increases in computational power, to new algo-
rithms, and a plethora of exciting new applications. In
this dissertation we are focusing on text classification
algorithms. Text classification is the process of orga-
nizing data into categories for its most effective and
efficient usage.
Nowadays there is a great choice of text classifi-
cation algorithms. There are 179 methods of classi-
fication by machine learning algorithms (Fern
´
andez-
Delgado et al., 2014). As researchers tackle more
ambitious problems, the models they use are also be-
coming more sophisticated. However, according to
the researches (Sebastiani, 2002) classifier ensembles
outperforms the best individual classifier. Classifier
ensembles (committees) are based on the idea that,
given a task that requires expert knowledge to per-
form, k experts may be better than one if their indi-
vidual judgments are appropriately combined.
The growing complexity of ML models inevitably
comes with the introduction of additional parameters,
which is often expressed via a vector of model pa-
rameters. Additional parameters express higher-level
properties of the learning model and therefore they
cannot be learned directly from the regular training
process; such parameters are designated as hyperpa-
rameters. Hyperparameters change the way the learn-
ing algorithm itself works (e.g. hyperparameters are
used to describe a thresholds, the number of neurons
in a hidden layer, the number of data points that a
leaf in a decision tree must contain to be eligible for
splitting). Each classification algorithm is tuned via
hyperparameters that affect the learning process and
the final accuracy of the prediction model. In the
context of text classification, the input (text) is pre–
processed by a set of operators and therefore each op-
erator also influences the prediction accuracy. These
hyperparameters are typically optimized in an outer
loop that evaluates the effectiveness of each hyperpa-
rameter configuration using cross-validation. Taking
into account each algorithms hyperparameters, there
is a staggeringly large number of possible alternatives
overall.
The design decisions range from the classifica-
tion algorithm, optimization parameters such as learn-
ing rates and text pre–processing parameters such as
stemming. Proper setting of these hyperparameters is
critical for performance on difficult problems. There
Aubakirov, S., Trigo, P. and Ahmed-Zaki, D.
Distributed Optimization of Classifier Committee Hyperparameters.
DOI: 10.5220/0006884101710179
In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 171-179
ISBN: 978-989-758-318-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
171

are many methods for optimizing over hyperparam-
eter settings, ranging from simplistic procedures like
grid or random search (Bergstra et al., 2011; Bergstra
and Bengio, 2012), to more sophisticated model–
based approaches using random forests (Hutter et al.,
2011) or Gaussian processes (Snoek et al., 2012).
Hence, in the context of the text classification
problem, we can formulate a feature space composed
of: a) data set, b) hyperparameters of the classifica-
tion algorithms, and c) textual pre–processing opera-
tors. According to (Garey and Johnson, 1990) the task
of selecting the right features is nontrivial and check-
ing all possible combinations is an NP–complete task.
The task of selecting the classifier algorithm becomes
resource intensive for the ensemble of classifiers and
it requires expert knowledge from various areas of
Computer Science (Machine Learning, Natural Lan-
guage Processing, High Performance Computing).
In this research, we propose a methodology to deal
with this complex task using an optimization model
that explores the feature space with the goal of maxi-
mizing the ensemble of classifiers accuracy. We out-
line the optimization model and describe each step
and show that we can approximate the maximization
goal using a regression model.
2 RELATED WORKS
The task of optimizing classification algorithms hy-
perparameter is addressed by many authors (Bergstra
et al., 2011; Forman, 2003; Lim et al., 2000; Das-
gupta et al., 2007; Thornton et al., 2012). A large
study of classification algorithms shows that not only
accuracy of the algorithm depends on selected fea-
tures and input data, but training time, scalability and
interpretability of algorithm (Lim et al., 2000). An-
other research (Dasgupta et al., 2007) points out the
challenges associated with automated text, such as
a) choosing an appropriate data structure to represent
the documents, b) choosing an appropriate objective
function to optimize in order to avoid overfitting, c)
obtain good generalization, and d) dealing with algo-
rithmic issues arising because of the high formal di-
mensionality of the data. This last challenge can be
addressed via a prior selection of a subset of the fea-
tures available for describing the data (Dasgupta et al.,
2007). Such selection occurs before applying a learn-
ing algorithm and setting its operational parameters.
A large number of studies on feature selection have
focused on text domains both for binary and multi-
class problems. This fails to investigate the best possi-
ble accuracy obtainable for any single class (Forman,
2003).
Those studies deal with feature selection and pro-
vide an in–depth analysis of the problem of simulta-
neously selecting a learning algorithm and setting its
hyperparameters. In the work (Thornton et al., 2012)
researchers provide a tool that effectively identifies
machine learning algorithms and hyperparameter set-
tings. Proposed approaches still require high com-
putational resources to evaluate each model. Most
feature selection studies are conducted in a non-
automatic way or in semi-automatic way. This fails
to explore all possible features, attributes and algo-
rithms.
In the next chapter we will present a methodology
to build effective automatic feature and algorithms se-
lection model. These include testing platform per-
formance against several types of classification algo-
rithms, training datasets and document representation
method.
Thus, problem solution has to be designed con-
sidering all defined features. We propose optimiza-
tion model that depends on (i) the quality of the sam-
ple sets, (ii) on classification algorithm hyperparame-
ter and (iii) on the document representation (text pre-
processing). In this context, the complexity of the
task comes from the size of feature space and com-
puting resources needed to explore all domain. We do
note the past work (Bergstra et al., 2011; Luo, 2016;
Friedrichs and Igel, 2005; Snoek et al., 2012) that dis-
cuss more the theoretical aspects of optimization, pre-
senting algorithms, but not concrete implementations
on a distributed computing architecture.
We also note the recent work that gives an exten-
sive analysis of the domain (Schaer et al., 2016). This
work shows that HPC tools and frameworks avail-
able nowadays does not fit following requirments:
(i) provide a full simulation of optimization process,
(ii) address hyperparameter optimization directly and
(iii) provide implementations for classification algo-
rithms. As a result of the work (Schaer et al., 2016),
distributed implementation of hyperparameter opti-
mization for medical image classification was devel-
oped. Nevertheless, the same problem in the text clas-
sification domain remains open. Thus, in the chapter
4 we introduce MapReduce and MPJ hybrid architec-
ture of the fully automatic optmimization algorithm.
In the chapter 3 we provide implementation details as
news classification case study.
Presented arguments lets one conclude that the
effectiveness of classification algorithm depends on
the following parameters: (i) ML algorithm itself,
(ii) training data set and (iii) document representa-
tion (text pre-processing). Most ML algorithms fur-
ther expose hyperparameters, which change the way
the learning algorithm itself works. Hyperparameters
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
172

express higher-level properties of the model such as
its convergence, tresholds or how fast it should learn.
Hyperparameters are usually fixed before the actual
training process begins. The complexity of the task
comes from the size of: (i) algorithm hyperparameter
space, (ii) size of data set, (iii) high dimensionality of
document feature space and (iv) computing resources
needed to explore this. The relevance of studying
such phenomena is confirmed by time costs of setting
up and evaluating each model, as well as by high own-
ership costs of conventional high-performance infras-
tructures. This suggests a challenge for ML and HPC
domains: given a dataset, to automatically and simul-
taneously choose a document representation feature
space, learning algorithm and set its hyperparameters
to optimize effectiveness.
In the next sections we will justify research mo-
tivation and give basic research background to serve
the bridge for the reader of the paper.
3 METHODS
Text classification (TC) is the task of assigning a
Boolean value to each pair hd
j
, c
i
i ∈ D × C, where
D is a domain of documents, C = {c
1
, . . . , c
|C|
} is a
set of predefined categories and |C| is the cardinality
of the set C. We will assume that the categories are
just symbolic labels, and no additional knowledge (of
a procedural or declarative nature) of their meaning
is available. Classifier ϕ
λ
: D × C → {T, F} approx-
imates unknown target function
ˆ
ϕ : D ×C → {T, F},
where λ is algorithm hyperparameter and λ ∈ Λ. Sup-
pose classifier has n hyperparameters {λ
1
, . . . , λ
n
} in
the domain Λ
1
, ..., Λ
n
. The hyperparamerer set Λ is
subset of the vector product: Λ ⊂ Λ
1
× ··· × Λ
n
.
More formally, the task is to approximate the un-
known target function
ˆ
ϕ : D ×C → {T, F} by means
of a function ϕ : D ×C → {T, F} called the classifier.
Then the goal is to minimize the value of |ϕ−
ˆ
ϕ|, how
to precisely define and measure this value (called ef-
fectiveness) will be discussed in section 3.1.
There is no clear guideline to choose a set of
learning methods and it is rare when one has a com-
plete knowledge about data distribution and also the
about the details of how the classification algorithm
behaves. Therefore, in practical pattern classifica-
tion tasks it is difficult to find a good single classifier.
Classifier ensembles are based on the idea that k clas-
sifiers may be better than one if their individual judg-
ments are appropriately combined. In TC, the idea is
to apply k different classifiers ϕ
1
, . . . , ϕ
k
to the same
task of deciding whether d
j
∈ c
i
, and then combine
their decision. A classifier committee is then char-
acterized as simplest majority voting (MV), whereby
the binary outputs of the k classifiers are pooled to-
gether, and the classification decision that reaches the
majority of
k+1
2
votes is taken, where k needs to be an
odd number. In the rest of the thesis we will deal with
the idea of majority voting classifier ensembles.
The combination of expert opinions is a topic
studied since the second half of the twentieth cen-
tury. In the beginning the studies were devoted to
applications such as democracy, economic and mili-
tary decisions. Multiple classifier combination meth-
ods can be considered some of the most robust and
accurate learning approaches (Jr., 2011). The fields
of multiple classifier systems and ensemble learning
developed various procedures to train a set of learn-
ing machines and combine their outputs. Such meth-
ods have been successfully applied to a wide range
of real problems, and are often, but not exclusively,
used to improve the performance of unstable or weak
classifiers. It is known from the ML literature that, in
order to guarantee good effectiveness, the classifiers
forming the committee should be as independent as
possible (Kagan and Joydeep, 1996).
Classifier ensemble is a set of learning algorithms
which decisions are combined to improve effective-
ness of the pattern recognition system. Much of the
efforts in classifier combination research focus on im-
proving the accuracy of difficult problems, managing
weaknesses and strenghts of each model in order to
give the best possible decision taking into account
all the ensemble. The use of combination of multi-
ple classifiers was demonstrated to be effective, un-
der some conditions, for several pattern recognition
applications and scenarios were also experimentally
and theoretically studied in the past years (Brown and
Kuncheva, 2010).
Many studies showed that classification problems
are often more accurate when using combination of
classifiers rather than an individual base learner (Se-
bastiani, 2002). For instance “weak” classifiers are
capable of outperform a highly specific classifier
(Kuncheva et al., 2001). These methods were widely
explored, for example, to stabilize results of random
classifiers and to improve the performance of weak
ones. Neural-network based classifiers that are unsta-
ble can be stabilized using MCS techniques (Breve
et al., 2007). Also, noisy data can be better han-
dled since the diversity of classifiers included in the
ensemble increases the robustness of the decisions.
Besides, there are many classifiers with potential to
improve both accuracy and speed when used in en-
sembles. All these advantages can be explored by re-
searches on the field of pattern recognition and ma-
chine learning. The formal definition of the ensemble
Distributed Optimization of Classifier Committee Hyperparameters
173

of classifiers is given below.
The classifier ensemble is defined as
¯
ϕ = hϕ
(1)
λ
, . . . ϕ
(k)
λ
i, where k is the number of
classification algorithms in the ensemble. The
decision to assign a Boolean value is taken on the
basis of a simple majority
k+1
2
, where k is always
odd. The set of all ensembles is defined as
¯
Φ.
Given a set of classification algorithms Φ =
{ϕ
(1)
λ
, . . . , ϕ
(|Φ|)
λ
}, appropriate hyperparameter space
Λ
(1)
. . . Λ
(|Φ|)
and the set of ensembles of classifiers
¯
Φ = {
¯
ϕ
(1)
. . .
¯
ϕ
(|
¯
Φ|)
}. Then the optimization of the
classification algorithm is determined by the formula
1.1, and the optimization of the hyperparameters of
the ensemble of classification algorithms according to
the formula 1.2:
ϕ
∗
λ
∗
= argmax
¯
ϕ
( j)
∈Φ,λ∈Λ
( j)
E(ϕ
j
λ
)
(1)
¯
ϕ
∗
= argmax
¯
ϕ
( j)
∈
¯
Φ
E(
¯
ϕ
j
)
(2)
, where E( ) the function of evaluating the accuracy
of the classifier.
3.1 The Effectiveness of Classifier
The evaluation of document classifiers is typically
conducted experimentally, rather than analytically
(Manning et al., 2008). The experimental evalua-
tion of a classifier usually measures its effectiveness,
that is, its ability to take the right classification deci-
sions. TC effectiveness is usually measured in terms
of the classic IR notions of precision (P) and recall
(R) (Manning et al., 2008). These are first defined for
the simple case where an TC algorithm returns a set
of classified documents.
These probabilities may be estimated in terms of
the contingency table for c
i
on a given test set. Here,
FP (false positives, a.k.a. errors of commission) is the
number of test documents incorrectly classified under
c
i
; TN (true negatives), T P (true positives), and FN
(false negatives, a.k.a. errors of omission) are defined
accordingly.
Precision P for a class c
i
is the number of T P di-
vided by the total number of documents labeled as
belonging to the c
i
.
Precision =
T P
T P + FP
= P
(3)
Recall (R) for a class c
i
in this context is defined as
the number of T P divided by the total number of doc-
uments that actually belong to the class c
i
Recall =
T P
T P + FN
= R
(4)
Our final goal is to evaluate the classifiers relative
to each other, rather than simply assess the effective-
ness of a single classifier. An extensive analysis of
various evalution metrics specifically for TC domain
based on contingency table, P and R may be found in
(Carletta, 1996; Fawcett, 2006; Manning et al., 2008;
Powers, 2008; Powers, 2012). Research (Carletta,
1996) states that the kappa statistic measure are easily
interpretable and allows different classifiers results to
be compared. The work (Manning et al., 2008) states
that different systems or variants of a single system
which are being compared for effectiveness have lit-
tle impact on the relative effectiveness ranking using
kappa statistics. The kappa statistic is used not only
to evaluate a single classifier, but also to evaluate clas-
sifiers amongst themselves.
In the (Powers, 2008; Powers, 2012) authors states
that Kappa does attempt to renormalize a debiased es-
timate of Accuracy, and is thus much more meaning-
ful than Recall, Precision, Accuracy, and their biased
derivatives. But they also assume that it is intrinsi-
cally non-linear, doesn’t account for error well, and
retains an influence of bias. Furthermore, in the (Pow-
ers, 2012) authors suggests Matthews correlation co-
efficient (MCC) instead of Kappa saying that for com-
parison of behaviour, Matthews Correlation is recom-
mended. Matthews Correlation coefficient is appro-
priate for comparing equally valid classifications or
ratings into an agreed number of classes.
Thus, in our work we use Kappa Cohen’s Coef-
ficient (Kappa 11) and Matthews correlation coeffi-
cient (MCC 10) as a classifier evaluation metrics. We
will also show standard F1 score (F
1
8), Accuracy
(ACC 6), Precision (P 3), Recall (R 4) and Error Rate
(ER 5) because it is often used as an evalutaion met-
rics in most text classification researches and it could
be used by other researchers as a benchmark. The
following shows the formulas for calculation the co-
efficients.
ER =
FN
FN + TP
(5)
ACC =
TP + TN
TP + TN + FP + FN
(6)
EACC =
(TP+TN)∗(TP+FP)
TP+TN+FP+FN
+
(FP+TN)∗(FN+TN)
TP+TN+FP+FN
TP + TN + FP + FN
(7)
F
1
= 2 ·
PPV · TPR
PPV + TPR
=
2TP
2TP + FP + FN
(8)
Kappa =
ACC − EACC
1 − EACC
(9)
MCC =
TP ×TN − FP ×FN
p
(TP +FP)(TP + FN)(TN +FP)(TN + FN)
(10)
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
174

Kappa =
ACC − EACC
1 − EACC
(11)
where
• IDF is inverse document frequency
• f (S
i
, R) is occurrence frequency of a word i from
sentence S in sentence R
• |R| is a length of sentence R
• avgDL is an average length of sentences in the
document
• k1 and b are parameters, k1 = 1.2, b = 0.75
3.2 The Feature Space
The first feature is classifier Λ
1
. Each classifier has
hyperparameters that affect the classification effec-
tiveness. In this work, we consider the well-known
classifiers K-Nearest Neighbors (KNN) and Naive
Bayes (NB) where K (from KNN) and -priori proba-
bilities (from NB) are hyperparameters that influence
accuracy. Our experiments have shown that KNN
classifiers accuracy dramatically low for K > 200,
that is why we decide to bound K from 1 to 200. We
have a set of hyperparameters features C = (0-200),
where values (1 − 200) mapped to K in KNN classi-
fier and value 0 mapped to NB classifier. We have a
set Λ
1
of 201 different features:
Λ
1
= [0, 1, 2...199, 200] (12)
The second feature is pp
3
- an input data text feature
selection by extracting n-grams. For our research, we
choose 1-gram, 2-gram, 3-gram, 4-gram, 5-gram and
altogether from 1 to 5 gram extraction. As a result,
we have a set Λ
2
of 6 different features:
Λ
2
= {1Gram, 2Gram, 3Gram,
4Gram, 5Gram, 1to5Gram}
(13)
The third features that affects classifier effective-
ness is an input data pre-processing. The goal of data
pre-processing (pp) is to clean and prepare the text
for classification and the whole process is as pipeline
with several stages, namely: (pp
1
) stemming, (pp
2
)
short words filtering and (pp
3
) n-gram extraction.
We consider that all input text is already pipelined
through text cleaning and stop words stages.
Thereby, we have a set Λ
3
consisting of pp
1
and
pp
2
operations. On pp
1
stage we decide whether in-
put text will be processed with stemmer (S) or not
(NS). On stage pp
2
we decide whether input text
will be processed with word length filter (LF) or not
(NLF). Length filter is dropping out the word that is
shorter than four symbols. There are combinations
of features pp
1
and pp
2
, for example, if we want to
apply both stemming and short word filtering. As a
result, we have a set Λ
3
of 4 different features:
Λ
3
= {S + LF, S + NLF, SN + LF, SN + NLF} (14)
The next is data set feature, for this research we use
different document text fields Λ
4
. As there are two
fields available, title and body, we have a set, Λ
4
, of
three different features:
Λ
4
= {body, title, body +title} (15)
Totally, we have a combination of 24 features text
pre-processing features, 201 classifiers hyperpareme-
ter features and 3 data set features. More formally
we have space ϕ
λ
, which is space of 14472 different
combinations of all features. By combining all fea-
tures, we assemble classifier. Assembled classifier is
a combination ϕ
λ
that can be expressed using formula
as follows:
ϕ
λ
= {λ
i
, λ
j
, λ
k
, λ
l
}
(16)
where,
i ∈ [0 − 200], λ
i
∈ Λ
1
, (17)
j ∈ [0 − 6], λ
j
∈ Λ
2
, (18)
k ∈ [0 − 3], λ
k
∈ Λ
3
, (19)
l ∈ [0 − 3], λ
l
∈ Λ
4
(20)
We propose tuple notation to describe each assembled
classifier, it is shown in figure 1.
Figure 1: Tuple notation describes each classifier with all
features.
4 ENSEMBLE OF CLASSIFIERS
EFFECTIVENESS
OPTIMIZATION
ARCHITECTURE
We built a classifiers ensemble based on work (Bauer
and Kohavi, 1999) to combine classifiers. To make a
decision we need a simple majority of voters. Sup-
pose we have five voters, then combination of all pos-
sible classifiers would be the combination of given
Distributed Optimization of Classifier Committee Hyperparameters
175

14472 set of classifiers of 5 elements. Which is
5 ∗ 10
18
possible combinations. We use a classical
genetic algorithm to deal with this complexity. The
chromosome will consist of 5 genes, where the gene
is one of the combinations of the classifier, analyzer
and field. By assigning each characteristic to a num-
ber, you can define a set of genes. Thus, the gene is
an array of 4 digits, where each of the digits is re-
sponsible for the characteristics of the classifier. An
example of chromosome shown in Figure 2.
Figure 2: An example of MapReduce processing of one
chromosome for voting classifier.
Each generation chromosome distributed using
MPJ to the slave nodes. Each slave nodes distributes
their task to the CPU cores using MapReduce Java
implementation. Slave nodes responsible for docu-
ment representation, feature selection, feature extrac-
tion, indexing, training and validating classifier. In the
end all slaves sends back K-fold cross validation re-
sults to master Node, which is producing next gener-
ation of chromosomes. Generation algorithm schema
is shown on figures 3.
We will use the value of the Kappa coefficient as
a fitness function. The stopping criteria for the ge-
netic algorithm is set to Kappa = 0.95. Selection
will occur using the roulette selection method. This
method increases the probability of selecting an in-
dividual with a high fitness function. The higher the
Kappa coefficient, the more likely it is to get into the
next generation. Optimization schema is shown in fig-
ure 4.
We use simple One-Point Crossover as a crossover
function. The point at which the crossing will oc-
cur selected randomly. The mutation of each chro-
mosome triggered with a 35% chance. This means
Figure 3: MPJ distributes chromosomes to slave nodes.
Java based MapReduce application computes classifier ef-
fectiveness.
Figure 4: Distributed optimization schema workflow.
that after each cycle of the algorithm, only 35% of the
population can mutate, and only 2 of the 5 genes will
mutate.
This simple genetic algorithm produces well-
stratified data to train prediction model. Figure 4
shows that we save each tuple as a key and accuracy
as the value. We execute algorithm until it generates
enough results to approximate accuracy function.
Proposed voting classifier description is a vector
in an N-dimensional space, where N is a number of
features of the classifier. Nearly any regression model
can be used to approximate relationship between fea-
tures and accuracy. As proof of concept, we built
multilayer perceptron (MLP) with one hidden layer
in order to predict voting classifier accuracy with-
out computation, training and testing classifier. The
prediction-learning schema is in figure 5.
Multilayer perceptron was trained using data that
genetic algorithm produced. In order to archive maxi-
mum performance, we implement a genetic algorithm
in a distributed computing manner using hybrid of
Java Message Passing Interface (MPJ-Express) and
MapReduce paradigm.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
176

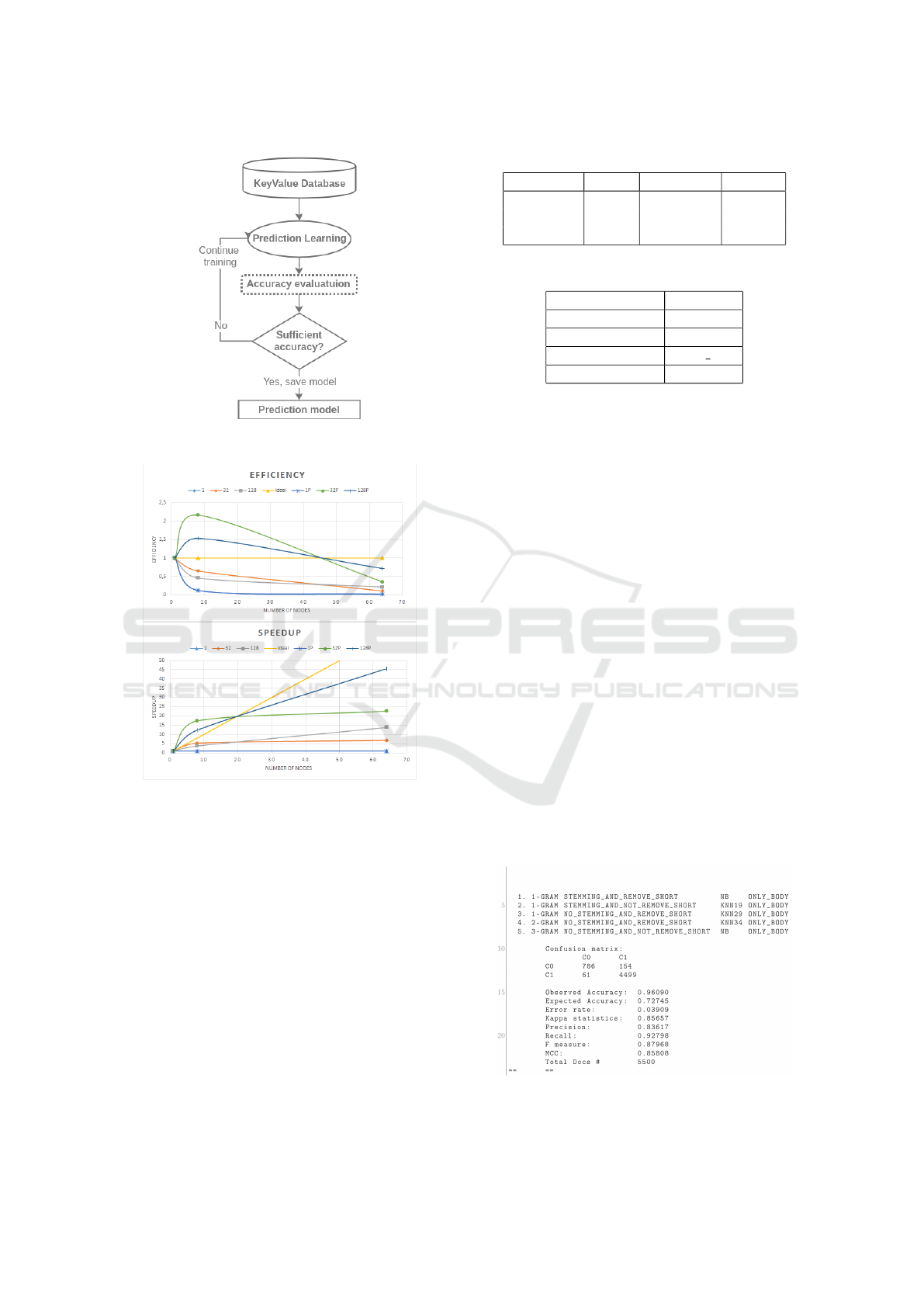
Figure 5: Process of training regression model.
Figure 6: Speedup ratio and parallel efficiency. Plots with
prefix “P” shows computation using prediction model.
5 RESULTS
Technical characteristics of the cluster is shown in ta-
bles 1 and 2. There are 16 nodes, each node has the
same characteristics. Figure 6 shows overall picture
for results of the experiments, parallelization gives
good efficiency and speedup on all platforms.
5.1 Speedup and Efficiency
We experimented on the task of distributed classi-
fier ensemble effectiveness optimization. The code
of classifier committee optimization using genetic al-
gorithm described in previous section. Experimental
result shows that the feature selection, feature extrac-
Table 1: Cluster specification.
CPU RAM HDD Net
Intel Core 500GB
i5-2500 16Gb 7200RPM 1Gbit/s
3.30GHz 6Gb/s
Table 2: Software specification.
Name Version
MPJ Express 0.44
Apache Hadoop 2.6.0
Java 1.8.0 131
Ubuntu OS 14.04
tion, data set and classifier hyperparameter has deep
influence to the effectiveness of classifier.
The speedup ratio and parallel efficiency plots are
shown in figure 6. Speedup and efficiency provide an
estimate for how well a code sped up if it was paral-
lelized. The yellow plot shows ideal speedup and ef-
ficiency, the ratio of one hundred percent parallelized
code.
The green (32P) and blue (128P) plot stand for 32
and 128 classifiers evaluation respectively. The prefix
“P” means that optimization process uses prediction
model in order to drop out classifiers with insufficient
accuracy. This helps to identify weak classifier before
implicit training, testing and evaluating. That is why
plots sometimes higher than an ideal line.
The proposed workflow finds the voting classifier
with the maximum Kappa coefficient of 0.85. The re-
sulted program output is shown in figure 7, chromo-
some vector representation is shown in listing 1. The
effectivness is not perfect, but according to (Landis
and Koch, 1977) almost perfect agreement. In addi-
tion, the goal of MLP was to predict accuracy and
avoid calculation of weak voting classifier. We in-
terpret these results as encouraging evidence for the
usefulness of MLP for deciding usefulness of voting
classifier.
Figure 7: Confusion matrix of the ensemble of classifiers
with the Kappa and MCC of 0.85.
Distributed Optimization of Classifier Committee Hyperparameters
177

Listing 1: Best chromosome vector representation in JSON
file format.
{
” chromosom e ” : {
” g e ne s ” : [
{
” c l a s s i f i e r ” : 0 ,
” a n a l y z e r ” : 0 ,
” f i l t e r ” : 0 ,
” f i e l d ” : 0
} ,
{
” c l a s s i f i e r ” : 19 ,
” a n a l y z e r ” : 0 ,
” f i l t e r ” : 1 ,
” f i e l d ” : 0
} ,
{
” c l a s s i f i e r ” : 29 ,
” a n a l y z e r ” : 0 ,
” f i l t e r ” : 2 ,
” f i e l d ” : 0
} ,
{
” c l a s s i f i e r ” : 34 ,
” a n a l y z e r ” : 1 ,
” f i l t e r ” : 2 ,
” f i e l d ” : 0
} ,
{
” c l a s s i f i e r ” : 0 ,
” a n a l y z e r ” : 2 ,
” f i l t e r ” : 3 ,
” f i e l d ” : 0
}
]
} ,
” f i t n e s s V a l u e ” : 0 . 8 56 5 7 1 0 47 3 6 4 91 0 1
}
Figure 8: Final optimization workflow. The dotted line
highlights the prediction model.
6 CONCLUSION
It is difficult nowadays to decide which classifica-
tion algorithm to use and how to preprocess text in-
put data. We design a workflow of algorithms that
can significantly reduce the amount of time to find
out correct attributes of the exact problem. Figure 8
shows proposed workflow of algorithms.
The proposed simulation tool is very effective and
has accuracy up to 0.85 value of Kappa and MCC
coefficient. Furthermore, the accuracy of the whole
workflow can be improved by selecting better approx-
imation model, for example, better MLP architecture.
7 COPYRIGHT FORM
The Author hereby grants to the publisher, i.e. Sci-
ence and Technology Publications, (SCITEPRESS)
Lda Consent to Publish and Transfer this Contribu-
tion.
REFERENCES
Bauer, E. and Kohavi, R. (1999). An empirical comparison
of voting classification algorithms: Bagging, boost-
ing, and variants. Machine Learning, 36(1):105–139.
Bergstra, J. and Bengio, Y. (2012). Random search for
hyper-parameter optimization. J. Mach. Learn. Res.,
13:281–305.
Bergstra, J. S., Bardenet, R., Bengio, Y., and K
´
egl, B.
(2011). Algorithms for hyper-parameter optimiza-
tion. In Shawe-Taylor, J., Zemel, R. S., Bartlett, P. L.,
Pereira, F., and Weinberger, K. Q., editors, Advances
in Neural Information Processing Systems 24, pages
2546–2554. Curran Associates, Inc.
Breve, F. A., Ponti-Junior, M. P., and Mascarenhas, N.
D. A. (2007). Multilayer perceptron classifier com-
bination for identification of materials on noisy soil
science multispectral images. In XX Brazilian Sym-
posium on Computer Graphics and Image Processing
(SIBGRAPI 2007), pages 239–244.
Brown, G. and Kuncheva, L. I. (2010). “Good” and “Bad”
Diversity in Majority Vote Ensembles, pages 124–133.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Carletta, J. (1996). Assessing agreement on classifica-
tion tasks: The kappa statistic. Comput. Linguist.,
22(2):249–254.
Dasgupta, A., Drineas, P., Harb, B., Josifovski, V., and
Mahoney, M. W. (2007). Feature selection methods
for text classification. In Proceedings of the 13th
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, KDD ’07, pages
230–239, New York, NY, USA. ACM.
Fawcett, T. (2006). An introduction to roc analysis. Pattern
Recogn. Lett., 27(8):861–874.
Fern
´
andez-Delgado, M., Cernadas, E., Barro, S., and
Amorim, D. (2014). Do we need hundreds of clas-
sifiers to solve real world classification problems? J.
Mach. Learn. Res., 15(1):3133–3181.
Forman, G. (2003). An extensive empirical study of fea-
ture selection metrics for text classification. J. Mach.
Learn. Res., 3:1289–1305.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
178

Friedrichs, F. and Igel, C. (2005). Evolutionary tuning of
multiple svm parameters. Neurocomput., 64:107–117.
Garey, M. R. and Johnson, D. S. (1990). Computers
and Intractability; A Guide to the Theory of NP-
Completeness. W. H. Freeman & Co., New York, NY,
USA.
Hutter, F., Hoos, H. H., and Leyton-Brown, K. (2011). Se-
quential Model-Based Optimization for General Algo-
rithm Configuration, pages 507–523. Springer Berlin
Heidelberg, Berlin, Heidelberg.
Jr., M. P. P. (2011). Combining classifiers: From the cre-
ation of ensembles to the decision fusion. In 2011 24th
SIBGRAPI Conference on Graphics, Patterns, and Im-
ages Tutorials, pages 1–10.
Kagan, T. and Joydeep, G. (1996). Error correlation and
error reduction in ensemble classifiers. Connection
Science, 8(3-4):385–404.
Kuncheva, L. I., Bezdek, J. C., and Duin, R. P. W.
(2001). Decision templates for multiple classifier fu-
sion: an experimental comparison. Pattern Recogni-
tion, 34:299–314.
Landis, J. R. and Koch, G. G. (1977). The measurement of
observer agreement for categorical data. Biometrics,
33(1).
Lim, T.-S., Loh, W.-Y., and Shih, Y.-S. (2000). A compar-
ison of prediction accuracy, complexity, and training
time of thirty-three old and new classification algo-
rithms. Machine Learning, 40(3):203–228.
Luo, G. (2016). Predict-ml: a tool for automating machine
learning model building with big clinical data. Health
Information Science and Systems, 4(1):5.
Manning, C. D., Raghavan, P., and Sch
¨
utze, H. (2008). In-
troduction to Information Retrieval. Cambridge Uni-
versity Press, New York, NY, USA.
Polikar, R. (2017). Ensemble learning.
Powers, D. (2008). Evaluation: From precision, recall and
f-factor to roc, informedness, markedness & correla-
tion. Journal of Machine Learning Technologies, 2.
Powers, D. M. W. (2012). The problem with kappa. In
Proceedings of the 13th Conference of the European
Chapter of the Association for Computational Lin-
guistics, EACL ’12, pages 345–355, Stroudsburg, PA,
USA. Association for Computational Linguistics.
Schaer, R., Muller, H., and Depeursinge, A. (2016). Opti-
mized distributed hyperparameter search and simula-
tion for lung texture classification in ct using hadoop.
J. Imaging, 2:19.
Sebastiani, F. (2002). Machine learning in automated text
categorization. ACM Comput. Surv., 34(1):1–47.
Snoek, J., Larochelle, H., and Adams, R. P. (2012). Prac-
tical bayesian optimization of machine learning algo-
rithms. In Proceedings of the 25th International Con-
ference on Neural Information Processing Systems -
Volume 2, NIPS’12, pages 2951–2959, USA. Curran
Associates Inc.
Thornton, C., Hutter, F., Hoos, H. H., and Leyton-Brown,
K. (2012). Auto-weka: Automated selection and
hyper-parameter optimization of classification algo-
rithms. CoRR, abs/1208.3719.
Distributed Optimization of Classifier Committee Hyperparameters
179