
Reliable In-Memory Data Management on Unreliable Hardware
Dirk Habich, Till Kolditz, Juliana Hildebrandt and Wolfgang Lehner
Database Systems Group, Technische Universit
¨
at Dresden, Germany
Keywords:
In-Memory, Database Systems, Error Detection, Error Correction, AN Encoding.
Abstract:
The key objective of database systems is to reliably manage data, whereby high query throughput and low
query latency are core requirements. To satisfy these requirements, database systems constantly adapt to novel
hardware features. Although it has been intensively studied and commonly accepted that hardware error rates
in terms of bit flips increase dramatically with the decrease of the underlying chip structures, most database
system research activities neglected this fact, leaving error (bit flip) detection as well as correction to the
underlying hardware. Especially for memory, silent data corruption (SDC) as a result of transient bit flips
leading to faulty data is mainly detected and corrected at the DRAM and memory-controller layer. However,
since future hardware becomes less reliable and error detection as well as correction by hardware becomes
more expensive, this free ride will come to an end in the near future. To further provide a reliable data
management, an emerging research direction will be employing specific and tailored protection techniques at
the database system level. Following that, we are currently developing and implementing an adopted system
design for state-of-the-art in-memory column stores. In this position paper, we summarize our vision, the
current state and outline future work of our research.
1 INTRODUCTION
We have already known for a long time that hardware
components are not perfect and soft errors in terms
of single bit flips happen all the time (transient bit
flips). Up to now, hardware-based protection is used
to mitigate these single bit flips. However, recent
studies have shown that future hardware is becom-
ing less and less reliable and the occurrence of multi-
bit flips instead of single bit flips is prevailing (Kim
et al., 2014; Rehman et al., 2016; Henkel et al., 2013;
Shafique et al., 2015). For example, repeatedly ac-
cessing one memory cell in DRAM modules causes
bit flips in physically-adjacent memory cells, whereby
one to four bits flips per 64-bit word have been dis-
covered (Kim et al., 2014; Mutlu, 2017). The reason
for this is a hardware failure mechanism called dis-
turbance error (Kim et al., 2014; Mutlu, 2017). In
this case, electromagnetic (cell-to-cell) interference
leads to bit flips and it is already known that this in-
terference effect increases with smaller feature sizes
and higher densities of transistors (Kim et al., 2014;
Mutlu, 2017). Furthermore, emerging non-volatile
memory technologies like PCM (phase change mem-
ory) (Lee et al., 2009), STT-MRAM (Kultursay et al.,
2013), and PRAM (Wong et al., 2012) exhibit sim-
ilar and perhaps even more reliability issues (Khan
et al., 2014; Khan et al., 2016; Liu et al., 2013; Mutlu,
2017). For instance, heat produced by writing one
PCM cell can alter the value stored in many nearby
cells (e.g., up to 11 cells in a 64 byte-block). Addi-
tionally, hardware aging effects will lead to changing
bit flip rates at run-time (Henkel et al., 2013).
Generally, all hardware components in the nano
transistor era will show an increasing unreliability be-
havior (Borkar, 2005; Henkel et al., 2013; Rehman
et al., 2016), but memory cells are more suscepti-
ble than logic gates (Henkel et al., 2013; Hwang
et al., 2012; Kim et al., 2007). To tackle the up-
coming increasing reliability concerns, there exist a
lot of hardware-oriented research activities (Borkar,
2005; Henkel et al., 2013; Khan et al., 2014; Khan
et al., 2016; Kim et al., 2007). However, these activ-
ities show that hardware-based approaches are very
effective on the one hand, but the protection is very
challenging and each technique introduces large per-
formance, chip area, and power overheads on the
other hand (Henkel et al., 2013; Rehman et al., 2016;
Shafique et al., 2015). Furthermore, the protection
techniques have to be implemented in a pessimistic
way to cover the aging aspect leading usually to an
over-provisioning. The whole is made more difficult
by Dark Silicon (Esmaeilzadeh et al., 2012): billions
of transistors can be put on a chip, but not all them can
Habich, D., Kolditz, T., Hildebrandt, J. and Lehner, W.
Reliable In-Memory Data Management on Unreliable Hardware.
DOI: 10.5220/0006884203650372
In Proceedings of the 7th Inter national Conference on Data Science, Technology and Applications (DATA 2018), pages 365-372
ISBN: 978-989-758-318-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
365

be used at the same time. This and the various new
disruptive hardware interference effects make the reli-
able hardware design and development very challeng-
ing, time consuming, and very expensive (Rehman
et al., 2016). The disadvantages outweigh the advan-
tages for hardware-based protection, so that the semi-
conductor as well as hardware/software communities
have recently experienced a shift towards mitigating
these reliability issues also at higher software layers,
rather than completely mitigating these issues only in
hardware (Henkel et al., 2013; Rehman et al., 2016;
Shafique et al., 2015).
Consequently, this shift will also affects database
systems, because data as well as query processing
have to be protected in software accordingly to further
guarantee a reliable data management on future un-
reliable hardware. Unfortunately, classical software-
based protection techniques are usually based on
data/code redundancy using dual or triple modular
redundancy (DMR/TMR). While DMR only allows
error detection, TMR can also correct errors (Pittelli
and Garcia-Molina, 1986; Pittelli and Garcia-Molina,
1989). However, the application of these techniques
with respect to in-memory database systems causes a
high overhead (Pittelli and Garcia-Molina, 1986; Pit-
telli and Garcia-Molina, 1989). For example, DMR
protection requires twice as much memory capac-
ity compared to a normal (unprotected) setting, since
data must be kept twice in different main memory lo-
cations. Furthermore, every query is redundantly ex-
ecuted with an additional voting at the end resulting
in a computational overhead slightly higher than 2x.
Thus, there is a clear need for database-specific pro-
tection approaches without sacrificing the overall per-
formance too much (B
¨
ohm et al., 2011). To tackle
that grand challenge, we present our overall vision
and summarize first promising results in this paper.
In detail, we make the following contributions:
1. We describe our big picture by introducing our as-
sumptions and based on that three requirements
for database-specific approaches (Section 2).
2. While Section 3 summarizes our novel developed
error detection approach (Kolditz et al., 2018),
Section 4 outlines our vision or research activities
for error correction.
Finally, we close the paper with related work in Sec-
tion 5 and a short conclusion in Section 6.
2 OVERALL VISION
In principle, any undetected and uncorrected bit flip
destroys the reliability objective of database systems
in form of false negatives (missing tuples), false posi-
Unreliable Hardware
Hardened
Dictionaries
Hardened Columns Redundant Columns
=
Error Detection
Error Correction
Memory
Trade-offs:
Scan
Join
Scan
Group
Sort
Challenges:
Ø Hardening data and data
structures to enable error detection
Ø Adjust processing to enable a
continuous error detection,
because bit flips can happen
anytime
Challenges:
Ø Adjust processing to
be able to correct
on-the-fly detected
bit flips
Ø Define necessary
data redundancy for
data correction
Storage Layer
Processing Layer
Changing error model All components unreliable
Reliability
Query Latency
Figure 1: Reliable In-Memory Column Store Architecture.
tives (tuples with invalid predicates) or inaccurate ag-
gregates in a silent way. So far, database systems
do not care about this reliability aspect because hard-
ware components usually provide appropriate protec-
tion techniques. However, this free-ride will come
to an end in the near future (Borkar, 2005; Henkel
et al., 2013; Rehman et al., 2016). To prepare state-
of-the-art in-memory database systems by developing
appropriate approaches, we assume in our work as il-
lustrated in Figure 1 that (i) all hardware components
are unreliable, (ii) multi-bit flips will occur regularly
rather than exceptionally, and (iii) bit flips are not
handled at the hardware layer. Furthermore, the bit
flip rate changes at runtime due to various effects like
heat (Henkel et al., 2013).
Based on these assumptions, major challenges for
in-memory database system are reliable data storage
as well as reliable query processing (B
¨
ohm et al.,
2011). To provide both reliability issues, we envi-
sion to tightly integrate protection techniques in in-
memory database systems and to use the available
database knowledge to specialize as well as to balance
protection and the associated overhead. That means,
our goal is to develop an appropriate solution satisfy-
ing the following requirements based on our assump-
tions:
(R1). Our solution has to detect as well as to correct
(i) errors (multi-bit flips) that modify data stored
in main memory, (ii) errors induced during trans-
ferring on interconnects, and (iii) errors induced
during computations during query processing (de-
tection capability).
(R2). Our solution has to be adaptable to different er-
ror model at runtime because the number and the
rate of bit flips may vary over hardware genera-
tions or due to hardware aging effects (run-time
adaptability).
(R3). Our solution has to introduce only the nec-
essary overhead in terms of memory consump-
tion and query runtime being required to protect
against a desired error model. That means, the
overhead should be as small as possible, but still
provide a reliable behavior (balanced overhead).
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
366

In our work, we mainly focus on state-of-the-art
in-memory columns stores (Abadi et al., 2013; Idreos
et al., 2012; Stonebraker et al., 2005) and our envi-
sioned reliable architecture is depicted in Figure 1. As
illustrated, we explicitly distinguish between error de-
tection and error correction on the one hand. On the
other hand, we have to consider the storage as well as
processing layer of column stores. From our point of
view, the most important part is error detection, be-
cause it is the prerequisite for error correction. If we
are not able to detect bit flips, no correction can be
triggered. Thus, we developed a novel approach for
error detection tailored for in-memory column stores
as summarized in the next section. In the following,
we want to extend this approach with error correction
capabilities.
3 ERROR DETECTION
For error detection, we developed a novel column
store-specific approach called AHEAD (Kolditz et al.,
2018) which is mainly based on error coding, but
we are not using a well-known error code like Ham-
ming (Hamming, 1950; Moon, 2005). However, our
approach has unique properties as shown later. That
means, we encode all data and data structures in way
that we are able to detect bit flips in base data as well
as during query processing. To represent the intention
of error detection, we introduce new terms for encod-
ing and decoding. We denote the encoding of data as
data hardening, since data is literally firmed so that
corruption becomes detectable. In contrast, we denote
as data softening the decoding of data, as it becomes
vulnerable to corruption again.
Generally, in-memory column stores maintain re-
lational data using the decomposition storage model
(DSM) (Copeland and Khoshafian, 1985), where each
column of a table is separately stored as a fixed-width
dense array (Abadi et al., 2013). To reconstruct the
tuples of a table, each column record is stored in
the same (array) position across all columns of a ta-
ble (Abadi et al., 2013). Column stores typically sup-
port a fixed set of basic data types, including inte-
gers, decimal (fixed-, or floating-point) numbers, and
strings. For fixed-width data types (e.g., integer, dec-
imal and floating-point), column stores utilize basic
arrays of the respective type for the values of a col-
umn (Abadi et al., 2013; Idreos et al., 2012). For
variable-width data types (e.g., strings), some kind
of dictionary encoding is applied to transform them
into fixed-width columns (Abadi et al., 2013; Abadi
et al., 2006; Binnig et al., 2009). The simplest form
constructs a dictionary for an entire column sorted on
Example
5 7 4 … 3
101
111
100
…
011
Hardening
Multiplication with A = 29
145
203
116
… 87
100
100
01
110
010
11
011
101
00
…
010
101
11
Logical Level
Physical Level
3 Data Bit Width
8 Hardened Data Bit Width
all 1 and 2 Bit Flips are detectable
Raw Data Array
Hardened Data Array
Figure 2: Example for Hardening Data Arrays.
frequency, and represents values as integer positions
in this dictionary (Abadi et al., 2013).
That means, in-memory column stores are based
on two main data structures as illustrated in Figure 1:
(i) dictionaries for variable-length data types and (ii)
column arrays for fixed-length data types. Thus, each
base table column is stored either by means of a single
data array or by a combination of a dictionary and a
data array containing fixed-width integer references
to the dictionary. The decision is made based on the
data type of the column. Therefore, we have to harden
both structures.
3.1 Hardened Data Arrays
For data arrays, we only have to harden values and
this is done using AN coding (Avizienis, 1971; Hoff-
mann et al., 2014) as illustrated in Figure 2. AN
coding is a representative of arithmetic error detect-
ing codes, where the hardened code words are com-
puted by multiplying a constant integer value A onto
each original data word. The multiplication modifies
the data word itself and all data is viewed as integers
as shown in Figure 2. As a result of this multipli-
cation, the domain of code words expands such that
only multiples of A become valid code words, and all
other integers are considered non-code words. The
used value of A has an impact on the detection ca-
pability as described later. For softening, A division
or multiplication of the inverse of A is required. Bit
flips are detected by testing the remainder of this op-
eration, which must be zero, otherwise the code word
was corrupted. A unique feature of arithmetic codes,
and thus AN coding, is the ability to operate directly
on hardened data by encoding the other operands,
too (Avizienis, 1971; Hoffmann et al., 2014).
3.1.1 Different Data Types
Regarding hardening arrays of integer data, this re-
quires only multiplication with a constant factor of A.
For decimal numbers, the case is a bit more complex:
for the sake of correctness and accuracy, database sys-
Reliable In-Memory Data Management on Unreliable Hardware
367

tems typically use fixed-point numbers and arithmetic
instead of native floating point numbers (float / dou-
ble) (Neumann, 2016). These fixed-point numbers
are usually represented as integer (Neumann, 2016),
which can be hardened like integers.
Table 1: Super As for detecting a guaranteed minimum
number of bit flips (min bfw). Numbers are: super
A/hardening overhead/hardened code bit length.
∗
=derived
by approximatio2n, bold=prime, tbc=to be computed.
min
bfw
Data Bit Width (Byte-aligned)
8 16 32
1 3/2/10 3/2/18 3/2/34
2 29/5/13 61/6/22 125/7/39
3 233/8/16 463/9/27 881/10/42
4 1,939/11/19 7,785/13/29 16, 041
∗
/14/46
5 13,963/14/22 63,877/16/32 tbc
6 55,831/16/24 tbc tbc
3.1.2 Parametrization of AN Coding
As mentioned above, AN coding has only one param-
eter A which has an impact on the error detection rate
as well as the necessary storage overhead. Now, to re-
liably detect b bit flips in each code word, a value for
A has to be used which guarantees a minimum Ham-
ming distance of b + 1, whereby A depends on the
data bit width l and on the number of detectable bit
flips (Avizienis, 1971; Hoffmann et al., 2014). More-
over, to reduce the necessary space overhead, it is usu-
ally not some arbitrary value for A sought but a small
one (called “super A”), so that the domain of code
words is small. We applied a brute force approach
to compute “super As” for different settings of l and
b, whereby the brute force approach consists of two
components:
Component 1: Determine minimum Hamming dis-
tance for a given A and l, and
Component 2: Iterate over all possible As to deter-
mine a small A with a minimum Hamming dis-
tance of b + 1, whereby component 1 is heavily
applied.
Table 1 lists an extract of computed “super As”.
For example, for 8-bit data and a minimum bit flip
weight of two, we have to use A=29 for the harden-
ing. As depicted, we require five additional bits for
the hardening. If we want to increase the minimum bit
flip weight to 3, we only have to use A=233 resulting
in a code word width of 16. In this case, the data over-
head increases from 62, 5% (13 bit code word width)
to 100% (16 bit code word width for 8 bit data).
Based on that, we are able to use this knowledge
for a balanced data hardening with regard to a specific
hardware error model (number of bit flips) and to spe-
cific data characteristics (data bit width). Addition-
ally, column data arrays can be re-hardened at run-
time with different As. Thus, the requirements (R2)
and (R3) are adequately addressed from the storage
perspective. Nevertheless, Table 1 also highlights that
the brute force approach for the computation of A is
very expensive, because we are currently not able to
compute a value for A for all settings of l and b. Thus,
a new approach have to be developed for this compu-
tation.
3.2 Hardened Dictionaries
Dictionaries are usually realized using index struc-
tures to efficiently support encoding and decod-
ing (Binnig et al., 2009). In contrast to data arrays, not
only the data values must be hardened, but also nec-
essary pointers within the index structures. To tackle
that issue, Kolditz et al. (Kolditz et al., 2014) al-
ready proposed various techniques to harden B-Trees,
which we are currently using in our approach. As
they have shown, hardening pointer-intensive struc-
tures are more challenging as hardening data arrays.
However, slightly increasing data redundancy at the
right places by incorporating context knowledge in-
creases error detection significantly (Kolditz et al.,
2014). Moreover, for dictionaries of integer data,
AN hardening can be applied on the dictionary en-
tries. The corresponding column (data array) con-
tains fixed-width, AN hardened integer references to
the dictionary.
3.3 Continuous Error Detection
To satisfy requirement (R1), we integrated bit flip de-
tection into each and every physical query operator
by checking each value. From our point of view,
this is the best solution, because bit flips caused by
any hardware components are continuously detected.
Moreover, each and every value is checked for bit
flips in the columns of base tables and intermediate
results. The integration can be seamlessly done for
both state-of-the-art processing models of column-
at-a-time (Abadi et al., 2013; Idreos et al., 2012)
and vector-at-a-time (Zukowski et al., 2012) with our
hardened storage concept. There are two reasons:
(i) the column structure is unchanged, only the data
width is increased and (ii) the values are multiplied
by A and can thus be processed as before.
We also fully implemented our error detection ap-
proach and conducted an experimental evaluation us-
ing the SSB benchmark (O’Neil et al., 2009). In
our evaluation, we compared our approach with the
Unprotected baseline and dual modular redundancy
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
368
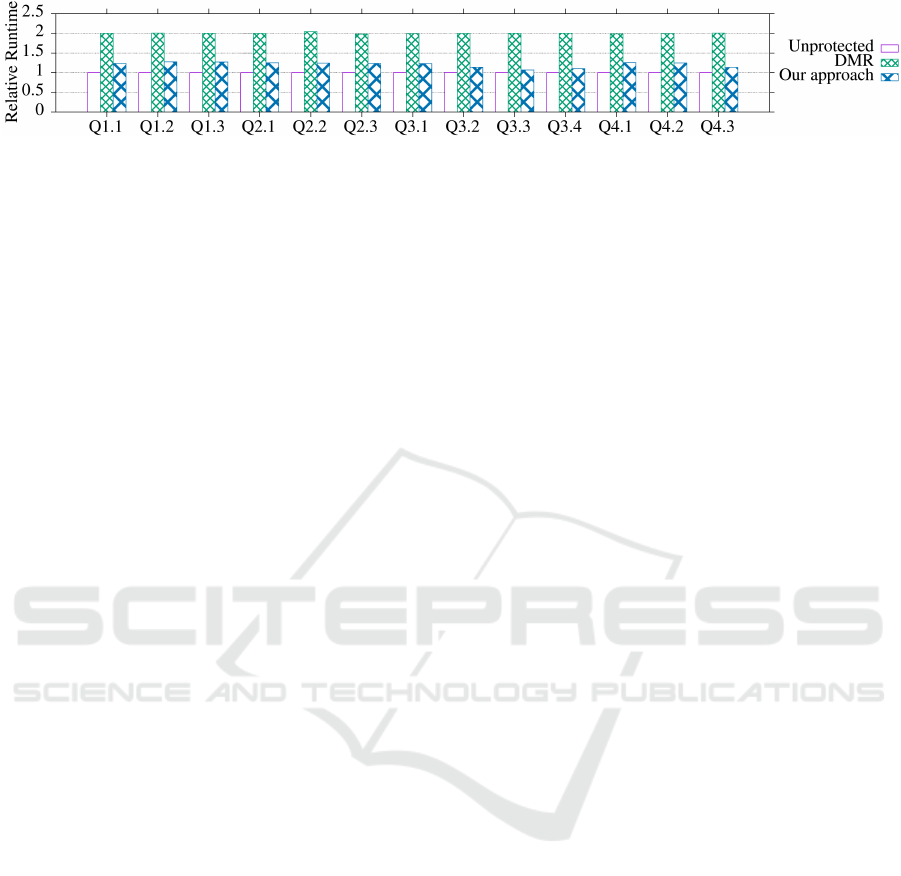
Figure 3: Relative SSB runtimes for vectorized (SSE4.2) execution (average over all scale factors).
(DMR). In the Unprotected baseline, data is always
compressed on a byte-level based on the column char-
acteristics. DMR uses the Unprotected setting and
replicates all data in main memory, executes each
query twice sequentially, and afterwards a voter com-
pares both results. Our approach hardens each col-
umn using the largest currently known A for the cor-
responding column data width from Table 1. Thus,
compared to Unprotected setting, our approach in-
creases the data width of each column to the next byte
level. For all approaches, we measured all 13 SSB
queries for vectorized (Intel SSE4.2) execution and
we varied the SSB scale factor from 1 to 10. Each
single experiment ran 10 times. Figure 3 shows vec-
torized (SSE4.2) runtimes relative to the Unprotected
baseline. On the one hand, DMR results in the ex-
pected runtime overhead of about 100%, because each
query is executed twice. On the other hand, the run-
time overhead of our approach is only between 7% to
28%. This is due to the tight integration of error de-
tection in each operator combined with our AN cod-
ing approach.
3.4 Future Work
Our future work in this direction is manifold, whereby
three aspects are very important: (i) develop new ap-
proach for the computation of the parameter value
A, (ii) investigate the interplay of data compression
and data hardening, and (iii) develop appropriate tech-
niques to protect internal query operator data struc-
tures like hash maps. For instance, the second aspects
is crucial, because in-memory column stores heavily
employ lightweight data compression to reduce the
necessary memory space and to address the access
bottleneck between main memory and CPU (Abadi
et al., 2006; Damme et al., 2017; Zukowski et al.,
2006). While both domains are orthogonal to each
other, their interplay is very important to keep the
overall memory footprint of the data as low as possi-
ble (Kolditz et al., 2015). With data hardening, com-
pression gains even more significance, since it can re-
duce the newly introduced storage overhead. How-
ever, combining both is challenging and we briefly
outline some aspects requiring closer investigation.
Fitness of Compression Algorithms. There is a high
number of lightweight data compression algorithms
(Abadi et al., 2006; Damme et al., 2017; Zukowski
et al., 2006), which differ in how far they are suited
for the combination with AN-coding.
Order of Hardening and Compression. Hardening
could be applied to compressed data, or vice-versa.
The decision depends on the compression algorithm:
While dictionary coding (Abadi et al., 2006) must
be applied before hardening to obtain integers from
variable-width data, null suppression (Abadi et al.,
2006; Damme et al., 2017; Lemire and Boytsov,
2015; Zukowski et al., 2006) could be applied before
or after.
Hardened Compression Meta Data. Most
lightweight compression algorithms store some meta
data along with the compressed data to enable decom-
pression. If hardening comes before compression, the
latter must harden the meta data on its own. For in-
stance, with run length encoding (Abadi et al., 2006;
Damme et al., 2017) of hardened data, the run values
will already be hardended, while the run lengths as
meta data still need to be hardened.
Detection and Re-encoding vs. Decompression.
Detection and re-encoding happen many times per
query. Conversely, decompression can often be de-
layed until the end of the query, since many operators
can process compressed data directly (Abadi et al.,
2013; Zukowski et al., 2006). Hence, detection and
re-encoding should not require decompression.
4 ERROR CORRECTION
Up to now, we only considered error detection. As
next, we want to extend our approach with the ability
of continuous error correction. In this case, detected
bit flips should be on-the-fly corrected during query
processing. At the moment, we are already able to
detect bit flips on value granularity and can find out
where the error occurred. Based on that property, we
believe that specific correction techniques can be de-
veloped and integrated in the query processing. For
example, if we detect a faulty code word in the input
of an operator, we can re-transmit this value, possibly
several times, to correct errors induced during trans-
mission. If we get a valid code word, processing can
Reliable In-Memory Data Management on Unreliable Hardware
369

Example
145
203
116
… 87
Hardened Data Array
Redundant Data
Column X (A=29)
122
61
183
…
305
Column Y (A=61)
267
264
299
…
392
+
Column Z = X+Y
Reconstruction by Z-Y
Reconstruction by Z-X
Figure 4: Example for Linear Combination.
continue with this correct code word. If we get an in-
valid code word, we can assume that bits are flipped
in main memory and then we require an appropriate
technique for error correction. For that, correcting bit
flips in memory requires data redundancy in any case.
Here, classical RAID-techniques or techniques from
the network coding domain like linear combinations
may be interesting to consult.
In particular, a very promising idea from our per-
spective is to use linear combinations of hardened
data columns array as illustrated in Figure 4 for the
error correction. In this example, a single redun-
dant column Z is created as a linear combination of
two columns X and Y . As depicted, the columns
X and Y can be appropriately reconstructed for cor-
rection, whereby the reconstruction is possible on a
value granularity. Fundamentally, AN coding and lin-
ear combinations perfectly fit together and they re-
quire less space overhead than triple modular redun-
dancy. Furthermore, the redundant data in form of
linear combinations are automatically hardened at the
same time, so that these data can be checked for bit
flips. Main research questions are:
1. Which linear combinations should be created at
all?
2. How can queries be answered on these linear com-
binations?
3. What does an efficient access to these linear com-
binations for value-based correction look like?
5 RELATED WORK
Fundamentally, hardware components fabricated with
nano-scale transistors face serious reliability issues
like soft errors, aging, thermal hot spots, and process
variations as a consequence of the aggressive transis-
tor miniaturization (Rehman et al., 2016). Addition-
ally, memory cells are more susceptible to soft errors
than logic gates (Henkel et al., 2013; Hwang et al.,
2012; Kim et al., 2007). These issues arise from mul-
tiple sources and they jeopardize the correct applica-
tion execution (Rehman et al., 2016). The recently
published book (Rehman et al., 2016) summarizes
state-of-the-art protection techniques in all hardware
as well as software layers and presents new results of
a large research initiative.
Hardware-Level Protection. Hardware protection
to mitigate soft errors can be done on three lay-
ers (Rehman et al., 2016): (i) transistor, (ii) circuit,
and (iii) architectural. On the transistor layer, several
techniques have been proposed to harden transistors
against radiation events like alpha particles or neutron
strikes (Itoh et al., 1980; Kohara et al., 1990). For
example, thick polyimide can be used for alpha parti-
cle protection (Itoh et al., 1980; Kohara et al., 1990).
However, this technique cannot be utilized for neutron
strikes (Rehman et al., 2016). In general, techniques
at this layer have in common that the protection re-
sults in adopted fabrication processes using special-
ized materials (Itoh et al., 1980; Kohara et al., 1990;
Rehman et al., 2016). Therefore, these techniques are
very effective, but they produce (i) substantial over-
head in terms of area and cost, and (ii) immense vali-
dation and verification costs.
At the circuit layer, redundant circuits and er-
ror detection/correction circuits are prominent exam-
ples (Dell, 1997; Ernst et al., 2004; Kim et al., 2007;
Rehman et al., 2016). For instance, the RAZOR ap-
proach introduces shadow flip flops in the pipeline
to recover from errors in logic gates (Ernst et al.,
2004). Memories and caches are usually protected
using error correcting codes (ECC) or parity tech-
niques. Current ECC memories are based on Ham-
ming using a (72,64) code, meaning that 64 bits of
data are enhanced with 8 bits of parity allowing sin-
gle error correction and double error detection. To
address multi bit flips advanced ECC schemes have
to be used. Examples are (i) IBM’s Chipkill ap-
proach, which computes the parity bits from differ-
ent memory words and even separate DIMMs instead
of physically adjacent bits (Dell, 1997), and (ii) (Kim
et al., 2007), which shows that other ECC codes like
BCH-codes (Moon, 2005) can be realized in hard-
ware. However, this increases the number of transis-
tors in hardware and consequently impacts the energy
demand, the overhead growing quickly as the code
strength is increased (Kim et al., 2007). Addition-
ally, reading and computing the enhanced ECC bits
can be a performance bottleneck during read opera-
tions (Kim et al., 2007).
At the architectural layer, the protection is based
upon the redundant execution either in space (using
duplicated hardware units) or in time (using the same
hardware multiple times for redundant execution and
comparing the results). Dual Modular Redundancy
(DMR) and Triple Modular Redundancy (TMR) are
traditional approaches. Generally, these techniques
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
370

lead to an increased power usage which may poten-
tially increase the temperature (Rehman et al., 2016).
Increased temperatures lead to higher soft error rate
and increased aging (Rehman et al., 2016).
To summarize, hardware-based protection has
been proposed at different layers. The techniques are
usually very effective, but they also have some draw-
backs in terms of (i) high chip area overhead leading
at the same time to more power overhead and (ii) per-
formance penalties. Furthermore, the high verifica-
tion/validation costs make the reliable hardware de-
sign and development very expensive and time con-
suming (Rehman et al., 2016). To overcome these
non-negligible drawbacks, a rich set of software-
based techniques has evolved.
Software-Level Protection. Classical software-
based protection techniques are (Goloubeva et al.,
2006; Rehman et al., 2016): (i) N-version pro-
gramming, (ii) code redundancy, (iii) control flow
checking, and (iv) checkpoint recovery. For in-
stance, N-version programming (Avizienis, 1985)
is based on implementing multiple program ver-
sions of the same specification which reduces the
probability of identical errors occurring in two or
more versions. State-of-the-art redundancy-based
techniques are Error Detection using Duplicated
Instructions (EDDI) (Oh et al., 2002) and Software
Implemented Fault Tolerance (SWIFT) (Reis et al.,
2005). Both provide software reliability by dupli-
cating instructions, and inserting comparison and
checking instructions. However, these techniques
incur significant performance overheads (Oh et al.,
2002; Reis et al., 2005).
Moreover, AN coding has also been used for
software-based fault tolerance (Hoffmann et al., 2014;
Schiffel, 2011; Ulbrich et al., 2012). For instance, the
work of Schiffel (Schiffel, 2011) allows to encode ex-
isting software binaries or to add encoding at compile
time, where not all variables’ states need to be known
in advance. However, in her work she only describes
encoding integers of size |D| ∈ {1, 8, 16, 32} bits and
pointers, where the encoded values are always 64 bits
large. Furthermore, protecting processors by AN cod-
ing was also suggested in (Forin, 1989).
6 CONCLUSION
A few years ago, Boehm et al. (B
¨
ohm et al., 2011)
pointed out the lack of data management techniques
dealing with an increasing number of bit flips in main
memory as a more and more relevant source of er-
rors. Thus, we presented our overall vision for a reli-
able data management on unreliable hardware in this
position paper, because recent studies show that fu-
ture hardware becomes less reliable. In particular,
we summarized our novel develop error detection ap-
proach, which is the first comprehensive database-
specific approach to tackle a reliable data manage-
ment on unreliable hardware.
REFERENCES
Abadi, D., Boncz, P. A., Harizopoulos, S., Idreos, S., and
Madden, S. (2013). The design and implementation
of modern column-oriented database systems. Foun-
dations and Trends in Databases, 5(3):197–280.
Abadi, D. J., Madden, S., and Ferreira, M. (2006). Integrat-
ing compression and execution in column-oriented
database systems. In SIGMOD 2006, pages 671–682.
Avizienis, A. (1971). Arithmetic error codes: Cost and
effectiveness studies for application in digital system
design. IEEE Trans. Computers, 20(11):1322–1331.
Avizienis, A. (1985). The n-version approach to fault-
tolerant software. IEEE Trans. Software Eng.,
11(12):1491–1501.
Binnig, C., Hildenbrand, S., and F
¨
arber, F. (2009).
Dictionary-based order-preserving string compression
for main memory column stores. In SIGMOD 2009,
pages 283–296.
B
¨
ohm, M., Lehner, W., and Fetzer, C. (2011). Resiliency-
aware data management. PVLDB, 4(12):1462–1465.
Borkar, S. Y. (2005). Designing reliable systems from unre-
liable components: The challenges of transistor vari-
ability and degradation. IEEE Micro, 25(6):10–16.
Copeland, G. P. and Khoshafian, S. (1985). A decompo-
sition storage model. In SIGMOD 1985, pages 268–
279.
Damme, P., Habich, D., Hildebrandt, J., and Lehner, W.
(2017). Lightweight data compression algorithms: An
experimental survey (experiments and analyses). In
EDBT 2017, pages 72–83.
Dell, T. J. (1997). A white paper on the benefits of chipkill-
correct ecc for pc server main memory. IBM Micro-
electronics Division, 11.
Ernst, D., Das, S., Lee, S., Blaauw, D., Austin, T., Mudge,
T., Kim, N. S., and Flautner, K. (2004). Razor: circuit-
level correction of timing errors for low-power opera-
tion. IEEE Micro, 24(6):10–20.
Esmaeilzadeh, H., Blem, E. R., Amant, R. S., Sankar-
alingam, K., and Burger, D. (2012). Dark silicon and
the end of multicore scaling. IEEE Micro, 32(3):122–
134.
Forin, P. (1989). Vital coded microprocessor: Principles and
application for various transit systems. IFAC-GCCT.
Goloubeva, O., Rebaudengo, M., Reorda, M. S., and Vi-
olante, M. (2006). Software-implemented hardware
fault tolerance. Springer Science & Business Media.
Hamming, R. W. (1950). Error detecting and error correct-
ing codes. Bell System technical journal, 29(2).
Reliable In-Memory Data Management on Unreliable Hardware
371

Henkel, J., Bauer, L., Dutt, N., Gupta, P., Nassif, S. R.,
Shafique, M., Tahoori, M. B., and Wehn, N. (2013).
Reliable on-chip systems in the nano-era: lessons
learnt and future trends. In DAC 2013, pages 99:1–
99:10.
Hoffmann, M., Ulbrich, P., Dietrich, C., Schirmeier, H.,
Lohmann, D., and Schr
¨
oder-Preikschat, W. (2014). A
practitioner’s guide to software-based soft-error miti-
gation using an-codes. In HASE 2014, pages 33–40.
Hwang, A. A., Stefanovici, I. A., and Schroeder, B. (2012).
Cosmic rays don’t strike twice: understanding the na-
ture of DRAM errors and the implications for system
design. In ASPLOS 2012, pages 111–122.
Idreos, S., Groffen, F., Nes, N., Manegold, S., Mullender,
K. S., and Kersten, M. L. (2012). Monetdb: Two
decades of research in column-oriented database ar-
chitectures. IEEE Data Eng. Bull., 35(1):40–45.
Itoh, K., Hori, R., Masuda, H., Kamigaki, Y., Kawamoto,
H., and Katto, H. (1980). A single 5v 64k dynamic
ram. In ISSCC 1980, volume 23, pages 228–229.
Khan, S., Lee, D., Kim, Y., Alameldeen, A. R., Wilkerson,
C., and Mutlu, O. (2014). The efficacy of error miti-
gation techniques for dram retention failures: A com-
parative experimental study. SIGMETRICS Perform.
Eval. Rev., 42(1):519–532.
Khan, S. M., Lee, D., and Mutlu, O. (2016). PARBOR:
an efficient system-level technique to detect data-
dependent failures in DRAM. In DSN 2016, pages
239–250.
Kim, J., Hardavellas, N., Mai, K., Falsafi, B., and Hoe,
J. (2007). Multi-bit error tolerant caches using two-
dimensional error coding. In Symposium on Microar-
chitecture 2007, pages 197–209.
Kim, Y., Daly, R., Kim, J., Fallin, C., Lee, J., Lee, D., Wilk-
erson, C., Lai, K., and Mutlu, O. (2014). Flipping bits
in memory without accessing them: An experimental
study of DRAM disturbance errors. In ISCA 2014,
pages 361–372.
Kohara, M., Mashiko, Y., Nakasaki, K., and Nunoshita, M.
(1990). Mechanism of electromigration in ceramic
packages induced by chip-coating polyimide. IEEE
Transactions on Components, Hybrids, and Manufac-
turing Technology, 13(4):873–878.
Kolditz, T., Habich, D., Damme, P., Lehner, W., Kuvaiskii,
D., Oleksenko, O., and Fetzer, C. (2015). Resiliency-
aware data compression for in-memory database sys-
tems. In DATA 2015, pages 326–331.
Kolditz, T., Habich, D., Lehner, W., Werner, M., and
de Bruijn, S. T. J. (2018). AHEAD: adaptable data
hardening for on-the-fly hardware error detection dur-
ing database query processing. In SIGMOD, pages
1619–1634.
Kolditz, T., Kissinger, T., Schlegel, B., Habich, D., and
Lehner, W. (2014). Online bit flip detection for in-
memory b-trees on unreliable hardware. In DaMoN
2014, pages 5:1–5:9.
Kultursay, E., Kandemir, M. T., Sivasubramaniam, A., and
Mutlu, O. (2013). Evaluating STT-RAM as an energy-
efficient main memory alternative. In ISPASS 2013,
pages 256–267.
Lee, B. C., Ipek, E., Mutlu, O., and Burger, D. (2009). Ar-
chitecting phase change memory as a scalable dram
alternative. In ISCA 2009, pages 2–13.
Lemire, D. and Boytsov, L. (2015). Decoding billions of in-
tegers per second through vectorization. Softw., Pract.
Exper., 45(1):1–29.
Liu, J., Jaiyen, B., Kim, Y., Wilkerson, C., and Mutlu, O.
(2013). An experimental study of data retention be-
havior in modern dram devices: Implications for re-
tention time profiling mechanisms. SIGARCH Com-
put. Archit. News, 41(3):60–71.
Moon, T. K. (2005). Error correction coding. Mathematical
Methods and Algorithms. Jhon Wiley and Son.
Mutlu, O. (2017). The rowhammer problem and other is-
sues we may face as memory becomes denser. In
DATE 2017, pages 1116–1121.
Neumann, T. (2016). The price of correctness.
http://databasearchitects.blogspot.de/2015/12/the-
price-of-correctness.html.
Oh, N., Shirvani, P. P., and McCluskey, E. J. (2002).
Error detection by duplicated instructions in super-
scalar processors. IEEE Transactions on Reliability,
51(1):63–75.
O’Neil, P., O’Neil, E., Chen, X., and Revilak, S. (2009).
The Star Schema Benchmark and Augmented Fact Ta-
ble Indexing, pages 237–252.
Pittelli, F. M. and Garcia-Molina, H. (1986). Database
processing with triple modular redundancy. In SRDS
1986, pages 95–103.
Pittelli, F. M. and Garcia-Molina, H. (1989). Reliable
scheduling in a TMR database system. ACM Trans.
Comput. Syst., 7(1):25–60.
Rehman, S., Shafique, M., and Henkel, J. (2016). Reliable
Software for Unreliable Hardware - A Cross Layer
Perspective. Springer.
Reis, G. A., Chang, J., Vachharajani, N., Rangan, R., and
August, D. I. (2005). SWIFT: software implemented
fault tolerance. In CGO 2005, pages 243–254.
Schiffel, U. (2011). Hardware error detection using AN-
Codes. PhD thesis, Dresden University of Technology.
Shafique, M. et al. (2015). Multi-layer software reliability
for unreliable hardware. it - Information Technology,
57(3):170–180.
Stonebraker, M., Abadi, D. J., Batkin, A., Chen, X., Cher-
niack, M., Ferreira, M., Lau, E., Lin, A., Madden,
S., O’Neil, E. J., O’Neil, P. E., Rasin, A., Tran, N.,
and Zdonik, S. B. (2005). C-store: A column-oriented
DBMS. In VLDB 2005, pages 553–564.
Ulbrich, P., Hoffmann, M., Kapitza, R., Lohmann, D.,
Schroder-Preikschat, W., and Schmid, R. (2012).
Eliminating single points of failure in software-based
redundancy. In EDCC 2012, pages 49–60.
Wong, H. P., Lee, H., Yu, S., Chen, Y., Wu, Y., Chen, P.,
Lee, B., Chen, F. T., and Tsai, M. (2012). Metal-oxide
RRAM. Proceedings of the IEEE, 100(6):1951–1970.
Zukowski, M., H
´
eman, S., Nes, N., and Boncz, P. A. (2006).
Super-scalar RAM-CPU cache compression. In ICDE
2006, page 59.
Zukowski, M., van de Wiel, M., and Boncz, P. A. (2012).
Vectorwise: A vectorized analytical DBMS. In ICDE
2012, pages 1349–1350.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
372
