Virtual Network Function Embedding in Multi-hop Wireless Networks

Zahra Jahedi and Thomas Kunz

Department of System and Computer Engineering, Carleton University, Ottawa, Canada

Keywords:

Wireless Multi-hop Network, Network Function, Network Function Virtualization, Network Function

Embedding, Integer Linear Programming.

Abstract:

The use of Network Function Virtualization (NFV) and Software Deﬁned Network (SDN) provides oppor-

tunities to offer services with lower CAPEX/OPEX for service providers and deploy new services quickly.

However, it will introduce new challenges. One of the main challenges is an optimized placement of the vir-

tualized functions based on the characteristics and available resources of the network. Placement of Network

Functions (NFs) can affect the path trafﬁc ﬂows take and consequently bandwidth usage in the network. While

most of the research is focused on the challenges of NFV in wired networks, it can also be applied to wireless

networks. However, the speciﬁc differences between the wired and wireless networks should be considered.

In this paper, we are expanding one of the comprehensive placement methods in the wired networks which

use Integer Linear Programming (ILP) to place a chain of NFs. The extended model formulates the main

characteristic of the wireless networks which is a scarcity of bandwidth due to interference. As our results

show, the interference in the wireless networks increases the bandwidth usage and consequently the average

NF deployment cost. To address this, we can either increase the number of nodes or the nodal resources to

achieve higher placement success rates.

1 INTRODUCTION

A Service Chain (SC) is a chain of high-level services,

where each service is composed of Network Func-

tions (NFs). A chain of NFs with predeﬁned parame-

ters is referred to as a Service Graph (SG). The place-

ment of all NFs of an SG can be referred to as a Net-

work Function Embedding Problem (NFEP). NFEP

can be explained as a way to map the Virtual Net-

work Functions (VNF) and the links between them to

the physical network. There are several types of al-

gorithms proposed to solve the NFEP. Previous stud-

ies are mostly focused on the placement of NFs in

wired networks while the use of NFV can bring com-

parable advantages to wireless networks. NFV intro-

duced new possibilities to wireless networks such as

network virtualization. Where subscribers can cus-

tomize their exclusive access networks while using

the shared infrastructure. The amount of literature

on wireless network virtualization shows the impor-

tance of NFV in the wireless networks. However,

there are only a few papers considering the problem

of NFEP in wireless networks. To our knowledge,

none of the proposed methods for NFEP in wireless

networks include the effect of interference in their

optimization model. It is assumed that the interfer-

ence is being handled by using orthogonal channels

in the network. However, this is only possible where

we have multi-channel multi-radio networks. Even in

those networks, there is interference.

We included the effect of interference in our op-

timization model. In (Sahhaf et al., 2015), the

NFEP has been formulated as an optimization prob-

lem which can be solved with Integer Linear Pro-

gramming (ILP). In this method, the objective is to

minimize the mapping cost based on the requirements

of the NFs and available resources in the network.

The cost of mapping is based on the consumed re-

sources by the NFs in the physical network which in-

cludes: (i) The total units of CPU, memory, and stor-

age used by NFs in physical nodes. (ii) The total units

of bandwidth used by virtual links in the physical net-

work.

The modeling results have been observed and

compared to the wired ones in order to analyze the

effect of interference on the ratio of accepted re-

quests. Based on the results and different scenarios

modeled with MATLAB, a couple of solutions have

been provided to increase the acceptance ratio in wire-

less multi-hop networks. The remainder of this pa-

Jahedi, Z. and Kunz, T.

Virtual Network Function Embedding in Multi-hop Wireless Networks.

DOI: 10.5220/0006887400330041

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 1: DCNET, ICE-B, OPTICS, SIGMAP and WINSYS, pages 33-41

ISBN: 978-989-758-319-3

per is organized as follows: Section II discusses re-

lated work on NFEP and the characteristics of the

optimization models introduced in the related papers.

Section III introduces the optimization model, its con-

straints, variables, and objective function. Section IV

describes the modeling environment and results. We

conclude the work in Section V.

2 RELATED WORK

Solving NFEP is known to be NP-hard (Sahhaf et al.,

2015). Designing a heuristic algorithm can be a solu-

tion for this matter. As our aim is to study the effect

of a multi-hop wireless network on the placement of

NFs, we only consider exact solutions in this paper.

The exact solution in most of the proposed approaches

formulates NFEP using Linear Programming and can

be differentiated based on the constraints and the ob-

jective function.

The amount of work on NFEP is considerable.

Most of the works in this domain are related to wired

networks. In (Bouet et al., 2015), the authors used

Integer Linear Programming (ILP) in order to ﬁnd

an optimum solution for placing Deep Packet Inspec-

tion (DPI) as a VNF in the network. In the proposed

method, the objective function is to minimize the acti-

vation and maintenance cost of the virtual DPI (vDPI)

and the considered constraint is the network’s avail-

able bandwidth. In (Mohammadkhan et al., 2015)

the authors used Mixed Integer Linear Programming

(MILP) to ﬁnd an optimum solution. The proposed

optimization is based on maximizing the number of

services that can be supported in a switch. In this so-

lution, the constraints are based on the number of free

cores, tolerable delay of ﬂows and links’ bandwidth.

The objectives of (Mohammadkhan et al., 2015) are

minimizing maximum link utilization and maximum

core utilization, which leads to the distribution of load

between available resources. Leivadeasa et al. pro-

posed a Mixed Integer Programing (MIP) formula-

tion with the nodes’ capacity and the bandwidth of

the links as the constraints in (Leivadeas et al., 2017).

It considers minimizing activation, maintenance cost,

and load balancing among the resources as the objec-

tive function (Leivadeas et al., 2017). (Botero et al.,

2012) is another proposed method based on an ILP

which aims at minimizing the resource consumption

and energy saving by turning off unused resources.

Finally, as mentioned earlier, (Sahhaf et al., 2015) is

considering the available resources of the nodes, the

available bandwidth of the links and the requested

QoS as constraints and minimizes the resources us-

age.

The topic of NFV in wireless networks has re-

ceived a signiﬁcant attention in the literature, where

most of the focus is on wireless network virtualiza-

tion. (Riggio et al., 2015) talks about virtual WiFi

where kernelbased virtual machines are used as a vir-

tual wireless LAN device. The authors of (Riggio

et al., 2015) provide an integer linear programming

for placing the VNFs in a hybrid wireless network

were there are forwarding nodes, some with process-

ing capacity, and some are access points. In this

paper, the optimization method is designed without

considering the effect of interference. Its authors as-

sumed that Orthogonal Frequency Division Multiple

Access (OFDMA) is being used in order to handle the

problem of interference. (Lv et al., 2012) considers

the embedding of virtual wireless mesh gateways and

the virtual links between them. The problem of inter-

ference between the wireless links has been solved by

considering multi-radio multi-channel networks. Its

authors assign orthogonal channels to the neighbor-

ing links. The same method has been used in (Park

and Kim, 2009) where the interference is being han-

dled separately from the optimization model. To our

knowledge, none of the papers considering NFEP in

the wireless networks include the effect of interfer-

ence in their optimization model. We model the inter-

ference and provide the related formulation in order

to consider interference as one of the constraints.

3 OPTIMIZATION METHOD

As the service requests arrive over time, the embed-

ding algorithm decides where to place the NFs in the

physical network subject to various constraints. Each

request has an associated duration. If the request is

accepted, the required resources will be assigned and

when the request expires the used resources will be

released.

We are using Integer Linear Programming (ILP)

as the optimization method. ILP consists of two parts,

an Objective function which calculates the cost of

each mapping and chooses the one with the lowest

cost, and the constraints, which apply the limitations

we have with regard to the resources in the physi-

cal network. ILP will choose the mapping that sat-

isﬁes all of the constraints and minimizes the objec-

tive function. In this section, we deﬁne the variables,

constraints and the objective function similar to the

optimization method in (Sahhaf et al., 2015) and then

introduce the extension of the model and the added

constraint for multi-hop wireless networks.

DCNET 2018 - International Conference on Data Communication Networking

3.1 Input Parameters

• Sets

– N

, set of physical nodes where u is represent-

ing node u ∈ N

– L

, set of physical links where E

∈ L

is rep-

resenting the physical link connecting node u to

– F, set of ﬂows where f is representing ﬂow f ∈

F. Each ﬂow f consists of a set of requested

NFs with required resources, SG

– N

, set of NFs where i ∈ N

represents NF

ﬂow f .

– L

, set of virtual links between NFs of ﬂow

f , where e

f ,i j

∈ L

represents the virtual link

which connects NF i to j.

• Constants

– C

, available processing units in physical node

– c

f ,i

, requested processing units for NF i of ﬂow

f .

– M

, available memory units in physical node u.

– m

f ,i

, requested memory units for NF i of ﬂow

f .

– S

, available storage units in physical node u.

– s

f ,i

, requested storage units for NF i of ﬂow f .

– BW

, available BW over the physical link be-

tween node u and v.

– bw

f ,e

i j

, requested BW for the link that is con-

necting NF, i to j in ﬂow f .

• Decision Variables

– x

f ,i,u

, a binary variable where one means that

function i from ﬂow f is placed in physical

node u.

– F

f ,e

i j

, a binary variable which is equal to one

when the virtual link between NFs i and j is

mapped to one or more physical links and phys-

ical link E

is one of them. In the case of map-

ping a virtual link to multiple physical links all

the related variables must be set to one.

3.2 Objective Function

As mentioned before, the objective is to minimize the

placement cost. The cost consists of resources that are

used in the physical network which include nodes’ re-

sources (processing, memory, and storage) and links’

BW. Term 1 shows the objective function where the

ﬁrst part considers the nodes’ resources and the sec-

ond part the BW usage. Term 2 is a more detailed ver-

sion of Term 1, expressing the same objective func-

tion in terms of the notation introduced earlier.

∑

u∈N

∑

i∈N

cost(i, u) +

∑

∈L

cost( f , E

) (1)

∑

u∈N

∑

i∈N

f ,i

+ s

f ,i

+ m

f ,i

) ∗ x

f ,i,u

∑

∈L

∑

i j

∈L

(bw

f ,e

i j

∗ F

f ,e

i j

) (2)

3.3 Constraints

Constraints are sets of equalities and inequalities

which are deﬁned based on the conditions the op-

timization model must satisfy. Over-assignment of

the physical resources will be prevented by the con-

straints. The ﬁrst three constraints ensure that the

summation of processing, memory and storage units

of the placed NFs do not exceed each node’s re-

sources.

∑

i∈N

f ,i

f ,i,u

≤ C

, ∀u ∈ N

(3)

∑

i∈N

f ,i

f ,i,u

≤ M

, ∀u ∈ N

(4)

∑

i∈N

f ,i

f ,i,u

≤ S

, ∀u ∈ N

(5)

Inequality 6 prevents over-assignment of bandwidth

in each physical link.

∑

∈L

∑

f ,i j

∈L

f ,e

i j

≤ BW

, ∀E

∈ L

(6)

Each virtual link between the NFs can be mapped

to one or more than one of the physical links. In case a

set of physical links connected to each other are cho-

sen to connect two NFs, Eq. 7 makes sure all the re-

lated physical links are chosen.

∑

∈L

,u=src

f ,e

i j

−

∑

∈L

,u=dst

f ,e

i j

= x

f ,i,u

− x

f , j,u

(7)

∀e

i j

∈ L

, ∀u ∈ N

Last but not least each NF should be placed in the

physical network once.

∑

u∈N

f ,i,u

= 1, ∀i ∈ N

(8)

Virtual Network Function Embedding in Multi-hop Wireless Networks

3.4 Extended Model for Wireless

Networks

The basic model is designed for wired networks. In

order to extend the model to be applicable to wireless

networks, a couple of changes must be made in the

constraints and objective function. The BW usage of

wireless links is different from wired ones. In a wired

network, it is sufﬁcient to require that the summation

of required bandwidth for the mapped virtual links

should not exceed the physical link’s bandwidth. In

multi-hop wireless networks, where nodes share ac-

cess to the common shared channel, using each link

will affect the adjacent links’ available bandwidth. In

order to consider this effect, we have to model the

interference between wireless links. We use the inter-

ference model in (Kunz et al., 2012) and redeﬁne the

constraint for wireless links.

The interference in wireless networks can be mod-

eled based on either the protocol or the physical

model. Each of these models deﬁnes conditions for a

successful transmission in the wireless network (Jain

et al., 2005). In our optimization model, we used the

protocol model. We assume in the case of a single

wireless channel, d

expresses the distance between

nodes u and v, and all nodes have the same identical

transmission range R. With these assumptions, the

transmission from u to v is successful if the following

two conditions are satisﬁed:

• d

≤ R

• Any node k, such that d

, d

≤ R, is not transmit-

ting.

These two conditions imply that transmission in the

link between nodes u and v will affect the BW usage

of all the links whose transmitter is within transmis-

sion range of the sender or the receiver. To formulate

this as one of the constraints in the optimization, an

interference set has been deﬁned for each link. It con-

sists of all the links that are connected to the nodes in

the transmission range of the sender or receiver.

∀E

∈ L

intset

= {E

∨ d

≤ R}

Then for the bandwidth constraint, instead of inequal-

ity 6, we have The following E.q 9. Where for each

of the wireless links E

the cumulative BW used by

mapped virtual links to the physical link E

and to the

physical links in the interference set of E

shouldn’t

exceed its available BW.

∑

i j

∈L

f ,e

i j

f ,e

i j

∑

i j

∈L

∑

∈intset

f ,e

i j

f ,e

i j

≤ BW

(9)

Also the second term in the objective function

changes to the following term in order to consider the

cost of BW usage due to interference.

∑

u∈N

∑

i∈N

f ,i

+ s

f ,i

+ m

f ,i

) ∗ x

f ,i,u

∑

∈L

∑

i j

∈L

(bw

f ,e

i j

∑

∈intset

f ,e

i j

) ∗ F

f ,e

i j

(10)

4 MODELING RESULTS

Our main goal is to apply the existing and extended

optimization method for placing NFs in multi-hop

wireless networks and study the impact of the wire-

less network characteristics on the results. We also

implemented the basic method as a way to capture the

NF placement under the assumptions of a wired net-

work. The placement rate and placement costs then

serve as a benchmark to compare our results against.

We ﬁrst applied our extended model to a wired net-

work topology and observed the differences in the

results. Next, we generated a number of multi-hop

wireless topologies and placed SGs based on both our

extended model and the basic model. In order to see

the impact of our approach in bigger networks we in-

creased the number of nodes and observed the results

as a function of network size.

In this section, we describe the modeling environ-

ment and its characteristics, then introduce the mea-

surement metrics. In the end, we discuss the results

of the modeling.

4.1 Modeling Environment

We used MATLAB to solve the ILP. The wired net-

work topology was chosen to be the same as the small

network in (Sahhaf et al., 2015) which was chosen

from the Internet Topology zoo (Knight, 2010). We

used the ’BT Europe’ topology which has 25 nodes

and 37 edges. In order to generate wireless topolo-

gies, we used the same method as (Kunz et al., 2012)

where the nodes are randomly deployed in a square

area, based on a uniform distribution. The square area

grows with the number of nodes such that the average

node density is constant and ranges from 346∗346m

for the 10 nodes network to 600 ∗ 600m

for the 30

nodes network (Kunz et al., 2012). The links in the

wireless network are based on the transmission range

and all of the generated topologies are connected.

DCNET 2018 - International Conference on Data Communication Networking

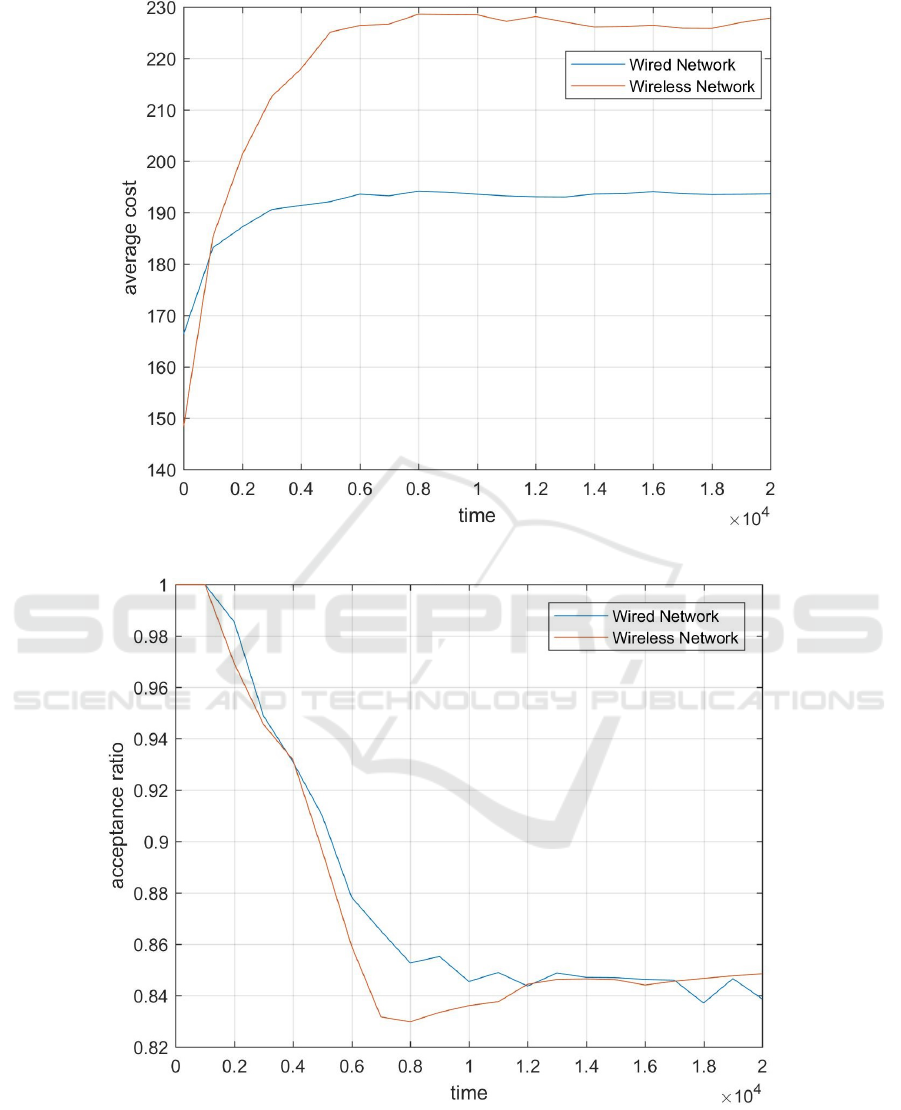
Figure 1: Average Cost in a Wired (With Basic Model) and Wireless Network (With Extended Model), ’BT Europe’ Topology.

Figure 2: Acceptance Ratio in a Wired (With Basic Model) and Wireless Network (With Extended Model), ’BT Europe’

Topology.

The parameter values were inspired by (Sahhaf

et al., 2015). Processing, memory and storage ca-

pacity of the nodes and bandwidth of the links are

numbers uniformly distributed between 100 and 150

in both network scenarios. The ﬂows arrive over

time following a Poisson process with an average rate

Virtual Network Function Embedding in Multi-hop Wireless Networks

of four ﬂows per 100 time units. Each ﬂow has a

lifetime, exponentially distributed with an average of

µ = 1000 time units and is accompanied by a Ser-

vice Graph, deﬁning the required NFs and their in-

terconnection to handle this ﬂow. The number of NFs

for each of the requests is a number uniformly dis-

tributed between 2 and 10. The computation, memory

and storage unit demands of each NF follows a uni-

form distribution between 1 and 20. The bandwidth

requirement of each link is between 1 and 50 units,

uniformly distributed.

4.2 Measurement Metrics

We used different metrics in order to compare the re-

sults and observe the impact of the wireless network’s

characteristics in the NFEP.

• Average cost: average of the units of computa-

tion, memory, and storage used for the deployed

service requests that are not expired.

• Acceptance ratio: The total number of accepted

requests divided by the total number of requests.

• Number of physical links used to deploy SGs: It

shows us over how many nodes the NFs have been

deployed in the wired and wireless network.

4.3 Results

In this section, we discuss the results of the model-

ing for wired and wireless networks. For the basic

model, we used the ’BT Europe’ topology from the

Internet Topology Zoo (Knight, 2010). This topol-

ogy has been chosen to be able to compare the results

to (Sahhaf et al., 2015). The rest of the results are

based on random wireless topologies that have been

generated as discussed above. In these topologies, we

kept the density of the nodes constant as the number

of the nodes increases. The program ran for 20000

seconds in order to reach a steady state where the

curves ﬂatten off after initial settling due to the ini-

tially unloaded network. Fig. 1 shows the average

cost of deploying requests over time in the wired and

wireless network. As was expected, the interference

model has caused higher bandwidth usage and higher

average cost for placing the NFs. Higher BW usage

in the wireless network lowers the number of requests

that can be placed in the network and reduces the ac-

ceptance ratio. The low reduction of the acceptance

ratio in Fig. 2 is due to the fact that, for the chosen

arrival rate of the requests and requested resources,

most of the SCs can be placed in one or two nodes.

Which limits the impact of interference in the accep-

tance ratio. The next set of ﬁgures shows the result by

running the basic and extended optimization model

for the randomly generated topologies. Fig. 3 shows

the average cost for different-sized wired and wireless

networks. Fig. 3 demonstrate clearly that increas-

ing the number of the nodes can decrease the average

cost. This is mainly due to the fact that the optimiza-

tion method tends to minimize the resource usage for

each SG; therefore, it chooses a placement that has

fewer physical links involved. This is conﬁrmed by

the next ﬁgure. Increasing the number of nodes will

increase the possibility to use fewer physical links and

consequently lower the average cost. This is why the

decrease in the wireless networks is higher than the

wired one. We measured the number of assigned links

for each accepted SG and also the number of the vir-

tual links that were requested for each SG in the net-

work. Fig. 4 shows the results of a 20 node wireless

network with random topology. We can see that the

majority of SG requests is placed completely in one

node, very few placements involve multiple nodes.

This is true even though the number of virtual links

of the SGs ranges from 1 to 9. Fig. 4 and 5 show

that there can be a trade-off between a number of the

nodes and BW usage in the network. Increasing the

number of nodes increases (overall) resources such as

memory, CPU, and storage. While this increases the

overall costs for deploying the network, it reduces the

average cost of deploying SGs.

Fig. 5 shows the results from a scenario where we

increased the node’s computation, memory and stor-

age by 50 units. In this scenario, we kept the num-

ber of the nodes constant (20 nodes) and increased

the available resources in each node. It can be seen

that, as the nodes’ resources are increased, the aver-

age deployment cost dropped in both the wireless and

wired network. However, the decrease is higher in

the wireless network case. This again shows a trade-

off between lowering the cost of the deployment of

NFs by using less bandwidth and increasing the cost

of the network by increasing the available resources

of the nodes. We compared the cost reduction in Fig.

6. This ﬁgure shows the cost reduction (in number

of units) when we increase the nodes’ resources. As

we can see, the number of units saved is much higher

in the wireless network. The cost added by increasing

the available resources in each node is 150 processing,

memory and storage units. This is a one-time cost and

for the network of 20 nodes, it will be 3000 units. We

can see that this increase leads to a large cost reduc-

tion over time. It can also be seen that by increasing

the available resources the average cost for the wired

and wireless networks becomes close to each other.

DCNET 2018 - International Conference on Data Communication Networking

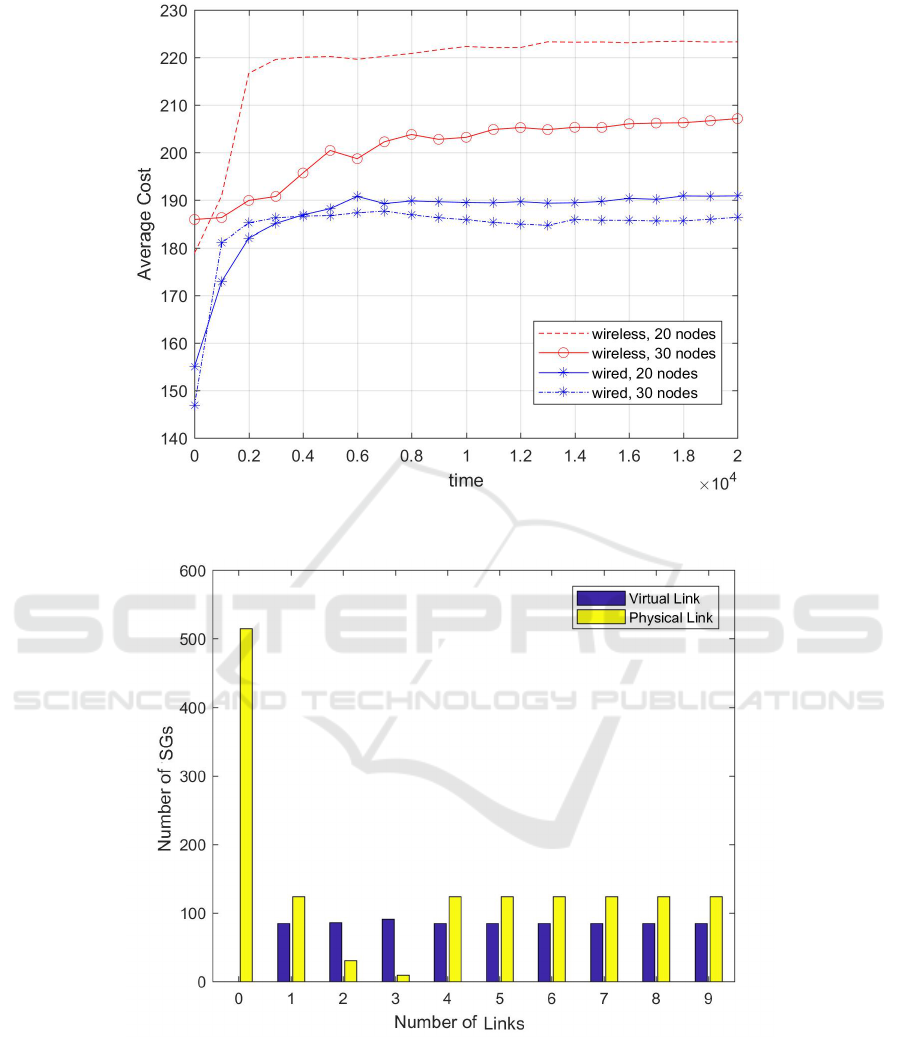
Figure 3: Average Cost in Wireless(With The Extended Model) and Wired Networks(With The Basic Model) with Increasing

Number of Nodes.

Figure 4: Number of Physical Links and Number of Virtual Links in the SG’s Requests (20 Nodes, Random Topology).

5 CONCLUSIONS

Placing NFs in a multi-hop wireless network can be

more challenging as there is more BW scarcity: wire-

less links interfere with and therefore reduce the avail-

able BW of links in their vicinity. This challenge

can affect the NF placement in comparison to wired

networks. In this paper, we extend an existing op-

timization method for a wired network and consider

the characteristics of the wireless network. The basic

and extended optimization model are applied to the

topology reported in (Sahhaf et al., 2015) to compare

Virtual Network Function Embedding in Multi-hop Wireless Networks

Figure 5: Average Cost in Wireless(with The Extended Model) and Wired Networks(with The Basic Model) with Increasing

Available Nodal Resources.

Figure 6: Cost Savings by Increasing Nodal Resources in Wired(with The Basic Model) and Wireless Network(with The

Extended Model) (20 Nodes, Random Topology).

the average cost and acceptance ratio. As expected,

the wireless interference caused higher BW usage and

slightly lowered the acceptance ratio in the wireless

network as shown during the time period of 400 sec-

onds to 1200 seconds. The basic and extended opti-

mization model were also applied to randomly gener-

ated wireless network topologies with multiple sizes

to compare the average cost, acceptance ratio and the

number of the physical links and virtual links used to

deploy SGs.

DCNET 2018 - International Conference on Data Communication Networking

We learned from the results that the interference

model in wireless networks causes an increase in the

average cost. Our results show that the bandwidth us-

age has a major impact on the placement of NFs. BW

is the only factor that can be reduced by using fewer

links for the deployment of SGs and that is the main

reason the optimization method tends to place the NFs

in fewer nodes. We show that increasing the avail-

able resources of the nodes or increasing the number

of nodes increases the acceptance ratio and reduces

the average cost. However, this also increases the de-

ployment cost of the network. This trade-off is more

obvious in the wireless network as the BW usage is

higher than the wired one. It can be deduced from

Fig. 5 and 6 that in the wireless network increasing

the available resources has the potential to result in

large cost savings.

Extending the experiments already performed in

this paper, future work will be devoted to including

more features of a wireless network in the NFEP. It

will be interesting to include the characteristics of

the multi-hop wireless networks such as the trafﬁc

pattern, the mobility, and nodes in the optimization

method. On the other hand, the optimization problem

can be more speciﬁc about the NF types to explore

how they will affect the trafﬁc rate and consequently

the BW usage.

REFERENCES

Botero, J. F., Hesselbach, X., Duelli, M., Schlosser, D., Fis-

cher, A., and de Meer, H. (2012). Energy efﬁcient

virtual network embedding. IEEE Communications

Letters, 16(5):756–759.

Bouet, M., Leguay, J., Combe, T., and Conan, V. (2015).

Costbased placement of vDPI functions in NFV in-

frastructures. International Journal of Network Man-

agement, 25(6):490–506.

Jain, K., Padhye, J., Padmanabhan, V. N., and Qiu, L.

(2005). Impact of interference on multi-hop wireless

network performance. Wireless Networks, 11(4):471–

487.

Knight, S. (2010). The internet topology zoo.

Kunz, T., Mahmood, K., and Li, L. (2012). Broadcasting

in multihop wireless networks: The case for multi-

source network coding. In IEEE International Con-

ference on Communications (ICC), pages 5157–5162.

IEEE.

Leivadeas, A., Falkner, M., Lambadaris, I., and Kesidis, G.

(2017). Optimal virtualized network function alloca-

tion for an SDN enabled cloud. Computer Standards

& Interfaces, 54:266–278.

Lv, P., Wang, X., and Xu, M. (2012). Virtual access net-

work embedding in wireless mesh networks. Ad Hoc

Networks, 10(7):1362–1378.

Mohammadkhan, A., Ghapani, S., Liu, G., Zhang, W., Ra-

makrishnan, K. K., and Wood, T. (2015). Virtual func-

tion placement and trafﬁc steering in ﬂexible and dy-

namic software deﬁned networks. In The 21st IEEE

International Workshop on Local and Metropolitan

Area Networks, pages 1–6. IEEE.

Park, K. and Kim, C. (2009). A framework for virtual net-

work embedding in wireless networks. In 4th Inter-

national Conference on Future Internet Technologies,

pages 5–7. ACM.

Riggio, R., Bradai, A., Rasheed, T., Schulz-Zander, J.,

Kuklinski, S., and Ahmed, T. (2015). Virtual net-

work functions orchestration in wireless networks. In

11th International Conference on Network and Ser-

vice Management (CNSM), pages 108–116. IFIP.

Sahhaf, S., Tavernier, W., Rost, M., Schmid, S., Colle,

D., Pickavet, M., and Demeester, P. (2015). Net-

work service chaining with optimized network func-

tion embedding supporting service decompositions.

The 21st IEEE International Workshop on Local and

Metropolitan Area Networks, 93:492–505.

Virtual Network Function Embedding in Multi-hop Wireless Networks