Improving the Characteristics of Two-Stage Fuel Pump

by Optimizing the Blades Geometry

Oleg Baturin, Daria Kolmakova, Grigorii Popov and Vasilii M. Zubanov

Department of Aircraft Engine Theory, Samara National Research University, Samara, Russian Federation

Keywords: Screw Centrifugal Pump, Blade, CFD, Optimization.

Abstract: The article presents a refining method for a two-stage screw centrifugal pump by the joint usage of

optimization software IOSO, meshing complex NUMECA and CFD software ANSYS CFX. The pump main

parameters: high-pressure stage rotor speed was 13300 rpm; low-pressure rotor speed was 3617 rpm by

gearbox; inlet total pressure was 0.4 MPa; outlet mass flow was 132.6 kg/s at the nominal mode. This article

describes the process of simplifying the calculation model for the optimization. The parameters of camber

lines of the low-pressure impeller, transition duct, and high-pressure impeller blades for two sections (hub

and shroud) were chosen as optimization parameters. The optimization goal was the increase of the pump

efficiency with preservation or slight increase in the pressure head. The efficiency was increased by 3%.

1 INTRODUCTION

Pumps are the integral part of both industrial

production and everyday human life (Andronov,

2004), centrifugal pumps are used in water supply and

disposal systems. A special place is occupied by the

screw centrifugal pumps as the devices for supplying

liquid components to the rocket engine. In this case,

the turbo-pump unit requires both high performance

and high reliability of operation. It is known

(Ivanov, 2006), more than 70% of crashes of liquid

propellant rocket engines occurred due to the

breakdown in the turbo-pump units.

Currently used turbo-pump units for liquid

propellant rocket engines (LPRE) were designed in

the 1960-1970. The geometry of the pumps was

projected initially by theoretical and empirical

dependencies, and they were designed by expensive

experimental development of the engine/pumps.

A modern CFD programs allows the simulation of

the pump workflow. After validating the simulation

results, these CFD models can be used to study the

effect of the pump parameters on its performance. It

is also possible to optimize the pump using verified

CFD model as a "black box".

An optimization of the pump geometry is carried

out for the following purposes:

1) improvement of the pump performance while

maintaining the pump reliability.

2) providing the same pump performance with

the reduced pump rotor speed. In this case, the

load on the rotor elements of the turbo-pump

unit will be decreased;

3) the combination of the first two approaches.

Investigation of the working process in previous

studies (Zubanov, 2015; Zubanov, 2016) showed the

presence of vortex zones in the high-performance

pumps. The high-performance fuel pump was

adopted as the study subject (Figure 1, 2).

The fuel pump main parameters with water as the

working fluid (based on experiment data) were the

following:

 high-pressure stage rotor speed was 13300 rpm,

low-pressure rotor speed was 3617 rpm by

gearbox;

 inlet total pressure was 0.4 MPa;

 outlet mass flow was 132.6 kg/s at nominal

mode.

Figure 3 shows the meridional section of the fuel

pump, in which vortex zones present in the following

regions:

 the periphery of the inlet edge of the low-

pressure screw (LPS) and high-pressure screw

(HPS) (areas 1 and 4);

 the periphery of the leading edge of the low-

pressure impeller (LPI) (area 2);

 the area closer to LPI stage outlet at the hub

(area 3);

Baturin, O., Kolmakova, D., Popov, G. and Zubanov, V.

Improving the Characteristics of Two-Stage Fuel Pump by Optimizing the Blades Geometry.

DOI: 10.5220/0006889903570364

In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 357-364

ISBN: 978-989-758-323-0

357

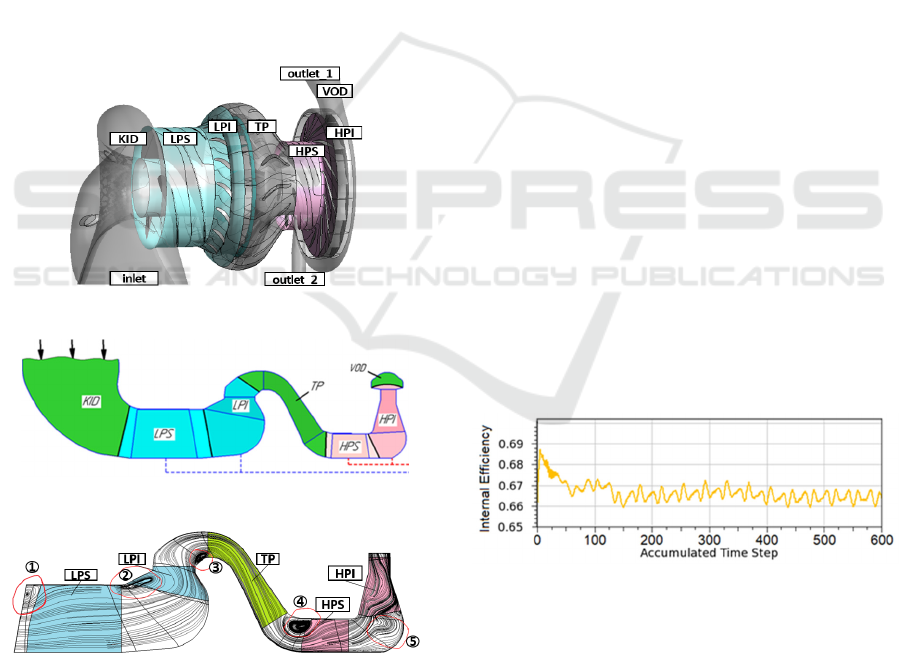
 the stagnation zone of the vortex near HPI hub

(area 5).

Vortices in regions 1 and 4 are due to the design

of the screws. But vortices 2, 3 and 5 in the pump are

undesirable. Thus, the decrease of the intensity of

vortices 2, 3, and 5 will increase the efficiency and

pressure head of the pump. This can be achieved by

changing the geometry of LPI, TP and HPI blades.

2 NOMENCLATURE

These are abbreviations of the pump parts (Figure 2):

 KID - Knee Inlet Duct;

 LPS - Low Pressure Screw passage;

 LPI - Low Pressure Impeller passage;

 TP - Transferring Passage;

 HPS - High Pressure Screw passage;

 HPI - High Pressure Impeller passage;

 VOD - Volute Outlet Duct.

Figure 1: 3D view of the pump under investigation.

Figure 2: Meridional section of the pump.

Figure 3: The pump meridional section with vortex zones.

3 METHODOLOGY

A proven CFD model will be used from the previous

study (Zubanov, 2016). Water was used as the

working fluid because the experimental test data for

water were available. The proven CFD model ensures

a coincidence of Pressure Head value with

experimental data with the accuracy of 6.9% at

nominal mode, and of Internal Efficiency - 2.0%. The

experimental data are presented in the form of points.

The IOSO program was used as an optimizer

(IOSO, 2017). The optimization algorithm requires

multiple iterations with CFD-model. The mesh model

size has a direct impact on the speed of calculation.

For optimization, it is important to have a mesh model

with the smallest number of elements, which

adequately repeats the pressure and efficiency

characteristics of the pump. This article describes the

process of simplifying the calculation model for the

optimization. A calculation will be performed with

the settings of the basic mesh model for the final

optimal variant of the pump design.

The physical processes in the pump are non-

stationary (Pinho, 2014; Reboud, 2003; NUMECA,

2017). While calculations in a stationary statement

are sufficient for most engineering tasks, the

parameters of efficiency and pressure head vary by

iterations in high-performance pumps for stationary

calculation. It was found in previous studies the time-

averaged parameters of efficiency and pressure head

for non-steady-state calculations coincide with the

parameters averaged over iterations for stationary

calculation. Therefore, further calculations will be

carried out in the stationary statement, with averaging

the last 100 iterations by a specially script. To

calculate one task 600 iterations were used, while the

oscillation of parameters remained constant after 400

iterations (Figure 4). The maximum level of

parameter variation for the last 100 iterations was also

controlled by a special script.

Figure 4: The internal efficiency parameter by the

accumulated time step.

4 OPTIMIZATION ALGORITHM

AND DESCRIPTION OF BLADE

PARAMETERIZATION

IOSO software was used as optimization program

(IOSO, 2017). This program has proven itself in

SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

358

many research studies (Jha, 2015; Matveev, 2014;

Yang, 2016). The optimization algorithm for the

investigated pump is shown in Figure 5.

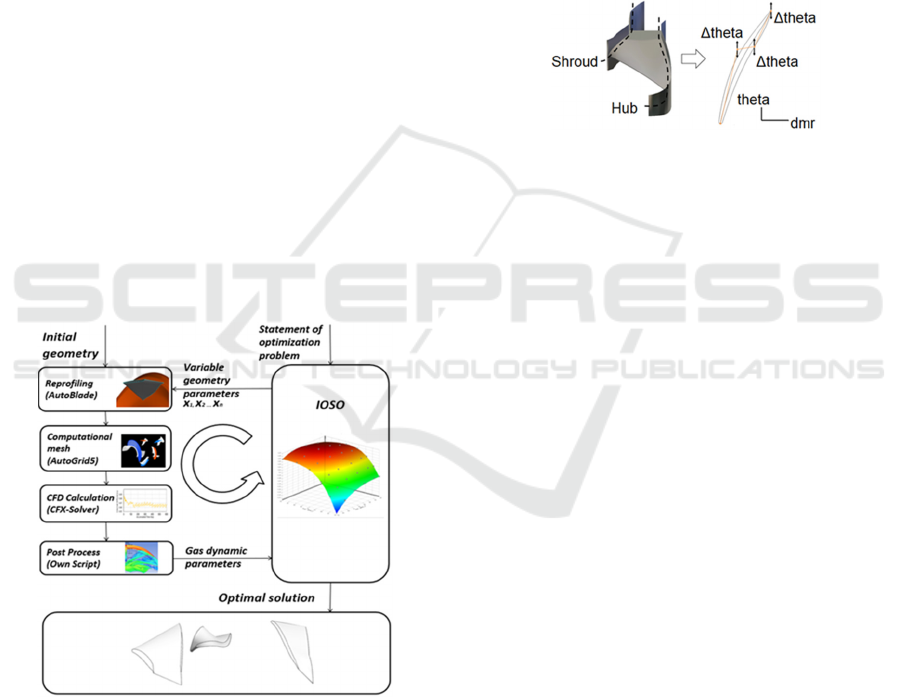
At each step of optimization, the optimizer IOSO

PM generates a Vector of variable parameters x

, x

, …, x

. The Vector describes the geometry of the

LPI, TP and HPI blades in a parametric form. The

Vector of variable parameters is transferred to the

reprofiling block, at which Numeca

AutoBlade (ANSYS CFX-Solver Modeling

Guide, 2011) program perform a conversion of the

blades by Vector data and save them in the form of

geometry files in a *.GeomTurbo format. Then, the

mesh model is created in the Numeca AutoBlade 5

program using new blades. At the next step, the CFD

calculation is performed with the new mesh model.

The processing of CFD-results is carried out by a

special script. As a result, several output files are

created containing pump operation parameters in the

text format. These parameters are then passed to the

optimizer IOSO.

The optimization goal was the increase of the

pump efficiency with preservation or slight increase

in the pressure head. This will reduce the load of the

main gas turbine. It is necessary because the main gas

turbine of the turbopump unit operates in oxidizing

environment (the mass ratio at the gas generator is

more than 56 for oxygen/kerosene components).

Figure 5: The optimization algorithm of the investigated

pump.

The blades fitting was performed in the Numeca

AutoBlade. The parameters of camber lines of the

LPI, TP and HPI blades for two sections (hub and

shroud) were chosen as optimization parameters.

Figure 6 shows the parameterization scheme of the

LPI blades. The camber lines of the LPI, TP and HPI

blades are described by Bezier curves. The camber

line of the LPI blade is described by three points-

poles, while the camber lines of the TP and HPI

requires at least four point-poles. This is due to the

large length of the TP and HPI blades. The

distribution of the cross sections along the blade

height was carried out according to the linear law.

The total number of independent variables was 22.

The pump model with fitted blades was called v0,

and a comparison of its characteristics with the basic

values shows the pressure head differs from the basic

value by 20 m, or 1%, and the efficiency differs by

0.013 or 2%. A good match of the mesh B2Bm2 level

with a mesh B2B0 level is revealed.

Figure 6: 2D parameterization of the LPI blades.

5 SIMPLIFICATION OF THE

PUMP MODEL FOR

OPTIMIZATION

Simplification of the pump model is necessary to

reduce the estimated time of CFD-calculation.

Simplified models were calculated with the

Mass Flow boundary condition, since changing the

geometry of the LPI, TP, and especially of the HPI

can lead to a displacement of the pump

characteristics.

The simplification of the pump model included:

 comparison of the results of simulations with

cavitation and without one;

 comparison of the results of stationary and

transient simulations of pump workflows;

 a study of the pump characteristics behavior,

depending on the mesh model level in the

blades passages (B2B section) and on the

flowpath amounts.

5.1 Simulations Results Comparison

with Cavitation and without One

The phenomenon of cavitation should be considered

in hydrodynamic investigations of the pumps,

because the water hammer effect, arising from the

cavitation, poses a serious risk to the pump reliability.

Also, neglecting the cavitation simulation in pumps

Improving the Characteristics of Two-Stage Fuel Pump by Optimizing the Blades Geometry

359

can lead to obtaining characteristics with a

sufficiently large error of 10-15% (Ding, 2011;

Athavale, 2002). To estimate this error for the pump,

the modeling of working processes with cavitation

was carried out. The simulation was performed with

the basic mesh model. Cavitation settings were the

following:

 doubled fluids: primary – liquid, secondary –

vapor;

 homogeneous model of multiphase;

 cavitation model of Rayleight-Plesset;

 bubbles mean diameter is 2 microns;

 saturation pressure is 3169 Pa;

 volume fraction at inlet: “1” for liquid, “0” for

vapor.

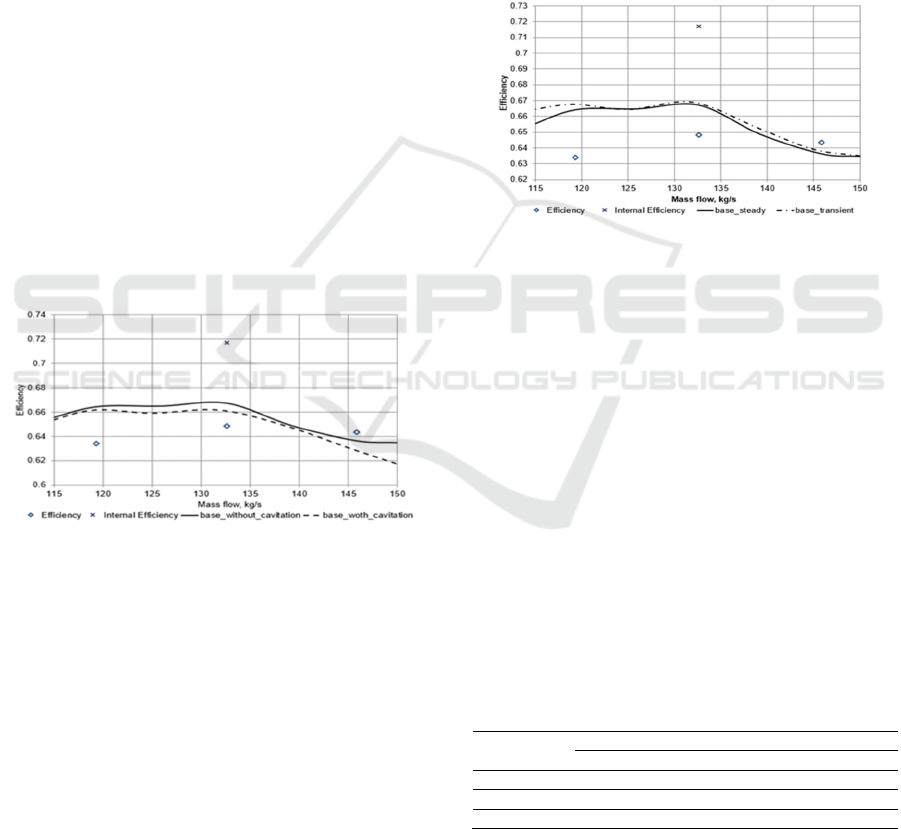
The results of comparison of efficiency are shown

in Figure 7. The pressure head characteristics are

practically the same, and the efficiency with

cavitation is lower by 1.0-2.9%.

Simulation of the pump considering cavitation

took in 1.9 times more processor-hours than

simulations without cavitation. The pressure and

efficiency characteristics are equidistant in the near-

nominal mode. Therefore, the modeling of workflows

in the pump was carried out without considering

cavitation for further research.

Figure 7: The internal efficiency characteristic of the

investigated pump without and with cavitation modeling.

5.2 Comparison of the Results of

Stationary and Transient

Simulations of Pump Workflows

In the «Methodology» section, the specific decision

on stationary modeling with averaging the last 100

iterations was mentioned. This section contains the

rationale for such approach.

The simulation was performed with the basic

mesh model. Settings for the transient modeling:

 the time step is 3.7594e-005 seconds. This

value corresponds to 1/10 of the transit time of

the HPI blade channel;

 Maximum Number of Coefficient Loops is 10;

 Number of Timesteps is 600.

The sustained operation of the pump required 300

iterations. The last 300 iterations (of total 600) were

used for averaging the transient results.

Figure 8 show the pump efficiency for stationary

and transient tasks that differ by less than 0.3%.

The simulation of non-stationary pump operation

was very resource-intensive task by 2.7 times more

than for the stationary simulation without cavitation.

Regarding the foregoing, the simulation of working

processes in the pump was carried out in the steady

state without cavitation for further investigations.

Figure 8: The internal efficiency characteristic of the

investigated pump for steady and transient cases.

5.3 Investigation of the Pump

Characteristics Dependence on the

Mesh Model

The basic mesh model of the vane units contained

2.81 million elements with 81 flowpaths by height.

The number of elements in the B2B section of the

vanes of the basic model was adopted as B2B0 level.

Two levels of B2B meshes were created with a

reduced number of points: B2Bm1 and B2Bm2. The

B2B levels differed by ~1.3 times according to the

recommendations given in (ANSYS CFX-Solver

Modeling Guide, 2011; Marchukov, 2017;

Jha, 2015). The number of points in 3D meshes

depending on B2B level and flowpaths number,

which are presented in Table 1.

Table 1: The number of points in the 3D mesh, X10

B2B

level

Flowpaths number

81 73 65 57

B2B0 3.08 2.80 2.51 2.22

B2Bm1 2.28 2.10 1.85 1.64

B2Bm2 1.77 1.60 1.44 1.27

All mesh models adequately predict the values

and behavior of the pressure head and internal

efficiency characteristics. Figures 9 and 10 show the

SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

360

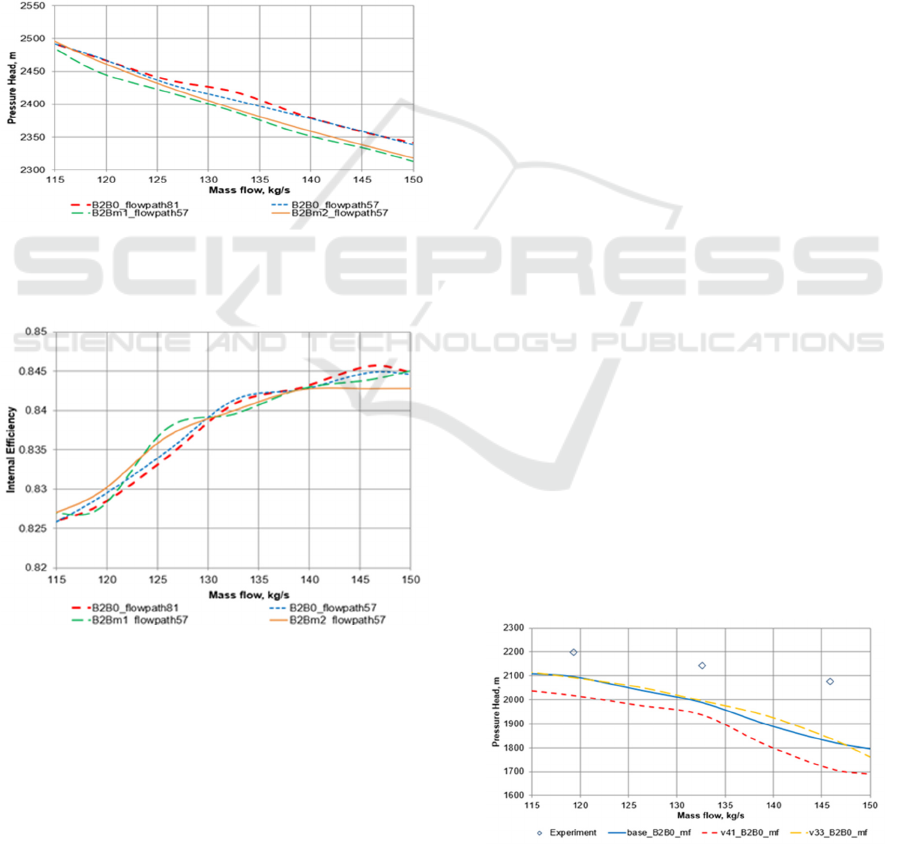
pressure head and efficiency characteristics of the

investigated pump for several mesh models. The

internal efficiency and pressure head values were

determined at the outlet of HPI stage, to determine the

influence of only the mesh parameters of the blade

elements on the pump characteristics.

The maximum difference of the pressure head at

the nominal mode for B2Bm2_flowpath57 mesh

model was 1% relative to the basic value, and of the

internal efficiency - 0.2% for the for

B2B0_flowpath57 mesh model. The mesh model

B2Bm2_flowpath57 was chosen for the optimization

task because it provides the fastest possible solution

time with the adequate prediction of the pump

characteristics.

Figure 9: The pressure head characteristic of the

investigated pump for several mesh models determined at

the outlet of the HPI stage.

Figure 10: The internal efficiency characteristic of the

investigated pump for several mesh models determined at

the outlet of the HPI stage.

6 OPTIMIZATION RESULTS

The optimization task was performed using B2Bm2

mesh model of blades and mesh models of KID and

VOD from rough mesh of previous study (Zubanov,

2015).

The optimization task of the pump had criteria:

 increase in the internal efficiency;

 preservation or a slight increase the pressure

head.

The optimization of the pump required more than

200 iterations. The Pareto front «efficiency-pressure

head» was obtained. For a detailed analysis, 2 points

were selected from the Pareto front:

 v33 is the variant of the pump with increased

internal efficiency by 3.3% and increased

pressure head by 6.8% at B2Bm2 mesh level

relative to variant v0;

 v41 is the variant of the pump with increased

internal efficiency by 5.4% and increased

pressure head by 0.2% at B2Bm2 mesh level

relative to variant v0.

Then calculations of variants v33 and v41 were

performed at B2B0 mesh level. The internal

efficiency and pressure head characteristics with

boundary condition Mass Flow at the outlet are

shown in Figures 11-12. The pressure head of pump

variant v41 is below the basic value at the parity level

of the internal efficiency in comparison with pump

variant v33. In addition, the internal efficiency of the

pump is sharper in the field of high mass flows. The

pump variant v33 seems preferable.

The internal efficiency of the pump variant v33

has the increased value by 3.1% and the increased

pressure head by 0.4% at nominal mode relative to the

basic values.

Figure 13 shows the blade-to-blade sections of

LPI, TP and HPI pump blades of basic and optimized

(v33) versions. LPI blade became more elongated

closer to the exit, the blade of the TP became more

curved, and provides a certain flow angle for the HPS.

The HPI blade underwent major change closer to the

outlet of HPI stage, especially at the shroud. It seems,

that such shape of the HPI blade ensures

compensation of Pressure Head losses in the

periphery of the HPS blade.

Figure 11: The pressure head characteristic of the pump

with boundary condition Mass Flow.

Improving the Characteristics of Two-Stage Fuel Pump by Optimizing the Blades Geometry

361

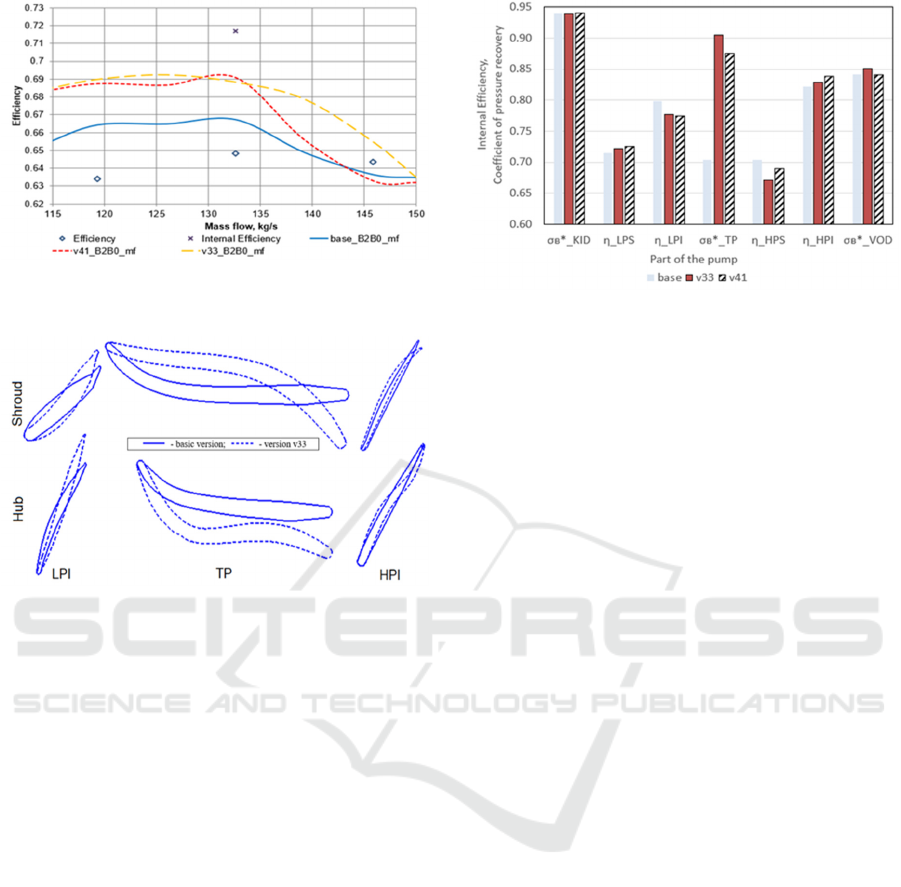
Figure 12: The internal efficiency characteristic of the

pump with boundary condition Mass Flow.

Figure 13: Blade-to-blade sections of LPI, TP and HPI

pump blades of base and optimized (v33) versions.

Analysis of the pressure head and efficiency

parameters by the pump parts was carried out for the

basic pump, v33 and v41 variants. Changing the

parameters of internal efficiency and pressure

recovery coefficient is shown in Figure 14. The

greatest change occurred in the TP part of the pump.

The pump variant v41 has higher efficiency for

the impeller than the pump variant v33, but v41 has

lower pressure recovery coefficient for the VOD.

Apparently, the calculation on the fine B2B0 mesh

level allowed to calculate the vortices shown in

Figure 3 more detailed.

Since only the LPI, TP and HPI blades were

subject to optimization, the efficiency of the LPS and

HPS blades should remain at the same level or

slightly change. The efficiency of the LPS blades

slightly increased due to the change in the shape of

the LPI blades. At the same time the efficiency of the

HPS blades decreased because of the change in the

velocity triangles associated with the change in the

shape of the TP and HPI blades. In general, the

efficiency of the pump increased by 3.1% with the

increased pressure head by 0.4% due to the

coordinated work of the stages (Popov, 2016).

Figure 14: The parameters of internal efficiency and

pressure recovery coefficient determined for the pump

parts.

7 STRENGTH ANALYSIS OF HPI

BLADE OPTIMAL GEOMETRY

The geometry of the HPI blades was significantly

changed during the optimization. To evaluate the

effect of loads acting on the optimized variant of

geometry, calculations are made to determine the

maximum equivalent stresses in the basic geometry

and in the optimized variant of the high-pressure

impeller. The calculation was carried out in ANSYS

Mechanical. Computational model was the impeller

sector, the cyclic symmetry condition was used. The

calculation did not consider the material ductility.

The pressure values on the solid surfaces were

interpolated from the CFD calculation. The

temperature field was 25 °C, given as constant for the

entire calculation model.

As a result of the calculation of two impeller

variants, the values of the maximum equivalent

stresses were obtained. For the basic variant the

maximum value of equivalent stress

σ_(von Mises stress)_base was 961.6 MPa, for the

optimized variant v33 - σ_(von Mises stress)_opt was

1038.3 MPa.

The material of HPI is chromium-nickel steel

VNL-1. It has the specific stress limit of 1079 MPa

(VIAM, 2017). According to J. E. Shigley

«stress-concentration factors need not be employed

when the material is ductile, and the loads are static»

(Shigley, 2001). According to the recommendations

in (VIAM, 2017) and (ANSYS Mechanical User's

Guide, 2013) «failure is most often declared if

yielding occurs across a complete section».

Therefore, the equivalent stresses region near the

maximum value was considered. A region occupying

1/4 of the maximum stress scale for each case was

SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

362

adopted as such region. The equivalent stresses for

the selected region was 722.3 MPa for the basic HPI

blade version and 779.2 MPa – for the optimized v33

version. Then the safety factor for the basic version is

1.49, and for the optimized version is 1.38.

8 CONCLUSIONS

Two optimization studies of powerful fuel pump were

performed. The first optimization task with CFD-

model, which does not contain KID and VOD parts

of the pump, did not allow to significantly increase

the pressure head and internal efficiency.

Nevertheless, optimization with the first CFD-model

correctly predicted the trends in the geometry

variation of the LPI and TP blades. Thus, it is possible

to perform optimization of the pump blades without

VOD part, while maintaining the geometry of the

blades in the stage before the output device. This can

be important for the gradual improvement of the

pump geometry, especially if the number of variable

parameters is limited by the capabilities of an

optimizer program.

The second optimization task provided the pump

with re-profiling geometry of the blades, which allow

to obtain the increased internal efficiency by 3.1%

and the increased pressure head by 0.4% at nominal

mode relative to the basic values.

The strength analysis of the HPI blade was

performed since the HPI blades were greatly changed

at the HPI stage exit area. The maximum equivalent

stresses increased by 76.7 MPa, and the safety factor

of HPI decreased from 1.49 to 1.38.

The obtained reserve can be used to boost the

rocket engine, and/or to reduce the loading of the

main turbine, which operates in aggressive oxidizing

environment.

Further optimization is planned for 3-4 sections

for all blade stages, including screws. Also, conjugate

optimization is planned to consider the strength

model.

ACKNOWLEDGEMENTS

This work was financially supported by the Ministry

of education and science of the Russian Federation in

the framework of the implementation of the Program

“Research and development on priority directions of

scientific-technological complex of Russia for 2014-

2020”.

REFERENCES

Andronov, A. L., 2004. Features of operation of centrifugal

pumps and the requirements for their electric drive.

Polzunovskii Almanac (Barnaul, Russia), Volume 1,

pp. 150-152.

Ivanov, V. K., Kashkarov, A. M., Romacenko, E. N.,

Tolstikov L.A., 2006. Turbopump units for LPRE

engineering, Volume 1, pp. 15 21.

Zubanov, V. M., Shabliy, L. S., Krivcov, A. V., 2015.

Rational Technique for Multistage Centrifugal Pump

CFD-Modeling. In Proceedings of the ASME Turbo

Expo, Paper No. GT2015-42070, pp. 1-9.

Zubanov, V. M., Shabliy, L. S., Krivcov, A. V., Matveev,

V. N., 2016. Technique for adequate CFD-modeling

of the pump with hydro-drive of the low-pressure stage.

In Proceedings of the ASME Turbo Expo, Paper No.

GT2016-57689, pp. 1-11.

IOSO Optimization Technology. Access mode:

http://www.iosotech.com.

Pinho, J., Lema, M., Rambaud, P., Steelant, J., 2014.

Multiphase investigation of water hammer

phenomenon using the full cavitation model. Journal of

Propulsion and Power, Volume 30, Issue 1, January

2014, pp. 105-113.

Reboud J. L., Pouffary B., Coutier-Delgosha O., Fortes –

Patella R., 2003. Numerical simulation of unsteady

cavitating flows: some applications and open problems.

Fifth International Symposium on Cavitation

(CAV2003), Japan, Paper No. CAV2003-IL-10, pp.

1-10.

NUMECA. Access mode: http://www.numeca.com/en.

ANSYS CFX-Solver Modeling Guide, 2011. ANSYS Inc.

Marchukov, E. Yu., Egorov, I., Popov, G., Salnikov, A.,

Goriachkin, E., Kolmakova, D., 2017. Multidiscipli-

nary optimization of the working process of uncooled

axial turbine according to efficiency and strength

criteria. Proceedings of the ASME Turbo Expo, Paper

No. GT2017-64843.

Jha, R., Dulikravich, G. S., Colaço, M. J., Egorov, I. N.,

Poloni, C., Chakraborti, N., Fan, M., Schwartz, J.,

Koch, C., 2015. Multi-objective design and

optimization of hard magnetic alloys free of rare earths.

Materials Science and Technology Conference and

Exhibition 2015.

Matveev, V. N., Baturin, O. V., Popov, G. M., Egorov, I.

N., 2014. Seven-stage axial compressor optimization.

Engineering Optimization IV - Proceedings of the 4th

International Conference on Engineering Optimiza-

tion, ENGOPT 2014, pp. 821-826.

Yang, C., Wu, H., 2016. Optimized aerodynamic design of

aggressive intermediate turbine duct with strut fairings

using genetic algorithms. ASME Paper GT2016-56639.

Ding, H., Visser, F. C., Jiang, Y., Furmanczyk, M., 2011.

Demonstration and validation of a 3D CFD simulation

tool predicting pump performance and cavitation for

industrial applications. Journal of Fluids Engineering,

Transactions of the ASME Volume 133, Issue 1, Article

number 011101, pp. 277-293.

Improving the Characteristics of Two-Stage Fuel Pump by Optimizing the Blades Geometry

363

Athavale, M. M., Li, H. Y., Jiang, Y. U., Singhal, A. K.,

2002. Application of the full cavitation model to pumps

and inducers International Journal of Rotating

Machinery, Volume 8, Issue 1, pp. 45-56.

Popov G., Goriachkin E., Kolmakova D. and Novikova

Yu., 2016. Multicriteria Optimization of Axial Low

Pressure Compressor of Gas Turbine Power Plant.

In Proceedings of the ASME Turbo Expo, Paper No.

GT2016-57856, pp. 1-10.

VIAM, 2017. Access mode: https://catalog.viam.ru.

Shigley J. E. and Mischke C. R., 2001. Mechanical

Enginering Design. McGraw-Hill.

ANSYS Mechanical User's Guide, 2013. ANSYS Inc.

SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

364