Optimization of Nozzle Shape of Hydrogen-Oxygen Rocket Engine

Valeriy Matveev, Vasilii Zubanov, Leonid Shabliy and Anastasia Korneeva

Department of Aircraft Engine Theory, Samara National Research University, Samara, Russian Federation

Keywords: Parametric Optimization, Rocket Engine, Combustion, Hydrogen, Oxygen, CFD-Simulation.

Abstract: The article presents a technique of parametric optimization of nozzle supercritical part of liquid-propellant

rocket engine. Main approaches for parametric optimization were given. Two optimizers were mentioned.

Thrust and specific impulse were chosen as optimization criteria. Simulation of chamber process was

performed in ANSYS CFX with combustion model Eddy Dissipation. Two variants of combustion were

considered: one global reaction and detailed chemical system with 8 components and 18 reactions.

Comparison of results gives more smooth contours of parameters for set with detailed system against variant

with one reaction for simulation of liquid-propellant rocket engine working with “hydrogen-oxygen”

propellants. In result of optimization the nozzle length was shortened up to 15% virtually without thrust loss

(0.18% reduction in thrust). Also the Pareto set in axis “thrust”-“nozzle length” was obtained.

1 INTRODUCTION

Chamber of liquid-propellant rocket engine (LPRE)

is the main unit of LPRE, in which fuel components

or burner gases create engine thrust during chemical

reactions and efflux from nozzle.

Operating processes of LPRE chamber

accompanied by energy losses. As is known, the

increase of thrust, specific impulse and other

operational parameters (Dobrovol'skij, 2005) of

modern LPRE is an actual problem of aerospace

engineering. At the same time, the cost of

experimental development of LPRE is significantly

higher than the estimated optimization studies, which

allows to create the LPRE with the best parameters at

the design stage, and it reduces the creation time and

the final product cost.

The technology of virtual computer simulation

allows solving optimization tasks using methods

based on multiple virtual simulations (Zubrilin, 2015;

Baturin, 2015) appeared relatively recently.

This paper presents the technique for optimizing

the shape of the expanding part of a LPRE nozzle

using virtual gas-dynamic modeling in ANSYS CFX

(Zubanov, 2015). The engine has a thrust of 100 kN,

and it designed for the interorbital transport vehicle

(Belousov, 2014).

2 THE MAIN APPROACHES FOR

OPTIMIZATION

The traditional approach to solving any optimization

problem is the general mathematical approach, where

the optimized value (for example, the LPRE thrust or

the specific impulse) is expressed as a function in an

explicit or implicit form with several the design

variables (geometric dimensions of LPRE elements,

gas-dynamic flow parameters in the chamber,

strength parameters, design constraints, etc.). Then,

the extrema of this function and the corresponding

values of the optimized parameters (Egorychev,

2016) are found using the tools of mathematical

analysis. Unfortunately, the complexity of creating an

adequate optimized function (verified mathematical

model) exceeds the experimental development of the

LPRE. After all, in order to correctly reflect in the

functional form the influence of some constructive

factor, for example, on the magnitude of thrust, it is

necessary to carry out and mathematically generalize

the corresponding experimental study.

The technology of virtual computer modeling

allows solving optimization tasks using methods

based on multiple virtual simulations (Kuzmenko,

2007; Shablii, 2014) appeared relatively recently. The

main feature of this approach is that the functional

dependence of N optimized parameters, optimized by

K criteria, is constructed in (N + K) - dimensional

space solely from data on the values of the criteria

Matveev, V., Zubanov, V., Shabliy, L. and Korneeva, A.

Optimization of Nozzle Shape of Hydrogen-Oxygen Rocket Engine.

DOI: 10.5220/0006890003650370

In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 365-370

ISBN: 978-989-758-323-0

365

obtained from virtual models constructed for the

corresponding combinations of parameters in the

region of interest, completely without analyzing the

physical effect of the parameters on the criteria. The

latter is a very important advantage of this approach,

since it allows to treat the virtual model as a "black

box" without analyzing the reasons for the influence

of certain parameters on the criteria. At the same time,

the evaluation of the mutual influence of a parameter

set on the considered criteria is performed

automatically by the optimization algorithm.

Algorithm of modern optimizers, such as ANSYS

Design eXplorer (ANSYS, 2015) and Sigma

Technology IOSO (Kuzmenko, 2007) allow

simultaneous optimization by several criteria,

depending on several hundred parameters (Egorov,

2007).

Figure 1 shows a diagram of the process of

constructing an approximating optimization surface

using as a virtual model the CFD model of the flow

in the chamber of a liquid rocket engine. Similarly,

lower-level models, both higher, up to the full three-

dimensional model of a virtual LPRE, can be applied,

which includes not only CFD modeling of currents in

all engine paths, considering phase transitions and

chemical transformations, but also a FEM-evaluation

of the structural strength of the structure. Similarly,

models of both low and high levels can be applied. As

models of a low level, the mathematical functions of

the traditional approach can be used. As models of a

high level, the full three-dimensional model of a

virtual LPRE including not only workflow CFD-

simulation in all engine paths, considering phase

transitions and chemical transformations, but also the

FEM-evaluation of structural strength can be used.

Also, combined and multilevel models can be used.

For example, modeling of fuel flow through pipelines

is carried out in a one-dimensional setting, the quality

of its spraying by nozzles is estimated by zero-

dimensional criterial dependencies, and modeling of

combustion in the chamber is performed in a three-

dimensional nonstationary setting. Naturally, since

the values obtained from the "black box" cover the

investigated area with a mesh model of finite density,

this approach to optimization contains a

methodological error: the approximating surface in

the general case cannot guarantee the search for a

global extremum under sharp changes in the criterion

(Figure 2). However, as practice shows, the existing

technologies of optimizer programs can reduce the

probability of error (Shabliy, 2014).

3 CFD-SIMULATION OF

COMBUSTION PROCESS IN

LPRE CHAMBER WITH FUEL

COMPONENTS «HYDROGEN

& OXYGEN»

This section presents the methodology of simulation

in ANSYS CFX of combustion process in the

chamber of small thrust rocket engine operating on

gaseous oxygen and hydrogen (Zubanov, 2017).

Chemical kinetics was modeled in two variants: using

a single global reaction (molecular formula) and set

of chemical reactions.

For first calculation, the single reaction in the pre-

processor СFX-Pre was chosen from the library

ANSYS CFX the global combustion reaction

“Hydrogen Oxygen”, which involves three

components: H2, O2, H2O. The reacting mixture of

these three gases, defined based on the selected

reaction was set as a working fluid. The mass flow

rate, the temperature and mass fraction components

were set as the input boundary conditions of

calculation area.

Figure 1: The optimization scheme through multiple virtual

simulations (for example, CFD simulation of a LPRE

chamber).

SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

366

Figure 2: Error estimating the global maximum of the

optimized criterion in the case of insufficient discretization

of the approximation domain.

The applied model of combustion Eddy

Dissipation was developed to describe turbulent

flows of a premixed mixtures. It suggests that

chemical reactions cause the reacting mixture to

equilibrium, i.e. the chemical reaction rate is

much higher than the rate of mixing of fuel and

oxidizer (Matveev, 2014). Using one global reaction

does not allow to fully describe a branched chain

reaction in mixtures of hydrogen with oxygen and

assess the education progress of the reaction

intermediates. A detailed kinetic scheme of

chemical reactions with these components includes

more than 20 elementary reactions with

participation of free radicals in the reacting mixture.

The set of reactions of (Gardiner, 1984),

described in more detail in (Zubanov, 2014) was

used in this study. It consists of 18 chemical

reactions (including reversible 5) with the

participation of 8 components: H

, O

, H

O, H, O,

OH, H

O, H

Figure 3: The temperature distribution along the length of

the chamber when using: a – single global reaction; b – set

of 18 reactions.

The rate of each reaction is determined by the

Arrhenius equation. The components and products

involved in this reaction, the stoichiometric

coefficients and the reaction order were set manually

for describe each reaction in CFX-Pre. The

parameters of the chemical reaction speed rate

(preexponential multiplier A, temperature exponent

n, activation energy E and activation temperature T

were taken from (Gardiner, 1984),

(Soloviova-Sokolova, 2016) and (Kozlov, 2015).

After reactions specifying all substances was

included in the reacting gas mixture of fluid domain.

Further steps of the modeling did not differ from the

previous simulation using global-reaction. When

modeling complicated systems of reactions, the

instability of the solution was increased that was

required to increase the number of iterations, and

consequently, increased the total solution time in

comparison with using a single global reaction.

Verification of shown above simulation

methodology was performed on the test small thrust

rocket engine (25 N thruster), since there were

experimental data for it. A comparison of the CFD

model results with experimental data showed that

the resulting specific impulse in the void

corresponds to the experimental one with an

accuracy of 3%.

After verification the current LPRE was

simulated. The obtained results (Figures 3 and 4)

show that the simulation with a single reaction

overestimates the local temperature, and the flow is

more uniform, axisymmetric. But the calculation

with a complicated system of reactions gives has

more gradual change in temperature along the length

of the chamber and looks more “physical”.

Figure 4: The Mach number distribution along the length of

the chamber when using: a – single global reaction; b – set

of 18 reactions.

Optimization of Nozzle Shape of Hydrogen-Oxygen Rocket Engine

367

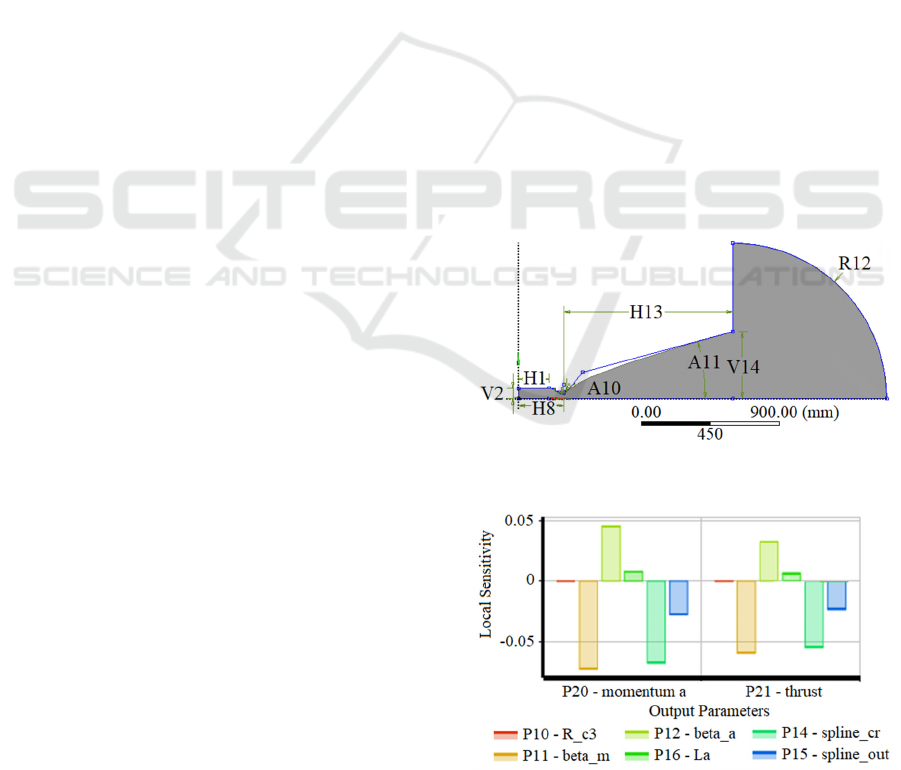
4 DESCRIPTION OF LPRE

CHAMBER PARAMETRIC

MODEL

The rocket engine with a thrust of 100 kN designed

for the interorbital transport vehicle was chosen as the

optimization object, because it should have a large

nozzle to provide the high specific impulse and thrust.

A virtual CFD model of the gas-dynamic flow in

the nozzle was created earlier (Figures 3 and 4). The

thrust, the specific impulse, and the static pressure

distribution on the inner surface were determined for

the given working conditions of the projected nozzle.

The working conditions of the projected nozzle were

the workflow parameters at the inlet, the pressure at

the inlet and outlet. It is noteworthy that the

simulation accuracy was acceptable for a multivariate

optimization study: the calculated thrust by CFD-

modeling of the base nozzle version, constructed

according to the technique (Egorychev, 2016), was

99.14 kN, and the specific impulse was 4323 m/s.

By the technique (Dobrovol'skij, 2005;

Egorychev, 2016) the thrust was 100 kN, and the

specific impulse was 4357 m/s with the combustion

chamber coefficient 0.98.

The expanding part of the nozzle composed of a

circular arcs and a Bezier-splines constructed by three

knots (Figure 5). The expanding part of the nozzle

was parameterized by six parameters with the

following ranges of variation (the basic value and

relative changes are indicated in parentheses):

 the length of the expanding nozzle part was

= 935…1155 (1100

%

%

) mm;

 the arc radius after the critical section was

= 2…20 (14

%

%

) mm;

 the expansion angle of the nozzle in the critical

section was β

= 30…70° (50°

%

%

;

 the expansion angle of the nozzle in the output

section was β

= 5…19° (15°

%

%

;

 the distance of the spline control points from its

ends for the critical (cr) section was

spline_cr = 1…99% (basic - 5%);

 the distance of the spline control points from its

ends for the output (out) section was

spline_out = 1…99% (basic - 5%).

For optimization, ANSYS Design Exploration

tools were used, namely: the sensitivity of the

parameters (Local Sensitivity), the construction of the

response surface in the second order polynomials

(Response Surface), and the optimization algorithm

for screening geometry variants (Screening

Optimization) (ANSYS, 2015; Shabliy, 2014).

5 OPTIMIZATION RESULTS

A preliminary assessment of the sensitivity of the

parameters showed that parameters βa and βm,

spline_cr and spline_out have the determining

influence on the thrust and momentum, while

parameter La affects to a lesser extent, and the

influence of parameter Rc3 is insignificant

(Figures 6 and 7).

In the first case, optimization was carried out

according to the criteria of maximum thrust and

specific impulse, and it was possible to increase the

thrust by 0.6%, and the specific impulse by 0.2%, and

with the nozzle length La reduced to 1093 mm (base

value of La was 1100 mm). Since the mass of the

engine depends strongly on the length of the nozzle,

it was decided to supplement the optimization task by

the criterion of minimizing La. As a result, the nozzle

was shortened by 15% (up to 936 mm) with a slight

(by 0.18%) reduction in thrust. Changes of the nozzle

shape, corresponding to the first (I) and the second

(II) tasks, are shown in Figure 8. The Pareto set

corresponding to the second task is shown in

Figure 9.

Thus, the technique for optimizing the shape of

the expanding part of a LPRE nozzle by calculation

was created to obtain maximum thrust with the

minimum nozzle length.

Figure 5: Parametrized nozzle model.

Figure 6: The sensitivity diagram for the geometric

parameters and optimizing criteria.

SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

368

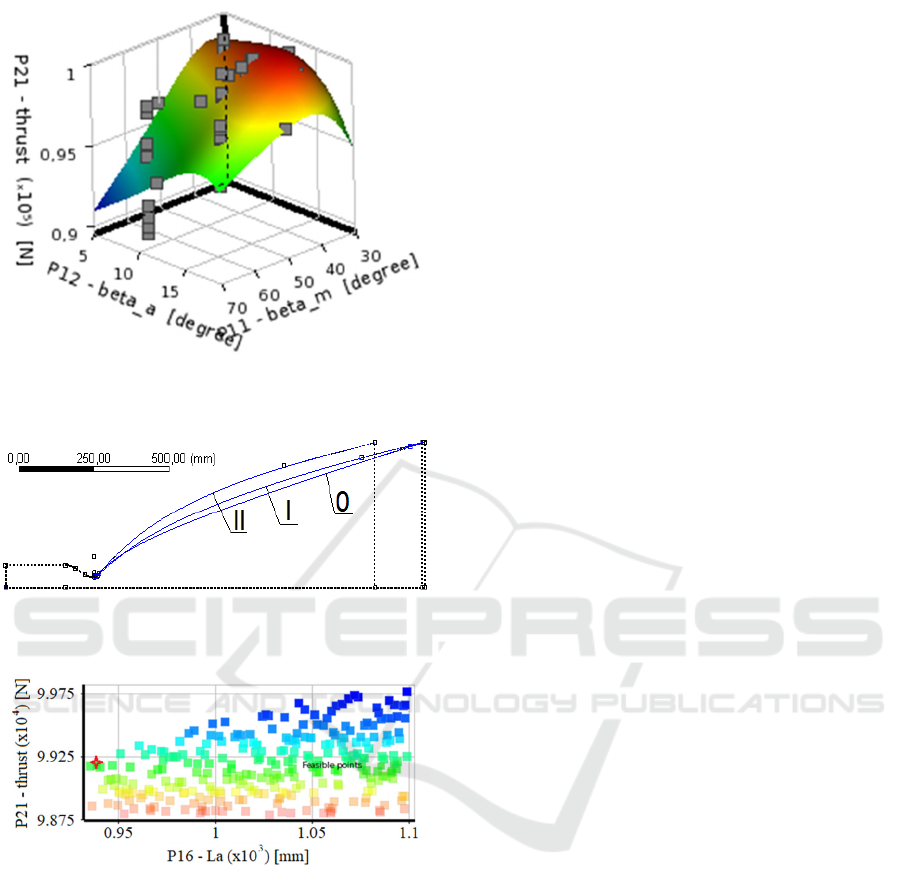
Figure 7: The response surface in assessing the effect of β

and β

on the thrust.

Figure 8: Changes the nozzle shape in comparison with the

basic version ("0").

Figure 9: The Pareto set "Length La - Thrust".

6 CONCLUSIONS

Based on the adequate CFD-model with the set of

reactions, the geometry optimization of the expanding

nozzle part of the rocket engine with the thrust of

100 kN for an interorbital transport vehicle was

carried out. The good solution was found of the set of

pareto: the nozzle was shortened by 15% with a slight

by 0.18% reduction in thrust.

CFD-modeling of the combustion process on

components “hydrogen-oxygen” shows that the gross

reaction results differ from the results obtained with

system of chemical reactions. In General, the EDM

model gives overestimated results on temperature in

comparison with results of thermodynamic

calculation of the chamber. But it can be used to

obtain reference solutions.

The technique for optimizing the shape of the

expanding part of a LPRE nozzle by calculation was

created to obtain maximum thrust with the minimum

nozzle length.

The technique can be used to optimize the nozzle

of a rocket engine for the second, third and

interorbital transport vehicle stages of launch

vehicles. But first of all it is required to obtain an

adequate CFD-model with combustion of a rocket

engine.

ACKNOWLEDGEMENTS

The work was completed with the financial support

of the Ministry of Education and Science of Russia in

the framework of the implementation of the Program

‘‘Research and development on priority directions of

scientific-technological complex of Russia for 2014–

2020” and within the basic part framework of the state

assignment and with Grant Council of the President

of the Russian Federation in the framework of the

SP-3790.2015.1 scholarship.

REFERENCES

Dobrovol'skij M. V. Zhidkostnye raketnye dvigateli.

Osnovy proektirovanija [Liquid propellant rocket

engines. Basics of designing]. Moscow: MSTU Publ.,

2005. 488 p.

Zubrilin, I. A., Dmitriev, D. N., Matveev, S. S., Matveev,

S. G. Numerical investigation of the nonreacting

swirling flow structure downstream of industrial gas

turbine burner with the central body. Paper presented at

the Proceedings of the ASME Turbo Expo, 2015, 4A

doi:10.1115/GT2015-42181.

Baturin, O. V., Popov, G. M., Goryachkin, E. S., Novikova,

Y. D. Application of 3D navier-stokes equations and

mathematical optimization techniques to improve the

efficiency of seven-stage axial compressor. Paper

presented at the SIMULTECH 2015 - 5th International

Conference on Simulation and Modeling

Methodologies, Technologies and Applications,

Proceedings, 227-232.

Vasiliy Zubanov, Vitaliy Egorychev, Leonid Shabliy.

Design of Rocket Engine for Spacecraft Using CFD-

Modeling. Procedia Engineering, 2015, V. 104, P. 29–

35. DOI: 10.1016/j.proeng.2015.04.093.

Belousov, A. I., Sedel'nikov, A. V. Problems in formation

and control of a required microacceleration level at

spacecraft design, tests, and operation. Russian

Optimization of Nozzle Shape of Hydrogen-Oxygen Rocket Engine

369

Aeronautics, 2014, 57(2), 111-117. doi:10.3103/

S1068799814020019

Egorychev, V. S., Ryazanov, A. I. A method of design

calculation for the two-component jet-jet gas nozzle

with outer mixing. Russian Aeronautics, 2016 59(4),

619–622. doi: 10.3103/S1068799816040280

Kuzmenko M. L., Shmotin Yu. N., Egorov I. N., Fedechkin

K. S. Optimization of the gas turbine engine parts using

methods of numerical simulation. Proceedings of the

ASME Turbo Expo, 2007, Vol. 6, pt. A, pp. 425-431.

DOI: 10.1115/GT2007-28205.

Shablii, L. S., Dmitrieva, I. B. Blade geometry

transformation in optimization problems from the point

cloud to the parametric form Russian Aeronautics

(Allerton Press Incorporation), 2014, 57(3), 276–282.

doi: 10.3103/S1068799814030106

ANSYS Inc. 2015 Workbench. Design Exploration User's

Guide

Egorov I. N., Kretinin G. V., Leshchenko I. A., Kuptzov S.

V. Multi-objective approach for robust design

optimization problems. Inverse Problems in Science

and Engineering, 2007, 15 (1), pp. 47–59.

DOI:10.1080/17415970600573916.

Shabliy L. S. and Cherniaev A. V. Optimization of

Compressor Blade Geometry for Efficiency and

Pressure Ratio Under Strength Constraint. ASME 2014

Gas Turbine India Conference GTINDIA2014-8132,

2014, DOI: 10.1115/GTINDIA2014-8132.

V. M. Zubanov, D. V. Stepanov, L. S. Shabliy. The

technique for Simulation of Transient Combustion

Processes in the Rocket Engine Operating with Gaseous

Fuel "Hydrogen and Oxygen" - IOP Conf. Series:

Journal of Physics: Conf. Series 803 (2017), (JPCS),

Paper No. 012187, doi:10.1088/1742-6596/803/1/

012187

Matveev, S. G., Zubrilin, I. A. Large-eddy simulation of

flow structure after a bluff-body flameholder with

different chemical kinetics mechanisms. Life Science

Journal, 2014, 11(11), 644-649.

Gardiner, W. C. Combustion Chemistry. Springer-Verlag

New York. 1984. 351 p.

Vasiliy Zubanov, Vitaliy Egorychev and Leonid Shabliy.

Hydrogen-Oxygen Rocket Engine Design Using CFD-

Modeling. Research Journal of Applied Sciences, 2014,

V. 9, Issue 10, Pp. 660-663. DOI: 10.3923/rjasci.2014.

660.663.

Soloviova-Sokolova, J. V., Alekseev, V. A., Matveev, S. S.,

Chechet, I. V., Matveev, S. G., Konnov, A. A. Laminar

burning velocities of benzene + air flames at room and

elevated temperatures. Fuel, 2016, 175, 302-309.

doi:10.1016/j.fuel.2016.02.054.

Kozlov, V. E., Chechet, I. V., Matveev, S. G., Titova, N. S.,

Starik, A. M. Modeling study of combustion and

pollutant formation in HCCI engine operating on

hydrogen rich fuel blends. International Journal of

Hydrogen Energy, 2015, doi:10.1016/j.ijhydene.2015.

12.078

Shabliy L and Cherniaev A 2014 Optimization of gas

turbine compressor blade parameters for gas-dynamic

efficiency under strength constraints Proceedings of the

4th International Conference on Simulation and

Modeling Methodologies, Technologies and

Applications SIMULTECH 2014 pp 523-528 doi:

10.5220/0004994905230528.

SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

370