
Estimation of the Effect of 3D Grid Parameters on the Simulation
of the Working Process of Axial Turbines
Grigorii Popov, Valery Matveev, Oleg Baturin, Iuliia Novikova,
Daria Kolmakova and Vasilii Zubanov
Department of Aircraft Engine Theory, Samara National Research University, Samara, Russian Federation
Keywords: Component, Axial Turbine, CFD, Finite Volume Mesh, Settings, Simulation Accuracy, Error, Optimization.
Abstract: This article describes the second part of the global work done by the authors aimed at finding the best settings
for a numerical model for calculations of axial uncooled turbines using the RANS approach. The authors
studied more than 80 papers published over the past 5 years in the examined field. Their analysis did not allow
to identify unified recommendations for the creation of numerical models. The selection of model parameters
is usually motivated by general considerations of numerical simulation, which follow from the method. In
none of the papers the selection of parameters is correlated with the structure of the flow in the turbine. Many
specific simulation issues were not covered at all. For the research, more than 1000 models of full-size axial
turbines (including multistage turbines) and their elements were created. They differed in the number, size,
parameters of the elements of finite volume meshes, in turbulence models, in the degree of simplification.
The results were compared with the experimental data. As a result, the following was obtained: 1. A method
for developing and optimizing the working process of turbines using numerical simulation based on the RANS
approach is proposed. The search for the optimal turbine configuration is carried out using light computational
models, which are based on the simplified channel geometry and the finite volume mesh. Their application
makes it possible to reliably find the optimal turbine configuration 2.8 times faster. The characteristics of the
selected variants are verified with the help of verification models that consider the real geometry of the
channels and have a minimum error. 2. Recommendations are given on the selection of parameters for finite
volume meshes and the selection of turbulence models for numerical models of the working process of axial
turbines designed to perform optimization and verification calculations.
NOMENCLATURE
GTU – gas turbine unit
GTE – gas turbine engine
LPT – Low pressure turbine
FT – free turbine
y+ – dimensionless distance
RANS - Reynolds-averaged Navier–Stokes equations
=
- cell expansion ratio of the finite
volume mesh
=
- maximum cell aspect ratio of the
finite volume mesh
y
FP1
–size of the element of the finite volume mesh
closest to the endwall.
y
B2B1
- size of the element of the finite volume mesh
closest to the blade surface
CIAM – Central Institute of Aviation Motors
ζ
PR
– profile losses
λ – specific velocity
β
1
– inlet flow angle of the cascade, degree
β
2
– outlet flow angle of the cascade, degree
–residual dispersion
F – F-ratio test
qMSE – mean square error
– mean relative square errors
ζ
EXP
mean
– mean experimental value of profile losses
S – calculation speed up
η
PR
– cascade efficiency
Т
∗
- gas expansion ration in turbine
Popov, G., Matveev, V., Baturin, O., Novikova, I., Kolmakova, D. and Zubanov, V.
Estimation of the Effect of 3D Grid Parameters on the Simulation of the Working Process of Axial Turbines.
DOI: 10.5220/0006890203710377
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 371-377
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
371

α
OUT
– outlet flow angle of the turbine, degree
Т
∗
- throughflow capacity of the turbine, m
.
n – rotational speed, rpm
∗
- isentropic rate of gas expansion in a turbine, m/s
E – efficiency of parallelization of a computational
task
B2B – two-dimensional blade passage
FV – finite volumes.
1 MOTIVATION AND
STATEMENT OF THE
RESEARCH PROBLEM
This paper is an integral part and a continuation of the
paper (Popov, 2018) in which it was shown that axial
uncooled turbine is widely used in aviation and
industrial gas turbine propulsion engineering.
Turbines are the components that significantly
determine the reliability, efficiency and cost of gas
turbine engines (Inozemcev, 2015). For this reason,
the problem of increasing the efficiency of turbines is
important and relevant. It is also important to develop
methods for designing and developing such turbines,
and primarily the methods for their numerical
simulation that is the most advanced calculation
method available to a modern engineer for evaluation
of the characteristics.
It was shown in (Popov, 2018) that the available
publications do not contain universal recommenda-
tions for numerical modeling of turbines. In (Popov,
2018), an approach was suggested, according to
which the selection of finite volume mesh should be
differentiated in accordance with the flow structure in
the blade row.
The selection of the values for 2D mesh
parameters must be carried out by the profile losses
determined during the simulation for individual blade
rows or by integral parameters of the turbines. The
paper (Popov, 2018) contains the results of the study
to substantiate this choice. Secondary losses have a
complex distribution along the height of the blade and
have effect only near the end surfaces of the flow
path. Therefore, when selecting the values of
and
, it is necessary to evaluate the distribution
of the flow parameters (for example, loss coefficients,
flow angle, total pressure) along the height of the flow
path. Below the development of recommendations for
the selection of the distribution of parameters along
the height of the turbine cascade and the results of
testing the received recommendations during the
simulation are described.
2 INVESTIGATION OF EFFECT
OF THE DISTRIBUTION OF
FINITE-VOLUME MESH
ELEMENTS ALONG THE
HEIGHT OF THE FLOW PART
TO THE SIMULATION
EFFICIENCY OF THE
WORKING PROCESS OF
TURBINE CASCADES
In the framework of the research, 9 meshes were
created for each cascade, the values of
and
parameters in which ranged from 1.2 to 1.7 and
from 250 to 4000, respectively. Each mesh was
simulated using 6 turbulence models. In total, 216
numerical models were created.
and
parameters have a qualitative and
quantitative effect on the calculated distribution of
secondary losses along the height of the flow part
=
. The increase in the
and
parameters leads to a decrease in the characteristic
loss peak on the distribution of secondary losses
along the height of the flow part (Figure 1), which is
also confirmed by the patterns of the flow structure in
the blade passages (Figure 2).
Figure 1: Influence of the
parameter at
=1.2
on the simulation of secondary losses (on the example of
cascade No. 34 (Venediktov, 1990).
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
372
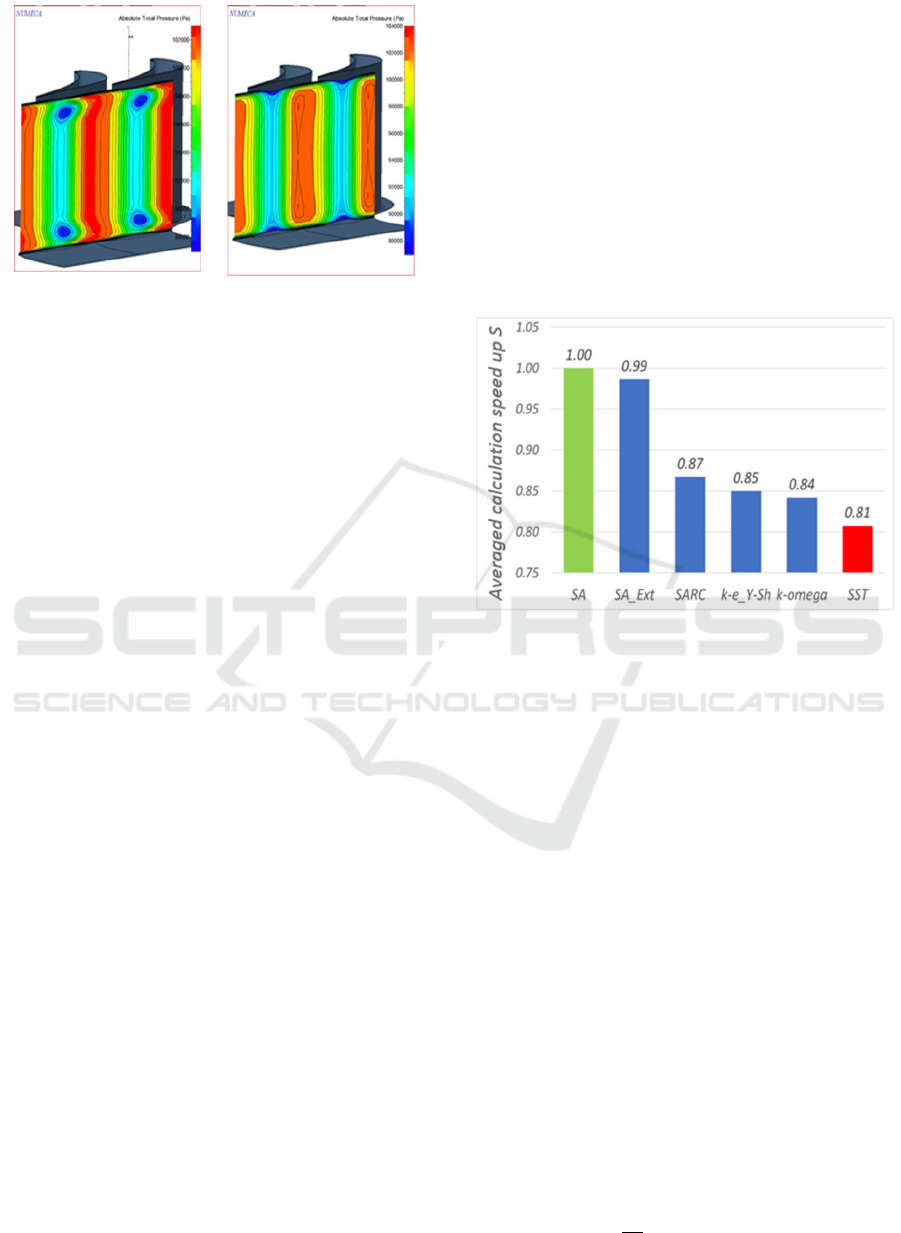
a)
=1.2;
=250
b)
=1.7;
= 4000
Figure 2: Influence of the
and
parameters on
the computed fields of turbulent viscosity at the outlet from
the cascade No. 34 (Venediktov etc., 1990).
Acceptable combinations of the
and
parameters that allow to describe the distribution of
secondary losses in blade height adequately to the
experimental data are:
=1.2,
=
250 … 2000, and
=1.2…1.7,
= 250.
The
and
parameters have a negligible
effect on the total loss coefficient
in the
cascades (the change in the calculated value of
with changing
and
parameters in the
indicated ranges does not exceed 0.002), but they
significantly decrease the value of the speed up
parameter S in the range of
<1.4 and
<
1000, reaching the value S = 0.46 for
<1.2 и
= 250.
Based on the performed studies, it was concluded
that rational combinations of the parameters
and
for simulation of the secondary flows of
turbine cascades are:
=1.2,
=
1000 … 2000.
Then, the influence of the turbulence model on the
efficiency of simulation of the secondary losses in
axial turbine cascades was studied. When conducting
the mesh studies, it was found that the selection of the
turbulence model has only a quantitative effect on the
characteristics of the cascades in the form of
=
, and, consequently, on the error in
determining the coefficients of profile losses and the
efficiency of the cascades. The smallest errors in the
calculation of the cascade characteristics are provided
by using SST and k-ω turbulence models. It was also
found that the selection of the turbulence model has a
certain effect on the speed up of the calculations S.
Figure 3 shows a histogram of the relative speed up
averaged over all cascade and meshes
. The
relative speed up
was defined as the ratio of
the calculation time of one iteration
,
of the
numerical model with the i-th mesh and the Spalart-
Allmaras turbulence model to the time of calculation
of one iteration
,
of the numerical model
with the i-th mesh and the j-th turbulence model:
=
,
/
,
. The greatest value
of speed up
is achieved using the Spalart-
Allmaras turbulence model. Thus, to perform
optimization calculations, it is advisable to use the
Spalart-Allmaras model, and SST and k-ω turbulence
models for the verification, since the least error in
determining the losses is achieved.
Figure 3: The averaged (over all meshes) calculation speed
up for various turbulence models.
3 INVESTIGATION OF THE
INFLUENCE OF VARIOUS
PARAMETERS OF FINITE
ELEMENT MESHES ON THE
SIMULATION EFFICIENCY OF
THE WORKING PROCESS OF
FULL-SIZE GAS TURBINES
One of the features of numerical simulation of the
working process of full-size axial uncooled turbines
is the need to determine three characteristics for them:
the dependences of throughflow capacity, efficiency
and the flow angle in absolute motion at the outlet of
the turbine from the expansion ratio to the total
pressure (
Т
∗
=
Т
∗
,
Т
∗
=
Т
∗
и
=
Т
∗
,
respectively). Other features of simulation of the
working process of turbines is the variety of structural
elements of stage, such as, for example, shroud
platform, as well as the need to determine the
characteristics for different modes of operation with
respect to the
∗
⁄
parameter.
Estimation of the Effect of 3D Grid Parameters on the Simulation of the Working Process of Axial Turbines
373

Therefore, in addition to checking the results of
studies for turbine cascades on the simulation
efficiency of the turbine working process as a whole
while varying the number of 2D B2B mesh elements,
parameter, the
and
parameters, the
turbulence models obtained earlier, additional studies
on the effect of the accounting the parietal cavities
over the shroud platforms on simulation efficiency,
and also on the evaluation of the simulation efficiency
for various values of the parameter
∗
⁄
were
carried out.
In total, ten uncooled axial turbines with
aerodynamically long blades were examined. The
number of stages in the selected turbines ranged from
1 to 4, the throughflow capacity
Т
∗
was in the range
from 0.3 m
.
to 3.0 m
.
, the value
of the loading parameter
∗
⁄
was up to 0.66.
In the beginning, the computational models of
turbines were created using the parameters of the
basic numerical models of the working process. They
did not contain the parietal cavities. The simulation
was performed using three turbulence models:
Spalart-Allmaras, k -ε Low Re Yang-Shih and k-ω (in
total 30 numerical models).
As a result of the conducted studies, it was
established that all the obtained calculation
characteristics are adequate to the available
characteristics of turbines obtained experimentally or
using verified mathematical models. At the same
time, the discrepancy between the existing and the
numerical values of the integral parameters of
turbines at the design point reached 4% (abs.)
(Figure 4, a). For this reason, the existing and
resultant numerical simulation data were recalculated
into a relative form:
=
Т
∗
.. The
relative values of the integral parameters of turbines
Т
∗
,
Т
∗
and
were determined using
expression:
=
,
where is the parameter value at an
arbitrary point of the characteristic curve,
is the parameter value at the design
point. All the relative characteristics obtained during
numerical simulation are adequate to the available
experimental characteristics (Figure 4, b). Thus, it
was concluded that all the basic numerical models of
the working process of turbines allow to determine
the behavior of the characteristics of turbines.
a) absolute characteristics
b) relative characteristics
Figure 4: Comparison of the calculated and experimental
characteristics of the NASA 4.5 turbine stage (Whitney,
1977), obtained using various turbulence models and basic
meshes.
Then, a study of the effect of the number of 2D
B2B mesh elements on the simulation efficiency of
the working process of axial uncooled turbines was
performed. Within the framework of the research
based on the basic meshes, 3 additional
computational meshes were created for each turbine
with 2D meshes B2B-2, B2B1 and B2B2, the number
of B2B elements varied from 6000 to 34000. The
calculation of each mesh was carried out using three
turbulence models. In total, 120 numerical models
were created. The studies confirmed the conclusions
made for the cascades about only the quantitative
influence of the number of B2B elements on the
calculation absolute characteristics; about a small
quantitative effect on the calculated parameters for
the number of elements 2 21000 (2D mesh
B2B1); about the insignificant influence of the
number of B2B elements on the absolute and relative
errors in determining the integral parameters of
turbines (Figure 5), as well as on increasing the
calculation speed up S to 2, while reducing the
number of 2D mesh elements to 6000 (corresponds to
B2B0 mesh). At the same time, the relative
characteristics of turbines when changing the number
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
374

of B2B elements practically do not change and are
adequate to the available relative characteristics.
Figure 5: The influence of the number of 2D mesh elements
on the absolute error in determining the efficiency of the
turbine.
Investigations on the effect of the
parameter
on the simulation efficiency performed in the range
of
from 0.2 to 5.0 using three turbulence
models also confirmed the conclusions drawn for the
cascades. The change in the
parameter does not
change the behavior of the calculation absolute
characteristics of turbines and only shifts them along
the ordinate axis. For
1, the influence of the
parameter on the calculated values of the integral
parameters of the turbines and on the error of their
determination is extremely insignificant. At the same
time, the relative characteristics of turbines with a
change in the
parameter practically do not
change and are adequate to the available relative
characteristics.
The next step was to investigate the effect of the
and
parameters on the simulation
efficiency of the turbine workflow. The range of
parameters during the study was:
=1.2…1.7,
= 1000 …4000.. Also, as for cascades, the
increase in
and
parameters lead to the
flattening of peaks due to secondary losses on the loss
distribution over the height of the flow part
(Figure 6). At the same time, permissible
combinations of the
and
parameters
allow adequately describing the distribution of losses
along the blade height:
1.4,
2000.
and
parameters in the permissible range
have practically no effect on the absolute and relative
characteristics of the turbines. At the same time, the
calculation speed up S significantly decreases with
decreasing the
and
parameters, reaching
the value S = 0.67 for
1.4,
2000.
Figure 6: The effect of the
parameter at
= 1000 on the simulated distribution of losses along
the blade height in a section behind first nozzle block of the
NASA turbine (Whitney, 1977).
Studies on the effect of accounting the cavities
over the shroud platforms on the simulation
efficiency showed that their presence does not
qualitatively affect the behavior of the characteristics,
but exerts a significant quantitative influence on
them, shifting the efficiency along the ordinate axis
by up to 1% (Figure 7), which leads to a significant
reduction in the error in the calculation of the
efficiency. At the same time, the calculation speed up
S is also significantly reduced (up to 0.74)
(J. Respondek, 2010).
Figure 7: The influence of the accounting of the shroud
platform on the calculation characteristics of the LPT.
Simulation of the turbine working process using
different meshes, turbulence models for various
values of the parameter
∗
⁄
showed that all
numerical models allow to estimate the
characteristics at off-design modes by
∗
⁄
in
Estimation of the Effect of 3D Grid Parameters on the Simulation of the Working Process of Axial Turbines
375

absolute and in a relative form without additional
errors.
At the final stage, the effect of the selection of
turbulence models on the simulation efficiency of the
working process of axial turbines was generalized.
All the described mesh studies for turbines were
performed using only three turbulence models and
allowed to establish that the selection of the
turbulence model does not change the behavior of the
characteristics, but only equidistantly shifts them
along the ordinate axis. Thus, all turbulence models
make it possible to evaluate trends in the turbine
parameters. The simulated workflow of some of the
turbines using the basic meshes and 7th turbulence
models only confirmed these conclusions. The
smallest errors in determining the integral parameters
of turbines are provided by using k-ω turbulence
model, and the greatest speed up S is when the
Spalart-Allmaras turbulence model is used.
4 GENERALIZATION OF THE
OBTAINED RESULTS:
RECOMMENDATIONS FOR
THE DEVELOPMENT OF
NUMERICAL MODELS OF
AXIAL UNCOOLED TURBINES
Based on the studies carried out, two methods were
developed for the creation of rational numerical
models for the working process of turbines with
aerodynamic long blades, designed to perform
optimization and verification calculations.
At the first stage of creating a rational numerical
model designed to perform optimization calculations,
the geometry of the computational domain is
constructed.
Then a mesh of finite volumes is constructed. For
optimization calculations it is necessary to use two-
dimensional meshes B2B-2 (6000 elem.), in which
the value of the dimensionless parameter
is 1.
The distribution of the elements along the height must
be specified using the
and
. parameters.
At the initial stages of optimization, it is advisable to
use meshes in which
<1.4,
< 2000.
When optimizing with a more accurate account of
secondary losses, meshes should be used in which
<1.2,
< 2000.
At the third stage of adjusting the parameters of
the numerical model, among other settings, it is
necessary to select the Spalart-Allmaras turbulence
model.
When configuring paralleling settings, it is
advisable to adhere to the approach that involves
running the maximum number of tasks
simultaneously on all processors.
This method allows to create rational optimization
numerical models that to estimate accurately the
trends in the integral parameters of turbines and have
high values of the speed up parameter up to 2.8.
The method of creating rational numerical models
intended for verification calculations differs from the
method for optimization models only by
recommendations on the selection of values of model
parameters.
For verification calculations, it is advisable to use
two-dimensional meshes B2B1 (21000 elem.). The
values of the parameters for the distribution of
elements along the height of the flow part should be
chosen from the interval:
<1.2,
= 1000 …2000. When carrying out the
verification calculations, it is necessary to consider
the parietal cavities over the shroud platforms. For
verifying calculations, the best results are shown by
the k - ω turbulence model.
Parallelization should be performed on the
maximum possible number of processors, but one
processor should account for at least 200 thousand
elements of the computational mesh.
This method allows the creation of rational
numerical models designed for verification
calculations, which determine the detailed flow
structure, which have minimal errors in determining
the integral parameters, but also a low value of the
speed up S (approximately 0.27...0.30).
5 CONCLUSIONS
This paper together with (Popov, 2018) describes the
main stages and results of the work aimed at
increasing the simulation efficiency (increasing
accuracy and reducing the calculation time) of the
workflow of uncooled axial turbines of aircraft
engines using the RANS approach.
To obtain the results, more than 80 papers by
different authors published over the last 5 years
related to numerical simulation of the working
process of axial turbines were studied. More than
1000 numerical models of axial turbines and their
elements were created, calculated and analyzed. The
obtained results were compared with the results of
experiments or calculations using verified methods.
All the results obtained during the study were
processed and generalized using the methods of
mathematical statistics.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
376

As a result of the work, the following results were
obtained:
1. A method for studying, improving and
optimizing the working process of axial turbines
using numerical simulation based on the RANS
approach is proposed. The essence of the method lies
in the fact that the search for the optimal
configuration of the turbine is carried out using light
computational models that are based on a simplified
channel geometry (neglecting the parasitic cavities,
fillets, etc.) and a light mesh of finite volumes. The
application of such models makes it possible to create
a rational optimization numerical models that allow
estimating the trends in the variation of the integral
parameters of turbines and having high values of the
speed up parameter (up to 2.8). The obtained results
should be checked with the help of verification
numerical models that consider the real geometry of
the channels and allow to determine the detailed flow
structure with minimal errors in calculating the
integral parameters.
2. A universal complex of parameters describing
the finite volume mesh of numerical models of axial
air turbines and based on the features of the flow
structure in the channels is proposed. The complex
includes: the number of elements along the
characteristic sides of 2D-mesh topological blocks;
dimensionless parameter y
, which determines the
values y
and y
, the cell expansion ratio along
the height of the flow part ER
, the maximum cell
aspect ratio along the height of the flow part MR
.
3. An original approach to the search for the best
parameters of a finite volume mesh was proposed and
implemented. In particular, the selection of the values
of the parameters of 2D mesh should be carried out
according to the calculated profile losses for
individual blade rows or by integral parameters of
turbines. The selection of ER
and MR
parameter
values must be performed based on the distribution of
flow parameters along the height of the flow part.
4. Recommendations were received on the setting
the parameters for finite volume meshes and the
selection of turbulence models for numerical models
of the working process of axial uncooled turbines
designed to perform optimization calculations. The
number of B2B mesh elements must contain more
than 6000 elements, the value of the y
parameter
is 1, the value of the MR
parameter is 2000, and the
ER
parameter value is less than 1.4. Simulation
should be performed using the Spalart-Allmaras
turbulence model.
5. Recommendations were received on the setting
the parameters for finite volume meshes and the
selection of turbulence models for numerical models
of the working process of axial uncooled turbines
designed to perform verification calculations. For
verification calculations it is advisable to use two-
dimensional B2B meshes with the number of
elements greater than 21000. The values of the
parameters for the distribution of the elements along
the height of the flow part should be chosen from the
interval: ER
<1.2, MR
= 1000 … 2000. When
carrying out verification calculations, parietal cavities
over the shroud platforms should be considered.
Simulation should be performed using k-ω turbulence
model.
ACKNOWLEDGEMENTS
This work was supported by the Ministry of
Education and scenes of the Russian Federation in the
framework of implementation of the Program of
increasing the competitiveness of Samara University
among the world's leading and educational centers for
2013-2020 years.
REFERENCES
Popov, G., Matveev, V., Baturin, O., Novikova, J., Volkov
A., 2018. Selection of parameters for blade-to-blade
finite-volume mesh for CFD simulation of axial
turbines. In press. Proceedings of International
Conference on Mechanical, System and Control
Engineering, ICMSC 2018.
Inozemcev, A. A., 2015. Development of a line of civil gas
turbine engines (Razvitie linejki grazhdanskih GTD).
Report, CIAM.
Venediktov, V. D., and Granovsky, A. V., 1990. The
Atlas of Experimental Performances of Cooled Gas
Turbine Blade Cascades (Atlas eksperimental'nykh
kharakteristik ploskikh reshetok okhlazhdaemykh
gazovykh turbin). CIAM.
Wilfert, G., Joerg, S., Rolt, A., Baker, N., and A. Touyeras,
2007. New Environmental Friendly Aero Engine Core
Concepts. Proceedings of the ISABE 2007, Paper 1120.
Whitney, W. J., Bebning, F. P., Moffit, T. P., Hotz, G. M.,
1977. Cold-air investigation of 4 ½ stage turbine with a
stage loading factor of 4.66 and high specific work
output. I – Overall Performance. NASA TM X-3498.
Respondek, J., 2010. Numerical simulation in the partial
differential equation controllability analysis with
physically meaningful constraints. Mathematics and
Computers in Simulation 81, P 120–132.
Estimation of the Effect of 3D Grid Parameters on the Simulation of the Working Process of Axial Turbines
377
