
An Approach for Adaptive Parameter Setting
in Manufacturing Processes
Sonja Strasser, Shailesh Tripathi and Richard Kerschbaumer
Production and Operations Management, University of Applied Sciences Upper Austria,
Wehrgrabengasse 1-3, Steyr, Austria
Keywords: Process Parameter Setting, Manufacturing, Model Selection, Regression Analysis, Machine Learning.
Abstract: In traditional manufacturing processes the selection of appropriate process parameters can be a difficult task
which relies on rule-based schemes, expertise and domain knowledge of highly skilled workers. Usually the
parameter settings remain the same for one production lot, if an acceptable quality is reached. However, each
part processed has its own history and slightly different properties. Individual parameter settings for each part
can further increase the quality and reduce scrap. Machine learning methods offer the opportunity to generate
models based on experimental data, which predict optimal parameters depending on the state of the produced
part and its manufacturing conditions. In this paper, we present an approach for selecting variables, building
and evaluating models for adaptive parameter settings in manufacturing processes and the application to a
real-world use case.
1 INTRODUCTION
Product and process quality is playing an increasingly
important role in the competitive success of
manufacturing companies (Robinson and Malhotra
2005). As a consequence, this trend forces
manufacturing companies to further improve their
production (Wuest et al., 2014).
In general, quality is defined as the degree to
which a commodity meets the requirements of the
customer (DIN EN ISO 9001:2015). In this context,
customers are not only the users of final products;
they can also be other companies in a supply chain
network. When a company is a supplier of
components, which serve as assembly parts in a final
product, then important quality requirements are
dimensions of parts, which have to be within
predefined tolerances. There exist International
Tolerance Grades of industrial processes, which
identify what tolerances a given process can produce
for a given dimension (ISO 286-1:2010). If an
industrial process is more precise, less scrap is
produced or even a higher tolerance class can be
achieved and the produced components can generate
more profit for the company.
The appropriate and prompt selection of process
parameters in manufacturing processes plays a
significant role to ensure the quality of the product, to
reduce the machining cost and to increase the
productivity of the process (Pawar and Rao, 2013). In
practice, the adjustment of process parameters to get
dimensions of a produced part in predefined
tolerances can be a difficult task. Traditional control
systems rely on rule-based schemes, expertise and
domain knowledge of highly skilled workers or on
trial and error. Furthermore, modern manufacturing
processes are becoming more and more complex and
modelling every aspect of a process in a rule- and
expert-based system is getting challenging or even
impossible.
The phase of parameter adjustment consumes
precious production time where scrap parts are
processed. Once an acceptable setting of parameters
is obtained, it is common to remain it unchanged for
the whole production lot. However, each part
processed has its own history and slightly different
properties. Individual parameter settings for each part
can further increase the quality and reduce scrap.
Machine learning (ML) methods offer the
opportunity to generate models based on
experimental data, which automatically predict
optimal parameters depending on the state of the
produced part and its manufacturing conditions.
This paper contributes to the application of ML
methods for parameter setting in manufacturing
processes and addresses the following research ques-
24
Strasser, S., Tripathi, S. and Kerschbaumer, R.
An Approach for Adaptive Parameter Setting in Manufacturing Processes.
DOI: 10.5220/0006894600240032
In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 24-32
ISBN: 978-989-758-318-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tions:
- How can ML methods be integrated in a
framework for adaptive parameter setting?
- Which ML methods are suitable in models for
adaptive parameters settings?
- Which accuracy can be reached when predicting
quality measures and is this accuracy sufficient
for practical applications?
We provide the related work to this topic in Section 2
and present the methodology of the developed
approach in Section 3. Afterwards, we apply and
evaluate our approach in a use case based on real-
world manufacturing data in Section 4. Concluding
remarks follow in the final Section 5.
2 RELATED WORK
There exist literature of parameter optimization and
parameter setting for different kinds of manufacturing
processes.
For the injection moulding process there are
different approaches. A common design method to
reduce the amount of simulation runs and to consider
interaction effects of parameters is the Taguchi
method (Oliaei et al., 2016; Tian et al., 2017). It is
used to find a better initial point for the optimization
and to reduce time for solving the problem. For the
optimisation of a multi-objective problem a
combination of Response Surface Methodology
(RSM) and non-dominated sorting genetic algorithm
II (NSGA II) is used (Park and Nguyen, 2014; Tian et
al., 2017). The function generated out of the RSM is
optimized with the NSGA II. As initial values for the
first iteration of the genetic algorithm it is possible to
use results from the Taguchi method or to generate
random values within a set range. Oliaei et al., (2016)
used an Artificial Neural Networks (ANN) with the
learning algorithm of back-propagation to optimize
the quality. In their work, they compared the results
of the Taguchi method with the results of the ANN.
In both methods the same sample set was used. The
results show that there is a slight difference between
them.
In Additive Manufacturing unsuitable process
parameters influence the quality of 3D printed parts
adversely. There exist various approaches to use
Machine Learning to choose optimal process
parameters for different technologies in 3D printing
(Fused Deposition Modeling, Selective Laser Melting
or Sintering). The most popular method used is
Artificial Neural Networks (ANN) (Collins et al.,
(2014), Ding et al., (2016)) which performs good due
to the provided flexibility. Although comparisons
show that in some cases regression is only slightly
worse (Xiong et al., (2014), Mohamed et al., 2016).
Cook et al., (2000) develop an ANN to model the
relationship between process operating parameters
and a critical strength parameter in a particleboard
manufacturing process. Then a genetic algorithm is
applied to determine the process parameter values,
which result in desired levels of the strength
parameter.
Park and Kim (1998) present a review on artificial
intelligence approach which attempt to automatically
adapt and optimize the CNC machining parameters
based on sensor information in real time. Again ANN
is the dominating method in this field of application.
Venkata Rao and Kalyankar (2013) present an
approach for process parameter optimization in a
multi-pass turning operation. They developed a
teaching-learning-based optimization algorithm,
which outperforms other optimization methods in
their multi-objective and single-objective examples.
It is stated that this algorithm can be easily modified
for parameter optimization of other manufacturing
processes, such as casting, forming and welding.
An approach for estimating control parameters of
a plasma nitriding process is presented in Kommenda
et al., (2015). They solve inverse optimization
problems to find good combinations of parameters
such that desired product qualities can be fulfilled
simultaneously.
As already slight variations of the product state
during production can lead to costly and time-
consuming rework or even scrap, Wuest et al., (2014)
suggest an approach based on recording of the
individual product’s state along the entire production
process. Whereas condition monitoring is mostly
focused on a single manufacturing process,
monitoring of the whole manufacturing programme
has to be further investigated (Choudhary et al.,
2009). Wuest et al., (2014) suggest a combination of
cluster analysis and support vector machines (SVM)
to achieve the goal of improved quality monitoring.
They provide a theoretical example to illustrate the
potential of the approach, but the application to a real-
life manufacturing process is missing.
This paper applies the concept of tracking the
individual product state to predict quality relevant
requirements of finished manufactured parts. As the
considered target variables are numeric (e.g.
dimensions of the part), instead of classification (e.g.
good and bad parts), methods for regression are
chosen. Furthermore, the developed approach is
evaluated on data from a real-life industrial
environment.
An Approach for Adaptive Parameter Setting in Manufacturing Processes
25

3 METHODOLOGY
In this section, an approach for the setting of process
parameters of a manufacturing process is developed.
The setting of the process parameter is adaptive for
each produced part depending on its properties and
previous manufacturing conditions. First, the
collection of the necessary process and product data
is presented. Then the basic concept of the parameter
setting is introduced. Based on this concept the next
steps are data pre-processing, the selection of a
suitable machine learning model and its evaluation
based on different criteria.
3.1 Data Collection
We consider a multi-stage manufacturing process,
consisting of N consecutive steps (Figure 1). In each
step a physical transformation of the product is
performed, so that, starting from the raw material in
step 1, the final product is finished in step N. The
approach, which is developed in this section, refers to
parts of one specific product type. If there are
multiple product types in the manufacturing system,
it is possible to apply this approach to each type
separately.
The basic idea is to record all relevant product and
process variables of each manufactured part. Due to
variations in material properties and manufacturing
conditions (e.g. machine and tool conditions,
environmental conditions, influence of human
workers) each part will be characterised by individual
values of the variables, which describe the life cycle
of the part during the manufacturing process. This
concept is introduced by Wuest et al., (2011) as
product state based view.
In our approach, it is important to distinguish
between independent and dependent variables. Some
of the product and process variables, like the type of
raw material or the adjustment of process parameters,
can be manually selected and are not influenced by
other recorded variables. Other variables, like quality
relevant properties of the part, depend on the values
of multiple variables, although the precise
relationships are not known in practice.
Figure 1: Product and Process Variables.
3.2 Basic Concept
The final objective is to determine appropriate,
adaptive parameter settings of the last production step
for a specific part based on its manufacturing life
cycle to fulfil the quality requirements. The selection
of multiple process parameters is likely to deliver a
manifold of solutions whereas the fulfilment of
multiple quality requirements won’t be feasible in
general. Therefore, we restrict our approach to the
determination of one process parameter of the last
production step (u), in order to fulfil a single relevant
quality requirement (z). The considered process
parameter belongs to the independent process
variables of step N and the quality requirement is part
of the dependent product variables of step N. In our
approach, we take only numeric quality measures into
account, like critical dimensions or the weight of the
part.
Figure 2: Basic Concept.
To achieve this goal, we suggest a two-step
approach (see Figure 2). First, we model the
relationship between the quality measure and relevant
product and process variables, including the selected
process parameter, by a function f.
ˆ
( , , )
ij ij
z f x y u
(1)
This function enables the prediction of the relevant
quality measure (
ˆ
z
) based on the life cycle of an
individual part. Then we calculate, if possible, the
inverse function of f. This inverse function
1
f
enables us to set a predefined optimal value for the
quality measure and to estimate the necessary process
parameter (
ˆ
u
) under consideration of the actual
product and process variables of a specific part.
1
ˆ
( , , )
ij ij
u f x y z
(2)
If f is no bijective function, Eq. (1) has to be solved
PROCESS
PRODUCT
STEP 1
STEP 2 STEP N
........
........
Proc
. Var. y
11
Proc
. Var. y
12
.....
Proc
. Var. y
1m
1
Prod
. Var. x
11
Prod
. Var. x
12
.....
Prod
. Var. x
1m
1
Proc
. Var. y
21
Proc
. Var. y
22
.....
Proc
. Var. y
2m
2
Prod
. Var. x
21
Prod
. Var. x
22
.....
Prod
. Var. x
2m
2
Prod
. Var. x
N1
Prod
. Var. x
N2
.....
Prod
. Var. x
Nm
N
Proc
. Var. y
N1
Proc
. Var. y
N2
.....
Proc
. Var. y
Nm
N
MODELING RELATIONSHIP
f
Product Variables
Process Variables
Process Parameter
f
-1
PARAMETER SETTING
Product Variables
Process Variables
Process Parameter
Quality Measure
Quality Measure
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
26

implicitly, for example by using Newton’s method.
However, in this case, multiple solutions can exist.
3.3 Data Pre-processing
There are some data pre-processing needed, in order
that we are able to apply regression models in the first
step of our approach. If there are nominal variables in
the set of the recorded product and process variables,
they have to be replaced by binary attributes (dummy
coding). A nominal variable with m levels has to be
transformed in m-1 dummy variables with 0 and 1 as
possible values.
The second point, which has to be checked, is the
collinearity of attributes, since it reduces the accuracy
of the regression model. It is likely that some of the
recorded product and process variables are correlated.
For example, if the height of the part is measured after
each process step, i.e. N times, then these N variables
are presumably more or less correlated. Here not only
correlation between two attributes has to be
considered, also multicollinearity has to be detected.
A way to assess multicollinearity is to compute
variance inflation factors (VIF). The smallest possible
value for VIF is 1, which indicates no collinearity.
Attributes with VIF values that exceed 5 or 10 should
be dropped from the regression analysis (James et al.,
2013).
In some cases, it can be useful to create new
features based on the recorded process and product
variables to increase the accuracy of the applied
machine learning model. Using domain knowledge of
experienced workers of the considered manufacturing
process can help in feature engineering as well as in
the selection of relevant variables.
3.4 Model and Variable Selection
For modelling the relationship between product and
process variables and the quality measure, regression
models and artificial neural networks (ANN) are
applied.
ANN are a flexible and widely spread method for
modelling complex relationships (Widrow et al.,
1994). A multi-layered architecture is built up from
one or more hidden layers placed between an input
and an output layer. Each layer consists of several
highly interconnected processing units, called
neurons, which sum weighted inputs and apply an
activation function for generating the output. The
weights are determined by training the neural network
with the goal to minimize the error between the actual
and predicted output values. Then a separate test set
of data is used to estimate the network’s performance
on new data. After all, the neural network serves as a
function that maps input values (product and process
variables) to output values (quality measures).
Although ANN deliver good models for prediction,
regression models are more transparent and easier to
interpret when applying them in the practice of
manufacturing companies.
When we choose a regression model, we first have
to answer the question, which variables from the set
of the recorded product and process variables of the
whole manufacturing process have the biggest
influence on the quality measure and therefore should
be used for modelling. From the point of view of the
practitioners in the companies, it is desirable to get a
model with a good accuracy, which only depends on
a few variables. This configuration would reduce the
cost and time for measuring and recording a huge
amount of data from the production process.
However, using too few variables will lead to bias and
the inclusion of too many of them is likely to cause
overfitting. A variety of methods for selecting
variables is available (Miller, 2002; James et al.,
2013), such as
Best subset selection
Forward selection
Backward elimination
Best subset selection fits a model to each combination
of possible numbers of prediction variables. If there
are p prediction variables, then
2
p
models are trained
and the best of them is selected. Because of the
computational effort, the application is only possible,
if p is not too high. Otherwise, stepwise methods, like
forward selection and backward elimination, are
alternatives, which only explore a restricted set of
combinations. Forward selection starts with the best
model containing only one variable and increases the
number of variables in each step by one. Conversely,
backward selection starts with all possible prediction
variables and reduces the number in each step by one.
Regardless of the applied method for variable
selection, performance measures for the comparison
of different models are necessary in order to pick out
the best model (Murtaugh, 2010). Different
techniques for model evaluation are introduced in the
next subsection 3.4.
If linear regression is not adequate to generate
models with good performance, the linearity
assumption can be relaxed by introducing polynomial
terms or generalized additive models. The selection
of the applied function types can be motivated by
known physical relationships of product and process
variables.
An Approach for Adaptive Parameter Setting in Manufacturing Processes
27

3.5 Model Evaluation and Parameter
Setting
Different models based on different sets of prediction
variables have to be compared in order to select the
best one. Residual Sum of Squares (RSS) and R² are
not suitable measures because they are based on the
training data and are getting better, when the number
of prediction variables increases. For model selection,
the test error has to be estimated directly (e.g. by
cross-validation) or indirectly (by adjusting the
training error to account for the bias due to
overfitting). In the first case, mean squared error
(MSE) or root mean squared error (RMSE) can be
applied. In the second case, the following criteria can
be used: Akaike information criterion (AIC),
Bayesian information criterion (BIC), C
p
value and
Adjusted R² (James et al., 2013).
One of these criteria or the cross-validation error
can be applied for model selection in order to get a
linear regression model f based on a selected set of
process and product variables or a neural net with an
optimal number of neurons in the hidden layer. In
variable selection, it must be observed that the
process parameter u, which has to be adjusted for
each individual part, is included in the set of selected
prediction variables. By calculating the inverse
function
1
f
of the linear function and inserting the
optimal value of the quality measure z and the
individual product and process variables of a part, an
estimation
ˆ
u
for the parameter setting is yield.
4 CASE STUDY
In this section, the developed approach is applied to a
real-world production process in metal processing
industry, which consists of three production steps.
The whole workflow for parameter setting was
implemented in R, an open-source software for
statistical computing. In the next subsection, we
describe the data, which was recorded in a
manufacturing company. There exist two relevant
quality measures of the finished part, so the approach
is applied twice and the results are reported in the
following sections.
4.1 Experimental Data
In an experiment, the data of 200 produced parts and
the associated process data were recorded. Together
with experts of the involved production processes,
relevant variables have been selected. Table 1 shows
the number of the analysed variables of each
production step. According to Figure 1, the following
notation is used:
ij
x
: j-th product variables of step i
ij
y
: j-th process variable of step i
Product variables include, for instance, the
dimensions of the part after each process step and its
weight. Important process variables are temperatures,
pressures and forces.
Both product variables of step 3 are important
quality measures, namely the height (
1 31
zx
) and
the diameter (
2 32
zx
) of the part. One of the process
variables of step 3 (
31
uy
) is the process parameter
which should be determined individually for each part
produced. With the exception of
23
y
, all product and
process variables are numeric. Since
23
y
is a nominal
attribute with 5 different levels, it is replaced by four
binary attributes (
231 232 233 234
, , ,y y y y
), such as
proposed in section 3.2.
Table 1: Number of Product and Process Variables.
4.2 Results for Quality Measure 1
Here the first quality measure, the height of the
finished part
1 31
zx
, is used as response variable in
a linear regression model. In this model, the second
quality measure
32
x
has to be excluded from the
analysis, because it is not available in advance when
using the regression model for prediction.
The calculation of VIF, using the R package “car”,
reveals that there is just one process variable with a
VIF higher than 10 (
16
VIF 12.16x
). After the
elimination of this variable, the VIF are calculated
again with the result that the maximum value is 7.56.
So this reduced data set is used for building the
regression model.
Since the number of variables is relatively small
in our application, best subset selection can be applied
for model selection. For this purpose we use the
“regsubsets” function from the R-package “leaps”.
Representative for the evaluation of the criteria
mentioned in Section 3.4, Figure 3 displays the results
of adjusted R².
Variables
Step 1 Step 2 Step 3 Total
Product Variables
6
6
2
14
Process
Variables
4
4
2
10
Total
10
10
4
24
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
28
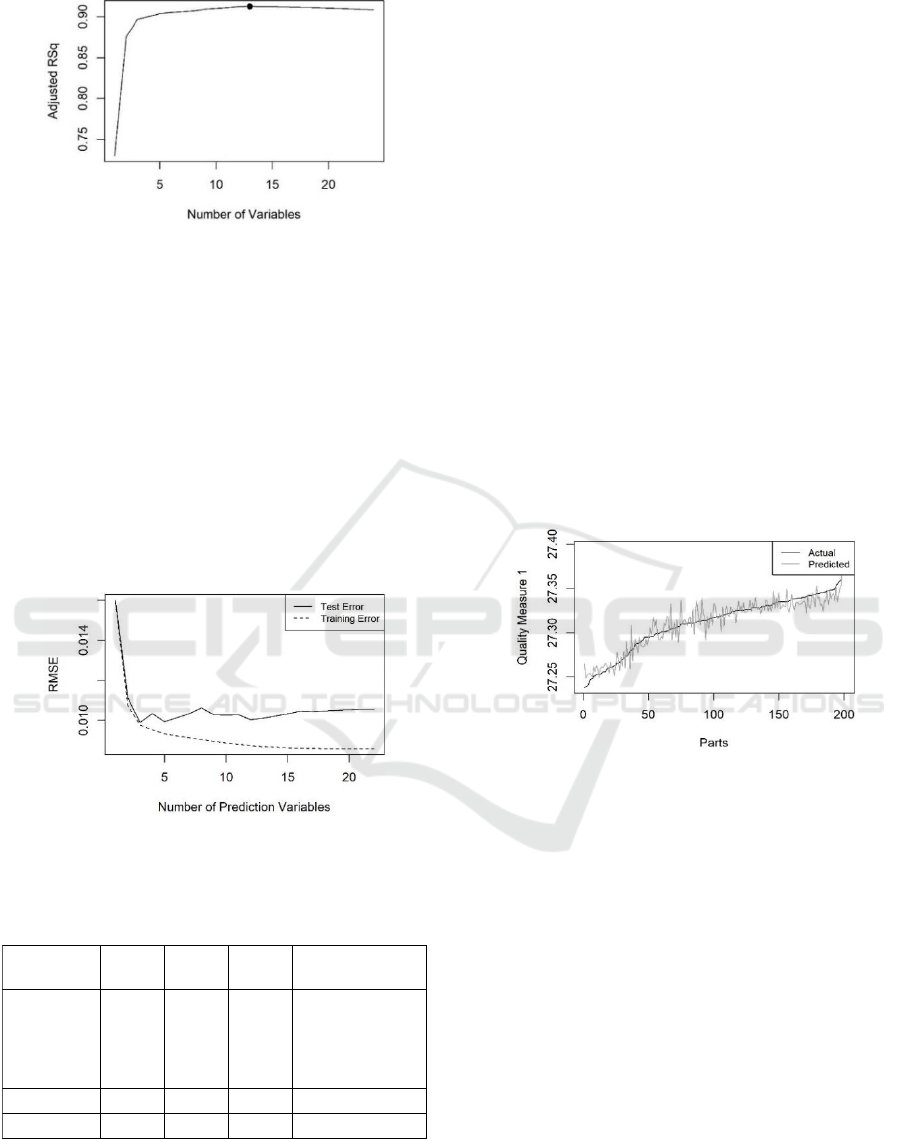
Figure 3: Adjusted R squared for Linear Regression
Models.
Although the optimal number of variables varies
from 5 to 13, all criteria reach good values with just a
view number of variables. A closer look at adjusted
R² reveals, that already 3 variables achieve a result
that is close to the optimal value.
Additionally, 10-fold cross-validation was
applied to best subset selection, to get a better
estimation of the test error. Figure 4 displays the
comparison of test and training error depending on
the number of prediction variables. This evaluation
indicates also that 3 to 5 variables are a good choice
for the regression model.
Figure 4: Cross-validation of Linear Regression Models for
Quality Measure 1.
Table 2: Comparison of Linear Regression Models for
Quality Measure 1.
Now the linear regression model is trained on the
whole dataset in order to obtain models with 3, 4, 5
and 8 variables. Table 2 compares the values of
adjusted R² and RMSE for these models and reveals
that all of these models lead to similar good results.
In all of the models the process parameter
u
, the
product variable
21
x
and the dummy coded process
variable
231
y
are selected.
The formula obtained by linear regression for
estimating quality measure 1 as a function of three
prediction variables is:
1 31 21 231
21 231
ˆ
ˆ
,,
18.477 0.772 0.289 0.012
z x f u x y
x u y
(3)
Therefore, we can see that the quality measure
increases when
21
x
increases and it decreases, when
the process parameter
u
increases or the binary
variable
231
y
has the value 1. The experts of the
manufacturing company confirm these relationships,
although for them it was surprising, that a linear
function with only three variables can provide good
estimates for this quality measure. Figure 5 provides
a graphical comparison of actual and predicted values
of the quality measure.
Figure 5: Actual vs. Predicted Values for Quality Measure
1 using Linear Regression.
In order to be able to better assess the results, it is
important to know that the optimal value for the
quality measure is 27.29 and the accepted tolerance is
0.06. Partly, there exist quite large deviations from
the optimal value, which is the consequence of the
rather large variations of possible parameters (in
comparison to serial operation) in the experiment to
get better insights in the relationships of product and
process variables. However, the deviation of
predicted values to actual values is less than the
tolerance.
Calculating the inverse function of f and inserting
the optimal value for the quality measure in Eq. (3)
yields a function for the process parameter:
1
21 231
27.29
ˆ
30.495 2.671 0.042
z
u x y
(4)
This equation can be applied to estimate the process
Number
of
Variables
3 4 5 8
Variables
u
x
21
y
231
u
x
21
y
231
y
32
u
x
11
x
21
y
231
y
32
u
x
14
x
21
y
231
, y
232
, y
233
, y
234
y
32
Adjusted
R² 0.897 0.900 0.904 0.907
RMSE
0.00977
0.00958
0.00939
0.00914
An Approach for Adaptive Parameter Setting in Manufacturing Processes
29

parameter u of step 3 individually for each part, just
by inserting one product variable and one process
variable of step 2.
For the purpose of benchmarking the results from
linear regression models, we also apply ANN for
regression. This is done by the “neuralnet” function
of the “neuralnet” package in R. We select a neural
net with one hidden layer and apply 10-fold cross-
validation to get the optimal number of neurons in this
hidden layer, using a range from 1 to 15. Figure 6
shows the training and test error as a function of the
number of neurons in the hidden layer, with a
minimum test error for four neurons. The training
errors of neural networks are comparable to the
training errors for linear regression models (see
Figure 4), but the test errors for ANN are significantly
higher. One reason for this could be the small number
of datasets for training the neural net. So already
models with three neurons tend to overfit the training
data and lead to relatively high test errors.
Figure 6: Cross-validation of Neural Networks for Quality
Measure 1.
When the neural net with four neurons in the
hidden layer is trained on the whole dataset, the
following performance is obtained:
² 0.967
0.00517
Adjusted R
RMSE
(5)
These values outperform the good results from linear
regression (see Table 2), however it is important to
note that the performance of the neural net on new
data is considerably worse than for linear regression.
Further drawbacks of neural nets in this application is
the number of variables applied (and the associated
measuring effort) and the impossibility to calculate an
inverse function, which is required for Eq. (2).
4.3 Results for Quality Measure 2
Now the same approach is applied to quality measure
2, the diameter of the finished part. Again the reduced
dataset without the product variable
16
x
, due to its
multicollinearity detected by calculating VIF, is used.
Only the response variable
31
x
is replaced by
32
x
.
However, the first results are not very promising.
Training a linear regression model on the whole
dataset using all variables delivers adjusted R² of only
0.07. A neural net can increase this value at 0.2, which
is also too less for practical applications. At this point,
feature engineering is necessary to improve the
results. A detailed analysis revealed that it is
favourable to replace the diameter in step 3 as
response variable by the change of the diameter from
step 2 to step 3:
2 2 32 22
z d x x
. Additionally we
introduced the change of the diameter from step 1 to
step 2 as a new feature
1 22 12
d x x
and excluded
the diameter
22
x
from the analysis for the sake of
collinearity.
First, best subset selection for linear regression
models in combination with a 10-fold cross-
validation is applied for model selection (Figure 7).
Also for the change of the diameter, a small number
of variables (2 – 5) is sufficient for a good predictive
model. In Table 3 linear models, which are trained on
the full data set with 2, 3, 4 and 5 variables, are
compared. Adjusted R² is nearly equally excellent for
all these models. For parameter setting, the first
model is not suitable, because the process parameter
u is not used for prediction. Selection of three
variables for prediction of the change in diameter
yields the function
2 2 12 1
12 1
ˆ
ˆ
,,
45.982 1.054 0.009 0.972
z d f u x d
x u d
(6)
Figure 7: Cross-validation of Linear Regression Models for
Change in Diameter.
Table 3: Comparison of Models for Change in Diameter.
Number
of
Variables
2 3 4 5
Variables
d
1
x
12
u
d
1
x
12
u
d
1
x
12
x
13
u
d
1
x
12
x
13
y
32
Adjusted
R² 0.974 0.975 0.976 0.976
RMSE
0.00304
0.00296
0.00294
0.00290
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
30

Figure 8 shows the comparison of actual and
predicted values for the change in diameter. The
accepted tolerance for this diameter is 0.012 and the
optimal value is 44.043, which can be applied for
calculating estimates of the necessary process
parameter for individual parts:
22 2
12 1 22
44.043
ˆ
215.44 117.11 108 111.11
xd
u x d x
(7)
Also for this quality measure we train a neural net
with one hidden layer and select the optimal number
of neurons with a 10-fold cross-validation. Here three
neurons lead to the minimum test error in the studied
range from 1 to 15 (see Figur). The performance of
the neural net, trained on the whole data set, can be
assessed by the following measures:
² 0.976
0.00275
Adjusted R
RMSE
(8)
Adjusted R² is roughly equal than the value for linear
regression models and RMSE is slightly better (see
Table 3). Taking into account the higher test error for
ANN (Figur) and the drawbacks already discussed for
quality measure 1, also for quality measure 2 the
linear regression model should be preferred.
Figure 8: Actual vs. Predicted Values for Change in
Diameter.
Figure 9: Cross-validation of Neural Networks for Change
in Diameter.
5 CONCLUSIONS
In this article, we present an approach for parameter
setting in manufacturing processes. The parameter
adjustment is adaptive to the properties and history of
each individual part. In the first step the relationship
between multiple input variables and a relevant
quality measure is investigated. Then this relationship
is used to calculate estimates for a specific process
parameter in order to get optimal quality measures.
The results of the case study, based on real-world
manufacturing data, show that even simple linear
regression models with a few product and process
variables provide good estimates for quality measures
and can be applied for parameter setting. We also
train neural nets to get a benchmark for the linear
regression models. The results reveal that neural nets
outperform linear regression on the training data, but
application on the test data shows a significantly
higher test error. Recording more data for training and
testing could be favourable for neural networks.
In further research, we want to extend the
approach to multiple quality measures, which are
weighted in an objective function. In order to
investigate the scalability of the presented approach,
we plan to apply it in a long-term study on a larger
data set of the considered real-world use case. To
evaluate the generality of our approach we intend the
application in other manufacturing processes as well.
ACKNOWLEDGEMENTS
This paper was funded through the projects ADAPT
and BAPDEC by the Government of Upper Austria
in their programme “Innovative Upper Austria 2020”.
REFERENCES
Barz, Christiane, and Rainer Kolisch. 2014. “Hierarchical
Multi-skill Resource Assignment in the
Telecommunications Industry.” Production and
Operations Management 23 (3): 489–503.
doi:10.1111/poms.12053.
Choudhary, A. K., J. A. Harding, and M. K. Tiwari. 2009.
“Data mining in manufacturing: A review based on the
kind of knowledge.” Journal of Intelligent
Manufacturing 20 (5): 501–21. doi:10.1007/s10845-
008-0145-x.
Collins, P. C., C. V. Haden, I. Ghamarian, B. J. Hayes, T.
Ales, G. Penso, V. Dixit, and G. Harlow. 2014.
“Progress Toward an Integration of Process–Structure–
Property–Performance Models for “Three-Dimensional
An Approach for Adaptive Parameter Setting in Manufacturing Processes
31

(3-D) Printing” of Titanium Alloys.” JOM 66 (7):
1299–1309. doi:10.1007/s11837-014-1007-y.
Cook, D. F., C. T. Ragsdale, and R. L. Major. 2000.
“Combining a neural network with a genetic algorithm
for process parameter optimization.” Engineering
Applications of Artificial Intelligence 13 (4): 391–96.
doi:10.1016/S0952-1976(00)00021-X.
Quality management systems - Fundamentals and
vocabulary (ISO 9000:2015). DIN EN ISO 9001:2015.
2015.
Ding, Donghong, Chen Shen, Zengxi Pan, Dominic Cuiuri,
Huijun Li, Nathan Larkin, and Stephen van Duin. 2016.
“Towards an automated robotic arc-welding-based
additive manufacturing system from CAD to finished
part.” Computer-Aided Design 73: 66–75.
Geometrical product specifications (GPS) — ISO code
system for tolerances on linear sizes. ISO 286-1:2010.
2010.
James, Gareth, Daniela Witten, Trevor Hastie, and Robert
Tibshirani. 2013. An introduction to statistical
learning: With applications in R. Springer texts in
statistics 103. New York: Springer.
Kommenda, M., B. Burlacu, R. Holecek, A. Gebeshuber,
and M. Affenzeller. 2015. “Heat treatment process
parameter estimation using heuristic optimization
algorithms.” In Proceedings of the European Modeling
and Simulation Symposium, edited by M Affenzeller,
Bruzzone, Jimenez, Longo, Merkuryev, and Zhang,
222–27.
Miller, Alan J. 2002. Subset selection in regression. 2nd ed.
Monographs on statistics and applied probability 95.
Boca Raton: Chapman & Hall/CRC.
Mohamed, Omar A., Syed H. Masood, and Jahar L.
Bhowmik. 2016. “Investigation of dynamic elastic
deformation of parts processed by fused deposition
modeling additive manufacturing.” Advances in
Production Engineering & Management 11 (3): 227–
38. doi:10.14743/apem2016.3.223.
Murtaugh, Paul A. 2010. “Methods of variable selection in
regression modeling.” Communications in Statistics -
Simulation and Computation 27 (3): 711–34.
doi:10.1080/03610919808813505.
Oliaei, Erfan, Behzad S. Heidari, Seyed M. Davachi,
Mozhgan Bahrami, Saeed Davoodi, Iman Hejazi, and
Javad Seyfi. 2016. “Warpage and Shrinkage
Optimization of Injection-Molded Plastic Spoon Parts
for Biodegradable Polymers Using Taguchi, ANOVA
and Artificial Neural Network Methods.” Journal of
Materials Science & Technology 32 (8): 710–20.
doi:10.1016/j.jmst.2016.05.010.
Park, Hong S., and Trung T. Nguyen. 2014. “Optimization
of injection molding process for car fender in
consideration of energy efficiency and product quality.”
Journal of Computational Design and Engineering 1
(4): 256–65. doi:10.7315/JCDE.2014.025.
Park, Kyung S., and Soung H. Kim. 1998. “Artificial
intelligence approaches to determination of CNC
machining parameters in manufacturing: A review.”
Artificial Intelligence in Engineering 12 (1-2): 127–34.
doi:10.1016/S0954-1810(97)00011-3.
Pawar, P. J., and R. V. Rao. 2013. “Parameter optimization
of machining processes using teaching–learning-based
optimization algorithm.” The International Journal of
Advanced Manufacturing Technology 67 (5): 995–
1006. doi:10.1007/s00170-012-4524-2.
Robinson, Carol J., and Manoj K. Malhotra. 2005.
“Defining the concept of supply chain quality
management and its relevance to academic and
industrial practice.” International Journal of
Production Economics 96 (3): 315–37.
doi:10.1016/j.ijpe.2004.06.055.
Tian, Maosheng, Xiaoyun Gong, Ling Yin, Haizhou Li,
Wuyi Ming, Zhen Zhang, and Jihong Chen. 2017.
“Multi-objective optimization of injection molding
process parameters in two stages for multiple quality
characteristics and energy efficiency using Taguchi
method and NSGA-II.” The International Journal of
Advanced Manufacturing Technology 89 (1-4): 241–
54. doi:10.1007/s00170-016-9065-7.
Venkata Rao, R., and V. D. Kalyankar. 2013. “Multi-pass
turning process parameter optimization using teaching–
learning-based optimization algorithm.” Scientia
Iranica 20 (3): 967–74.
doi:10.1016/j.scient.2013.01.002.
Widrow, Bernard, David E. Rumelhart, and Michael A.
Lehr. 1994. “Neural networks: Applications in industry,
business and science.” Communications of the ACM 37
(3): 93–105. doi:10.1145/175247.175257.
Wuest, Thorsten, Christopher Irgens, and Klaus-Dieter
Thoben. 2014. “An approach to monitoring quality in
manufacturing using supervised machine learning on
product state data.” Journal of Intelligent
Manufacturing 25 (5): 1167–80. doi:10.1007/s10845-
013-0761-y.
Wuest, Thorsten, Dieter Klein, and Klaus-Dieter Thoben.
2011. “State of steel products in industrial production
processes.” Procedia Engineering 10: 2220–25.
Xiong, Jun, Guangjun Zhang, Jianwen Hu, and Lin Wu.
2014. “Bead geometry prediction for robotic GMAW-
based rapid manufacturing through a neural network
and a second-order regression analysis.” Journal of
Intelligent Manufacturing 25 (1): 157–63.
doi:10.1007/s10845-012-0682-1.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
32
