Simulation of Snowboarding

on Snow Surface Modelled with Particle Elements

Tatuya Yoshida

, Akihiro Hojo

and Humiyasu Kuratani

Faculty of Engineering, University of Fukui, 3-9-1 Bunkyo, Fukui-shi, Japan

Graduate school of Engineering, University of Fukui, 3-9-1 Bunkyo, Fukui-shi, Japan

Keywords: Sports Equipment, Snowboard Turn, Snow, Motion Analysis, Distinct Elemental Method.

Abstract: One approach for an efficient development of snowboards is quantification of prototype performance. A

simulation model which represents the discrete behaviour of snow with particle elements is developed to

evaluate snowboarding performance of prototypes. The particle behaviour is calculated using the discrete

element method (DEM). A snowboard is considered to be a rigid body in the simulation. Four snowboards

with different sidecuts are modelled to evaluate the influence on the turn. The simulation is able to confirm

the difference of trajectory due to the sidecut radius. The smaller sidecut radius increases the attack angle of

the board. As the result, lateral force acting on the board increases and the turn become sharply.

1 INTRODUCTION

Several analytical and experimental studies have

found that the mechanical properties of skis and

snowboards affect their performance (Brennan et al.,

2003; Buffinton et al., 2010). In the actual design

process for skis and snowboards, designers consider

the material used, the manner in which it is

laminated and the board thickness. Many prototype

models are evaluated for static and dynamic

properties, such as bending and torsional stiffness,

natural frequency and damping in the laboratory．

After the lab testing process, test riders evaluate the

prototype boards based on subjective opinions about

the performances under various conditions. This

process is time-intensive and costly because of the

necessity to make many iterations of prototypes.

Moreover, manufacturers generally rely on a trial-

and-error procedure. In field tests, it is difficult to

evaluate different prototypes under the same

conditions. This makes the performance results from

field tests difficult to evaluate quantitatively.

One approach to solve this technical problem is

the development of numerical simulations that

model key aspects of snowboarding performance. In

a simulation, the snow surface can be modelled with

identical conditions for quantitatively testing each

iteration of a design. Moreover, the simulation

makes it possible to quantitatively predict the

manner in which changes to the board design will

affect it’s performance. This allows us to easily

realise the desired characteristics of the snowboard

and can reduce the time and costs needed for

prototyping snowboard designs: a first prototype is

edsigned based on simulation results and the model

shows gideline of design modification after

evaluations of test riders.

Skis and snowboards push snow away from the

board surface as they slide down a slope. Some

snow is scattered while another type snow is

deformed and packed. Although one study (Federolf

et al., 2010) represented snow as a continuous body

using the finite element method, a simulation model

that considers both the discrete behaviour and large

deformation of snow may be necessary when the

deformation of the snow surface becomes large. The

finite element method is not suitable to reproduce

snow in some case because Skis and snowboards

turn carve snow and grooves with their edge.

In this study, we develop a simulation model to

reproduce the discrete behaviour of snow by

calculating interaction forces between a board and

snow particles. We evaluated the influence of the

sidecut radius on the turning behaviour using the

simulation. The reaction force from slope, rotation

angle and attitude of the board affect the

snowboarding turn and are evaluated by the

simulation.

Yoshida, T., Hojo, A. and Kuratani, H.

Simulation of Snowboarding on Snow Surface Modelled with Particle Elements.

DOI: 10.5220/0006896400230026

In Proceedings of the 6th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2018), pages 23-26

ISBN: 978-989-758-325-4

2 METHODS

2.1 Snow Model

In this simulation model, snow is modelled as

particle elements. The particle behaviour is

calculated using the discrete element method (DEM).

Based on the Voigt model shown in Figure 1, the

model calculates the contact forces between snow

particles. In Figure 1, k is the spring coefficient,

the damping coefficient and

is the friction

coefficient. The subscript n indicates the normal

direction, and the subscript t indicates the tangential

direction. By setting these parameters appropriately,

the DEM can reproduce the discrete behaviour of

snow. The motion equation that expresses the

behaviour of particle i is shown in the following

equation.



+ F

nj

+ F



(1)

is the mass of the particle i, x

is the position

vector for particle i and g is the gravitational

acceleration vector. F

and F

are the contact force

vectors applied by particle j in the normal and

tangential directions. In this equation, all contact

forces acting on particle i are calculated and

summed up.

The interaction forces between a snow particles

and the modelled snowboard are calculated with the

above method, and they are also calculated using the

Voigt model.

Figure 1: Snow modelling with particle element method.

2.2 Snowboard Model

A snowboard is considered to be a rigid body in the

simulation. The motion of the snowboard is

reproduced by numerically solving motion equations

with six degrees of freedom, including translational

and rotational motion. When the board contacts

snow particles, the interaction force is determined by

the method shown in the previous section and the

calculated force is considered to be an external force

acting the board.

3 SIMULATION CONDITIONS

3.1 Shape of Snowboard

Four snowboards were modelled to evaluate the

influence of sidecut radius. The sidecut radii of the

models are 15 m (R15), 10 m (R10) and 5 m (R5). A

board without a sidecut was also modelled. The

modelled boards are illustrated in Figure 2. A

coordinate system local to the board is located at the

centre of each board. The x axis is set along the

longitudinal direction of the board. The y axis points

along the width of the board, and the z axis points in

the vertical direction to the board. The board

dimensions, mass and moment of inertia are shown

in Table 1. To verify the effect of the sidecut

geometry, the mass and moment of inertia the board

are kept constant for all the modelled boards.

Furthermore, to represent a rider simply and

consistently, a concentrated mass of 60 kg is located

at the centre of the board coordinate system.

Figure 2: Geometry of the modelled snowboard.

Table 1: Board properties.

Length Width Mass

Inertia moment

1.5 m 0.3 m 3.3 kg 0.02 kgm

0.62 kgm

0.65 kgm

3.2 Slope Condition

We set up a slope tilted at an angle of 10° in the

simulated environment. Many particle elements

cover the slope and reproduce granular snow with

parameters modified from those used by Abe et al.

(2011).

3.3 Initial Attitude and Load Torque

The initial Attitude of the board is rotated 10° about

the y axis to be parallel to the slope and the x axis of

the board coordinate system is parallel with the fall

line of the slope. Then, the boards are given an

Normal direction Tangential direction

Voigt model

R15 R10 R5Straight

R=5 m

Traveling direction

icSPORTS 2018 - 6th International Congress on Sport Sciences Research and Technology Support

initial velocity of 1 m/s in the x axis direction and

slide down the slope.

During the whole simulation, a torque of −30

Nm is applied about the x axis to a board.

Simultaneously, a 5 Nm torque is applied about the z

axis for 0.4 s following the start of the run. In order

to evaluate influence of the sidecut radius on turn

behaviour, loading conditions to each board are

matched.

4 RESULT AND DISCUSSION

Figure 3 shows the trajectories of each board’s

centre during the simulated run. In the global

coordinate system, the X and Y axes are located on

the horizontal plane, and the Z axis points in the

vertical direction. The amount of movement in the Y

direction is increased as the sidecut radius decreases.

This is consistent with general theory about the

manner in which snowboards behave. Although the

trajectories of the straight board and the R15 board

are similar, the R5 board turns considerably after

torque is applied, consequently running off the side

of the slope.

Figure 4 shows the forces acting on the board in

the Y direction from the slope. These forces are

averaged over 0.1 s. The force in the Y direction

increases as the sidecut radius decreases. Thus, the

influence of sidecut radius appears in the reaction

force supplied by the snow surface.

In addition, the attack angle, which is the angle

formed by the travelling direction of the board and

the x axis of the board coordinate system, is shown

in Figure 5. These angles are averaged over 0.1 s.

The reaction force from the slope acting in the

direction opposite to the travelling direction

increases the y axis force component because the

attack angle increases (Figure 6). The y axis force

component corresponds to the centripetal force on

the board as it turns. However, as the attack angle

increases further, the y axis force component (board

coordinates system) increases, but the force in the

global Y direction may decrease. In these conditions,

the turn becomes a skid turn.

Comparing the attack angle between the different

sidecut radii, the small sidecut radius increases the

angle. Because this increases the reaction force in

the y direction of the board coordinate system, the

movement of the turn also increases as the result.

However, by focusing on the variation of the force

in time, it is observed that the attack angle decreases

when the sidecut radius is R15 or more, and

decreases when the sidecut radius is R10 or less. In

the case of R10 or less, the attack angle tends to be

large. However, the force in the y direction of the

board R5 decreases because of the large attack angle

when the attack angle is at the maximum (from 0.7s

to 0.8s).

Figure 3: Board trajectories.

Figure 4: Reaction force acting on the board.

Figure 5: Influence of sidecut radius on attack angle.

100

120

140

Force along Y direction [N]

Time [s]

Straight R15 R10 R5

Attack angle [°]

Time [s]

Straight R15 R10 R5

Simulation of Snowboarding on Snow Surface Modelled with Particle Elements

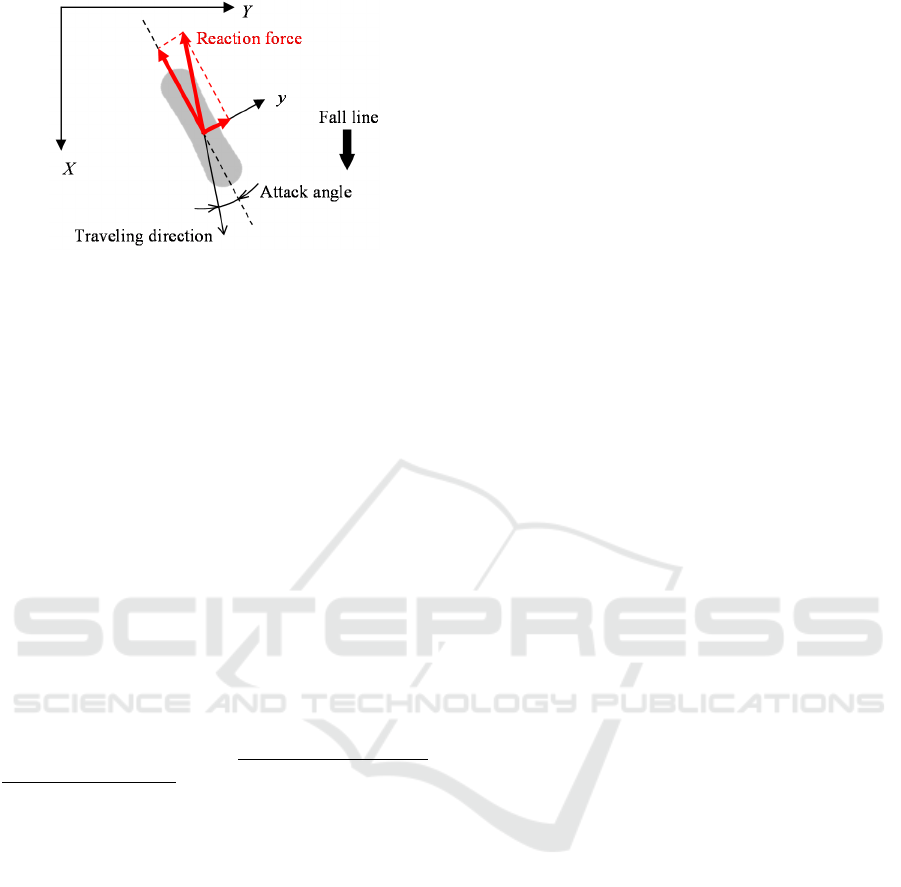
Figure 6: Attack angle.

5 CONCLUSIONS

A simulation model which represents snow surface

with particle elements was developed to quantify

snowboarding performance of prototypes. The

model evaluated the turn characteristics of the

modelled snowboards with different sidecuts and

helps to understand their tendency. The particle

element allows to evaluate the reaction force from

the snow surface in detail. Moreover it was possible

to understand the influence of the characteristics on

the reaction force due to the shape and attitude of the

board.

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI Grant

Number JP17K14614.

REFERENCES

Brennan, S. M., Kollár, L. P., Springer, G. S., 2003,

Modelling the mechanical characteristics and on-snow

performance of snowboards. Sports Engineering, 6(4),

193–206.

Buffinton, K. W., Shooter, S. B., Thorpe, I. J., Krywicki, J.

J., 2003, Laboratory, computational and field studies

of snowboard dynamics. Sports Engineering, 6(3),

129–137.

Federolf, P., Lüthi, A., Roos, M., Dual, J., 2010,

Parameter study using a finite element simulation of a

carving Alpine ski to investigate the turn radius and its

dependence on edging angle, load, and snow

properties. Sports Engineering, 12(3), 135–141.

Abe, M., Fujino, T., Saito, F., Takahata, K., Iwamoto, K.,

2011, Three-dimensional dynamic simulation analysis

of snow removal characteristics of rotary equipment,

Journal of System Design and Dynamics, 5(5), 982–

993.

icSPORTS 2018 - 6th International Congress on Sport Sciences Research and Technology Support