
Blind PDF Document Watermarking Robust Against PCA and ICA
Attacks
Makram W. Hatoum
1
, Rony Darazi
2
and Jean-Franc¸ois Couchot
1
1
FEMTO-ST Institute, University of Bourgogne Franche-Comt
´
e, UMR 6174 CNRS, France
2
TICKET Lab, Antonine University, Hadat-Baabda, Lebanon
Keywords:
Digital Watermarking, Portable Document Format, QIM Watermarking, BSS, Security, Transparency,
Robustness.
Abstract:
Spread Transform Dither Modulation (STDM) is a blind watermarking scheme used for its high robustness
against re-quantization and random noise attacks. It has been applied mainly on images, speech, and PDF
documents. The key of this scheme is the projection vector aiming at spreading the embedded message over
a set of cover elements. However, it has been recently shown that such a key vector can be estimated thanks
to Blind Source Separation (BSS) techniques, e.g. Principal Component Analysis (PCA) and Independent
Component Analysis (ICA). This security breach can be harnessed by an opponent to copy, remove, or modify
the embedded watermark. In this position paper, a CAR-STDM (Component Analysis Resistant-STDM) is
designed and its application on PDF documents is presented. The security is guaranteed by the use of a
cryptographically secure number generator, preventing algebraic approaches (as BSS ones) from finding the
key. First experimental results show that the Secure-STDM achieves the security against the aforementioned
BSS techniques. It is further shown that CAR-STDM preserves its robustness against AWGN and Salt&Peper
attacks, and keeps furthermore its transparency.
1 INTRODUCTION
Digital networks are essential communication mecha-
nisms that are used to transmit any sort of information
such as text, audio, and image. The rapid growth of
the volume of exchanged data over the internet provi-
des a significant number of problems such as illegal
distribution, authentication, duplication and malici-
ous tampering of the digital data. Authors and data
providers are concerned about protecting their data
or work, to be distributed in a network environment.
Among many approaches of protection, digital wa-
termarking is undoubtedly the one that has received
the most attention and interest. Watermarking is the
practice of transparently, which alter a digital content
like image, video, audio, and text, for various pur-
poses, such as copyright protection, authentication,
access control, and broadcast monitoring (Cox et al.,
2007).
The watermarking approaches are classically applied
into the spatial domain and frequency domain. In
the first one, the watermark is embedded directly into
the cover work by changing the intensity values of
the signal. In the second one, the watermark is em-
bedded into the frequency domain transform, such
as the DCT, DFT, and DWT. Over the last decade,
several watermarking schemes have been proposed,
which can be classified into the additive class know
by Spread Spectrum (SS) schemes (Cox et al., 1996),
and the substitutive class known by Quantization In-
dex Modulation (QIM) (Chen and Wornell, 2001a).
Spread Transform Dither Modulation (STDM) is an
extension of QIM that is more robust against re-
quantization and random noise attacks. With the
STDM method, each bit of the watermark is inserted
into a sample vector x after quantizing the projection
of x onto a projection vector p.
The watermarking schemes are characterized by a
number of properties such as payload, impercepti-
bility, robustness, and security. Payload defines the
amount of data that can be embedded in the original
signal. Imperceptibility refers to the perceptual simi-
larity between the original signal and the watermar-
ked one. Robustness refers to the ability to uncover
the watermark after several types of attacks such as
additive noise, compression, and filtering. The secu-
rity constraint has received little attention, while the
most of the watermarking schemes have been driven
by the improvement of the above requirements. The
security relies on the goals and the power of an adver-
420
Hatoum, M., Darazi, R. and Couchot, J-F.
Blind PDF Document Watermarking Robust Against PCA and ICA Attacks.
DOI: 10.5220/0006899604200427
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 420-427
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sary to copy, modify or remove the watermark. (Bas
and Hurri, 2006) show that STDM can be attacked
successfully using a Blind Source Separation (BSS)
technique called Independent Component Analysis
(ICA), by estimating the projection vector p of STDM
used during the embedding process. (Cao, 2014) pro-
ved that an attacker can estimate the projection vector
p using another BSS technique called Principal Com-
ponent Analysis (PCA). Therefore, they proposed an
improved method for STDM called ISTDM in order
to resist such kind of BSS attack.
Portable Document Format, a digital form for repre-
senting documents, was developed and specified by
Adobe Systems Society (Iso, 2008). Several methods
have been proposed in PDF and Text documents. (Por
and Delina, 2008) presented an approach in informa-
tion hiding, using inter-paragraph and inter-word spa-
cing, characterized by a large capacity for embedding
the hidden bits. This method misses the main con-
straint of robustness. When deleting the space bet-
ween words and paragraphs, the hidden data is de-
stroyed. (Wang and Tsai, 2008) proposed an imper-
ceivable modification of PDF object parameters. The
main drawback of this method is the low embedding
capacity. (Lee and Tsai, 2010) presented two methods
to embed the secret messages in a PDF file using the
alternative space coding method and the null space
coding method. In those methods, The ASCII code 20
(original white space) and the ASCII code A0 (non-
breaking space) are used as the watermarking space.
An opponent could simply modify or remove the em-
bedded message by replacing the ASCII code A0 by
20. (Alizadeh-Fahimeh et al., 2012) composed two
different algorithms using the TJ method. The first
one has a lower capacity level, and the second one
has a higher embedding capacity with a lower secu-
rity level. (Lin et al., 2013) presented a study ba-
sed on PDF files of iso-8859 encoding. It consists
of hiding information without detecting any irregula-
rity while reading the PDF file. The main drawback
is that the hiding information is removed when the
PDF file is opened directly without using PDF reader.
A blind digital watermarking scheme for PDF docu-
ments is proposed by (Bitar et al., 2017). This method
consists of embedding the secret message in the x-
coordinates of a group of characters, taking into con-
sideration the transparency-robustness trade-off. (Ku-
ribayashi et al., 2017) used the space lengths between
characters as a watermarking space, and the water-
mark is embedded using the DCT transform, based on
the DM-QIM, but this method still missing the expe-
rimental tests concerning the robustness constraints.
This position paper introduces the CAR-STDM
(Component Analysis Resistant-STDM) for blind
PDF watermarking robust against PCA and ICA at-
tacks. This paper recalls some backgrounds on
STDM and BSS attacks in Section 2. The proposed
method is presented in Section 3. The evaluation of
the proposed approach is presented in section 4. Fi-
nally, in Section 5 conclusion and future work are gi-
ven.
2 BACKGROUND
2.1 Spread Transform Dither
Modulation
QIM methods proposed by (Chen and Wornell,
2001a) use knowledge of the host signal at the enco-
der, and show an achievable trade-off among the ro-
bustness, degradation of the host signal, and the em-
bedding rate. QIM watermarking algorithm quantizes
each signal sample x, using a quantizer Q
m
, based on
the message bit m ∈ {0, 1}. We are going to take Q
0
for m = 0, and Q
1
for m=1.
Q
0
(x,∆) = round
x − d
0
∆
∆ + d
0
(1)
Q
1
(x,∆) = round
x − d
1
∆
∆ + d
1
(2)
where ∆: represents the Quantization Factor,
round(.): rounding value to the nearest integer,
d
0
and d
1
: real values represent the dither level
d
0
= −
∆
4
and d
1
=
∆
4
. (3)
STDM is a special case of QIM, it is called Spread
Transform Dither Modulation due to the spreading of
the embedding-induced distortion into all groups of
samples instead of one. Each bit of the secret mes-
sage is inserted into a sample vector x of length N
producing a vector y. Instead of quantizing the host
signal itself, the quantization occurs entirely in the
projection of x onto a projection vector p. The quan-
tized signal is given by:
y = x +
round
x
T
p − d
m
∆
∆ + d
m
− x
T
p
p (4)
where x
T
is the transpose of x, and d
m
is defined as in
equation (3).
Equation (4) can be seen as the host signal x augmen-
ted with the quantization error q
0
:
q
0
=
round
x
T
p − d
m
∆
∆ + d
m
− x
T
p
p (5)
Blind PDF Document Watermarking Robust Against PCA and ICA Attacks
421

To extract the embedded message, the detection can
be performed with a minimum distance decoder as the
form:
ˆm = argmin
m∈{0,1}
| y
T
p − Q
m
(y
T
p,∆) | (6)
2.2 BSS Techniques
Beside imperceptibility and robustness, the security
constraint is an important requirement for the wa-
termarking schemes. While increasing the security,
we guarantee that the embedded watermark is safe
against the opponent, whose aim is to estimate the
private key. Among Blind Source Separation (BSS)
techniques, we focus here on Principal Component
Analysis (PCA) and Independent Component Analy-
sis (ICA) recalled hereafter.
2.2.1 ICA Attack
An attacker may estimate the projection vector p of
STDM using a blind source separation technique cal-
led Independent Component Analysis (ICA), which
is a computational and statistical technique for re-
covering a set of independent signals from sets of
random variables or signals by some simple assump-
tions of their statistical properties (Hyvarinen, 1999;
Hyv
¨
arinen et al., 2004).
In ICA, the measure is based on non-gaussianity, and
this is according to the central limit theorem; the
average of independent variables will have a distri-
bution that is closer to Gaussian, and the mixture of
components will be more Gaussian. Reciprocally, the
individual signals will be independent if we break
the Gaussian observation down into a set of non-
Gaussian mixtures, each with distributions that are
non-Gaussian as possible.
ICA technique could be used to estimate a mixing ma-
trix A and the independent sources X from a set of wa-
termarked contents Y using the matrix formulation:
Y = AX (7)
While using FastICA, which is a popular ICA algo-
rithm that achieves a fast operation and reliability of
the extracted basis vector (Bas and Hurri, 2006), we
are able to compute the matrices A and X and extract
the estimated projection vector ˆp located in one of the
columns of the matrix A.
A limitation of ICA technique is the fact that the se-
cret carrier could be estimated up to sign, but this will
be solved by multiplying the independent components
by -1 without affecting the model. Another ambiguity
of ICA is that the estimated independent components
may appear in an arbitrary (column) order, but one of
them would be the proper estimated secret carrier.
2.2.2 PCA Attack
Another technique called Principal Component Ana-
lysis (PCA) could be used by an attacker to estimate
the projection vector p as done in (Cao, 2014). PCA
identify a smaller number of uncorrelated variables
known as principal components from a complex data
set. It is a variable reduction procedure, which is use-
ful to be applied on a number of redundant variables.
Reducing the observed variables into a smaller num-
ber of principal components will account for most of
the variance in the observed variables. Therefore, we
could extract the relevant information from the com-
plex data, and this is achieved by computing the ei-
genvector with the highest eigenvalue. A helpful stra-
tegy for an opponent is the Known Original Attack
(KOA). In such a case, the original signal is known,
and the opponent goal is to gain information about the
structure of the secret key, in order to hack later on
several watermarked signal. By this way, the attacker
will get the quantization error q
0
presented in equa-
tion (5) and will try to estimate the projection vector
ˆp using PCA.
STDM spreads the distortion into a sample vector x,
based on the projection vector p as shown in equation
(4). By this way, the watermark energy is focused in
the projection vector after the STDM embedding. The
quantization error q
0
as shown in equation (5), makes
the variables correlated because the same projection
vector p is used during the embedding process. Using
PCA, we are able to estimate the principal compo-
nent, which is the eigenvector of the highest eigenva-
lue, and in our case, this principal component would
be the estimated projection vector ˆp. By this way, the
attacker will be able to estimate the projection vector
and will get the possibility to copy, modify or remove
the watermark.
As we will see in Section 4, the opponent can estimate
the projection vector using PCA or ICA, therefore we
applied a simple modification to the STDM watermar-
king scheme to overcome such kind of attacks.
3 PROPOSED CAR-STDM
METHOD
The projection vector p is an essential part of the
STDM watermarking method, that is used as a se-
cret key to embed and extract the watermark. The
observation of several watermarked signals can pro-
vide sufficient information for an attacker to estimate
the projection vector, by using the PCA or ICA at-
tacks. The proposed scheme takes into account the
security constraint and tries to overcome such kind of
SECRYPT 2018 - International Conference on Security and Cryptography
422
BSS attacks.
3.1 Embedding Process
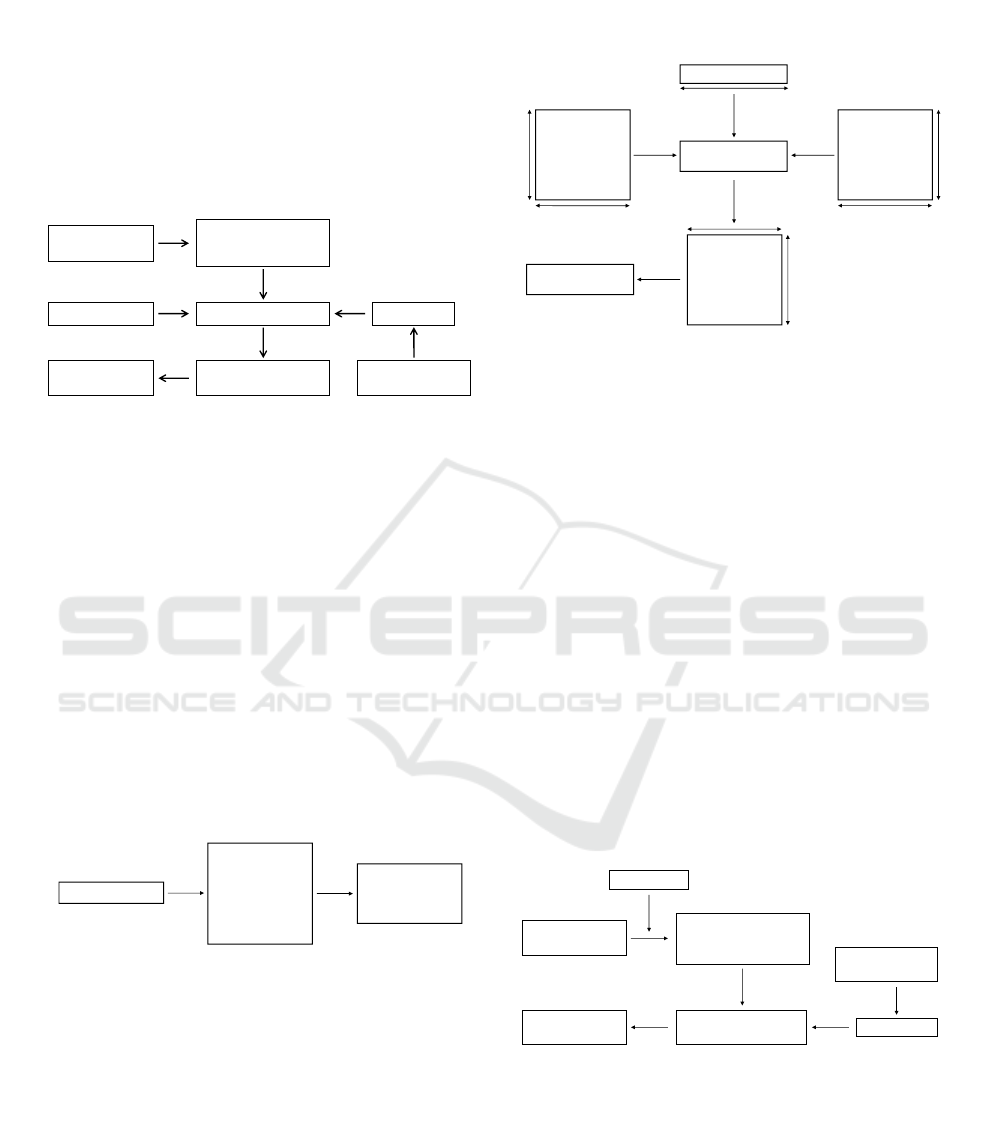
The embedding process is divided into 4 main steps as
shown in Figure 1. The main idea is to have a number
of projection vectors equal to the number of the bits
to be embedded.
Original
document
Watermark
2- Projection vector
generator
Secret key k
1- Extract and re-
arrange the x-
coordinates
3- STDM
4- Re-write the modified
x-coordinates
Watermarked
document
Figure 1: Embedding Block diagram.
The first step consists of reading the original docu-
ment, extracting the x-coordinates c
i
of the existing
characters and rearranging them into a matrix X of
size L × N. Each character in the PDF document is
located horizontally and vertically based on the coor-
dinate pair (x,y). The x-coordinates values are non-
constant, therefore they are exploited as the watermar-
king space in order to embed the watermark.
For the second step, we use one secret key k shared
between the embedder and decoder as a seed of a
cryptographically secure pseudorandom number ge-
nerator (PRNG) to produce L projection vectors. This
step is further denoted as ”Projection vector genera-
tor” and is illustrated in Figure 2.
Projection Vector Generator
Secret key k
Main Projection Vector
p
= [
v
1
v
2
v
3
………..
v
N
]
p
1
= [
v
1
v
2
v
3
..….v
N
]
p
2
= [
……..…………
]
.
.
.
.
p
j
= [
……..…………
]
p
1
= [
v
1
……….……
v
N
]
.
.
p
L
= [
……………………
]
Figure 2: Projection Vector Generator.
The third step consists of embedding each bit of the
watermark into the x-coordinates values using equa-
tion (4). We will use one projection vector per em-
bedded bit, for that we only have to replace p with p
i
in equation (4).
The last step consists of rearranging and re-writing
the modified x-coordinate of each character into the
watermarked document.
e.g. Assume that b of length L is the binary represen-
tation of the secret message. Each bit of b will be em-
bedded into the host signal X using a projection vector
p
i
of length N. For instance, suppose that we have a
p
1
= [
v
1
v
2
….……
v
N
]
p
2
= [………………...]
.
.
.
p
L
= [………………...]
b =
[
bit
1
…………
bit
L
]
x
1
= [
c
1
c
2
...….…
c
N
]
x
2
= […………….…..]
.
.
.
x
L
= [………………...]
y
1
= [
c’
1
c’
2
…….
c’
N
]
y
2
= [………………...]
.
.
.
y
L
= [……………...….]
STDM
bit
i
p
i
x
i
y
i
L
L
N
L
N
L
N
Matrix X
Watermark
Secret key k
Matrix Y
Watermarked
document
Figure 3: Embedding the i
th
bit of the secret message into a
set of x-coordinates x
i
using a projection vector p
i
.
PDF file containing 800 characters through which we
will embed a watermark of length L=24 bits. If we
consider that the length of projection vector N=8; in
this case, we need 192 characters (24×8) to embed
the watermark. Hence 192 characters will be selected
from the original document and the x-coordinates will
be rearranged into a matrix X. Using the secret key k,
24 projection vectors will be extracted from the pro-
jection vector generator and each bit will be projected
into 8 x-coordinates using different projection vector.
This technique is supposed to enhance the security of
the traditional STDM, and hence nullify the effect of
the PCA and ICA attacks.
3.2 Extraction Process
The extraction process is divided into 2 main steps as
shown in Figure 4.
Extracted
watermark
Watermarked
document
1- Extract and rearrange
the x-coordinates into a
matrix S
2- Minimum distance
decoder
Secret key k
Attacks
Projection vector
generator
Figure 4: Extraction Block diagram.
The first step consists of reading the watermarked do-
cument and extracting the x-coordinates of the exis-
ting characters and rearranging them into a matrix S
of size L × N. Matrix S is the watermarked matrix Y
subject to various attacks.
The second step consists of extracting the embedded
message by using the minimum distance decoder, ba-
Blind PDF Document Watermarking Robust Against PCA and ICA Attacks
423

sed on the secret key k as of the form:
ˆm
i
= argmin
m∈{0,1}
| s
T
p
i
− Q
m
(s
T
p
i
,∆) | (8)
where s corresponds to a vector of x-coordinates of
length N, and p
i
represents the projection vector, used
to extract the i
th
bit of the secret message.
4 EVALUATION OF THE
PROPOSED APPROACH
In this section, we compare the performance of the
traditional STDM watermarking scheme and the pro-
posed CAR-STDM watermarking scheme in terms of
security (Section 4.1), transparency (Section 4.2), and
robustness (Section 4.3). In a practical point of view,
same embedding parameters have been used such as
the length of the host signal and the secret message,
dither level, and quantization step. All the experi-
ments were conducted while varying the quantization
step ∆, and the simulations were repeated 500 times.
The embedded PRNG is BSS (Blum et al., 1986),
Blum Blum Shub as an instance of cryptographically
secure PRNG.
4.1 Security
PCA and ICA have been used to compare the security
level of the traditional STDM watermarking scheme
and the proposed CAR-STDM watermarking scheme.
The security level is measured by comparing the Bit
Error Rate (BER) of the extracted message to the ori-
ginal one after the estimation of the projection vector
used at the encoder using the PCA and ICA attacks.
Experiments are done while modifying the length of
the embedded message from 200 to 2000 bits, and the
length of the projection vector from 8 to 32. The ori-
ginal document chosen during the experimental tests
contains 64000 characters. BER has been used as the
error measurement between the original watermark m
and the extracted watermark ˆm. If the BER tends to
0, means that the extracted watermark is similar to the
original one, which means that the opponent gets an
accurate estimation of the projection vector.
Figure 5 and Figure 6 show that the CAR-STDM
achieves a high level of security, where the BER of the
extracted watermark is close to a random guess of 0.5.
This high security level is due to the fact that multi-
ple projection vectors are used during the embedding
process instead of one, which nullifies the effect of
PCA and ICA attacks to estimate the projection vec-
tors, and prevents the opponent to copy, modify or
remove the watermark.
Figure 5: The comparison between the proposed CAR-
STDM and the traditional STDM while modifying the
length of the projection vector from 8 to 32 and the num-
ber of observations from 200 to 2000, while applying the
ICA attack.
Figure 6: The comparison between the proposed CAR-
STDM and the traditional STDM while modifying the
length of the projection vector from 8 to 32 and the num-
ber of observations from 200 to 2000, while applying the
PCA attack.
In the traditional STDM method, a single projection
vector is used during the embedding process, which
decreases the security level. PCA and ICA can ex-
actly estimate the projection vector due to the fact
that the watermark energy is focused in the projection
vector after the STDM embedding. Even if we vary
the length of projection vector, the BER of the extrac-
ted watermark always tends to 0, which means that
the opponent will get an accurate estimation of the
projection vector through the PCA and ICA attacks.
With the CAR-STDM, a unique projection vector p
i
is generated to embed each i
th
bit of the watermark,
which will makes the watermarked vectors uncorrela-
SECRYPT 2018 - International Conference on Security and Cryptography
424

Table 1: Distortin values when applying STDM and CAR-
STDM.
∆ D
s
STDM (MSE) CAR-STDM (MSE)
0.1 0.00002 2.2444×10
−5
2.3127×10
−5
0.5 0.00053 6.3574×10
−4
5.9178×10
−4
1 0.00214 0.0023 0.0020
1.5 0.00481 0.0058 0.0067
2 0.08550 0.0090 0.0087
2.5 0.01335 0.0144 0.0150
3 0.01923 0.0198 0.0199
5 0.05342 0.0687 0.0665
8 0.13675 0.1612 0.1618
10 0.21367 0.1886 0.1739
ted from each other, and void the effect of PCA. At
the same time, we will not get any relevant informa-
tion from the watermarked vectors, which will block
the effect of ICA to estimate the projection vectors.
Since we use a cryptographically secure PRNG for
building each projection vector, any algebraic method
will fail to estimate the projection vectors. The obtai-
ned practical results are coherent with this theoretical
analysis.
While increasing the security of the watermarking
scheme, we should preserve the efficiency in term of
transparency and robustness. Therefore, we compa-
red the CAR-STDM to the traditional STDM to make
sure that the modification did not affect the efficiency
of the main watermarking scheme.
4.2 Transparency
The transparency of the proposed CAR-STDM and
the traditional STDM has been tested using several
values of quantization step ∆. We consider a part of
the original document containing 952 characters, and
a watermark message ”LAW” is encoded using 8 bits
per character in order to form a total of 24 bits. For
that, the length of the projection vector used during
the embedding and decoding concept is N=952/24 ≈
39.
Table 1 presents the distortion plots of each value of
∆, and the error measurements between the watermar-
ked document and the original one, using the Mean
Square Error (MSE) and the average expected distor-
tion D
s
(Chen and Wornell, 2001b) presented as:
D
s
= ∆
2
/12N (9)
When ∆ increases, the error values increase as well.
As expected, the error values of the CAR-STDM
and the Traditional STDM watermarking methods are
very close to each other. As shown in Figure 7, we get
a slight modification in the characters position when
(a) ∆=3
(b) ∆=5
(c) ∆=10
Figure 7: Perceptual visualization of the watermarked do-
cument using the proposed CAR-STDM for ∆=3, ∆=5 and
∆=10 gradually from top to bottom.
∆ is smaller or equal to 3 and a notable modification
when ∆ is greatest than 3.
4.3 Robustness
The robustness experiments were conducted by ap-
plying the Gaussian and Salt&Pepper watermarking
attacks to the x-coordinates of the characters in the
watermarked document with two density values (d =
0.1 and d = 0.25). Therefore, different robustness
threshold levels are computed respectively from the
experiments of each type of attacks. Only the digits
after the decimal point are modified. The Bit Error
Rate (BER) was computed, by comparing the original
watermark to the extracted one, to make the objective
performance comparison. As shown in Figure 8
and Figure 9 the values of the proposed CAR-STDM
and the traditional STDM are very close to each other
and achieve a higher level of robustness. The robus-
tness increases with a higher value of ∆. Figure 10
shows the robustness of the CAR-STDM versus the
traditional STDM under the AWGN attack, where the
strength of the AWGN attack is evaluated by mean of
the Watermark to Noise ratio (WNR):
W NR = 10 log
10
(
σ
2
w
σ
2
n
) (10)
The BER assesses the robustness level of the water-
marking technique. As shown in Figure 10, for ∆
Blind PDF Document Watermarking Robust Against PCA and ICA Attacks
425

Figure 8: Comparison between the proposed CAR-STDM
and the traditional STDM in terms of BER under Gaussian
attack.
Figure 9: Comparison between the proposed CAR-
STDM and the traditional STDM in terms of BER under
Salt&Pepper attack.
Figure 10: The robustness of the proposed CAR-STDM to
that of STDM against the AWGN while varying the WNR.
equal to 2.5, the BER is equal to 0 when the WNR
is greater or equal to 10, and the BER is greater than
0.12 when the WNR is smaller than 4. Consequently,
the robustness of the CAR-STDM and the traditional
STDM increases while ∆ increases.
4.4 Our Method VS Related Work
(Cao, 2014) proved that an attacker could estimate the
projection vector of STDM, for that they proposed an
improved method called ISTDM. In this method, the
host signal is divided into two mutually orthogonal
subspaces with the same dimension. The first one
is called a reference subspace, and the other one is
called an embedding subspace. ISTDM embed the
watermark only in the embedding subspace using the
STDM algorithm, in which the projection vector p
is the projection of the normalized host signal onto
the reference subspace. This method has been tested
using a Gaussian-distributed with mean vector 0 as a
host signal. In addition to that, the capacity has de-
creased, and only the half size of the host signal could
be used to embed the watermark.
In contrast, our proposed watermarking scheme em-
beds the watermark in a PDF document for copyright
protection under a sufficient transparency-robustness
tradeoff while taking into account the security con-
straint. We exploited the x-coordinates values of cha-
racters as real cover elements to embed the water-
mark. Furthermore, CAR-STDM could not be attac-
ked by any algebraic methods such as PCA and ICA
and preserved the capacity of STDM, therefore the
watermark could be embedded in all the cover ele-
ments.
5 CONCLUSION AND FUTURE
WORK
In this position paper, we have presented the
Component Analysis Resistant-STDM watermarking
scheme. Unlike the traditional STDM watermarking,
the CAR-STDM uses multiple projection vectors at
the encoder and the decoder. The simple but effective
idea is to produce one projection vector per an embed-
ded bit thanks to a cryptographically secure PRNG,
whose seed is a key shared between the encoder and
the decoder.
The x-coordinates values of character PDF elements
have been used as cover elements to embed the wa-
termark in this article, but any element can be used
as support to contain the mark. Theoretically spea-
king, any algebraic attack such as PCA and ICA fails
with this proposal. The experimental results confirm
SECRYPT 2018 - International Conference on Security and Cryptography
426

that the CAR-STDM approach achieves the security
against such kind of BSS attacks, with higher level
of transparency and robustness against AWGN and
Salt&Peper attacks.
As for future enhancements, we plan to execute the
theoretical proof of the security analysis and to in-
clude further improvements by exploring new secure
subspaces to embed the watermark.
ACKNOWLEDGEMENTS
This work is partially funded with support from the
National Council for Scientific Research in Lebanon
CNRS-L, the Hubert Curien CEDRE programme, the
Agence Universitaire de la Francophonie AUF-PCSI
programme, and the Labex ACTION program (con-
tract ANR-11-LABX-01-01).
REFERENCES
Alizadeh-Fahimeh, F., Canceill-Nicolas, N., Dabkiewicz-
Sebastian, S., and Vandevenne-Diederik, D. (2012).
Using steganography to hide messages inside pdf fi-
les. SSN Project Report.
Bas, P. and Hurri, J. (2006). Vulnerability of dm watermar-
king of non-iid host signals to attacks utilising the sta-
tistics of independent components. IEE Proceedings-
Information Security, 153(3):127–139.
Bitar, A. W., Darazi, R., Couchot, J.-F., and Couturier, R.
(2017). Blind digital watermarking in pdf documents
using spread transform dither modulation. Multimedia
Tools and Applications, 76(1):143–161.
Blum, L., Blum, M., and Shub, M. (1986). A simple un-
predictable pseudo-random number generator. SIAM
Journal on computing, 15(2):364–383.
Cao, J. (2014). Improved spread transform dither modu-
lation: a new modulation technique for secure water-
marking. In International Workshop on Digital Water-
marking, pages 399–409. Springer.
Chen, B. and Wornell, G. W. (2001a). Quantization in-
dex modulation: A class of provably good met-
hods for digital watermarking and information em-
bedding. IEEE Transactions on Information Theory,
47(4):1423–1443.
Chen, B. and Wornell, G. W. (2001b). Quantization index
modulation methods for digital watermarking and in-
formation embedding of multimedia. Journal of VLSI
signal processing systems for signal, image and video
technology, 27(1-2):7–33.
Cox, I., Miller, M., Bloom, J., Fridrich, J., and Kalker,
T. (2007). Digital watermarking and steganography.
Morgan Kaufmann.
Cox, I. J., Kilian, J., Leighton, T., and Shamoon, T. (1996).
Secure spread spectrum watermarking for images, au-
dio and video. In Image Processing, 1996. Procee-
dings., International Conference on, volume 3, pages
243–246. IEEE.
Hyvarinen, A. (1999). Fast and robust fixed-point algo-
rithms for independent component analysis. IEEE
transactions on Neural Networks, 10(3):626–634.
Hyv
¨
arinen, A., Karhunen, J., and Oja, E. (2004). Indepen-
dent component analysis, volume 46. John Wiley &
Sons.
Iso, T. (2008). 171/sc 2: Iso 32000–1: 2008 document
management-portable document format-part 1: Pdf
1.7.
Kuribayashi, M., Fukushima, T., and Funabiki, N. (2017).
Data hiding for text document in pdf file. In Interna-
tional Conference on Intelligent Information Hiding
and Multimedia Signal Processing, pages 390–398.
Springer.
Lee, I.-S. and Tsai, W.-H. (2010). A new approach to co-
vert communication via pdf files. Signal processing,
90(2):557–565.
Lin, H.-F., Lu, L.-W., Gun, C.-Y., and Chen, C.-Y. (2013).
A copyright protection scheme based on pdf. Int J
Innov Comput Inf Control, 9(1):1–6.
Por, L. Y. and Delina, B. (2008). Information hiding: A new
approach in text steganography. In WSEAS Internatio-
nal Conference. Proceedings. Mathematics and Com-
puters in Science and Engineering, number 7. World
Scientific and Engineering Academy and Society.
Wang, C. and Tsai, W. (2008). Data hiding in pdf fi-
les and applications by imperceivable modifications of
pdf object parameters. In Proceedings of 2008 Confe-
rence on Computer Vision, Graphics and Image Pro-
cessing, Ilan, Taiwan, Republic of China. Asia Uni-
versity.
Blind PDF Document Watermarking Robust Against PCA and ICA Attacks
427
