A Comparative Study on the Performance of MOPSO and MOCS as

Auto-tuning Methods of PID Controllers for Robot Manipulators

Ahmed Zidan, Svenja Tappe and Tobias Ortmaier

Institute of Mechatronic Systems, Leibniz Universit

at Hannover, 30167 Hanover, Germany

Keywords:

Robot Manipulators, Particle Swarm Optimization, Cuckoo Search, Multi-Objective Optimization, PID

Control, Automatic Tuning.

Abstract:

An auto-tuning method of PID controllers for robot manipulators using multi-objective optimization techni-

que is proposed. Two approaches are introduced based on the multi-objective particle swarm optimization

(MOPSO) and multi-objective cuckoo search (MOCS), respectively. The main goal of this work is to intro-

duce a comparative study on the performance of both algorithms with respects to their applicability to the

auto-tuning process. For this sake, necessary metrics are considered such as the hyperarea difference and the

overall Pareto spread, among others. In order to generate a sufﬁcient amount of statistical data, a simula-

tion of the robot Puma 560 is implemented. Using a relatively accurate model of the robot dynamics, a PID

controller is applied and an optimization problem is conﬁgured. Two objective functions are deﬁned, namely

the integral of absolute error and the variance of control action. In addition, two constraints are considered

regarding the maximal position error and maximal motor torque. After deﬁning the optimization problem,

the two algorithms are implemented as auto-tuning methods of the controller gains. Execution of the tuning

process is repeated 30 times to test the statistical power of the obtained results. After that, an experiment on a

real robot is performed to gain an overview on the practical application of the proposed method. Finally, the

performance of both algorithms are compared and conclusions about the efﬁciency of each one are made.

1 INTRODUCTION

PID control structures provide simple, robust and ef-

fective solutions for most applications of control engi-

neering. They are with more than 95% share by far the

most used controller in industrial processes. These

good characteristics of PID controllers are conditio-

ned by accurate tuning of the controller gains. Howe-

ver, it was shown in (Desborough and Miller, 2002)

that up to 80% of twenty six thousand PID controllers

are not performing perfectly, one of the most impor-

tant reasons is the poor tuning of the controllers.

Robotic manipulators are highly non linear, highly

coupled, Multi-Input Multi-Output (MIMO) dynamic

systems, while PID controller has a linear structure,

and therefore, tuning the controller parameters for

such systems depending on analytical approaches is

a very difﬁcult task.

In the last decades, optimization algorithms have

attracted the attention of researchers in many diffe-

rent ﬁelds. The increased development of these algo-

rithms enabled researchers to apply them on difﬁcult

designing tasks where the previous knowledge of the

problem characteristics and the ability to analyze the

studied system are somehow limited.

In the ﬁeld of robotic manipulators, a number

of optimization methods (e. g. Genetic Algorithms

(GA) (Kim et al., 2012), Particle Swarm Optimization

(PSO) (Zidan et al., 2017)) has been applied to auto-

tune the PID controllers. In the presence of a large

number of optimization algorithms, comparative stu-

dies are introduced to evaluate their performance and

emphasize their positive and negative aspects. Howe-

ver, only a limited number of comparative studies can

be related to the tuning problem of PID controllers

for robot manipulators. For example, genetic algo-

rithm (GA) is compared to simulated annealing (SA)

in (Kwok and Sheng, 1994) while performing a trajec-

tory tracking movement. Ga is found to be giving the

best tracking accuracy. In (Ouyang and Pano, 2015),

a comparison study of GA, PSO, and DE (Differen-

tial Evolution) is performed with respect to different

performance-measuring functions and it is concluded

that DE surpasses the other two algorithms.

New promising algorithms are increasingly deve-

loping, and therefore, the need for performing more

240

Zidan, A., Tappe, S. and Ortmaier, T.

A Comparative Study on the Performance of MOPSO and MOCS as Auto-tuning Methods of PID Controllers for Robot Manipulators.

DOI: 10.5220/0006899802400247

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 240-247

ISBN: 978-989-758-321-6

tests on these algorithms and introducing comparative

studies between them increases as well. One of the

new and very successful algorithms is the cuckoo se-

arch (CS) proposed by (Yang and Deb, 2009), which,

to the author’s knowledge, has not been implemented

yet as an auto-tuning method for robot manipulators.

Regarding the problem at hand, the optimization

of the controller is affected by many factors, and des-

cribing it in the form of a single-objective optimi-

zation problem might be oversimpliﬁed and insufﬁ-

cient. For example in trajectory tracking control, the

main objective is to achieve the most possibly accu-

rate tracking, but this might be associated with relati-

vely high variance in the control action (joint torque)

or even with high oscillations in the motion. The-

refore, it is helpful to take more than one objective

function into consideration and handle the problem as

a multi-objective problem.

This consideration has already been introduced in

some works. (Ayala and dos Santos Coelho, 2012)

proposed an approach based on a multi-objective evo-

lutionary algorithm (MOEA), which aimed to tune

the PID controller gains by taking two conﬂicting ob-

jective functions into consideration: minimization of

position errors and minimization of the control sig-

nal variation (joint torques). Also in (Pierezan et al.,

2014), a comparative study between different multi-

objective optimization techniques has been introdu-

ced and an improved multi-objective particle swarm

optimization (I-MOPSO) has been proposed.

We introduced in a previous work (Zidan et al.,

2017) a practical auto-tuning method for a PD con-

troller using PSO algorithm, where the problem is

handled from a practical point of view and the pro-

blem of the necessary constraints is solved efﬁciently.

In this work, more attention is directed towards des-

cribing the problem from a multi-objective point of

view, and in the same time, implementing and compa-

ring the cuckoo search algorithm to the previously tes-

ted particle swarm optimization. In this comparison,

suitable metrics are considered in order to achieve

accurate results and reach helpful conclusions in order

to choose the best approach for similar applications.

The reminder of this paper is organized as follows.

In Section 2, the optimization problem with the ne-

cessary objective functions and constraints is deﬁned,

while Section 3 introduces the CS and the MOCS al-

gorithms brieﬂy. Section 4 introduces the PSO algo-

rithm and the chosen approach to form the MOPSO

algorithm. The metrics used for comparing the two

algorithms are introduced in Section 5. The experi-

mental results are presented in Section 6, ﬁrstly based

on a simulation where statistical data are generated,

and after that an experiment on a real robot is per-

formed and its results are shown. Finally, Section 7

discusses the conclusions of this work.

2 OPTIMIZATION OF PID

CONTROLLER FOR ROBOT

MANIPULATORS

This work considers a serial robot manipulator con-

trolled by an independent PID controller for every

joint of the robot. PID controller is a very desirable

choice because of its simplicity, efﬁciency and inde-

pendence of model knowledge. However, tuning the

controller gains for a complex nonlinear system such

as robot manipulator is not an easy task. The tuning is

done usually by using manual or experimental tuning

methods, which are unable to obtain critical damping

behavior and, therefore, settle for an overdamped one.

Recently after the rapid increase of computing power,

it became possible to use heuristic optimization met-

hods to solve the practical problems of such systems.

The auto-tuning process can be handled as an opti-

mization problem by deﬁning one or more objective

functions representing the control design criteria, then

determining any necessary conditions regarding the

stability of the controller as the constraints of the op-

timization problem. Finally, the algorithm will work

as a searching mechanism and after a sufﬁcient num-

ber of iterations, the best control parameters that meet

the design requirements will be found.

In this problem, it is desired to ﬁnd the control

parameters that lead to the best accuracy in the trajec-

tory tracking of the robot. However, the gains should

not be too high in such a way that it could lead to very

high variations in the control action within small time

intervals, which increase the risk of damaging the ro-

bot actuators. Depending on these two requirements,

the optimization parameters are deﬁned to be the PID

gains k

, k

and k

. The cost function that represents

the tracking accuracy is the integral of the absolute

error (IAE), which is calculated in practice using the

following formula:

IAE =

∑

i=1

e(i)|∆T , (1)

and the cost function representing the control actions

variance (CAV ) is given by:

CAV =

M−1

∑

i=1

|τ

τ(i + 1)− τ

τ(i)|. (2)

Where ∆T is the sampling time, M is the total num-

ber of samples along the trajectory, e

e is the position

error signal and τ

τ is the torque signal. Usually by the

A Comparative Study on the Performance of MOPSO and MOCS as Auto-tuning Methods of PID Controllers for Robot Manipulators

241

tuning procedure of the controller’s gains in robotic

manipulators, it is important to limit the gain values

in order to avoid driving the robot into unstable situ-

ations. This can be achieved by monitoring the robot

movement and stop it if one of these situations is de-

tected, such as high position error, high motor torque

or high excited oscillations.

In this work, the auto-tuning method is tested on

a simulation model of a robot and, additionally, on a

real robot. In the simulation case, the ﬂexibility of

the joints and the links are neglected, therefore, it is

not necessary to detect oscillations in the movement.

However, when the auto-tuning is performed on real

robots, oscillations constraints are crucial and must be

considered. Handling oscillations has been done in a

previous work (Zidan et al., 2017) by deﬁning an in-

dex that can detect unwanted oscillations and conse-

quently terminate the movement. In general, to detect

a constraint violations, maximum limits are deﬁned

as thresholds of the constraints (a maximum position

error, a maximum torque and a maximum value of the

oscillation index). If one of these limits is exceeded,

the movement has to be stopped immediately.

Based on the foregoing, the optimization problem

can be deﬁned as follows:

K = (

) = arg min

(IAE,CAV),

|τ

τ| ≤ τ

max

, |e

e| ≤ e

max

, |h

osc

| ≤ h

osc,max

With h

osc

being a vector of the oscillation index va-

lues in the robot links, and h

osc,max

being a vector of

the maximum limits of index values corresponding to

the tolerance interval of oscillations.

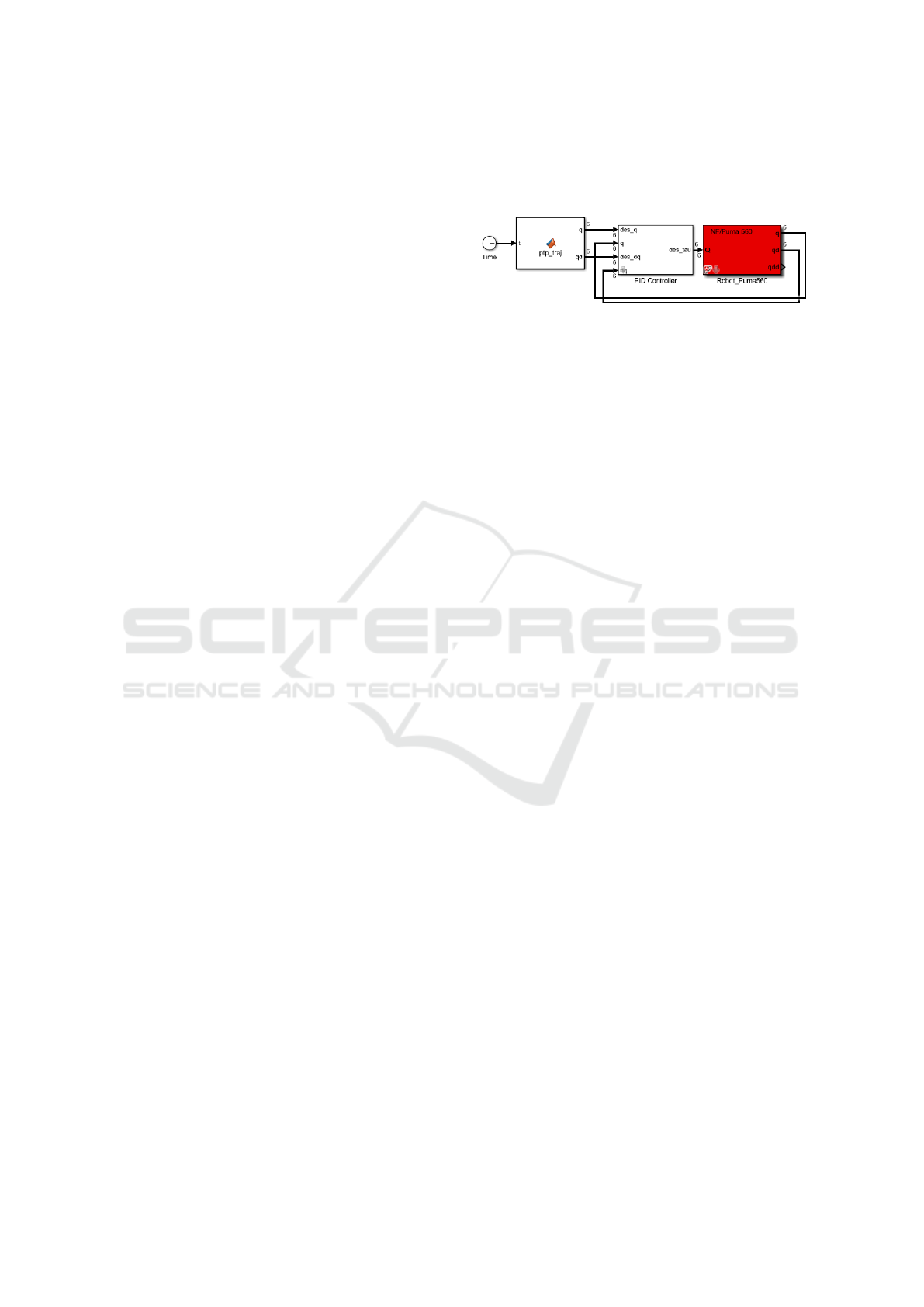
For the simulation case, a model of the robot Puma

560 is used to test the proposed method. This ro-

bot is built using the robotic toolbox designed by Pe-

ter Corke (Corke, 2017), which is a Matlab/Simulink

toolbox supplied with many functions that can be used

to model the kinematics and the dynamics of several

types of robots besides many other functions. By

using the built-in functions for Puma 560 dynamics,

one can add a PID position controller and use Simu-

link to simulate the movement of the robot as shown

in Figure 1 and ﬁnally evaluate the accuracy and the

efﬁciency of the movement. It is worth mentioning,

that the simulation is relatively simpliﬁed in compa-

rison to a real robot, where many other factors af-

fects the robot movement such as the ﬂexibility of

the joints/links, measurements noise and unmodeled

friction. However, the main focus of this work is on

comparing the performance of the two optimization

algorithms which requires a sufﬁcient number of exe-

cutions of the auto-tuning process in order to collect

enough statistical data. Getting these data from a real

robot would require letting the robot perform the de-

sired movement for thousands of times and, therefore,

would take a very long time.

Figure 1: Simulink model of Puma 560, PID controller and

a ptp trajectory generator.

3 CUCKOO SEARCH AND

MULTI-OBJECTIVE CUCKOO

Cuckoo search is an optimization algorithm ﬁrst intro-

duced in (Yang and Deb, 2009). It imitates the brood

parasitism behavior of some cuckoo species. These

cuckoo birds lay their eggs in the nests of other birds,

by some species the eggs can take very close shape

to the host bird’s eggs, which makes it harder for the

host bird to detect the intruder egg. By the propo-

sed cuckoo search algorithm, the hosts nests are re-

presented as the population of the algorithm, where

the number of hosts will be ﬁxed through the search.

The cuckoo birds are represented by the new indivi-

duals generated in every iteration. It is assumed that

every cuckoo bird lays only one egg at a time. The

new egg replaces the original egg in the host nest if

its evaluation (cost value) is better. In addition, there

is the possibility of the host nest to detect the intruder

egg and get rid of it (or abandoned the nest to another

location). This possibility is modeled by a probability

function which is the probability of detecting this egg.

This probability value pa ∈ [0 1] is actually the only

parameter which needs to be tuned in the algorithm.

In addition, CS algorithm uses a strong tool in ge-

nerating new eggs based on the concept of L

evy ﬂig-

hts (Barthelemy et al., 2008), which is proven to be

more efﬁcient than a random walk technique where

the individuals are generated randomly. The genera-

tion of new solutions is given as follows:

(t + 1) = x

(t) + α ⊕ L ´evy(β), (3)

where α depends on the difference between solution

qualities, the product ⊕ is an entry-wise multiplica-

tion, and L ´evy(β) is a function provides a random

walk while their random steps are drawn from a L´evy

distribution for large steps which has an inﬁnite vari-

ance and large steps.

L ´evy ∼ u = t

−1−β

, (0 < β ≥ 2) . (4)

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

242

In (Yang and Deb, 2013), the single objective

CS algorithm is extended to handle optimization pro-

blems with multiple objectives. In order to achieve

that, the analogy to the cuckoo behavior is modiﬁed

in which every objective function is represented by

an egg in the nest, i.e. in k objectives problem, every

nest will have k eggs, and each egg has its own quality

(cost value). When a nest is abandoned by the proba-

bility pa, a nest with k eggs takes its place considering

the similarities between the eggs. This approach is the

one used in this work to perform the auto-tuning met-

hod.

4 PARTICLE SWARM

OPTIMIZATION AND

MULTI-OBJECTIVE PARTICLE

SWARM OPTIMIZATION

Particle swarm optimization (PSO), ﬁrst introduced in

(Eberhart and Kennedy, 1995), is a population-based

algorithm simulating the movement of a swarm of

particles in a predeﬁned search space. The number of

optimization parameters is the number of dimensions

of the search space. Every generation has a constant

number of particles, which move in the next generati-

ons in the search space until ﬁnding the position with

the best quality. The movement of the particles is de-

ﬁned by the following equations:

(i + 1) = ω(i)V

(i) + c

(i) − X

(i))

+ c

(G(i) − X

(i)),

(5)

(i + 1) = X

(i) + V

(i + 1).

(6)

Where i indicates the current iteration, j indicates

a particle of the swarm, X

(i) is the position vector

of the particle j, V

(i) is the velocity vector of the

particle j, c

and c

are the cognitive and the social

acceleration coefﬁcients respectively, ω is the inertia

factor and γ

and γ

∈ [0 1] are random variables with

uniformly distributed values.

There is no standard way to choose the swarm size

and the maximum number of iterations. However,

both parameters must be high enough in order to gua-

rantee a convergence of the objective value towards

the global minimum.

The inertia weight is deﬁned to be a linear decre-

ased function as follows:

ω = ω

max

−

(ω

max

− ω

min

max

, (7)

where N

max

is the maximum number of iterations, N

is the current number of iterations, ω

max

and ω

min

are

the maximum and the minimum values of the inertia

weight respectively. The chosen values in this work

are ω

max

= 0.9 and ω

min

= 0.4, as it was suggested in

(Shi and Eberhart, 1998).

Regarding the case of multi-objectives, different

modiﬁcation approaches are introduced as MOPSO

algorithms. In this work, the MOPSO algorithm de-

ﬁned in (Coello et al., 2004) is applied where an ex-

ternal repository is used to store the non-dominated

solutions and an adaptive grid is constructed to pro-

duce well-distributed Pareto frontier.

5 EVALUATION OF PARETO

SOLUTIONS

Unlike single objective optimization algorithms,

multi-objective algorithms provide several optimal

solutions to the problem and offer some sort of com-

promise between the objective functions (assuming

that these functions contradict each other). Given

these solutions, the designer is supposed to evaluate

their goodness and choose one suitable to the problem

at hand.

In the case where the designer is trying to decide

between two or more optimization algorithm, diffe-

rent metrics from those of single objective problems

are required. In some cases, the designer can test the

algorithms on a similar problem for which the true Pa-

reto frontier is already known, and then perform the

comparison. For this case several metrics are intro-

duced in the literature as those in (Zitzler and Thiele,

1998). For cases such as the one in this work, the true

Pareto frontier can not be known in advance, and the-

refore, the known metrics need to be adjusted or even

new ones must be developed. The work of (Wu and

Azarm, 2001) has introduced several metrics for this

sake and are found to be very suitable for the auto-

tuning problem. These metrics are introduced brieﬂy

with the corresponding formulas.

1. Hyperarea Difference: This metric is meant to

produce an estimation of the difference between

the area in objective space, which is dominated by

the true Pareto solutions (the actual Pareto front),

and the one dominated by the resulted Pareto so-

lutions (the Pareto front resulted from the optimi-

zation algorithm). This metric can be modiﬁed to

an equivalent one when the true Pareto solution

is unknown and different optimization algorithms

are compared. In this metric, it is sufﬁcient to es-

timate the area dominated by the resulted Pareto

frontier (gray rectangles shown in Figure 2) and

then compare the areas between algorithms. The

A Comparative Study on the Performance of MOPSO and MOCS as Auto-tuning Methods of PID Controllers for Robot Manipulators

243

Figure 2: Example of a Pareto frontier and the dominated

region.

one with a bigger area has for sure smaller diffe-

rence hyperarea with the true Pareto frontier, and

therefore, generates better solutions.

(Wu and Azarm, 2001) proposed a general for-

mula to calculate the dominated region. In case

of only two objective functions, this formula can

be simpliﬁed to the calculation of the area of the

rectangles determined by the solutions. This area

is given as follows:

DA =

n−1

∑

i=1

(1 − f

(i))( f

(i + 1) − f

(i))+

(1 − f

(n))(1 − f

(n)),

(8)

with n being the total number of solutions and

(i) being the value of the jth objective function

with respect to the ith solution. The objective

functions are considered here to be normalized

and scaled to the interval [0 1].

2. Overall Pareto Spread: This metric estimates the

range, in which the Pareto solutions are spread.

The wider this range is, the more preferred the so-

lutions set is. This metric is calculated as follows:

OS =

∏

j=1

|max

i=1

( f

(i)) − min

i=1

( f

(i))|, (9)

with m being the total number of objective functi-

ons and n the total number of Pareto solutions.

3. Number of Distinct Solutions: Usually when

comparing two set of Pareto solutions, the one

with higher number of solutions is preferred. Ho-

wever, this criteria can be misleading in the case

where many solutions are too close to each ot-

her. This metric solve the problem by conside-

ring only the solutions that are sufﬁciently dis-

tinct from each other (separated by long enough

distance). It is simply calculated by setting a con-

stant number ε and counting the number of solu-

tions with a separating distance ≥ ε from other

solutions.

6 EXPERIMENTAL RESULTS

6.1 Performance Evaluation based on a

Robot Simulation

The proposed auto-tuning method is tested in a simu-

lation of a Puma 560 robot controlled by a classical

PID controller. For this sake, a point to point trajec-

tory is applied on the ﬁrst three joints. The simula-

tion is executed using Simulink environment for the

time period 0 – 4 sec. At the end of execution, the

two objective functions are evaluated and these values

are sent to the corresponding optimization algorithm,

where the set of Pareto solutions are found. To gua-

rantee a fair comparison of the two algorithms, the

same number of population is set for both of them (40

individuals). In addition, the same maximum num-

ber of iterations is set before ending the search (100

iterations). The constraints are dealt with using the

sudden death method, where a very high value is as-

signed to the two objective functions once a high error

or high moment value is detected. Every algorithm

is applied to do the auto-tuning for 30 times. Then

the Pareto solutions and their corresponding gain va-

lues are collected for the comparison phase. To eva-

luate the performance of the two algorithms, the me-

trics introduced in Section 5 are used. The evaluation

requires ﬁrst a normalization of the objective values,

which will give them always a value in the interval

[0 1]. This is achieved by deﬁning a minimal and a

maximal limit of the objective values, which are de-

termined experimentally by applying 10 different set

of gain values, calculate the objective values of them,

and multiply the maximum value by a sufﬁcient fac-

tor. The minimum value of both objectives is set to be

0, while the maximum values are IAE

max

= 2.5[rad ·s]

and CAV

max

= 1500[N · m]. The normalization is then

simply achieved by dividing the calculated objective

value to the corresponding maximum value.

At this point, the evaluation metrics can be calcu-

lated for every execution of the algorithms and later

compare the results.

The ﬁrst metric is the number of Pareto solutions

found by each algorithm. As shown in Figure 3,

MOPSO gave clearly higher number of solutions by

all the executions. However, after determining the

number of distinct solutions with a limit ε = 0.01, the

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

244

Figure 3: Number of Pareto solutions in 30 executions.

Figure 4: Number of distinct solutions in 30 executions.

Figure 5: Dominated hyperareas in 30 executions.

superiority of MOPSO vanishes and MOCS takes the

advantage as shown in Figure 4. This indicates that

MOPSO generates solutions in a narrow range and

shows the importance of the second metric to avoid

the misleading results of the ﬁrst.

Regarding the hyperarea difference, MOCS have

by all executions bigger dominating area as shown

in Figure 5 and, therefore, have lower hyperarea of

non-inferior solutions, which indicates that the Pareto

frontier of MOCS is closer to the true Pareto frontier

than MOPSO.

Another important metric is the overall Pareto

spread. Once again, MOCS has advantage in this me-

tric over MOPSO as shown in Figure 6.

The previous results indicate that despite the hig-

her number of MOPSO in general, those solutions are

concentrated in narrow region of the objective space.

However, MOCS gives more accurately distributed

solutions at the end and, therefore, wider range of so-

lutions for the designer to choose from.

Depending on the robot task and design require-

ments, one of the Pareto solutions can ﬁnally be cho-

sen and the corresponding set of gain values are used

Figure 6: Overall Pareto spread in 30 executions.

Figure 7: Best compromise solutions in 30 executions.

to tune the controller. Because of the conﬂict between

the two objectives, a compromise is needed here bet-

ween the accuracy and the controller variance. Assu-

ming that both objectives have the same importance,

an appropriate choice, which represents the best made

compromise, is the one with minimal average of ob-

jective values between all solutions

bcs = min(

IAE(P)+CAV (P)

). (10)

With P being the resulted set of Pareto solutions. Fi-

gure 7 shows the distribution of the best compromise

solutions for the 30 executions of the two algorithms.

MOCS generates clearly solutions with a lower bcs

values to prove again its superiority over MOPSO.

6.2 Performance Evaluation based on a

Real Robot

After comparing the two algorithms in a simulation of

the robot Puma 560, a more realistic test is done on a

real robot. The goal of this test is not to collect statisti-

cal data describing the behavior of the algorithms, but

to perform a realization of the auto-tuning method as

a practical process and take an overview on the perfor-

mance of the algorithms. For this sake, a 7-DOF ro-

bot is used to perform a trajectory tracking movement.

The robot is built of specially designed modules cal-

led PowerCube from the company “Schunk”. In this

experiment, PID controllers are used to control the

joints (3, 4, 6) which are shown in Figure 8. All the

joints here are rotational and actuated by brushless dc-

motors. The desired trajectories are shown in Figure

A Comparative Study on the Performance of MOPSO and MOCS as Auto-tuning Methods of PID Controllers for Robot Manipulators

245

Figure 8: PowerCube robot.

Figure 9: Desired trajectories of a circular movement.

9, which generate a circular movement of the end ef-

fector.

For a real robot, the maximum number of iterati-

ons by the optimization algorithms has to be more li-

mited compared to the simulation, otherwise the auto-

tuning process will take an extremely long time. The

population number and the maximum number of ite-

rations are set to be 10 and 20, respectively, i. e. a

total number of movement executions equals 200 for

every algorithm, which is much less than the 4000

executions used by the simulation. Performing the

200 movements takes about 1 hour, which is an accep-

Table 1: Performance evaluations of MOPSO and MOCS

after experiments on a real robot.

Performance measures MOPSO MOCS

Number of solutions 18 13

Number of distinct solutions 16 10

Dominated hyperarea 0.3641 0.3892

Overall Pareto spread 0.1763 0.1383

Best compromise solution 0.4543 0.4296

Figure 10: Pareto solutions of MOPSO and MOCS corre-

sponding to real robot movements.

table period of time. After looking at the results,

it was found that the difference in performance was

not as clear as in the test on a simulation. Figure

10 shows the Pareto solutions of both MOPSO and

MOCS, which appear to look relatively close to each

other. Table 1 gives the results of the performance

metrics for this test. The difference in the results is

too small to decide which is better. Therefore, based

on this experiment it is fare to say that both algorithms

did equally well.

6.3 Discussion

Based on the simulation results and statistics,

MOCS shows clearly better performance compared to

MOPSO. Adding to that the simplicity of MOCS and

low number of parameters which needs to be set (only

one parameter), one concludes that this algorithm is

very promising and worth to be considered as an auto-

tuning mechanism for PID controller even with such

complex systems as robot manipulators. On the other

hand, there is probably still a room for improvement

for MOPSO regarding the diversity of the determined

Pareto solutions, which despite its high count, are re-

latively concentrated in a narrow region of the Pareto

frontier.

However, performance evaluations after testing

the auto-tuning method on a real robot did not show

the superiority of MOCS as it was for the simula-

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

246

tion. This indicates that MOCS might need a rela-

tively high number of populations and executions in

order to achieve its best performance. On the other

hand, the high number of iterations in the simulation

test showed clearly the tendency of MOPSO to ge-

nerate solutions which are more concentrated in the

neighborhood of the leader particle (best global solu-

tion). This tendency was not emphasized as clearly in

the second experiment where only a limited number

of iterations is used.

7 CONCLUSION

In this work, an auto-tuning method of PID control-

lers for robot manipulators is introduced. Two multi-

objective optimization methods are considered, na-

mely MOCS and MOPSO. The main contribution of

this work is to compare the performance of the two

algorithms in the sense of achieving a good tracking

accuracy of a predeﬁned trajectory without causing

a control action with high variations. The necessary

metrics for the comparison are considered and des-

cribed. Statistics taken from a simulation of the ro-

bot Puma 560 show clearly that MOCS is performing

much better than MOPSO with respect to all the con-

sidered metrics. The main advantage of MOCS co-

mes from the fact that its Pareto solutions have higher

spread and cover bigger region of the objective space

than the solutions of MOPSO. However, an experi-

ment on a real robot, where only a limited number of

iterations is used, showed that both algorithms perfor-

med equally well. This indicates that sufﬁciently high

number of populations and iterations might be neces-

sary for MOCS to achieve its best performance.

REFERENCES

Ayala, H. V. H. and dos Santos Coelho, L. (2012). Tuning of

pid controller based on a multiobjective genetic algo-

rithm applied to a robotic manipulator. Expert Systems

with Applications, 39(10):8968–8974.

Barthelemy, P., Bertolotti, J., and Wiersma, D. S. (2008). A

evy ﬂight for light. Nature, 453(7194):495.

Coello, C. A. C., Pulido, G. T., and Lechuga, M. S. (2004).

Handling multiple objectives with particle swarm op-

timization. IEEE Transactions on evolutionary com-

putation, 8(3):256–279.

Corke, P. (2017). Robotics, Vision and Control: Funda-

mental Algorithms In MATLAB

 Second, Completely

Revised, volume 118. Springer.

Desborough, L. and Miller, R. (2002). Increasing customer

value of industrial control performance monitoring-

honeywell’s experience. AIChE symposium series,

(326):169–189.

Eberhart, R. and Kennedy, J. (1995). A new optimizer using

particle swarm theory. Micro Machine and Human

Science, 1995. MHS’95., Proceedings of the Sixth In-

ternational Symposium on, pages 39–43.

Kim, E.-J., Seki, K., Iwasaki, M., and Lee, S.-H. (2012).

Ga-based practical auto-tuning technique for indus-

trial robot controller with system identiﬁcation. IEEE

Journal of Industry Applications, 1(1):62–69.

Kwok, D. and Sheng, F. (1994). Genetic algorithm and si-

mulated annealing for optimal robot arm pid control.

Evolutionary Computation, 1994. IEEE World Con-

gress on Computational Intelligence., Proceedings of

the First IEEE Conference on, pages 707–713.

Ouyang, P. and Pano, V. (2015). Comparative study of de,

pso and ga for position domain pid controller tuning.

Algorithms, 8(3):697–711.

Pierezan, J., Ayala, H. H., da Cruz, L. F., Freire, R. Z., and

Coelho, L. d. S. (2014). Improved multiobjective par-

ticle swarm optimization for designing pid controllers

applied to robotic manipulator. Computational Intelli-

gence in Control and Automation (CICA), 2014 IEEE

Symposium on, pages 1–8.

Shi, Y. and Eberhart, R. C. (1998). Parameter selection

in particle swarm optimization. International Confe-

rence on Evolutionary Programming, pages 591–600.

Wu, J. and Azarm, S. (2001). Metrics for quality assessment

of a multiobjective design optimization solution set.

Journal of Mechanical Design, 123(1):18–25.

Yang, X.-S. and Deb, S. (2009). Cuckoo search via l

evy

ﬂights. pages 210–214.

Yang, X.-S. and Deb, S. (2013). Multiobjective cuckoo se-

arch for design optimization. Computers & Operati-

ons Research, 40(6):1616–1624.

Zidan, A., Kotlarski, J., and Ortmaier, T. (2017). A practi-

cal approach for the auto-tuning of pd controllers for

robotic manipulators using particle swarm optimiza-

tion. 14th International Conference on Informatics in

Control, Automation and Robotics, pages 34–40.

Zitzler, E. and Thiele, L. (1998). Multiobjective optimiza-

tion using evolutionary algorithmsa comparative case

study. pages 292–301.

A Comparative Study on the Performance of MOPSO and MOCS as Auto-tuning Methods of PID Controllers for Robot Manipulators

247