Gain-Scheduling Position Control Approaches for Electromagnetic
Actuated Clutch Systems
Claudia-Adina Bojan-Dragos, Mircea-Bogdan Radac, Radu-Emil Precup, Elena-Lorena Hedrea,
Alexandra-Iulia Szedlak-Stinean and Stefan Preitl
Department of Automation and Applied Informatics, Politehnica University Timisoara,
Bd. V. Parvan 2, Timisoara, Romania
Keywords: Electromagnetic Actuated Clutch Systems, Gain-Scheduling Control, Nonlinear System, Simulation
Results.
Abstract: The paper proposes three Gain-Scheduling (GS) control design approaches dedicated to the position control
of electromagnetic actuated clutch systems. The initial nonlinear mathematical model of the plant is
simplified and next linearized at six operating points to use it in the design approaches. Starting with
classical Proportional-Integral (PI) controllers, three GS control versions, namely Lagrange, Cauchy and
Switching GS, are next designed to ensure zero steady-state control error and the switching between PI
controllers. All control solutions are tested and validated on the nonlinear model of the plant and a
comparative analysis is included.
1 INTRODUCTION
The paper is focused on the development of three
gain-scheduling control solutions (CSs) for
electromagnetic actuated clutch systems (the plant)
in the framework of electrically driven clutches
which belong to vehicular power train system.
Several classical and modern control solutions
for electromagnetic actuated clutch systems have
been proposed recently including the following
ones: two electromagnetic clutch water pumps that
can control the coolant in terms of a nonlinear
servo are designed in (Shin et al., 2013) using a
model-free approach based on an online self-
organizing adaptive fuzzy controller. A nonlinear
feedforward–feedback control scheme is proposed
in (Gao et al., 2014) to improve the performance of
the position tracking control that consist of steady-
state-like control, feedforward control based on
reference dynamics, and state dependent feedback
control. The design of an estimator for each clutch
of the dual clutch transmission is carried out in (Oh
et al., 2014) using shaft model-based observer,
unknown input observers, and adaptive output
torque observer. A position controller for a clutch
actuator is suggested in (Losero et al., 2016) using
a quasi-Linear Parameter Varying (LPV) Takagi-
Sugeno representation and, in order to use
unmeasured values in the controller, a Takagi-
Sugeno switching observer. A parallel adaptive
feedforward and bang-bang controller is proposed
in (Temporelli et al., 2017) to control the clutch
pressure with an electromechanical clutch actuator.
A controller for an electromagnetic linear clutch
actuator is given in (Ranjan et al., 2017).
Since linear controllers can usually ensure the
CS performance specifications only in some
neighbourhood of a single operating point, the
Gain-Scheduling (GS) technique is popular as it
generalizes the performance specifications over
various operating points. An analysis of GS
controllers which can vary slowly and can capture
the plant’s nonlinearities and the conditions which
guarantee the stability using Lyapunov’s stability
theory, robustness and performance of the overall
gain-scheduled design are given in (Shamma and
Athans, 1990; Veselý and Ilka, 2013), with recent
results outlined as follows: a Proportional-Integral
(PI) GS CS for second-order LPV systems, which
excludes time varying delay and uses a Smith
predictor, is given in (Puig et al., 2012). GS deals
in (Andonovski et al., 2015) with the adaptation of
gains of a robust evolving cloud-based controller
Bojan-Dragos, C-A., Radac, M-B., Precup, R-E., Hedrea, E-L., Szedlak-Stinean, A-I. and Preitl, S.
Gain-Scheduling Position Control Approaches for Electromagnetic Actuated Clutch Systems.
DOI: 10.5220/0006900404110418
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 411-418
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
411

(RECCo) designed for a class of nonlinear
processes; the robust modification of the adaptive
laws and the performance analysis are introduced.
A practical implementation of RECCo with
normalized data space for a heat-exchanger plant is
shown in (Andonovski et al., 2016). Other
interesting GS (adaptive) control techniques for
real practical applications are discussed in
(Haidegger et al., 2012; Costa et al., 2015; Precup
et al., 2015; Yang and Yan, 2016; Precup et al.,
2017).
This paper continues with the modelling of a
nonlinear electromagnetic actuator system in
Section 2. Six linear PI controllers are designed in
Section 3 based on the linearized mathematical
models (MMs) of the plant. Three GS controllers
are next suggested to ensure the switching between
these linear PI controllers and to improve the
performance indices. The parameters of the
suggested controllers can be relatively easily
adapted to the modifications of the operating
points. The simulation results and comparisons
between the suggested GS controllers are given in
Section 4. Section 5 presents the conclusions.
2 MATHEMATICAL MODELING
OF CONTROLLED PLANT
In this paper, the controlled plant is an
electromagnetic actuator as part of a clutch system.
The state-space MM of the electromagnetic
actuated clutch is built around a magnetically
actuated mass spring damper system, Figure 1 (Di
Cairano et al., 2007). The mass m moves linearly
under the effect of the magnetic force F, which is
generated by the coil. Additional forces which
acting on the mass are generated by the spring and
the damper.
Figure 1: Schematic structure of the magnetically actuated
mass-spring-damper system.
Using the equations given in (Di Cairano et al.,
2007; Bishop, 2008), the dynamic behaviours of
the mechanical (M-S) and electromagnetic
subsystems (EM-S) are characterized by
).4/()/(
),/(2
,:)(
:)(
222
aba
ba
kxdkikF
xdkik
RiVSEM
kxxcFxmSM
λ=−+=
−+=λ
−=λ−
−−=−


(1)
Based on (1), the following simplified nonlinear
state-space model of the plant can be accepted
(Dragos et al., 2012a, Dragos et al., 2012b):
,1000
,)]2/()([)]
/(1[)]2/()( [
],)
( /[)()/()/(
,
1
1321
313
2
1
2
3212
21
xy
ukxdkxxxd
kxkxdkRx
xd
kmxkxmcxmkx
xx
ab
bab
ba
=
−++−+
−−+−=
−+
+−−=
=



(2)
with the following characteristic variables: u
∈
[0,
12] [V] is the control input, x
1
∈
[0, 0.004] [m] is
the mass position, x
2
[m/s] is mechanical
subsystem’s speed and
λ=
3
x
[V⋅ s] is the
magnetic flux; y [m] is the output variable, i.e., the
measured mass position, m=1 [kg] is the mass,
d=0.004 [m] is the distance between contact
position and spring neutral position, R=1.2 [Ω] is
the resistance, c=700 [N s/m] coefficient of the
damper, k=37500 [N/m] is stiffness of the spring,
k
a
=0.5 is a constant k
b
=0.375 is a constant, i
∈
[0,
10] [A] is the current, and F
∈
[0, 150] [N] is the
external magnetic force.
To design the proposed CS, the reduced model
(2) is linearized at six operating points (o.p.s) with
the following coordinates
),,(
)()(
3
)(
1
)( jjjj
uxxP
,
where j is the index of the current operating point,
6,1=j
:
).76.119.8,,0038.0(),8.109,,0033.0(
),6.98,,0027.0(),4.87,,0023.0(
),2.76,,0021.0(),65,,002.0(
)6()5(
)4()3(
)2()1(
PP
PP
PP
(3)
The simplified linearized state-space models
(Ln-Ms) are
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
412

[]
,,,
],001000[
,
)2/(
0
0
,
0
010
,,
,
,
31
)(
13)(33)(
)(
)(
)(
33
)(
32
)(
23
)(
22
)(
21
)(
)(13)(
)(
3
)(
2
)(
1
)(
)(
)(
)(
)()()()()(
x
j
Txjxj
j
T
ab
j
jj
jjjj
jxj
T
jjjj
j
j
Tj
jjjjj
kkaa
aaa
u
xxx
y
u
ℜ∈ℜ∈ℜ∈
=










=










=
ℜ∈Δℜ∈Δ
ΔΔΔ=Δ
Δ=Δ
Δ+Δ=Δ
cbA
c
bA
x
x
xc
bxAx

(4)
with the matrix parameters
).2/(),2/(,/
),/(2,/,/
)(
31
)(
3330
)(
32
2
30
)(
23
)(
22
)(
21
ab
j
ab
j
b
j
ba
jjj
kkbkkRakxa
kmxkamcamka
⋅=⋅⋅−==
⋅⋅=−=−=
(5)
The variables in (4) are:
)(
0
)()( jjj
xxx
γγγ
−=Δ
,
)(
0
)()( jjj
yyy −=Δ
,
3,1,6,1 == γ j
, representing the
differences of the variables
)( j
x
γ
and
)( j
y
with
respect to their values at the current operating point
)( j
P
, and referred to as
)(
0
j
x
γ
and
)(
0
j
y
, respectively.
The transfer function (t.f) corresponding to Ln-
Ms (4) has the general expression
,
)1()(
/
)()(
3,1
)(
)(
3,1
)(
3,1
)()(
)(1)(
)(
)(
∏∏
∏
==
=
−
+
=
−
=
−=
η
η
η
η
η
η
sT
k
ps
pk
ssH
j
j
CP
j
jj
P
jj
j
Tj
P
bAIc
(6)
where
∏
=η
η
=
3,1
)()()(
/
jj
P
j
CP
pkk
, I is the third-order
identity matrix and the time constants of the plant
are
6,1,3,1,/1
)()(
==η−=
ηη
jpT
jj
. The numerical
values of the t.f.s.
)(
)(
sH
j
P
at six operating points
are synthesized in Table 1 (Dragos et al., 2012b).
3 DESIGN OF POSITION
CONTROL SOLUTIONS
Four CSs are developed and analyzed as follows to
obtain good performance of electromagnetic
actuated clutch systems: PI controller and three PI
gain-scheduling controllers.
Table 1: The numerical values of
)(
)(
sH
j
P
.
)( j
P
,
6,1=j
6,1),(
)(
=jsH
j
P
)1(
P
,
)0016.01)(016.01)(064.01(
3.0
sss +++
)2(
P
,
)0016.01)(0164.01)(066.01(
38.0
sss +++
)3(
P
,
)0016.01)(0162.01)(07.01(
47.0
sss +++
)4(
P
,
)0016.01)(016.01)(077.01(
58.0
sss +++
)5(
P
,
)0016.01)(0157.01)(087.01(
745.0
sss +++
)6(
P
,
)0016.01)(0154.01)(098.01(
9.0
sss +++
3.1 Design of PI Controllers
Depending on the operating points, six control
solutions with PI controllers have been designed to
ensure a small overshoot, offering an adequate phase
margin (
o
60=ϕ
m
) and a relatively small settling
time.
The Modulus Optimum method is applied to
initially tune the parameters of PI controllers
(Åström and Hägglund, 1995):
,/)1()(
)()()(
ssTksH
j
c
j
c
j
PI
+=
(7)
where
)2/(1
)()()( jj
CP
j
c
Tkk
Σ
⋅⋅=
is the controller gain,
)(
1
)( jj
c
TT =
is the integral time constant. The
numerical values of tuning parameters are:
89
)1(
=
c
k
,
064.0
)1(
=
c
T
,
95.72
)2(
=
c
k
,
066.0
)2(
=
c
T
88.59
)3(
=
c
k
,
07.0
)3(
=
c
T
,
79.48
)4(
=
c
k
,
077.0
)4(
=
c
T
,
92.38
)5(
=
c
k
,
087.0
)5(
=
c
T
92.31
)6(
=
c
k
,
098.0
)6(
=
c
T
.
The continuous PI controller (7) is discretized
using Tustin’s method with the sampling period
T
s
=0.003 s. Six discrete-time PI controllers with the
following t.f.s are obtained:
),1/()()(
11
10
1)( −−−
−+= zzqqzH
j
PI
(8)
where
1−
z
is the backward shift operator. The
numerical values of tuning parameters are:
Gain-Scheduling Position Control Approaches for Electromagnetic Actuated Clutch Systems
413

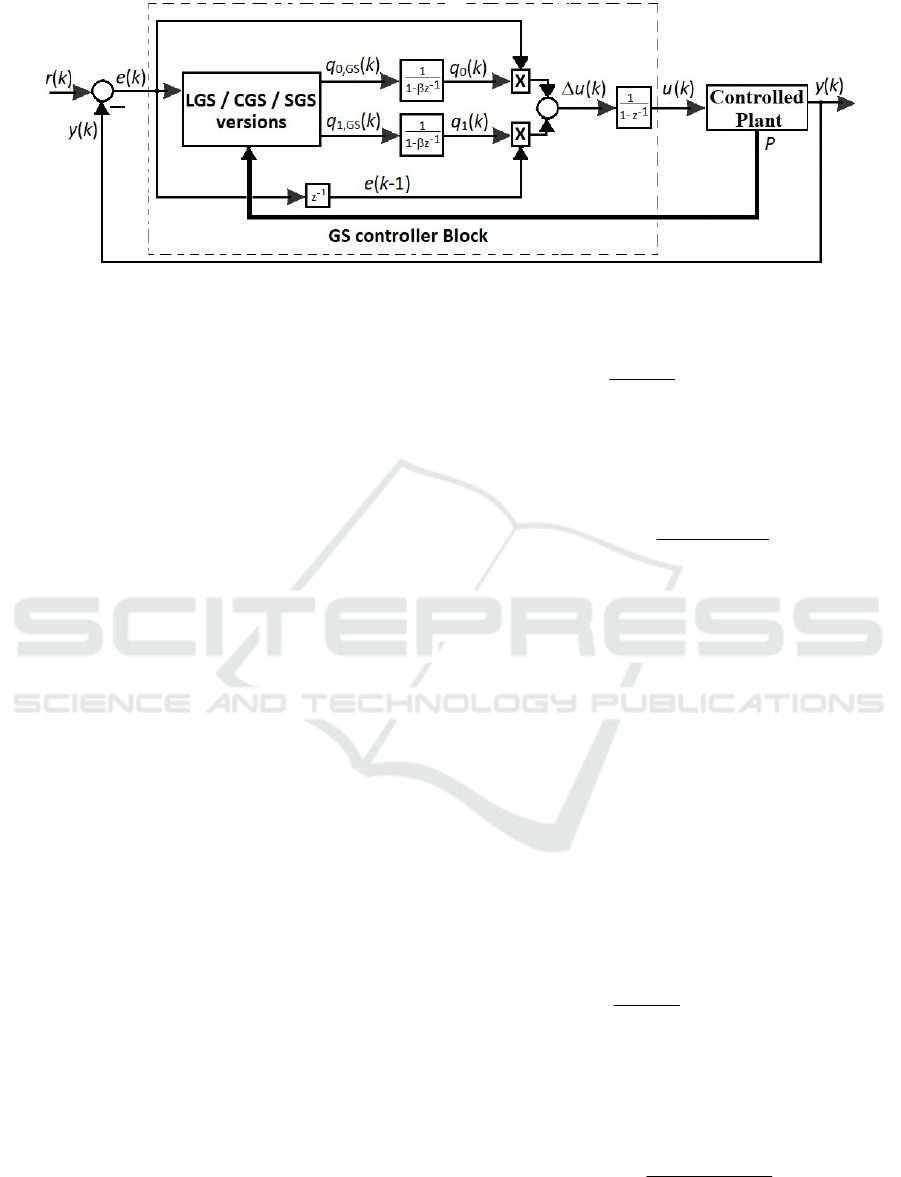
Figure 2: Schematic structure of the magnetically actuated mass-spring-damper system.
96.5
)1(
0
=q
,
70.5
)1(
1
−=q
,
06.5
)2(
0
=q
,
82.4
)2(
1
−=q
,
38.4
)3(
0
=q
,
20.4
)3(
1
−=q
,
92.3
)4(
0
=q
,
77.3
)4(
1
−=q
,
51.3
)5(
0
=q
,
40.3
)5(
1
−=q
,
33.3
)6(
0
=q
,
23.3
)6(
1
−=q
.
3.2 Gain-scheduling Control Solutions
Design
In order to ensure the switching between these six
discrete PI controllers, three GS control solutions,
namely Lagrange, Cauchy and Switching GS, Figure
2, are developed:
),1()()()()1()(
10
−++−= kekqkekqkuku
(9)
where
k is the discrete time argument, e(k)=r(k)–y(k)
is the control error sequence, y(k) is the process
output sequence,
r(k) is the reference input
sequence.
The discrete-time PI tuning parameters
}1,0{, ∈iq
ik
are
),()1()(
,
kqkqkq
GSiii
+−⋅β=
(10)
extended or not with a first-order lag filter, where
the parameter
}5.0,4.0,3.0,2.0,1.0,0{∈
β
controls
the transition speed between different controller
parameters, and
)(
,
kq
GSi
are regarded as reference
inputs calculated as follows.
The proposed Lagrange GS (LGS) control
solution is the first GS version, and it is based on a
generalization to the multivariable case of the
Lagrange interpolating parameter value method:
},1,0{,
1
)(
1
)(
)(
,
∈














⋅
α
α
=


=
=
iqq
n
j
j
i
n
j
j
LGS
j
LGS
LGSi
(11)
where
∏
≠=
−
−
=α
n
jll
lj
l
j
LGS
PP
PP
,0
2)()(
2)(
)(
||||
||||
,
(12)
the superscripts
j denote different operating points,
7=n
, LGS is Lagrange GS version,
||||
)( j
PP −
is
the Euclidean distance between the current operating
point in the form of
T
EMEM
uivxP ),,,(
111
=
) and
the nearest operating point
P
(j)
. All coefficients
)( j
LGS
α
in the first summation in (11) are normalized to add
up to 1.
The Cauchy GS control solution is the second
GS version which is based on a Cauchy kernel
distance metric (Andonovski et al., 2016). This
approach directly takes into account all previous
data samples using :
},1,0{,
1
)(
1
)(
)(
,
∈














⋅
α
α
=


=
=
iqq
n
j
j
i
n
j
j
CGS
j
CGS
CGSi
(13)
where

=
−+
=α
n
j
j
j
CGS
PP
1
2)(
)(
||||1
1
,
(14)
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
414

and CGS is Cauchy GS version,
||||
)( j
PP −
is the
Euclidean distance between the current operating
point
P and the nearest operating point P
(j)
.
The Switching GS (SGS) control solution is the
third version. It is based on the switching between PI
controllers and the PI controller parameters
correspond to the nearest operating point during the
real-time experiments. The selection is supported by
the Euclidean distance metric resulting in
},1,0{ ,
1
)(
1
)(
)(
,
∈














⋅
α
α
=


=
=
iqq
n
j
j
i
n
j
j
SGS
j
SGS
SGSi
(15)
where
},1,0{ ,||||minarg
,
2)(
,1
*
)(
,
*
∈−=
=
=
iPPj
qq
j
nj
j
iSGSi
(16)
and
SGS is Switching GS version.
4 SIMULATION RESULTS
The proposed adaptive control structures presented
above are tested and validated by six simulation
results. A staircase change of the reference input
signal was employed and the control structures
responses were tested on the time frame of 10 s. The
illustrated results include the evolutions of mass
position
x
1
(t) versus time t for Lagrange, Cauchy and
Switching GS control solutions designed for the
electromagnetic actuator as part of clutches system
for
}5.0,4.0,3.0,2.0,1.0,0{∈
β
. Due to the lack of
space, in this paper, only the results corresponding
to
0=
β
,
3.0=
β
and
5.0=
β
are illustrated in
Figures 3, 4 and 5.
The mean square error
GS
MSE
J
is computed for all
three GS versions as:
,))()((
1
J
1
2
MSE
GS

=
−=
N
t
dd
d
tytr
N
(17)
where
}SGS,CGS,LGS{GS∈
is the designed
control solution,
)(
d
tr
is the reference input at time
Table 2: The mean square errors.
GS
MSE
J
β
0 0.1 0.2 0.3 0.4 0.5
LGS
8.52⋅10
–2
8.12⋅10
–2
7.72⋅10
–2
7.33⋅10
–2
6.94⋅10
–2
6.57⋅10
–2
CGS
8.31⋅10
–2
7.93⋅10
–2
7.55⋅10
–2
7.17⋅10
–2
6.80⋅10
–2
6.44⋅10
–2
SGS
8.68⋅10
–2
8.28⋅10
–2
7.89⋅10
–2
7.51⋅10
–2
7.14⋅10
–2
6.77⋅10
–2
Figure 3: Mass position x
1
versus time (t) in all the three GS versions (namely CGS, LGS, SGS) for
0=
β
.
Gain-Scheduling Position Control Approaches for Electromagnetic Actuated Clutch Systems
415

Figure 4: Mass position x
1
versus time (t) in all the three GS versions (namely CGS, LGS, SGS) for
3.0=
β
.
Figure 5: Mass position x
1
versus time (t) in all the three GS versions (namely CGS, LGS, SGS) for
5.0=
β
.
moment
Nt
d
...1=
, N=3333 is the number of
samples and
)(
d
ty
is the measured mass position
at time moment
t
d
=1…N. The values are presented
in Table 2.
The conclusion drawn by analyzing the plots
given in Figures 3, 4 and 5, and after comparing
the results presented in Table 2 is that the zero
steady-state control error is ensured in all versions
and the reference input is well tracked.
Analyzing in terms of GS versions the smallest
mean square error is obtained in CGS version and
the biggest mean square error is obtained in SGS
version, and analyzing in terms of
β
the smallest
mean square error is obtained for
5.0=
β
and the
biggest mean square error is obtained for
0=
β
in
all GS versions.
The above analysis of control system
performance can lead to different results for other
controlled plants. Such suggestive examples of
plants include motion control (Korondi et al.,
1996), chaotic systems (Precup et al., 2007), large-
scale complex systems (Filip, 2008; Fan and Liu,
2016), multi-tank systems (Precup et al., 2013),
evolving systems (Blažič et al., 2014), node
localization (Derr and Manic, 2015; Wang et al.,
2017), turbojet engines (Fozo et al., 2017), routing
problems (Osaba et al., 2017) and neural networks
(Dumitrache et al., 1999; Alique et al., 2000;
Fioriti and Chinnici, 2017; Saadat et al., 2017;
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
416

Wagarachchi and Karunananda, 2017). Although
they do not seem to be directly related to this
paper, they point out the generality of GS
approaches described in the previous sections.
5 CONCLUSIONS
This paper has presented the design of gain-
scheduling control approaches viewed as adaptive
control approaches developed to deal with the
nonlinearities of the electromagnetic actuator and
to ensure the switching between PI controllers. The
simulation results prove that the GS-based control
systems guarantee the performance improvement
(zero steady-state control error, small settling times
and small overshoots) with respect to staircase
changes of the reference input.
Future research will be focused on the
improvement of the performance indices by
designing of CSs with PI(D) fuzzy gain-scheduling
controllers, with model predictive controllers and
hybrid structures applied to mechatronics systems.
REFERENCES
Alique, A., Haber, R. E., Haber, R. H., Ros, S.,
Gonzalez, C., 2000. Neural network-based model for
the prediction of cutting force in milling process. A
progress study on a real case. In Proceedings of 15
th
IEEE International Symposium on Intelligent
Control. Patras, Greece, 121-125.
Andonovski, G., Blažič, S., Angelov, P., Škrjanc, I.,
2015. Analysis of adaptation law of the robust
evolving cloud-based controller, In Proceedings of
2015 International Conference on Evolving and
Adaptive Intelligent Systems, Douai, France, 1-7.
Andonovski, G., Angelov, P., Blažič, S., Škrjanc, I.,
2016. A practical implementation of robust evolving
cloud-based controller with normalized data space
for heat-exchanger plant. Applied Soft Computing.
48, 29-38.
Åström, K. J., Hägglund, T., 1995. PID Controllers
Theory: Design and Tuning. Instrument Society of
America, Research Triangle Park, NC, USA.
Bishop, R. H., 2008. Mechatronic Systems, Sensors, and
Actuators: Fundamentals and Modeling. CRC Press,
Boca Raton, FL, USA.
Blažič, S., Škrjanc, I., Matko, D., 2014. A robust fuzzy
adaptive law for evolving control systems. Evolving
Systems. 5 (1), 3-10.
Costa, B. S. J., Angelov, P. P., Guedes, L. A., 2015.
Fully unsupervised fault detection and identification
based on recursive density estimation and self-
evolving cloud-based classifier, Neurocomputing.
150 (A), 289-303.
Derr, K. W., Manic, M., 2015. Wireless sensor networks
- node localization for various industry problems.
IEEE Transactions on Industrial Informatics. 11(3),
752-762.
Di Cairano, S., Bemporad, A., Kolmanovsky, I. V.,
Hrovat, D., 2007. Model predictive control of
magnetically actuated mass spring dampers for
automotive applications, International Journal of
Control. 80, 1701-1716.
Dragos, C.-A., Precup, R.-E., Preitl, S., Petriu, E. M.,
Stinean, A.-I., 2012a. Takagi-Sugeno fuzzy control
solutions for mechatronic applications, International
Journal of Artificial Intelligence. 8 (S12), 45-65.
Dragos, C.-A., Preitl, S., Precup, R.-E., Petriu, E. M.,
Stinean, A.-I., 2012b. Adaptive control solutions for
the position control of electromagnetic actuated
clutch systems. In Proceedings of 2012 IEEE
Intelligent Vehicles Symposium. Alcala de Henares,
Spain, 81-86.
Dumitrache, I., Constantin, N., Drăgoicea, M., 1999.
Retele neurale: identificarea si conducerea
proceselor. Matrix Rom, Bucharest.
Fan, Z., Liu, X., 2016. Energy synchronized
transmission control for energy-harvesting sensor
networks. International Journal of Computers
Communications and Control. 11 (21), 194-208.
Filip, F. G., 2008. Decision support and control for
large-scale complex systems. Annual Reviews in
Control. 32 (1), 61-70.
Fioriti, V., Chinnici, M., 2017. Node seniority ranking in
networks. Studies in Informatics and Control. 26 (4),
397-402.
Fozo, L., Andoga, R., Beneda, K., Kolesár, J., 2017.
Effect of operating point selection on non-linear
experimental identification of iSTC-21v and TKT-1
small turbojet engines. Periodica Polytechnica
Transportation Engineering. 45 (3), 141-147.
Gao, B., Chen, H., Liu, Q., Chu, H., 2014. Position
control of electric clutch actuator using a triple-step
nonlinear method, IEEE Transactions on Industrial
Electronics. 61 (12), 6995-7003.
Haidegger, T., Kovács, L., Precup, R.-E., Benyó, B.,
Benyó, Z., Preitl, S., 2012. Simulation and control
for telerobots in space medicine. Acta Astronautica.
181 (1), 390-402.
Korondi, P., Hashimoto, H., Gajdar, T., Suto, Z., 1996.
Optimal sliding mode design for motion control. In
Proceedings of 1996 IEEE International Symposium
on Industrial Electronics. Warsaw, Poland, 277-282.
Losero, R., Guerra, T.-M., Lauber, J., Maurel, P., 2016.
Electro-mechanical clutch actuator control based on
output switched Takagi-Sugeno controller. IFAC-
PapersOnLine, 49 (5), 85-90.
Oh, J. J., Choi, S. B., Kim, J., 2014. Driveline modeling
and estimation of individual clutch torque during
gear shifts for dual clutch transmission.
Mechatronics. 24 (5), 449-463.
Osaba, E., Yang, X.-S., Diaz, F., Onieva, E., Masegosa,
A., Perallos, A., 2017. A discrete firefly algorithm to
Gain-Scheduling Position Control Approaches for Electromagnetic Actuated Clutch Systems
417

solve a rich vehicle routing problem modelling a
newspaper distribution system with recycling policy.
Soft Computing. 21 (18), 5295-5308.
Precup, R.-E., Angelov, P., Costa, B. S. J., Sayed-
Mouchaweh, M., 2015. An overview on fault
diagnosis and nature-inspired optimal control of
industrial process applications. Computers in
Industry. 74, 75-94.
Precup, R.-E., David, R.-C., Petriu, E. M., 2017. Grey
wolf optimizer algorithm-based tuning of fuzzy
control systems with reduced parametric sensitivity.
IEEE Transactions on Industrial Electronics. 64 (1),
527-534.
Precup, R.-E., Tomescu, M. L., Preitl, S., 2007. Lorenz
system stabilization using fuzzy controllers.
International Journal of Computers
Communications and Control. 2 (3), 279-287.
Precup, R.-E., Tomescu, M. L., Preitl, S., Petriu, E. M.,
Fodor, J., Pozna, C., 2013. Stability analysis and
design of a class of MIMO fuzzy control systems.
Journal of Intelligent and Fuzzy Systems. 25 (1),
145-155.
Puig, V., Bolea, Y., Blesa, J., 2012. Robust fain-
scheduled Smith PID controllers for second order
LPV systems with time varying delay. IFAC
Proceedings Volumes. 45(3), 199-204.
Ranjan, A., Prasanth, S., Cherian, F., Baskar, P., 2017.
Design and control of electromagnetic clutch
actuation system for automated manual transmission.
IOP Conference Series: Materials Science and
Engineering. 263, 1-13.
Saadat, J., Moallem, P., Koofigar, H., 2017. Training
echo state neural network using harmony search
algorithm. International Journal of Artificial
Intelligence. 15 (1), 163-179.
Shamma, J. S., Athans, M., 1990. Analysis of gain
scheduled control for nonlinear plants. IEEE
Transactions on Automatic Control. 35 (8), 898-907.
Shin, Y. H., Kim, S. C., Kim, M. S., 2013. Use of
electromagnetic clutch water pumps in vehicle
engine cooling systems to reduce fuel consumption.
Energy. 57, 624-631.
Temporelli, R., Micheau, P., Boisvert, M., 2017. Control
of an electromechanical clutch actuator by a parallel
adaptive feedforward and bang-bang controller:
Simulation and experimental result. IFAC-
PapersOnLine. 50 (1), 4787-4793.
Veselý, V., Ilka, A., 2013. Gain-scheduled PID
controller design, Journal of Process Control. 23
(8), 1141-1148.
Wagarachchi, M., Karunananda, A., 2017. Optimization
of artificial neural network architecture using
neuroplasticity. International Journal of Artificial
Intelligence. 15 (1), 112-125.
Wang, Y.-M., Zhang, F.-J., Cui, T., 2017. Fault
diagnosis and fault-tolerant control for Manifold
Absolute Pressure sensor (MAP) of Diesel engine
based on Elman network observer. Control
Engineering and Applied Informatics. 19 (2), 90-
100.
Yang, Y.-N., Yan, Y., 2016. Attitude Regulation for
Unmanned Quadrotors Using Adaptive Fuzzy Gain-
scheduling Sliding Mode Control, Aerospace
Science and Technology, 54, 208-217.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
418