
Managing Weighted Preferences with Constraints in Interactive
Applications
Bandar Mohammed
1
, Malek Mouhoub
1
, Eisa Alanazi
2
and Samira Sadaoui
1
1
Department of Computer Science, University of Regina, Regina, SK, Canada
2
Department of Computer Science, Umm Al-Qura University, Mecca, Saudi Arabia
Keywords:
Preference Reasoning, Constrained Optimization, CP-nets, Weighted CP-nets.
Abstract:
Developing intelligent and interactive systems with visual user interfaces is essential for any website and
mobile device. In this study, we propose a new web-based shopping system to elicit buyer’s requirements and
preferences and to provide a set of suggestions accordingly. This process is achieved by first representing the
elicited information through graphical models and then solving the underlying constrained problem. More
precisely, we have used the Weighted CP-nets (WCP-net) graphical model to allow the user to express fine-
grained preferences on the product attributes and their values in a quantitative or a conditional qualitative
form. The latter has been extended in this paper to include constraints between attributes. A backtrack search
algorithm is then performed to solve the constrained WCP-net and to return a set of Pareto optimal solutions
satisfying all the constraints and maximizing all the preferences.
1 INTRODUCTION
Nowadays, client preferences, such as web services
(Santhanam et al., 2008; Brafman and Domshlak,
2009a), play a key role in customized artificial in-
telligence applications. Several online websites in-
clude some communication with customers to be able
to comprehend and respond to their needs. When a
client is enthusiastic about purchasing a new product,
he will access the web to search for it. However, ex-
isting shopping sites offering clients new goods are
still problematic. Clients may not be pleased if these
sites are difficult to use as they do not want to deal
with complications or spend too much time brows-
ing through the sites. Corporations may not see this
as a serious issue when designing shopping websites
that are not user friendly. Additionally, the results
produced by these websites do not usually meet the
specifications of clients. To be successful, these ap-
plications should improve the consumer interaction.
Increasing the satisfaction of users can be achieved
by assist them in eliciting their preferences and re-
quirements as done in matchmaking systems (Jiang
and Sadaoui, 2012) and online auctions (Sadaoui and
Shil, 2016). Furthermore, several of these websites
are available in a restricted environment. While ex-
pressing his preferences for a laptop for example, the
customer cannot select parts that are not compatible
with each other. Hence, we should consider a sce-
nario where both preferences and constraints co-exist
together (Sadaoui and Shil, 2016). This has motivated
us to develop an interactive shopping application that
maximizes the user’s desires while satisfying some re-
quirements. This application is based on the Weighted
CP-nets (WCP-net) graphical model that we extend to
include constraints between attributes. A backtrack
search algorithm is then performed to solve the con-
strained WCP-net and to return a set of Pareto optimal
solutions satisfying all the constraints and maximiz-
ing all the preferences.
The rest of the paper is structured as follows. The
following section provides a brief background about
preferences and related graphical models as well as
constraint satisfaction. Section 3 presents the ex-
tended model Weighted CP-nets. Section 4 describes
our interactive shopping system based on Weighted
CP-nets. Finally, Section 5 lists concluding remarks
and future works.
2 BACKGROUND
Preference reasoning is an important subject in the
area of artificial intelligence, computer science and fi-
nances (Walsh, 2007; Brafman and Domshlak, 2009b;
Mohammed, B., Mouhoub, M., Alanazi, E. and Sadaoui, S.
Managing Weighted Preferences with Constraints in Interactive Applications.
DOI: 10.5220/0006902002550260
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 255-260
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
255

Boutilier et al., 1999). Managing preferences is cru-
cial in those applications where customers search for
the best outcome meeting their requirements. There-
fore, developing an application to manage constraints
and preferences is necessary in the decision mak-
ing process (Walsh, 2007; Chevaleyre et al., 2008;
Rossi, 2005). Nevertheless, there are lots of chal-
lenges when reasoning is conducted, especially when
constraints and preferences co-exit together (Brafman
and Domshlak, 2009b; Rossi, 2005). Preferences ex-
ist in various forms: qualitative conditional and quan-
titative. Quantitative preferences are called cardinal
or soft constraints while qualitative preferences are
called ordinal and often include conditional prefer-
ences. Many models have been proposed to handle
these types of preferences.
A Constraint Satisfaction Problem (CSP) is a
well-known framework for solving constraint prob-
lems (Dechter, 2003). The CSP includes a set of vari-
ables, each one is defined on a discrete domain of
values, and a set of constraints restricting the values
that the variables can simultaneously take (Dechter,
2003). A solution to a CSP is a complete assignment
of values to variables such that all constraints are sat-
isfied (Dechter, 2003).
A Conditional Preference Network (CP-net) is a
graphical model for representing qualitative and con-
ditional preferences (Boutilier et al., 2004; Braf-
man and Dimopoulos, 2003). Nodes represent vari-
ables or attributes, and arcs the conditional prefer-
ences (Boutilier et al., 2004; Brafman and Dimopou-
los, 2003). The CP-net expresses conditional qual-
itative statements; for example, I prefer Pepsi more
than orange juice when the main dish includes red
meat (Boutilier et al., 2004; Brafman and Dimopou-
los, 2003).
WCP-nets is a weighted extension to CP-nets
allowing users to state their preferences in a fine-
grained way (Wang et al., 2012). More precisely,
user’s preferences can be defined at different scales
(Wang et al., 2012; Xu et al., 2009). Here, the signif-
icance relation (weight) among attributes can be ex-
pressed by showing the range in which an attribute is
more significant than another (Wang et al., 2012; Xu
et al., 2009).
3 MANAGING WEIGHTED
PREFERENCES WITH
CONSTRAINTS
3.1 Problem Statement
We consider the problem where the qualitative pref-
erences come with weights corresponding to their de-
gree of importance. More precisely, the problem is
defined as follows: a multivalued domain over a set
of n variables V = {V
1
,V
2
, . . . ,V
n
}. Each variable V
i
is associated with a set of possible values dom(V
i
) =
{v
i
1
, v
i
2
, . . . , v
i
m
i
}. The set of variables V is the result of
combining two disjoint sets V = V
Qual
∪V
Quan
. V
Qual
is the set of variables that represent the Weighted
CP-net while V
Quan
is the set where each variable
V
i
∈ V
Quan
has a utility function µ(V
i
) associated to
it. A utility function for variable V
i
is a mapping from
dom(V
i
) to [1, 10]. We also consider the presence of
a set of constraints C over the variables in V . Con-
sequently, a solution (i.e. mapping from V to its do-
main) is feasible if and only if it satisfies all the con-
straints in C . Thus, the problem can be viewed as a
triple ϕ = hN , U, C i where:
• N is a Weighted CP-net over a subset of variables
V
Qual
⊂ V
• U is a set of utility functions over V
Quan
⊂ V
• and C is a set of constraints over V
Given ϕ, the aim is to find a set of solutions that
are feasible according to C and optimized according
to both N and U. In other words, the goal is to look
for the Pareto set of optimal solutions. A feasible so-
lution is Pareto if it is not dominated by any other fea-
sible solutions. The Pareto set is the set of all Pareto
optimal solutions.
Figure 1: An Example of a WCP-net and Quantitative Pref-
erences.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
256

3.2 Solving Method
The proposed solving method is shown in Algorithms
1, 2 and 3. Algorithm 1 returns the Pareto set accord-
ing to the CP-net (qualitative preferences) and the set
of constraints. This is basically a backtrack search
algorithm assigning variables sorted in a topological
order. Once the Pareto set is obtained, 2 and 3 are
then applied to determine weights to each optimal
solution (based on the quantitative preferences) and
to return an ordering of these solutions.
To better describe the solving method, let us con-
sider the example depicted in Figure 1. The WCP-
net is defined as a set of two variables (Memory and
Screen), each with its own preference table. For the
variable Memory, the client prefers 12 GB of mem-
ory three times more than 8 GB. For the screen vari-
able, when the memory value is 12 GB, the client
prefers a 13-inch screen two times more than a 15-
inch. For a memory of 8 GB, the client prefers a 15-
inch screen four times more than a 13-inch. The rela-
tion and level among attributes can be clearly defined
as well. For instance, the variable memory (parent)
is preferred five times more than the variable screen
(child). Quantitative preferences are defined as a set
of two variables (Processor and HardDrive), each one
with its preference table. For the variable Processor,
the client has a preference for a 2.7 GHz processing
speed at a value level of 8 and a 2.9 GHz speed at a
value level of 4. For the HardDrive variable, the client
shows a value level of 5 for a 1TB and a value level
of 2 for a 2TB. We will show through the following
equations how to compute the weighted values of the
qualitative data represented as a WCP-net for the two
variables Memory and Screen in order to sum those
weights with the values level of the quantitative pref-
erences. WM and WS represent the weights for vari-
ables Memory and Screen respectively.
WM + WS = 1 (1)
WM + WS = 5WS + WS = 6WS = 1 (2)
WS = 0.16 (3)
WM = 0.84 (4)
(12GB, 13 − inch) = (0 × 0.84) + (0 × 0.16) = 0
(5)
(12GB, 15 − inch) = (0 × 0.84) + (2 × 0.16) = 0.32
(6)
(8GB, 13 − inch) = (3 × 0.84) + (4 × 0.16) = 3.16
(7)
(8GB, 15 − inch) = (3 × 0.84) + (0 × 0.16) = 2.52
(8)
The best outcome has less weight according to the
WCP-net and the quantitative preferences (12 GB, 13-
inch, 2.9 GHz, 2 TB) = (0+4+2) = 6. The worst out-
come has a high weight (8 GB, 13-inch, 2.7 GHz,
1 TB) = (3.16 + 8 + 5) =16.16. It is assumed that
there are two hard constraints, a global constraint
being the client’s budget, and a local constraint be-
ing the available attributes such as speed, screen size
and hard drive capacity. The maximum price and lo-
cal constraints can be expressed as incompatible tu-
ples among different components of the product such
as laptop. As an example, the two component (12
GB, 15-inch) and (2.7 GHz, 2 TB) are incompatible.
Therefore any tuple in the optimal solution with those
components will not be listed as a set of optimal solu-
tions because they do not satisfy the local constraints.
Once the set of qualitative data with a weighted exten-
sion to CP-nets along with quantitative preferences is
obtained, the list of optimal solutions has to satisfy the
hard constraints. For example, tuple (12 GB, 13-inch,
2.9 GHz, 2 TB) satisfies the local constraints.
Algorithm 1: WPrefC method - finding Pareto set.
Input: CP-net N and a set of constraints C
Output: The Pareto Set S (initially empty)
1. let > be topological ordering over N
2. let T be a stack
3. push {} into T
4. while (T is not empty)
5. n ← pop first element
6. if (n is complete assignment)
7. if (n is not dominated by any element in S )
8. add n to S
9. else
10. for every value v
i
of next variable V
i
w. r. t. >
11. if (n ∪ (V
i
, v
i
) is consistent with C )
12. push n ∪ (V
i
, v
i
) into T
13. Return S
4 SYSTEM DESCRIPTION
Our online shopping system has been developed using
the following software:
1. Programming environment: Microsoft Visual Stu-
dio 2013 (ASP.NET - C Sharp).
2. Programming languages: Visual C Sharp
2012/2013 (ASP.NET MVC 5 Web Application),
HTML and JavaScript.
Managing Weighted Preferences with Constraints in Interactive Applications
257
Algorithm 2: WPrefC method - assigning weights to all tu-
ples of the CP-Net.
Input: Pareto Solutions S
Output: Ordering and assigning weights to CP-Net
tuples >
W Pre fC
over S
1. let >
W Pre fC
← {}
2. for every two elements s
i
, s
j
∈ S
3. for k = 1 to |V |
4. if V
k
(s
i
) is equally preferred to V
k
(s
j
)
5. (s
i
, s
j
) = 1 and add (s
i
, s
j
) to >
W Pre fC
6. else
7. if V
k
(s
i
) is mildly preferred to V
k
(s
j
)
7. (s
i
, s
j
) = 2 and add (s
i
, s
j
) to >
W Pre fC
8. else
8. if V
k
(s
i
) is strongly preferred to V
k
(s
j
)
9. (s
i
, s
j
) = 3 and add (s
i
, s
j
) to >
W Pre fC
10. else
8. if V
k
(s
i
) is very strongly preferred to V
k
(s
j
)
11. (s
i
, s
j
) = 4 and add (s
i
, s
j
) to >
W Pre fC
12. else
8. V
k
(s
i
) is extremely preferred to V
k
(s
j
)
13. (s
i
, s
j
) = 5 and add (s
i
, s
j
) to >
W Pre fC
14. if V
k
(s
i
) 6= V
k
(s
j
)
15. if V
k
(s
i
) is better than V
k
(s
j
)
16. add (s
i
, s
j
) to >
W Pre fC
17. else
18. add (s
j
, s
i
) to >
W Pre fC
19. Return >
W Pre fC
Algorithm 3: WPrefC method - combining qualitative and
quantitative.
Input: f
1
and f
2
mapping functions, constraints C
Output: A set of ranked feasible solutions S
1. S ←
/
0
2. while (O
Qual
6=
/
0)
3. o
1
← min( f
1
(O
Qual
))
4. copy ← Q
Quan
5. while (copy 6=
/
0)
6. o
2
← min( f
2
(copy))
7. if (o
1
× o
2
consistent with C )
8. add o
1
× o
2
to S
9. remove o
2
from copy
10. remove o
1
from O
Qual
11. Return S
3. Operating system: Web Hosting under Windows 7
and supporting .NET Runtime Version (ASP.NET
4.5) and PHP Runtime Version (PHP 5.4).
4. Database: SQL Server Database 2012.
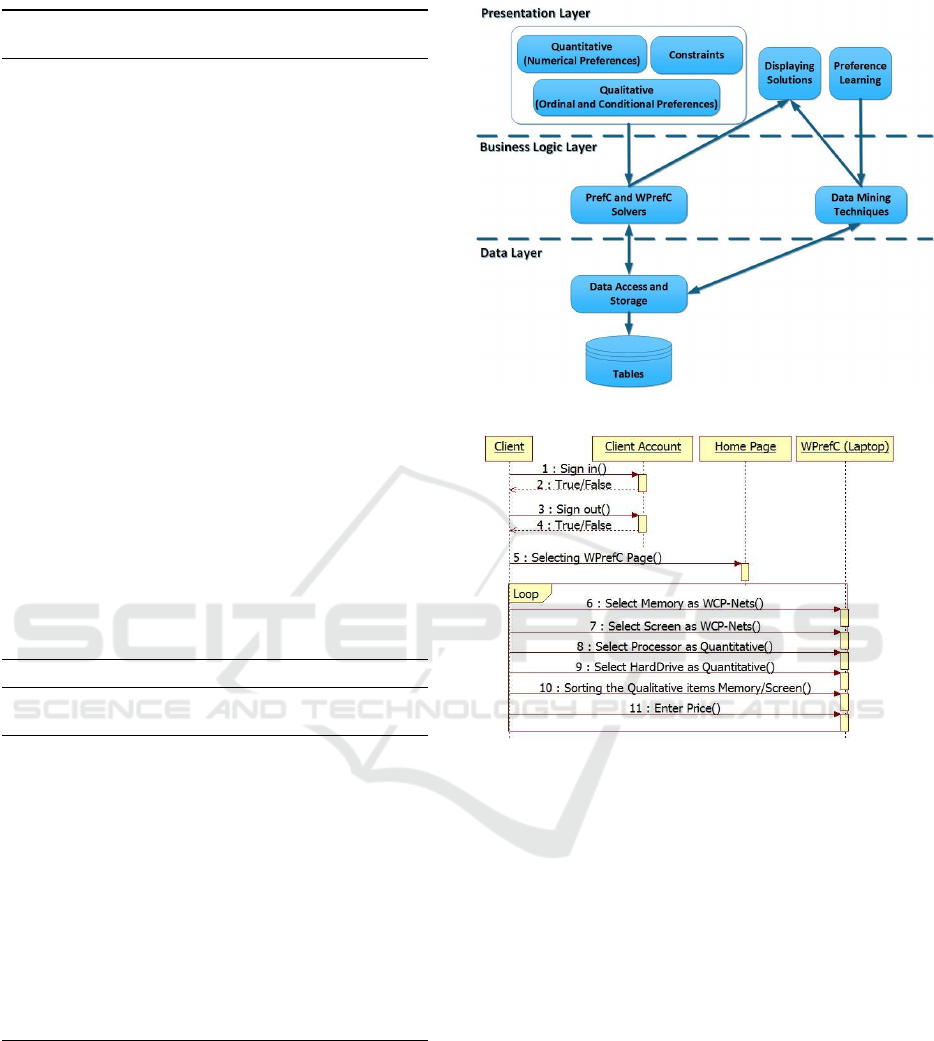
The architecture of our e-shopping system follows
the 3-layer style as depicted in Figure 2. The graphic
user interface allows clients to register and sign in in
Figure 2: Software Architecture.
Figure 3: Sequence Diagram.
order to use the system features and also takes care of
the constraint and preference elicitation phase. The
business logic layer implements the WPrefC solver.
The database layer takes care of the information stor-
age and retrieval. Figure 3 illustrates the interactions
among the different components of our system when
purchasing a laptop. Clients first select the WPrefC
page in order to express their quantitative and qualita-
tive preferences for the product.
Figure 4 shows the Graphic user interface of our
Online Shopping System.
5 CONCLUSION
We proposed in this paper an online shopping system
based on WPrefC technique - Weighted Preferences
with Constraints for interactive applications that lets
the clients elicit their requirements when buying a
product online. WPrefC technique was introduced
in order to resolve the issues of CP-nets and to al-
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
258

Figure 4: GUI of our Online Shopping System.
low users to state their preferences in a fine-grained
way (Wang et al., 2012). Clients are able to express
their preferences either numerically (quantitative) or
ordinaly (qualitative), and then the system will dis-
play a list of optimal solutions by meeting the clients’
needs and satisfying the constraints.
For future work, we would like to manage prefer-
ences along with dynamic hard constraints where the
client is able either to add or delete some hard con-
straints and notice the influence of those changes on
the outcomes. Another research direction is to com-
bine quantitative preferences and qualitative prefer-
ences into one solver/algorithm rather than solving
quantitative preferences and qualitative preferences
separately along with hard constraints.
REFERENCES
Boutilier, C., Brafman, R. I., Domshlak, C., Hoos, H. H.,
and Poole, D. (2004). Cp-nets: A tool for representing
and reasoning with conditional ceteris paribus prefer-
ence statements. J. Artif. Intell. Res.(JAIR), 21:135–
191.
Managing Weighted Preferences with Constraints in Interactive Applications
259

Boutilier, C., Brafman, R. I., Hoos, H. H., and Poole, D.
(1999). Reasoning with conditional ceteris paribus
preference statements. In uai99, pages 71–80.
Brafman, R. and Domshlak, C. (2009a). Preference
handling-an introductory tutorial. AI magazine,
30(1):58.
Brafman, R. I. and Dimopoulos, Y. (2003). A new look
at the semantics and optimization methods of cp-
networks. In IJCAI, pages 1033–1038.
Brafman, R. I. and Domshlak, C. (2009b). Preference
handling - an introductory tutorial. AI Magazine,
30(1):58–86.
Chevaleyre, Y., Endriss, U., Lang, J., and Maudet, N.
(2008). Preference handling in combinatorial do-
mains: From ai to social choice. AI Magazine,
29(4):37–46.
Dechter, R. (2003). Constraint processing. Morgan Kauf-
mann.
Jiang, W. and Sadaoui, S. (2012). Evaluating and ranking
semantic offers according to users’ interests. Journal
of Electronic Commerce Research, 13(1):1–22.
Rossi, F. (2005). Preference reasoning. In van Beek, P.,
editor, CP, volume 3709 of Lecture Notes in Computer
Science, pages 9–12. Springer.
Sadaoui, S. and Shil, S. K. (2016). A multi-attribute auc-
tion mechanism based on conditional constraints and
conditional qualitative preferences. Journal of The-
oretical and Applied Electronic Commerce Research,
11(1):1–25.
Santhanam, G. R., Basu, S., and Honavar, V. (2008). Tcp-
compose–a tcp-net based algorithm for efficient com-
position of web services using qualitative preferences.
In Service-Oriented Computing–ICSOC 2008, pages
453–467. Springer.
Walsh, T. (2007). Representing and reasoning with prefer-
ences. AI Magazine, 28(4):59–70.
Wang, H., Zhang, J., Sun, W., Song, H., Guo, G., and Zhou,
X. (2012). Wcp-nets: a weighted extension to cp-nets
for web service selection. In Service-Oriented Com-
puting, pages 298–312. Springer.
Xu, H., Hipel, K. W., and Kilgour, D. M. (2009). Multiple
levels of preference in interactive strategic decisions.
Discrete Applied Mathematics, 157(15):3300–3313.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
260
