Comparison of Constraint-handling Techniques Used in Artiﬁcial Bee

Colony Algorithm for Auto-Tuning of State Feedback Speed Controller

for PMSM

Rafal Szczepanski

,Tomasz Tarczewski

, Krystian Erwinski

and Lech M. Grzesiak

Department of Automatics and Measurement Systems, Nicolaus Copernicus University,

Grudziadzka 5, 87-100 Torun, Poland

Institute of Control and Industrial Electronics, Warsaw University of Technology, Koszykowa 75, 00-662 Warsaw, Poland

Keywords:

Constraint-handling Technique, Augmented Lagrangian, Deb’s Rules, Optimization, Artiﬁcial Bee Colony,

State Feedback Speed Controller, PMSM.

Abstract:

This article focuses on comparison of two constraint-handling techniques: Deb’s Rules (DR) and Augmented

Lagrangian (AL) applied to Artiﬁcial Bee Colony (ABC) algorithm that is used for auto-tuning of state feed-

back speed controller (SFC) for permanent magnet synchronous motor (PMSM). The task of the optimization

algorithm is to determine the elements of Q and R weighting matrices in linear quadratic regulator (LQR) op-

timization process. Chosen matrices guarantee the best performance according to given optimization criteria.

Safety and proper operation of the motor requires the use of constraint-handling (C-H) technique. The ABC in

its original version cannot handle the constrained optimization problems, therefore necessary modiﬁcations of

considered optimization algorithm are depicted. Simulation and experimental results showed that AL techni-

que allows to obtain a better convergence of ABC algorithm and a better performance of the PMSM drive than

DR technique.

1 INTRODUCTION

Optimization problems are present in all branches

of applied sciences and engineering sciences. Most

practical applications require limiting of physical va-

riables, which involve equality or inequality con-

straints. Over the past years, nature-inspired opti-

mization algorithms, such as Artiﬁcial Bee Colony

(ABC), Particle Swarm Optimization (PSO), Gene-

tic Algorithm (GA), Flower Pollination Algorithm

(FPA), Ant-Colony (AC), Grey Wolf Optimizer Al-

gorithm (GWO) and many others, have gained popu-

larity in solving engineering optimization problems

(Kaminski and Najdek, 2018), (Wang et al., 2016),

(Senberber and Bagis, 2017). Most of nature-inspired

algorithms, in their original versions, can solve only

unconstrained optimization problems. Therefore re-

searchers had to apply C-H techniques (Gionfra et al.,

2017), (Deb, 2000), (Khalilpourazari and Khalilpou-

razary, 2018), (Long et al., 2017), (Tarczewski and

Grzesiak, 2018), (Szczepanski et al., 2017). There

are many techniques to handling constraints (Mezura-

Montes and Coello, 2011), but the most commonly

used groups are: penalty functions and, separation of

objective function and constraints. First group allows

transformation of constrained optimization problems

into unconstrained optimization problems by adding

penalty functions to the objective function for each

constraint. In order to favor selection of a feasible

(e.g. valid) solution, the penalty functions decrease

the ﬁtness of an infeasible solution. The opposite

idea of C-H technique is based on separation of the

objective function and constraints. Keeping both va-

lues apart allows for optimization on an unconstrained

problem by calculating ﬁtness of solution with dif-

ferent equations for feasible and infeasible solution

or tournament selection. Mathematically, the equa-

lity constrained optimization problem can be presen-

ted as:

Minimize

subject to:

f (x)

h(x) = 0

(1)

where f : R

→ R, h : R

→ R

and x

, i = 1, ...,n is

bounded by lower and upper limits l

≤ x

≤ u

which

deﬁne the search space.

The reliable comparison of C-H techniques re-

quires non-trivial constrained optimization problem.

In this paper, an auto-tuning process of state feed-

Szczepanski, R., Tarczewski, T., Erwinski, K. and Grzesiak, L.

Comparison of Constraint-handling Techniques Used in Artiﬁcial Bee Colony Algorithm for Auto-Tuning of State Feedback Speed Controller for PMSM.

DOI: 10.5220/0006904002690276

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 269-276

ISBN: 978-989-758-321-6

269

back speed controller for PMSM has been chosen.

PMSM has wide range of applications (e.g. electri-

cal and hybrid vehicles, CNC machines, ventilating

and air conditioning applications (Chan, 1993), (Liu

et al., 2016), (Dai et al., 2007), (Lin et al., 2006),

(Abrahamsen et al., 2000). Variable speed drives with

PMSMs are commonly controlled by cascade of PI

controllers or by state feedback controller. The latter

control structure is applied in the proposed approach

due to superior dynamical properties, with particular

emphasis on disturbance compensation (Tarczewski

and Grzesiak, 2016). Since all state-space variables

of the plant are simultaneously controlled by a sin-

gle controller, the design process requires selection

of all coefﬁcients at the same time. This is a non-

trivial task, especially for complex control systems.

The trial-and-error method is commonly used to tune

SFC regardless of linear-quadratic or pole-placement

design technique. In (Franklin et al., 1998), Bry-

son’s method is described for initial guess of diago-

nal elements of penalty matrices. The pole-placement

technique is based on location of poles, which usu-

ally requires expert knowledge. A novel usage of

nature-inspired optimization algorithm to auto-tuning

SFC for PMSM was proposed in (Tarczewski and Gr-

zesiak, 2018), where DR technique has been applied

as C-H technique. To the best our knowledge, usage

of AL technique for the above described optimization

problem and comparison of C-H techniques for auto-

tuning of state-space controller were not presented be-

fore.

In this paper LQR is used to tune SFC gains. Ho-

wever the coefﬁcients of penalty matrices are obtai-

ned by applying ABC algorithm. Two C-H techni-

ques are investigated to analyze the performance of

constrained, nature-inspired optimization algorithm.

2 STATE FEEDBACK SPEED

CONTROLLER FOR PMSM

The knowledge of state-space description of PMSM

fed by voltage-source inverter (VSI) is necessary for

synthesis process of state feedback speed controller

for PMSM. It was assumed that: (i) all state-space

variables of the motor are directly measured using ap-

propriate sensors and calculations and, (ii) a single

SFC controls all state-space variables.

2.1 Linearized Model of the PMSM

In order to design SFC for PMSM, state-space repre-

sentation of the plant (i.e. PMSM fed by VSI) should

be introduced. The following assumptions will be

adopted to design a linear description of the drive’s

model:

• a simple feedback linearization procedure will be

employed,

• VSI’s dynamic behavior and non-linearities will

be neglected,

• a PMSM with surface mounted magnets will be

considered, and therefore L

= L

• load torque cannot be measured, and therefore it

will be omitted,

• reference signal’s internal model will be included.

The aforementioned assumptions lead to the follo-

wing representation of the considered plant in d-q re-

ference frame (Tarczewski and Grzesiak, 2018):

(t)

= A

(t) +B

(t) + F

(t) (2)

with:







−

0 0 0

0 −

0 0

0 −

−

0 0 1 0







, F







−1













0 0







, x

(t) =







(t)







(t) =





(t)





, r

(t) = ω

m re f

(t),

where: R

, L

– resistance and inductance of the

PMSM stator, J

– moment of inertia, K

– torque

constant, B

– viscous friction, i

(t), i

(t) – current

space vector components, ω

(t) – angular speed of

the PMSM shaft, K

– gain of VSI, u

(t), u

(t)

– linear components of control voltages, ω

m re f

(t)

– reference value of angular speed. The last state-

space variable has been introduced to ensure steady-

state error-free operation for step changes of reference

speed and load torque. It is speciﬁed by the following

formula:

(t) =

[ω

(τ) − ω

mre f

(τ)]dτ (3)

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

270

Shown in (2), linear components of control voltages

are obtained by using feedback linearization proce-

dure described in (Grzesiak and Tarczewski, 2012):

(t) = u

(t) + u

(t) (4)

(t) = u

(t) − u

(t) (5)

with:

(t) = pω

(t)L

(t)/K

(6)

(t) = pω

(t)(L

(t) + ψ

)/K

(7)

where: u

(t), u

(t) – space vector components of

inverter control voltages, u

(t), u

(t) – non-linear

components of control voltages, p – the number of

pole pairs, ψ

– permanent magnet ﬂux linkage.

2.2 State Feedback Controller

A discrete state feedback speed controller obtained

for (2) has the following form:

(n) = −Kx

(n) = −K

x(n) − K

(n) (8)

with:

K = [K

] =



ω1

ω2



(9)

where: n – a discrete sample time index, k

, k

ω1

and k

ω2

– gain coefﬁcients

of SFC. Proper selection of gain coefﬁcients is not

trivial, because all of them should be simultane-

ously chosen. These could be determined by using

linear-quadratic optimization (Grzesiak and Tarczew-

ski, 2011) or pole placement technique (Grzesiak and

Tarczewski, 2012). In the proposed approach the ﬁrst

one is used. The method minimizes discrete perfor-

mance index for weighting matrices Q and R:

LQR

∞

∑

n=0



(n)Qx

(n) + u

(n)Ru

(n)



(10)

with

Q = diag(





R = diag(





)

(11)

where: q

, q

, r

and r

are coefﬁcients of pen-

alty matrices. The trial-and-error manual approach to

determine those values could be time-consuming and

challenging process for the control system conside-

red. In this paper the Artiﬁcial Bee Colony algorithm

will be employed to obtain Q and R values.

3 CONSTRAINED ARTIFICIAL

BEE COLONY ALGORITHM

An Artiﬁcial Bee Colony optimization algorithm has

been proposed by Karaboga in 2005. It is based on

the intelligent foraging behavior of honey bee swarm

(Karaboga and Basturk, 2007). In the next years Ka-

raboga proved experimentally that ABC has better

performance than other popular nature-inspired algo-

rithms (Karaboga and Basturk, 2008).

3.1 Artiﬁcial Bee Colony Algorithm

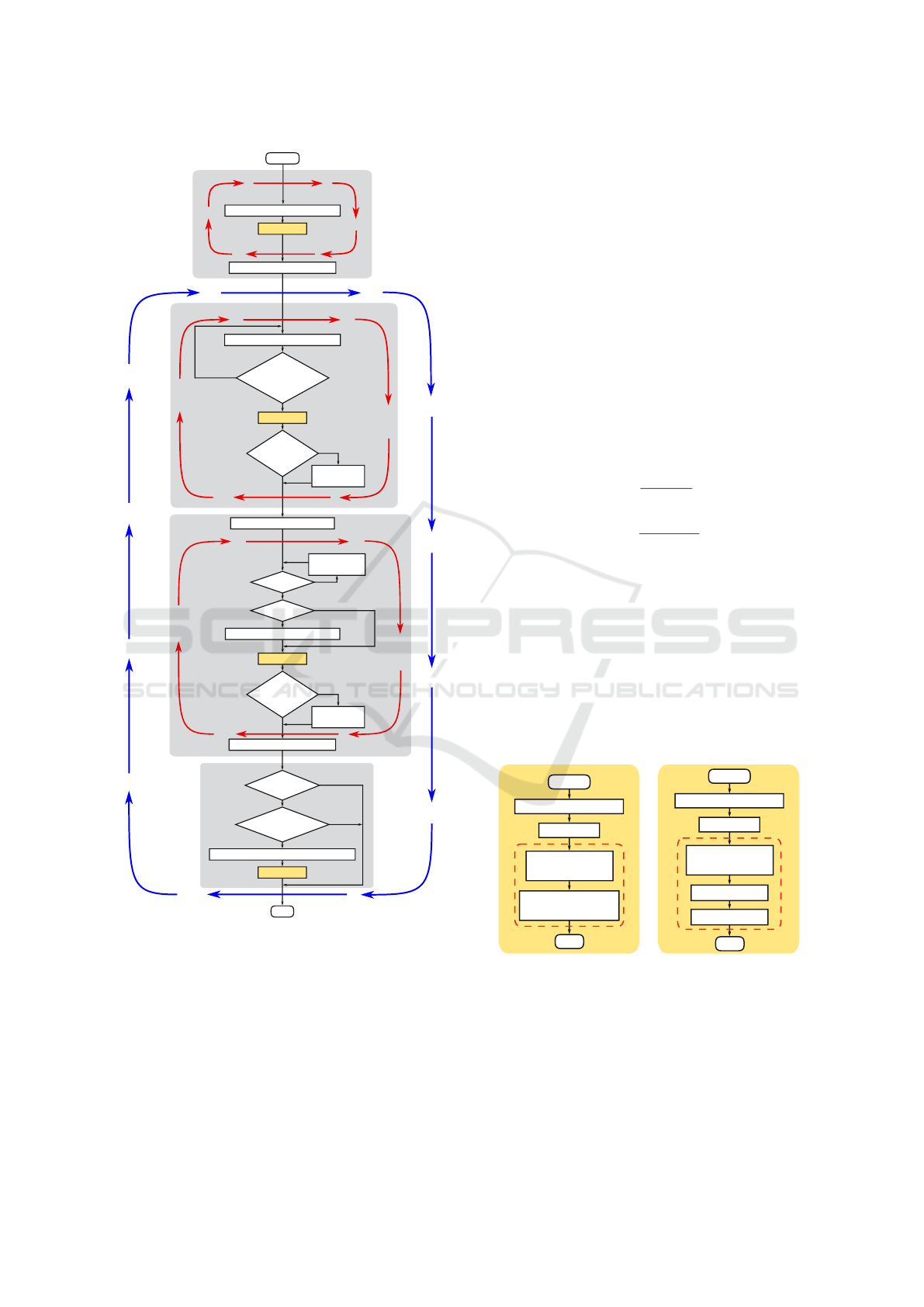
The block diagram of the ABC algorithm is shown in

Fig. 1. The algorithm divides the colony into three

groups: employed bees, onlooker bees and scouts.

Employed bees look for a new food source in the

randomly chosen neighbourhood.

Onlooker bees go from their actual food source to

another food source depending on the nectar amount

in the source. The last group, scouts, only appear

when a food source is abandoned and a new one has

to be found. An employed bee becomes a scout when

the number of failed attempts exceeds the predeﬁned

parameter called limit. After initialization, the algo-

rithm repeats all aforementioned phases MCN times.

To reduce the diversity of new food sources produ-

ced by employed and onlooker bees, the modiﬁca-

tion rate MR is introduced. The parameter determi-

nes probability of change in dimension. Well mat-

ched MR allows to reduce diversity without conver-

gence reduction. Values of ABC used in the conside-

red auto-tuning problem are listed in Table 1.

Table 1: Artiﬁcial Bee Colony parameters.

Parameter & (Symbol) Value

No of optimized parameters (D) 6

No of colony size (NP) 10

No of food sources (FN) NP/2

Maximum no of cycles (MCN) 50

Control parameter (limit) FN × D

Scout production period (SPP) FN × D

Modiﬁcation rate (MR) 0.8

Lower bounds (lb

÷ lb

) 1 × 10

−3

Upper bounds (ub

÷ ub

) 1 × 10

Weighting coefﬁcient (α) 1 × 10

−3

In order to apply the ABC for automatic selection

of Q and R values that assure satisfactory behavior of

the drive, an optimization performance index should

be deﬁned. On the basis of information contained in

(Tarczewski and Grzesiak, 2018), the following for-

mula was chosen:

f (x) =

∑

n=0



(x,n)nT

+ e

(x,n)nT

+ α∆u

(x,n)



(12)

with:

(x,n) = ω

(x,n) − ω

mre f

(x,n)

Comparison of Constraint-handling Techniques Used in Artiﬁcial Bee Colony Algorithm for Auto-Tuning of State Feedback Speed

Controller for PMSM

271

START

the probability calculation

remember the best solution

evaluation

random generation of Q & R

> rn?

MR> rn?

generation of a new Q & R

evaluation

END

generation of a new Q & R

remember the best solution

INITIALIZATION

EMPLOYED BEES PHASE

ONLOOKER BEES PHASE

SCOUTS PHASE

for each food source

is at least one

parameter changed?

is solution

improved?

increment

trial counter

for each food source

check for the

next solution

is solution

improved?

increment

trial counter

repeat MCN times

random generation of a new Q & R

evaluation

trial counter≥limit?

is SPP

reached?

Figure 1: The block diagram of Artiﬁcial Bee Colony algo-

rithm.

(x,n) = i

(x,n) − i

dre f

(x,n)

∆u

(x,n) = [u

(x,n) − u

(x,n − 1)]/T

where: α – manually selected coefﬁcient, i

dre f

(x,n) –

the reference value of d-axis current. From (12) it can

be seen, that the performance index has three com-

ponents: the ﬁrst one is responsible for steady-state

error-free operation and dynamical properties of the

drive’s angular velocity, the second one should assure

zero d-axis current control strategy, and the last one

is responsible for minimization of chattering in q-axis

control signal.

It should be noted, that despite of performance in-

dex selection, an original version of ABC (i.e. non-

constrained) cannot be directly employed for auto-

tuning of SFC. Since safe operation of the drive re-

quires limitation of q-axis current and q-axis control

signal, a constraint-handling technique should be app-

lied. The constraints are computed from the following

formulas:

(x) =

∑

n=0

MAX(0,c

(x,n))

(x) =

∑

n=0

MAX(0,c

(x,n))

(13)

with:

(x,n) =

(x,n)|

q max

− 1

(x,n) =

(x,n)|

sq max

− 1

Although C-H method based on Deb’s Rules has

been recently employed to auto-tuning of SFC (Tar-

czewski and Grzesiak, 2018), it is worth to examine

the impact of other techniques on the convergence

of ABC algorithm as well as on the performance of

the PMSM drive. For that reason, Powell-Hestenes-

Rockafellar Augmented Lagrangian (Powell, 1967),

(Hestenes, 1969), (Rockafellar, 1974) will be com-

pared with Deb’s Rules (Deb, 2000) C-H technique.

Due to this, two variants of the evaluation block will

be used. Their contents are shown in Fig. 2.

controller calculation

START

END

simulation

f(x) and violation

calculation

tournament selection

(Deb's rules)

controller calculation

START

END

simulation

f(x) and h(x)

calculation

L(x) calculation

minimize L(x)

EvALUATION

a) b)

Augmented Lagrangian technique

Deb's rules technique

Figure 2: Content of evaluation block.

3.2 Deb’s Rules Technique

In 2000 Deb proposed a C-H technique based on se-

paration of objective function and constraints. No-

wadays this method is known as Deb’s Rules (DR)

and it is used with many nature-inspired optimization

algorithms (e.g. PSO (Gionfra et al., 2017), ABC

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

272

(Tarczewski and Grzesiak, 2018), GA (Deb, 2000)).

The DR introduces only one additional variable cal-

led violation, which is deﬁned as:

violation = kh(x)k

∞

(14)

solution →

(

f easible if violation ≤ 0

in f easible if violation > 0

In order to compare two solutions, the following rules

are used:

• for feasible solution and infeasible solution, the

feasible one is selected,

• for two feasible solutions, the one having better

objective function value is selected

• for two infeasible solutions, the one having smal-

ler violation parameter value is selected

Above rules guarantee that, the solution will be feasi-

ble or the value of violation will be minimized. The

main advantages of DR are: (i) the lack of parameters

that have to be chosen individually for the problem,

and (ii) a simple implementation.

3.3 Augmented Lagrangian Technique

Augmented Lagrangian (AL) technique works by

using additional formulas, called penalty functions,

to the objective function for each violated con-

straint. The augmented objective function (Augmen-

ted Lagrangian) has the following form (Birgin and

Mart

ınez, 2008):

L(x,λ , ρ) = f (x) +

∑

i=1



(x) +



(15)

where λ : R

and ρ > 0. The algorithm updates aug-

mented lagrangian multipliers λ and penalty parame-

ter ρ automatically during optimization process by

using following formulas:

(k+1)

= γρ

(16)

(k+1)

= MAX

min

,MIN



max

,λ

+ ρ

(k+1)

(x)

i

(17)

where: λ

min

= −10

, λ

max

= 10

, ρ

min

= 10

−6

max

= 10 and γ = 10. It is worth to point out that afo-

rementioned values are directly taken from (Andreani

et al., 2007).

Initially AL multipliers are equal to zeros and the

penalty parameter is deﬁned as:

initial

= MAX



min

,MIN



max

2 | f (x

) |

kh(x



(18)

It was assumed that for kh(x

)k equal to zero, the pen-

alty parameter takes the minimum value. To avoid

unnecessary modiﬁcations of the penalty parameter ρ

the Infeasibility - Complementarity Measure (ICM)

parameter is introduced using the following formula:

ICM = kABS(MAX(h

(x),−

)) i = 1...mk

∞

(19)

The ﬁnal updating formula of the penalty parameter

is deﬁned as:

(k+1)

(

αρ

if ICM

(k+1)

ICM

otherwise

(20)

Finally, the last parameter needed for integration

of the AL technique with ABC algorithm is an upda-

ting frequency of λ and ρ. Considered value was de-

termined by using trial-and-error method. If parame-

ters will be updated too rarely it could cause prema-

ture convergence of the ABC algorithm in infeasible

local minimum which may result in rejection of every

infeasible solution too early. In the second case, the

operation of AL technique would be similar to DR.

The experimentally selected parameter λ is updated

every two iterations of ABC algorithm.

4 NUMERICAL RESULTS

The algorithms were examined on a computer with

Intel i5-7500 @ 3.4GHz CPU with 16GB memory in

MATLAB/Simulink environment. The main parame-

ters of the PMSM drive employed during auto-tuning

process are listed in Table 2. The laboratory stand

consists of two PMSM drives (Tarczewski and Grze-

siak, 2018). The main drive is used for evaluation of

SFC algorithms, while the second one is employed to

produce load torque.

Table 2: The main parameters of the PMSM drive.

Parameter (Symbol) Value [Unit]

Rated power (P

) 628 [W]

Rated current (I

) 3 [A]

Rated torque (T

) 1.05 [Nm]

Rated speed (Ω

) 366 [rad/s]

Resistance (R

) 0.85 [Ω]

Inductance (L

) 4 [mH]

Torque constant (K

) 0.35 [Nm/A]

No of pole pairs (p) 3

Viscous friction (B

) 2.2 × 10

−3

[Nms/rad]

Moment of inertia (J

) 2 × 10

−4

[kgm

]

VSI gain (K

) 95

Switching frequency 16 [kHz]

Comparison of Constraint-handling Techniques Used in Artiﬁcial Bee Colony Algorithm for Auto-Tuning of State Feedback Speed

Controller for PMSM

273

0 10 20 30 40 50

-6

0 10 20 30 40 50

200

400

0 10 20 30 40 50

100

0 10 20 30 40 50

100

0.3

200

0.6

100

0.3

200

0.6

f(x)

L(x,λ,ρ)

t [s] t [s]

iteration

24.97 24.61

25.32

usq

Figure 3: Progress of: a) the objective function and plant response for DR technique; a) the objective function and plant

response for AL technique, c) the AL function, AL multiplier and penalty parameter.

The number of objective function’s evaluation was

the same for both C-H techniques, which results in

very similar computation times, c.a. 14 minutes. Re-

petition of gained result is shown in Fig. 4. It can be

seen, that application of AL as C-H technique gives a

better repetition and assures a smaller mean value of

the objective function in comparison to DR.

The best determined coefﬁcients of Q and R ma-

trices for both C-H techniques are summarized in Ta-

ble 3, while coefﬁcients of SFC are listed in Table 4,

respectively.

Table 3: Coefﬁcients of: Q and R matrices.

DR AL

1.25 × 10

5.49 × 10

1.29 × 10

50.2

4.3 5.0

9.38 × 10

9.2 × 10

7.01 × 10

4.23 × 10

2.92 × 10

1.51 × 10

Table 4: Coefﬁcients of SFC.

DR AL

0.3097 0.5749

0 0

0.4436 0.4174

0.0839 0.1270

3.3655 5.2356

The progress of the objective functions, AL

function, AL parameters and the response of the plant

are shown in Fig 3. It is worth to point out that the DR

technique never goes under constrained global mini-

mum value of the objective function, which is cau-

sed by the tournament selection, and AL technique

1 2 3 4 5 6 7 8 9 10

f(x)

run

AL: mean=25.3; std=0.90

DR: mean=28.1; std=6.94

Figure 4: Final objective function values after 10 runs for

ABC algorithm with DR and AL techniques.

10 20 30 40 50

no.

10 20 30 40 50

iteration

no.

found a better solution

found a worse solution

rejected due to violation of constraints

found a better solution

found a worse solution

Figure 5: Decisions taken by ABC algorithm during com-

parison of solutions for: a) DR technique, b) AL technique.

allows to reach infeasible solutions and then the algo-

rithm imposes penalties for violated constraints. The

DR technique approaches the solution only from the

side of feasible solutions while the AL technique al-

lows for approaching the solution from both sides.

The slope from side of feasible solutions is caused

by minimizing the objective function and the slope

from side of infeasible solutions is caused by mi-

nimizing penalty functions (minimizing violation of

constraints). In late iterations, when all food sour-

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

274

0 0.2 0.4 0.6

-0.25

0.25

0.5

0 0.2 0.4 0.6

100

0 0.2 0.4 0.6

-0.25

0.25

0.5

0 0.2 0.4 0.6

100

mref

t [s] t [s]

[rad/s]

[A] u

[V]

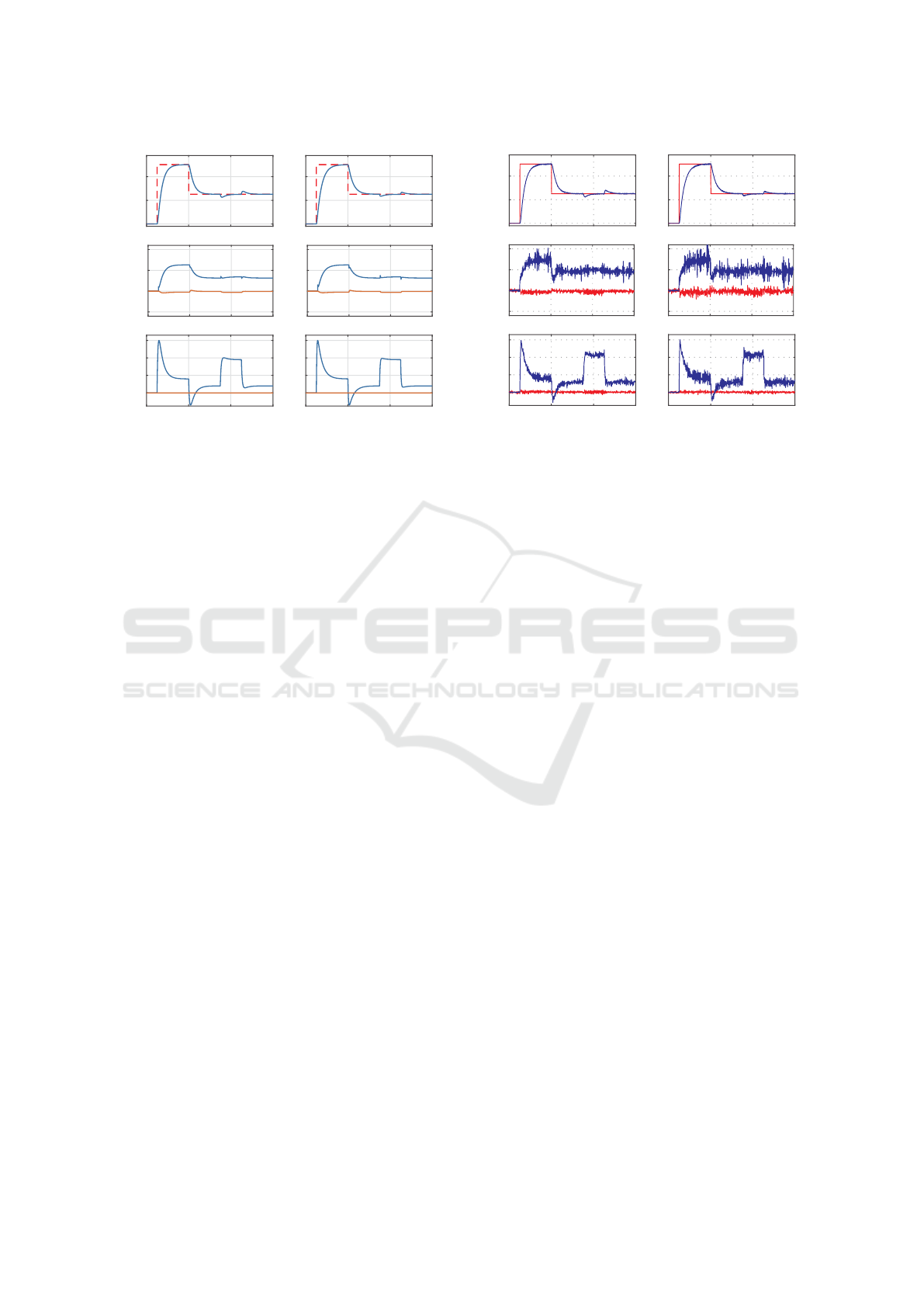
Figure 6: Simulation responses of the PMSM with SFC

coefﬁcients found by using ABC algorithm with: a) DR

technique, b) AL technique.

ces of ABC algorithm are near the global minimum,

the most of new food sources are rejected by DR, be-

cause these violate constraints. Taken decisions about

new food source for both C-H techniques are shown

in Fig. 5.

The comparison of simulation results obtained for

PMSM with SFC tuned by ABC with DR and AL C-

H techniques is shown in Fig. 6. Result of experi-

ment carried out with the same reference signals (i.e.

values of angular speed and load torque) on physical

drive is presented in Fig. 7. From simulation and ex-

perimental responses it can be seen, that all control

objectives are fulﬁlled. Angular speed is controlled

without steady-state error and load torque imposed

on the PMSM shaft for t ∈ (0.35; 0.45) s is properly

compensated. Recorded waveforms of current space

vector components clearly illustrate, that zero d-axis

control strategy is successfully employed and both C-

H techniques imposed on q-axis current work well (its

maximum value does not exceed rated one).

5 CONCLUSION

This paper presented comparison of popular

constraint-handling techniques: Deb’s rules and Aug-

mented Lagrangian used with novel, nature-based

Artiﬁcial Bee Colony algorithm to solve practical

engineering problem, which is auto-tuning of SFC for

PMSM. Both C-H techniques have been successfully

used. These allow to satisfy imposed constraints

and to return a feasible solution. DR technique

owes its popularity to lack of parameters and easy

implementation. AL technique requires selection of

several parameters for proper optimization, but in

0 0.2 0.4 0.6

100

0 0.2 0.4 0.6

-0.25

0.25

0.5

0 0.2 0.4 0.6

100

0 0.2 0.4 0.6

-0.25

0.25

0.5

0 0.2 0.4 0.6

[rad/s]

[A] u

[V]

t [s] t [s]

mref

Figure 7: Experimental responses of the PMSM with SFC

coefﬁcients found by using ABC algorithm with: a) DR

technique, b) AL technique.

this paper the recommended default parameters have

been used. In AL technique a frequency of parameter

updating should also be chosen, what was done by

using trial-and-error approach. Stability and perfor-

mance of obtained solution compensates additional

parameters that need to be chosen individually for

problem. On the basis of simulation and experimental

results, it was found that AL technique allows to ﬁnd

a better solution and also to reduce standard deviation

between runs.

Regardless of employed C-H technique, obtained

weighting matrices assure steady-state error-free ope-

ration of the drive and satisfactory dynamical beha-

vior. To the best our knowledge, Augmented Lagran-

gian technique for auto-tunning of SFC was not pre-

sented before. On the basis of obtained results, we

recommend to use AL C-H technique in ABC algo-

rithm for the discussed problem.

REFERENCES

Abrahamsen, F., Blaabjerg, F., and Pedersen, J. K. (2000).

Efﬁciency improvement of variable speed electrical

drives for hvac applications. In Energy Efﬁciency Im-

provements in Electronic Motors and Drives, pages

130–135. Springer.

Andreani, R., Birgin, E. G., Mart

ınez, J. M., and Schuverdt,

M. L. (2007). On augmented Lagrangian methods

with general lower-level constraints. SIAM J. Optim.,

18(4):1286–1309.

Birgin, E. G. and Mart

ınez, J. M. (2008). Improving ulti-

mate convergence of an augmented Lagrangian met-

hod. Optim. Method Softw., 23(2):177–195.

Chan, C. C. (1993). An overview of electric vehicle techno-

logy. Proc. of the IEEE, 81(9):1202–1213.

Comparison of Constraint-handling Techniques Used in Artiﬁcial Bee Colony Algorithm for Auto-Tuning of State Feedback Speed

Controller for PMSM

275

Dai, Y., Song, L., and Cui, S. (2007). Development of pmsm

drives for hybrid electric car applications. IEEE Trans.

Magn., 43(1):434–437.

Deb, K. (2000). An efﬁcient constraint handling method for

genetic algorithms. Comput. Meth. Appl. Mech. Eng.,

186(2-4):311–338.

Franklin, G. F., Powell, J. D., and Workman, M. L. (1998).

Digital control of dynamic systems. Addison-Wesley

Menlo Park, CA.

Gionfra, N., Sandou, G., Siguerdidjane, H., Loevenbruck,

P., and Faille, D. (2017). A novel distributed particle

swarm optimization algorithm for the optimal power

ﬂow problem. In IEEE CCTA Conf., pages 656–661.

Grzesiak, L. M. and Tarczewski, T. (2011). Permanent mag-

net synchronous motor discrete linear quadratic speed

controller. In 2011 IEEE ISIE Symp., pages 667–672.

Grzesiak, L. M. and Tarczewski, T. (2012). PMSM ser-

vodrive control system with a state feedback and a

load torque feedforward compensation. COMPEL,

32(1):364–382.

Hestenes, M. R. (1969). Multiplier and gradient methods.

J. Optim. Theory Appl., 4(5):303–320.

Kaminski, M. and Najdek, K. (2018). Adaptive neural con-

troller based on RBF model applied for electrical drive

with PMSM motor. Przeglad Elektrotechniczny, pages

94–98 (in Polish).

Karaboga, D. and Basturk, B. (2007). A powerful and ef-

ﬁcient algorithm for numerical function optimization:

artiﬁcial bee colony (ABC) algorithm. J. Glob. Op-

tim., 39(3):459–471.

Karaboga, D. and Basturk, B. (2008). On the performance

of artiﬁcial bee colony (ABC) algorithm. Appl. Soft.

Comput., 8(1):687–697.

Khalilpourazari, S. and Khalilpourazary, S. (2018). Opti-

mization of production time in the multi-pass milling

process via a robust grey wolf optimizer. Neural Com-

puting and Applications, 29(12):1321–1336.

Lin, F.-J., Shieh, H.-J., Shieh, P.-H., and Shen, P.-H. (2006).

An adaptive recurrent-neural-network motion control-

ler for X-Y table in CNC Machine. IEEE Trans. Syst.

Man Cybern. Part B-Cybern., 36(2):286–299.

Liu, X., Chen, H., Zhao, J., and Belahcen, A. (2016). Re-

search on the performances and parameters of interior

pmsm used for electric vehicles. IEEE Transactions

on Industrial Electronics, 63(6):3533–3545.

Long, W., Liang, X., Cai, S., Jiao, J., and Zhang, W. (2017).

An improved artiﬁcial bee colony with modiﬁed aug-

mented Lagrangian for constrained optimization. Soft

Comput.

Mezura-Montes, E. and Coello, C. A. C. (2011). Constraint-

handling in nature-inspired numerical optimization:

past, present and future. Swarm Evol. Comput.,

1(4):173–194.

Powell, M. (1967). ”A method for non-linear constraints in

minimization problems”. Atomic Energy Res. Estab.

Theoretical Physics Div. ; AERE TP 310. U.K.A.E.A.

Rockafellar, R. T. (1974). Augmented lagrange multi-

plier functions and duality in nonconvex program-

ming. SIAM J. Control, 12(2):268–285.

Senberber, H. and Bagis, A. (2017). Fractional pid con-

troller design for fractional order systems using abc

algorithm. In Electronics, 2017, pages 1–7. IEEE.

Szczepanski, R., Erwinski, K., and Paprocki, M. (2017).

Accelerating PSO based feedrate optimization for

NURBS toolpaths using parallel computation with

OpenMP. In 22nd Int. MMAR Conf., pages 431–436.

Tarczewski, T. and Grzesiak, L. M. (2016). Constrained

state feedback speed control of PMSM based on mo-

del predictive approach. IEEE Trans. Ind. Electron.,

63(6):3867–3875.

Tarczewski, T. and Grzesiak, L. M. (2018). An applica-

tion of novel nature-inspired optimization algorithms

to auto-tuning state feedback speed controller for

PMSM. IEEE Trans. Ind. Appl., 54(3):2913–2925.

Wang, X., Ufnalski, B., and Grzesiak, L. M. (2016). Adap-

tive speed control in the PMSM drive for a non-

stationary repetitive process using particle swarms.

In Compatibility, Power Electronics and Power Engi-

neering (CPE-POWERENG), 2016 10th International

Conference on, pages 464–471. IEEE.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

276